符号理論
Erasure コーディング ::
\( \def\vector#1{\boldsymbol{#1}} \)

誤り検出訂正

Takami Torao #ECC
  • このエントリーをはてなブックマークに追加

概要

誤り検出訂正 (error detection and correction) はデータの伝送やデータ保存時におけるエラー (誤り) の検出と訂正を行うための手法。データは、伝送やストレージで生じる物理的なノイズや機器の不具合によって情報の欠損が生じ正確性を損なう可能性があるが、誤り検出訂正によってそれらのエラーを検出し訂正することで正確性と信頼性を向上させることができる。

誤り検出はデータの受信時にエラーが起きているか検知することをのみ目的としている。比較的信頼性の高い通信チャネルでのデータ伝送は、誤り訂正のための冗長なビットを常に送信するより、誤り検出と自動再送のプロトコルを実装することが多い。

Table of Contents

  1. 概要
    1. シャノンの定理
    2. 線形符号
  2. ハミング符号
    1. アルゴリズム
      1. 符号化
      2. 誤り検出訂正と復号化
    2. ハミング符号以前の符号
  3. 参考文献

アルファベット (alphabet) は記号の有限集合である。例えば 2 進数で表現されるデータのアルファベットは \(\mathcal{A}=\{0,1\}\) である。符号化対象のデータを構成するアルファベットを情報源アルファベット (source alphabet)、符号化によって生成される符号を構成するアルファベットを符号アルファベット (code alphabet) と呼ぶ。一般に符号アルファベットは符号化の目的や伝送路の技術に依存する。

情報を符号化することによって得られる固定長のアルファベット列を符号語 (code word) と呼び、符号語の集合を符号 (code) と呼ぶ。符号への変換が 1:1 であるなら一意復元可能 (uniquely decodable) であり、エンコード (符号化) 処理によって生成され符号語はデコード (復号化) 処理によって元の情報に復元することができる。サーディナス-パターソンのアルゴリズム (Sardinas–Patterson algorithm) は可変長の符号が一意復元可能であるかを判断するアルゴリズムである。

誤り訂正符号の場合、一般に符号語はデータ復元のための冗長ビットのような情報も含んでいる。

ハミング距離 (Hamming distance) は同じ長さを持つ 2 つのデータ列の差異を表すための指標である。具体的には双方のデータ列で同じ位置だが異なる値を持つ要素の数によって表される。ハミング距離が小さいほど 2 つのデータ列は類似していることを意味している。誤り訂正符号では、ハミング距離が一定値以上であることによって特定のビットのエラーが検出または訂正可能であることが保証される。

アルファベット \(\mathcal{A}\) に属し同じ長さ \(n\) を持つ 2 つのデータ列 \(\vector{x}=x_1,\ldots,x_n\) と \(\vector{y}=y_1,\ldots,y_n\) のハミング距離を \(d(\vector{x},\vector{y})=\sum_{i=1}^n d(x_i,y_i)\) で表すことができる。ここで \(x_i=y_i\) のとき \(d(x_i,y_i)=0\)、\(x_i\ne y_i\) のとき \(d(x_i,y_i)=1\) とする。

シャノンの定理

シャノンの定理 (Shannon's theorem)、または通信路符号化定理 (noisy-channel coding theorem) は通信チャネルのノイズによってデータ破損が起きた場合の誤り訂正符号の最大効率を説明している。これは、チャネル容量 \(C\) とデータ転送レート \(R\) の間で \(R \lt C\) である限り、受信側でエラーの確率を任意に小さくできる符号化が存在することを示している。つまり通信チャネルにどれほどのノイズが含まれるとしても、チャネル容量 (データサイズ) が許す限り受信側でのエラーの発生確率を任意に小さくできるということ意味する。ただしシャノンの定理は可能性を示しているだけで具体的な符号化アルゴリズムは特定していない。

線形符号

線形符号 (linear code) は線形結合の演算によって符号語を生成する誤り検出訂正符号である。加算またはスカラー乗算のみで符号を生成するため変換効率が良い。

線形符号における要素数 \(q\) のアルファベットは位数 \(q\) の有限体 \(\mathbb{F}_q\) の性質を持つ (代表的な例は 2 を法とする整数環 \(\mathbb{Z}\) の剰余環が形成する有限体 \(\mathbb{Z}/2\mathbb{Z}=\)\(\mathbb{F}_2=\)\(\{0,1\}\) である)。長さ \(n\) で \(k \le q\) 種類のアルファベットで構成される (つまり位数 \(k\) の) 符号 \(\mathcal{C}\) を \([n,k]\)-符号と呼ぶ。アルファベット \(\mathbb{F}_q\) 上の長さ \(n\) の符号語列はベクトル \(\vector{a}=(a_1,\ldots,a_n)\), \(a_i\in \mathbb{F}_q\) である。したがって有限体 \(\mathbb{F}_q\) 上の \([n,k]\)-符号は \(\mathbb{F}_q^n\) の \(k\)-次元部分空間であるアルファベット \(\mathbb{F}_q\) を持つ符号である。

アルファベットが位数 \(q\) を持つ符号は \(q\) 元符号 (\(q\)-ary code) と呼ばれる。例えば \(\mathcal{A}=\{0,1\}\) は \(q=2\) より 2 元符号 (binary code) である。符号 \(\mathcal{C}\) に含まれる符号語の数を \(|\mathcal{C}|\) と表記し、符号 \(\mathcal{C}\) のサイズと呼ぶ。また長さ \(n\) の符号 \(\mathcal{C}\) の情報レートは \(\log_q \frac{|\mathcal{C}|}{n}\) であり、長さ \(n\) の線形符号はデータを \(n\) ビットのブロックに分割し、各ブロックを固定長の符号語に変換する。

長さ \(k\) の情報列 \(\vector{x}=x_1,\ldots,x_k\) が符号化関数によって長さ \(n\) の情報列 \(\vector{y} = y_1,\ldots,y_n\) に変換され、確率的なノイズの影響を受けるチャネル経由で伝送されて \(\vector{y}' = y'_1,\ldots,y'_n\) として受信されたとする。\(\vector{y}'\) は復号化関数によって復号化される。シャノンの定理では符号の長さ \(n\) を十分大きくしたとき、漸近的に任意に小さくできる復号時のエラー発生確率を決定することで、ある符号化レート \(\frac{k}{n}\) の上限を定まることを示している。

\(G\) を \(k \times n\) の生成行列としたとき、符号化は \(\vector{y} = \vector{x} G\) と表現することができる。また \(G H^\top = 0\) となるような \(H\) を検査行列と呼ぶ。\(\vector{y} H^\top = 0\) である。

ハミング符号

ハミング符号 (Hamming code) は 1947 年にハミングによって導入された初期の誤り訂正符号 (線形符号) である。冗長ビットを追加することで誤り検出が可能となり、さらに誤り検出結果の組み合わせからエラービットの位置を特定し訂正することができる。

ハミング符号は符号に含まれる 1 ビットの反転 (誤り) を検出し訂正することができるが、2 ビット以上の反転は誤った訂正を引き起こす。ハミング符号にパリティビットを加えた拡張ハミング符号 (extended Hamming code, Hamming codes with additional parity) は「1 ビットまでの誤り訂正、2 ビットまでの誤り検出」を行うことができる。ハミング符号は冗長性が限られる一方で演算が単純で比較的高速であるため、メモリの ECC 機構のような比較的安定したチャネルで高速な誤り訂正が必要なケースに適用されている。

代表的な設定は \(\mathbb{F}_2\) 上で \(k=4\) ビットを \(n=7\) ビットに変換する \([7,4]\)-符号である。ただし、冗長ビット数を \(c\) として、\(k=n-c\) ビットのデータを \(n=2^c-1\) ビットに符号化して誤り検出訂正を行うように一般化できる (\(c=3\) のとき \([7,4]\)-符号となる)。転送レートは \([7,4]\)-ハミング符号で \(R=4/7\) となるため同時代の 3 反復符号の \(R=1/3\) より遙かに良好である。

アルゴリズム

この説明では \([7,4]\)-ハミング符号を用いて 4 ビット列 \(\vector{a}=a_1 a_2 a_3 a_4\) を 7 ビット列 \(\vector{u}=u_1 u_2 u_3 u_4 u_5 u_6 u_7\) に符号化する。基本的な考え方は以下の通り。

  1. \(\vector{a}\) の 4 ビットを用いて 3 ビット ✕ 3 の集合を作る。このとき:

    • 集合内でのビットの和が 0 となるようにパリティビットを追加する。このとき、符号 \(\vector{u}\) のいずれかのビットが反転したときに、少なくとも一つの集合の和が 1 となって誤りを検出できるように \(\vector{a}\) のビットを分配する。

    • それぞれの集合の和の並びを 3 ビット値とみなしたとき、\(u_i\) が反転した場合にその値が \(i\) を示すように配置することで、反転した位置を特定できるので誤りを訂正ができる。

  2. 元の 4 ビット + パリティ 3 ビットを並べて 7 ビットの符号 \(\vector{u}\) とする。

これはしばしば集合の交差を用いた例で説明されている。まず Fig 1 左のように 3 つの集合 \(A\), \(B\), \(C\) の各交差に符号 \(\vector{u}\) の各ビットを配置する。次に、Fig 1 中央のように集合の交差となる \(i=3,5,6,7\) の領域に \(\vector{a}\) の各ビットを配置する。最後に、\(A\), \(B\), \(C\) それぞれの集合の元の和が 0 となるように冗長ビット (パリティビットとも言える) \(u_1\), \(u_2\), \(u_4\) を決定する。

Fig 1.

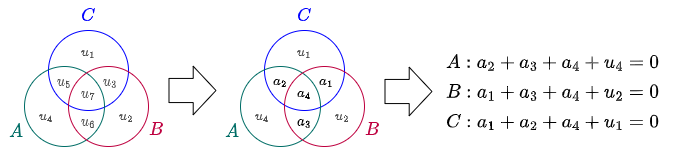
集合 \(A\), \(B\), \(C\) それぞれの和を並べて 3 ビット値 \(i\) とすると、\(\vector{u}\) に反転が起きていないときは \(i=0\)、\(u_1\) の反転は \(i=1\)、\(u_2\) の反転は \(i=2\)、… と \(i\) が \(\vector{u}\) 内の反転したビットの位置を示していることが分かる。

符号化

この考えに基づいて \([7,4]\)-ハミング符号を行う。まず \(\vector{a}\) の各ビットを式 (\(\ref{binhamcode_src}\)) に示す位置の \(u_i\) と置き換える。\[ \begin{equation} \vector{a} = \left( \begin{array}{l} a_1 \\ a_2 \\ a_3 \\ a_4 \end{array} \right) = \left( \begin{array}{l} u_3 \\ u_5 \\ u_6 \\ u_7 \end{array} \right) \label{binhamcode_src} \end{equation} \]

次に残りの冗長ビット \(u_1\), \(u_2\), \(u_4\) を式 (\(\ref{binhamcode_redbits}\)) の性質を持つように決定すると: \[ \begin{equation} \left( \begin{array}{l} u_4 + u_5 + u_6 + u_7 \\ u_2 + u_3 + u_6 + u_7 \\ u_1 + u_3 + u_5 + u_7 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right) \label{binhamcode_redbits} \end{equation} \]

結果的に \([7,4]\)-ハミング符号は式 (\(\ref{binham}\)) の変換となる。\[ \begin{equation} \vector{u} = \left( \begin{array}{l} u_1 \\ u_2 \\ u_3 \\ u_4 \\ u_5 \\ u_6 \\ u_7 \end{array} \right) = \left( \begin{array}{l} a_1 + a_2 + a_4 \\ a_1 + a_3 + a_4 \\ a_1 \\ a_2 + a_3 + a_4 \\ a_2 \\ a_3 \\ a_4 \end{array} \right) \label{binham} \end{equation} \] ここで \(a_x + a_y + a_z\) はより計算効率の良い XOR 演算子 \(\oplus\) に置き換えることもできる。

この符号の 8 ビット目にパリティビット \(u_8=\sum_{i=1}^7 u_i\) を追加することで \([8,4]\)-拡張ハミング符号とすることができる。

誤り検出訂正と復号化

式 (\(\ref{binham}\)) で得られた符号 \(\vector{u}\) を伝送し再構成された符号を \(\vector{u}'\) とする。ここで符号 \(\vector{u}'\) に含まれる反転は最大でも 1 ビットと仮定する。

\(\vector{u}'\) に式 (\(\ref{binhamcode_redbits}\)) を適用した結果が \((0,0,0)\) であればいずれのビットも反転していないことは明らかである (つまり \(\vector{u}'=\vector{u}\))。そうでない場合、式 (\(\ref{binhamcode_redbits}\)) による反転ビット \(u'_i\) の位置は \((0,0,1)\) で \(u'_1\)、\((0,1,0)\) で \(u'_2\)、\((0,1,1)\) で \(u'_3\)、…、\((1,1,1)\) で \(u'_7\) となる。したがって式 (\(\ref{binhamcode_redbits}\)) が示す \(u_i\) のビットを反転すれば符号 \(\vector{u}'\) に含まれるエラーを訂正し \(\vector{u}\) を復元することができる。

\([8,4]\)-拡張ハミング符号では 2 ビットまでの反転を仮定する。式 (\(\ref{binhamcode_redbits}\)) が \((0,0,0)\) ではない場合、\(u'_8 \ne \sum u'_i\) であれば 1 ビットの反転であるため上記の方法で訂正することができる。\(u'_8 = \sum u'_i\) では 2 ビットの反転が起きていることが分かる (ただし訂正はできない)。

誤り訂正後の復号化は式 (\(\ref{binhamcode_src}\)) のとおりである。

ハミング符号以前の符号

ハミング符号より前にも誤り検出訂正符号はあったが効果的ではなかった。

反復符号 (repetition code)

すべてのビットを固定回数繰り返す符号。例えば 3 反復符号は 1011 を 111000111111 と表し、3 つの並びが 110 だったときは 3 ビット目が反転しているとみなして 1 とする \([3,1]\)-符号である。

参考文献

  1. G.A.ジョーンズ, J.M.ジョーンズ. 情報理論と符号理論 (2012) 丸善出版 ISBN 4621063421