論文翻訳: Computing Extremely Accurate Quantiles Using \(t\)-Digests
Ted Dunning†
MapR Technologies, Inc
Santa Clara, CA
E-mail: ted.dunning@gmail.com
Otmar Ertl
Dynatrace
Linz, Austria
E-mail: otmar.ertl@gmail.com
 概要
概要
我々は非常に小さなスケッチで、特に分布のテール部分において高い精度を実現するランクベースの統計の近似値を計算するオンラインアルゴリズムを提示する。特に、この方法は他の多くの方法とは異なり、絶対精度ではなく \(\max(q,1-q)\) に対する相対精度で分位点 \(q\) を算出することができる。この新しいアルゴリズムは歪んだ分布や順序付けされたデータセットに対しても堅牢で、個別に計算されたダイジェストを精度を損なうことなく結合することができる。
このアルゴリズムのオープンソース Java 実装は著者のウェブサイトから入手可能である。また Go および Python による独自実装も入手できる。
Table of Contents
Keywords: quantiles, 分位数, median, 中央値, rank statistics, ランク統計, t-digest
 1. 導入
1. 導入
数値の集合が与えられたとき、すべてのサンプルを保持したり、すべてのデータが処理されるまで待ったりすることなく、中央値、95 パーセンタイル、またはトリム平均などのランクに基づく統計をオンラインで計算することが望ましいことがよくある。多くの場合、データはストリーミング方式で処理されるので小さなデータ構造のみをメモリに保持する必要があるという追加の要件がある。従来、このような統計は、データをソートし補間によって関心のある分位点を見つけるか、特定の分位数範囲内のすべてのサンプルを再処理することによって計算されてきた。このソート方法は、非常に大きなデータセットの場合や、多数のサブセットの分異数を計算しなければならない場合には実行不可能である。この実行不可能な状況によりオンライン近似アルゴリズムへの関心が高まっている。これまでのアルゴリズムでは、定数またはわずかに増加するメモリ使用量で分位数の近似値を計算することが可能であったが、これらのアルゴリズムでは一定の相対精度を確保することはできなかった。ここで説明する \(t\)-digest は厳密にオンライン方式で動作しながら一定のメモリ制限と一定の相対精度を提供する。
 1.1. 過去の研究
1.1. 過去の研究
オンラインで分位数を計算する初期のアルゴリズムの一つは Chen ら (Chen et al., 2000) で説明されている。その研究では特定の分位数を計算するために同時に推定された確率密度に比例する値で推定値を増減させていた。この方法では、密度を推定するにはさらに多くの分位数を推定しなければならないという循環的な問題に悩まされている。さらにこの手法ではトリム平均などのハイブリッド量の計算はできない。
Munro と Paterson のアルゴリズム (Munro & Paterson, 1980) は中央値の正確な推定値を得るための代替アルゴリズムを提供している。これは、データセット全体が観測されるまでに、これまでに確認された \(s \ll N\) となるような \(N\) 個のサンプルから \(s\) 個のサンプルを維持することで行われる。データがランダムな順序で提示され、\(s=\theta(N^{1/2} \log N)\) である場合、Munro と Paterson のアルゴリズムは中央値を含むサンプルセットを維持できる可能性が高くなる。このアルゴリズムはメモリに比例するコストで事前に指定されたいくつかの分位数を同時に求めるように適応できる。しかし正確な結果が求められる場合は Munro-Paterson アルゴリズムはメモリ消費量が多すぎる。ただしメモリを少なくしても近似値の結果を得ることはできる。
より微妙な問題は、Sawzall (Pike et al., 2005) および Datafu ライブラリ (DFU, 2019) における Munro と Paterson アルゴリズムの実装では目的の分位数の GCD から計算された多数のバケットを使用することである。つまり 99、99.9、99.99 パーセンタイルを計算する場合 1 万個のバケットが必要となり、それぞれに多数のサンプルを保持する必要がある。ここで示す結果では Munro と Paterson のアルゴリズムのこの実装を MP01 と呼ぶ。
Munro と Paterson の研究で最も重要な成果の一つは、ある任意の分位数を \(p\) パスで正確に計算するには \(\Omega(N^{1/p})\) のメモリが必要であるという証明だった。オンラインの場合は \(p=1\) となり、オンラインアルゴリズムでは特定の分位数の正確な値を生成することは保証できないことを意味する。この結果とオンラインの場合の重要性により、その後の研究は分位数の近似値を生成するアルゴリズムに焦点が当てられるようになった。
Greenwald と Khanna (Greenwald & Khanna, 2001) は制御可能な精度で分位数の推定値を算出できる、まさにそのような近似アルゴリズムを提供した。このアルゴリズム (この論文では以降 GK01 と呼ぶ) は Munro と Paterson のアルゴリズムよりメモリ使用量が少なく、あらかじめ指定された分位数に対して近似値を提供する。
別の方法については Shrivastava ら (Shrivastaba et al., 2004) が説明している。この研究では入力値は固定サイズの整数であると想定されている。このような整数は、葉が整数に対応し内部ノードがビット単位の接頭辞に対応する完全な平衡二分木に簡単に配置できる。この木は Q-digest として知られるデータ構造の基礎となる。Q-digest の考え方は、非圧縮ではさまざまな値のカウントがツリーの葉に割り当てられるというものである。このツリーを圧縮するには、サブツリーを折りたたんで葉からのカウントをサブツリーを表す単一のノードに集約する。これにより、折りたたまれたサブツリーの最大カウントはそれまでに観測された整数の総数のごく一部であるしきい値よりも小さくなる。任意の分位数は、ツリーを左接頭辞順にトラバースし、合計が目的の割合に達するまでカウントを累積することで計算できる。その時点で、最後にトラバースしたサブツリーのカウントを使用して、制御可能な小さな誤差の範囲内で目的の分位数を補間することができる。それぞれの折りたたまれたサブツリーのカウントは制限されているため誤差も制限される。
Q-digest の主な利点は
- 必要な空間は圧縮係数 \(k\) に比例して制限される
- 任意の分位数の推定値の最大誤差は \(1/k\) に比例する
- 目的の分位数を事前に指定する必要がない
一方 Q-digest には、想定される値の集合が事前に分かっていなければならず、\(q\) の定数誤差を持つ分位数推定値を生成するという 2 つの問題がある。このため、実際には Q-digest の適用は整数で識別できるサンプルに限定される。Q-digest を順序付き集合の任意の要素に対して平衡木を使用するように適応することは難しい。この問題は、ツリーの再バランスがサブツリーの回転を伴い、これらの回転には複雑な方法で以前に折りたたまれたカウントの再割り当てが必要になる可能性があるためである。この際割り当てはアルゴリズムの精度に重大な影響を与える可能性があり、いずれにしてもカウントの問題と平衡木を維持する問題を切り離すことができないため実装がはるかに複雑になる。
 1.2. 新しい貢献
1.2. 新しい貢献
ここで紹介する手法では、実数値のサンプルをクラスタリングして形成される \(t\)-digest と呼ばれる新しいデータ構造を導入する。\(t\)-digest は、サンプルがメトリクスを持つ任意の空間から取得されるのではなく \(\mathbb{R}^1\) から取得される点、またクラスタが特別な方法でサイズ制限されるという点で \(k\)-means などのよりよく知られているクラスタリング手法と異なる。\(t\)-digest は近似的な分位数の計算を目的として設計されたこれまでの構造とはいくつかの重要な点で異なっている。まず、\(t\)-digest ではデータがクラスタ化されて要約されるが、異なるクラスタに含まれるデータの範囲が重複する可能性がある。次に、ビンはその上限と下限ではなくビンに寄与するサンプル数を表す重心 (centroid) 値と累積重みによって要約される。さらに、サンプルは以前の方法のように一定の絶対誤差を維持するのではなく、相対誤差が制限されるように極端な分位数に対応するビンに寄与するサンプルが少数となるように集約される。
\(t\)-digest では \(q\) 分位数の推定精度は \(q(1-q)\) に対してほぼ一定である。これは \(q\) に依存しない誤差があった以前のアルゴリズムとは対照的である。\(t\)-digest の相対誤差の制限は、一般的に要求される 0 または 1 に近い \(q\) 分位数を計算する際に便利である。Q-digest アルゴリズムと同様に、\(t\)-digest の精度とサイズのトレードオフは、必要なメモリ量が \(\Theta(\delta)\) にのみ比例する単一の圧縮パラメータ \(\delta\) を設定することによって制御できる。
 2. \(t\)-digest
2. \(t\)-digest
\(t\)-digest は実数値のサンプルをクラスタリングし、各クラスタの平均とサンプル数を保持することによって生成される。このクラスタリングは、分布のテール部分付近で特に高い精度で分位数関連の統計を推定するために使用できる。アルゴリズム的には数値の集合から \(t\)-digest を生成する重要な方法が 2 つある。1 つは入力サンプルのバッファを維持する方法である。バッファがいっぱいになると、内容がソートされ、以前のサンプルから計算された重心とマージされる。このマージ形式の \(t\)-digest アルゴリズムにはすべてのメモリ構造を静的に割り当てることができるという利点がある。償却ベースでは、この buffer-and-merge アルゴリズムは特に入力バッファが大きい場合に非常に高速になる。もう一つの主要な \(t\)-digest アルゴリズムは、最も近いクラスタに新しいサンプルが一つずつ追加される従来のクラスタリングアルゴリズムに似ている。ここでは両方のアルゴリズムについて説明する。両方のアルゴリズムのリファレンス実装はオープンソースソフトウェアとして入手可能である。
 2.1. 基本概念
2.1. 基本概念
\(n\) 個のサンプル \(\{x_1 \ldots x_n\} = X \subset \mathbb{R}^1\) を取る。ダイジェストを、\(X\) の互いに疎なサンプル集合 (disjoint set) \(\pi_i \subset X\) で構成されるパーティションとして定義する。このパーティションのサブセット \(\pi_i\) はクラスタと呼ぶ。クラスタ \(\mathcal{C}\) のサンプル数は \(|\mathcal{C}|\) と表記され、通常はクラスタの重みと呼ばれる。
ダイジェスト内の各クラスタ \(\mathcal{C}\) には \(|\mathcal{C}| \gt 0\) のサンプルがあり、関連する平均 \(\bar{\mathcal{C}} = \sum_{x \in \mathcal{C}} x/|\mathcal{C}|\) が存在する。ダイジェスト内のクラスタは、その平均に従って部分順序付けできる。同一の平均を持つクラスタには、クラスタを一貫してインデックス付けできるように任意の固定順序が割り当てられる。この完全順序付けを前提として、各クラスタ \(\mathcal{C}_i\) の左側と右側のクラスタの重みの合計として、クラスタ \(\mathcal{C}_i\) の左と右のクラスタの重みを定義する。つまり \[ \begin{eqnarray*} \mathcal{W}_{\rm left}(\mathcal{C}_i) & = & \sum_{j \lt i} |\mathcal{C}_j| \\ \mathcal{W}_{\rm right}(\mathcal{C}_i) & = & \sum_{j \gt i} |\mathcal{C}_j| \end{eqnarray*} \]
これまでのところ、異なる点集合の要素の順序付けについては制約がないことに注意。\[ \begin{equation} i \gt j \Rightarrow x \gt y \text{ for } x \in \pi_i \text{ and } y \in \pi_i \label{eq1} \end{equation} \] であれば、ダイジェストは強く順序付けられていると呼ぶ。また \[ \begin{equation} i \gt j + \Delta \Rightarrow x \gt y \text{ for } x \in \pi_i \text{ and } y \in \pi_i \label{eq2} \end{equation} \] であれば、ダイジェストは弱く順序付けられていると呼ぶ。ここで \(\Delta \ge 1\) は正のオフセットである。
このようなダイジェストは、すべてのクラスタが単位重みを持つか、または以下に定義されるスケール関数を用いて重みが制限されている場合に \(t\)-digest と呼ばれる。重みの制限に違反せずに 2 つの連続するクラスタがマージできない場合、\(t\)-digest は完全にマージされていると呼ばれる。
 2.2. 簡単な開始
2.2. 簡単な開始
すべてのサンプル \(X = x_1 \ldots x_n\) が昇順で提示され、同値は任意に分割されるとする。サンプルは順序付けられているため、各サンプルのインデックスを使用して新しい値の経験的分位点の値を決定できる。
各クラスタが 1 点を持つような単純なダイジェストを作成すると、このダイジェストは強く順序付けられた \(t\)-digest になるが、完全にはマージされない可能性が高い。
連続するサンプルを左から右に貪欲にグループ化して、連続するサンプルのサブシーケンスを \(X=\{\pi_1|\pi_2|\ldots|\pi_n\}\) とできる。ここで \(\pi_i=\{x_{{\tt left}(i)} \ldots x_{{\tt right}(i)}\}\) は各 \(\pi_i\) がサイズ制限に従って可能な限り多くのサンプルを持つようにする。結果は \(t\)-digest であり、強く順序付けされた完全なマージでもある。
\(t\)-digest の重要な考え方の 1 つは、各クラスタサイズは補間によって正確な分位推定を取得できるほど小さく、かつクラスタが多くなりすぎない程度に選択されることである。重要なことは、相対精度をほぼ一定にするために両端付近のクラスタを強制的に小さくする一方で、中間のサブシーケンスを大きくすることである。もう一つの重要なアイディアは \(t\)-digest を段階的に構築できる実用的なアルゴリズムがあり、結果が厳密に順序付けられていないとしても非常に役立つほど十分に近いということである。
 2.3. クラスタサイズの制限
2.3. クラスタサイズの制限
\(t\)-digest は、ダイジェストの先頭または末尾付近のクラスタを小さくして 1 つのサンプルのみを含むように強制するスケール関数を使用してサイズ制限が課される。スケール関数は、分布のテール部分における非常に正確な分位推定値と、中央値付近における妥当な精度との間で適切なトレードオフを実現するように選択される。
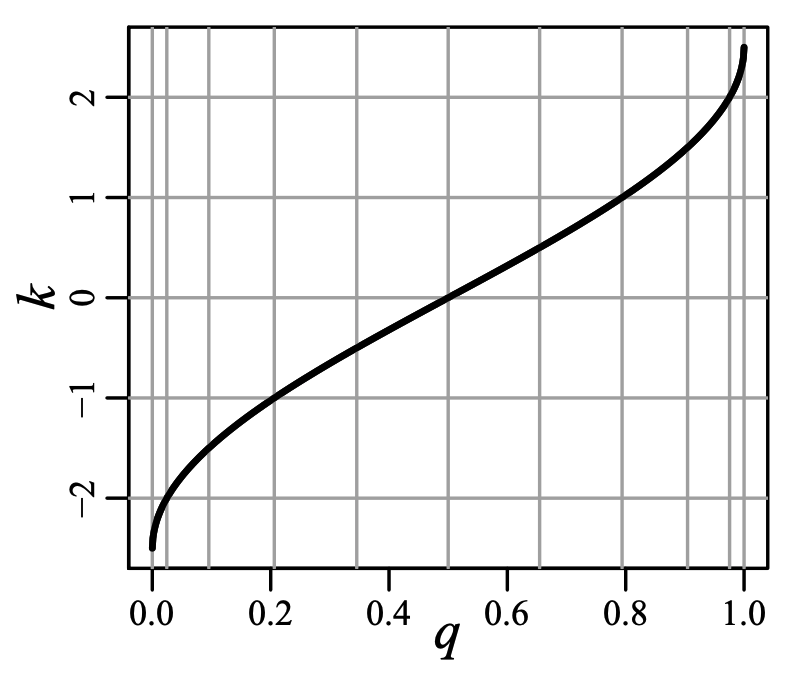
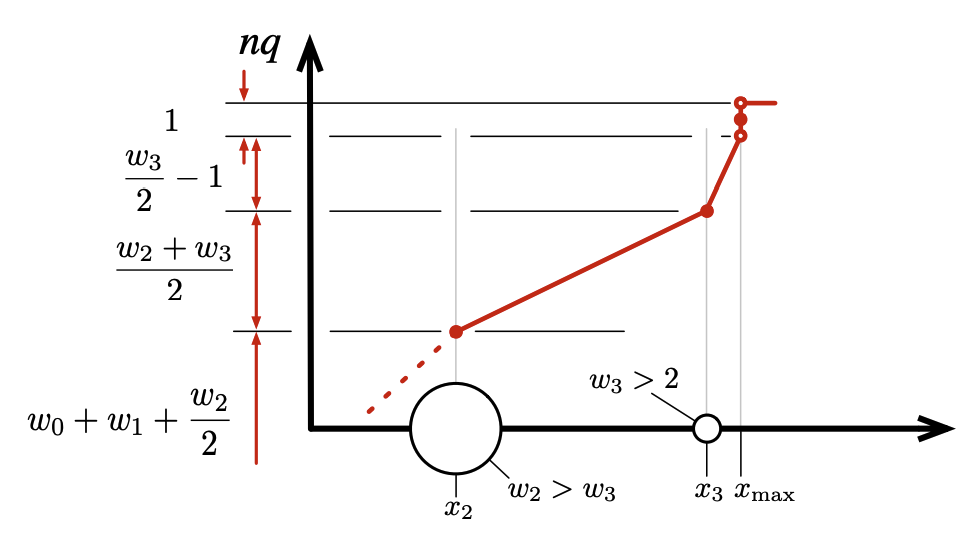
このようにクラスタのサイズを制限するために、圧縮パラメータ \(\delta\) を持つ分位数 \(q\) から概念上のインデックス \(k\) までの非減少関数 (non-decreasing function) としてスケール関数を定義する。\(t\)-digest でよく使用されるスケール関数の 1 つとして \[ \begin{equation} k_1(q) = \frac{\delta}{2\pi} \sin^{-1}(2q-1) \label{eq3} \end{equation} \] が挙げられる。他のスケール関数と同様に \(k_1\) は非減少で、最小値は \(k(0)=-\delta/4\)、最大値は \(k(1)=\delta/4\) である。Fig. 1 は \(\delta=10\) に対する \(k\) と \(q\) の関係を示している。この図では横軸は \(k\) の整数値で等間隔に区切られている。縦軸はスケール関数と等間隔に区切られた横軸の交点から引かれている。\(q=0\) と \(q=1\) 付近では縦軸がどれほど接近しているかに注目して欲しい。
スケール関数は \(t\)-digest のサイズ上限を定義するために必要なメカニズムを提供する。1 つ以上のサンプルを含むすべてのクラスタ \(\mathcal{C}\) の \(k\)-サイズ (\(|\mathcal{C}|_k\) と表記) は最大で 1 の必要がある。\[ \begin{equation} |\mathcal{C}|_k = k(q_{\rm right}) - k(q_{\rm left}) \le 1 \label{eq4} \end{equation} \] ここで \[ \begin{eqnarray*} q_{\rm left} & = & \mathcal{W}_{\rm left}(\mathcal{C}) / n \\ q_{\rm right} & = & q_{\rm left} + |\mathcal{C}| / n \end{eqnarray*} \] である。完全にマージされた \(t\)-digest では、隣接するクラスタは結果が大きくなりすぎるためマージできない。\[ \begin{equation} | \mathcal{C}_i \cup \mathcal{C}_{i+1} |_k = | \mathcal{C}_i |_k + | \mathcal{C}_{i+1} |_k \gt 1 \label{eq5} \end{equation} \] 式 \(\ref{eq4}\) と \(\ref{eq5}\) で示される条件を併せて考えると \(n \gg \delta\) 個のサンプルで \(k_1\) を使用する完全にマージされた \(t\)-digest ではクラスタ数は最大でも \(\lceil \delta \rceil\) であることが示唆される。クラスタ数の加減は \(\lfloor \delta/2 \rfloor\) に近い。
 2.4. スケール関数の効果
2.4. スケール関数の効果
これまでのところスケール関数に必要とされている唯一の特性は非減少であるということだけである。そのため \(k_1\) の代わりにスケール関数 \(k_0(q)=\delta q/2\) を使用することができる。線形スケール関数を使用するとクラスタサイズがほぼ均一になり \(q\) における一定の絶対誤差が得られる。これはこれまでに報告されたほとんどの分位近似アルゴリズムの挙動と類似している。
Fig. 2 は、\(q\) の極値付近でクラスタを小さく保つスケール関数を用いて構築された、強く順序付けされ完全にマージされた \(t\)-digest において、\(q\) のテール付近の推定がどのように改善されるかを示している。この図は \(u \sim {\rm Uniform}(0,1)\) となるような \(x \sim \log u\) を使用してサンプリングされた 10,000 個のデータポイントの最初のパーセンタイルを大まかに示している。左のパネルではデータポイントが 100 のクラスタに分けられてそれぞれ 100 のデータポイントを含んでおり、左側のビンのみが表示されている。等サイズのビンを使用しているため、図の左のパネルにおける \(q\) の補間値にはかなりの避けられない誤差が生じている。一方、右側のパネルでは、ほぼ同じ数のビン (100 ではなく 102) で \(t\)-degit を示しているが \(q=0\) 付近のビンのポイント数はかなり少ない。
もちろん、すべてのサンプルはどこかのビンに入らなければならないため、いくつかのビンを 100 より少ないサンプルで満たすには、他のビンに 100 を超えるサンプルがあるか、またはビンを増やす必要がある。しかし \(q=0\) または \(q=1\) 付近のビンに少ないサンプルを入れることは精度を大幅に向上させるが、\(q=1/2\) 付近のビンのサイズを大きくすることは精度をわずかに低下させることに注意。この特定の例では、最初のビンは 2 サンプルしかないため誤差はゼロであり、2 番目のビンは 10 サンプルしかないため 100 サンプルのクラスタで生じる誤差よりはるかに小さい。一方、\(q=1/2\) 付近のクラスタには均一な場合よりも約 1.6 倍のサンプルがあり、同じサイズのビンに比べて誤差はわずかにしか増加しない。全体的な効果としては極端な部分の分位推定精度が大幅に向上するが、中央値付近ではわずかに低下するだけである。テール部分での精度がどの程度改善されるかは \(t\)-digest がどの程度厳密に順序付けられているかに大きく依存する。
 2.5. 独立した \(t\)-digest のマージ
2.5. 独立した \(t\)-digest のマージ
前のセクションでは、\(t\)-digest を形成するアルゴリズムはサンプルのセットを入力として受け取った。しかしこのアルゴリズムが重み付けされたサンプルの集合に適用されることを妨げるものは何もない。ここの重みがスケール関数によって課されるサイズ制限よりも小さい限り、結果は適切に形成された \(t\)-digest となる。
別々のシーケンス \(X\) と \(Y\) から独立した \(t\)-digest \(t_X\) と \(t_Y\) を形成すると、これらの \(t\)-digest は \(X\) と \(Y\) の分位数を個別に計算し、その結果を組み合わせることで \(X \cup Y\) の分位数を推定するのに利用できることは明らかである。しかし、2 つの \(t\)-digest の順序付けられた和が有効な \(t\)-digest になることを保証するようにスケール係数を選択すればより有用である。スケール係数 \(k_0\) と \(k_1\) は、後述する \(k_2\) と \(k_3\) のスケール係数と同様にどちらもこの特性を持っているが、候補となるスケール関数がこの性質を持つ保証はない。
他のダイジェストをマージして形成されたダイジェストは、連続するクラスタがサイズ制限を満たすのであれば、重心を結合することで完全にマージされるように強制できる。結果として得られる \(t\)-digest は、同じサイズ制限を満たすとしても元データすべてから一度に \(t\)-digest \(t_{X \cup Y}\) を計算した場合と同じになるとは限らない。特に \(t_X\) と \(t_Y\) が個別に強く順序付けされていても、それらの和集合 \(t_X \cup t_Y\) は一般に弱く順序付けされているだけである。これは例えば、マージされる 2 つのダイジェストにおいて重心がほぼ同じ位置にある場合に発生することがある。このように厳密な順序付けが失われると厳密な誤差範囲を計算することが難しくなる。
実際には、他のダイジェストをマージして形成された \(t\)-digest は、順序付けられたデータや多数の繰り返し値を含むデータなどの高度に構造化されたデータセットであっても依然として正確な分位推定値を生成するが、マージされたダイジェストの順序付けがどの程度弱いかはまだよく分かっていない。実証結果のセクションではこれらの問題がどのように作用するかを検討する。
\(t\)-digest をマージする機能により、入力データの互いに疎なパーティションから独立した \(t\)-digest を生成し、それを結合して完全なデータセットを表す \(t\)-digest を作成できるため、大規模なデータセットの並列処理が比較的簡単になる。
同様の分割統治戦略を使用して \(t\)-digest は OLAP システムで使用できるようになる。この考え方は、入力データセットを選択要因の一意の組み合わせに対応する部分集合に分割することにより、データの部分集合の分位数を含むクエリーを迅速に近似できるというものである。そして、選択要因の一意の組み合わせごとに 1 つの \(t\)-digest が事前に計算される。すべての関心のあるクエリーがこのようなプリミティブな部分集合の互いに疎な結合によって満たされる限り、対応する \(t\)-digest を結合して目的の結果を計算することができる。
 2.6. 漸近的マージアルゴリズム
2.6. 漸近的マージアルゴリズム
\(t\)-digest をマージすると精度が向上するという観察は、大量のデータから \(t\)-digest を作成する実用的なアルゴリズムを示唆している。基本的な考え方はデータをバッファに収集することである。バッファがいっぱいになったとき、または最終的な結果が必要になったとき、バッファの内容を以前に作成された重心とともにソートし、組み合わせによってサイズ制限が満たされるたびに点または重心をマージするために 1 回のパスを実行する。任意の大きさのバッファを使用すると、このアルゴリズムはソートされたデータから \(t\)-digest を作成するための元のアプローチと同じになる。しかしバッファサイズが小さい場合、大量のデータを処理するために多くのマージパスが必要となる。
バッファのサンプルを既存の重心集合にマージするアルゴリズムを Algorithm 1 に示す。サイズ制限のチェックは \(C'\) の出力値と同じ回数だけ \(k\) と \(k-1\) を評価するように最適化されていることに注意。これは新しい重心が出力されるたびに \(q_{\rm limit} = k^{-1} (k(q)+1)\) を計算することによって行われる。これにより条件を \(q\) の比較で表現できるため、多くのポイントがマージされても \(k\) を追加で呼び出す必要はない。\(n \gg \lfloor \delta \rfloor\) の場合、スケール関数またはその逆関数の評価は通常 \(\log\) や \(\sin^{-1}\) の呼び出しが含まれるため、これにより大幅な速度向上が期待できる。またこのアルゴリズムでは、プリミティブ値の静的に割り当てられた 4 つの配列のみを使用し、動的な割り当てや構造体をボックス化/アンボックス化をすべて回避していることにも注意。
- 入力: シーケンス \(C=[c_1 \ldots c_m]\), 実数を含む \(t\)-digest, 重み付けされた重心の成分 sum と count を平均の昇順に並べたもの, データバッファ \(X=x_1,\ldots,x_n\), 重み付けられた点, および圧縮係数 \(\delta\)
- 出力: \(t\)-digest を形成する重み付けされた重心の新しい順序の集合 \(C'\)。
| 1. | \( X \leftarrow {\tt sort}(C \cup X); \) | |
| 2. | \( S = \sum_i x_i{\tt .count}; \) | |
| 3. | \( C' = [\,], q_0 = 0; \) | |
| 4. | \( q_{\it limit} = k^{-1}(k(q_0,\delta)+1,\delta); \) | |
| 5. | \( \sigma = x_1; \) | |
| 6. | \( {\bf for} \ i \in 2...(m+n) {\tt :} \) | |
| 7. | \( \hspace{12pt}q = q_0 + (\sigma{\tt .count} + x_i{\tt .count}) / S; \) | |
| 8. | \( \hspace{12pt}{\bf if} \ q \le q_{\it limit}{\tt :} \) | |
| 9. | \( \hspace{24pt}\sigma \leftarrow \sigma + x_i; \) | |
| 10. | \( \hspace{12pt}{\bf else}{\tt :} \) | |
| 11. | \( \hspace{24pt}C'{\tt .append}(\sigma); \) | |
| 12. | \( \hspace{24pt}q_0 \leftarrow q_0 + \sigma{\tt .count} / S; \) | |
| 13. | \( \hspace{24pt}q_{\it limit} \leftarrow k^{-1} (k(q_0, \sigma) + 1, \sigma); \) | |
| 14. | \( \hspace{24pt}\sigma \leftarrow x_i; \) | |
| 15. | \( C'{\tt .append}(\sigma); \) | |
| 16. | \( {\bf return} \ C' \) | |
\(t\)-digest のマージ変種の実行コストは、頻繁に行われるバッファ挿入と希に行われるマージの混合である。バッファ挿入は、配列の書き込み、インデックスのインクリメント、オーバーフローテストで構成されるため非常に高速である。マージはバッファソートとマージ自体で構成される。マージにはバッファと既存の重心の両方をスキャンすることに加えて、すべての一般的なスケール関数の \(\lceil \delta \rceil\) によって制限される結果のサイズにほぼ等しいスケール関数の呼び出し回数が含まれている。\(c_1\) を入力バッファサイズとすると、支配的なコストはソートとスケール関数の呼び出しであるため、入力値あたりの償却コストはおよそ \(C_1 \log c_1 + C_2 \lceil \delta \rceil / c_1\) となる。ここで \(C_1\) と \(C_2\) はそれぞれソート関数とスケール関数のコストを表すパラメータである。この全体的な償却コストは \(c_1 \approx \delta C_2/C_1\) で最小となる。比例定数は実験的に決定する必要があるが、マイクロベンチマークでは \(C_2/C_1\) は Intel i7 プロセッサのシングルコアで 5 から 20 の範囲にあることが示されている。これらのマイクロベンチマークではバッファサイズを \(10 \lceil \delta \rceil\) に増やすと平均速度が大幅に向上するが、それ以上にバッファサイズを増やしても効果はほとんどない。
スケール関数 \(k_1\) の場合、\(\sin^{-1}\) の評価を高速化することでさらなる最適化が可能である。ドメイン \([0,1]\) 全体にわたって \(\sin^{-1}\) の非常に高速で品質の良い近似値を構築することは困難だが、近似値が使用されるドメインを \(q \in [\epsilon,1-\epsilon]\) に限定することで単純かつ高速な近似が利用可能になる。ここで \(\epsilon \approx 0.01\) である。
また、\(q\) から各候補のクラスタに入ることができるサンプルの最大数を直接推定することで \(k\) と \(k-1\) の評価を回避することもできる。このような推定では特にテール付近で許容されるサンプル数が過小評価されるのが一般的だが、\(t\)-digest のサイズが大幅に増加することなく精度を多少向上させることができる。
最後に、ここで示したようなマージに基づくアルゴリズムでは、実際にはサンプルが既存の重心とマージされる際に常に昇順で考慮されるという事実のために問題が発生する可能性がある。このため \(q=0\) 付近の重心が非対称に大きくなり、ダイジェストが構築される際に重心が少しずれるというという影響が生じる可能性がある。このずれは結果として得られるダイジェストが望んでいるより弱い順序になっていることを意味する。この問題はマージのスキャン順序を交互に変更することで (1 回目のパスで昇順、次のパスで降順) ある程度軽減できる。
別のアプローチは、点を追加している間に一時的に大きい圧縮パラメータ \(\delta\) の値を使用する階層化マージを使用することである。ダイジェストが格納されると最終的なマージパスが実行され、ダイジェストが最終的な圧縮パラメータで完全に統合される。これは空間、速度、精度の 3 方向のトレードオフという文脈である程度とらえることができる。一定のメモリ使用で最高速度を得るには大きいバッファと小さい \(\delta\) 値を使用することができる。最高の精度を得るには大きなバッファと階層化マージを使用できる。最小のメモリを得るには小さいバッファと単一の \(\delta\) 値を使用する必要がある。
このトレードオフの具体例を挙げると、高い精度を実現するためには一般的に行われているように \(10\times\delta\) のバッファサイズを使用するが、マージは \(3\times\delta\) の圧縮パラメータで行うことができる。この場合、必要なメモリは通常使用されるものより増えないが、マージの頻度が 20% ほど高くなり、マージ間で保持される重心の数が 3 倍になるため各マージのコストが少し高くなる。結果のダイジェストが、増分的に構築されることにより順序パラメータ \(\Delta \le 3\) などの弱い順序付けのみである場合、最終的なマージにより重心の数と順序パラメータがともに約 3 分の 1 のファクターで減少するため、ダイジェストはほぼ強い順序付けの状態に減少させる可能性が高い。実際には順序付けパラメータの減少によりエラーが大幅に小さくなる。
階層化マージは \(t\)-digest を並列実行で使用する場合にも有用である。これについては並列計算のセクションで詳しく説明する。
 2.7. クラスタリングの変種
2.7. クラスタリングの変種
\(t\)-digest アルゴリズムのマージ変種において、バッファに単一の要素のみを含めて新しい点が追加されるたびにマージが行われるようにすると、アルゴリズムは新しい特性を持ち、バッファリングやマージよりもクラスタリングに近くなる。
\(t\)-digest を構築するクラスタリングアルゴリズムの基本的なアウトラインは非常に単純である。最初はからの順序付き重心リスト \(C=[c_1\ldots c_m]\) が保持される。各重心は平均とカウントで構成されている。重み \(w_n\) を持つ新しい値 \(x_n\) を追加するには、\(x_n\) との距離が最小となる重心の集合を見つける。この集合は \(w_n\) を追加した後の \(k\) サイズがサイズ制限を満たす重心のみを保持することで縮小される。複数の重心が残っている場合は最大の重みを持つ重心が選択される。許容可能な重心が見つかった場合、新しい… \((x_n,w_n)\) がその重心に追加される。もし満足できる重心が見つからなければ \((x_n,w_n)\) は重み \(w_n\) を持つ重心を形成するために使われる。
このクラスタリングの変種を Algorithm 2 として示す。
特定の挿入順序により重心の数が無制限に増加する可能性がある。例えば \(X\) の値が昇順または降順の場合、\(C\) には挿入されたサンプルの数だけ重心を含むことになる。これは \(X\) の新しい値が常に新しい最大値 (または最小値) であり、したがって常に新しい重心を形成するためである。これを避けるためにはクラスタ数が過剰に増えるたびに Algorithm 1 を用いてクラスタを統合できる。
- 入力: 重み付けられた重心の順序付き集合 \(C=\{\}\), 実数値のシーケンス, 重み付けられた点 \(X=\{(x_1,w_1),\ldots (x_N,w_N)\}\), 精度の許容範囲 \(\delta\), および通常は \(3...10\) 範囲内の過剰増加の制限値 \(K\)
- 出力: 重み付き重心の最終的な集合 \(C=[c_1 \ldots c_m]\)
| 1. | \( {\bf for} \ (x_n,w_n) \in X{\tt :} \) | |
| 2. | \( \hspace{12pt}z = \min |c_i{\tt .mean} - x|; \) | |
| 3. | \( \hspace{12pt}S = \{c_i: |c_i{\tt .mean} - x| = z \land |c_i + w_1|_k \lt 1\}; \) | |
| 4. | \( \hspace{12pt}{\bf if} \ |S| \gt 0{\tt :} \) | |
| 5. | \( \hspace{24pt} \)// 距離の降順で並べ替え | |
| 6. | \( \hspace{24pt}S{\tt .sort}({\it key} = \lambda(c)\{-c{\tt .sum}\}); \) | |
| 7. | \( \hspace{24pt}c \leftarrow S{\tt .first}(); \) | |
| 8. | \( \hspace{24pt}c{\tt .count} \leftarrow c{\tt .count} + w_n; \) | |
| 9. | \( \hspace{24pt}c{\tt .mean} \leftarrow c{\tt .mean} + (x_n - c{\tt .mean})/c{\tt .sum}; \) | |
| 10. | \( \hspace{12pt}{\bf else}{\tt :} \) | |
| 11. | \( \hspace{24pt}C \leftarrow C + (x_n, w_n); \) | |
| 12. | \( \hspace{12pt}{\bf if} \ |C| \gt K \delta{\tt :} \) | |
| 13. | \( \hspace{24pt}C \leftarrow {\tt merge}(C, \{\}); \) | |
| 14. | \( C \leftarrow {\tt merge}(C, \{\}); \) | |
| 15. | \( {\bf return} \ C \) | |
 2.8. 代替のスケール関数
2.8. 代替のスケール関数
これまでに説明した \(k_1\) と \(k_0\) のスケールだけが唯一の可能な関数ではない。実際、精度とサイズの重要なトレードオフを提供する重要な関数が存在する。これら 4 つの関数は全体として便利なスケール関数として機能する。\[ \begin{eqnarray} k_0(q) & = & \frac{\delta}{2}q \\ k_1(q) & = & \frac{\delta}{2 \pi} \sin^{-1}(2q-1) \\ k_2(q) & = & \frac{\delta}{4 \log n/\delta + 24} \log \frac{q}{1-q} \\ k_3(q) & = & \frac{\delta}{4 \log n/\delta + 21} \begin{cases} \log 2q & \text{if $q \le 1/2$} \\ -\log 2(1-q) & \text{if $q \gt 1/2$} \end{cases} \end{eqnarray} \] \(t\)-digest を構築するこれらのスケール関数はそれぞれ次の 2 つの保証を提供する。
完全にマージされた \(t\)-digest 内の重心の数はサンプル数が無制限に増加するにつれて \(\lceil \delta \rceil\) によって制限される (上記の \(k_2\) と \(k_3\) ではクラスタ数がおよそ \(\log \log n\) で増加し始める \(10^{60}\) サンプルまでのみ提供される)。
複数の \(t\)-digest の重心の結合はサイズ制限を満たすため個々のダイジェストの最小の \(\delta\) に等しい値の \(\delta\) に対する \(t\)-digest となる。
\(k_2\) と \(k_3\) の非正規化バージョンを使用することもできる: \[ \begin{eqnarray} k'_2(q) & = & \delta \log \frac{q}{1-q} \\ k'_3(q) & = & \delta \begin{cases} \log 2q & \text{if $q \le 1/2$} \\ -\log 2(1-q) & \text{if $q \gt 1/2$} \end{cases} \end{eqnarray} \] これらの非正規化スケール関数を使用すると \(t\)-digest 内の重心の数は概ね \(\log n\) に比例して増加する。
\(k_2\) と \(k_3\) スケール関数の主な利点は \(q=0\) および \(q=1\) 付近のクラスタサイズを \(k_1\) よりさらに厳しく制限することである。一方、\(k_1\) ではクラスタのサイズは \(\sqrt{q(1-q)}\) に比例して制限されるが、\(k_2\) と \(k_3\) ではそれぞれ \(q(1-q)\) と \(\min(q,1-q)\) に比例してクラスタのサイズを制限する。
このクラスタサイズのより厳密な規制により、ダイジェスト内のクラスタの弱い順序付けやクラスタに対するサンプルの不均一な分布による誤差は、\(q\) の極端な値の近くに小さなクラスタを配置することで補正される。特に \(k_3\) スケール関数は \(q=0\) または \(q=1\) 付近のクラスタに 1 つのサンプルのみを配置することで極値付近での誤差をゼロにする。
 2.9. 累積分布関数の補間
2.9. 累積分布関数の補間
一般に、完全にマージされた \(t\)-digest の情報はサンプルがクラスタ化される際に情報が失われているため、特定の値 \(x\) の経験的分位数 (empirical quantile) \(q\) を正確に決定するには不十分である。唯一の例外は、クラスタに 1 つのサンプルのみが含まれており、その重心がその 1 つのサンプルと同じである場合である。
\(t\)-digest の現在の実装で採用されているアプローチは、元のデータのサンプルの分布についていくつかの単純化された仮定を置くことである。これは:
クラスタのサンプルは、複数のサンプルがある場合、重心の左側のサンプルと右側のサンプルに均等に分割される。
2 つのクラスタ間のサンプルは、それらの間で均一に分散される。
最初の仮定は期待される分布に関する詳細情報が無い場合に実行できる最善の仮定であることは明らかである。2 番目の仮定は、各クラスタに関連付けられたサンプルが隣接する重心を超えない場合に \(t\)-digest 内のクラスタの数が増えるため、連続分布に対して漸近的に真となる。実際には \(t\)-digest 内のクラスタは十分に局所化されており、非常に偏った分布であっても極値の分位精度は良好である。
これらの仮定に基づいて 4 つの重要なケースがある。すなはち a) 複数のサンプルを含むクラスタ間の補間、b) 複数のサンプルを含むクラスタと 1 つのサンプルのみを持つクラスタ間の補間、c) 1 つのサンプルのみを持つクラスタ間の補間、および d) 最初と最後のクラスタ間の補間である。
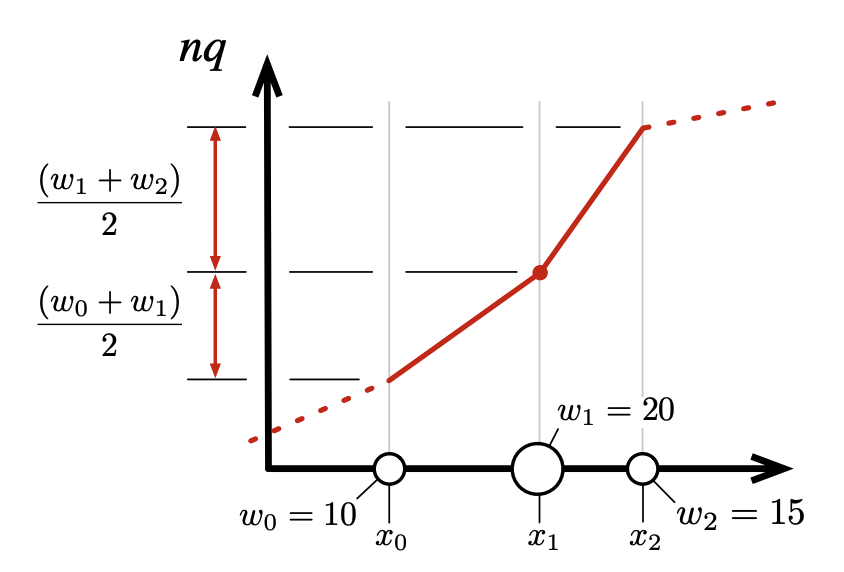
両方のクラスタに複数のサンプルがある場合、経験的分布関数は 2 つの連続する重心間の線形近似を使用して近似され、各重心の重みの半分をそれらの間の感覚に割り当てる。これはクラスタの中心点が重心にあると言っているのと同じである。これは Fig. 3 に示されている。
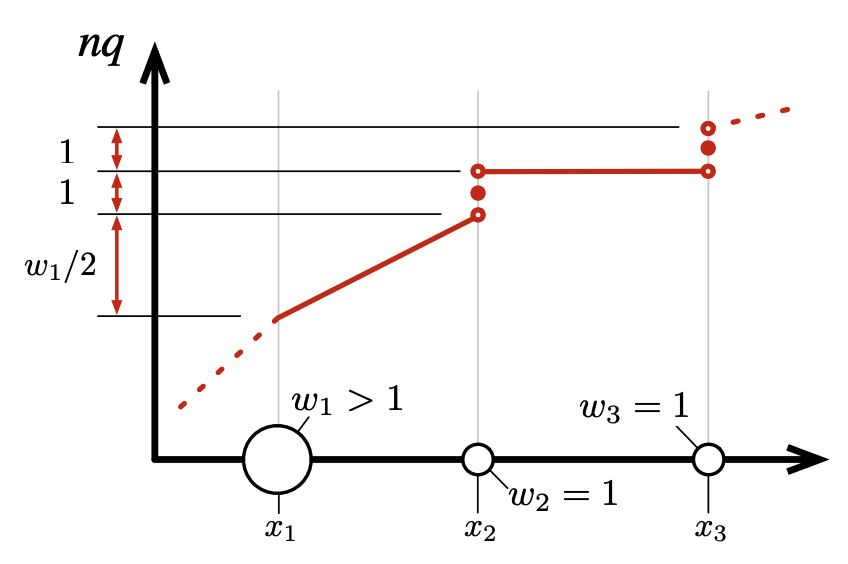
ただしクラスタが 1 つしかサンプルを含まない場合、この 1 つのサンプルがそのクラスタの重心に正確に配置されていることに注意することでこの補間を改善できる。Fig. 4 に示されているように補間を改善できる。隣接するクラスタが複数のサンプルを持つ場合はほぼ以前と同様に補間できるが、次のクラスタ自体がシングルトンである場合は補間を完全に回避できる。
最後に考慮すべきケースはダイジェスト内の最初または最後のクラスタである。このような末端のクラスタが 1 つのサンプルしか持たない場合 \(x_{\rm max}\) はまさにその 1 つのサンプルによるものであることがわかる。クラスタが 2 つのサンプルを持つ場合、それらの 2 つのサンプルは \(x_{\rm max}\) と \(x_n-(x_{\rm max}-x)\) に位置していることが分かっているので、2 つのシングルトンとして扱うことができる。ただしサンプルが 2 つ以上ある場合は、サンプルの半分が重心の前、もう半分が重心の後ろにあるものとしてクラスタを扱うのが有利である。後ろ半分のサンプルについては、1 つは \(x_{\rm max}\) にあるはずなのでそれをシングルトンとして扱い、残りを補間することができる。もちろん最初のクラスタを扱うときはこの議論は逆となり、最初と最後、左と右が逆になる。これはダイジェストの最後のクラスタについて Fig. 5 に示されている。
 3. 経験的評価
3. 経験的評価
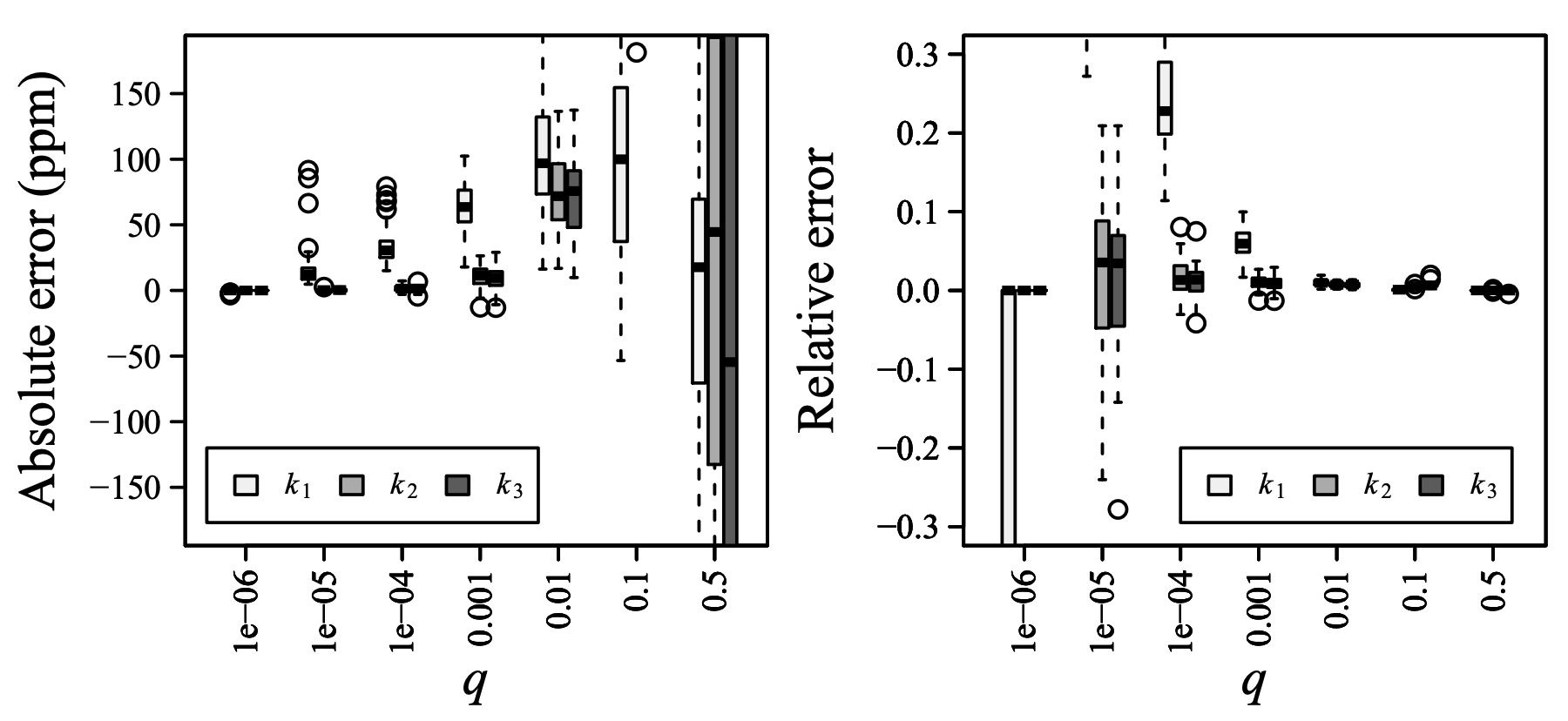
Fig. 6 は \(t\)-digest における分位推定の精度を検証したものである。意図したように、分位推定における絶対誤差は小さく、スケール関数 \(k_1\), \(k_2\) および \(k_3\) に対して \(q=0\) と \(q=1\) 付近 (左パネル) で減少している。垂直スケールのためこの図ではよく見えないが、\(q \in [0.1,0.9]\) の中間領域では \(k_1\) の絶対誤差は \(k_2\), \(k_3\) よりいくらか改善される。
すべてのスケール関数は \(q\) の値が極端になるほど絶対誤差が減少するパターンを示しているが、\(k_2\) と \(k_3\) は \(q \le 0.001\) または \(q \ge 0.999\) で 1 桁の百万分の一の誤差を達成している。これは \(\delta=100\) の場合に合計で約 50〜60 個の重心しか保持されないことを考えると驚くほど良好である。
\(q\) が極端になるほど 3 つのスケール関数すべてで絶対誤差が減少するにもかかわらず、相対誤差はそれほど制御されていない。これは Fig. 6 の→パネルに示されている。スケール関数 \(k_2\) と \(k_3\) は \(q=0.001\) まで相対誤差を良好に制御しているが、\(q=10^{-5}\) と \(q=10^{-4}\) では相対誤差が少し増加する。寄り小さな \(q\) の値では、関連するすべての重心には 1 つのサンプルしかないため誤差はゼロとなる。\(k_1\) に対しては状況はそれほど好ましくはなく、相対誤差は \(q=0.0001\) から劇的に増加し、\(q=10^{-5}\) でスケールから外れる。
 3.1. D\(t\)-digest クラスタの重なり度合い
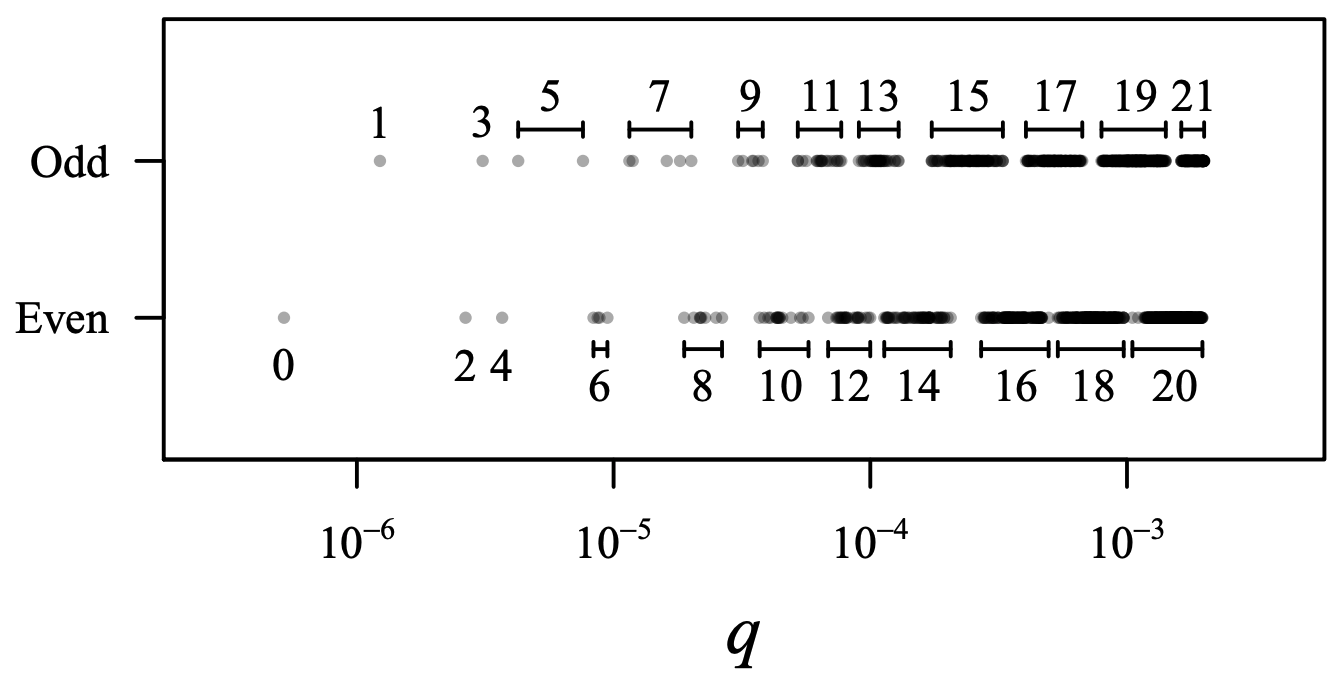
3.1. D\(t\)-digest クラスタの重なり度合い
Fig. 7 は階層化マージ戦略が高品質のクラスタを生成するのにどれほど効果的かを示している。この戦略では約 20% 多いマージ操作が必要であり、各マージ操作のコストは通常の 2 倍未満である。結果として得られるクラスタは厳密に順序付けられているわけではないが、クラスタ間の重複は隣接するクラスタに限られている。ここに示したダイジェストは \(\delta=316\) の作業圧縮を使用し、マージの方向を交互に変えながら合計 \(10^6\) 個のサンプルを挿入して作成された。最終的なダイジェストは \(\delta=100\) で最終的なマージステップを行い、作業クラスタのマージはおよそ 3:1 となった。一方向のマージステップで構築中に \(\delta=100\) を維持すると、クラスタ間の重なりは隣接する 3〜4 個のクラスタまで及ぶのが一般的で精度が大幅に低下する。
 3.2. \(t\)-digest の永続化
3.2. \(t\)-digest の永続化
今回の実験で使用した精度設定とテストデータでは、\(t\)-digest には 50〜60 個の重心が含まれていた。したがって \(t\)-digest の結果はこの数の重心平均と重みを保存することで保存できる。重心を倍精度浮動小数点、カウントを 4 バイト整数として保存する場合、ここで説明した精度テストから得られる \(t\)-digest に必要なストレージは 800 バイト未満となる。
ただしこのサイズは減らすことができる。1 つの簡単な選択肢は重心平均間の差を保存し、各クラスタサイズを格納するために可変バイトエンコーディングを使用することである。連続する平均値間の差は平均値そのものよりも約 2 桁小さいため、単精度浮動小数点を使用してこれらの差を保存すると、個々で説明するテストでの \(t\)-digest を 500 バイト未満で保存しながら平均の精度を約 10 桁回復することができる。これは 32 ビット整数とほぼ同等だが、\(t\)-digest の動的範囲はかなり広くなり精度もかなり向上する。
 3.3. 空間と精度のトレードオフ
3.3. 空間と精度のトレードオフ
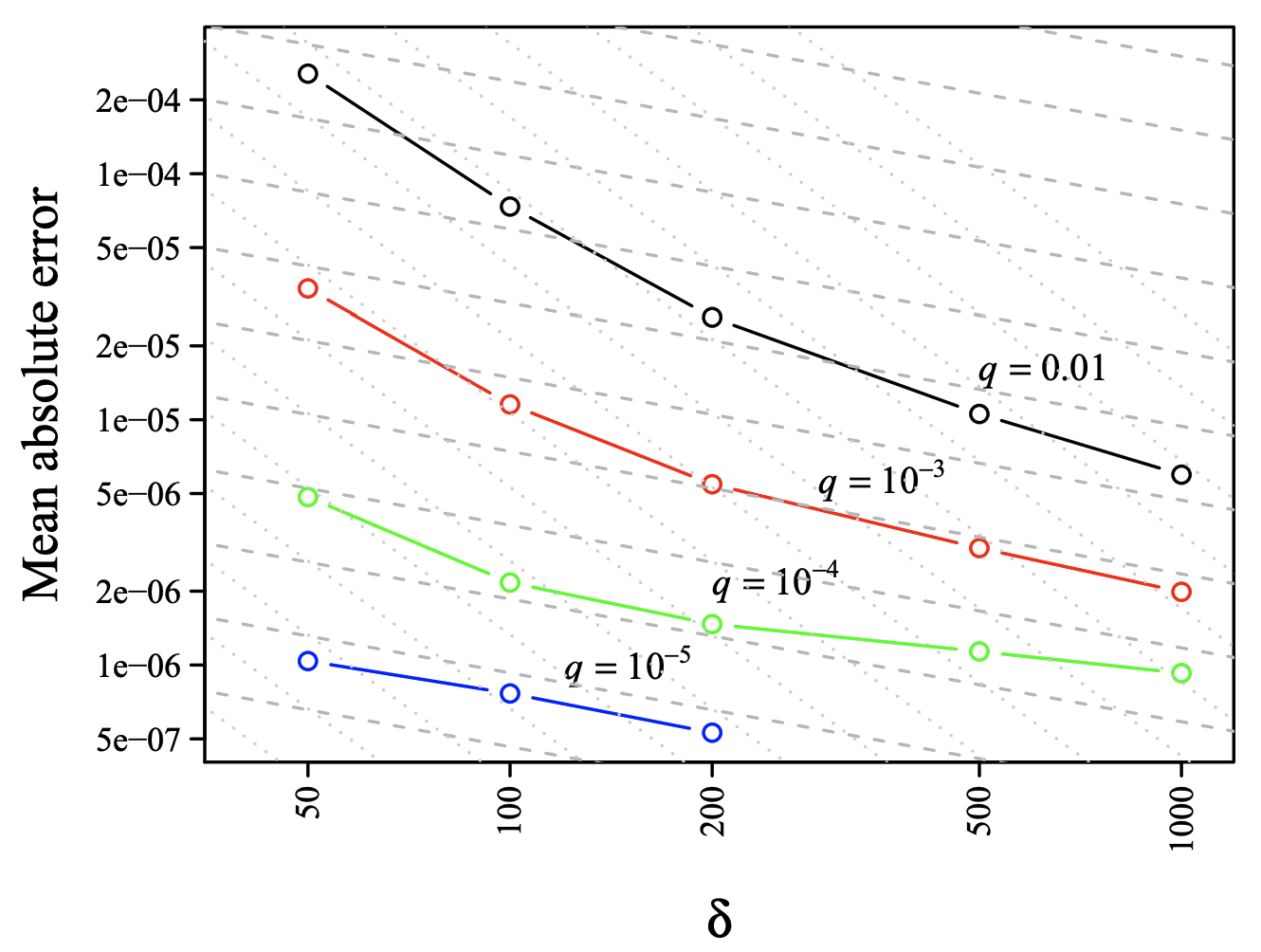
当然のことながら、圧縮パラメータ \(\delta\) によって制御される \(t\)-digest のサイズと分位数を推定できる精度の間にはトレードオフがある。Fig. 8 は異なる分位数に対するトレードオフを示している。特に興味深いのは、\(\delta\) の値が小さい場合、誤差は保持される重心の数 (または等価的に圧縮パラメータ \(\delta\)) の 2 乗でほぼ減少し、\(\delta\) の値が大きい場合は平方根で減少するように見えることである。\(t\)-digest の基礎となる当初の (現在では正しくないか、少なくとも不完全であることが知られている) 直感では、ステップサイズが小さくなるにつれて、連続曲線の段階的な近似の場合のように、ダイジェスト内のクラスタのサイズの 2 乗で誤差が減少することを示唆していた。実際、数値実験では、\(t\)-digest の誤差の主な原因は各クラスタの平均と中央値の差およびクラスタ内のサンプルの実際の分布と線形補間との偏差であることが示唆されている。これらの誤差源はいずれもクラスタ内のサンプル数の逆平方根でスケールされるはずである。
特に、特定の \(q\) の値に対するクラスタサイズは \(\delta\) に正比例するはずなので、観測された \(\delta\) による誤差のスケーリングは本来の直感とは矛盾し、誤差の平方根スケーリングを指示するように見える。この矛盾は \(k_1\) が相対誤差の点で \(k_2\) や \(k_3\) ほど上手く機能しない理由を説明するが、\(\delta\) による誤差のスケーリングの厳密な説明はまだ得られていない。しかし実用的には \(t\)-digest は明らかに良い結果を出している。
 3.4. \(t\)-digest の並列計算
3.4. \(t\)-digest の並列計算
大規模な計算では、入力の別々の部分で \(t\)-digest のような集計を並列に計算し、それらの集計を結合できることが重要である。
例えば Hadoop などの map-reduce フレームワークでは combiner 関数を使用して複数の mapper の出力で \(t\)-digest を構築し、単一の reducer を使用して combiner の出力を結合し、データセット全体の \(t\)-digest を計算することができる。
別の例として Apache Druid のような特定のデータベースがある。このデータベースではツリー構造のインデックスが維持され、プログラマは格納されているデータの特定の集計をインデックスの内部ノードに保持できるように指定できる。この利点は、インデックスの連続するサブ範囲全体で集計をほぼ瞬時に実行できることである。\(N\) をツリーの深さとすると、すべてのデータの実行中の集約を保持するのにかかる労力は合計で \(O(\log(N))\) 増加するだけでありコストは非常に低い。多くの実用的なケースではツリーは 2 または 3 レベル以下でも十分に高速な応答が可能である。例えば 30 年までの任意の期間について 30 秒単位で分位数を計算したい場合、最大で約 300 個のダイジェストをマージする必要があるため、30 秒、2.5 時間、31 日の間隔で \(t\)-digest を保持するだけでも十分である。
\(t\)-digest をマージする最も簡単な方法は Algorithm 1 を使用することである。このアルゴリズムはマージする \(t\)-digest からすべての重心をソートし、\(t\)-digest のサイズ基準を維持しながら可能な限り統合する。非並列実装と同様に、階層化マージはデータが小さいダイジェストに挿入されるときに \(\delta\) の値が大きくなり、ダイジェストを結合するときに \(\delta\) の値が小さくなる場合に有用である。
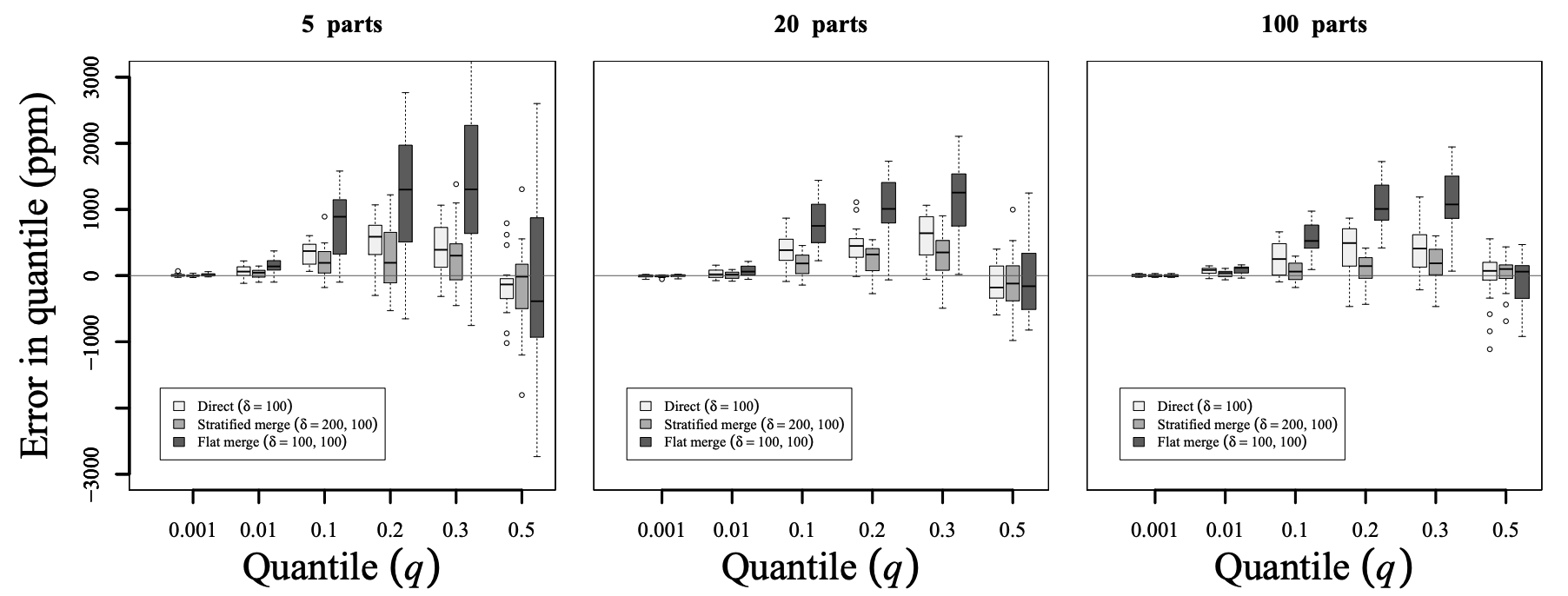
Fig. 9 はこれがどのようになるかを示している。この図は 20 回の試行で 1,000,000 サンプルを要約したときに達成された精度を示している。左から右のパネルは 5, 20, 100 のサブダイジェストをマージした結果が示されている。各パネル内の 3 本のバーは、内部的に \(\delta=300\) を使用する単一のダイジェスト、100 の階層化マージ、サブダイジェストで \(\delta=200\)、結果に \(\delta=100\) を使用するマージダイジェスト、および \(\delta=100\) の非階層化マージの使用を表している。すべての並列度で非階層化マージの結果は、非マージ階層化の結果より悪かった。階層化並列のマージは、5-way 並列処理で少し変動はあるものの、非並列マージと同等であったが、並列度が高くなるにつれて徐々に精度が向上した。
速度の点では、\(t\)-digest のマージは比較的安価である。ある実験では 1,000 個のダイジェストを使用してそれぞれ 1,000,000 個のサンプルを要約し、それらのダイジェストを 1 つのダイジェストにマージした各ダイジェストを埋めるのに約 150 ms、1000 個のダイジェストをすべてマージするのに約 150ms かかった。この例では各ダイジェストは約 1kB なので合計で約 1MB のダイジェストをマージに移す必要がある。全体として、十分なハードウェア (およそ 1000 コア) があれば 10 億のデータポイントから 0.5 秒未満で \(t\)-digest を生成できることを意味する。
 3.5. Q-digest との比較
3.5. Q-digest との比較
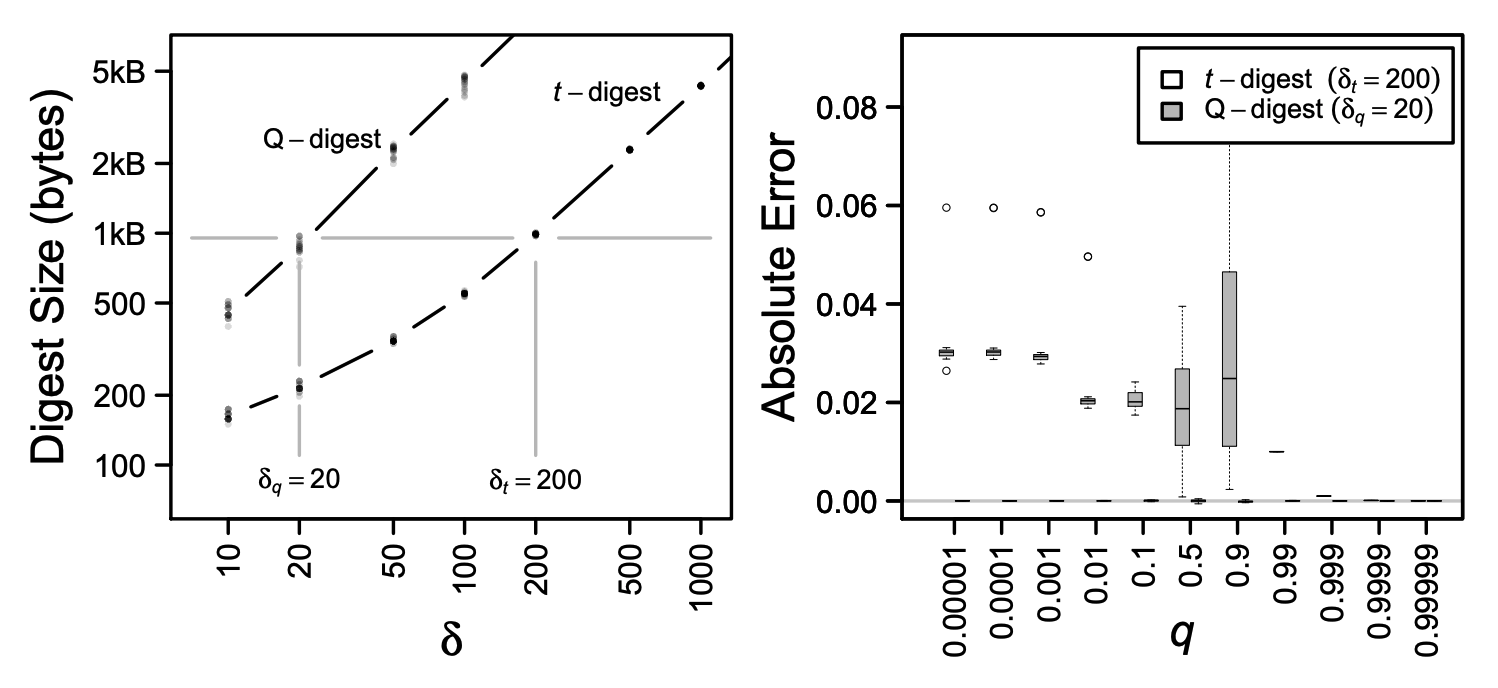
誤差サイズに関しては、同じサイズのダイジェストを比較した場合、\(t\)-digest の 4.0 プレビュー実装は人気のある stream-lib パッケージ (Lib, 2019) の Q-digest (Shrivastava et al., 2004) の実装より優れてる。これは Fig. 10 に示されている。左側のパネルでは、圧縮パラメータ \(q\) とサイズの関係が、両種類のダイジェストに 10 万個の均一に分散されたサンプルが挿入される 20 回の試行に対しそれぞれのダイジェストについて示されている。ダイジェストのサイズを強制的に等しくするために Q-digest では \(\delta_q=20\)、\(t\)-digest では \(\delta_t=200\) の圧縮パラメータが選択された。これにより、左のパネルに示すように Q-digest では約 874 バイト、\(t\)-digest では約 990 バイトの平均ダイジェストサイズが得られる。右のパネルはこれらの条件下での誤差を比較したもので、\(t\)-digest の誤差が \(q\) のすべての値において 1 桁以上小さいことを示している (実際には 2 桁以上)。\(t\)-digest は \(q=0\) に近い値では Q-digest よりも絶対誤差が 3〜5 桁小さい。歪度 (skew) が高い分布で比較した場合は \(t\)-digest に有利であることがさらに顕著となる。この比較で選択されたパラメータはサンプル数に依存することに注意。これは Q-digest のサイズはサンプル数にほぼ対数的に増加するが、\(t\)-digest のサイズは厳密に制限されており、サンプル数が \(2\delta\) を超えるとほぼ一定となるためである。
 4. 考察
4. 考察
\(t\)-digest は精度とサイズの点でこれまでの最先端であった Q-digest を上回る新しいオンラインアルゴリズムである。\(t\)-digest は分位数やトリム平均などさまざまなランクベースの統計の正確なオンライン推定値を提供する。アルゴリズムのコアとなるアイディアは単純で高い精度が保証される。\(t\)-digest は並列アプリケーションや OLAP スタイルのインデックスでも使用できる。
\(t\)-digest アルゴリズムはオープンソースで十分にテストされた実装の形で利用可能であると著者は主張している (Dunning, 2018)。これは既に Netflix や Microsoft などの大企業で社内監視に採用されており、Apache Mahout や stream-lib などのオープンソースライブラリに含まれており、Apache Lucene や Elasticsearch などの著名なオープンソースプロジェクトに組み込まれている。
 References
References
- Chen, Fei, Lambert, Diane, & Pinheiro, Jos´e C. 2000. Incremental Quantile Estimation for Massive Tracking. Pages 516–522 of: In Proceedings of KDD.
- DFU. 2019. The Apache Datafu Project. https://datafu.apache.org/. [Online; accessed 23-January-2018].
- Dunning, Ted. 2018. The t-digest Library. https://github.com/tdunning/t-digest/. [Online; accessed 23-January-2018].
- Greenwald, Michael, & Khanna, Sanjeev. 2001. Space-efficient Online Computation of Quantile Summaries. Pages 58–66 of: Proceedings of the 2001 ACM SIGMOD International Conference on Management of Data. SIGMOD ’01. New York, NY, USA: ACM.
- Lib, Stream. 2019. Stream summarizer and cardinality estimator. https://github.com/addthis/stream-lib. [Online; accessed 11-February-2019].
- Munro, J.I., & Paterson, M.S. 1980. Selection and sorting with limited storage. Theoretical Computer Science, 12(3), 315 – 323.
- Pike, Rob, Dorward, Sean, Griesemer, Robert, & Quinlan, Sean. 2005. Interpreting the Data: Parallel Analysis with Sawzall. Scientific Programming Journal, 13, 277–298.
- Shrivastava, Nisheeth, Buragohain, Chiranjeeb, Agrawal, Divyakant, & Suri, Subhash. 2004 (09). Medians and Beyond: New Aggregation Techniques for Sensor Networks. In: SenSys’04 - Proceedings of the Second International Conference on Embedded Networked Sensor Systems.
翻訳抄
大規模データセットから \(k\) 番目に小さい要素の近似値を効率的に見つけるためのアルゴリズム \(t\)-digest についての 2019 年の論文。
- DUNNING, Ted; ERTL, Otmar. Computing extremely accurate quantiles using \(t\)-digests. arXiv preprint arXiv:1902.04023, 2019.