論文翻訳: Graph Drawing by Force–Directed Placement
THOMAS M. J. FRUCHTERMAN AND EDWARD M. REINGOLD
Department of Computer Science, University of Illinois at Urbana-Champaign,
1304 W. Springfield Avenue, Urbana, IL 61801-2987, U.S.A.
 SUMMARY
SUMMARY
直線の辺を持つ一般的な無向グラフを描画するための Eades [1] の spring-embedder モデルの改良を紹介する。我々の発見は辺の長さが均一になるようにめざし、自然システムにおける力学に類似させることでシンプルでエレガント、概念的に直感的なアルゴリズムを開発する。
KEY WORDS: Graph drawing, Force-directed placement, Multi-level techniques, Simulated annealing
Table of Contents
- SUMMARY
- グラフ描画問題
- 過去の研究
- 新手法
- 実装
- 拡張の例 - 五角柱
- 対称グラフ
- 平面的グラフ
- LAYOUTS THAT APPEAR TO BE THREE-DIMENSIONAL
- THREE-DIMENSIONAL LAYOUT
- GRID VARIANT
- 考察
- REFERENCES
- 翻訳抄
 グラフ描画問題
グラフ描画問題
グラフ \(G(V,E)\) は頂点の集合 \(V\) と辺の集合 \(E\) であり、辺は頂点のペアを結んでいる [2]。通常、グラフは頂点を平面上の点とし、辺をそれらを結ぶ線分または曲線として描画される。グラフの種類や表現目的に応じて様々な表現方法がある。ここで我々は最も一般的な種類のグラフ、つまり直線の辺で描かれた一般的な無向グラフに焦点を当てる。この論文では、物理システムの単純化されたシミュレーションを実行することで見た目が美しいグラフの 2 次元画像を生成しようとするアルゴリズムを紹介する。
我々は一般に受け入れられている美的基準 (aesthetic criteria) に従って一般的な無向グラフを描画することに関心がある [3]:
- フレーム内の頂点を均等に配置する
- 辺の交差を最小にする
- 辺の長さを均一にする
- 固有の対称性を繁栄する
- フレームに合わせる
我々のアルゴリズムはこれらの目標を明示的に目指しているわけではないが、対称性、均等な分布、均一な辺の長さを繁栄することに最も優れている。我々の実装の目標は速度と単純さである。
 過去の研究
過去の研究
我々の無向グラフ描画アルゴリズムは Eades [1] の研究に基づいており、これは force-directed placement [4] と呼ばれる VLSI 配線技術から発展したものである。まず Eades の 'メタファー' についての説明を引用する。
基本的な考え方は次の通りである。グラフを埋め込む [レイアウトする] には、頂点を鋼鉄のリングに置き換え、各辺をバネに置き換えて機械システムを形成する。… 頂点はある初期レイアウトに配置され、リングにかかるバネの力によって系が最小エネルギー状態に遷移するように放される。
Eades はグラフをリングとバネの物理的なシステムとしてモデル化したが、彼の実装はフックの法則*を反映したものではなく、むしろバネが及ぼす力について独自の公式を選択した。物理的現実からのもう一つの重要な逸脱は力学の適用である。反発力はすべての頂点の間で計算されるが、引力は隣接する頂点の間でのみ計算される。これにより隣接間の引力は \(\Theta(|E|)\) で計算されるため時間複雑性が軽減されるが、反発力は依然として \(\Theta(|E|^2)\) であるため、これらの \(n\)-体アルゴリズム [6] の大きな弱点である。
Kamada と Kawai [7, 8] は Eades のアルゴリズムに独自の変形を加えている。彼らもグラフをバネのシステムとしてモデル化したが、Eades がフックの法則を放棄したのに対して Kamada と Kawai はそれに基づいて微分方程式を解いてレイアウトを最適化した。Eades は頂点がすぐ近くにあることだけが重要であると考え隣接間の引力のみを計算したが、Kamada と Kawai のアルゴリズムは隣接していない頂点間の理想的な距離、2 つの頂点間の理想的な距離はその最短経路の長さに比例するという強力な概念を追加した。
Kamada と Kawaiはグラフ描画の問題を鋼鉄のリングをつなぐバネの系の総エネルギーを減少させる過程と考えた。すべてのバネの圧縮または張力の和を最小化することにより、リングまたは頂点は互いに最も理想的な距離に近くなる。彼らはグラフの総エネルギーを次のように定式化した。\[ E = \frac{1}{2} \sum_{1\le i \lt j \le |V|} k_{ij} (|p_i - p_j| - l_{ij})^2 \] ここで \(p_i\) は頂点 \(v_i\) に対応するリングの位置、k_{ij}\) は \(p_i\) と \(p_j\) の間のバネのバネ定数、\(l_{ij}\) は頂点 \(v_i\) と頂点 \(v_j\) の間の最適距離である。このエネルギーは拡張点の偏微分方程式を解いて新しい位置を求め、新しい位置が新しい状態のエネルギーを最小化する方向にリングを移動することによって減少する。頂点の再配置はエネルギーがあらかじめ設定されたしきい値を下回るまで繰り返される。Eades のアプローチとの重要な違いは、各反復で移動する頂点は 1 つだけなので、内部ループはシステムのエネルギーに対するその頂点の寄与を再計算するのに \(\Theta(|V|)\) 時間をかけるだけで良いことである。
Davidson と Harel [9] もシステムのエネルギーを削減してグラフをレイアウトしようと試みているが、VLSI の配置や他の最適化問題に古くから根ざしている方法、すなはち焼きなまし法 (simulated annealing) [10, 11] を使用している。焼きなまし法は強力で一般的な最適化アルゴリズムだが計算コストが高い。グラフの描画はエネルギーを最小化する問題であり最適化の一つであるといえる。焼きなまし法を適用するにはエネルギー関数を選択する必要がある。Davidson と Harel は頂点の分布、境界への近さ、辺の長さ、辺の交差の高を組み合わせた柔軟な関数を選択した。これらの項の重みは異なる美的基準を強調するために変更することができる。
Davidson と Harel は様々な美的基準を柔軟に満たし最高品質の図を作成しようと務めた。焼きなまし法を使用して基本的な構成を見つけた後、それを一度数ピクセルずつ調整し、「上り坂」の動きを禁止する「微調整」オプションを備えている。このアイディアについては本論文の後半で取り上げる予定である。内部ループで \(\Theta(|V|)\) の時間複雑性のみの更新を使用しているにもかかわらず、焼きなまし法は非常に遅く、グラフの対話型時間には実用的ではない。
- *フックの法則はバネの挙動を記述する巨視的近似である。我々はこれを物理学の入門書から引用する [5]:
バネを圧縮または伸張して放すと、変位が大きすぎない限り元の長さ、つまり自然な長さに戻る。… それが分る … \(\Delta x\) が小さい場合、バネが及ぼす力はほぼ \(\Delta x\) に比例する。フックの法則として知られるこの結果は \[ F_x = -k(x-x_0) = -k\Delta x \] と書くことができ、ここで経験的に決定された定数 \(k\) はバネの 力定数 (force constant) と呼ばれる。
 新手法
新手法
我々のグラフ描画の原則は 2 つしかない:
- 隣接する頂点は互いに近くに描べきである。
- 互いに近すぎる頂点は描くべきではない。
頂点をどの程度近づけて配置するかは、頂点の数と利用可能な空間による。一部のグラフでは複雑すぎて魅力的に描画できないものもある。我々の漠然としたガイドラインは素粒子物理学の結果を思い起こさせる [5]:
約 1 fm [フェムトメートル] の距離では強い核力が引力となって 2 つの陽子間には電気力の約 10 倍の力が働く。この力は距離が増すにつれて急激に減少し、この距離が約 15 倍になると完全に無視できるようになる。2 つの核子が約 0.4 fm 以内の距離にあるとき、強い核力は反発する。したがって原子核は崩壊しない。
次のような例を考える: 頂点は亜原子粒子や天体のように振る舞い、互いに引力と反発力を及ぼし合う。その力が運動を引き起こす。我々のアルゴリズムは分子や衛星のシミュレーションに似ており \(n\)-体問題と呼ばれることもある。しかし Eades に倣えば忠実なシミュレーションをする必要はなく、非現実的な力を非現実的な方法で適用することができる。そこで Eades のように隣接する調弦だけが互いに引き合うようにし、すべての頂点は互いに反発するようにする。これは上記の 2 つのガイドラインの非対称性と一致する。
我々はバネやマクロ宇宙重力などの自然システムからヒントを得たが、「力」の名前が正しくないことを指摘しなければならない。我々は力を使ってあらゆる量子の速度 (velocity) (量子の時間は単一であるため変位) を計算するが、真の力は加速度 (acceleration) を引き起こす。実際の定義は動的平衡 (振り子、軌道) につながる一方で、我々は静的平衡を求めるため、この区別は非常に重要である。
アルゴリズムの疑似コードを Figure 1 に示す。初期構成、入力、出力については何も述べていない。初期構成はすべてを指定することも、部分的に指定することもできるが、通常、頂点はフレーム内にランダムに配置される。\(f_a\) と \(f_r\) には異なる関数が選ばれている可能性がある。
各反復には 3 つのステップがある: まず拡張点に対する引力の効果を計算し、次に反発力の効果を計算し、最後に温度によって変位の合計を制限する。頂点が同じ位置にある場合に特別なケースが発生する。我々の実装は 2 つの点がランダムに選ばれた向きでわずかな距離だけ離れている可のように動作する。これは頂点を分離する激しい反発力につながる。
Figure 1 は「温度」と「冷却」の説明を省略している。このアイディアは、頂点の変位はある最大値に制限され、この最大値は時間の経過と共に減少するというものである。つまりレイアウトが良くなるにつれて調整量はどんどん細かくなって行く。例えば温度は初期幅 (つまりフレームの幅の 10 分の 1 など) で開始し、逆線形に 0 まで減衰することができる。より効率的な冷却機能については後述する。
| 1. | \( {\it area} := W * L; \) | // \(W\) と \(L\) はフレームの幅と長さ |
| 2. | \( G := (V, E); \) | // 頂点は初期配置をランダムに割り当てられている |
| 3. | \( k := \sqrt{{\it area} / |V|}; \) | |
| 4. | \( {\bf function} \ f_a(x) := {\bf begin \ return} \ x^2 / k \ {\bf end}; \) | |
| 5. | \( {\bf function} \ f_r(x) := {\bf begin \ return} \ k^2 / x \ {\bf end}; \) | |
| 6. | \( \) | |
| 7. | \( {\bf for} \ i := 1 \ {\bf to} \ {\it iterations} \ {\bf do \ begin} \) | |
| 8. | \( \hspace{12pt} \)// 反発力を算出 | |
| 9. | \( \hspace{12pt}{\bf for} \ v \ {\bf in} \ V \ {\bf do \ begin} \) | |
| 10. | \( \hspace{24pt} \)// 拡張点は \({\it .pos}\) と \({\it .disp}\) の 2 つのベクトルを持つ | |
| 11. | \( \hspace{24pt}v.{\it disp} := 0; \) | |
| 12. | \( \hspace{24pt}{\bf for} \ u \ {\bf in} \ V \ {\bf do} \) | |
| 13. | \( \hspace{36pt}{\bf if} (u \ne v) \ {\bf then \ begin} \) | |
| 14. | \( \hspace{48pt} \)// \(\Delta\) は差を表す略語 | |
| 15. | \( \hspace{48pt} \)// 2 つの頂点の位置を結ぶベクトル | |
| 16. | \( \hspace{48pt}\Delta := v.{\it pos} - u.{\it pos}; \) | |
| 17. | \( \hspace{48pt}v.{\it disp} := v.{\it disp} + (\Delta / |\Delta|) * f_r(|\Delta|) \) | |
| 18. | \( \hspace{36pt}{\bf end} \) | |
| 19. | \( \hspace{24pt}{\bf end} \) | |
| 20. | \( \) | |
| 21. | \( \hspace{24pt} \)// 引力を算出 | |
| 22. | \( \hspace{24pt}{\bf for} \ e \ {\bf in} \ E \ {\bf do \ begin} \) | |
| 23. | \( \hspace{36pt} \)// 各辺は頂点 \(.v\) と \(.u\) の順序づけられたペア | |
| 24. | \( \hspace{36pt}\Delta := e.v.{\it pos} - e.u.{\it pos}; \) | |
| 25. | \( \hspace{36pt}e.v.{\it disp} := e.v.{\it disp} - (\Delta / |\Delta|) * f_a(|\Delta|); \) | |
| 26. | \( \hspace{36pt}e.u.{\it disp} := e.u.{\it disp} + (\Delta / |\Delta|) * f_a(|\Delta|) \) | |
| 27. | \( \hspace{24pt}{\bf end} \) | |
| 28. | \( \) | |
| 29. | \( \hspace{24pt} \)// 最大変位を温度 \(t\) に制限し、フレーム外への変位を防ぐ | |
| 30. | \( \hspace{24pt}{\bf for} \ v \ {\bf in} \ V \ {\bf do \ begin} \) | |
| 31. | \( \hspace{36pt}v.{\it pos} := v.{\it pos} + (v.disp / |v.disp|) * \min(v.disp, t); \) | |
| 32. | \( \hspace{36pt}v.pos.x := \min(W/2, \max(-W/2, v.pos.x)); \) | |
| 33. | \( \hspace{36pt}v.pos.y := \min(L/2, \max(-L/2, v.pos.y)) \) | |
| 34. | \( \hspace{24pt}{\bf end} \) | |
| 35. | \( \hspace{24pt} \)// レイアウトがより良い構成に近づくにつれて温度を下げる | |
| 36. | \( \hspace{24pt}t := {\it cool}(t) \) | |
| 37. | \( \hspace{12pt}{\bf end} \) | |
| 38. | \( {\bf end} \) | |
 力のモデリング
力のモデリング
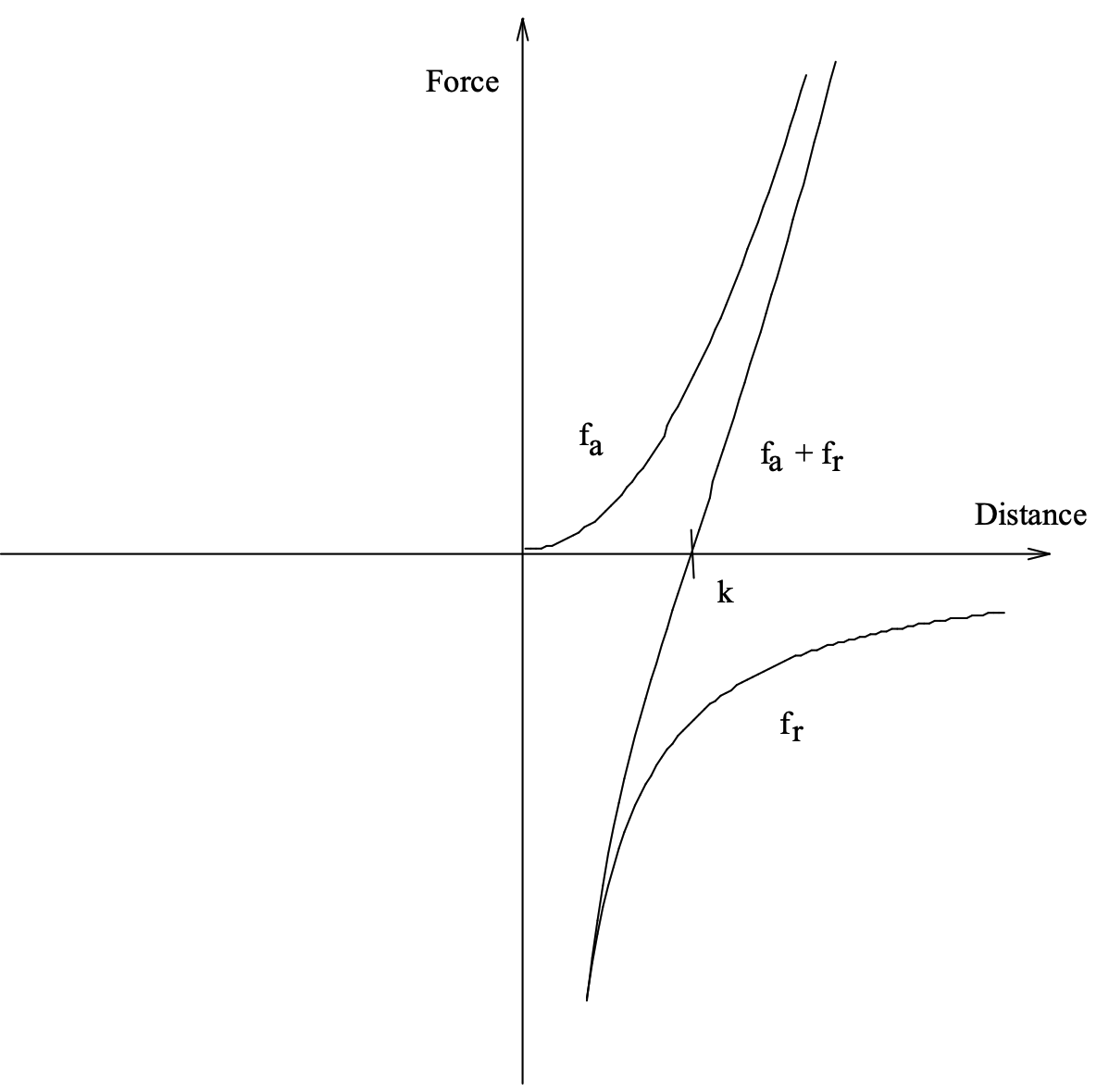
頂点の最適な距離は \[ k = C \sqrt{\frac{\mbox{area}}{\mbox{number of vertices}}} \] として計算される。ここで定数 \(C\) は実験的に求められる。直感的には、2 つの頂点が離れていれば離れているほど、あるいは近ければ近いほど現在のレイアウトを考慮する必要があり修正が激しくなることが予想される。\(f_a\) と \(f_r\) をそれぞれ引力と反発力とし、2 つの頂点間の距離を \(d\) とすると次のようになる: \[ \begin{eqnarray*} f_a(d) & = & d^2/k, \\ f_r(d) & = & -k^2/d \end{eqnarray*} \] Figure 2 はこれらの力とその合計の距離に対する関係を示している。引力と反発力の合計が \(x\)-軸と交差する点は、2 つの力が正確に打ち消し合う点であり、これは頂点間の理想的な距離 \(k\) である。
この 2 つの関数はフックの法則に似ており、いくつかの実験の後、我々の目的を実現するものであることが自然に示唆された。我々は他にも \[ \begin{eqnarray*} f_a(d) & = & d/k \\ f_r(d) & = & -k/d \end{eqnarray*} \] のように我々のガイドラインを満たすと思われるいくつかの関数を実験した。しかし後者の関数は焼きなまし法で言うところの極小値 (local minima) を克服できないように見えたため、頂点が初期値の悪い別の頂点を飛び越える可能性が低くなるなど、より複雑なグラフに対してはうまく機能しなかった。焼きなまし法ではより良い配置に到達するためにさらに悪い配置を経由することによって悪い配置を克服することを hill-climbing として知られている。焼きなまし法は悪い配置への移行を受け入れるかどうかを確率的に決定するが、我々の力による配置は決定論的に常に最低地点を探す。これは、我々のシミュレーションが離散的であり、頂点は短距離での反発効果に直面することなく単一のタイムステップで別の頂点を飛び越えることができる点を除いて、極小値または「谷」で立ち往生することが多くなる可能性がある。高次のべき乗を使う力の法則は二次関数と同等の結果をもたらす傾向があるため計算が容易な方を選択した。
Eades の方程式は次のようなものだった。\[ \begin{eqnarray*} f_a(d) & = & k_a \log d \\ f_r(d) & = & k_r / d^2 \end{eqnarray*} \] 後に示すように、我々は Eades の式と同等の結果を達成したが、計算効率が悪いため彼の \(f_a\) 式は却下した。
 フレーム
フレーム
我々はユーザが指定したフレームにグラフを閉じ込めなければならない。当初、反発力を与えるがそれ自体は異動しないダミーの頂点をグラフの周囲に配置した。Davidson と Harel も最初は全く同じ戦略をとった。そして彼らは頂点が境界付近にあるときのコストが逆二次関数的に増加する項をエネルギー関数の中に入れることで、壁を傾斜したポテンシャル障壁としてモデル化した。我々はフレームを不動のオブジェクトと見なして、フレームを 4 つの「壁」としてモデル化することにした。それぞれの壁は、頂点を越えて押し出す力と全く同じ「垂直」の力を及ぼすので、実際の壁のようにフレームを停止する。
我々はこの概念を任意の線分で構成される境界線に拡張することをまだ満足に実装できていない。凹領域内にグラフを描く場合、頂点だけではなく辺も境界を超えないようにしなければならない。これにより我々のアルゴリズムに \(\Theta(|V||E|)\) の時間複雑性を追加することになるが、このような任意の領域はグラフの中央にテキスト用の島を確保するのに便利であろう。例えばくさび形の頂点に木の根を固定し、くさび形の領域に木を描こうとするかもしれない。
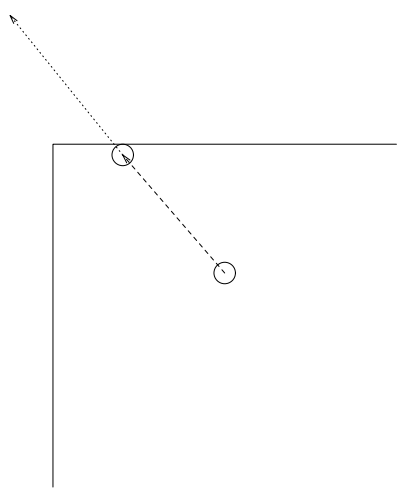
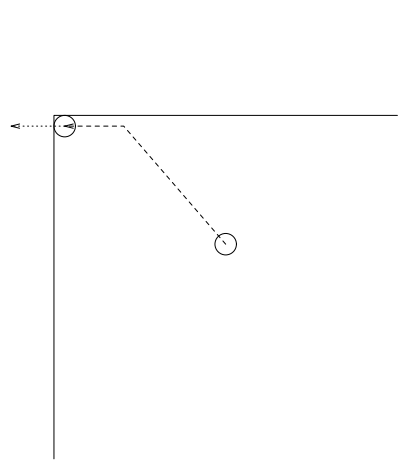
物理的な壁に基づいてフレームをモデル化するにはいくつかのアプローチがある。最も簡単なのは「粘着性」頂点で、最初に衝突 (非弾性衝突) した壁の場所に付着し、その頂点にかかる力のベクトルが壁から離れる成分だけになるまでそこに留まる (Figure 3 参照)。もう一つのアプローチは壁への衝突を弾性衝突としてモデル化することだが、この場合、壁にぶつかる順序を決定する必要があり、おそらく頂点が何度も「跳ね返る」こととなり、膨大な計算が必要となるだろう。このアプローチはコンピュータグラフィックスのシェーディングに使用されるような、現実的だが計算量の多い方法のレイトレーシング [12] を彷彿とさせる (Figure 4 参照)。
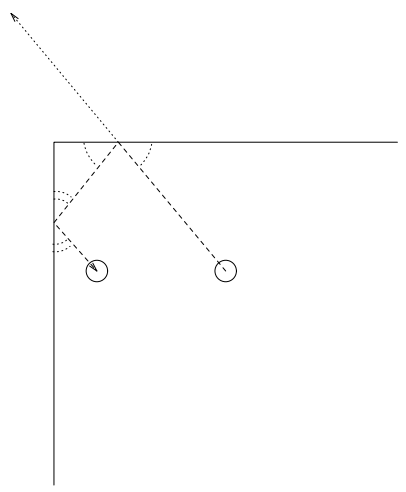
我々は壁に垂直な変位成分を壁で止めることを選択した。すべての壁が座標系に直交しているため、これはグラフを囲むボックスに実装するのが簡単かつ効率的であった。Figure 5 は、頂点が枠の外に提案されている軌跡を上部の境界によって止められている様子を示しているが、Figure 6 では頂点は左の境界に到達して左上隅に留まるまで左へスライドすることが許されている (任意の線でできた境界の場合は境界線に垂直な軌跡の成分を見つけるためにドット積を計算しなければならない)。実際には、結果のグラフが境界線に近づかない程度に小さくなるように力の強さを選択し、フィルターを適用してグラフをフレームいっぱいに拡大することが多い。
 アルゴリズムの高速化
アルゴリズムの高速化
単純な \(n\)-体シミュレーションの改良として古くから知られているものは、離れた物体の影響を一つの極として近似することである [13]。こうすることで \(n\)-体シミュレーションの複雑性を \(\Theta(n^2)\) から \(\Theta(n \log n)\) に削減できる。我々は天体、科学、亜原子粒子系を忠実に模倣する必要はない。これにより、頂点は近傍にのみ引き寄せられる - これには \(\Theta(|E|)\) の複雑性がある - という時間短縮のための調整が可能となった。それでも全ての頂点が他のすべての頂点からの反発力を計算しなければならないが、これは \(\Theta(|V|^2)\) の複雑性である。反発力は距離の逆に譲渡して現象する。より遠い頂点の寄与を無視できるだろうか?
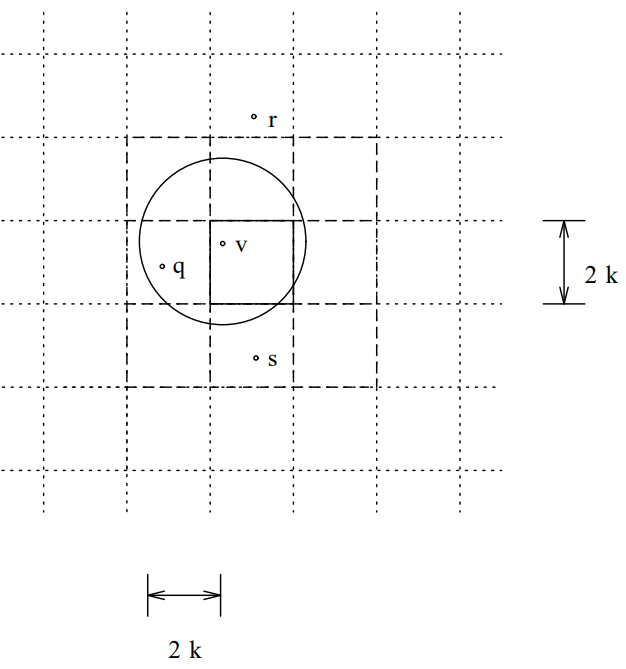
本論文では、前のセクションで説明した基本的なアルゴリズムと、以後 grid-variant と呼ぶアルゴリズムを適用した結果について述べる。これは互いに近接する頂点間の反発力のみを計算するために画面を正方形のグリッドに分割するようにアルゴリズムを書き直し、各反復において各頂点をそのグリッドの正方形に配置し、その頂点とグリッドの近接する正方形の頂点との間の反発力のみを計算する。引力は通常通り計算する。これはすべての頂点に反発力を適用するのとほぼ等価だが、次の方法で計算する: \[ f_r = \frac{k^2}{d} u (2k - d) \] ここで \[ u(x) = \left\{ \begin{array}{cl} 1 & \mbox{if $x \gt 0$} \\ 0 & \mbox{otherwise} \end{array} \right. \] 実際にはグリッドボックスの形状が正方形であるために歪みが生じ、すべての方向で落下距離 (fall-off distance) を同じにする必要があることに気づいた (反発力は該当地点の中心から半径 \(2k\) の円形領域内のすべての頂点から加えられる)。Figure 7 では、頂点 \(v\) は頂点 \(q\) から反発されるが、グリッドのすぐ隣の正方形の外にある \(r\) や、考慮されたが遠すぎて却下された \(s\) からは反発力を受けない。
フレームが幅 \(W\)、長さ \(L\) の場合、頂点あたりの面積は \[ A = \frac{WL}{|V|} \] であり \[ k = \sqrt{A} \] である。\(2k\) の距離を超えると頂点の反発を無視するため、\(2k\) はグリッドボックスの大きさの長さである。\[ \mbox{Number of grid boxes} = \frac{W}{2k} \frac{L}{2k} = WL \frac{|V|}{4WL} = \frac{|V|}{4} \] 大胆に頂点の分布がほぼ一様であると仮定すると反発力の計算は \(\Theta(|V|)\) となる。
焼きなまし法の重要な考慮点は温度 \(T\) に応じた冷却スケジュールを選択することであり、極小値を回避し、最適なレイアウトを見つける能力と、より迅速な終了の要求とのバランスを取ることである。焼きなまし法の温度に相当するのは反復中の拡張点の最大変位を制限し、その最大変位ごとに変更することである。
焼きなまし法に関する多くの研究はその高速化に重点が置かれており、より優れた、より一般的な冷却スケジュールの開発に多くの努力が費やされている。焼結法 (simulated sintering) 焼きなまし法の変種であり、焼きなまし法ではランダムな配置から妥当な配置に移行するのに無駄な労力を費やしているため、より計算効率の高い方法を適用して良好な初期配置を生成し、その後、低温での焼きなまし法を適用してより微妙な調整を行う方が良いという仮説に基づいている [14, 11]。実際、これは計算負荷の高い最終調整フェーズで Davidson とHarel が行ったことと似ている。Grover [14] が VLSI の初期レイアウトに提案しているのは Min-Cut Placement [15] である。初期レイアウトを迅速に生成するためのもう一つの選択肢は焼き入れ (quenching) であり、焼きなまし法を数回繰り返して急速に冷却を行うものである。我々のシステムを概念的に単純化するために焼結法に似た処理を行うが、別のアルゴリズムの導入を避けるために焼き入れに力学指向類推 (force-directed analogy) を使用する。
我々はいくつかの主観的な実験を実施して異なる冷却スケジュールで異なるグラフを描画し、異なる反復回数を使用した結果を比較した。主に「急冷」と「煮沸」の組み合わせで温度の定常的な低下を比較した。最初の段階は高温で始まり定常的かつ急速に冷却され、二番目の段階は一定の温度である。後者のスケジュールによる結果はより良く必要な反復回数も少なくなった。
 時間複雑性
時間複雑性
我々のアルゴリズムを導入するにあたり、基本アルゴリズムの個々の反復の時間複雑性が \(\Theta(|V|^2+|E|)\) であることを示し、グリッドの変種では \(\Theta(|V|+|E|)\) であることを提案したが、グラフを魅力的にレイアウトするために必要な反復の回数はいったい何回だろうか。アルゴリズムがいつ終了するかを説明しようとするとき、文献にはその場限りの議論がたくさんある。Eades は "シミュレーションステップを 100 回実行するとほぼすべてのグラフが最小エネルギー状態に達する…" と単純に主張している。Davidson と Harel、および Kamada と Kawai は状態エネルギーの明示的な表現に基づいて終了条件を設定したが、これらの条件がどのように満たされるかについてはほとんど分析できていない。実際、Kamada と Kawai は時間複雑性分析を行う際に最も外側のループに反復回数を含めていなかった! 我々も反復回数を \(|V|\) や \(|E|\) の関数にする実験を行って、それを正当化することはほとんどできなかったが、我々は Davidson と Harel 同様により良い冷却スケジュールを選択することで劇的な違いが生まれるのではないかと考え、これについては前に議論した。
このアルゴリズムは、エネルギーがしきい値に達し、グラフがおそらく最終的な状態になったときに終了するという意識的な状態エネルギーの概念を適用していた。対照的に、我々のアルゴリズムの終了は Eades の場合と同様、推測に基づいている。ただしレイアウトが「中途半端」な状態になった場合、プログラムの中間出力を保存して初期構成として使用し、さらに煮沸してレイアウトを修正することで最初から始めるよりも少ないコストでレイアウトを修正できる。また中間レイアウトを保存することで、すでにレイアウトされているグラフに辺や頂点を追加するなど、他の形のインクリメンタルなレイアウトが容易になる。
 実装
実装
我々は "トリックの詰め合わせ" ではなくシンプルで一貫した方法を望んでいた。たとえば効率的であっても平面性テスト (planarity testing) や平面化 (planarization) は避けた。また我々は焼きなまし法などの遅くて複座砂手法を避け、適度な大きさのグラフであれば対話的に行えるような十分な速度の実装を心がけた。
我々は様々な力学のモデルを簡単にテストできるように柔軟な実験フレームワークを構築した。加算、減算、乗算、除算、mod、log、平方根、指数、および単位ステップ関数を用いて awk に似た構文 [16] を使用して任意の複雑な関数を指定できた。
我々はアルゴリズムを C [17, 18] で実装した。速度を上げるために整数演算を使用することを早い段階で決定した。これには、優位性を保つために式を慎重に順序づける必要がしばしばあったが、それは功を奏した。Jon Bentley [6] の助言に従い平方根などのコストのかかる演算を最小限に抑えた。平方根の代わりに二乗が使われることも多い。実験には、力学やその他のパラメータを指定するための "小さな言語" が役に立った。多くのアイディアがこの方法で評価され、その価値が証明されればハードコードされた (グリッド近似や焼結など)。
レイアウトプログラムにはいくつかのバリエーションがある。基本的なバージョンは我々のレイアウトアルゴリズムと自然の力との類似性から Nature と呼ばれている。Nature3d と呼ばれる 3 次元のレイアウトを行うものもあり、\(O(|V|)\) の内部ループを実装したものは Naturev と呼ばれている。3 つともテキスト入力を受け取りテキスト出力を生成する。入力ファイルの形式は出力ファイルの形式と同じだが、入力に必ずしも頂点の座標が含まれるわけではない。存在する場合は、それらは初期構成を指定するが、そうでなければ頂点はランダムに配置される。したがって Nature を 1 回通過しても満足の行くレイアウトが得られなければグラフを再提出することができる。両者の違いは異なるオブジェクトファイルへのリンクの問題である。
 拡張の例 - 五角柱
拡張の例 - 五角柱
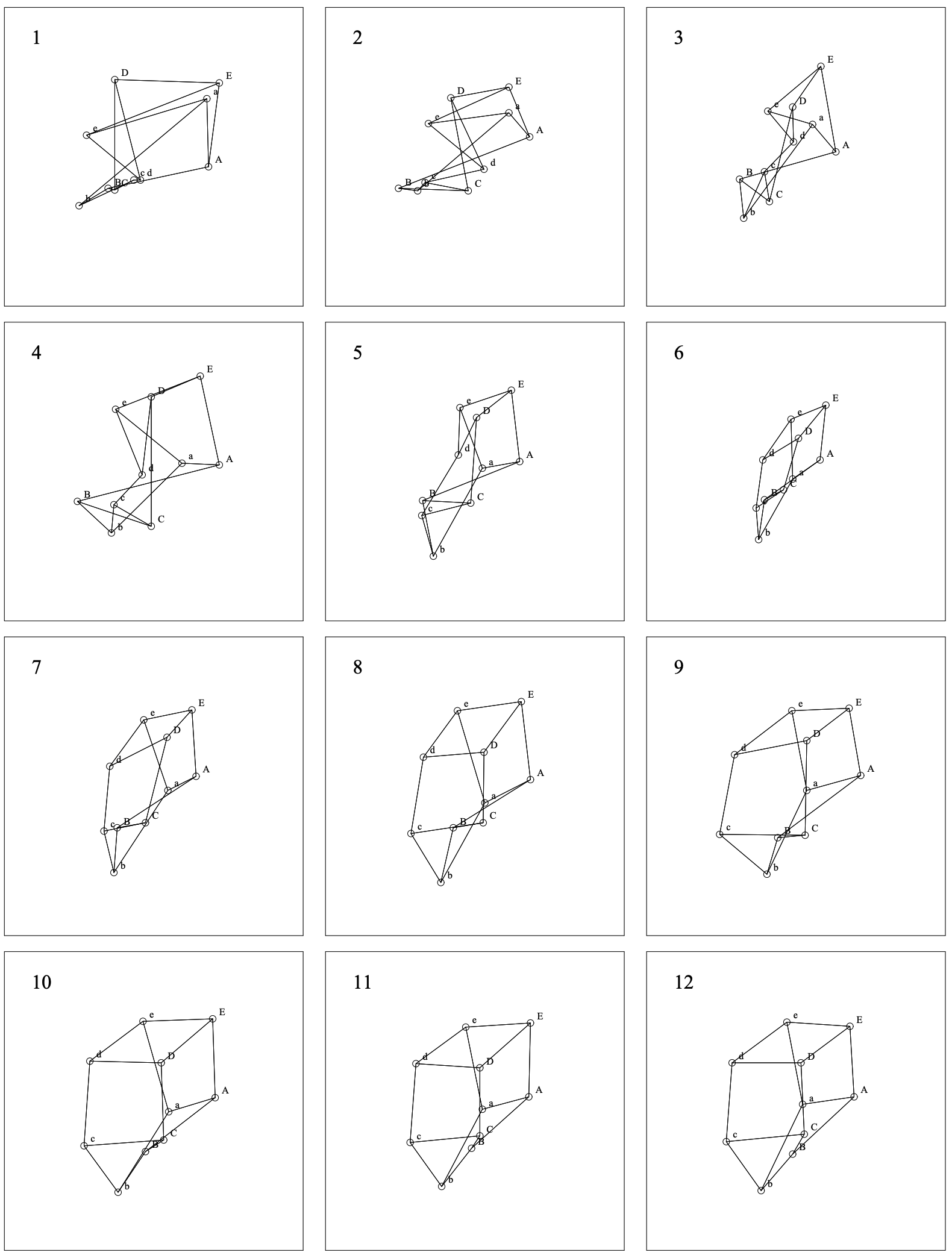
実際のアルゴリズムを示すために Figure 8 と Figure 9 に五角柱をレイアウトするステップを示す。最初のフレームにはランダムな初期位置にあるすべての頂点が表示されている。最初の 12 フレームは焼き入れを、後の 12 フレームは煮沸を示している。この論文の図に枠がある場合、それは境界が我々のアルゴリズムの一部であることを表している。他のほとんどの図には枠がないが、これはフィルターによって拡大縮小されていることを意味する。
 対称グラフ
対称グラフ
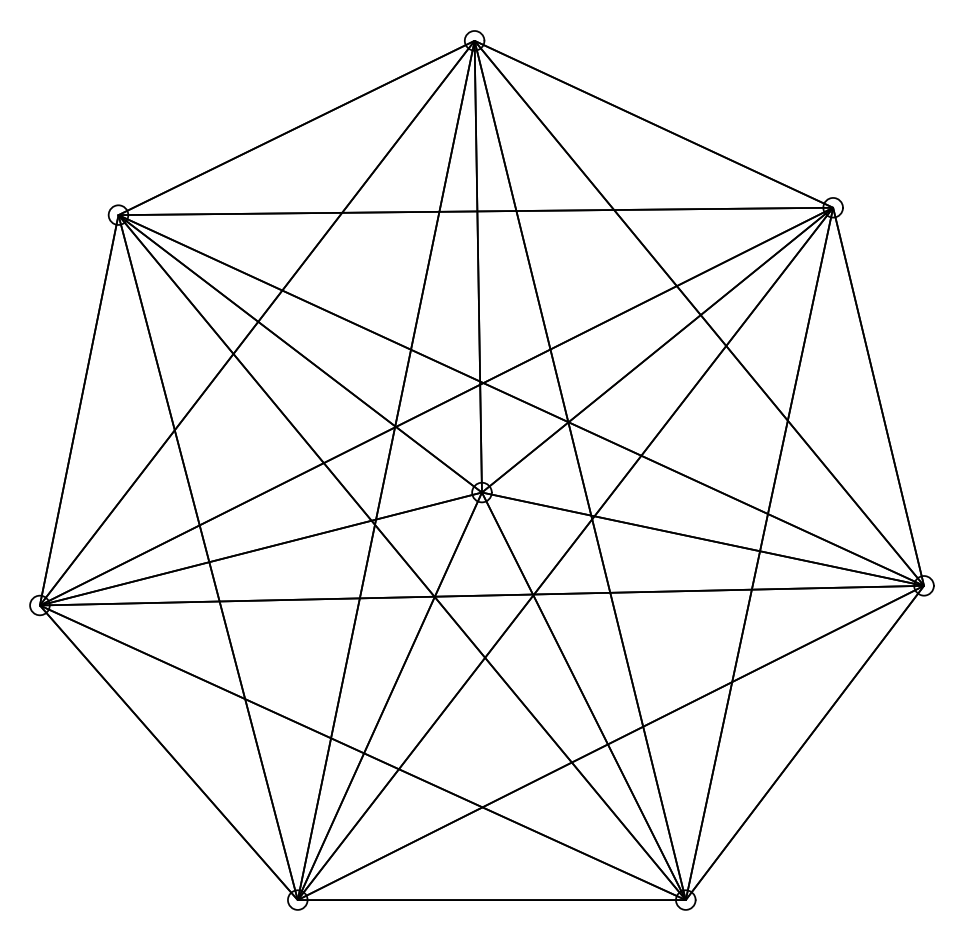
我々のアルゴリズムから得られる最も自然で好ましい結果は、根底にある力学法則のパラダイムが最も明らかとあんる、対称性の高いグラフから得られるものだろう。グラフレイアウトに関する論文でよく使われるグラフの 1 つが \(K_5\) (Figure 10) である。我々の形式では、元の論文の図番号と引用を示すことによって図のキャプション内のすべてのグラフを識別する。これらは引用された論文に掲載されているとおりにそれらの図を複製したものである。前者のキャプションは引用した論文で議論されているアルゴリズムによって生成された表現を識別するものであり、後者は単に著者によって提案されただけのものでそのアルゴリズムによって生成されたものではない。
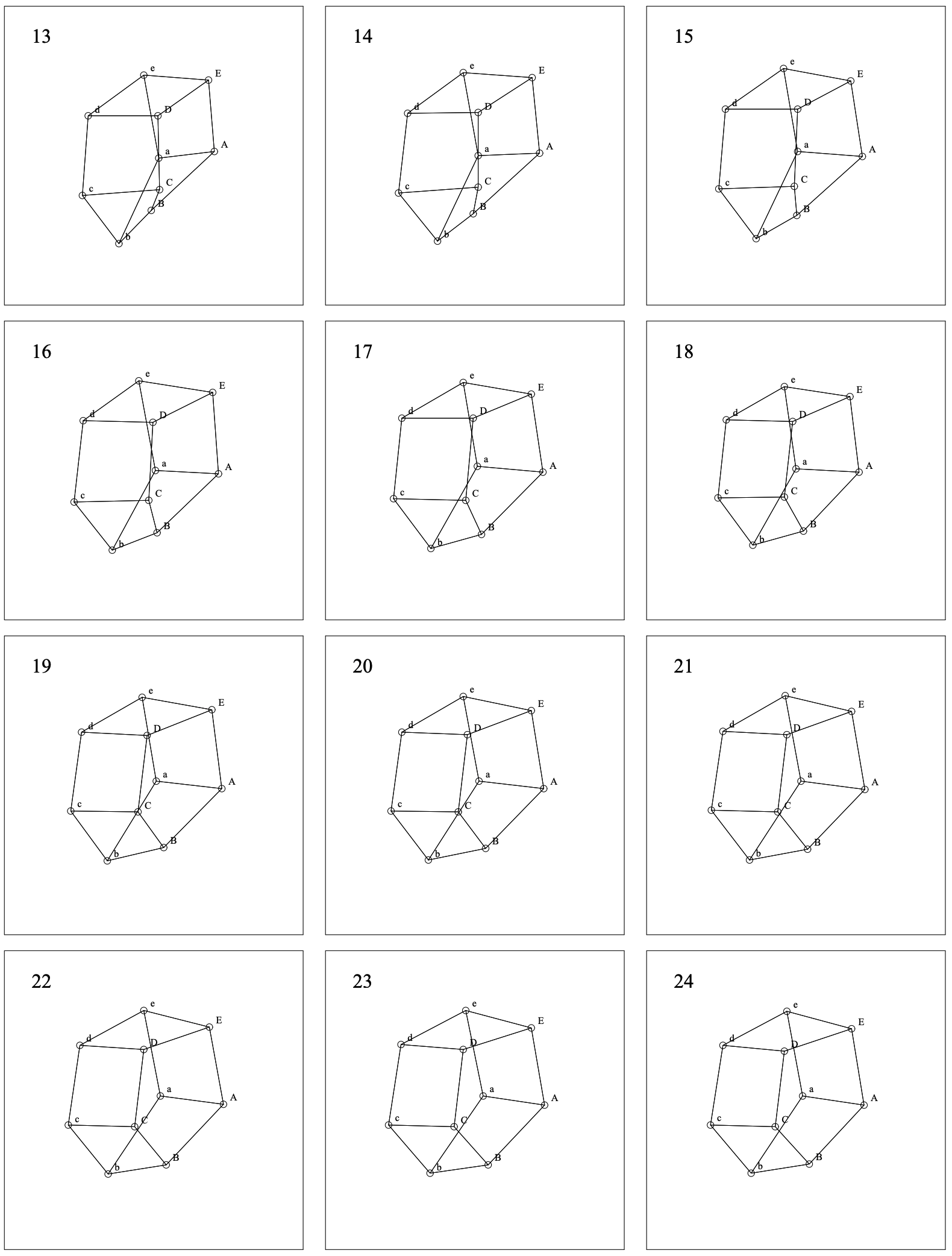
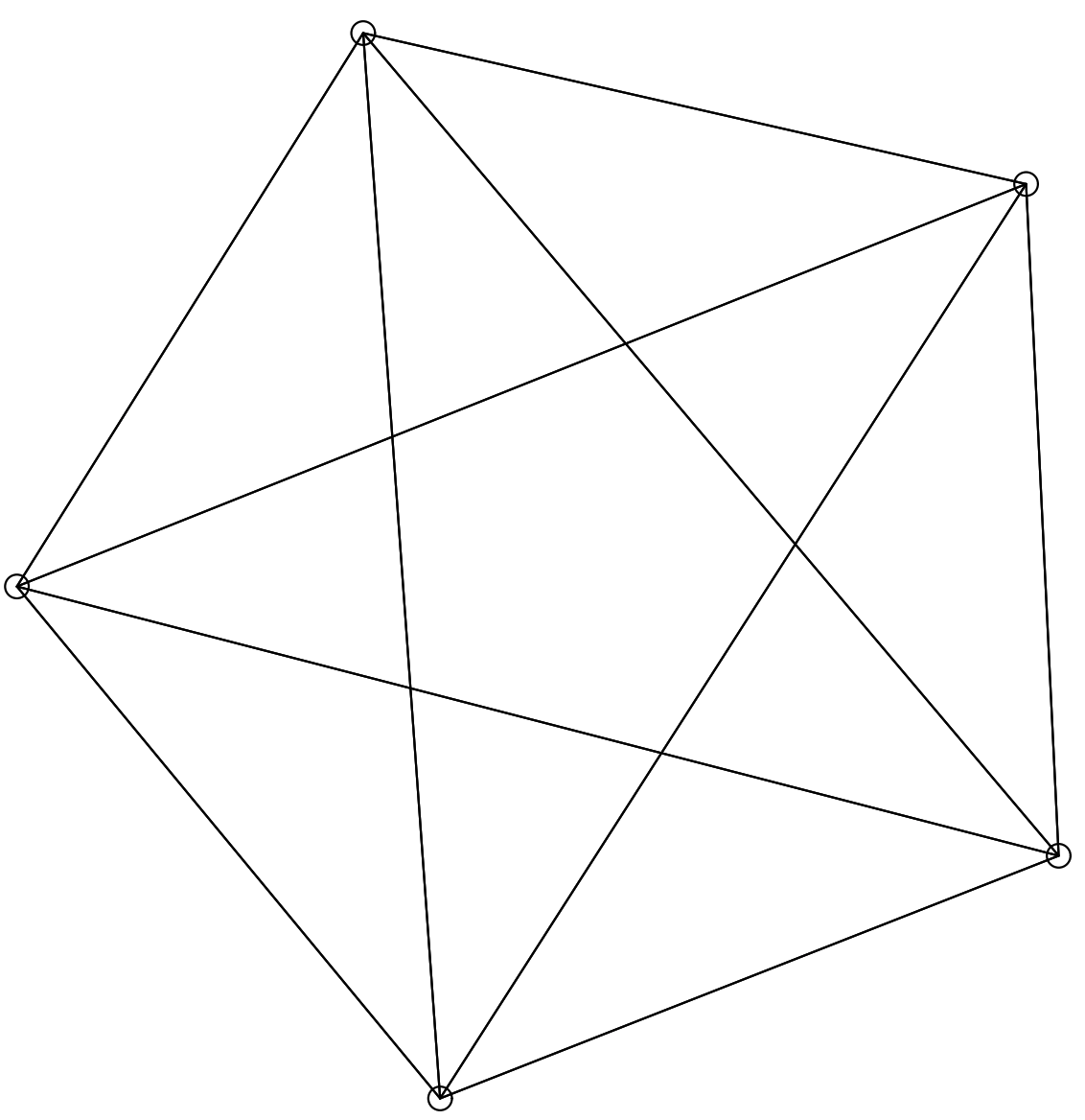
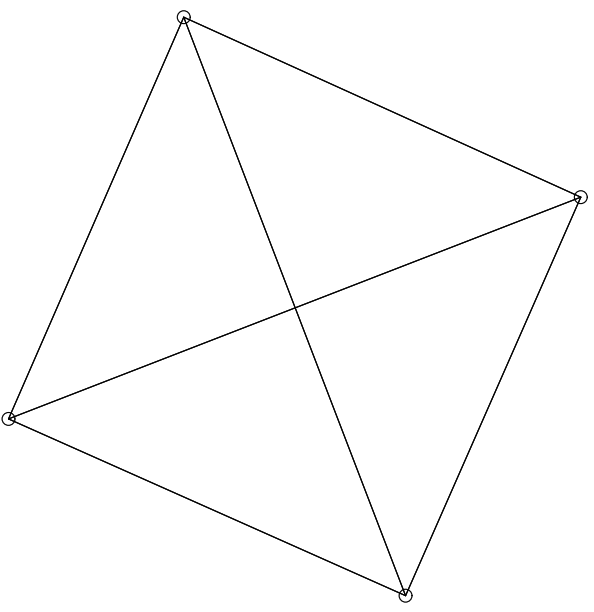
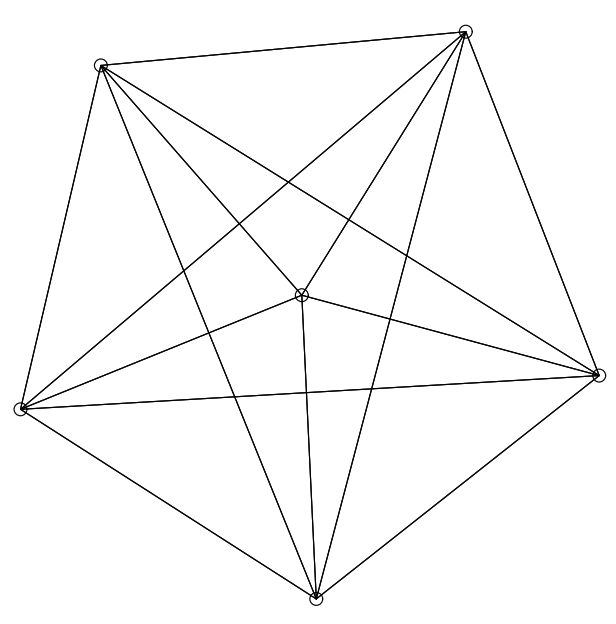
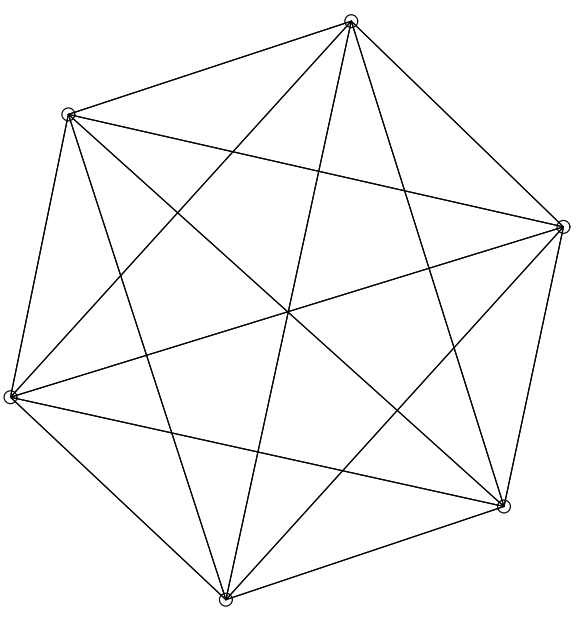
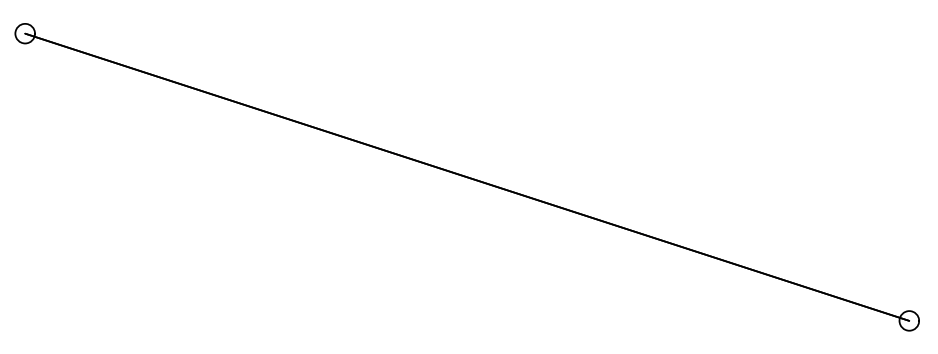
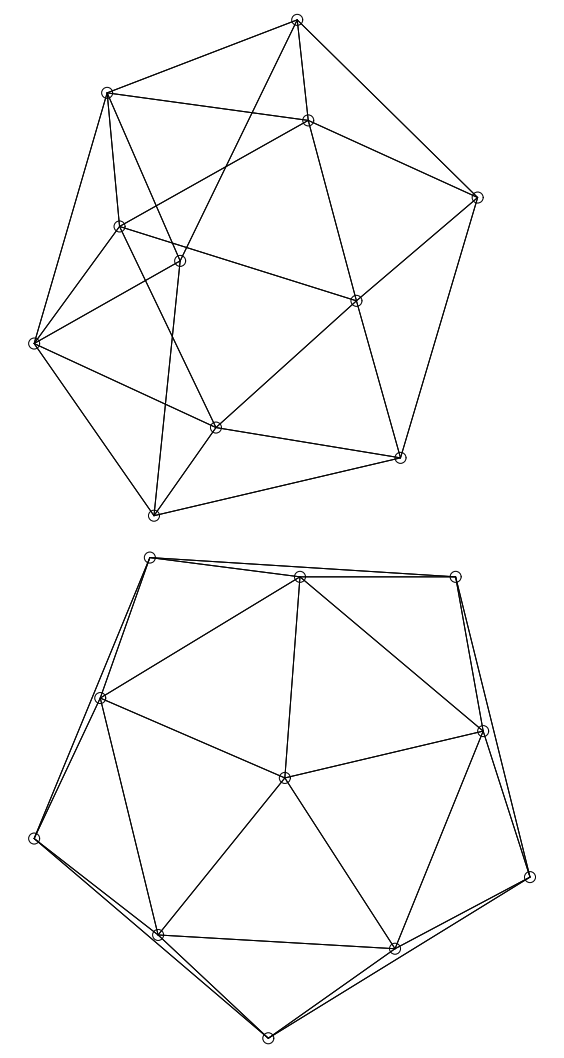
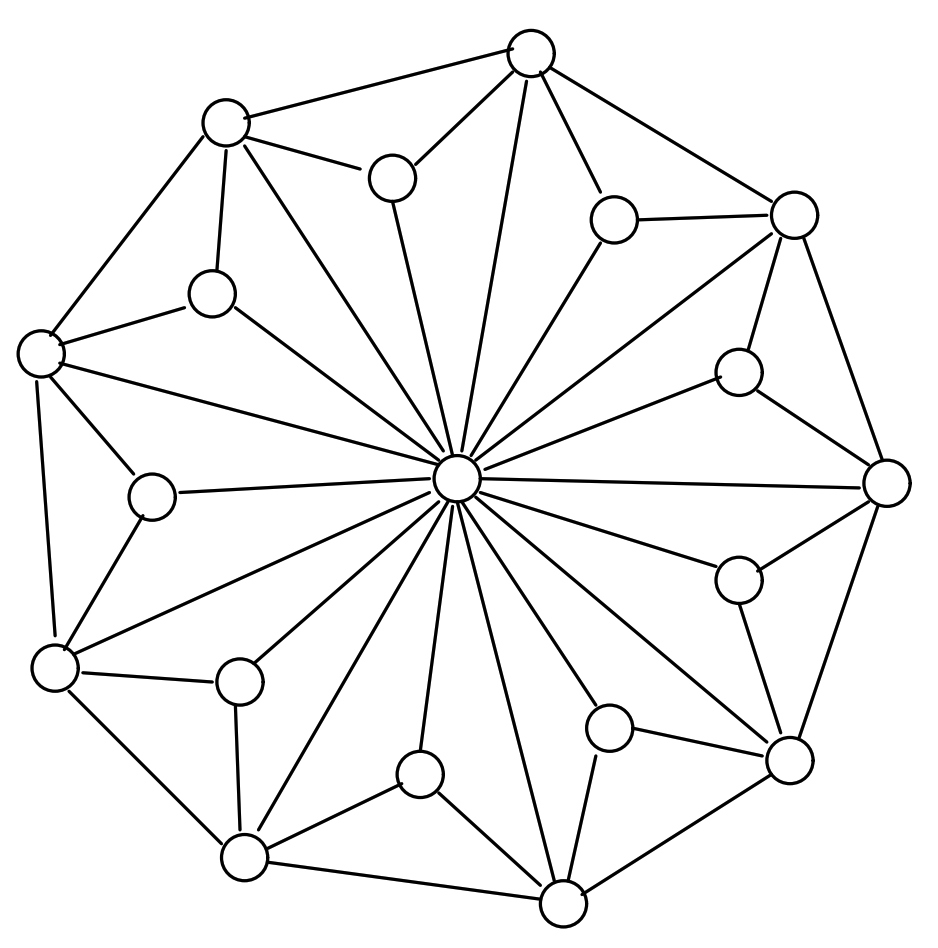
\(K_5\) と他の完全ブラフ \(K_4\) (Figure 11)、\(K_6\) (Figure 12 と Figure 13)、\(K_8\) (Figure 14) は平衡状態における引力と反発力のバランスを示している。\(K_4\) は平面的 (planar; 辺が交差していないグラフ) だがそう表現されていないことに注意。平面表現には歪曲した辺が必要だが、おそらくここで生成される表現ほど人間にとって自然でない。完全グラフは次数が高くなるほど小さくなり、辺の密度が高くなるほど平衡に達する距離が短くなる。頂点間の理想的な距離の計算は、\(K_2\) Figure 15 の単純なケースでのみ理想的に説明したとおりに機能するが、すべての図は拡大フィルターを通しているためすべてほぼ同じサイズとなっている。単純な平面、またはほぼ平面の対称グラフの例では、Figure 16 の 3 つと、最初に Kamada と Kawai [7] で登場した Figure 17、Davidson と Harel [9] で登場した Figure 18 の 1 つが挙げられる。Kamada と Kawai が提示したグラフは特に簡単で、我々のレンダリングは本質的に彼らのものと同じである。
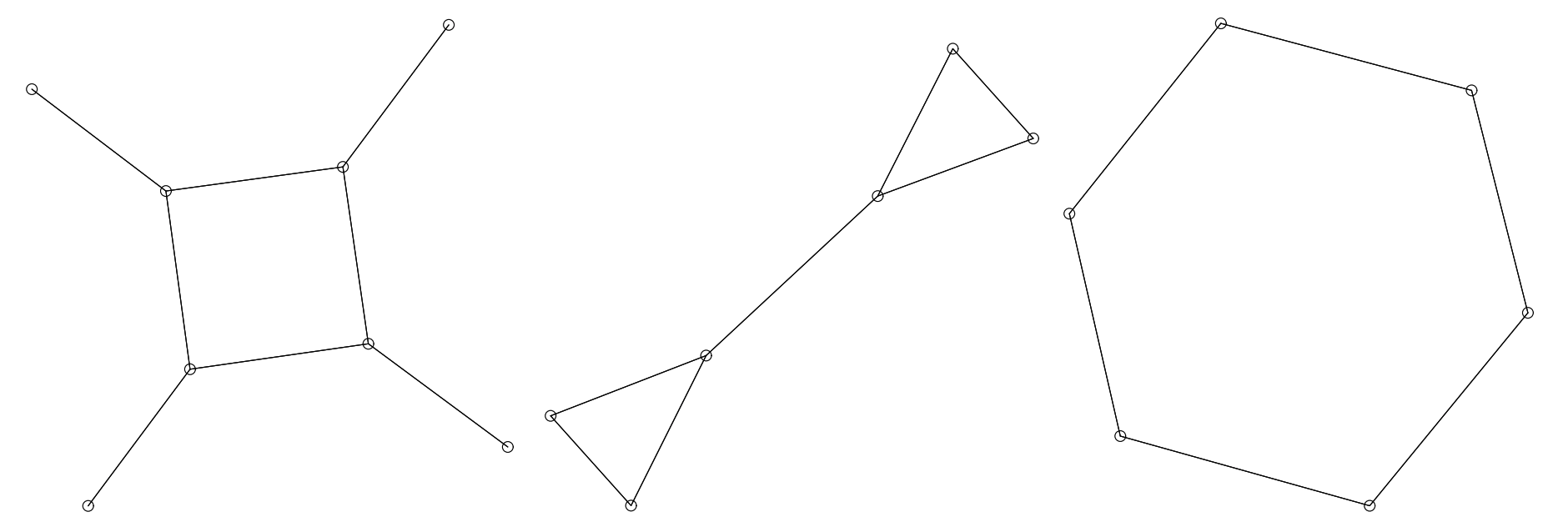
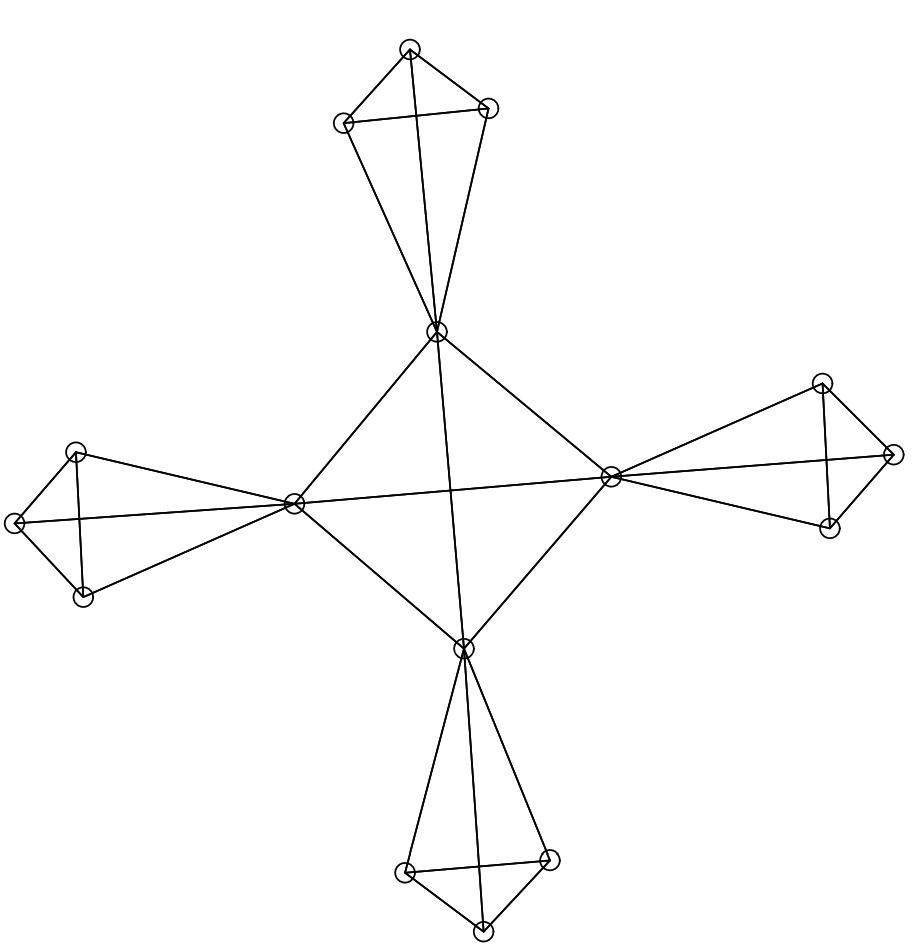
もう一つの対称性の高いグラフは \(K_{3,3}\) である (Figure 19 と Figure 20)。最初の表現は許容できるものではあるが、対称性の次元が一つ欠けているためおそらく他のものほどよくはない。Heywood グラフ (Figure 21) は Davidson と Harel から引用されたものだが、彼らのアルゴリズムではこれは達成されていない。彼らのレイアウトは Figure 22 である。それでもおそらく我々の Figure 12 よりは望ましい。両方の手法が失敗するのはおそらく対称レンダリングが近傍間に長い距離を必要とするからであろう。
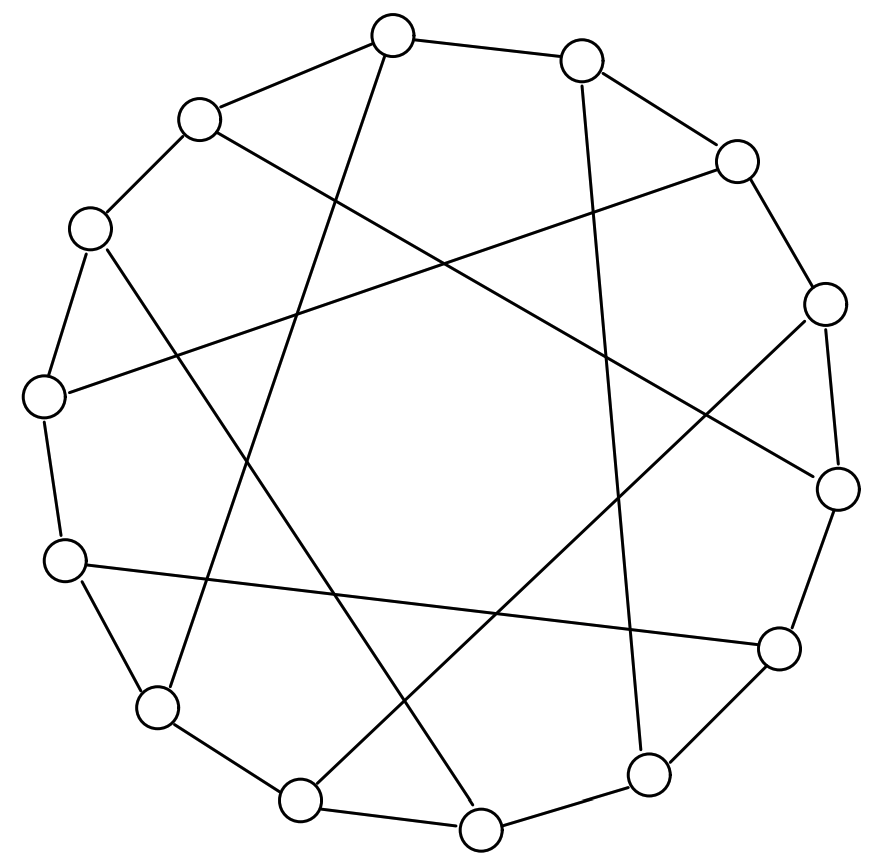
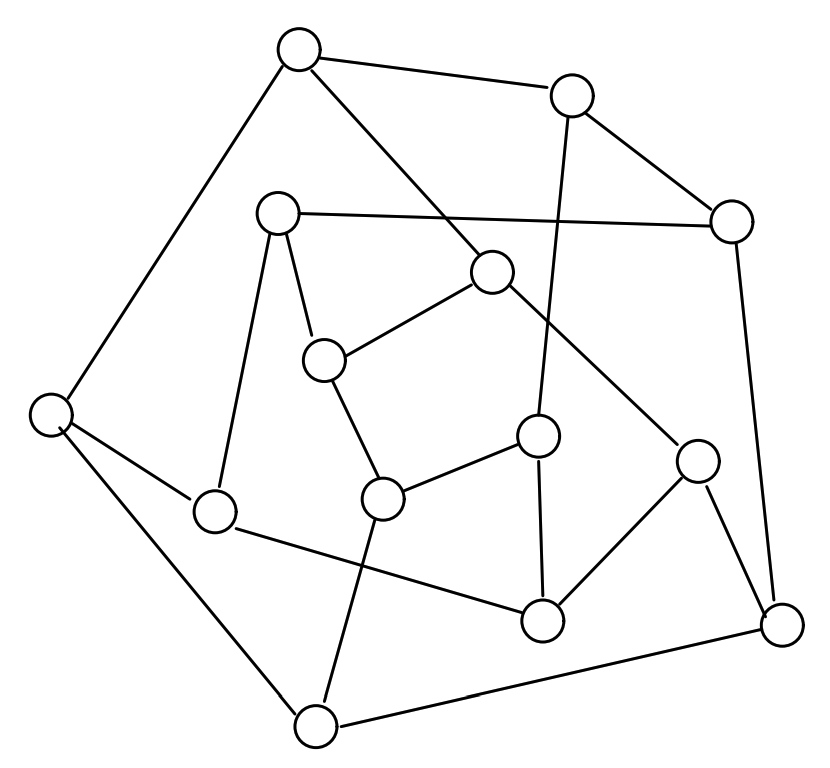
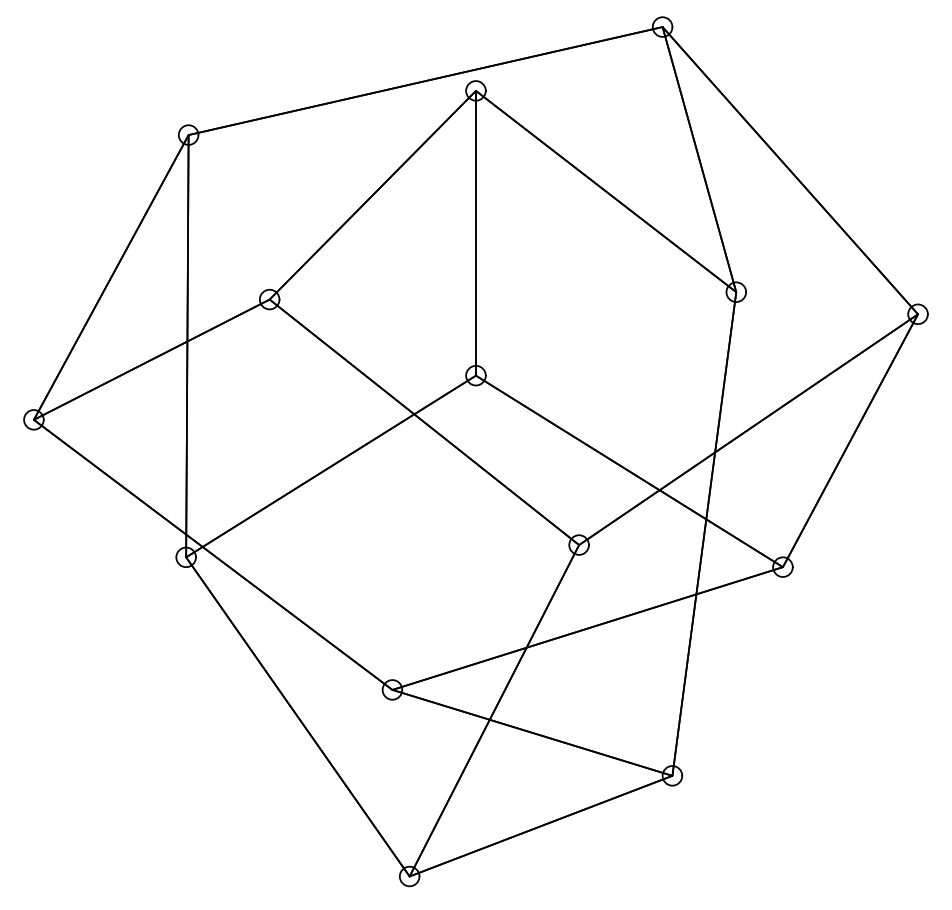
我々のアルゴリズムが対称グラフで遭遇する他の問題は、Davidson と Harel [9] の最初の図である Figure 24 に示されている。オリジナルの図 Figure 25 は問題をもう少し明確にしている。このグラフは平面であり、Davidson と Harel は平面的表現を生成したが、内側の頂点からの反発力によってより魅力的で安定した構成を達成することができない。
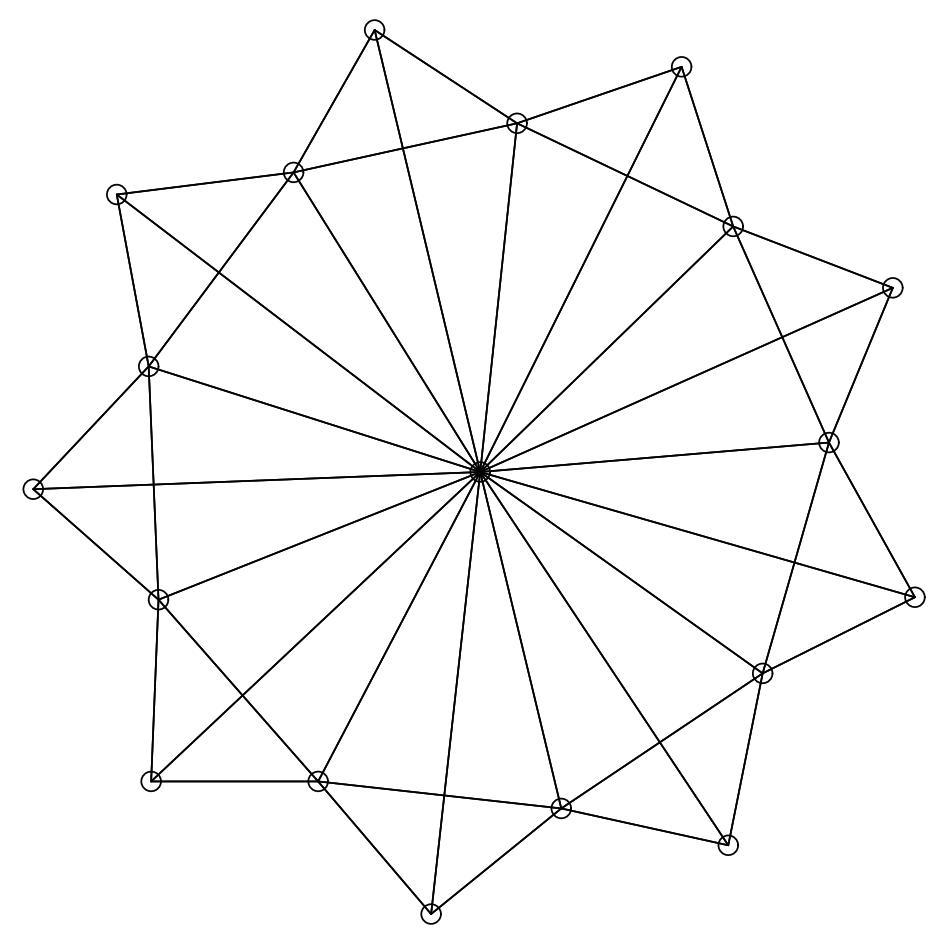
Davidson と Harel の論文の目玉は Figure 26 である。我々の表現である Figure 27 にはある点で欠陥がある。Davidson と Harel はグラフを完全に平面にするために、2 つの隣接する頂点の間に最も外側の頂点 \(p\), \(q\), \(n\), \(o\) を描画した。比較として、Davidson と Harel が提供する時間複雑性の公式を使用すると彼らのこの図を生成するのに 10 分かかるが、我々のアルゴリズムは同等のマシンで 30 秒である。
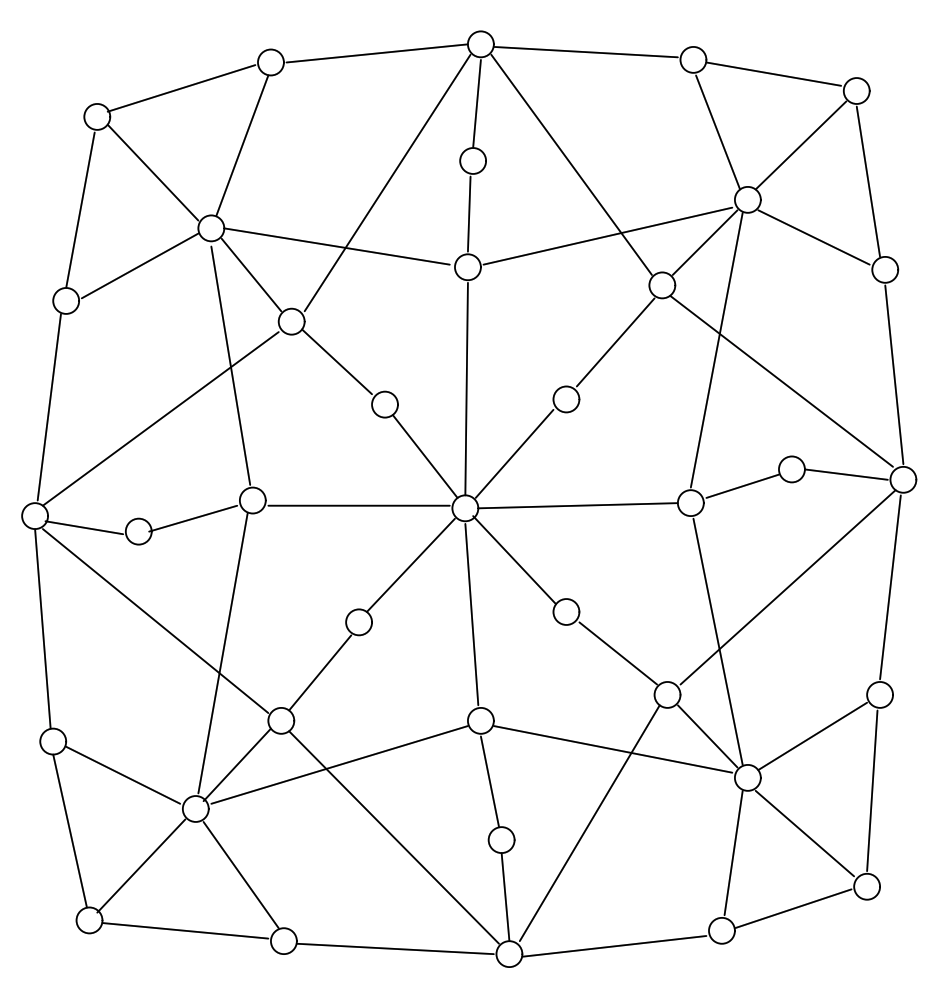
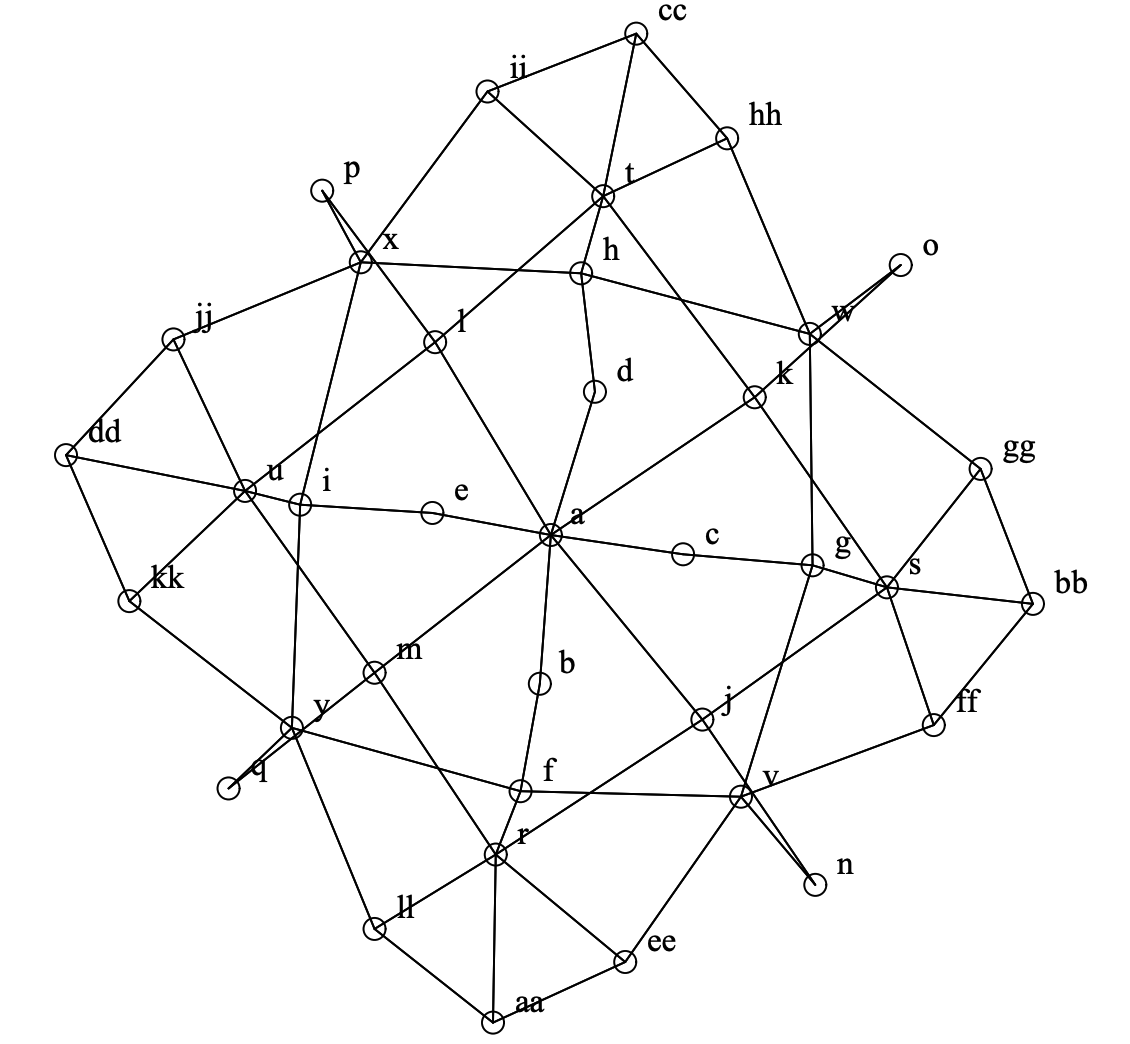
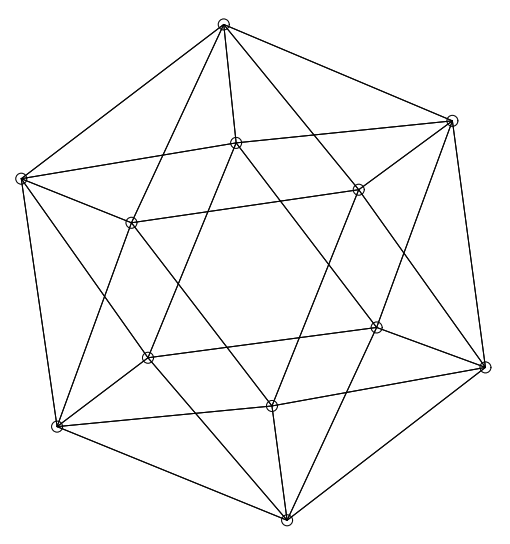
Figure 28 は 1 つの入射辺を欠いた正二十面体の 2 つの異なるレイアウトを表している。最初のレイアウトは正二十面体の伝統的な立体表現に似ている (ただしある頂点を欠いている)。もう一つのレイアウトは平面だが、一部の辺が見にくくなっている。これまで論議してきたすべての方法のうち Davidson と Harel の焼きなまし法だけが、頂点が辺で隠れることを明確に避けようとしている。Figure 29 は正二十面体である。平面ではないが (正二十面体は平面である) レイアウトは非常に魅力的である。
 平面的グラフ
平面的グラフ
このセクションでは他の論文から我々が描きやすいと思った非対称の図をいくつか作成する。これらのグラフはほぼ平面である。各図のレイアウトはグラフの出典として引用した論文のレイアウトとほぼ同じである。
Kamada と Kawai は、Figure 36 と Figure 37 のような同型グラフは (回転と反射により) 同一のレイアウトを持つ一方で、Figure 38 と Figure 39 のように類似しているが同型ではないグラフは似ているが異なるレイアウトになることを示した。我々の結果はこれと一致している。
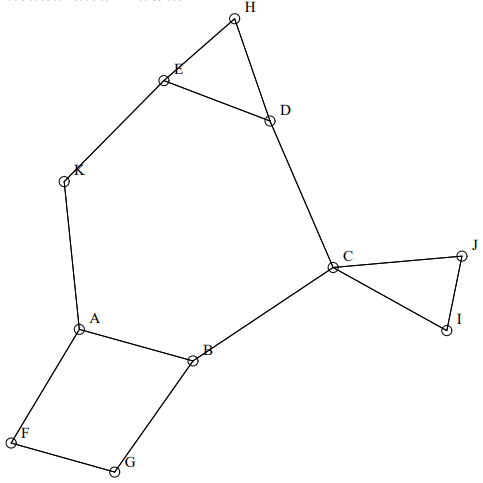
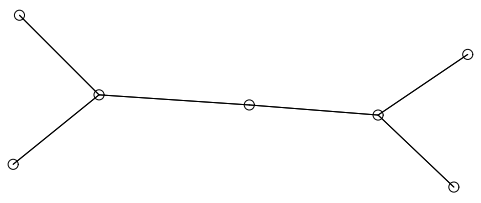
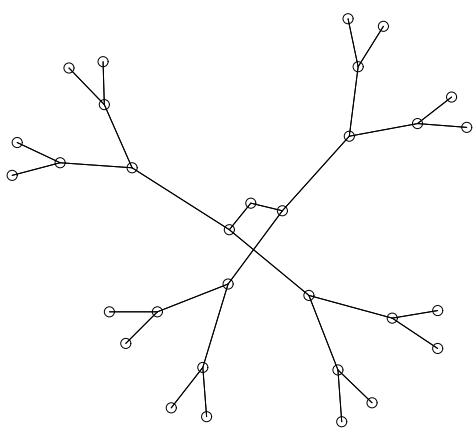
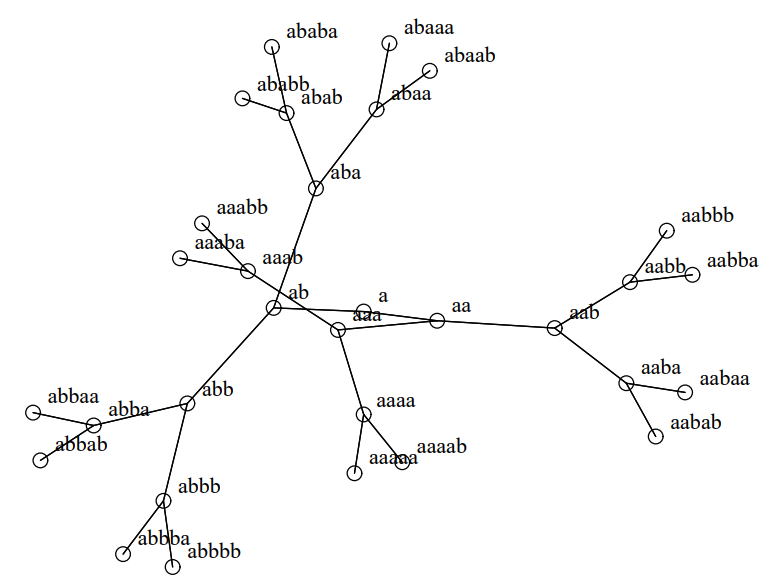
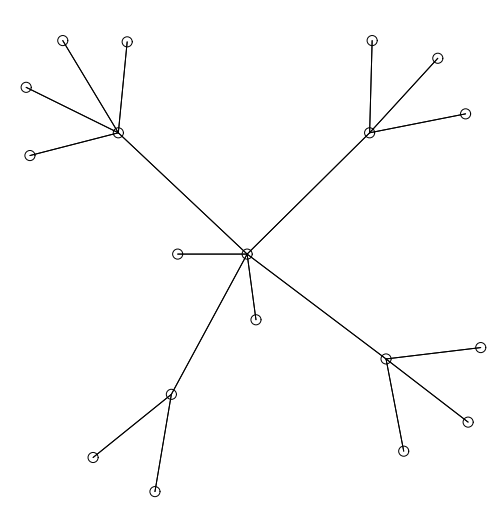
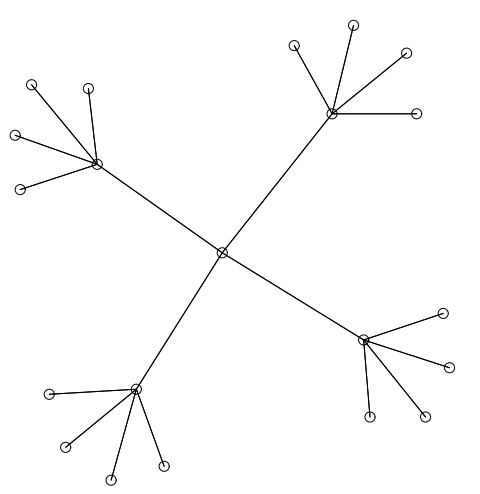
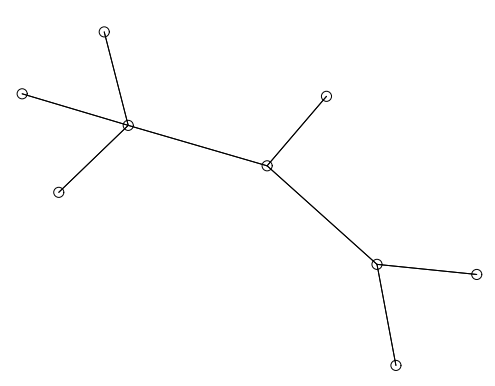
単純な二分木を Figure 40 に示す。他の多くのアルゴリズムがそうであるように、我々のアルゴリズムも根から放射線状に広がるように木を描画する。辺の交差に直接ペナルティを与えない我々のアルゴリズムの問題点のいくつかを Figure 41 に示す。ここでフレーム内の頂点を詰め込んでいるため第 2 レベルの子が互いに交差する。我々のアルゴリズムの初期の実装でも同様の問題が発生したが、より深刻な程度は Figure 42 に示すブロッキングの影響だった。頂点 \(aaab\), \(aaaba\), \(aaabb\) は祖先 \(aaa\) に引き寄せられるが、頂点 \(ab\) と \(aba\) によってもたらされるポテンシャル障壁を乗り越えることができない。我々はこのようなブロックする力が克服される方法を示唆するような自然界における類似性を見つけようとした。電子による量子ジャンプが思い浮かんだが、この問題を解決するために使用したヒューリスティックは 5 回の反復ごとに反発力をオフにするというものだった。このヒューリスティックは役に立つが、Figure 41 のような多数の頂点を含む問題を克服することはできない。グラフ全体を移動できるマルチグリッド技術を適用すれば何らかの助けになるかも知れないが、その手法は焼きなまし手法などの最適化アルゴリズムに適しているかも知れない。
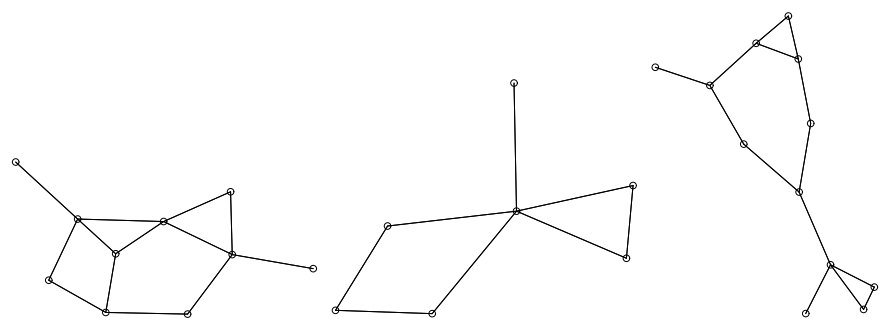
さらに、Figure 43, Figure 44, Figure 45, Figure 46 は一部は二分木ではない 4 つのツリーの例である。後者の 2 つについては根がどこにあるか分らない。実際、現在の実装では辺の方向が示されていないため、これらは実際には木ではなく回路のない無向平面グラフである。そして他の例ではどの頂点が根であるかが分っていると思い込んでいた。
 LAYOUTS THAT APPEAR TO BE THREE-DIMENSIONAL
LAYOUTS THAT APPEAR TO BE THREE-DIMENSIONAL
 THREE-DIMENSIONAL LAYOUT
THREE-DIMENSIONAL LAYOUT
 GRID VARIANT
GRID VARIANT
 考察
考察
我々のアルゴリズムの第一の利点は速度である。多くのグラフは 1 秒未満で描画され、SPARC ステーション 1 ではすべて 10 秒未満で描画された。我々はこれを "対話的" 速度であると考える。
Davidson と Harel のアルゴリズムは、より複雑なグラフに対してわずかに高いレベルの美しさと柔軟性を達成できるようである。おそらく 3 次元のバリアントを使用してグラフをレイアウトし、グリッドやマルチレベルのアプローチを使用することも可能だろうが、その場合、より複雑な実装に直面し実行時間に大きなペナルティが発生する。
主な目標はユーザがオプションをいじったり、力学の法則を変更したり、反復回数を増やしたり、\(\Theta(|V|)\) または 3 次元のバリアントに切り替えたりすることなく、アルゴリズムがほぼ常にうまく機能することであった。エネルギーに関する明確な概念がなく、停止条件を検出できなかったため、単純に毎回 50 回の反復を使用した。これは単純なグラフでは過剰だったが、小さなグラフではどのような場合でも 1 回の反復にかかる時間が短く、アルゴリズムが非常に高速であるため問題にはならなかった。
 REFERENCES
REFERENCES
- P. Eades, “A heuristic for graph drawing,” Congressus Numerantium, 42, 149–160 (1984).
- F. Harary, Graph Theory Addison–Wesley, Reading, MA, 1969.
- P. Eades and R. Tamassia, “Algorithms for drawing graphs: an annotated bibliography,” Technical Report CS-89-09, University of Queensland, October 1989.
- N. Quinn and M. Breur. “A force directed component placement procedure for printed circuit boards,” IEEE Transactions on Circuits and Systems, CAS-26, (6), 377–388 (1979).
- P. A. Tipler, Physics, 2nd Edition, Worth Publishers, New York, NY, 1982.
- J. Bentley, Programming Pearls, Addison–Wesley, Reading, MA, 1986.
- T. Kamada and S. Kawai, “Automatic display of network structures for human understanding,” Technical Report 88-007, Department of Information Science, Tokyo University, February 1988.
- T. Kamada and S. Kawai, “An algorithm for drawing general undirected graphs,” Information Processing Letters, 31, (1), 7–15 (1989).
- R. Davidson and D. Harel, “Drawing graphs nicely using simulated annealing,” submitted for publication, July 1989.
- S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi, “Optimization by simulated annealing,” Science, 220, (4598), 671–680 (1983).
- R. Otten and L. van Ginneken, The Annealing Algorithm, Kluwer Academic Publishers, Boston, MA, 1989.
- D. Hearn and M. P. Baker, Computer Graphics, Prentice–Hall, Englewood Cliffs, NJ, 1986.
- A. Appel, “An efficient algorithm for many–body simulations,” SIAM Journal on Scientific and Statistical Computing, 6, (1), 85–103 (1985).
- L. K. Grover, “Standard cell placement using simulated sintering,” Proceedings 24th Design Automation Conference, 56–59 (1987).
- M. A. Breuer, “Min-cut placement,” Journal of Design Automation and Fault Tolerant Computing, 1, (4). 343–382 (1977).
- B. W. Kernighan, A. V. Aho, and P. J. Weinberger, The AWK Programming Language, Addison–Wesley, Reading, MA, 1989.
- B. Stoustrup, The C++ Programming Language, Addison–Wesley, Reading, MA, 1986.
- S. C. Dewhurst and K. T. Stark, Programming in C++, Prentice–Hall, Englewood Cliffs, NJ, 1989.
- T. Kamada and S. Kawai, “A Simple Method for Computing General Position in Displaying Three–Dimensional Objects,” Computer Vision, Graphics, and Image Processing, 41, 43–56 (1988).
翻訳抄
Force-Directed Placement を用いてノード間の引力と反発力を調整してグラフ構造を 2 次元上に均等に配置する手法を提案している 1991 年の論文。Fruchterman-Reingold アルゴリズムとも呼ばれる。
- FRUCHTERMAN, Thomas MJ; REINGOLD, Edward M. Graph drawing by force‐directed placement. Software: Practice and experience, 1991, 21.11: 1129-1164.