情報検索
\( \def\vector#1{\boldsymbol{#1}} \)

全文検索

Takami Torao
  • このエントリーをはてなブックマークに追加

概要

全文検索 (full-text search) はテキストデータベースや文書集合として存在する構造化されていないテキストから特定の単語やフレーズを検索し、その出現位置や関連する文書を取得するための検索技術である。単純なキーワード検索と異なり、ランキング付けや表記揺れを考慮した検索によってよりユーザの目的に近い検索結果を提供する。

テキストの先頭から末尾までを単純にスキャンしてキーワードやパターンに一致する位置をすべて見つけ出す方法を逐次検索 (sequential search) と呼ぶ。ただし、逐次検索は非常に遅く大規模な文書集合に対しては実用的ではない。一般的な全文検索エンジンは非構造化テキストから構造化されたインデックスを作成し索引検索 (index search) を行うことで大規模な文書集合に対しても効率的に検索を行うことができる。

Table of Contents

  1. 概要
  2. テキスト解析
    1. トークン化
      1. 形態素解析
      2. N-gram
    2. 正規化
    3. ストップワード
  3. インデックス作成
  4. 検索
    1. AND 検索
    2. OR 検索
    3. フレーズ検索
  5. ランキング付きの検索
    1. 類似度を使用したランキング
      1. TF-IDF
      2. コサイン類似度
      3. ランキング OR 検索
    2. 機械学習によるランキング
    3. 近接度によるランキング
  6. 参考文献

テキスト解析

全文検索におけるテキスト解析 (text analysis) は文書を効率的に検索できるようにテキストを構造化する。インデックス (索引) を作成するための前処理である。

トークン化

トークン化 (tokenization) は文書を検索対象となる単位のトークン (token) に分割するテキスト解析の最初のステップである。トークンかを行う処理をトークナイザー (tokenizer) と呼ぶ。

トークン化の方法は言語や用途によって異なる。例えば英語では単純に空白文字を区切り文字として利用できる一方で、単語の区切りの曖昧な日本語では一般に MeCab, Kuromoji, ChaSen といった形態素解析器や N-gram を利用する。

形態素解析

形態素解析は辞書を用いて単語の活用形や品詞などからトークンの区切りを推定する。IPAdic は MeCab や Kuromoji などで広く使われている形態素解析に利用可能な辞書であり、他にも Juman, UniDic などの辞書が利用できる。

例えば「東京都知事選挙」を形態素解析すると「東京」「都知事」「選挙」の 3 つのトークンに分割される。形態素解析器は文書の意味を理解するために重要な情報を提供するが、辞書に登録されていない単語や造語に対しては適切な解析ができないという欠点がある。形態素解析を使用する場合、新しい言葉に対応するために継続的な辞書のメンテナンスが必要である。

N-gram

N-gram は文章を \(N\) 文字ごとに区切りトークン化する手法である。\(N=1\) の場合を unigram (ユニグラム)、\(N=2\) を bigram (バイグラム)、\(N=3\) を trigram (トライグラム) などと呼ぶ。N-gram は OCR で読み込んだようなノイズの多い文章や、形態素解析器が利用できない未知の言語の文章をトークン化するのに適している。

例えば「東京都知事選挙」を 2-gram でトークン化すると「東京」「京都」「都知」「知事」「事選」「選挙」となる。N-gram を使った全文検索は形態素解析と比べて精度が低い反面、辞書を使用しないため新しい単語や造語、業界特有の言い回しなどにも適応できる利点がある。

正規化

トークン化された文字列は活用や表記などの表現上の変化を含んでいるため、それらが検索時に意味的に同じ言葉として正しくヒットするように一貫した形式に変換する必要がある。

ここでは正規化されたトークンのことをターム (term) と呼ぶ。正規化されたタームの集合を bag-of-words (BoW) と呼ぶ。

N-gram によって切り出されたトークンは意味づけされていないためいくつかの正規化手法は難しい。

ストップワード

一般的でどのような文章にも含まれる助詞や冠詞などのタームは検索時にノイズとして作用することが多く、またインデックスを肥大化する要因にもなる。そのようなタームをインデックスに含めない (検索対象外とする) ために指定するタームの集合をストップワード (stop word) と呼ぶ。例えば「は」「が」「the」「is/are」などのタームはストップワードに含まれることが多い。

ただし、最近の検索エンジンではインデックス時にはストップワードの除外処理を行わず、検索時に選択的にストップワードを除外する使い方が多くなっている [2]。

インデックス作成

全文検索の基本的なアルゴリズムは転置インデックス (inverted index) と呼ばれるデータ構造を用いる。このデータ構造は事実上すべての情報検索システムが中核に採用している [1]。転置インデックスは、文書集合に含まれるターム (正規化されたトークン) とその出現位置を記録したデータ構造である。1 つのタームに対する出現位置のリストをポスティングリスト (posting list) と呼ぶ。ポスティングリストの位置情報は昇順にソートされている。

タームに県連づけられた文書ID集合(ポスティングリスト) / posting list
Fig 1. タームに関連付けられたポスティングリスト (出現位置リスト)。

例として 3 つの文書をテキスト解析して作成した転置インデックスを Fig 1 に示す。それぞれの文書はテキスト解析を受けてタームに分割され、それぞれのタームに対して出現位置として文書 ID が関連付けられ転置インデックスに記録されている。

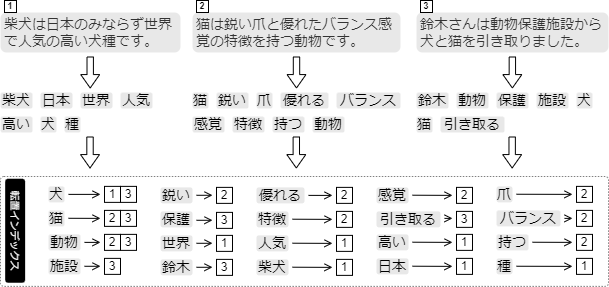
転置インデックスの作成 / inverse index
Fig 2. 3 つの文書をテキスト解析し転置インデックスを作成する過程。

転置インデックスに含まれているタームの集合を辞書 (dictionary) と呼ぶ。

検索エンジンやデータベースに情報を問い合わせるための入力をクエリー (query) と呼ぶ。全文検索でのクエリーは、ユーザが求めている特定の情報を記述するキーワードやフレーズで構成される。

AND 検索 (AND search) は複数のキーワードがすべて含まれる文書を検索する手法である。例えばクエリー cats AND dogs と検索すると "cats" と "dogs" の両方が含まれる文書が検索される。

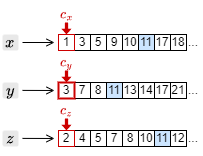
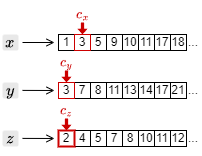
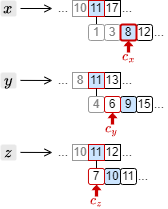
例としてクエリー \(x\) AND \(y\) AND \(z\) に対する検索方法を考える。まず、転置インデックスの中から \(x\), \(y\), \(z\) のポスティングリストを取得し、それぞれの先頭にカーソルを置いたところから開始する。

1. もっとも大きい文書 ID はカーソル \(c_y\) の指している 3 であるため、それ以外の \(c_x\) と \(c_z\) のカーソルを 3 以上の文書 ID を検出するまで進める。

2. カーソルを進めたことで、もっとも大きい文書 ID は \(c_z\) の指す 4 となった。このため、それ以外の \(c_x\) と \(c_y\) のカーソルを 4 以上の文書 ID を検出するまで進める。

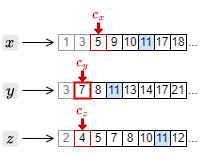
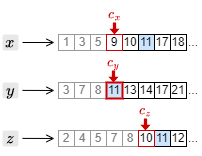
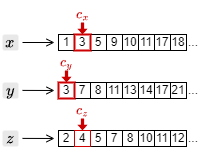
3. カーソルを進めたことで、もっとも大きい文書 ID は \(c_y\) の指す 7 となった。このため、それ以外の \(c_x\) と \(c_z\) のカーソルを 7 以上の文書 ID を検出するまで進める。

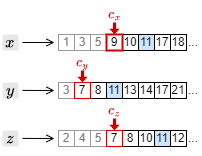
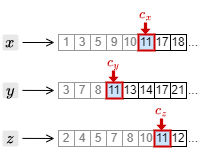
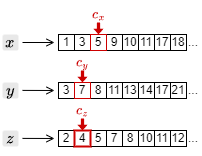
4. カーソルを進めたことで、もっとも大きい文書 ID は \(c_x\) の指す 9 となった。このため、それ以外の \(c_y\) と \(c_z\) のカーソルを 9 以上の文書 ID を検出するまで進める。

5. カーソルを進めたことで、もっとも大きい文書 ID は \(c_y\) の指す 11 となった。このため、それ以外の \(c_x\) と \(c_z\) のカーソルを 11 以上の文書 ID を検出するまで進める。

6. カーソルを進めたことで、すべてのカーソルの文書 ID が 11 となった。したがって文書 ID = 11 の文書をクエリーに一致する文書として取り出す。

このような処理を \(x\), \(y\), \(z\) のポスティングリストの末尾まで繰り返すことで、クエリー \(x\) AND \(y\) AND \(z\) に一致する文書 ID の集合を取り出すことができる。

OR 検索 (OR search) は複数のキーワードのいずれかが含まれる文書を検索する手法である。例えばクエリー cats OR dogs を用いて検索すると "cats" または "dogs" が含まれる文書を検索する。

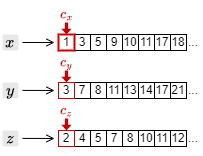
クエリー \(x\) OR \(y\) OR \(z\) に一致する文書 ID の集合を取り出すためには、AND 検索と同様に \(x\), \(y\), \(z\) のポスティングリストを取得し、それぞれの先頭にカーソルを置いたところから開始する。

1. カーソルの中でもっとも小さい文書 ID の 1 を取得し、\(c_x\) を一つ進める。

2. カーソルの中で最も小さい文書 ID の 2 を取得し、\(c_z\) を一つ進める。

3. カーソルの中で最も小さい文書 ID の 3 を取得し、\(c_x\) と \(c_y\) を一つ進める。

4. カーソルの中で最も小さい文書 ID の 3 を取得し、\(c_z\) を一つ進める。

上記の処理を \(x\), \(y\), \(z\) のポスティングリストの末尾まで繰り返すことで、クエリー \(x\) OR \(y\) OR \(z\) に一致する文書 ID の集合を取り出すことができる。

フレーズ検索 (phrase search) は複数の単語が特定の順序で連続して現われる文書を検索する手法である。例えばクエリー "information retrieval" と検索すると、ターム information の直後に retrieval が存在する文書だけが検索対象となる。

フレーズ検索では文書 ID に加えてそのタームが文書中のどこに現われたかを示す情報が必要になる。フレーズ検索の転置インデックスのポスティングリストは [文書ID]\(\mapsto\)[文書内位置リスト] 形式の位置情報で構成されているものとする。

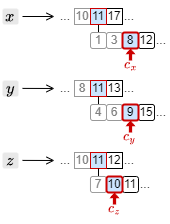
クエリー "\(x\) \(y\) \(z\)" のフレーズ検索ではまず AND 検索ですべてのタームを含む文書 ID を特定し、その文書内位置リストの先頭にカーソルを設定する。

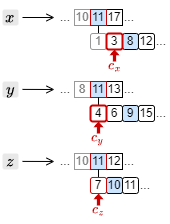
1. \(c_x\) が 1、\(c_y\) が 4 であることから、\(c_x \ge 3\) となる位置まで \(c_x\) を移動する。

2. \(c_x\), \(c_y\) が 3, 4 を指しているが、\(c_z\) が 7 を指していることから、\(c_x \ge 5\), \(c_y \ge 6\) となる位置までそれぞれを移動する。

3. \(c_x\) が 8 に対して \(c_y\) が 6、\(c_z\) が 7 を指していることから、\(c_y \ge 9\), \(c_z \ge 10\) となる位置までそれぞれを移動する。

4. \(c_x\) が 8 に対して \(c_y\) が 9、\(c_z\) が 10 となったことからこの位置に検索対象のフレーズが存在することが分る。

ランキング付きの検索

ランキング (ranking) は検索クエリーに一致した文章のうち、よりユーザの関心が高いと考えられる結果を上位に配置するプロセスである。前セクションで説明した転置インデックスを用いてクエリーがどのように文書と一致判定されるかに加えて、このセクションでは検索結果にどのように順位付けするかを説明する。

ランキングは一般的に検索クエリーと文書との類似度を算出し、よりクエリーと関連する文書を上位に表示する。例えば Apache Solr や Elasticsearch ではデフォルトのスコアリングに BM25 を使用して類似度を算出している。さらに、実用的な検索システムでは検索対象の属性情報 (価格や評価数、リリース日など) を用いてスコアを再調整することが一般的である。この属性情報によるスコアリングの調整はブースト (boost) と呼ばれ、類似度との関連をチューニングすることでランキングの精度を向上させる。

類似度を使用したランキング

基本的なランキング手法では、文書 \(d\) にクエリーに含まれるターム \(t\) が出現する頻度であるターム頻度 (term frequency) から類似度を算出して比較する。転置インデックスに基づくランキングでは TF-IDF とコサイン類似度を使用することができる。

TF-IDF

TF (term frequency) (\(\ref{tf}\)) は特定のターム \(t\) が文書 \(d\) 内で出現する頻度であり、文書内でのそのタームの重要性を表す。\[ \begin{equation} {\rm tf}_{t,d} = \frac{n_{t,d}}{\sum_{\forall i \in d} n_{i,d}} \label{tf} \end{equation} \] ここで \(n_{t,d}\) はある文書 \(d\) においてターム \(t\) が出現する回数、\(\sum_{\forall i \in d} n_{i,d}\) は文書 \(d\) に含まれているすべてのタームの出現数の総和である。

IDF (inverse document frequency) (\(\ref{idf}\)) は特定のタームが全体の文書集合においてどれだけ一般的かを表しており、その単語の希少性を表している。\[ \begin{equation} {\rm idf}_t = \log \frac{N}{N_t} \label{idf} \end{equation} \] ここで \(N\) は文書の総数、\(N_t \gt 0\) はターム \(t\) を含む文書数である。

最終的に \({\rm tf\mbox{-}idf}\) は \({\rm tf}\) と \({\rm idf}\) を乗算することで得られる特徴ベクトルである。\[ \begin{equation} {\rm tf\mbox{-}idf}_d = ({\rm tf}_{1,d} \times {\rm idf}_1, \ldots, {\rm tf}_{t,d} \times {\rm idf}_t, \ldots, {\rm tf}_{n,d} \times {\rm idf}_n) \label{tfidf} \end{equation} \]

コサイン類似度

コサイン類似度 (cosine similarity) は 2 つのベクトル間の類似度を計る指標である。ベクトルがなす角度が小さいほど 1 に近づき類似度が高いと見なすことができる。ある文書を (TF-IDF のような) 特徴ベクトルで表現した文書ベクトル \(\vector{d}\) と、検索クエリーを同様に特徴ベクトルで表現したクエリーベクトル \(\vector{q}\) のコサイン類似度は式 (\(\ref{cossim}\)) のように表される。\[ \begin{equation} {\rm sim}(\vector{d},\vector{q}) = \frac{\vector{d} \cdot \vector{q}}{|\vector{d}||\vector{q}|} \label{cossim} \end{equation} \] ただし検索においては過去の研究から「ベクトル長による正規化をしない方が検索精度が上がる」ことが知られている [2] ことから、式 (\(\ref{cossim}\)) の分子のみをスコアとして考慮する。さらに、クエリーベクトルについては \({\rm tf\mbox{-}idf}\) ではなく「タームが出現するかどうか」を 1 と 0 で表すのみとすると、\(\vector{d}\) との内積演算は「クエリーに含まれているタームの \(\vector{d}\) における要素の値を足し合わせる」操作のみでスコアを算出することができる。\[ \begin{equation} {\rm score}(\vector{d},\vector{q}) = \vector{d} \cdot \vector{q} = \sum_{\forall t \in q} \left\{ {\rm tf}_{t,d} \times {\rm idf}_t \right\} \label{cossim2} \end{equation} \]

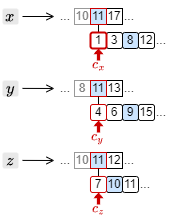
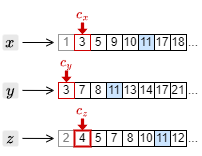
例として TF-IDF を使用したランキング付き OR 検索について説明する。転置インデックスを作成するときに \({\rm tf}_{t,d}\) はポスティングリストの各文書 ID に、\({\rm idf}_t\) はターム集合の各タームにそれぞれ関連付けて保存されているものとする。

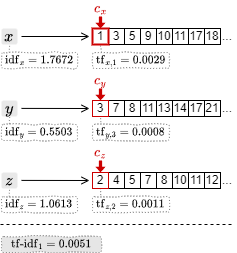
1. カーソルの中で最も小さい文書 ID の 1 を取得して \(c_x\) を一つ進める。ここで \({\rm tf\mbox{-}idf}_1 = 1.7672\times 0.0029\) を算出してスコアを得る。

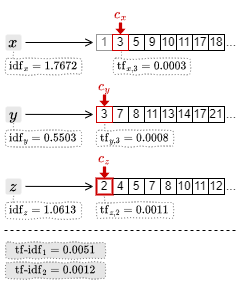
2. カーソルの中で最も小さい文書 ID の 2 を取得して \(c_z\) を一つ進める。ここで \({\rm tf\mbox{-}idf}_2 = 1.0613\times 0.0011\) を算出してスコアを得る。

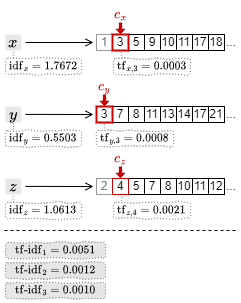
3. カーソルの中で最も小さい文書 ID の 3 を取得して \(c_x\) と \(c_y\) を一つ進める。ここで \({\rm tf\mbox{-}idf}_3 = 1.7672\times 0.0003+0.5503\times 0.0003\) を算出してスコアを得る。

4. 同様の操作でそれぞれのポスティングリストの末尾まで処理を進める。得られた \({\rm tf\mbox{-}idf}_d\) リストを降順にソートしたものがランキング付きの検索結果となる。

機械学習によるランキング

検索システムでの機械学習は「文書の順序関係」を予測するために利用する。この手法はランキング学習 (learning to rank; LTR) と呼ばれる。TF-IDF や BM25 といった従来の手法は主に単語の頻度などの静的な特徴量に依存している。ランキング学習モデルはユーザのクリックやメタデータ、履歴など、さまざまな特徴量を統合してランク付けを行うことができる。

近接度によるランキング

ターム近接度 (term proximity) によるランキングは、複数の検索タームが互いに近くに出現する文書の方がランクが上に評価されるべきであるという考えに基づく。

参考文献

  1. Stefan Buttcher, Charles L. A. Clarke, Gordon V. Cormack. 情報検索 :検索エンジンの実装と評価. 森北出版 (2020)
  2. 打田智子, 古澤智裕, 大谷純, 加藤遼, 鈴木翔吾, 河野晋策. 検索システム実務者のための開発改善ガイドブック. ラムダノート (2022)