論文翻訳: NIST SP 800-22: A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications / 暗号アプリケーションのための乱数・擬似乱数生成器の統計的検定スイート
Andrew Rukhin,Juan Soto,James Nechvatal, Miles Smid, Elaine Barker, Stefan Leigh, Mark Levenson, Mark Vangel, David Banks, Alan Heckert, James Dray, San Vo
 Abstract
Abstract
この論文では乱数・疑似乱数生成器の選択と検定に関するいくつかの側面を論じる。このような生成器の出力は鍵素材の生成など多くの暗号アプリケーションで使用できる。暗号アプリケーションでの使用に適した生成器はほかのアプリケーションよりも強い要件を満たさなければならない場合がある。特に入力に関する知識がなければ出力が予測不可能でなければならない。この文書では生成器を適切に特徴づけて選択するためのいくつかの基準について議論する。また統計的検定と暗号解読学の関係についても説明し、推奨される統計的検定をいくつか提示する。これらの検定は生成器が特定の暗号アプリケーションに適しているかを判断する最初のステップとして有用であろう。しかし一連の統計的検定は特定のアプリケーションでの使用に適した生成器を完全に証明することはできない。つまり統計的検定は暗号解読学の代わりとして機能しない。生成器の設計と暗号解読学はこの論文の範囲外である。
キーワード: 乱数生成器, 仮説検定, P-値
Table of Contents
- Abstract
- 1. 乱数検定の導入
- 2. 乱数生成検定
- 2.1 頻度 (モノビット) 検定
- 2.2 ブロック内頻度検定
- 2.3 連検定
- 2.4 ブロック内最大連検定
- 2.5 Binary Matrix Rank Test
- 2.6 Discrete Fourier Transform (Spectral) Test
- 2.7 Non-overlapping Template Matching Test
- 2.8 Overlapping Template Matching Test
- 2.9 マウラーの "普遍統計" 検定
- 2.10 Linear Complexity Test
- 2.11 Serial Test
- 2.12 Approximate Entropy Test
- 2.13 Cumulative Sums (Cusum) Test
- 2.14 ランダム偏差検定
- 2.15 ランダム偏差変種検定
- 3. 検定の技術的説明
- 3.1 頻度 (モノビット) 検定
- 3.2 ブロック内頻度検定
- 3.3 Runs Test
- 3.4 Test for the Longest Run of Ones in a Block
- 3.5 Binary Matrix Rank Test
- 3.6 Discrete Fourier Transform (Specral) Test
- 3.7 Non-Overlapping Template Matching Test
- 3.8 Overlapping Template Matching Test
- 3.9 Maurer's "Universal Statistical" Test
- 3.10 Linear Complexity Test
- 3.11 Serial Test
- 3.12 Approximate Entropy Test
- 3.13 Cumulative Sums (Cusum) Test
- 3.14 Random Excursions Test
- 3.15 Random Excursions Variant Test
- 4. 検定の戦略と結果の解釈
- 5. ユーザガイド
- List of Appendices
- 翻訳抄
 1. 乱数検定の導入
1. 乱数検定の導入
乱数や疑似乱数の必要性は多くの暗号アプリケーションで生じている。例えば一般的な暗号システムではランダムな方法で生成する必要のある鍵を採用している。また多くの暗号プロトコルは電子署名の生成や認証プロトコルのチャレンジの生成など、様々な場面で乱数や疑似乱数の入力を必要とする。
この文書は暗号、モデリング、シミュレーションなど様々な用途に使用される乱数・疑似乱数生成器のランダム性検定について説明したものである。この文書では暗号用途でランダム性が要求されるアプリケーションに焦点を当てる。この文書では乱数に関する統計的検定について説明する。米国国立標準技術研究所 (NIST) はこれらの手法がバイナリ列 (binary sequence) のランダム性からの逸脱を検出するために有用であると考えている。しかし試験者はランダム性からの明らかな逸脱が、生成器の不十分な設計によるものか、試験されるバイナリ列に現れる異常によるものかを十分に注意する必要がある (つまり特定の生成器によって生成されるランダム列では一定数の失敗が予想される)。検定結果の正しい解釈を決定するのは試験者次第である。検定戦略と検定結果の解釈についてはセクション 4 を参照。
 1.1 総論
1.1 総論
乱数列の生成には、乱数生成器 (RNGs - セクション 1.1.3 参照) と疑似乱数生成器 (PRNGs - セクション 1.1.4 参照) の 2 種類の基本的な生成器が使用されている。
 1.1.1 ランダム性
1.1.1 ランダム性
ランダムなビット列は "0" と "1" でラベル付けされた偏りのない "公平な" コインフリップの結果と解釈することができる。各フリップは正確に \(1/2\) の確率で "0" か "1" を生成することができる。さらにコインフリップは互いに独立しており、前のコインフリップの結果は後のコインフリップに影響を与えることはない。"0" と "1" はランダムに分布する (そして \(0,1]\) は一様に分布する) ため、偏りのない "公平な" コインは完全なランダムビットストリーム生成器となる。列のすべての要素は互いに独立して生成され、既に生成された要素の数に関係なく、列の次の要素の値を予測することはできない。
暗号化の目的で偏りのないコインを使用することは明らかに非現実的である。しかしこのような真の乱数列による理想化された生成器の仮想的な出力は、乱数及び疑似乱数生成器の評価のベンチマークとして機能する。
 1.1.2 予測不可能性
1.1.2 予測不可能性
暗号アプリケーション向けに生成される乱数・疑似乱数は予測不可能であるべきである。PRNG の場合、シードが未知であれば乱数列の以前の乱数が分かっていても次の出力値は予想できない。この性質は前方予測不可能性として知られている。また生成された乱数値からシードを決定することも可能であってはならない (つまり後方予測不可能性も必要である)。シードとそのシードから生成された値との間には相関関係がなく、シーケンスの各要素は確率が \(1/2\) の独立したランダムイベントの結果であるように見える必要がある。
前方予測不可能性を確保するためにはシードの取得に注意が必要である。シードと生成アルゴリズムがわかっている場合、PRNG によって生成される値は完全に予測可能である。多くの場合、生成アルゴリズムは後悔されているためシードは秘匿する必要があり、シード自体も予測不可能でなければならない。
 1.1.3 乱数生成器 (RINGs)
1.1.3 乱数生成器 (RINGs)
第一のタイプのシーケンス生成器は乱数生成器 (RNG) である。RNG は非決定論的なソース (つまりエントロピーソース) と何らかの処理機能 (つまりエントロピー蒸留 (distillation) プロセス) を使用してランダム性を生成する。エントロピーソースの弱点である非乱数性 (たとえば 0 または 1 の長い列の発生) を克服するために蒸留プロセスが必要とされる。エントロピーソースは通常、電気回路のノイズ、ユーザプロセスのタイミング (例えばキーストロークやマウス操作)、また半導体の量子効果などの物理量で構成される。またこれらの入力を様々に組み合わせて使用することもできる。
RNG の出力は乱数として直接使用することも、疑似乱数生成器 (PRNG) に入力することもできる。PNG の出力を直接 (つまりそれ以上の処理なしで) 使用するのであれば、統計検定によって RNG からの入力の物理的ソースがランダムに見えていることを確信するための判断なランダム性の基準を満たす必要がある。例えば電子ノイズのような物理的ソースは波や他の周期的な現象などの規則的な構造の重ね合わせを含むことがある。これはランダムに見えるかもしれないが統計的検定を用いてランダムではないと判断される。
暗号化の目的では RNG の出力は予測不可能である必要がある。しかし物理的なソース (例えば日付/時刻ベクトル) の中にはかなり予測可能なものもある。これらの問題は異なる種類のソースからの出力を組み合わせて RNG の入力として使用することで軽減できる。しかし RNG から得られる出力を統計的検定で評価すると依然として欠点がある可能性がある。また高品質な乱数の生成には時間がかかりすぎることから大量の乱数が必要な場合には好ましくない場合がある。大量の乱数を生成するには疑似乱数生成器を用いることが望ましいと考えられる。
 1.1.4 疑似乱数生成器 (PRNGs)
1.1.4 疑似乱数生成器 (PRNGs)
第二のタイプの生成器は疑似乱数生成器 (PRNG) である。PRNG は 1 つ以上の入力を使用して複数の "疑似乱数" を生成する。PRNG への入力はシードと呼ばれる。予測不可能性が必要とされる文脈ではシード自体がランダムで予測不可能でなければならない。したがってデフォルトでは PRNG は RNG の出力からシードを取得するh津用がある。つまり PRNG には必携として RNG が必要である。
通常 PRNG の出力はシードの決定論的関数である。つまりすべての真のランダム性はシード生成に限定される。個の決定論的な性質から "疑似乱数" という用語が生まれた。疑似乱数列の各要素はそのシードから再現可能であるため、疑似乱数列の再現や検証が必要な場合はシードのみを保存する必要がある。
皮肉なことに、疑似乱数は物理的なソースから得られる乱数よりもランダムであるように見えることがよくある。疑似乱数列が適切に構築されている場合、乱数列の各値は追加のランダム性を導入するように見える変換を介して前の値から生成される。このような一連の返還により入力と出力の間の統計的な自己相関を排除できる。したがって PRNG の出力は RNG より統計的な性質が良く、RNG より拘束に生成される可能性がある。
 1.1.5 検定
1.1.5 検定
様々な統計検定を乱数列に適用して真にランダムな列と比較、評価することができる。ランダム性は確立的な特性である。ランダムなシーケンスの特性は確率論の観点から特徴づけられ説明できる。真にランダムな乱数列に適用される統計検定の結果は先駆的に知られており、確率的な用語で記述することができる。統計的検定には無限の可能性があり、それぞれが "パターン" の有無を評価する。パターンが検出された場合、そのシーケンスがランダムでないことを示す。シーケンスがランダムかどうかを判断するための検定は非常に多く存在するため、特定の有限セットの検定が "完全" と見なされることはない。さらに、統計的検定の結果は特定の生成器に関する誤った結論を避けるためにある程度の注意と慎重さを持って解釈されなければならない (セクション 4 参照)。
統計的検定は特定の帰無仮説 (\(H_0\)) を検定するために定式化される。この文書のでは検定対象の帰無仮説は検定対象のシーケンスがランダムであるというものである。この帰無仮説に関連する対立仮説 (\(H_a\)) は、この文書ではシーケンスがランダムではないというものである。適用される各検定について帰無仮説を受理するか棄却するか、つまり、生成されたシーケンスに基づいて生成器がランダムな値を生成しているか (またはしていないか) の決定または結論が導き出される。
各検定で関連するランダム性統計量を選択し帰無仮説の受理または棄却を決定するために使用する必要がある。ランダム性の仮定の下でこのような統計量には可能な値の分布を持っている。帰無仮説の下でこの統計量の理論的な参照分布 (reference distribution) は数学的手法によって決定される。個の参照分布から棄却値 (critical value) が決定される (通常、この値は分布のテールの "はるか彼方"、例えば 99% ポイントにある)。検定ではデータ (検定対象のシーケンス) に対して検定統計値が算出される。この検定統計値は棄却値と比較される。もし検定統計量が棄却値を超えていればランダム性の帰無仮説は棄却される。そうでなければ、帰無仮説 (ランダム性仮説) は棄却されない (つまり仮説は受理される)。
実際には、統計的仮説検定が機能するのは参照分布と棄却値がランダム性の暫定的な仮定に依存し、その下で生成されるためである。もしランダム性の仮定が実際の手元のデータに当てはまるのであれば、データの結果として産出された統計検定量は非常に低い確率 (例えば 0.01%) で棄却値を超えることになる。一方、算出された検定統計量が棄却値を超える場合 (つまり低確率事象が実際に発生した場合)、統計的仮説検定の観点からは低確率事象は自然には発生しないはずである。したがって算出された検定統計量の値が棄却値を超えると、元のランダム性の過程が疑わしい、または誤っているという結論となる。この場合、統計的仮説検定では \(H_0\) (ランダム性) を棄却し \(H_a\) (非ランダム性) を受理するという結論が得られる。
統計的仮説検定とは \(H_0\) を受理するか (データはランダムである)、\(H_a\) を受理するか (データは非ランダムである) の 2 つの可能性を持つ結論生成手続き conclusion-generation procedure) である。次の \(2\times 2\) 表は手元にあるデータの真の (未知の) 状態と検定手順で得られた結論とを関連付けたものである。データが本当にランダムであったときに帰無仮説が棄却される (データが非ランダムであると結論付ける) 結論はわずかな確率で起き得る。このような結論をタイプ I エラーと呼ぶ。データが本当に非ランダムであったときに帰無仮説を受理する (つまりデータが実際にランダムだと結論付ける) 結論をタイプ II エラーと呼ぶ。データが本当にランダムであれば \(H_0\) を受理し、データがランダムでない場合は \(H_0\) を棄却するという結論は正しい。タイプ I エラーの確率はしばしば検定の有意水準 (level of significance) と呼ばれる。この確率は検定前に設定でき \(\alpha\) と表記される。\(\alpha\) は実際にはランダムであるシーケンスに対して検定がランダムでないと示す確率である。つまり "良い" 生成器によって生成された乱数列であっても非ランダムな性質に見えるということである。暗号技術における \(\alpha\) の一般的な値は約 0.01 である。
| 真の状況 | 結論 | |
|---|---|---|
| \(H_0\) を受理 | \(H_a\) を受理 (\(H_0\) を棄却) | |
| データはランダム (\(H_0\) が真) | 過誤なし | タイプ I エラー |
| データは非ランダム (\(H_a\) が真) | タイプ II エラー | 過誤なし |
タイプ II エラーの確率は \(\beta\) と表記される。検定では \(\beta\) はランダムでないシーケンスがランダムであることを検定が示す確率、つまり、"悪い" 生成器がランダムな特性を持つように見えるシーケンスを生成する確率である。\(\alpha\) と異なり \(\beta\) は個定義ではない、なぜなら、データストリームが非ランダムになり得る方法は無限にあり、それぞれの異なる方法によって異なる \(\beta\) が得られるためである。タイプ II エラー \(\beta\) の計算は多くの非ランダム性が考えられるため \(\alpha\) の計算より困難である。
以下の検定の主な目的の一つはタイプ II エラーの確率を最小限にすること、つまり、生成器が実際には不良であったときに、生成器によって生成されたシーケンスを良好であるものとして受理する確率を最小限に抑えることである。確率 \(\alpha\) と \(\beta\) は相互に関連付けられており、検定されるシーケンスのサイズ \(n\) とも関連付けられており、そのうちの 2 つが指定されれば 3 つ目の値は自動的に決定されるようになっている。実務者は通常、サンプルサイズ \(n\) と \(\alpha\) の値 (タイプ I エラーの確率、すなはち有意水準) を選択する。そして最小の \(\beta\) (タイプ II エラーの確率) を生成する特定の統計の棄却点を選択する。つまりシーケンスが本当はランダムであるにもかかわらず不良生成器が生成したシーケンスと判断する許容可能な確率と共に適切な標本サイズが選択される。そしてシーケンスをランダムと誤認する確率が最小になるような許容範囲のカットオフポイントが選択される。
各検定はデータの関数である計算された検定統計値に基づいている。検定統計量を \(S\)、棄却値を \(t\) とすると、タイプ I エラーの確率は \(P(S\gt t\,||\,H_0 \mbox{ is true})\) \(=\) \(P(\mbox{reject }H_0\,|\,H_0\mbox{ is true})\) であり、タイプ II エラーの確率は \(P(S \le t\,||\,H_0\mbox{ is false})\) \(=\) \(P(\mbox{accept }H_0\,|\,H_0\mbox{ is false})\) である。検定統計量は帰無仮説に対する証拠の強さを要約する P 値を計算するために使用される。これらの検定における各 P 値は、検定によって評価される非ランダム性の種類が与えられた場合に、完全な乱数生成器が被検シーケンスよりもランダム性の低いシーケンスを生成する確率である。検定の P 値が 1 に等しい場合、そのシーケンスは完全なランダム性を持っているように見えることを示す。P 値が 0 であればそのシーケンスは完全に非ランダムであることを示す。有意水準 (\(\alpha\)) を選択することができる。P 値 \(\ge \alpha\) であれば帰無仮説は受理される。つまりシーケンスはランダムであるように見える。P 値 \(\lt \alpha\) であれば帰無仮説は棄却される。つまりシーケンスは非ランダムに見える。パラメータ \(\alpha\) はタイプ I エラーの確率を示す。典型的に \(\alpha\) は \([0.001,0.01]\) の範囲で選択される。
\(\alpha\) が 0.001 の場合は、シーケンスが真にランダムであれば 1000 個のシーケンスのうち 1 つのシーケンスが検定により棄却されると予想されることを示す。P 値 \(\ge 0.001\) の場合、シーケンスは 99.9% の信頼度でランダムであると見なされる。P 値 \(\lt 0.001\) の場合、シーケンスは 99.9% の信頼度で非ランダムであると見なされる。
\(\alpha\) が 0.01 の場合は 100 個のシーケンスのうち 1 個が棄却されると予想されることを示す。P 値 \(\ge 0.01\) は 99% の信頼度でシーケンスがランダムであると考えられることを意味する。P 値 \(\lt 0.01\) は 99% の信頼度でシーケンスが非ランダム出るという結論になることを意味する。
この文書の例では \(\alpha\) は 0.01 に選択されている。多くの場合、例に使用するパラメータは推奨値とは一致しないため例は説明のためのものであることに注意。
 1.1.6 ランダム性、予測不可能性および検定に関する考慮事項
1.1.6 ランダム性、予測不可能性および検定に関する考慮事項
検定されるランダムな 2 進数列に関して次の仮定を置く:
一様性 (uniformity): ランダムまたは疑似ランダムビット列の生成のどの時点でも 0 または 1 の発生確率は等しい。つまりそれぞれの確率はちょうど \(1/2\) である。\(n=\)ビット列長としたとき、予想される 0 (または 1) の数は \(n/2\) である。
スケーラビリティ: シーケンスに適用可能な検定はランダムに抽出された部分シーケンスにも適用できる。シーケンスがランダムであればそのような部分シーケンスもランダムであるはずである。したがって抽出された部分シーケンスはランダム性の検定に合格するはずである。
一貫性 (consistency): 生成器の動作は開始値 (シード) 全体で一貫している必要がある。単一のシードからの出力に基づいて PRNG を検定したり、単一の物理的出力から生成された出力に基づいて RNG を検定することは不適切である。
 1.2 定義
1.2 定義
| 用語 | 定義 |
|---|---|
| 漸近的解析 (Asymptotic Analysis) | 注目する関数の極限近似を導き出す統計的手法。 |
| 漸近分布 (Asymptotic Distribution) | \(n\) が無限大に近づくと発生する検定統計量の極限分布。 |
| ベルヌーイ乱数変数 (Bernoulli Random Variable) | 確率 \(p\) で 1 の値を取り、確率 \(1-p\) で 0 の値を取る確率変数。 |
| 2進数列 (Binary Sequence) | 0 と 1 のシーケンス。 |
| 二項分布 (Binomial Distribution) | 確率変数が \(n\) 回の独立したベルヌーイ試行の成功回数であり、1 回の試行の成功確率が \(p\) であるような整数 \(n\) と確率 \(p\) が存在する場合、確率変数は二項分布である。 |
| ビット列 (Bit String) | ビットのシーケンス。 |
| ブロック (Block) | ビット列の部分集合。ブロックはあらかじめ決められた長さを持つ。 |
| 中央極限定理 (Central Limit Theorem) | 平均 \(\mu\)、分散 \(\sigma^2\) を持つ母集団からのサイズ \(n\) の無作為標本において、標本サイズが大きくなるにつれ標本平均の分布は平均 \(\mu\) と分散 \(\sigma^2/n\) でほぼ正規分布となる。 |
| 相補誤差関数 (Complementary Error Function) | Erfc 参照。 |
| 合流型超幾何関数 (Confluent Hypergeometric Function) | 合流型超幾何関数は次のように定義される。\[ \Theta(a;b;z)=\frac{\Gamma(b)}{\Gamma(a)\Gamma(b-a)}\int_0^1 e^{zt}t^{a-1}(1-t)^{b-a-1}dt,\ 0\lt a \lt b \] |
| 棄却値 (Critical Value) | 検定統計量が小さな確率で超える値 (有意水準)。これは検定統計量の "見立て" または計算値 (つまり検定統計量値) で、ランダム性の帰無仮説が真である場合に小さな確率 (例えば 5%) で起きるという構造。 |
| 累積分布関数 (CDF) \(F(x)\) (Cumulative Distribution Function) | すべての値 \(x\) について、確率変数 \(X\) が \(x\) 以下である確率を与える関数。つまり \[ F(x)=P(X\le x) \] |
| エントロピー (Entropy) | 閉じた系における無秩序またはランダム性の尺度。確率 \(p_1,\ldots,p_n\) を持つ確率変数 \(X\) の不確実性のエントロピーは次のように定義される。\[ H(X)=-\sum_{i=1}^n p_i \log p_i \] |
| エントロピーソース (Entropy Source) | 出力自体がランダムに見えるか、何らかのフィルタリング/蒸留プロセスを適用することでランダムに見える情報の物理ソース。この出力は RNG または PRINGの入力として使用される。 |
| Erfc | セクション 5.5.3 で定義される相補誤差関数 \({\rm erfc}(z)\)。この関数は通常の \({\rm cdf}\) と関係がある。 |
| 幾何確率変数 (Geometric Random Variable) | 確率 \(p^k(1-p)\) の非負整数である \(k\) を値とする確率変数。確率変数 \(x\) は無限に続くベルヌーイ試行において失敗の前の成功数である。 |
| グローバル構造体/グローバル値 (Global Structure/Global Value) | 検定コード内のすべてのルーチンで利用可能な構造体/値。 |
| igamc | セクション 5.5.3 で定義されている不完全Γ関数 \(Q(a,x)\)。 |
| 不完全ガンマ関数 (Incomplete Gamma Function) | igamc の定義参照。 |
| 対立仮説 (Alternative Hypothesis) | 帰無仮説が偽と判定されたときに分析者が真と見なすステートメント \(H_a\) (例えば \(H_a\):シーケンスは非ランダム)。 |
| 帰無仮説 (Null Hypothesis) | 観測されたシーケンスに想定されるデフォルトの条件/特性に関するステートメント \(H_0\)。この文書の目的では帰無仮説 \(H_0\) はシーケンスがランダムであるというものである。もし \(H_0\) が現実に真である場合、検定統計量の参照分布と棄却値が導出されるだろう。 |
| コルモゴロフ–スミルノフ検定 (Kolmogorov-Smirnov Test)) | あるデータが特定の確率分布に由来しているかを判断するために用いる統計的検定。 |
| 有意水準 (\(\alpha\)) (Level of Significance) | 帰無仮説を誤って棄却する確率、すはなち、仮説が実際には真であるにもかかわらず帰無仮説が偽であると結論づける確率。典型的な値は 0.05, 0.01 または 0.001 で、0.0001 のような小さな値が使われることもある。有意水準とは、ある列が実際にはランダムであるのに非ランダムであると結論づける確率のことである。タイプ I エラー、\(\alpha\) エラーと同義。 |
| 線形依存 (Linear Dependence) | 2 値階数行列検定の文脈において、線形依存とは線形独立な \(m\) ビットベクトルの線形結合として表現することのできる \(m\) ビットベクトルを指す。 |
| Maple | 記号代数式の操作と簡略化、任意の拡張精度数学、2 次元および 3 次元グラフィックス、およびプログラミングのための完全な数学的環境を提供する対話型コンピュータ代数システム。 |
| MATLAB | 数値計算、高度なグラフィックスと可視化、および高水準プログラミング言語を組み合わせた統合的なテクニカルコンピュータ環境。MATLAB にはデータ分析と可視化、数値・記号計算、工学・科学グラフィック、モデリング、シミュレーション、プロトタイピング、プログラミング、パリケーション開発、GUI 設計のための機能が含まれている。 |
| 正規 (ガウス) 分布 (Normal Distribution) | 密度関数が次のように表される連続分布。ここで \(\mu\) と \(\sigma\) は位置とスケールのパラメータである。\[ f(x;\mu;\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \] |
| P 値 (P-value) | 帰無仮説を考慮したときに、選ばれた検定統計量が観測された検定統計量と同じかそれよりも悪い値を取る確率 (ランダム性の帰無仮説の元で)。P 値はしばしば "末尾確率" (tail probability) と呼ばれる。 |
| ポアソン分布 - §3.8 (Poisson Distribution) | ポアソン分布は (いくつかの) 離散的な確率変数をモデル化したものである。典型的なポアソン確率変数は、ある時間区間に発生するまれな事象の数のカウントである。 |
| 確率密度関数 (PDF) (Probability Density Function) | 検定統計量の "局所" 確率分布を提供する関数。有限の標本サイズ \(n\) より、確率密度関数はヒストグラムで近似される。 |
| 確率分布 (Probability Distribution) | 確率変数の取り得る結果 (現実) に確率を割り当てること。 |
| 疑似乱数生成器 (PRNG) (Pseudorandom Number Generator) | 長さ \(k\) の真にランダムなバイナリ列が与えられたとき、ランダムに見える長さ \(l \gg k\) のバイナリ列を出力する決定論的アルゴリズム。生成器への入力をシードと呼び、出力を疑似乱数ビット列と呼ぶ。 |
| 乱数生成器 (RNG) (Random Number Generator) | 真にランダムなデータを生成することを目的とした機構。 |
| 乱数バイナリ列 (Random Binary Sequence) | 各ビットが "0" または "1" である確率が \(1/2\) であるビット列。各ビットの値はシーケンス内の他のビットとは独立している。つまり各ビットは予測不可能である。 |
| 確率変数 (Random Variable) | 確率変数は、取り得る各結果に対する確率値の体系的な分布割り当てができるという点で通常の (科学や工学の) 決定論的変数と異なる。 |
| (行列の) 階数 (Rank) | \({\rm GF}(2)\) 乗の線形代数における行列の階数を指す。諸島的な行操作によって行列を行階段形 (row-echelon form) に縮小した後、行列内の線形に独立した行また破裂の数を決定するために非ゼロの行の数をカウントする。 |
| 連 (Run) | 同様のビットの中断のないシーケンス (つまりすべて 0 またはすべて 1)。 |
| シード (Seed) | 疑似乱数生成器の入力。シードが異なると異なる疑似乱数列が生成される。 |
| SHA-1 | 連邦情報処理規格 180-1 で定義されたセキュアハッシュアルゴリズム。 |
| 標準正規累積分布関数 (Standard Normal Cumulative Distribution Function) | セクション 5.5.3 の定義参照。これは平均 0、分散 1 の正規関数である。 |
| 統計的独立事象 (Statistically Independent Events) | 2 つの事象は、一方の事象の発生が他の事象の発生の可能性に影響を与えない場合、独立である。事象 \(A\) と \(B\) の独立性の数学的定式化は、\(A\) と \(B\) の両方の発生確率が \(A\) と \(B\) の確率の積に等しい (すなはち \(P(A\mbox{ and }B)=P(A)P(B)\))。 |
| (仮説の) 統計検定 (Statistical Test) | 帰無仮説を棄却するかどうかを決定するために計算および使用されるデータ (バイナリストリーム) の関数。実験者が帰無仮説 \(H_0\) を受理するか棄却するかに関する結論を生成することを目的とする体系的な統計規則。 |
| ワード (Word) | 一定のパターン/テンプレートからなる定義済みの部分列 (例: 010, 0110) |
 1.3 略語
1.3 略語
| 略語 | 定義 |
|---|---|
| ANSI | 米国国家規格協会 |
| FIPS | 連邦情報処理標準 |
| NIST | アメリカ国立標準技術研究所 |
| RNG | 乱数生成器 |
| SHA-1 | セキュアハッシュアルゴリズム |
 1.4 数学的記号
1.4 数学的記号
この文書では一般に次の表記法を用いている。しかしこの文書内の検定は複数の著者によって設計、記述されており、若干異なる表記が使用されている可能性がある。読者は各検定で使用される表記法をとかの検定で使用される表記法とは分けて考えることを推奨する。
| 記号 | 意味 |
|---|---|
| \(\lfloor x \rfloor\) | \(x\) の床関数。与えられた正の実数 \(x\) に対して \(\lfloor x \rfloor = x - g\)、ここで \(\lfloor x \rfloor\) は非負整数、\(0 \le g \lt 1\) である。 |
| \(\alpha\) | 有意水準。 |
| \(d\) | 観測された頻度成分と期待される頻度成分の差を正規化したもの。セクション 2.6 と 3.6 参照。 |
| \(\nabla \Phi_m^2(obs)\); \(\nabla^2\Phi_m^2(obs)\) | 観測値が期待値とどの程度一致しているかを示す指標。セクション 2.11 と 3.11 参照。 |
| \(E[\ ]\) | 確率変数の期待値。 |
| \(\epsilon\) | 検定対象の 0 ビットと 1 ビットの元の入力列。 |
| \(\epsilon_i\) | 元のシーケンス \(\epsilon\) の \(i\) 番目のビット。 |
| \(H_0\) | 帰無仮説。つまりシーケンスがランダムであるというステートメント。 |
| \(\log(x)\) | \(x\) の自然対数。\(\log(x)=\log_e(x)=\ln(x)\)。 |
| \(\log^2(x)\) | \(\frac{\ln(x)}{\ln(2)}\) で定義される。ここで \(\ln\) は自然対数である。 |
| \(M\) | 検定される部分列 (ブロック) 内のビット数。 |
| \(N\) | 検定される \(M\) ビットブロックの数。 |
| \(n\) | 検定されるストリームのビット数。 |
| \(f_n\) | 一致する \(L\)-ビットテンプレート間の \(\log_2\) 距離の合計。つまり \(L\)-ビットテンプレート間の距離の桁数の総和。セクション 2.9 と 3.9 参照。 |
| \(\pi\) | 特定の検定において別途定義されていない限り 3.14159... |
| \(\sigma\) | 確率変数の標準偏差 \(\sqrt{\int(x-\mu)^2 f(x) dx}\)。 |
| \(\sigma^2\) | 確率変数の分散 = (標準偏差)² |
| \(s_{obs}\) | 頻度検定で統計量として使用される観測値。 |
| \(S_n\) | 値 \(X_i=\{-1,+1\}\) に対する \(n\) 番目の部分和。すなはち \(X_i\) の最初の \(n\) 個の和。 |
| \(\sum\) | 和算記号。 |
| \(\Phi\) | 標準正規累積分布関数 (セクション 5.5.3 参照)。 |
| \(\xi_j\) | 特定のサイクルである状態が発生する総回数。セクション 2.15 と 3.15 参照。 |
| \(X_i\) | ランダム性を検定する \(\pm 1\) からなる列の要素。ここで \(X_i=2\epsilon_i-1\) である。 |
| \(\chi^2\) | [論理的な] カイ二乗分布。検定統計量として使用される。また \(\chi^2\) 分布に従う検定統計量もある。 |
| \(\chi^2(obs)\) | 観測値に対して算出されたカイ二乗統計量。セクション 2.2, 2.4, 2.5, 2.7, 2.8, 2.10, 2.12, 2.14 およびセクション 3 の対応するセクションを参照。 |
| \(V_n\) | ランダム性の仮定の下で長さ \(n\) のシーケンスで発生するであろう連の期待値。セクション 2.3, 3.3 参照。 |
| \(V_n(obs)\) | 長さ \(n\) のシーケンスで観測された連の数。セクション 2.3 と 3.3 参照。 |
 2. 乱数生成検定
2. 乱数生成検定
NIST 検定スイートは、ハードウェアまたはソフトウェアベースの暗号論的乱数・疑似乱数生成器によって生成される (任意の長さの) バイナリ列のランダム性を検定するために開発された 15 の検定で構成される統計パッケージである。これらの検定はシーケンスに依存しうる様々な種類の非ランダム性に焦点をあてている。一部の検定は様々な部分検定に分解できる。15 の検定は次の通り。
- 頻度 (モノビット) 検定 (The Frequency (Monobit) Test)
- ブロック内頻度検定 (Frequency Test within a BLock)
連 検定 (The Runs Test)- ブロック内最大連検定 (Tests for the Longest-Run-of-Ones in a Block)
- バイナリ行列階数検定 (The Binary Matrix Rank Test)
- 離散フーリエ変換 (スペクトル) 検定 (The Discrete Fourier Transform (Spectral) Test)
- Non-overlapping Template Matching 検定 (The Non-overlapping Template Matching Test)
- Overlapping Template Matching 検定 (The Overlapping Template Matching Test)
- マウラーの "普遍統計" 検定 (Maurer's "Universal Statistical" Test)
- 線形複雑度検定 (The Linear Complexity Test)
- 直列性検定 (The Serial Test)
- 近似エントロピー検定 (The Approximate Entropy Test)
- 累積和 (Cusums) 検定 (The Cumulative Sums (Cumsums) Test)
- ランダムエクスカージョン検定 (The Random Excursions Test)
- ランダムエクスカージョン変種検定 (The Random Excursions Variant Test)
このセクション (セクション 2) は 15 のサブセクションで構成され、各検定に 1 つのサブセクションがある。各サブセクションでは特定の検定に関するハイレベルな概要を説明する。セクション 3 に対応するサブセクションでは、各検定の技術的な詳細を提供する。
セクション 4 では検定戦略と検定結果の解釈について述べる。検定スイート内の検定の適用順序は任意である。ただし頻度検定を最初に実行することを推奨する。これはシーケンス内の非ランダム性、特に非一様性の存在に関する最も基本的な証拠を提供するためである。この検定が失敗した場合、他の検定が失敗する可能性も高くなる。(注: 最も時間のかかる統計検定は線形複雑性検定である。セクション 2.10 および 3.10 参照。)
セクション 5 では検定のセットアップと実行に関するユーザガイドと、プログラムのレイアウトに関する説明を提供する。統計パッケージにはソースコードとサンプルデータセットが含まれている。検定コードは ANSI C で開発されている。一部の入力はパラメータを呼び出すのではなくグローバルな値であると仮定されている。
検定スイートの多くの検定は標準正規とカイ二乗 (\(\chi^2\)) を参照分布として持っている。検定対象のシーケンスが実際に非ランダムである場合、算出された検定統計量は参照分布の極端な領域に収まる。標準正規分布 (つまり釣鐘型曲線) を使用して RNG から取得した検定統計量の値と、ランダム性の仮定の下での統計量の期待値を比較する。標準正規分布の検定統計量は \(z=(x-\mu)/\sigma\) である。ここで \(x\) は標本検定統計値、\(\mu\) と \(\sigma^2\) は検定統計量の期待値と分散である。χ² 分布 (つまり左にゆがんだ曲線) は標本測定値の観測頻度と仮設分布の対応する期待頻度を比較するために使用される。この検定統計量は \(\displaystyle \chi^2=\sum \left( (o_i - e_i)^2/e_i\right)\) である。ここで \(o_i\) と \(e_i\) はそれぞれ測定値の観測頻度と期待頻度である。
この検定スイートの多くの検定ではシーケンスの長さ \(n\) のサイズが大きい (\(10^3\) から \(10^7\) オーダー) という仮定が成されている。そのように大きな \(n\) 個の標本サイズに対して漸近的参照分布が導入され、検定を実行するために適用されている。しかしより小さな \(n\) を使用する場合、漸近参照分布は不適切であり、一般に計算が困難な正確な分布に置き換える必要があるだろう。
注: セクション 2 の多くの例では、例として \(n=10\) のように小さな標本サイズが使用されている。このような例では通常の近似には適用できない。
 2.1 頻度 (モノビット) 検定
2.1 頻度 (モノビット) 検定
 2.1.1 検定目的
2.1.1 検定目的
この検定の焦点はシーケンス全体の 0 と 1 の割合である。この検定の目的は、シーケンス内の 1 と 0 の数が真のランダムなシーケンスで期待される数とほぼ同じであるかどうかを判断することである。この検定では 1 の割合が 1/2 に近いかどうか、つまりシーケンス内の 1 と 0 の数がほぼ同じであることを評価する。以降のすべての検定はこの検定の合格に依存する。
 2.1.2 関数実行
2.1.2 関数実行
\({\rm Frequency}(n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
 2.1.3 検定統計量と参照分布
2.1.3 検定統計量と参照分布
検定統計量の参照分布は正規分布の半分である (\(n\) が大きい場合)。(注: \(z\) が正規分布であれば (ここで \(z=s_{obs}/\sqrt{2}\); セクション 3.1 参照。)、\(|z|\) は正規分布の半分として分布する。) もし \(s_{obs}\) のシーケンスがランダムであれば、プラスとマイナスの値は互いに打ち消し合う傾向にある。1 または 0 が多すぎると検定統計量は 0 よりも大きくなる傾向がある。
 2.1.4 検定内容
2.1.4 検定内容
\(\pm 1\) への変換: 入力シーケンス (\(\xi\)) の 0 と 1 を -1 と +1 に変換して加算し \(S_n=X_1+X_2+\ldots+X_n\) を算出する。ここで \(X_i=2\epsilon_i-1\) である。例えば \(\epsilon=\)1011010101 であれば \(n=10\) であり \(S_n=\)1+(-1)+1+1+(-1)+1+(-1)+1+(-1)+1=2 である。
検定統計量 \(s_{obs}=\frac{|S_n|}{\sqrt{n}}\) を算出する。例えばこのセクションでは \(s_{obs}=\frac{|2|}{\sqrt{10}}=.632455532\) である。
P 値\(= {\rm erfc}(\frac{s_{obs}}{\sqrt{2}})\) を算出する。ここで \({\rm erfc}\) はセクション 5.5.3 で定義されている相補誤差関数である。このセクションの例では P 値\(={\rm erfc}(\frac{.632455532}{\sqrt{2}})=0.527089\) である。
 2.1.5 決定規則 (1%水準)
2.1.5 決定規則 (1%水準)
算出された P 値が \(\lt 0.01\) の場合、シーケンスは非ランダムであると結論づける。そうでなければシーケンスはランダムであると結論づける。
 2.1.6 結論と結果の解釈
2.1.6 結論と結果の解釈
セクション 2.1.4 のステップ 3 で得られた P 値は \(\ge 0.01\) (つまり P 値=0.527089) であるためシーケンスはランダムであるという結論となる。
なお P 値が小さい (\(\lt 0.01\)) 場合、\(|S_n|\) または \(|s_{obs}|\) が大きいことが原因であると考えられる。\(S_n\) の値が大きな正であるとき 1 が多すぎることを示し、大きな負であるとき 0 が多すぎることを示している。
 2.1.7 推奨入力サイズ
2.1.7 推奨入力サイズ
検定する各シーケンスは最低 100 ビット (つまり \(n \ge 100\)) で構成することを推奨する。
 2.1.8 例
2.1.8 例
| (入力) | \(\begin{eqnarray*}\epsilon&=&11001001000011111101101010100010001000010110100011\\&&00001000110100110001001100011001100010100010111000\end{eqnarray*}\) |
| (入力) | \(n=100\) |
| (処理) | \(S_{100}=-16\) |
| (処理) | \(s_{obs}=1.6\) |
| (出力) | \(P\mbox{-}{\rm value}=0.109599\) |
| (結論) | \(P\mbox{-}{\rm value}\gt 0.01\) であるためシーケンスがランダムであることを受理する。 |
 2.2 ブロック内頻度検定
2.2 ブロック内頻度検定
 2.2.1 検定目的
2.2.1 検定目的
この検定の焦点は \(M\)-ビットブロック内の 1 の割合である。この検定の目的は、ランダム性の仮定の下で予想されるように \(M\) ビットブロック内の 1 の頻度が約 \(M/2\) であるかどうかを判断する。ブロックサイズ \(M=1\) ではこの検定は検定 1 の頻度 (モノビット) 検定に縮退する。
 2.2.2 関数実行
2.2.2 関数実行
\({\rm BlockFrequency}(M,n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
 2.2.3 検定統計量と参照分布
2.2.3 検定統計量と参照分布
検定統計量の参照分布は \(\chi^2\) 分布である。
 2.2.4 検定内容
2.2.4 検定内容
入力シーケンスを \(\displaystyle N=\left\lfloor \frac{n}{M} \right\rfloor\) の non-overlapping ブロックに分割する。未使用のビットは破棄する。
例えば \(n=10\), \(M=3\), \(\epsilon=0110011010\) であれば 011, 001, 101 という 3 ブロック (\(N=3\)) が作られることになる。最後の 0 は破棄される。
各 \(M\) ビットブロックの 1 の割合 \(\pi_i\) を \(1 \le i \le N\) に対して \(\displaystyle \pi_i=\frac{\displaystyle \sum_{j=1}^M \epsilon_{(i-1)M+j}}{M}\) で求める。
このセクションの例では \(\pi_1=2/3\), \(\pi_2=1/3\), \(\pi_3=2/3\) である。
\(\chi^2\) 統計量を算出する: \(\displaystyle \chi^2(obs)=4M\sum_{i=1}^N(\pi_i-1/2)^2\)
このセクションの例では \(\displaystyle\chi^2(obs)=4\times 3\left((2/3-1/2)^2+(1/3-1/2)^2+(2/3-1/2)^2\right)=1\) である。
\(P\mbox{-}{\rm value}={\bf igamc}(N/2,\chi^2(obs)/2)\) を算出する。ここで \({\bf igamc}\) はセクション 5.5.3 で定義されている \(Q(a,x)\) の不完全ガンマ関数である。
このセクションをセクション 3.2 の技術的説明と比較する場合 \(Q(a,x)=1-P(a,x)\) であることに注意。
このセクションの例では \(P\mbox{-}{\rm value}={\bf igamc}\left(\frac{3}{2},\frac{1}{2}\right)=0.801252\) である。
 2.2.5 決定規則 (1%水準)
2.2.5 決定規則 (1%水準)
算出された P 値が \(\lt 0.01\) であればそのシーケンスは非ランダムであると結論づける。そうでなければシーケンスはランダムであると結論づける。
 2.2.6 結論と結果の解釈
2.2.6 結論と結果の解釈
セクション 2.2.4 のステップ 4 で得られた P 値は \(\ge 0.01\) (つまり \(P\mbox{-}{\rm value}=0.801252\)) であるためシーケンスはランダムであるという結論になる。
小さな P 値 (\(\lt 0.01\)) は、少なくとも 1 つのブロックにおいて 1 と 0 の割合が等しいということから大きく外れていることを示すものであることに注意。
 2.2.7 推奨入力サイズ
2.2.7 推奨入力サイズ
検定する各シーケンスは最低 100 ビット (つまり \(n \ge 100\)) で構成することを推奨する。\(N \ge MN\) に注意。ブロックサイズ \(M\) は \(M \ge 20\), \(M \gt .01n\), \(N \lt 100\) となるように選択すべきである。
 2.2.8 例
2.2.8 例
| (入力) | \(\begin{eqnarray*}\epsilon&=&11001001000011111101101010100010001000010110100011 \\ &&00001000110100110001001100011001100010100010111000\end{eqnarray*}\) |
| (入力) | \(n=100\) |
| (入力) | \(M=10\) |
| (処理) | \(N=10\) |
| (処理) | \(\chi^2=7.2\) |
| (出力) | \(P\mbox{-}{\rm value}=0.706438\) |
| (結論) | \(P\mbox{-}{\rm value}\gt 0.01\) であるためシーケンスがランダムであることを受理する。 |
 2.3 連検定
2.3 連検定
 2.3.1 検定目的
2.3.1 検定目的
この検定の焦点はシーケンス内の連 (run) の総数である。連とは同一ビットの途切れのない連続である。長さ \(k\) の連は正確に \(k\) 個の同一のビットで構成され、その前後は反対の値のビットで区切られている。連検定の目的は様々な長さの 1 と 0 の連の数がランダムなシーケンスに対して予想通りであるかを判断する。特に、この検定はそのような 0 と 1 の間の振動が速すぎるか遅すぎるかを判断する。
 2.3.2 関数実行
2.3.2 関数実行
\({\rm Runs}(n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
 2.3.3 検定統計量と参照分布
2.3.3 検定統計量と参照分布
検定統計量の参照分布は \(\chi^2\) 分布である。
 2.3.4 検定内容
2.3.4 検定内容
注: 連検定は前提条件として頻度検定を実施する。
検定前に入力シーケンス中の 1 の割合 \(\pi\) を算出する: \(\displaystyle\pi=\frac{\sum_j \epsilon_j}{n}\)
例えば \(\epsilon=1001101011\) であれば \(n=10\), \(\pi=6/10=3/5\) である。
前提条件となる頻度検定に合格しているかどうかを判断する。もし \(|\pi-1/2| \ge \tau\) であることを示すことができれば連検定を実施する必要はない (つまり検定 1 の頻度 (モノビット) 検定に合格しなかったのでこの検定を実行する必要はない)。もし検定が適用できなければ P 値は 0.0000 に設定される。なお、この検定の \(\tau=\frac{2}{\sqrt{n}}\) は検定コードに事前定義されている。
このセクションの例では \(\tau=2/\sqrt{10}\approx 0.63246\) であるため \(|\pi-1/2|=|3/5-1/2|=0.1\lt\tau\) となり検定は実施されない (訳注: 実施されるの誤記?)。
観測値 \(\pi\) は選択された境界の中にあるため連検定は適用可能である。
検定統計量 \(\displaystyle V_n(obs)=\sum_{k=1}^{n-1}r(k)+1\) を算出する。ここで \(\epsilon_k=\epsilon_{k+1}\) であれば \(r(k)=0\) であり、そうでなければ \(r(k)=1\) である。
\(\epsilon=1\ 00\ 11\ 0\ 1\ 0\ 11\) より\[V_{10}(obs)=(1+0+1+0+1+1+1+1+0)+1=7\]
\(\displaystyle P\mbox{-}{\rm value}={\bf erfc}\left(\frac{|V_n(obs)-2n\pi(1-\pi)|}{2\sqrt{2n}\pi(1-\pi)}\right)\) を算出する。
例えば \(\displaystyle P\mbox{-}{\rm value}={\bf erfc}\left(\frac{7-\left(2\cdot 10\cdot \frac{3}{5}\left(1-\frac{3}{5}\right)\right)}{2\cdot \sqrt{2\cdot 10}\cdot\frac{3}{5}\cdot\left(1-\frac{3}{5}\right)}\right)=0.147232\)
 2.3.5 決定規則 (1%水準)
2.3.5 決定規則 (1%水準)
算出された P 値が \(\lt 0.01\) であればそのシーケンスは非ランダムであると結論づける。そうでなければシーケンスはランダムであると結論づける。
 2.3.6 結論と結果の解釈
2.3.6 結論と結果の解釈
セクション 2.3.4 のステップ 4 で得られた P 値は \(\ge 0.01\) (つまり \(P\mbox{-}{\rm value}=0.147232\)) であるためシーケンスはランダムであるという結論になる。
\(V_n(obs)\) の値が大きいとビット列の振動が速すぎることを示し、小さいと振動が遅すぎることを示していることに注意。(振動 (oscillation) とは 1 から 0 への変化、またはその逆の変化と見なされる。) 速い揺れは例えば 1 ビットごとに揺れ動く 010101010 のように変化が多いときに起きる。ゆっくりとした振動を伴うストリームはランダム列で期待されるよりも少ない連となる。例えば 100 個の 1、73 個の 0、127 個の 1 で構成されるシーケンス (合計 300 ビット) は 150 回の連が期待されるのに対して 3 つの連しか存在しない。
 2.3.7 推奨入力サイズ
2.3.7 推奨入力サイズ
検定する各シーケンスは最低 100 ビット (つまり \(n \ge 100\)) で構成することを推奨する。
 2.3.8 例
2.3.8 例
| (入力) | \(\begin{eqnarray*}\epsilon&=&11001001000011111101101010100010001000010110100011 \\ &&00001000110100110001001100011001100010100010111000\end{eqnarray*}\) |
| (入力) | \(n=100\) |
| (入力) | \(\tau=0.02\) |
| (処理) | \(\pi=0.42\) |
| (処理) | \(V_n(obs)=52\) |
| (出力) | \(P\mbox{-}{\rm value}=0.500798\) |
| (結論) | \(P\mbox{-}{\rm value}\gt 0.01\) であるためシーケンスがランダムであることを受理する。 |
 2.4 ブロック内最大連検定
2.4 ブロック内最大連検定
 2.4.1 検定目的
2.4.1 検定目的
この検定の焦点は \(M\) ビットブロック内の 1 の最大連である。この検定の目的は、シーケンス内の 1 の最大連の長さが真のランダムなシーケンスで期待される 1 の最大連の長さと一致するかどうかを判断することである。1 の最大連の長さが不規則であることは 0 の最大連の長さも不規則であることを意味することに注意。したがって 1 についての検定のみが必要である。セクション 4.4 を参照。
 2.4.2 関数実行
2.4.2 関数実行
\({\rm LongestRunOfOnes}(n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
| Minimum \(n\) | \(M\) |
|---|---|
| 128 | 8 |
| 6272 | 128 |
| 750,000 | 10^4 |
 2.4.3 検定統計量と参照分布
2.4.3 検定統計量と参照分布
統計検定料の参照分布は \(\chi^2\) 分布である。
 2.5 Binary Matrix Rank Test
2.5 Binary Matrix Rank Test
 2.6 Discrete Fourier Transform (Spectral) Test
2.6 Discrete Fourier Transform (Spectral) Test
 2.7 Non-overlapping Template Matching Test
2.7 Non-overlapping Template Matching Test
 2.8 Overlapping Template Matching Test
2.8 Overlapping Template Matching Test
 2.9 マウラーの "普遍統計" 検定
2.9 マウラーの "普遍統計" 検定
 2.9.1 検定目的
2.9.1 検定目的
この検定の焦点は一致パターン間のビット数 (圧縮可能なビット列の長さに関連する指標) である。この検定の目的は、情報劣化を伴わずに有意に圧縮できるかどうかを検出することである。著しく圧縮可能なシーケンスは非ランダムであると考えられる。
 2.9.2 関数実行
2.9.2 関数実行
\({\rm Universal}(L,Q,n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
 2.9.3 検定統計量と参照分布
2.9.3 検定統計量と参照分布
検定統計量の参照分布はセクション 2.1 の頻度検定と同様に半正規分布 (正規分布の片側変形) である。
 2.9.4 検定内容
2.9.4 検定内容
\(n\) ビットシーケンス (\(\epsilon\)) は、\(Q\) 個の \(L\) ビット非オーバーラップブロックからなる初期化セグメントと、\(K\) 個の \(L\) ビット非オーバーラップブロックからなるテストセグメントに分割される。シーケンスの残りの \(L\) ビットブロックを形成できないビットは破棄される。最初の \(Q\) ブロックは検定の初期化に使用され、残りの \(K\) ブロックはテストブロックである (\(K=\lfloor n/L \rfloor - Q\))。
例えば \(\epsilon = 01011010011101010111\) であれば \(n=20\) であり、\(L=2\), \(Q=4\) とすると \(K\) \(= \lfloor n/L \rfloor-Q\) \(= \lfloor 20/2 \rfloor - 4\) \( = 6\) である。初期化セグメントは 01011010 でテストセグメントは 011101010111 となる。\(L\) ビットブロックは次の表のように表される。
ブロック タイプ 内容 1 初期化セグメント 01 2 01 3 10 4 10 5 テストセグメント 01 6 11 7 01 8 01 9 01 10 11 初期化セグメントを使用して各 \(L\) ビット値ごとに表が作成される (つまり \(L\) ビット値は表へのインデックスとして使用される)。各 \(L\) ビットブロックが最後に出現したブロック番号が表に記録される (つまり 1 から \(Q\) までの \(i\) について \(T_j=i\)、ここで \(j\) は \(i\) 番目の \(L\) ビットブロックの内容の 10 進数表現である)。
このセクションの例では 4 つの初期化ブロックを使用して次の表が作成される。
可能な \(L\) ビット値 00
(\(T_0\)に保存される)01
(\(T_1\)に保存される)10
(\(T_2\)に保存される)11
(\(T_3\)に保存される)初期化 0 2 4 0 テストセグメント内の \(K\) 個のブロックをそれぞれ調べ、同じ \(L\) ビットブロックが最後に出現してからのブロック数を求める (つまり \(i-T_j\))。表の値を現在のブロックの位置で置き換える (つまり \(T_j=i\))。同じ \(L\) ビットブロックの再出現間の距離を計算し、\(K\) 個のブロックで検出されたすべての差の累積 \(\log_2\) 和に加える (つまり \({\it sum} = {\it sum} + \log_2(i-T_j)\))。
このセクションの例では表と累積和は次のように求められる:
ブロック 5 (第 1 テストブロック): 表の "01" 行 (つまり \(T_1\)) に 5 が置かれ、\({\it sum}\) \(= \log_2(5-2)\) \(=1.584962501\) である。
ブロック 6: 表の "11" 行 (つまり \(T_3\)) に 6 が置かれ、\({\it sum}\) \(= 1.584962501\) \(+ \log_2(6-0)\) \(= 1.584962501\) \(+ 2.584962501\) \(= 4.169925002\) である。
ブロック 7: 表の "01" 行 (つまり \(T_1\)) に 7 が置かれ、\({\it sum}\) \(= 4.169925002\) \(+ log2(7-5)\) \(= 4.169925002\) \(+ 1\) \(= 5.169925002\) である。
ブロック 8: 表の "01" 行 (つまり \(T_1\)) に 8 が置かれ、\({\it sum}\) \(= 5.169925002\) \(+ log2(8-7)\) \(= 5.169925002\) \(+ 0\) \(= 5.169925002\) である。
ブロック 9: 表の "01" 行 (つまり \(T_1\)) に 9 が置かれ、\({\it sum}\) \(= 5.169925002\) \(+ log2(9-8)\) \(= 5.169925002\) \(+ 0\) \(= 5.169925002\) である。
ブロック 10: 表の "11" 行 (つまり \(T_3\)) に 10 が置かれ、\({\it sum}\) \(= 5.169925002\) \(+ log2(10-6)\) \(= 5.169925002\) \(+ 2\) \(= 7.169925002\) である。
テーブルの状態は次のようになる:
初期化ブロック 可能な \(L\) ビット値 00 01 10 11 4 0 2 4 0 5 0 5 4 0 6 0 5 4 6 7 0 7 4 6 8 0 8 4 6 9 0 9 4 6 10 0 9 4 10 検定統計量の算出: \(f_n=\frac{1}{K} \sum_{i=Q+1}^{Q+K} \log_2(i-T_j)\)、ここで \(T_j\) は \(i\) 番目の \(L\) ブロックの内容の 10 進数表現に対応する表項目である。
このセクションの例では \(f_n=\frac{7.169925002}{6} = 1.1949875\) である。
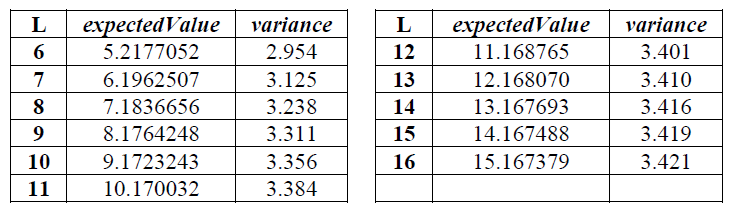
P 値\(= {\bf erfc}\left(\left|\frac{f_n-{\it expectecValue}(L)}{\sqrt{2}\sigma}\right|\right)\) を算出する。ここで \({\bf erfc}\) はセクション 5.5.3 で定義されており、\({\it expectedValue}(L)\) と \(\sigma\) は事前に計算された値2の表 (下記の表参照) からの取得する。ランダム性の仮定の下で標本平均 \({\it expectedValue}(L)\) は与えられた \(L\) ビット長に対して計算された統計量の理論上の期待値である。理論的な標準偏差は \(\sigma=c\sqrt{\frac{{\it variance}(L)}{K}}\) で与えられ、ここで \(c=0.7-\frac{0.8}{L}+\left(4+\frac{32}{L}\right)\frac{K^{-3/L}}{15}\) である。
このセクションの例では \(P\mbox{-}{\it value}={\bf erfc}\left(\left|\frac{1.1949875-1.5374383}{\sqrt{2}\sqrt{1.338}}\right|\right)=0.767189\) である。長さ 2 のブロックは検定には推奨されないので \(L=2\) の期待値と分散は上の表では提供されていないことに注意。しかしこの \(L\) の値は例題で扱いやすい値である。\(L=2\) の場合の期待値と分散は上記の表には示されていないがリファレンスで示した文献3から引用した。
 2.9.5 決定規則 (1%水準)
2.9.5 決定規則 (1%水準)
算出された P 値が \(\lt 0.01\) の場合、シーケンスは非ランダムであると結論づける。そうでなければシーケンスはランダムであると結論づける。
 2.9.6 結論と結果の解釈
2.9.6 結論と結果の解釈
セクション 2.9.4 のステップ 5 で得られた P 値は \(\ge 0.01\) (つまり P 値=0.767189) であるためシーケンスはランダムであるという結論となる。
セクション 2.9.4 のステップ 5 の表に示すように \(\varphi\) の理論的な期待値が計算されている。\(f_n\) が \({\it expectedValud}(L)\) と大きく異なる場合、シーケンスは大幅に圧縮可能である。
 2.9.7 推奨入力サイズ
2.9.7 推奨入力サイズ
この検定は長いビット列を必要とし \(n \ge (Q+K)L\))、、それは \(L\) ビットブロックの 2 つのセグメントに分けられ、\(6 \le L \le 16\) となるように選択されるべきである。最初のセグメントは \(Q\) 個の初期化ブロックからなり、\(Q=10\cdot 2^L\) となるように選択すべきである。第 2 セグメントは \(K\) 個のテストブロックからなり \(K=\lceil n/L \rceil-Q\approx 1000 \cdot 2^L\) となる。\(L\), \(Q\), \(n\) の値は次のように選ぶべきである。
 2.9.8 例
2.9.8 例
| (入力) | \(\epsilon=\)G-SHA-14で構築したバイナリ列 |
| (入力) | \(n=1048576\), \(L=7\), \(Q=1280\) |
| (注意) | 4 ビットは破棄される。 |
| (処理) | \(c=0.591311\), \(\sigma=0.002703\), \(K=148516\), \({\it sum}=919924.038020\) |
| (処理) | \(f_n=6.194107\), \({\it expectedValue}=6.196251\), \(\sigma=3.125\) |
| (出力) | \(P\mbox{-}{\rm value}=0.427733\) |
| (結論) | \(P\mbox{-}{\rm value}\gt 0.01\) であるためシーケンスがランダムであることを受理する。 |
 2.10 Linear Complexity Test
2.10 Linear Complexity Test
 2.11 Serial Test
2.11 Serial Test
 2.12 Approximate Entropy Test
2.12 Approximate Entropy Test
 2.13 Cumulative Sums (Cusum) Test
2.13 Cumulative Sums (Cusum) Test
 2.14 ランダム偏差検定
2.14 ランダム偏差検定
 2.14.1 検定目的
2.14.1 検定目的
この検定の焦点は累積和ランダムウォークにおいてちょうど \(K\) 回の訪問を持つサイクルの数である。累積和ランダムウォークは、\((0,1)\) シーケンスを適切な \((-1,+1)\) シーケンスに変換した後の部分和から導出される。ランダムウォークの 1 サイクルは、原点から始まり原点に戻る単位長のランダムなステップの列で構成されている。この検定の目的は、1 サイクル内の特定の状態への訪問回数がランダムなシーケンスで期待される階数から逸脱しているかを判断することである。この検定は実際には 8 つの検定 (および結論) のシリーズであり、各状態 -4, -3, -2, -1 と +1, +2, +3, +4 に対して 1 つの検定と結論がある。
 2.14.2 関数実行
2.14.2 関数実行
\({\rm RandomExcursions}(n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
 2.14.3 検定統計量と参照分布
2.14.3 検定統計量と参照分布
統計量の参照分布は \(\chi^2\) 分布である。
 2.14.4 検定内容
2.14.4 検定内容
正規化された \((-1,+1)\) シーケンス \(X\) を形成する: 入力シーケンス (\(\epsilon\)) の 0 と 1 は \(X_i=2\epsilon_i-1\) を介して \(-1\) と \(+1\) の値に変更される。
例えば \(\epsilon=0110110101\) は \(n=10\) で \(X=-1,1,1,-1,1,1,-1,1,-1,1\) である。
それぞれが \(X_1\) から始まる、連続するより大きな部分列の部分和 \(S_i\) を計算し集合 \(S={S_i\}\) を作る。\[ \begin{eqnarray*} S_1 & = & X_1 \\ S_2 & = & X_1 + X_2 \\ S_3 & = & X_1 + X_2 + X_3 \\ \vdots \\ S_k & = & X_1 + X_2 + X_3 + \ldots + X_k \\ \vdots \\ S_n & = & X_1 + X_2 + X_3 + \ldots + X_k + \ldots + X_n \end{eqnarray*} \]
このセクションの例では \[ \begin{array}{rclrcl} S_1 & = & -1 & S_6 & = & 2 \\ S_2 & = & 0 & S_7 & = & 1 \\ S_3 & = & 1 & S_8 & = & 2 \\ S_4 & = & 0 & S_9 & = & 1 \\ S_5 & = & 1 & S_{10} & = & 2 \\ \end{array} \] より集合 \(S=\{-1,0,1,0,1,2,1,2,1,2\}\) とする。
集合 \(S\) の前後に 0 を付けて新しい列 \(S'\) をつくる。つまり \(S'=0,s_1,s_2,\ldots,s_n,0\) とする。
このセクションの例では \(S'=0,-1,0,1,0,1,2,1,2,0\) とし、その結果のランダムウォークは次のようになる。
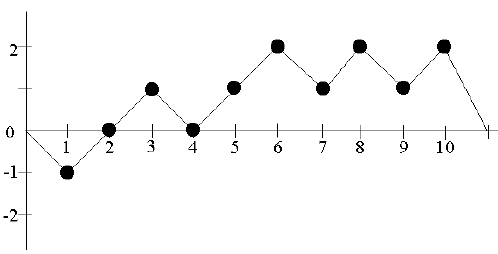
ランダムウォーク (\(S'\)) の例 \(J\) を \(S'\) のゼロ交差の総数とする。ここでゼロ交差とは開始時のゼロの後に発生する \(S'\) のゼロ値である。\(J\) はまた \(S'\) のサイクル数でもある。ここで \(S'\) のサイクルは、ゼロの発生後にゼロ以外の値の連続があり別のゼロで終わる \(S'\) の部分和である。あるサイクルの終了ゼロは別のサイクルの開始ゼロとなっているかもしれない。\(S'\) のサイクル数はゼロ公差の数である。\(J \lt 500\) であれば検定を中止する。
このセクションの例では \(S'=\{0,-1,0,1,0,1,2,1,2,1,2,0\}\) より \(J=3\) である (\(S'\) の位置 3, 5, 12 にゼロがある)。このゼロ公差は上記のプロットで簡単に確認できる。\(J=3\) より \(\{0,-1,0\}\), \(\{0,1,0\}\), \(\{0,1,2,1,2,1,2,0\}\) からなる 3 つのサイクルが存在することになる。
各サイクルで、値 \(-4\ge x\ge -1\) と \(1\ge x\ge 4\) を持つ非ゼロの状態数 \(x\) について、各サイクル内で各 \(x\) の頻度を計算する。
このセクションの例ではステップ 3 で第 1 サイクルに -1 が 1 回、第 2 サイクルに 1 回、第 3 サイクルに 1 と 2 が各 3 回出現していることになる。これは次の表を使って可視化することができる。
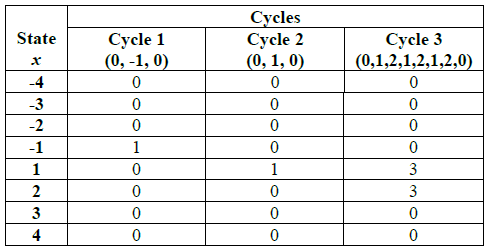
\(x\) の 8 個の状態それぞれについて、\(k=0,1,\ldots,5\) に対して \(v_k(x)=\)状態 \(x\) が全サイクル中にちょうど \(k\) 回発生するサイクルの総数とする (\(k=5\) の場合、頻度\(\ge 5\) はすべて \(v_5(x)\) に格納される)。なお \(\sum_{k=0}^5 v_k(x) = J\) である。
このセクションの例では
\(v_0(-1)=2\) (-1 状態は 2 つのサイクルで正確に 0 回発生)、
\(v_1(-1)=1\) (-1 状態は 1 つのサイクルで 1 回だけ発生)、
\(v_2(-1)=v_3(-1)=v_4(-1)=v_5(-1)=0\) (-1 状態は 0 個のサイクルで正確に \(\{2,3,4,\ge 5\}\) 回発生)。\(v_0(1)=1\) (1 状態は 1 つのサイクルで正確に 0 回発生)、
\(v_1(1)=1\) (1 状態は 1 つのサイクル 1 回だけ発生)、
\(v_3(1)=1\) (1 状態は 1 つのサイクルで正確に 3 回発生)、
\(v_2(1)=v_4(1)=v_5(1)=0\) (1 状態は 0 個のサイクルで正確に \(\{1,4,\ge t\}\) 回発生)。\(v_0(2)=2\) (2 状態は 2 つのサイクルで正確に 0 回発生)、
\(v_3(2)=1\) (2 状態は 1 つのサイクルで正確に 3 回発生)、
\(v_1(2)=v_2(2)=v_4(2)=v_5(2)=0\) (1 状態 (訳注: 2の誤記?) は 0 個のサイクルで正確に \(\{1,2,4,\ge 5\}\) 回発生)。\(v_0(-4)=3\) (-4 状態は 3 つのサイクルで正確に 0 回発生)、
\(v_1(-4)=v_2(-4)=v_3(-4)=v_4(-4)=v_5(-4)=0\) (-4 状態は 0 個のサイクルで正確に \(\{1,2,3,4,\ge 5\}\) 回発生)。
などなど…
これは次の表を用いて表される:
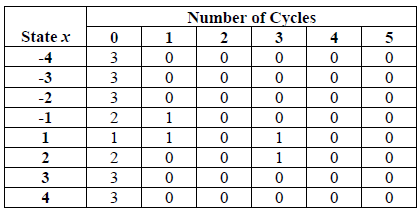
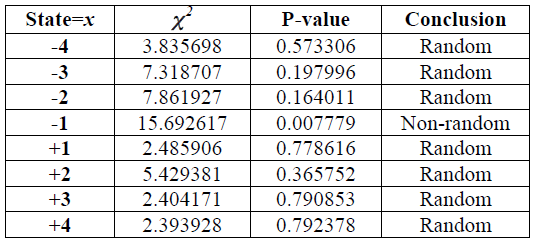
\(x\) の 8 個の状態それぞれに対して検定統計量 \(\chi^2(obs)=\sum_{k=0}^5\frac{(v_k(x)-J\pi_k(x))^2}{J\pi_k(x)}\) を算出する。ここで \(\pi_k(x)\) はランダムな分布の中で状態 \(x\) が \(k\) 回発生する確率である (\(\pi_k\) 値の表はセクション 3.14 参照)。\(\pi_k(x)\) の値とその計算方法はセクション 3.14 に記載されている。\(\chi^2\) は 8 個生成されることに注意 (つまり \(x=-4,-3,-2,-1,1,2,3,4\) に対して)。
このセクションの例では、\(x=1\) のとき \(\chi^2=\frac{(1-3(0.5))^2}{3(0.5)}+\frac{(1-3(0.25))^2}{3(0.25)}+\frac{(0-3(0.125))^2}{3(0.125)}+\frac{(1-3(0.0625))^2}{3(0.0625)}+\frac{(0-3(0.0312))^2}{3(0.0312)}+\frac{(0-3(0.0312))^2}{3(0.0312)} = 4.333033\) である。
\(x\) の各状態に対して P 値\(= {\bf igamc}(5/2,\chi^2(obs)/2)\) を算出する。8 個の P 値が生成される。
このセクションの例では \(x=1\) のとき \(P\mbox{-}{\it value}={\bf igamc}\left(\frac{5}{2},\frac{4.333033}{2}\right)=0.502529\) である。
 2.14.5 決定規則 (1%水準)
2.14.5 決定規則 (1%水準)
算出された P 値が \(\lt 0.01\) の場合、シーケンスは非ランダムであると結論づける。そうでなければシーケンスはランダムであると結論づける。
 2.14.6 結論と結果の解釈
2.14.6 結論と結果の解釈
セクション 2.14.4 のステップ 8 で得られた P 値は \(\ge 0.01\) (つまり P 値=0.502529) であるためシーケンスはランダムであるという結論となる。
大きすぎる \(\chi-2(obs)\) はすべてのサイクルにおいてある状態に対する論理分布からのずれを示すことに注意。
 2.14.7 推奨入力サイズ
2.14.7 推奨入力サイズ
検定する各シーケンスは最低 1,000,000 ビット (つまり \(n \ge 10^6\)) で構成することを推奨する。
 2.14.8 例
2.14.8 例
 2.15 ランダム偏差変種検定
2.15 ランダム偏差変種検定
 2.15.1 検定目的
2.15.1 検定目的
この検定の焦点は累積和ランダムウォークにおいて特定の状態が訪問される (つまり発生する) 総回数である。この検定の目的は、ランダムウォークにおける様々な状態への訪問回数の期待値からの逸脱を検出することである。この検定は実際には 18 個の検定 (および結論) のシリーズであり、各状態 -9, -8, …, -1 と +1, +2, …, +9 に対して 1 つの検定と結論がある。
 2.15.2 関数実行
2.15.2 関数実行
\({\rm RandomExcursionsVariant}(n)\)
関数によって使用されるが検定コードによって提供される追加の入力:
 2.15.3 検定統計量と参照分布
2.15.3 検定統計量と参照分布
検定統計量の参照分布は半正規分布 (\(n\) が大きい場合) である。(注: \(\xi\) が正規分布であれば \(|\xi|\) は半正規分布である。) シーケンスがランダムであれば検定統計量は約 0 となり、1 か 0 が多すぎれば検定統計量は大きくなる。
 2.15.4 検定内容
2.15.4 検定内容
正規化された \((-1,+1)\) シーケンス \(X\) を形成する: 入力シーケンス (\(\epsilon\)) の 0 と 1 は \(X_i=2\epsilon_i-1\) を介して \(-1\) と \(+1\) の値に変更される。
例えば \(\epsilon=0110110101\) は \(n=10\) で \(X=-1,1,1,-1,1,1,-1,1,-1,1\) である。
それぞれが \(X_1\) から始まる、連続するより大きな部分列の部分和 \(S_i\) を計算し集合 \(S={S_i\}\) を作る。\[ \begin{eqnarray*} S_1 & = & X_1 \\ S_2 & = & X_1 + X_2 \\ S_3 & = & X_1 + X_2 + X_3 \\ \vdots \\ S_k & = & X_1 + X_2 + X_3 + \ldots + X_k \\ \vdots \\ S_n & = & X_1 + X_2 + X_3 + \ldots + X_k \ldots + X_n \\ \end{eqnarray*} \]
このセクションの例では \[ \begin{array}{rclrcl} S_1 & = & -1 & S_6 & = & 2 \\ S_2 & = & 0 & S_7 & = & 1 \\ S_3 & = & 1 & S_8 & = & 2 \\ S_4 & = & 0 & S_9 & = & 1 \\ S_5 & = & 1 & S_{10} & = & 2 \\ \end{array} \] より集合 \(S=\{-1,0,1,0,1,2,1,2,1,2\}\) とする。
集合 \(S\) の前後に 0 を付けて新しい列 \(S'\) をつくる。つまり \(S'=0,s_1,s_2,\ldots,s_n,0\) とする。
このセクションの例では \(S'=0,-1,0,1,0,1,2,1,2,0\) とし、その結果のランダムウォークは次のようになる。

ランダムウォーク (\(S'\)) の例 \(x\) の 18 個の非ゼロ状態それぞれについて、\(\xi(x)=\)その状態 \(x\) が全 \(J\) サイクルに渡って発生した総回数を計算する。
このセクションの例では \(\xi(-1)=1\), \(xi(1)=4\), \(xi(2)=3\), その他すべては \(\xi(x)=0\) である。
各 \(\xi(x)\) について P 値 \(={\bf erfc}\left(\frac{|\xi(x)-J|}{\sqrt{2J(4|x|-2)}}\right)\) を計算する。8 個の P 値が算出される。\({\bf erfc}\) の定義についてはセクション 5.5.3 参照。
このセクションの例では、\(x=1\) のとき \(P\mbox{-}{\it value}={\bf erfc}\left(\frac{4-3}{\sqrt{2\cdot 3(4|1|-2)}}\right)=0.683091\) である。
 2.15.5 決定規則 (1%水準)
2.15.5 決定規則 (1%水準)
算出された P 値が \(\lt 0.01\) の場合、シーケンスは非ランダムであると結論づける。そうでなければシーケンスはランダムであると結論づける。
 2.15.6 結論と結果の解釈
2.15.6 結論と結果の解釈
セクション 2.15.4 のステップ 7 (訳注: ステップ 5 の誤記?) で得られた P 値は \(\ge 0.01\) (つまり P 値=0.683091) であるためシーケンスはランダムであるという結論となる。
 2.15.7 推奨入力サイズ
2.15.7 推奨入力サイズ
検定する各シーケンスは最低 1,000,000 ビット (つまり \(n \ge 10^6\)) で構成することを推奨する。
 2.15.8 例
2.15.8 例
| (入力) | \(\epsilon=\)"\(e\) の1,000,000ビットまでの2進数展開" |
| (入力) | \(n=1000000=10^6\) |
| (処理) | \(J=1490\) 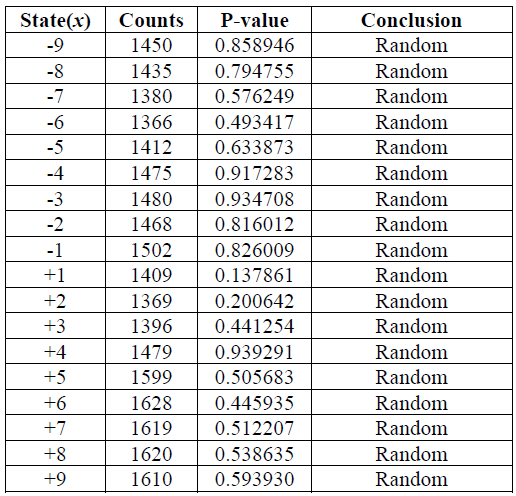
|
| (結論) | \(x\) の 18 の状態それぞれについて P 値 \(\ge 0.01\) であるためシーケンスはランダムであると結論づけられる。 |
- 2“Handbook of Applied Cryptography” より。
- 3“Handbook of Applied Cryptography” より。
- 4FIPS 186-2 で定義されている。
- 6カイ二乗計算の経験則を満たすには、セクション 3.14 の表で求めた最小値の \(J\) 倍が \(\ge 5\) でなければならない。
 3. 検定の技術的説明
3. 検定の技術的説明
このセクションは NIST 検定スイートにおける検定の数学的背景を含んでいる。各サブセクションはセクション 2 の該当するサブセクションに対応する。各サブセクションに関連する参考文献は、そのサブセクションの最後に記載されている。
 3.1 頻度 (モノビット) 検定
3.1 頻度 (モノビット) 検定
最も基本的な検定は帰無仮説の検定である。独立同分布のベルヌーイ確率変数の列 (\(X\) または \(\epsilon\)、ここで \(X=2\epsilon-1\) であり、したがって \(S_n=X_1+X\ldots+X_n=2(\epsilon_1+\ldots+\epsilon_n)-n\)) において 1 の確率は 1/2 である。古典的な De Moivre-Laplace 定理により十分な試行回数では \(\sqrt{n}\) で正規化された二項和の分布は標準正規分布によって厳密に近似される。この検定では 1 の割合が 1/2 に近いことを評価するためにその近似を利用する。後続のすべての検定は、この最初の基本検定に合格することを条件としている。
この検定はランダムウォーク \(S_n=X_1+\ldots+X_n\) に対するよく知られた中央極限定理から導かれる。中央極限定理によれば \[ \begin{equation} \lim_{n\to\infty}P\left(\frac{S_n}{\sqrt{n}} \le z\right) = \Phi(z) \equiv \frac{1}{\sqrt{2}} \int_{-\infty}^z e^{-u^2/2} du \label{e1} \end{equation} \] この古典的な結果は最も単純なランダム性の検定の基礎となる。これは正の \(z\) に対して \[ P\left(\frac{|S_n|}{\sqrt{n}} \le z\right) = 2\Phi(z)-1 \] を意味する。
統計量 \(s=|S_n|/\sqrt{n}\) に基づく検定により、観測値 \(|s(obs)|=|X_1+\ldots+X_n|/\sqrt{n}\) を評価して対応する P 値を計算する。ここで \(2[1-\Phi(|s(obs)|)]={\rm erfc}(|s(obs)|/\sqrt{n})\) である。ここで \({\rm erfc}\) は (相補) 誤差関数 \[ {\rm erfc}(z)=\frac{2}{\sqrt{\pi}} \int_z^\infty e^{-u^2} du \] である。
 3.2 ブロック内頻度検定
3.2 ブロック内頻度検定
この検定では検定シーケンスをいくつかの重ならないサブシーケンスに分解し、経験的な頻度が理想的な 1/2 に一様に一致するかどうかをカイ二乗検定を適用して、1 の頻度が 50% の理想値から局所的に逸脱していることを検出しようというものである。P 値が小さいと言うことは少なくとも 1 つの部分列で 1 と 0 の比率が等しいと言うことから大きく外れていることを示している。0 と 1 (または同等の -1 と 1) の列はいくつかの不連続な部分列に分割される。それぞれの部分列について 1 の割合が計算される。カイ二乗統計量はこれらの部分列の比率を理想的な 1/2 と比較する。この統計量は部分列の数に等しい自由度を持つカイ二乗分布として参照される。
この検定のパラメータは \(M\) と \(N\) であるため \(n=MN\) となる。つまり元のビット列はそれぞれの長さが \(M\) となる \(N\) 個の部分列に分割される。これらの部分列のそれぞれについて、1 の確率は 1 の相対頻度 \(\pi_i\), \(i=1,\ldots,N\) から推定される。ランダム性仮説の元での合計 \[ X^2(obs) = 4M\sum_{i=1}^N \left[ \pi_i - \frac{1}{2} \right]^2 \] は自由度 \(N\) の \(X^2\) 分布を持つ。報告される P 値は \[ \frac{\int_{X^2(obs)}^\infty e^{-u/2} u^{N/2-1} du}{\Gamma(N/2) 2^{N/2}} = \frac{\int_{X^2(obs)/2}^\infty e^{-u} u^{N/2-1} du9}{\Gamma(N/2)} = {\rm igamc}\left(\frac{N}{2}, \frac{X^2(obs)}{2}\right) \] である。
 3.3 Runs Test
3.3 Runs Test
 3.4 Test for the Longest Run of Ones in a Block
3.4 Test for the Longest Run of Ones in a Block
 3.5 Binary Matrix Rank Test
3.5 Binary Matrix Rank Test
 3.6 Discrete Fourier Transform (Specral) Test
3.6 Discrete Fourier Transform (Specral) Test
 3.7 Non-Overlapping Template Matching Test
3.7 Non-Overlapping Template Matching Test
 3.8 Overlapping Template Matching Test
3.8 Overlapping Template Matching Test
 3.9 Maurer's "Universal Statistical" Test
3.9 Maurer's "Universal Statistical" Test
 3.10 Linear Complexity Test
3.10 Linear Complexity Test
 3.11 Serial Test
3.11 Serial Test
 3.12 Approximate Entropy Test
3.12 Approximate Entropy Test
 3.13 Cumulative Sums (Cusum) Test
3.13 Cumulative Sums (Cusum) Test
 3.14 Random Excursions Test
3.14 Random Excursions Test
 3.15 Random Excursions Variant Test
3.15 Random Excursions Variant Test
 4. 検定の戦略と結果の解釈
4. 検定の戦略と結果の解釈
このセクションでは (1) 乱数生成器の統計分析の戦略、(2) NIST 統計検定スイートを用いた経験的結果 (empirical results) の解釈、(3) 一般的な推奨事項とガイドラインの 3 つのトピックについて説明する。
 4.1 RNG の統計分析の戦略
4.1 RNG の統計分析の戦略
現実に乱数生成器の統計分析には多くの異なる戦略がある。NIST は Figure 1 に示すような戦略を採用している。Figure 1 は乱数生成器の統計検定に関わる 5 つの段階のアーキテクチャ図を示している。
- ステージ 1: 生成器の選択
-
評価用のハードウェアまたはソフトウェアベースの生成器を選択する。生成器は指定された長さ \(n\) の 0 と 1 のバイナリ列を生成する必要がある。選択できる疑似乱数生成器 (PRNG) の例には ANSI X9.17 (Appendix C) の DES ベースの PRNG、および FIPS 186 (Appendix 3) に規定されているセキュアハッシュアルゴリズム (SHA-1) とデータ暗号化基準 (DES) に基づいた 2 つの方式がある。
- ステージ 2: バイナリ列の生成
-
長さ \(n\) の固定シーケンスと、事前に選択された生成器に対して、\(m\) 個のバイナリ列を構築し、シーケンスをファイル7に保存する。
- ステージ 3: 統計検定スイートを実行
-
ステージ 2 で生成されたファイルと目的のシーケンス長を使用して NIST 統計検定スイートを起動する。適用する統計検定と関連する入力パラメータ (ブロック長など) を選択する。
- ステージ 4: p 値を調べる
-
各統計検定の検定統計量や P 値など、関連する中間値を含む出力ファイルが検定スイートによって生成される。これらの P 値に基づいてシーケンスの品質に関する結論を下すことができる。
- ステージ 5: 評価: 合否判定
-
各統計検定について (シーケンスのセットに対応する) P 値のセットが生成される。一定の有意水準では P 値のある割合が失敗を示すと予想される。例えば有意水準 0.01 (すなはち \(\alpha=0.01\)) の場合、約 1% のシーケンスが不合格になると予想される。シーケンスが統計的検定に合格するのは P 値 \(\ge \alpha\)、そうでなければ不合格となる。各統計検定について、合格するシーケンスの割合が計算され、それに応じて分析される。より詳細な解析は追加の統計処理 (セクション 4.2.2 参照) を用いて実施する必要がある。
 4.2 経験的結果の解釈
4.2 経験的結果の解釈
経験的検証により発生する可能性のある事象の代表的な 3 つのシナリオを説明する。ケース 1: P 値がランダム性からの逸脱を示していない分析。ケース 2: ランダム性からの逸脱を明確に示す分析。ケース 3: 結論が出ない分析。
経験的結果の解釈は様々な方法で行うことができる。NIST が採用した 2 つのアプローチには (1) 統計的検定に合格した配列の割合の検討と、(2) 一様性を確認するための P 値分析が含まれている。ファイル finalAnalysisReport.txt にはこれらの 2 つの形式の解析結果が含まれている。
これらのアプローチのいずれかが失敗した場合 (つまり対応する無機仮説を棄却する必要がある場合)、その現象が統計的異常であるか、非ランダム性の明確な証拠であるかを判断するために、生成器の様々な標本に対して追加の数値実験を行う必要がある。
 4.2.1 検定に合格するシーケンスの割合
4.2.1 検定に合格するシーケンスの割合
特定の統計的検定に関する経験的結果が与えられたときに合格するシーケンスの割合を計算する。例えば 1000 個のバイナリ列 (つまり \(m=1000\)) が (有意水準) \(\alpha=0.01\) で検定されたとき、996 個のバイナリ列の P 値が 0.01 以上である場合、比率は 996/1000 = 0.9960 である。
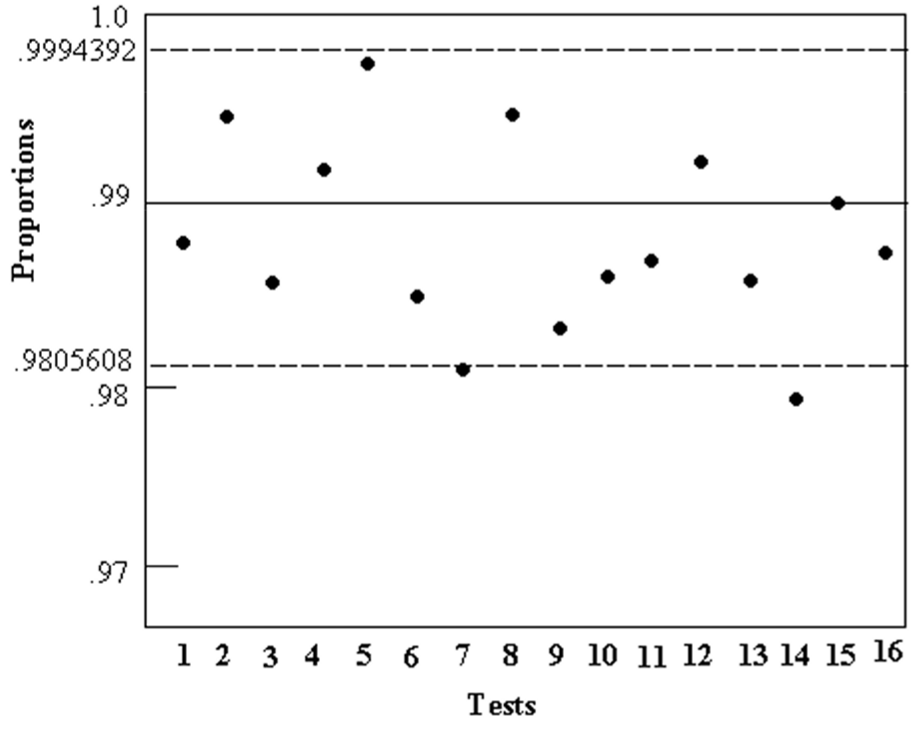
許容比率の範囲は \(\displaystyle \hat{p}\pm 3\sqrt{\frac{\hat{p}(1-\hat{p})}{m}}\) のように定義される信頼区間を用いて決定される。ここで \(\hat{p}=1-\alpha\)、\(m\) は標本サイズである。比率がこの範囲外であればデータが非ランダムであるという根拠がある。他の標準偏差の値を使用できることに注意。上記の例では信頼区間は \(.99\pm 3\sqrt{\frac{.99(.01)}{1000}}=.99\pm 0.0094392\) である (つまり比率は 0.9805607 より上にあるはずである)。これは Figure 4-1 に示すグラフを使って説明できる。信頼区間は二項分布の近似として正規分布を用いて計算された。これは大きなサンプルサイズ (例えば \(n\ge 1000\)) に対して合理的に正確である。
 4.2.2 P 値の一様分布
4.2.2 P 値の一様分布
P 値の分布が一様であることの確証を調べる。これはヒストグラム (Figure 4-2 参照) を使用して視覚的に説明できる。これにより 0 と 1 の区間が 10 個の小区間に分割され、各小区間内にある P 値がカウントされて表示される。
一様性は、χ² 検定を適用し、任意の統計検定で得られた P 値に対する適合度分布検定に対応する P 値を決定することで決定することもできる (つまり P 値の P 値)。これは \(\displaystyle \chi^2=\sum_{i=1}^{10}\frac{(F_i-s/10)^2}{s/10}\) を計算することで達成される。ここで \(F_i\) は小区間 \(i\) の P 値の数であり、\(s\) は標本サイズである。P 値は P 値\({}_T={\bf igamc}(9/2,\chi^2/2)\) となるように計算される。P 値\({}_T\ge 0.0001\) の場合、シーケンスは一様に分布していると見なすことができる。また統計的に意味のある結果を提供するには少なくとも 55 個のシーケンスを処理する必要がある。
 4.3 一般的な推奨事項とガイドライン
4.3 一般的な推奨事項とガイドライン
現実に、あるデータセットが統計的検定に不合格となった理由を説明するために多くの理由を挙げることができる。以下は考えられる説明のリストである。このリストは NIST の統計検定の取り組みに基づいて編集されたものである。
- 誤ってプログラムされた統計的検定.
特に明記されていない限り、統計検定は特定の問題クラスを扱うように調整されていると想定する必要がある。NIST の検定コードは入力パラメータを選択できるように記述されているため、コードは様々な方法で一般化されている。残念ながらこれらは必ずしもコーディングの用意さには繋がるわけではない。
いくつかの統計検定は人為的な上限で制約されている。例えばランダムエクスカージョン検定では \(\max\{1000,n/128\}\) サイクル以下と仮定している。実験条件によってはおそらく固定パラメータを増やす必要があるかも知れない。
- 未開発の (未熟な) 統計的検定.
確率論や複雑系理論が十分に開発または理解されておらず、統計的検定の厳密な分析ができない場合がある。
時間の経過に伴って統計的検定は新しい結果に照らして改訂される。多くの統計的検定が漸近的近似に基づいているため、近似がどの程度良いかを判断するために慎重な作業が必要である。
- 乱数生成器の実装が不適切.
ハードウェア PNG やソフトウェア PNG が、設計上の欠陥やコーディングの実装ミスにより故障した可能性は十分に考えられる。いずれの場合も、このような可能性を排除するために慎重な検討が必要である。
- 検定入力データの適用に不適切に記述されたコード.
精査が必要なもう一つの領域は検定データの適用 (harnessing) である。(P)RNG によって生成された検定データは統計検定で使用する前に処理する必要がある。例えば (P)RNG 空の出力ストリームを適切な大きさのブロックに分割したり、0 を負値に変換するなどの加工が必要な場合がある。過去には統計検定の失敗がデータを処理するためのコードのエラーに起因すると判断されることがあった。
- P 値を算出するための不十分な数学的ルーチン.
可能な限り優れた近似を行うために高品質の数学ソフトウェアを使用する必要がある。特に不完全Γ関数は定数 \(a\) の値が大きくなると近似が難しくなり、最終的には数値近似に起因する問題により P 値の公式が偽の値を示すことになる。その可能性を減らすために NIST は好ましい入力パラメータを規定している。
- 入力パラメータの選択が間違っている.
実際には、統計的検定では有効と思われるすべての入力パラメータに対して信頼できる結果を提供するわけではない。検定ごとに制約があることを認識することが重要である。例えば近似エントロピー検定を考えると、\(10^6\) 程度のシーケンス長の場合、\(\log_2 n\) 程度のブロック長が許容されると予想される。しかし残念ながらそうではない。経験的な証拠によると \(m=14\) を超えると観測された検定統計量は期待値と食い違うようになる (特に SHA-1 のような既知の優良ジェネレータの場合)。したがって、特定の統計検定は入力パラメータの影響を受けやすい可能性がある。
シーケンス長、標本サイズ、ブロックサイズ、テンプレートといった数値実験の入力パラメータについてはしばしば考慮する必要がある。
シーケンス長
統計的検定のためにどの程度の長さのシーケンスを取るべきかという判断は難しい。FIPS 140-1 統計検定を調べるとシーケンスは約 20,000 ビット長であるべきことが明らかである。
しかし、マウラーの普遍統計検定などの一部の統計検定では非常に長いシーケンス長が必要になるという意味で、比較的短いシーケンス長をとることが難しいことは問題である。その理由の一つは極限分布を決定する際に漸近的な近似が用いられるという認識である。特定の検定統計の分布に関する記述は長いシーケンスよりも短いシーケンスの方が対処は困難である。
標本サイズ
標本サイズの問題は有意水準の選択と関連している。NIST はこれらの検定においてユーザは有意水準を 0.001 以上 0.018 以下となるように固定することを推奨する8。有意水準に不釣り合いな標本サイズは適切ではない場合がある。例えば有意水準 (\(\alpha\)) が 0.001 とした場合、1000 シーケンスごとに 1 シーケンスが棄却されることが予想される。もし 100 シーケンスのみの標本が選択された場合、棄却が観測されることはほとんどない。この場合、十分に大きなサンプルが使用されなかった可能性が高いにもかかわらず生成器がランダムなシーケンスを生成していたという結論が導き出される可能性がある。したがってサンプルは有意水準の逆数 (\(\alpha^{-1}\)) のオーダーである必要がある。つまり有意水準が 0.001 であればサンプルは少なくとも 1000 個のシーケンスが必要である。理想的には多くの異なる標本を分析する必要がある。
ブロックサイズ
ブロックサイズは個々の統計検定に依存する。マウラーの普遍統計検定ではブロックサイズの範囲は 1~16 である。ただし特定のブロックサイズごとに最小のシーケンス長を使用する必要がある。ブロックサイズが 16 に固定されている場合、10 億ビットを超えるシーケンスが必要になるが、ユーザによってはそれは実現不可能かも知れない。
直感的にはブロックサイズが大きいほど近似エントロピー検定などのシーケンスの解析からより多くの情報を取得できるように思われる。しかし大きすぎるブロックサイズも選択すべきではない。さもなくば検定統計量が明確な確率分布によってより適切に近似されるため、実験結果が誤解を招き不正確になる可能性がある。実際には NIST は \(\lfloor \log_2 n \rfloor\) (\(n\) はシーケンス長) 以下のブロックサイズを選択することを推奨する。
テンプレート
特定の統計的検定は全体的な非ランダム性を検出するのに適している。しかし他の統計的検定はシーケンス内に存在する \(m\) ビットパターンが多すぎることを検出するために開発された検定など、局所的な非ランダム性を評価するのに適している。それでも \(\lfloor \log_2 n \rfloor\) より大きいブロックサイズのテンプレートを選択すべきでないことは理にかなっている。なzれなら頻度カウントはほとんどの場合に有用な情報を提供しないゼロの近傍となるためである。したがって適切な選択を行う必要がある。
その他の考慮事項
原則としてランダム性検定に関してよくある質問が多くある。おそらくもっともよくある質問は "いくつの検定を採用すべきか?" であろう。実際には誰もこの質問に真に答えることはできない。検定は可能な限り互いに独立したものであるべきと考えている。
もう一つのよくある質問は、マウラーの普遍統計検定の代わりにモノビット検定 (頻度検定) を提供する必要性についてである。マウラーの普遍統計検定はモノビット検定を適用する必要性に取って代わるという認識がある。これは無限の長さのシーケンスでは当てはまるかも知れない。しかし有限のバイナリ列がマウラーの普遍統計検定に合格してもモノビット検定で不合格になる場合があることに留意することが重要である。このため NIST では頻度検定を適用することを推奨している。この検定の結果が帰無仮説を支持する場合、ユーザは他の統計検定の適用に進むことができる。
 4.4 複数の検定の適用
4.4 複数の検定の適用
複数の検定の適用に関する懸念から、NIST は検定間の依存性を判断するための調査を実施した。検定の性能はシーケンスから得られた P 値に対してコルモゴロフ–スミルノフ検定を用いて一様性の検定を行うことで確認した。しかし一様性を検定するために生成されたシーケンスが十分にランダムであるという仮定が必要であった。スイートには多くの検定がある。いくつかの検定は直感的に独立した答えが得られるはずである (例えば頻度検定と頻度を条件とする連検定はランダム性の全く異なる側面を評価するはずである)。その他の累積和検定や連検定などでは相関する可能性が高い P 値が得られる。
冗長な検定を排除するために検定間の依存関係を理解し、スイート内の検定が妥当な範囲のパターン化された動作を検出できることを確認するために、結果の P 値の要因分析を行った。より正確には、独立性を評価するために長さ \(n\) の 2 進疑似乱数のシーケンスを \(m\) 個生成し、そのランダム性を決定するためにスイートのすべての \(k=161\) 個の検定に適用し、各検定で有意確率が得られた。シーケンス \(j\) に対する検定 \(i\) の有意確率を \(p_{ij}\) とする。
一様分布 \(p_{ij}\) が与えられると変換 \(z_{ij}=\Phi^{-1}(p_{ij})\) は正規分布の変数を導く。\(i\) 番目のシーケンスに対応する変換された有意確率のベクトルを \(z_j\) とする。\(z_1,\ldots,z_m\) に対して主成分分析を行った。通常、変動制の大部分を説明するには少数の成分で十分であり、これらの成分の数は一連の検定が及ぶ非ランダム性の "次元" 数の定量化に使用できる。このデータの主成分分析を行った。この分析では、検定の数に等しい 161 の因子が抽出される。最初の因子は最大の変動性を説明するものである。多くの検定が相関している場合、それらの P 値はこの因子に大きく依存し、この因子によって説明される全変動性の割合は大きくなる。2 番目の因子は、2 番目の因子が 1 番目の因子と直交するという制約の下で、2 番目に大きい変動性の割合を説明し、以降の因子についても同様である。長さ 1,000,000 の Blum-Blum-Shub シーケンスに基づいて最初の 50 の因子に対応する分数をプロットした。このグラフは検定間に大きな冗長性がないことを示した。
\(z_1,\ldots,z_m\) から形成される相関行列は統計ソフトウェア (SAS) を介して構築された。これらの行列の構造からも同じ結論が支持された。検定間の重複の程度は非常に小さいと考えられる。
- 7サンプルデータは George Marsaglia の乱数 CD-ROM (http://stat.fsu.edu/pub/diehard/cdrom/) から入手することもできる。
- 8なお FIPS 140-2 ではパワーアップ検定の有意水準は 0.0001 に設定されている。
 5. ユーザガイド
5. ユーザガイド
このセクションでは NIST の検定コードで利用可能な、NIST によって開発された統計検定のセットアップと適切な使用方法について説明する。使用したアルゴリズムとデータ構造の説明もこのセクションに含まれている。
 5.1 パッケージについて
5.1 パッケージについて
このツールボックスは暗号論的 (P)RNG の統計的検定の実施に関心のある人のために特別に設計された。またプロジェクトの開発段階で使用された PRNG のいくつかの実装も含まれている。
このパッケージは (P)RNG のランダム性を評価する課題に取り組むもので、次のことに役に立つ:
- 弱い (またはパターン化された) バイナリ列を生成する (P)RNG の識別。
- 新しい (P)RNG の設計。
- (P)RNG の実装が正しいかの検証。
- 標準で詳述されている (P)RNG の研究。
- 現在使用されている (P)RNG によるランダム性の程度の調査。
NIST 統計検定スイートの開発の目的は次の通り:
- プラットフォーム独立: ソースコードは ANSI C で書かれているが、ターゲットとなるプラットフォームやコンパイラによっては多少の修正が必要である。
- 柔軟性: ユーザは独自の数学ソフトウェアルーチンを自由に導入できる。
- 拡張性: 新しい統計検定を容易に取り入れることができる。
- 汎用性: PRNG, RNG, 暗号アルゴリズムの検定に有用である。
- 移植性: 些細な修正によりソースコードを異なるプラットフォームに移植することができる。NIST のソースコードは Visual Studio 2005 コンパイラを実行する Windows XP システムと、gcc を実行する Ubuntu Linux システムに移植された。
- 直交性: 多様な検定セットが提供されている。
- 効率性: 可能な限り線形時間または線形空間のアルゴリズムを使用した。
 5.2 システム要件
5.2 システム要件
このソフトウェアパッケージは当初 Solaris オペレーティングシステムの SUN ワークステーションで開発された。すべてのソースコードは ANSI C で記述されている。最新の改訂は Intel Core 2 Duo プロセッサを搭載した Apple MacBook Pro で gcc コンパイラを使用して作成された。
実際には、検定の正しい解釈を保証するために移植の改訂で小さな修正を加えなければならないかも知れない。ユーザが別のプラットフォームでコードをコンパイルして実行した場合に備えて、標本データと各統計検定の対応する結果が提供されている。このようにしてユーザは移植された統計検定スイートが正しく機能しているという確証を得ることができる。詳細については Appendix B を参照。
統計検定の大部分では実行するためにメモリを動的に割り当てる必要がある。ワークスペースを提供できない場合、統計検定は診断メッセージを返す。
 5.3 開始までの流れ
5.3 開始までの流れ
ワークステーションに NIST 検定コードのコピーをセットアップするには次の手順で行う。
sts.tarファイルをルートディレクトリにコピーし、tar -xvf sts.tar命令でソースコードをアンバンドルする。6 個のサブディレクトリと 1 つのファイルが作成されているはずである。サブディレクトリは
data/,experiments/,include/,obj/,src/,templates/でファイルはmakefileである。data/サブディレクトリは調査中の既存の RNG データファイル用に予約されている。現在、ASCII の 0 と 1 で構成されるデータファイルと、バイナリデータファイルの 2 つの形式がサポートされている。experiments/サブディレクトリは統計検定の経験的結果を格納する。そこにはAlgorithmTesting/,BBS/,CCG/,G-SHA1/,LCG/,MODEXP/,MP/,QCG1/,QCG2/,XOR/を含むいくつかのサブディレクトリがある。これらのサブディレクトリの最初のものを除くすべては対応する PRNG の結果を保存するためのものである。AlgorithmTesting/サブディレクトリはdata/サブディレクトリに格納された RNG データに対応する経験的結果のデフォルトのサブディレクトリである。include/サブディレクトリは統計的検定、疑似乱数生成器、その他関連ルーチンのヘッダーファイルが含まれている。obj/サブディレクトリは統計的検定、疑似乱数生成器、その他関連ルーチンのオブジェクトファイルが含まれている。src/サブディレクトリには各統計検定のソースコードが含まれている。templates/サブディレクトリには NonOverlapping Templates 統計検定で使用する様々なブロックサイズの一連の非周期的なテンプレートが含まれている。ユーザによる所定の修正をいくつかのファイルに導入することができる。これについてはセクション 5.5.2 および Appendix A で後述する。
makefileを編集する。次の行を変更する。CC(ANSI C コンパイラ)ROOTDIR(rng/のような、手順の前半で指定したルートディレクトリ)
ここで
makefileを実行する。プロジェクトディレクトリにassessと言う名前の実行ファイルができるはずである。これでデータを評価することができる。
assess <sequenceLengt>、例えばassess 1000000のように入力する。
メニュープロンプトに従う。
 5.4 データ入力と経験的結果の出力
5.4 データ入力と経験的結果の出力
 5.4.1 データ入力
5.4.1 データ入力
データ入力には 2 つの方法がある。ユーザが RNG を実装するスタンドアロンプログラムまたはハードウェアデバイスを持っている場合、ユーザは任意の長さのファイルを必要な数だけ作成することができる。ファイルには 0 と 1 で構成される ASCII 文字、または各バイトに 8 ビット分の 0 と 1 が含まれるバイナリデータとして保存されたバイナリ列を含む必要がある。NIST 統計検定スイートはこれらのファイルを独自に検査することができる。
ストレージ容量に問題がある場合、ユーザは参照実装を変更して評価中の PRNG 実装をプラグインすることができる。ビットストリームはバイナリ列を含むイプシロンデータ構造に直接格納される。
 5.4.2 経験的結果の出力
5.4.2 経験的結果の出力
経験的結果の出力ログは、データセットに適応された各統計検定の検定統計量、中間パラメータ、P 値などの計算情報にそれぞれ対応する stats と results の 2 つのファイルに保存される。
これらのファイルが適切に作成されていない婆、出力用にファイルを開くことが原因である可能性が高い。詳細は Appendix C を参照。
 5.4.3 検定データファイル
5.4.3 検定データファイル
6 個の標本ファイルが作成され data/ サブディレクトリに保存されている。これらのファイルのうち 4 つは 1,000,000 ビットを超えるいくつかの古典的な数値の Mathematica9によるバイナリ展開に対応するものである。これらのファイルは data.e, data.pi, data.sqrt2, data.sqrt3 である。これらのファイルの作成に使用された Mathematica プログラムは Appendix F にある。5 番目のファイル data.sha1 は SHA-1 ハッシュ関数を使用して作成された。最後のサンプルファイルは偏った PRNG によって生成されたもので、特定の統計検定に失敗することを意図している。
 5.5 プログラムレイアウト
5.5 プログラムレイアウト
検定スイートパッケージは統計検定と (疑似) 乱数生成器、経験的結果 (階層) ディレクトリ、およびデータを含む一連のモジュールに分解されている。
NIST 検定スイートの 3 つの主要コンポーネントは統計検定、基板となる数学ソフトウェア、調査対象の疑似乱数生成器である。その他のコンポーネントにはソースコードライブラリファイル、データディレクトリおよびサンプルデータファイルと経験的結果ログをそれぞれ含む階層ディレイクトリ (experiments/) が含まれる。
 5.5.1 一般プログラム
5.5.1 一般プログラム
NIST 検定スイートには乱数および疑似乱数生成器によって生成されるバイナリ列の調査と評価に役立つ 15 の検定が含まれている。この分野のこれまでの研究と同様に、ある仮説に基づいた分布の元で 1 の連続数やビットストリームに現れるパターンの回数のような特定の検定統計量を採用する統計検定を考案する必要がある。検定スイートの検定の大部分は、(1) 何らかの方法で 0 と 1 の分布を調べる、(2) スペクトル法を利用してビットストリームの調波を調べる、(3) 確率論や情報理論に基づく一般的なパターンマッチング技術によってパターンの検出を試みる、のいずれかである。
 5.5.2 グローバルパラメータ
5.5.2 グローバルパラメータ
実際にはユーザがこのソフトウェアを未知の領域で実行した場合に多くの問題が発生する可能性がある。検定手順 (つまり \(10^6\)) を遙かに超えるシーケンス長が選択されることはあり得ることである。メモリに余裕があればそこのソフトウェアが失敗することはないはずである。しかし、多くの場合、データ構造とワークスペースに対してユーザ定義の制限が設けられている。このような状況では NUMOFTEMPLATES などの特定のパラメータを増やす必要があるかも知れない。ユーザが変更できるいくつかのパラメータを Table 5-1 に示す。
| ソースコードパラメータ | デフォルトパラメータ | 詳述/定義 |
|---|---|---|
ALPHA |
0.01 | 有意水準 |
MAXNUMOFTEMPLATES |
40 | Non-overlapping Templates 検定 |
NUMOFTESTS |
16 | 検定の最大数 |
NUMOFGENERATORS |
12 | PRNG の最大数 |
パラメータ ALPHA は受理範囲と棄却範囲を決定する有意水準を示す。NIST は ALPHA を \([0.001,0.01]\) の範囲にすることを推奨する。
パラメータ MAXNUMOFTEMPLATES は Non-overlapping Template Matching 検定で実行できる非周期的テンプレートの最大数を示す。サイズ \(m=9\) のテンプレートに対して最大 148 の非周期的なテンプレートを適用できる。
パラメータ NUMOFTESTS と NUMOFGENERATORS はそれぞれ検定スイートで定義できる検定の最大数と、検定スイートで使用された生成器の最大数に対応する。
 5.5.3 数学ソフトウェア
5.5.3 数学ソフトウェア
検定スイートに必要な特殊関数は不完全ガンマ関数と相補誤差関数である。標準正規関数とも呼ばれる累積分布関数も必要だが、これは誤差関数で表すことができる。
参照実装の開発に関する最初の懸念事項の一つは、統計検定に必要な特殊関数に対して信頼できる数学ソフトウェアを得るために必要な依存関係だった。この問題を解決するために検定スイートは次のライブラリを使用する。
高速フーリエ変換ルーチンは http://www.netlib.org/fftpack/fft.c で入手した。このコードで使用されている正規関数は誤差関数で表現されている。
標準正規 (累積分布) 関数 \[ \Phi(z) = \frac{1}{\sqrt{2}} \int_{-\infty}^z e^{-u^2/2} du \]
このパッケージで使用される相補誤差関数 (erfc) は math.h ヘッダファイルとそれに対応する数学ライブラリに含まれる ANSI C 関数である。このライブラリはコンパイル時にインクルードする必要がある。
相補誤差関数 \[ {\rm erfc}(z) = \frac{2}{\sqrt{\pi}} \int_z^\infty e^{-u^2} du \]
不完全ガンマ関数は書籍 Handbook of Applied Mathematical Functions [1] と Numerical Recipes in C [6] に説明されている近似式に基づいている。パラメータ \(a\) と \(x\) の値に応じて不完全ガンマ関数は連続分数展開または級数展開のいずれかを使って近似できる。
ガンマ関数 \[ \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt \]
不完全ガンマ関数 \[ P(a,x) \equiv \frac{\gamma(a,x)}{\Gamma(a)} \equiv \frac{1}{\Gamma(a)} \int_0^x e^{-t} t^{a-1} dt \] ここで \(P(a,0)=0\) かつ \(P(a,\infty)=1\)。
不完全ガンマ関数 \[ Q(a,x) \equiv 1 - P(a,x) \equiv \frac{\Gamma(a,x)}{\Gamma(a)} \equiv \frac{1}{\Gamma(a)} \int_x^\infty e^{-t} t^{a-1} dt \] ここで \(Q(a,0)=1\) かつ \(Q(a,\infty)=0\)。
NIST は検定ソフトウェアで Cephes C 言語特殊関数ライブラリを使用することを選択した。Cephes は http://www.moshier.net/ の Cephes または GAMS サーバの http://gams.nist.gov/serve.cgi/Package/CEPHES/ にある。使用される特定の関数は igamc (相補不完全ガンマ関数) と lgam (対数ガンマ関数) である。
 5.6 検定コードの実行
5.6 検定コードの実行
NIST 統計検定スイートモノローグのサンプルを以下に示す。なおこのセクションでの太字の項目は入力を表している。
nIST 統計検定スイートを起動するには assess と入力し、その後に目的のビットストリーム長 \(n\) を入力区する (例: assess 100000)。分析するデータと適用する統計検定を選択するために一連のメニュープロンプトが表示される。最初の画面は次のように表示される。

ユーザは特定のデータセットまたは PRNG を選択したら、適用する統計的検定を選択する必要がある。次の画面が表示される。

この場合、利用可能な統計的検定のサブセットを適用することに関心があることを示すために 0 を選択している。次のような画面が表示される。

上に示したように適用された唯一の検定は番号 9 の Non-overlapping templates 検定である。次に必要なサンプルサイズの問い合わせが行われる。

これは data.pi ファイルから 10 個のシーケンスが解析される。ファイルがデータ指定モードとして選択されたので、後続の問い合わせはデータ表現に関して行われる。ユーザはファイルが ASCII 形式のビット列かバイナリ形式の 16 進数列かを指定する必要がある。

データは 0 と 1 の長い列で構成されているため 0 が選択された。すべての必要な入力パラメータが与えられると検定スイートはシーケンスの解析に進む。

検定プロセスか完了すると経験的結果は experiments/ サブディレクトリで見ることができる。

完了後、経験的結果の分析を簡略化するために詳細な分析を行う。解析は 2 種類行われる。1 つは統計的検定に合格したシーケンスの比率を調べるもの。もう 1 つは各統計検定の P 値の分布を調べるものである。詳細は次のセクションで説明する。
 5.7 結果の解釈
5.7 結果の解釈
結果の解釈を容易にするために分析ルーチンが含まれている。統計的検定が完了すると finalAnalysisReport というファイルが生成される。このレポートはセクション 4.2 で説明した経験的結果の要約が含まれている。結果は \(p\) 行 \(q\) 列のテーブルで表されている。行数 \(p\) は適用された統計検定の数に相当する。列数 \(q=13\) は次のように配置されている: 1 列目から 10 列目は P 値の頻度に対応し10、11 列目はカイ二乗検定を適用して生じた P 値11、12 列目は合格したバイナリ列の割合、13 列目は対応する統計的検定である。Figure 5-1 に例を示す。

- 9Mathematica は Stephen Wolfram によるコンピュータ代数システム。http://www.wolfram.com/.
- 10単位区間を10個の離散的なビンに分割している。
- 11\(i\) 番目の統計検定で P 値の一様性を評価するために使用される。処理されたシーケンスが 10 個未満の場合、値は未定義である。セクション 4.2 で述べたように P 値の一様性について統計的に意味のある結果を導き出すためには少なくとも 55 のシーケンスを処理する必要がある。
 List of Appendices
List of Appendices
 Appendix A - Source Code
Appendix A - Source Code
 Appendix B - Empirical Results for Sample Data
Appendix B - Empirical Results for Sample Data
 Appendix C - Extending the Test Suite
Appendix C - Extending the Test Suite
 Appendix D - Description of Reference Pseudorandom Number Generators
Appendix D - Description of Reference Pseudorandom Number Generators
 Appendix E - Numerical Algorithm Issues
Appendix E - Numerical Algorithm Issues
 Appendix F - Supproting Software
Appendix F - Supproting Software
 Appendix G - References
Appendix G - References
- M. Abramowitz and I. Stegun, Handbook of Mathematical Functions, Applied Mathematics Series. Vol. 55, Washington: National Bureau of Standards, 1964; reprinted 1968 by Dover Publications, New York.
- T. Cormen, C. Leiserson, & R. Rivest, Introduction to Algorithms. Cambridge, MA: The MIT Press, 1990.
- Gustafson et al., “A computer package for measuring strength of encryption algorithms,” Journal of Computers & Security. Vol. 13, No. 8, 1994, pp. 687-697.
- U. Maurer, “A Universal Statistical Test for Random Bit Generators,” Journal of Cryptology. Vol. 5, No. 2, 1992, pp. 89-105.
- A. Menezes, et al., Handbook of Applied Cryptography. CRC Press, Inc., 1997. See http://www.cacr.math.uwaterloo.ca/hac/about/chap5.pdf.
- W. Press, S. Teukolsky, W. Vetterling, Numerical Recipes in C : The Art of Scientific Computing, 2nd Edition. Cambridge University Press, January 1993.
- G. Marsaglia, DIEHARD Statistical Tests: http://www.stat.fsu.edu/pub/diehard/.
- T. Ritter, “Randomness Tests and Related Topics, http://www.ciphersbyritter.com/RES/RANDTEST.HTM.
- American National Standards Institute: Financial Institution Key Management (Wholesale), American Bankers Association, ANSI X9.17 - 1985 (Reaffirmed 1991).
- FIPS 140-1, Security Requirements for Cryptographic Modules, Federal Information Processing Standards Publication 140-1. U.S. Department of Commerce/NIST, National Technical Information Service, Springfield, VA, 1994.
- FIPS 180-1, Secure Hash Standard, Federal Information Processing Standards Publication 180-1. U.S. Department of Commerce/NIST, National Technical Information Service, Springfield, VA, April 17, 1995.
- FIPS 186, Digital Signature Standard (DSS), Federal Information Processing Standards Publication 186. U.S. Department of Commerce/NIST, National Technical Information Service, Springfield, VA, May 19, 1994.
- MAPLE, A Computer Algebra System (CAS). Available from Waterloo Maple Inc.; http://www.maplesoft.com.
翻訳抄
NIST SP 800-22 として刊行された (疑似) 乱数生成器のランダム性の検定に関する 2001 年の論文。15 の検定で構成されている。この論文に基づいた検定スイートは NIST SP 800-22: Download Documentation and Software からダウンロードできる。
- RUKHIN, Andrew, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications. Booz-allen and hamilton inc mclean va, 2001.