論文翻訳: Fast Generation of Discrete Random Variables
Florida State University
University of Hong Kong
University of Hong Kong
 Abstract
Abstract
我々はシンプルかつ高速で、公開されている方法と比較して平均で 10 倍、その中でも最も高速な方法の 5 倍以上の速度を持つ関数を用いて離散ランダム変数を生成するための 2 つの方法を記述し C 言語によるプログラムを提供する。この 2 つの方法を実装するための一般的な手順と、最も重要な 3 つの離散分布: ポアソン分布、二項分布、総幾何学分布に対する具体的な手順を提供する。
Keywords: 乱数, 離散変数, ポアソン, 二項, 総幾何学
Table of Contents
- Abstract
- 1. 導入
- 2. 方法 I: 圧縮テーブル検索
- 3. 方法 II. テーブル + 正方ヒストグラム
- 4. 正方ヒストグラム法
- 5. Comparisons
- 6. 添付
- References
- 翻訳抄
 1. 導入
1. 導入
ここで説明する方法は 1960 年代初頭に開発されたものであり (Marsaglia 1963)、二つ目の方法は 70 年代のデバイスに基づいたバリエーションある (Walker 1974)。その間の数年間は、これらの方法と比較してそん色のない方法はほとんど見つけることができなかった。これらの方法は数百のメモリ割り当てが重荷となる時代に開発されたものであり、数千の配置が容易に利用できる現在ではさらに適切と考えられる。生成関数は数行の C コードのみで済む。2 つの関数のリストは、生成関数が必要とするパラメータを設定するためのコードと同様に、ファイルの参照セクションに含まれている。
 2. 方法 I: 圧縮テーブル検索
2. 方法 I: 圧縮テーブル検索
Marsaglia (1963) で詳述され 1964 NSB ハンドブック (Abramowitz and Stegun 1964) で提唱された簡単な例について考える。以下の表で与えられた分布を持つ確率変数 \(X\) について:
| value | prob |
|---|---|
| a | .2245 |
| b | .1271 |
| c | .3452 |
| d | .3032 |
コンピュータで \(X\) を実現する最も速い方法はおそらく 2245 個の a, 1271 個の b, 3452 個の c, 3032 個の d で構成される 1 万エントリを持つ \(T[10000]\) テーブルを作成することであろう。このとき \(i\) を \(0 \le i \lt 10000\) となるランダムな整数とすると \(x=T[i]\) で完了する。これには 10k のテーブルが必要である ─ 現代の標準ではそれほど大きくないが、確率を 10 進数でさらに表現した場合、結果のテーブルは非常に大きくなる可能性がある。ここで、小さいテーブルでほぼ同じ速度でうまく行くか見てみよう。
我々は配列 \(T\) の 10000 要素から一様に選択しているため、任意の方法でテーブルに要素を自由に配置できる。古い Fortran の表記を使用して 4*a, 2*b, 5*c がそれぞれ 4 個の a, 2 個の b, 5 個の c で埋めることを意味するとして、次のようにテーブルを埋める: 2000*a, 1000*b, 3000*c, 3000*d, 200*a, 200*b, 400*c, 40*a, 70*b, 50*c, 30*d, 5*a, b, c, c, d, d。グループ化は各値の確率の桁を用いて先頭、2番目、3番目, ... の順に決定される。
我々には 2245 個の a, 1271 個の b といった合計で 10000 個の要素があるが、\(T\) テーブルの最初の 9000 個の要素は 1000 個の要素の 9 ブロックと同一である。\(T\) のこれら 9000 個の要素を無視し、代わりに確率 9000/10000 で \(\{a,a,b,c,c,c,d,d,d\}\) から 1 つの要素を選択することもできる。
同様に \(T[9000]\) から \(T[9799]\) までの 800 要素は 100 個の要素の 8 ブロックと同一にすぎないため、確率 800/10000 で小さな配列 \(\{a,a,b,b,c,c,c,c\}\) から 1 つの要素を選択できる。
最終的に \(T[9800]\) から \(T[9989]\) の 190 個の要素は 10 個の要素の 9 ブロックと同一に過ぎないため、確率 190/10000 で \(\{a,a,a,a,b,b,b,b,b,b,b,c,c,c,c,c,d,d,d\}\) から要素を選択できる。したがって \(0 \le i \lt 10000\) のランダムな整数 \(i\) に対して次のように \(X\) を生成すると空間がかなり節約され (10000 から 46 へ)、良好な速度は維持される (約 90%):
// Setup:
A[9] = {a, a, b, c, c, c, d, d, d};
B[8] = {a, a, b, b, c, c, c, c};
C[19] = {a, a, a, a, b, b, b, b, b, b, b, c, c, c, c, c, d, d, d};
D[10] = {a, a, a, a, a, b, c, c, d, d};
// Generating procedure, given random i in 0<=i<=9999:
if(i < 9000) return A[i / 1000];
if(i < 9800) return B[(i - 9000) / 100];
if(i < 9990) return C[(i 0 9800) / 10];
return D[i - 9990];基数 10 の数字を使用するのではなく、確率の数字から基数 100 までのテーブルを作成することもできる。この場合 2 つのテーブル A と B のみになる。複数のテーブルエントリに対して Fortran 表記を使って:
A[98] = {22*a, 12*b, 34*c, 30*d}
B[200] = {45*a, 71*b, 52*c, 32*d}テーブル空間の合計は 298 で基数 10 の 46 を超えているが、基数 10000 の 10000 よりは遙かに小さくなっている。生成手順は 10000 テーブルの場合とほぼ同じ程度の速さである。
if(i < 9800) return A[i / 100];
return B[i - 9800];もちろん、テーブルルックアップ方式はこのような単純な離散分布にとってやりすぎかもしれない。しかし上記の方法は数百の値と 8 桁以上の確率を持つ離散分布に非常に効率的に適用できる。実際に我々は分母が 230 の有理数として確率を表現する実装を提供する。そして基数 64 を使用すると各確率は基数 64 の "桁" を 5 つ持つことになり、上記の例と似ているがおそらくその何倍もの大きさの 5 つの小さなテーブルを提供するだろう。さらに、上記の整数除算である i/1000, (i-9000)/100 などの類推は 6 ビットの "桁" をシフトさせることで実現され非常に高速な生成手順が得られるだろう。
基礎となる離散分布を考慮すると生成関数は以下のようになる:
/* Uses 5 compact tables; jxr is global static Xorshift RNG */
int Dran(){
unsigned long j;
jxr ^= jxr << 13; jxr ^= jxr >> 17; jxr ^= jxr << 5; j = (jxr >> 2);
if(j < t1) return AA[j >> 24];
if(j < t2) return BB[(j - t1) >> 18];
if(j < t3) return CC[(j - t2) >> 12];
if(j < t4) return DD[(j - t3) >> 6];
return EE[j - t4];
}初期化手続きでは確率を使用して静的なグローバル変数 AA, BB, CC, DD, EE 配列と、テーブルのサイズによって決定されるパラメータ t1, t2, t3, t4 を設定する。Marsaglia (2003) で説明されている Xorshift RNG を使用している; これはランダム性テストで非常にうまく機能し高速であるため、それから与えられた数百の乱数のどれもが使用できる。
コンパクトテーブル法の具体的な比較を次に示す:
- ポアソン分布 \(\lambda=100\) を分母 \(2^{30}\) で最も近い有理数に (分子のみを保持して) 表現するとき、基数 64 を使用して 5 個のテーブルを作成すると、テーブルエントリは 10202 となり、C 言語の関数は秒間 6000 万個を超えるポアソン 100 変量を生成する (Intel 1800MHz CPU)。
- 同じように表現された二項確率 \(n=100\), \(p=.345\) の場合、5 つのテーブルには合計 5102 個のエントリがあり、速度は同等で 6000万/秒を超える。
- 基数 1024 を使用すると 3 つのテーブルの項合計はポアソン 100 分布では約 90020 要素、\(n=100\), \(p=.345\) の二項確率では 47057 となる。どちらの場合も速度は 5 テーブル版より速く約 7000 万/秒である。
- 基数 \(2^{15}\) の数字からの 2 つのテーブルに基づくバージョンは、3 テーブル版より少しだけ高速であるが 10 倍のテーブルエントリを必要とする。
- ポアソン分布や他の無数の確率を持つ離散変量に対して、サイズ \(2^{31}\) (\(10^{9.33}\)) のサンプルの場合、発生数の期待値が 0.5 を超えるもののみを選択する。その他の確率はゼロとみなされる。確率が \(5\times 10 - 10\) 未満の発生を考慮する必要がある異常な状況では、特別なテール処理手続きを使用する必要がある。
基数桁の選択がどのようなものであっても設定と生成の手順はほとんど同じである。付属の C プログラムは確率を基数 64 の 5 桁で表現した 5 テーブルのバージョンである。
コンパクト化したテーブルに必要な実際のメモリ空間は、莉算段ダム変数の可能な値の数である \(n\) に依存することに注意。\(n \le 256\) の場合、テーブルエントリはバイト (C 言語では char) だが、\(n \gt 256\) の場合は各テーブルエントリに 16 ビット (C 言語では short int) が必要となる。65536 以上の値を取る離散ランダム変数に遭遇した場合、テーブルエントリは各 32 ビットを必要とする。
 3. 方法 II. テーブル + 正方ヒストグラム
3. 方法 II. テーブル + 正方ヒストグラム
二つ目の方法ではあまり多くの値を必要としないようである:
- 32 ビットの乱数整数から 1 バイトを使用してサイズが 256 のテーブルのエントリを取得する。テーブル化された値が正であればそれを返す。
- そうでなければ、単一のテーブルでカバーされていない値の間で変量を生成するために、より遅い方法を使用する。
\(p_0,p_1,\ldots,p_{n-1}\) の確率で \(0,1,\ldots,n-1\) の値を取る離散ランダム変数の手順をセットアップするにはそれぞれの \(p_i\) を \[ p_i = \frac{k_i + \theta_i}{256} \] で表す。ここで \(k_i\) は整数で \(0 \le \theta_i \lt 1\) である。(\(k\) は 256 を底とする \(p\) の展開の最初の数字である。) ここでテーブル \(J[256]\) を埋める。\(k_0\) を 0 で、\(k_1\) を 1 で、…, \(k_{n-1}\) を \((n-1)\) で埋める。もしテーブルを埋められないのであれば (一般的に 2-15 の未割り当てセルを持つだろう) 残りの \(J[\ ]\) は -1 をで埋める。
次に、必要な変量 \(D\) を生成するために: \(i\) をランダムな 32 ビット整数とし、\(j\) を \(i\) の右端 8 ビットから形成する (C 言語では j = i & 255;)。\(J[j] \ge 0\) であれば \(J[j]\) を返し、そうでなければ以下で説明する、合計して 1 になるように正規化された確率 \(\theta_0\), \(\theta_1\), …, \(\theta_{n-1}\) の正方ヒストグラム法による \(D\) を返す。正方ヒストグラムに必要な単一の一様 \([,1)\) 変量は \(i/2^{32}\) の浮動小数点バージョンで形成できる。ここで \(i\) は右端 8 ビットがテーブルの参照インデックスを決定するランダムな 32 ビット整数である。
この結果として高速でシンプルな手続きとなる。これはサイズ \(n\) のテーブル \(K[\ ]\) と \(V[\ ]\) を使用する正方ヒストグラムの事前セットアップに依存する。この方法は、指定された離散変量を 4,000 万/秒で生成する。コンパクトテーブル法ほど高速ではないが、利用可能なほとんどの方法よりも遙かに高速である。
 4. 正方ヒストグラム法
4. 正方ヒストグラム法
正方ヒストグラムを次の図み示す:
全ての正方ヒストグラムには \(n\) 個の等幅の列 (この例では \(n=5\)) が含まれており、各列には下部と上部がある。各列の下部は列のインデックス \(0,1,\ldots,n-1\) に "属して" おり、各列の上部は列上のインデックスラベルに "属して" いて配列 \(K[n]\) に格納される。(上部は空の場合がある。) 各列には、列内容の所有権が変わる位置を示す配列 \(V[n]\) を含んでいる分割ポイントがある。この例では C 言語の表記で \(K[5] = \{2,4,3,0,2\}\) と \(V[5] = \{.15,.38,.57,.74,.96\}\) である。
この例では正方ヒストグラムの高さは \(.20\) である。配列 \(V\) の分割点は \(\{.15, .18, .17, .14, .16\}\) ではなく \(.15\), \(.20+.18\), \(.40+.17\), \(.60+.14\), \(.80+.16\) であることに注意。これは、列のインデックスが分かればそれを決定した一様数の範囲が分かるため、分割ポイントの上か下かを判断するために必要な計算が減るためである。
次に、離散確率変数を生成するために正方ヒストグラムから一様に点を選択し、その点が含まれる領域のラベルを返す。正方ヒストグラムでランダムな点を取得するための通常の 2 つの一様変数の代わりに、配列 \(K[n]\) および \(V[n]\) を使用して単一の一様 \([0,1)\) 変量 \(U\) から結果を取得できる: \[ j = \lfloor 5U \rfloor; \ \ \mbox{if $U \lt V[j]$ return j; else return $K[j]$} \]
このルールは確率 .21, .18, .26, .17, .18 (各インデックスに属する領域の合計) を持つ値 0, 1, 2, 3, 4 を取るランダム変数 \(J\) を生成する高速で簡単な方法を提供する。そして、そのような単純なルールは \(p_0, p_1\, \ldots, p_{n-1}\), \(\sum p_i = 1\) の確率で 0, 1, 2, …, \(n-1\) を取る任意の離散ランダム変数として機能するだろう。
必要なことは、高さ \(p_0, p_1, \ldots, p_{n-1}\) のバーを使用して \(0, 1, \ldots, n-1\) の通常のヒストグラムを作成し Robin Hood ルール ─ 最も裕福な人から最も貧しい人に平均を引き上げる ─ を使用して、全てが平均となり正方ヒストグラムが形成されるまで一つづつ、次々と行うことである。
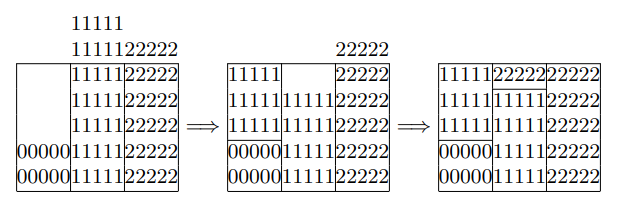
単純な正方ヒストグラム形成の例で説明する。確率 \(\frac{2}{15}, \frac{7}{15}, \frac{6}{16}\) で \(0,1,2\) を取るランダム変数 \(J\) を仮定する。正方ヒストグラムの平均の高さは 5/15 となるため、これらの確率によって与えられる高さでヒストグラムを形成し、ヒストグラムに予想されるの最終的な形式の中または上に描画する。我々は Robin Hood 法を繰り返す。まず最も貧しい列 0 を平均まで上げ、列 1 の "富" を減らし、次に新しく最も豊かな列 2 から取り出して、減少した列 1 を平均まで上げる。
これで配列 \(K[3] = \{1,2,2\}\) および \(V[3] = \{\frac{2}{15}, \frac{9}{15}, \frac{15}{15}\}\) の正方ヒストグラムと、均一 \([0,1)\) 変量 \(U\) を使用した生成規則 \(j=\lfloor 3U \rfloor\) if \(U \lt V[j]\) return \(j\), else return \(K[j]\) ができた。\(V\) 配列の値がどのように決定されるかに注意。\(j=0\) の場合、\(0 \le U \lt 5/15\) で \(U \lt 2/15\) をテストすると、"0" 列が "0" に属する 2 つの部分または "1" に属するような 3 つの部分に分割される。同様に \(5/15 \le U \lt 10/15\) 範囲は "1" 列の選択に繋がり、\(U \lt 9/15\) をテストするとその列が "1" と単一部の "2" に属する 4 つの部分に分割される。
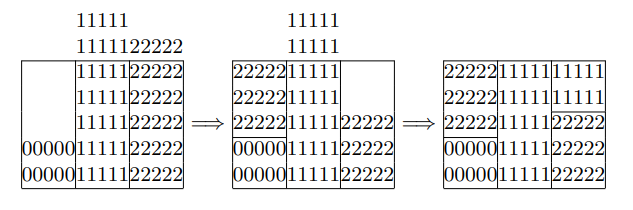
しかし正方ヒストグラムを作成する別の方法もある。上記と同様に初期列値 \(\frac{2}{15}, \frac{7}{15}, \frac{6}{15}\) から開始し最初のステップとして 2 番目に裕福な "2" を取り最も貧しい "0" を平均まで引き上げて終了すると仮定する。このとき正方プロセスは終了する:
我々は配列 \(K[3]=\{2,1,1\}\) と \(V[3]=\{\frac{2}{15},\frac{10}{15},\frac{13}{15}\}\) と同じ生成ルールで終了する: \(j=\lfloor 3U \rfloor\); if \(U \lt V[j]\) return \(j\), else return \(K[j]\)。ただし、今回我々は総確率 \(\frac{5}{15}\) で "else" 部分を実行することに注意。これは総確率がより小さい \(4/15\) の "else" 部分が必要な先の方法である Robin Hood 法とは対照的である。
生成手順 \[ j = \lfloor nU \rfloor; \ \ \mbox{if $U \lt V[j]$ return $j$; else return $K[j]$}; \] の "else" 部分を必要とする頻度は "over-area" に比例する; つまり分割ポイントの上にある最終的な正方ヒストグラムの部分である。最適な正方は最小限の over-area (面積) を提供する。Robin Hood 法は常に最適ではないが経験的にそれに近いだろう。特定のヒストグラムの最適な正方を見つけることは NP 困難であることが知られている。それは参考文献 Marsaglia and Tsang (1987) で論議されている。我々の正方ヒストグラム法は Walker (1974) で提案されたアプローチをより効率的かつ透過的に実装するために開発された。
合計が 1 で平均が \(a=1/n\) である初期確率 \(p_0,p_1,\ldots,p_{n-1}\) が与えられたとする。正方ヒストグラムの Robin Hood 法のアルゴリズムは次のようになる。
最初に \(0\) から \(n-1\) までの \(i\) に対して \(K[i] = i\) かつ \(V[i] = (i+1)*a\) で初期化する。次に次の 2 ステップを \(n-1\) 回実行する:
- 最小の確率 \(p_i\) と最大の確率 \(p_j\) を見つけ出す。
- \(K[i]=j\); \(V[i]=(i-1)*a+p_i\); を設定し、\(p_j\) を \(p_j-(a-p_i)\); に置き換え、\(p_i\) を \(a\) に置き換える。
これにより生成手順が提供される: \[ j = \lfloor nU \rfloor; \ \ \mbox{if $U \lt V[j]$ return $j$, else return $K[j]$} \]
 5. Comparisons
5. Comparisons
我々はポアソン変量、二項変量、超幾何学変量の生成に関する文献のいくつかの高速な方法と我々の 2 つの方法とを比較する。
一様変量の比率 (Stadlober and Zechner 1999) は単純な計算と合理的な棄却率を備えた棄却アルゴリズムである。
パッチワーク棄却 (Stadlober, E. 1989) は Marsaglia and Tsang (1984) と Marsaglia and Tsang (1998) からの Monty Python 法のアイディアを (それと言及なしに) 適用する。これらは単純な三角形関数 (hat function) を使用し、頻度関数 \(f(x)\) の下の領域を再配置して三角形関数の下の領域をできるだけ多く埋めるようにしている。その結果として非常に低い棄却率を実現している。これらの 2 つの手法はいずれも任意の分布に適用できるため、二項式、ポアソン式、超幾何学式の 3 つの比較すべてに含まれている。
我々はまた特定の分布のために設計された 2 つの手法と比較する:
- PD (acceptance complement) (Ahrens and Dieter 1982) はポアソン変量のために設計された最速の手法の一つであると考えられていた。
- BTPE (triangle-parallelogram-exponential rejection) (Kachitvichyanukul and Schmeiser 1988) はメジャー化関数とマイナー化関数を組み合わせて二項分布から標本抽出する。
比較のための C コードは Windows XP 上の Pentium IV 2.26GHz の Microsoft Visual C++ 6.0 と DOS ウィンドウ上の gcc でコンパイルしてリンクしたが、Unix システム上でコンパイルしても同様の結果が得られた。比較を公平にするために Marsaglia (2003) の高速 Xorshift 法を用いて一様乱数を生成した。
二項分布、ポアソン分布、および超幾何分布から 1 億個の変量を生成するための実行時間を後述の表に示す。結果は、我々の方法 I (圧縮テーブル検索) が最も優れた性能を示し、異なるパラメータに対してほぼ不変の速度であることを示している。方法 II (テーブル + 正方ヒストグラム) は方法 I とほぼ同じ程度の速度であることが多いが、第一段階の成功率が低いパラメータでは遅くなり、より頻繁に正方ヒストグラムを必要とするようになる。Stadlober-Zechner パッチワーク棄却法は他の 4 つの手法の中では最良のようだが、その最速値は我々の手法 I の 1/5 しかない。我々の方法は競合する方法より 5 倍から 15 倍早く、平均すると 10 倍である。あなたは速度だけでなく複雑さやプログラムのサイズ、(あなたの視点での) 優雅さなど、独自の方法や他の方法と比較してみてください。
パラメータの特定の値について我々の方法 I または方法 II のセットアップ時間とメモリコストはシンプルで直接的な方法をより適したものにする可能性がある。表 1, 2, 3 を参照。
 6. 添付
6. 添付
ここで説明した 2 つの方法の C 言語版をジャーナルの "Browse files" セクションに掲載するために提供する。最初に 5tbl.c、次に TplusSQ.c をコンパイルして実行することを推奨する。それぞれポアソン分布、二項分布、超幾何分布のパラメータの選択を求める。それぞれの手法はその分布に適用され、出力に対してカイ二乗検定を行う。そして理解のため、または離散分布に適用するのに有用な部分を抽出するために 2 つのファイルの構成を調べたいと思うかもしれない。
5tbls.c ファイルには基数 64 桁で表される 30 ビットの確率に基づいてコンパクトテーブル法の 5 つのテーブルを作成する void get5tlbs(void) が含まれている。
これらの確率は PoissP(), BinomP() または HyperGeometricP() によって作成される。パラメータ lambda が与えられると PoissP() はポアソン確率のテーブル P[] を、形式 \(j/2^{30}\) の有理数の分子として生成する。\(2^{31}p \lt 1\) となるような \(p\) はゼロと見なされる。
void BinomP(int n, double p) は二項分布の静的な int 配列 P[] を有理数 \(j/2^{30}\) の分子として作成する。\(2^{31}p \lt 1\) となるような \(p\) は、超幾何分布に対する関数 HypergeometricP() によって生成される \(p\) と同様にゼロとみなされる。
int Dran() は 32 ビットの xorshift 整数を使用して 5 つのテーブルの適切な一つから離散ランダム値を返す関数である。
void Dtest(int n) は Dran() を使用して \(n\) 個の値のサンプルを生成し、有効性テストを実行してセル数をグループ化し、機体数が \(\gt 20\) となるようにする。含まれている Phi() と Chisquare() 関数を使用する。
ファイル TplusSQ.c は、今回の Dran() 関数が方法 II: テーブル + 正方ヒストグラムに基づいていることを除いて、関数 Dran() によってもたらされるポアソン、二項、超幾何の出力もテストを行う。パラメータと配列は DSQset() 関数によってセットアップされる。この関数は整数配列 P[] を生成するための PoissP(), BinomP() または HyperGeometricP() と同じルーチンに依存している。DSQset() は各整数確率 P[i] を double p[i] に変換する。そして p[i] は J[256] 高速テーブル検索と正方ヒストグラムのための配列 K[] と V[] を生成sるための p[i]=\(\frac{k_i+\theta_i}{256}\) として表される。そして離散変量生成器 Dran() は方法 II に必要な形式をとる。
これら 2 つの方法のうち 1 つまたはそれと別の方法を他の種類の離散分布に適用したい場合、(整数) 確率、\(j/2^{30}\) で表される分布の確率の 30 ビットの分子 \(j\) のテーブル P[] を生成する PoissP(), BinomP() または HyperGeometricP() 関数の代わりに独自のルーチンを作成しなければならないだろう。そしてルーチン get5tbls() は Dran() 生成器が方法 I のために必要とする 5 つのテーブルを作成するか、または DSQset() が Dran() 生成器のテーブル+正方ヒストグラム版のための J, K そして V を作成するだろう。
そして、\(10^8\) の標本に Dtest(100000000) 関数を適用して誤検出がないかをテストした後、指定された離散分布から非常に高速でシンプルなランダム変数生成器を提供するために、適切な Dran() 関数を使用することができる。いくつかのパラメータ選択や特定の分布については、他の方法の方が適用しやすく、必要とするメモリも少ないかもしれない。しかし、ここで提唱した 2 つの方法は、離散分布の多様性を考慮して検討する価値があるかもしれない。
 References
References
- Abramowitz M, Stegun IA (eds.) (1964). Handbook of Mathematical Functions. U.S. Government Printing Office, Washington D.C.
- Ahrens JH, Dieter U (1982). “Computer Generation of Poisson Deviates from Modified Normal Distributions.” ACM Transaction on Mathematical Software(TOMS), 8.
- Kachitvichyanukul V, Schmeiser BW (1988). “Binomial Random Variate Generation.” Communications of the ACM, 31(2).
- Marsaglia G (1963). “Generating Discrete Random Variables in a Computer.” Communications of the ACM, 6, 37–38.
- Marsaglia G (2003). “Xorshift RNGs.” Journal of Statistical Software, 8(14).
- Marsaglia G, Tsang WW (1984). “A Fast, Easily Implemented Method for Sampling from Decreasing or Symmetric Unimodal Density Functions.” SIAM Journal Scientific and Statistical Computing, 5, 349–359.
- Marsaglia G, Tsang WW (1987). “A Decision Tree Algorithm for Squaring the Histogram in Random Number Generation.” Ars Combinatoria, 23A, 291–301.
- Marsaglia G, Tsang WW (1998). “The Monty Python Method for Generating Random Variables.” ACM Transactions on Mathematical Software, 24(3), 341–350.
- Stadlober E, Zechner H (1999). “The patchwork Rejection Technique for Sampling from Unimodal Distributions.” ACM Transaction on Modeling and Computer Simulation (TOMACS), 9.
- Stadlober,E (1989). “Ratio of Uniforms as a Convenient Method for Sampling from Classical Discrete Distributions.” Proceedings of the 21st ACM conference on Winter simulation.
- Tsang WW (1981). Analysis of the Square-the-Histogram Method for Generating Discrete Random Variables. Master’s thesis, Computer Science, Washington State University.
- Walker AJ (1974). “Fast Generation of Uniformly Distributed Pseudorandom Numbers with Floating Point Representation.” Electronics Letters, 10, 553–554.
翻訳抄
Walker のエイリアス法を改良して正方ヒストグラムを使う方法で高速に重み付きランダムサンプリングを行うアルゴリズムに関する 2004 年の論文。
- G. Marsaglia, W. W. Tsang, and J. Wang. Fast Generation of Discrete Random Variables, Journal of Statistical Software, 11(3):1-11, 2004.