B+Tree
葉間のリンク、及びキーに関連付けられたデータの描画は省略している。
概要
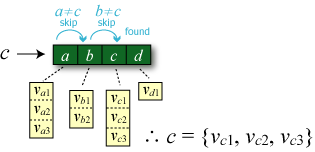
B-Tree の派生型である B+Tree は、個々のキーの検索効率を下げる代わりに、ある範囲のデータをまとめて取得するケースに適した構造を持つ。B-Tree が中間ノードにもデータエントリを保持していたのに対して、B+Tree では末端の葉にのみエントリを保持し、葉は相互にリンクしたリストの構造を持っている。
このようなソートされたリンクリスト構造を併せ持つことで B+Tree ではキーの範囲条件 \(x_0 \leq k \lt x_1\) に一致するデータを効率的に取得することができる (B-Tree では何度も中間ノードに上る必要があった)。
中間ノード及び葉のそれぞれに格納可能な最大エントリ数を \(M \geq 2\)、最小エントリ数を \(1 \leq t \leq \lfloor \frac{M}{2} \rfloor\) とする (以下の説明図では \(M=4\)、\(t=2\) としている)。
検索操作
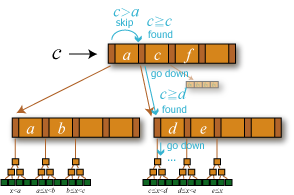
- B+Tree のルートノードから評価を開始する。
- 評価対象のノードが葉の場合、その葉が持つエントリからキーに該当するエントリを逐次検索し、その結果をもって検索操作を終了する。
- 評価対象のノードが中間ノードの場合、サブノードの境界値がキー以上である位置のサブノードに対して再帰的に 2. 以降を繰り返す。
挿入操作
- 検索と同じ手順で挿入対象のエントリが入る葉を特定する。
- 葉が既に同じキーを持つエントリを保持していた場合、キーの重複を許すのであればキーに関連付けられたデータを追加し挿入操作を終了 (葉のエントリ数は変化しない)。キーの重複を許さない場合は重複エラーとし挿入操作を終了する。
キーの重複が許可されている B+Tree へのエントリ挿入
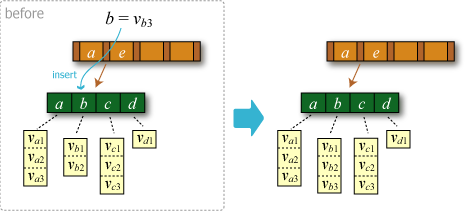
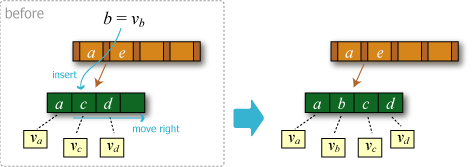
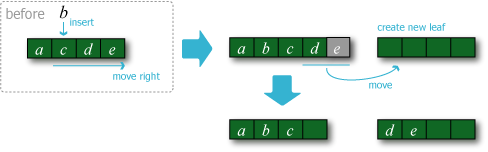
- 葉がキーと同じエントリを保持していない場合は新たにエントリを追加する。この操作によって葉のエントリ数が \(M\) を超えていなければ挿入操作を終了する。
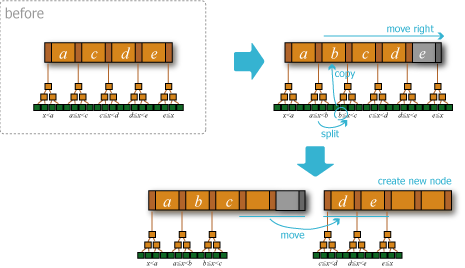
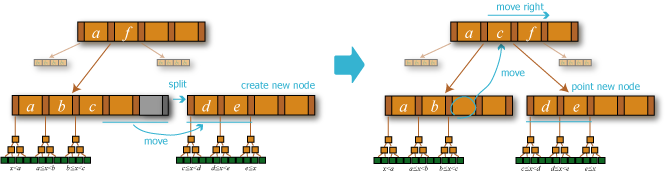
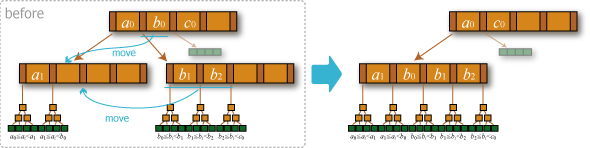
- 分割: エントリの挿入によって葉のエントリ数が \(M\) を超えた場合、新しい葉を作成し後半のエントリを移動する。
\(M+1\) が奇数の場合、余剰の 1 エントリ分をどちらのノードに配分しても良い。どちらかと言えばエントリは昇順に追加されることが多いと仮定すれば、前方に配分すると密な木に、後方に配分すると疎な木になるだろう。 - 分割前の葉がルートだった場合、新しい中間ノードを作成し 2 つに分離した葉をポイントしてルートをその中間ノードに変更して挿入操作を終了する。
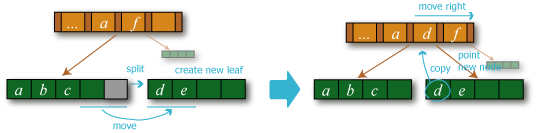
- 分割前の葉がルートではない場合 (中間ノードを親に持つ場合)、親の中間ノードに新しい葉のエントリを追加する。これ以降は、分割した葉のぞれぞれを単一の葉からなる 2 つのサブツリーとみなした親の中間ノードについての説明である。
- 中間ノードの保持するサブツリー数が \(M+1\) 以下の場合、挿入操作を終了する。
- 分割: 中間ノードの保持するサブツリー数が \(M+1\) を超えている場合、中間ノードを分離する。
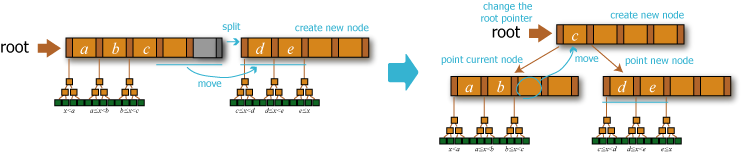
- 分割前の中間ノードがルートだった場合 (中間ノードが親を持たない場合)、新しい中間ノードを作成し 2 つに分離したサブツリーをポイントしてルートをその中間ノードに設定し挿入操作を終了する。
- 分割前の中間ノードがルートではなかった場合 (親の中間ノードを持つ場合)、親の中間ノードに新しく作成した中間ノードのポインタとその境界値を挿入する。
- 親の中間ノードに対して 7. 以降を再帰的に繰り返す。
削除操作
- 検索と同じ手順で削除対象のエントリを含む葉を特定する。
- 葉に削除対象のエントリが存在しない場合は削除操作を終了する。
- 葉に削除対象のエントリが存在する場合はそれを削除する (葉の先頭のエントリが削除された場合、上位の中間ノードが持つ境界値と厳密に一致しなくなることに注意)。葉がルートか、葉に含まれるエントリ数が \(t\) 以上であれば削除操作を終了する。もし \(t\) 未満であれば B+Tree の制約を満たすために操作を続ける。
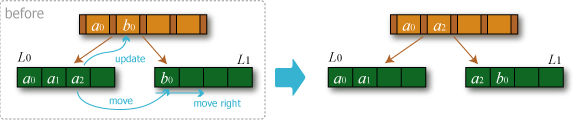
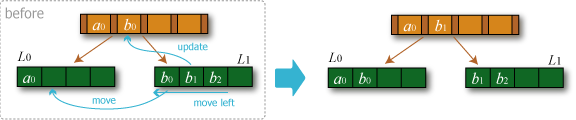
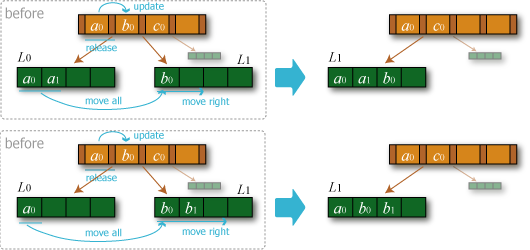
- 補填: 削除が行われた葉と同じ親を持つ兄弟の直前または直後の葉が \(t+1\) 個以上のエントリを保持している場合、それから 1 エントリ分を補填して削除操作を終了する。
直前の葉から 1 エントリ分を補填する場合
直後の葉から 1 エントリ分を補填する場合
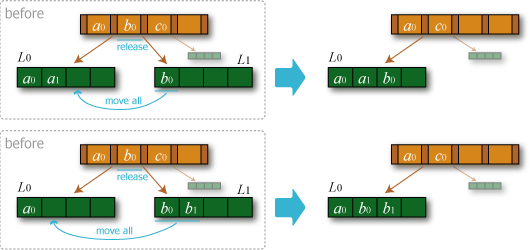
- 統合: 前後の葉が \(t\) 以下のエントリしか持っていない場合、そのどちらかと全エントリをマージし、親の中間ノードから空いた葉の境界値とポインタを削除するして開放する。なお、前後どちらの葉に統合しても同じ結果となるが、後方の葉への統合は先頭のエントリが変わることから手数が多くなる。このためノードのマージは前詰め手順で行うと良い。
前方の葉にマージする場合
以下、マージされた葉の親の中間ノードに対する操作として説明を続ける。
後方の葉にマージする場合
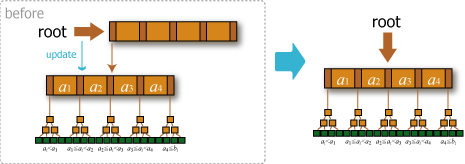
- 中間ノードがルートで 2 つ以上のサブツリーを保持している場合は削除操作を終了する。
- 中間ノードがルートで 1 つのサブツリーしか保持していない場合はルート直下の子ノードをルートに昇格させ、ルートだった中間ノードを開放し削除操作を終了する。
直前の中間ノードから補填する場合
- 中間ノードのエントリ数が \(t\) 以上であれば削除操作を終了する。もし \(t\) 未満であれば操作を続ける。
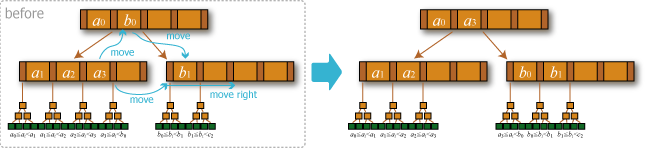
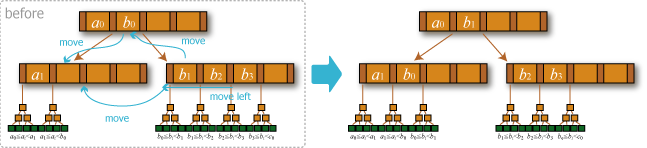
- 補填: 削除が行われた中間ノードと同じ親を持つ兄弟の直前または直後の中間ノードが \(t+1\) 個以上のエントリを保持している場合、それから 1 エントリ分を補填して削除操作を終了する。
直前の中間ノードから補填する場合
直後の中間ノードから補填する場合
- 統合: 前後の中間ノードが \(t\) 以下のエントリしか持っていない場合、そのどちらかと全エントリをマージし、親の中間ノードから空いた中間ノードの境界値とポインタを削除するして開放する。葉と同様に後方の中間ノードにマージすると手順が多くなる。図は省略。
前方の中間ノードにマージする場合
- 親の中間ノードに対して再帰的に 5. 以降を繰り返す。