Count-Min スケッチ

概要

Count-Min スケッチ (count-min sketch) [1] は大規模データセットにおいて頻度や重み付け合計を効率的に推定するための確率的データ構造である。膨大な数の要素を複数のハッシュ関数を用いて異なるカウンターにマッピングし、その最小値を参照することで頻度を推定する。この手法は結果として得られる合計頻度に誤差を含むが、要素ごとにカウンターを設けるよりはるかにメモリ使用量が少なく、挿入やクエリーも高速である。データストリーム分析、ネットワークトラフィックのモニタリング、検索クエリーの頻度分析などに広く利用されている。

Table of Contents

1. 概要
2. アルゴリズム
   1. 設定
   2. 更新
   3. 照会
   4. 誤差パラメータ
   5. レンジクエリー
3. 適用例
   1. Heavy Hitting の抽出
4. 参考文献

アルゴリズム

要素 \(x\) と対応する量 \(c\) からなるペア \((x,c)\) を供給するデータストリームを想定する。Count-Min スケッチの目的はある時点 \(t\) までにデータストリームから得られた任意の要素 \(x\) に対応する \(c\) の合計値の近似を推定することである。

Count-Min スケッチはデータストリームから得られた要素 \(x\) を \(d\) 個のハッシュ関数でのハッシュ化し、そのハッシュ値に対応する \(d\) 個のカウンターに \(c\) を加算する。異なる要素 \(x\) と \(y\) でハッシュ値が衝突する可能性があるが、Count-Min スケッチは真の合計からの想定誤差 \(\epsilon\) と想定誤差を超える確率 \(\delta\) を決めることができる。

ハッシュの衝突による加算の重複を考慮すると、\(c \gt 0\) の場合 (つまり増加のみの場合)、ある要素 \(x\) に対するすべてのカウンターは少なくとも \(x\) の「真の合計値」以上の値を持つはずである。さらに、その中でもっとも小さな合計値が真の値にもっとも近い合計値である。Count-Min スケッチはこの最小値を採用することで合計の近似値を推定する。

なお、Count-Min スケッチでは \(c\) が負の値をとることを許容することもでき、この場合は最小値ではなく中央値を採用する。この記事の内容は \(c \gt 0\) のケースを対象にしている。

設定

Count-Min スケッチのカウンターは \(w \times d\) の 2 次元整数配列で表される。初期状態のカウンターはすべて 0 が設定されるものとする。\(d\) と \(w\) は誤差パラメータ \((\epsilon,\delta)\) に基づいて式 (\(\ref{dw}\)) のように定めることができる。\[ \begin{equation} \left\{ \begin{array}{rcl} d & = & \lceil \log_e \frac{1}{\delta} \rceil \\ w & = & \lceil \frac{e}{\epsilon} \rceil \end{array} \right. \label{dw} \end{equation} \] また \(\{0,\ldots,w-1\}\) のハッシュ値を生成する \(d\) 個のハッシュ関数 \(h_0\), ..., \(h_{d-1}\) を pair-wise 独立族からランダムに選択する。

例として Fig 1 のような \(d=3\), \(w=8\) の構造を持つ Count-Min スケッチについて考える。逆算してこの誤差パラメータは \(\epsilon \le \frac{e}{8}\) と \(\delta \le e^{-3}\) の上限を持つ。

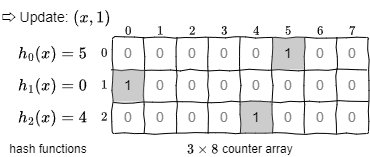
更新

データストリームから要素と量のペア \((x,c)\) の入力があったとき、Count-Min スケッチはまず要素 \(x\) に対してハッシュ関数を適用して \(d\) 個のハッシュ値を生成する。次にカウンター配列でハッシュ値に該当するそれぞれのカウンターに \(c\) を加算する。ある時点 \(t\) の入力を \((x_t,c_t)\) としたとき、各カウンターの状態 \(a_{t,j,i}\) は式 (\(\ref{update}\)) のように更新される。\[ \begin{equation} \forall j \in \{0,\ldots,d-1\}, \ \ a_{t,j,i} \leftarrow \begin{cases} a_{t-1,j,i} + c_t & \text{if $i = h_i(x_t)$,} \\ a_{t-1,j,i} & \text{Otherwise.} \end{cases} \label{update} \end{equation} \]

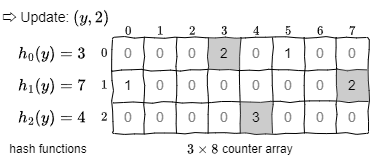
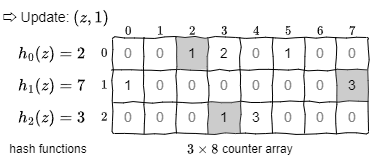
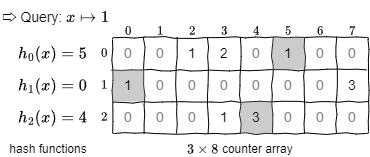
Fig 2 の例では Count-Min スケッチを \((x,1)\), \((y,2)\), \((z,1)\) で更新している。いくつかのカウンターはハッシュの衝突により異なる要素に対して重複して加算されていることに注意。

照会

更新された Count-Min スケッチからある要素 \(x\) の合計推定値を得るには、更新と同様に \(d\) 個のハッシュ値を生成し、配列内の該当するカウンターで最も小さい値 (\(c\) が正の場合)、または中央値 (\(c\) に負値を許容する場合) を採用する。

Fig 3 の例では一連の更新の後に \(x\) を照会し、該当するカウンター内の最小値である 1 が推定合計値として返される。

誤差パラメータ

2 つの誤差パラメータのうち \(\epsilon\) は過大評価の範囲 (実際より多く見積もってしまう範囲)、\(\delta\) は誤差がその過大評価の想定範囲から外れる確率を表している。

ある時点 \(t\) までのデータストリーム \((x_1,c_1)\), ..., \((x_t,c_t)\) において、すべての要素の頻度の合計を \(N=\sum_{i=1}^t c_i\)、ある要素 \(a\) の真の合計頻度を \(f_a\) としたとき、Count-Min スケッチで得られる \(a\) の推定合計頻度 \(\hat{f}_a\) は \(1-\delta\) の確率で式 (\(\ref{err}\)) を満たす [1, 2]。\[ \begin{equation} f_a \le \hat{f}_a \le f_a + \epsilon N \label{err} \end{equation} \] 例に用いた \(d=3\), \(w=8\) の Count-Min スケッチから得られる推定合計頻度は、\(1-\delta=1-e^{-3}=0.950\) の確率で真の合計頻度から \(\epsilon N=\frac{e}{8}\times 4=+1.359\) の範囲に収まっていることが保証されている。

式 (\(\ref{err}\)) における誤差の項 \(\epsilon N\) はどの要素でも一定である点に注意。これは \(f_a \gg f_b\) のような状況で \(\hat{f}_a\) に比べて \(\hat{f}_b\) の含む誤差の割合が大きくなる事を示している。これは真の合計頻度が大きい方がより相対誤差が少ないという意味であり、直感的には推定合計頻度が大きい方が相対誤差が少ない可能性が高いと言い換えることができる。

誤差パラメータ \((\epsilon,\delta)\) からカウンター配列の \(d\), \(w\) が決まることから、Count-Min スケッチの空間計算量は式 (\(\ref{o}\)) のように表すことができる。\[ \begin{equation} O\left( \frac{e \log_e \frac{1}{\delta}}{\epsilon} \right) \label{o} \end{equation} \] Count-Min スケッチはデータストリームから得られる入力数 \(t\) に依存せず (\(\ref{o}\)) のような小さなメモリ空間だけで十分に機能する。ただし、全要素の合計頻度 \(N\) が増えるに連れて過大評価の範囲が大きくなる点に注意する必要がある。

レンジクエリー

Count-Min スケッチでレンジクエリー (range query; 範囲クエリー) を実装する場合、前述のような点クエリーを繰り返して実装することも可能だが 2 つの問題がある。一つ目は誤差が累積すること。過大評価された誤差は範囲 \(r\) 内で最大で \(|r| \epsilon N\) に累積する可能性がある。これは \(|r|\) が大きい場合に特に問題である。二つ目は単純に加算のコストが \(O(|r|)\) となることである。

二進レンジ (dyadic range; 二進区間) とはパラメータ \(x\) と \(y\) に対して \([x 2^y + 1, (x+1)2^y]\) となる範囲である。任意の範囲は最大で \(2 \log_2 n\) 個の二進レンジに分解できることに注目する。例えば範囲 \([48,107]\) は重複しない 6 個の二進レンジ \([48,48]\), \([49,64]\), \([65,96]\), \([97,104]\), \([105,106]\), \([107,107]\) で正準に (canonically) カバーされる。つまり、すべての二進レンジで頻度をカウントしておけば 6 回の加算のみで \([48,107]\) 範囲のレンジクエリーを計算することができることになる。これは 60 個の点クエリーを繰り返して加算するより誤差が少なく計算効率も良い。

二進レンジを使用してレンジクエリーに近似的に応答するために、\(1+\log_2 n\) 個の Count-Min スケッチを用意し、それぞれ \(y \in \{0,1,\ldots,\log_2 n\}\) の二進レンジに含まれる頻度としてカウントする。レンジクエリーは要求のあった範囲を各層の二進レンジに分解し、それぞれ頻度を参照して合計頻度の推定値を得る。任意の範囲を二進レンジに分解する計算方法は [2] を参照。

Fig 4 の例は最大 \([0,15]\) 範囲の要素 (\(n=16\)) を持つ Count-Min スケッチの 5 層構造である。それぞれの層は \(y\) に対応する二進レンジを要素としてその頻度を保存する。要素 10 の頻度を更新する場合、上層の Count-Min スケッチから \([0,15]\), \([8,15]\), \([8,11]\), \([10,11]\), \([10,10]\) の頻度を更新する (図左)。\([3,9]\) のレンジクエリーでは \([3,3]\), \([4,7]\), \([8,9]\) の頻度を参照して合計すれば良い (図右)。

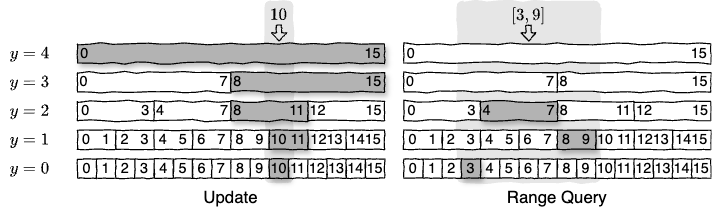
二進レンジ Count-Min スケッチ構造の更新とクエリーは、時間計算量 \(O(\log(n) \log \frac{1}{\delta})\)、空間計算量 \(O(\frac{\log n}{\epsilon} \log \frac{1}{\delta})\) である。ある範囲 \([a,b]\) の真の合計頻度を \(f_{a,b}\) としたとき、二進レンジを使った Count-Min スケッチの構造で得られるレンジクエリー \([a,b]\) の推定合計頻度 \(\hat{f}_{a,b}\) は \(1-\delta\) の確率で式 (\(\ref{err_rng}\)) を満たす [1]。\[ \begin{equation} f_{a,b} \le \hat{f}_{a,b} \le f_{a,b} + 2 \epsilon N \log_2 n \label{err_rng} \end{equation} \] 式 (\(\ref{err_rng}\)) より、\(\epsilon' = \frac{\epsilon}{2 \log_2 n}\) となるように空間を調整すれば単体の Count-Min スケッチでの点クエリーと同等の誤差を持つレンジクエリー向け構造が構築できることが分かる。

適用例

ハッシュテーブルのような決定論的な構造と比べて Count-Min スケッチが有利な点は (1) 要素 \(x\) の種類が非常に多い (時に無限となる) 状況である。ただし、結果の頻度に誤差を含むことから、(2) 頻度が完全に正確でなくてもシステムの機能には支障がないケースに限られる。

思いつく範囲で (1) の対象は、検索キーワードなどユーザが自由に入力できる値、IP アドレス、URL、地理データの位置情報メッシュ、スマフォなどの小型デバイスの識別子や電話番号、ゲームや映像での敵キャラや弾などのオブジェクト、ページングなどのデータの領域、など。また (2) の対象は、グラフやヒートマップのように全体的な印象として人間が認知する出力、効率化のための自動のシステム最適化、動画の再生回数や投稿のインプレッション数、など。これらの組み合わせで実用的な例があれば Count-Min スケッチの適用を検討する価値があるだろう。

• 自然言語処理: 自然言語処理では文書に含まれる単語の出現頻度が頻繁に使われている。[2] では単語の分布的類似性を見つけるための点相互情報 (PMI; point-wise mutual information) を得るために Count-Min スケッチを応用している。

• 分位数: レンジクエリーにより中央値やパーセンタイルのような分位数 (quantile) の近似値を探索する。

Heavy Hitting の抽出

ジップの法則 (Zipf's law) とは、一部の要素が全体の頻度をほとんどの頻度を締め、それ以外の大多数が極めて小さい頻度となるような、現実世界で頻繁に見られるモデルである。例えば EC サイトでは、少数の売れ筋商品が全体の販売数の大多数を占め、それ以降は販売数の少ない多数のロングテール商品が占める形となる。Count-Min スケッチは前述のように推定合計頻度が大きい方が相対誤差が少ないことから、このようなモデルで頻度の大きい上位の要素を抽出するようなタスクで有効である。

Count-Min スケッチは更新と同時に新しいカウンター値を取得してその時点の推定合計頻度を得ることができる。これにヒープ (heap) のようなデータ構造を組み合わせると、頻度の上位を占める Heavy Hitting (大ヒット) 要素を少ない計算量で更新し続けることができる。

• キャッシュ戦略の最適化: Web 検索やデータベースでは高頻度にアクセスされるクエリーの検索結果をキャッシュして次回以降の応答を高速する手法が一般的に行われている。ただし検索キーワードや SQL は膨大なパターンとなることから、すべてのクエリーの頻度を保存して計測する方法は現実的ではない。Count-Min スケッチで Heavy Hitting を保持することで、どのクエリーの頻度が高くキャッシュすべきかを少ないメモリ空間と計算量で決定することができる。

  また、データベースのバッファプールのようにページ単位で読み書きが行われる設計では、頻繁にアクセスされるページを優先的にメモリに保持しておくことでデータのアクセス速度を改善することができる。

参考文献

1. Cormode, G., Muthukrishnan, S. (2004). An Improved Data Stream Summary: The Count-Min Sketch and Its Applications. In: Farach-Colton, M. (eds) LATIN 2004 : Theoretical Informatics. LATIN 2004. Lecture Notes in Computer Science, vol 2976. Springer, Berlin, Heidelberg.
2. Dzejla Medjedovic, Emin Tahirovic, Ines Dedovic. 大規模データセットのためのアルゴリズムとデータ構造. マイナビ出版 (2024)