論文翻訳: Cuckoo Filter: Practically Better Than Bloom
Bin Fan, David G. Andersen, Michael Kaminsky†, Michael D. Mitzenmacher‡
Carnegie Mellon University, †Intel Labs, ‡Harvard University
{binfan,dga}@cs.cmu.edu, michael.e.kaminsky@intel.com, michaelm@eecs.harvard.edu
 概要
概要
多くのネットワーキングシステムにおいて Bloom フィルターは高速な集合メンバーシップテストに使用されている。これは非常に優れた空間効率でごく一部の偽陽性 (false positive) 応答を許容する。しかし Bloom フィルターは集合から要素を削除することができず、"標準的な" Bloom フィルターを拡張して削除をサポートしようとするこれまでの試みはいずれも空間または性能のいずれかを低下させるものであった。
我々は近似集合メンバーシップテストのための Bloom フィルターを置き換えることのできる Cuckoo フィルターと呼ばれる新しいデータ構造を提案する。Cuckoo フィルターは要素の動的な追加と削除をサポートし Bloom フィルターよりもさらに高い性能を達成する。多くの要素を保存し適度に低い偽陽性を目標とするアプリケーションでは、Cuckoo フィルターは空間最適化された Bloom フィルターよりも空間オーバーヘッドが低い。我々の実験結果では、Cuckoo フィルターは Bloom フィルターに削除をサポートするように拡張した従来のデータ構造より時間と空間の両方で大幅に優れていることを示している。
Table of Contents
- 概要
- 1. 導入
- 2. 背景と関連研究
- 3 Cuckoo フィルターアルゴリズム
- 4. 漸近的な挙動
- 5. 空間の最適化
- 6. Bloom フィルターとの比較
- 7. 評価
- 8. 結論
- 9. ACKNOWLEDGEMENTS
- 10. REFERENCES
- 翻訳抄
 Categories and Subject Descriptors
Categories and Subject Descriptors
E.1 [Data]: Data Structures; E.4 [Data]: Data Compaction and Compression
 Keywords
Keywords
Cuckoo hashing; Bloom filters; compression
 1. 導入
1. 導入
多くのデータベース、キャッシュ、ルータ、ストレージシステムは近似集合メンバーシップ (approximate set membership) テストを使用して特定の要素が (通常は大きな) 集合に含まれるかどうかを、小さな偽陽性 (false positive) の確率をもって判断する。このテストで最も広く使われているデータ構造は Bloom フィルター [3] であり、そのメモリ効率の高さから広く研究されている。Bloom フィルターは、確率的ルーティングテーブルに必要な空間削減 [25]、IP アドレスの最長接頭辞マッチングの高速化 [9]、ネットワーク状態の管理と監視の改善 [24, 4]、パケット内のマルチキャスト転送情報のエンコード [15] など、多くのアプリケーションに使用されている [6]。
標準的な Bloom フィルターの制限はフィルター全体を再構築しないと既存の要素を削除できないことである (さもなくば一般にあまり好ましくない偽陰性をもたらす可能性がある)。いくつかのアプローチでは標準の Bloom フィルターを拡張して削除をサポートしているが空間や性能に大きなオーバーヘッドを伴う。カウンティング Bloom フィルター (Counting Bloom Filter) [12] は複数のアプリケーション [24, 25, 9] で提案されているが、通常、空間最適化された Bloom フィルターと同じ偽陽性率を維持するために 3-4 倍の空間を使用する。他の変種として \(d\)-left カウンティング Bloom フィルター [5] があるがそれでも 1.5 倍大きく、Quotient フィルター (商フィルター) [2] は Bloom フィルターと同等の空間オーバーヘッドを得るために検索 (lookup) 性能が大幅に低下する。
この論文では、近似集合メンバーシップテストで削除をサポートしても標準の Bloom フィルターと比較して空間や性能に高いオーバーヘッドを課す必要がないことを示している。我々は 4 つの主要な利点を提供する実用的なデータ構造である Cuckoo フィルターを提案する。
要素の動的な追加と削除をサポートする;
従来の Bloom フィルターに比べて、満杯に近い場合 (例えば 95% の空間使用率) でも高い検索性能を提供する;
Quotient フィルターのような代替手法よりも実装が簡単である;
目標の偽陽性率が 3% 未満であれば、多くの実用的なアプリケーションにおいて Bloom フィルターよりも使用する空間が少ない。
Cuckoo フィルターは Cuckoo ハッシュテーブル [21] のコンパクトな変形で、Key-Value ペアの代わりに、挿入された各要素のフィンガープリント (ハッシュ関数を使用して要素から導出されたビット列) のみを格納する。フィルターはフィンガープリントで密に埋められており (例えば 95% のエントリが占有されている) 高い空間効率が得られる。要素 \(x\) の集合メンバーシップクエリーは単に \(x\) のフィンガープリントについてハッシュテーブルを検索し、同一のフィンガープリントが見つかった場合に true を返す。
Cuckoo フィルターを構築する場合、そのフィンガープリントのサイズは目標とする偽陽性率 \(\epsilon\) によって決まる。その値が小さいほどより多くの誤ったクエリーを拒否するためにより長いフィンガープリントが必要となる。興味深いことに、実際の多くのワークロードでは Cuckoo フィルターが Bloom フィルターより実際に優れていることを示す一方で、Cuckoo フィルターで使用される最小フィンガープリントのサイズは (セクション 4 で説明するように) テーブルのエントリ数と共に対数的に増加することから、これらは漸近的に悪くなっている。結果としてテーブルが大きいほど要素ごとの空間のオーバーヘッドが大きくなるが、この余分な空間の使用はより低い偽陽性率をもたらす。要素数が数十億以下の実用的な問題では \(\epsilon \lt 3\%\) であれば Cuckoo フィルターは削除をサポートしながら削除不可能で空間最適化された Bloom フィルターよりも少ない空間を使用する。
Cuckoo フィルターはフィンガープリントのみがフィルターに格納されており、各要素の元となるキーと値のビットはもはや検索できないことから通常のハッシュテーブルとは大きく異なる。完全なキーが保存されないため、Cuckoo フィルターはハッシュ値に基づいて既存のキーを移動することも、新しい要素を挿入するための標準的な Cuckoo ハッシュを実行することもできない。この違いは Cuckoo ハッシュに適用される標準的な手法、分析、最適化が必ずしも Cuckoo フィルターに引き継がれるわけではないことを意味している。
この論文による技術的貢献は以下の通りである。
標準的な Cuckoo ハッシングの変種である部分キー Cuckoo ハッシングを適用して要素の動的な追加と削除をサポートする Cuckoo フィルターを構築する (セクション 3)。
部分キー Cuckoo ハッシングが現実世界のほとんどのアプリケーションで高いテーブル占有率を保証する理由を探る (セクション 4)。
空間効率において Bloom フィルターを上回る Cuckoo フィルターの最適化 (セクション 5)。
 2. 背景と関連研究
2. 背景と関連研究
 2.1 Bloom フィルターとその変種
2.1 Bloom フィルターとその変種
Table 1 にまとめたように、標準の Bloom フィルターと削除のサポートや検索性能の向上を含む変種を比較する。これらのデータ構造はセクション 7 で経験的に評価される。Cuckoo フィルターはこれらのデータ構造より高い空間効率と性能を達成している。
標準的な Bloom フィルター [3] は Insert と Lookup の 2 つの操作をサポートする要素集合のコンパクトな表現を提供する。Boom フィルターはクエリが "間違いなく存在しない" (definitely not) (誤りなし) か "おそらく存在する" (probably yes) (誤りの可能性 \(\epsilon\) あり) のどちらかを偽陽性率を調整しながら返す。\(\epsilon\) が低いほどフィルターが必要とする空間は大きくなる。
Bloom フィルターは \(k\) 個のハッシュ関数と、すべてのビットが初期状態で "0" に設定されたビット配列で構成される。要素を挿入するには、その要素を \(k\) 個のハッシュ関数でビット配列内の \(k\) 個の位置にハッシュし、すべての \(k\) 個のビットを "1" に設定する。検索は同様に処理されるが、配列内の対応する \(k\) 個のビットを読み取る点が異なる。それらすべてのビットが設定されていればクエリーは true を返し、そうでなければ false を返す。Bloom フィルターは削除をサポートしていない。
Bloom フィルターは空間効率が非常に優れているが最適とは言えない [20]。偽陽性の場合、空間最適化された Bloom フィルターは \(k=\log_2(1/\epsilon)\) 個のハッシュ関数を使用する。このような Bloom フィルターは各要素を \(1.44\log_2(1/\epsilon)\) ビットで格納することができる。これは要素のサイズや総数ではなく \(\epsilon\) にのみ依存する。情報理論的な最小値は要素ごとに \(\log_2(1/\epsilon)\) ビットを必要とするため、空間最適化 Bloom フィルターは情報理論的な下限値に対して 44% の空間オーバーヘッドを課すことになる。
情報理論上の最適値は、フィンガープリント (長さ \(1/\epsilon\)) と完全なハッシュテーブルを使用することで静的な集合に対して基本的に達成可能である [6]。削除を効率的に処理するために、我々は完全なハッシュテーブルを最適に設計された Cuckoo ハッシュテーブルに置き換える。
カウンティング Bloom フィルター [12] は削除を許容するように Bloom フィルターを拡張したものである。カウンティング Bloom フィルターはビット配列の代わりにカウンターの配列を使用する。挿入操作は \(k\) 個のビットを設定する代わりに単に \(k\) 個のカウンターの値をインクリメントし、検索操作は必要な各カウンターが 0 でないかどうかをチェックする。削除操作はこれら \(k\) 個のカウンターの値をデクリメントする。Bloom フィルターの特性を保持するために、算術オーバーフロー (つまり取り得る最大値を持つカウンターをインクリメントすること) を防ぐため配列の各カウンターは十分大きくなければならない。実際にはカウンターは 4 ビット以上で構成されるため、カウンター Bloom フィルターは標準的な Bloom フィルターよりも 4 倍以上の空間を必要とする。(さらに複雑になるが、オーバーフローしたカウンターを管理する二次ハッシュテーブル構造を導入することでより少ない空間でカウンター Bloom フィルターを構築できる。)
Blocked Bloom フィルター [22] は削除をサポートしないが検索でより優れた空間的局所性を提供する。Blocked Bloom フィルターは小さな Bloom フィルターの配列で構成され、それぞれの Bloom フィルターは CPU キャッシュラインに収まる。各要素はハッシュパーティショニングによって決定されたこれらの小さな Bloom フィルターのうちの 1 つだけに格納される。その結果、どのクエリーでもその Bloom フィルターをロードするキャッシュミスは最大でも 1 回となり性能が大幅に向上する。欠点は、小さな Bloom フィルターの配列全体で負荷が不均衡になるため偽陽性率が高くなることである。
\(d\)-left カウンティング Bloom フィルター [5] は我々がここで使うアプローチと似ている。\(d\)-left ハッシング [19] を使ったハッシュテーブルは保存された要素のフィンガープリントを保存する。これらのフィルターはフィンガープリントを削除することで要素を削除する。カウンティング Bloom フィルターと比較して空間コストを 50% 削減し、空間最適化された削除不可能な Bloom フィルターと比較して通常は 1.5~2 倍の空間が必要となる。ここで示したように Cuckoo フィルターは \(d\)-left カウンティング Bloom フィルターよりも優れた空間効率を達成しておりシンプルさなどの利点もある。
Quotient フィルター [2] もまた削除をサポートするためにフィンガープリントを格納するコンパクトなハッシュテーブルである。Quotient フィルターはより優れた空間的局所性を提供するために線形プローブと同様の技術を使用してフィンガープリントを特定する。ただし各エントリをエンコードするために追加のメタデータを必要とし、同様の標準 Bloom フィルターよりも 10~25% 多くの空間を必要とする。さらにそのすべての操作はターゲットの要素に到達する前にテーブルエントリのシーケンスをデコードする必要があり、ハッシュテーブルを埋めれば埋めるほどこれらのシーケンスは長くなる。その結果ハッシュテーブルの使用率が 75% を超えるとその性能は著しく低下する。
その他の変種: Bloom フィルターを空間および/または性能の面で改善するために他の変種が提案されている。Rank-Index ハッシング [14] は圧縮されたフィンガープリントを保存するために線形チェーン法ハッシュテーブルを構築する。\(d\)-left カウンティング Bloom フィルターと似ており、それよりも空間効率が幾分良いもののチェーンコストを削減する内部インデックスの更新は非常に効果であるため動的な設定ではあまり魅力的ではない。Putze らは 2 種類の Bloom フィルター変種を提案している [22]。1 つは前述の Blocked Bloom フィルターである。もう 1 つは Golomb-Compressed Sequence と呼ばれるもので、すべての要素のフィンガープリントをソートされたリストに保存する。その空間は最適に近いがデータ構造は静的であり、エンコードされたシーケンスをデコードするために一定でない検索時間を必要とする。そのためこの論文では他のフィルターとは評価しない。Pagh らは Cleary [8] に基づいて漸近的に空間最適なデータ構造 [20] を提案した。しかしこのデータ構造は代替のデータ構造よりも大幅に複雑であり高性能な実装には適さないようである。対照的に Cuckoo フィルターは実装が容易である。
 2.2 Cuckoo ハッシュテーブル
2.2 Cuckoo ハッシュテーブル
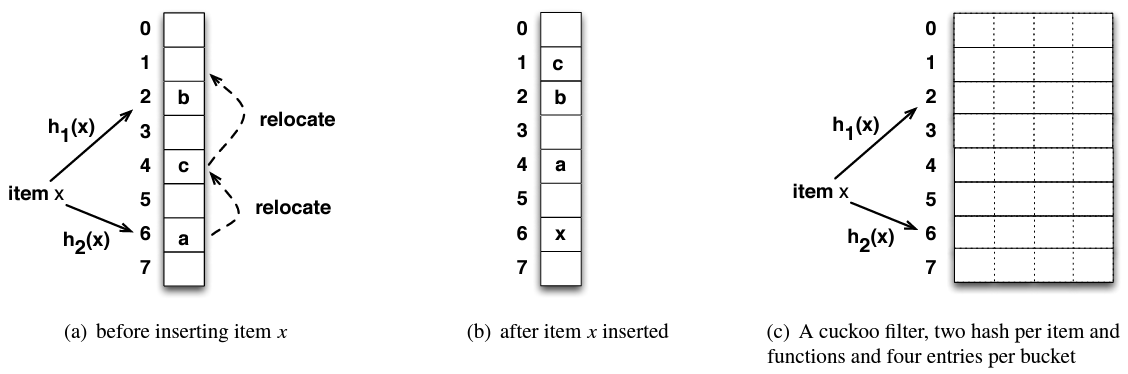
Cuckoo ハッシングの基本: 基本的な Cuckoo ハッシュテーブル [12] はバケットの配列で構成され、各要素はハッシュ関数 \(h_1(x)\) と \(h_2(x)\) によって決定される 2 つの候補バケットを持つ。検索手順は両方のバケットをチェックしてどちらかにこの要素が含まれているかを確認する。Figure 1(a) は 8 つのバケットからなるハッシュテーブルに新しい要素 \(x\) を挿入する例を示している。ここで \(x\) はバケット 2 または 6 のどちらかに配置できる。\(x\) の 2 つのバケットのどちらかが空であれば、アルゴリズムはその空いているバケットに \(x\) を挿入し挿入操作が完了する。この例のようにどちらのバケットにも空きがない場合、要素は候補バケットの 1 つ (例えばバケット 6) を選択し、既存のアイテム (この場合は "a") を追い出し、この犠牲となった要素 (victim item) をそれ自身の代替位置に再挿入する。この例では "a" を移動させることで既存の要素 "c" がバケット 4 からバケット 1 にキックされる別の再配置がトリガーされる。この手順は Figure 1(b) に示すように空きのバケットが見つかるまで、または再配置の最大回数に達するまで (例えば我々の実装では 500 回) 繰り返される。空のバケットが見つからなかった場合、このハッシュテーブルは満杯で挿入できないと判断される。Cuckoo ハッシングは一連の置換を実行できるが、その償却挿入時間は \(O(1)\) である。
Cuckoo ハッシングは新しい要素を挿入する際に以前の要素の配置決定を改善するため高い空間占有率を保証する。Cuckoo ハッシングのほとんどの実用的な実装は、[10] で提案されているように、複数の要素を保持するバケットを使用することで上記の基本的な説明を拡張している。すべてのハッシュ関数が完全にランダムであると仮定して、\(k\) 個のハッシュ関数とサイズ \(b\) のバケットを使用した場合に可能な最大負荷が分析されている [13]。Cuckoo ハッシュテーブルのパラメータを適切に設定すれば (セクション 5 で検討) テーブル空間の 95% を高い確率で満たすことができる。
Cuckoo ハッシュを集合メンバーシップに使用: 最近、いくつかのアプリケーションでは集合メンバーシップ情報を提供するために標準的な Cuckoo ハッシュテーブルが使用されている。トランザクショナルメモリをサポートするために Sanchez らは各トランザクションのメモリアドレスの読み書きの集合を Cuckoo ハッシュテーブルに格納し、このテーブルが一杯になったら Bloom フィルターに変換することを提案した [23]。彼らの設計では標準的な Cuckoo ハッシュテーブルを使用していたため Cuckoo フィルターよりもはるかに多くの空間を必要としていた。高速でメモリ効率の良い Key-Value ストア [17, 11] とソフトウェアベースのイーサネットスイッチ [26] の構築に関する我々の以前の研究ではすべての内部データ構造として Cuckoo ハッシュテーブルを適用していた。この研究は部分キー Cuckoo ハッシング (partial-key cuckoo hashing) と呼ばれる最適化によってハッシュテーブルの性能を向上させることに動機づけられ、またそれに焦点を当てたものだった。しかしこの論文で示すように、この技術はこれまで研究されていなかった Bloom フィルターに代わる新しいアプローチを構築することを可能とした。結果としてこの論文では部分キー Cuckoo ハッシングも適用するが、より重要なのは (Key-Value クエリーではなく) 集合メンバーシップテストを提供するために特にこの技術を採用することの詳細な分析を提供し、さらに代替の集合メンバーシップデータ構造と Cuckoo フィルターの性能を比較する。
Cuckoo フィルターの課題: Cuckoo フィルターの空間効率を高めるために、我々は高速検索と高いテーブル占有率 (例えばハッシュテーブルのスロットが 95% 埋まっているような) を提供する多方向連想 Cuckoo ハッシュテーブル (multi-way associative cuckoo hash table) を使用する。ハッシュテーブルのサイズをさらに縮小するために各要素はまず一定サイズのフィンガープリントにハッシュされてからこのハッシュテーブルに挿入される。このデータ構造を適用する課題は挿入プロセスを再設計し要素ごとに空間使用量を最小限に抑えるためにハッシュテーブルを慎重に構成することである:
第一に、ハッシュテーブルにフィンガープリントのみを保存すると標準的な Cuckoo ハッシュのアプローチを使用して要素を挿入できなくなる。なぜなら Cuckoo ハッシングでの挿入アルゴリズムは既存のフィンガープリントを代替の位置に再配置できなければならないためである。空間効率は悪いが簡単な解決策は、挿入された各要素を全体として (おそらくテーブルの外部に) 保存することである。元の要素 ("キー") があればその代替の場所を計算するのは簡単である。対照的に Cuckoo フィルターは部分キー Cuckoo ハッシングを使いフィンガープリントのみに基づいてアイテムの代替の位置を見つける (セクション 3)。
第二に、Cuckoo フィルターは各要素をハッシュテーブル内の複数の可能な場所に関連付ける。要素を格納する場所におけるこの柔軟性はテーブルの占有率を向上させるが、各検索でより多くの可能性のある場所を調査するときに同じ偽陽性率を維持するには、より長いフィンガープリントのためにより多くの空間を必要とする。セクション 5 では要素あたりの平均空間コストを最小化するためにテーブルの占有率とそのサイズのバランスを最適化する我々の分析を紹介する。
 3 Cuckoo フィルターアルゴリズム
3 Cuckoo フィルターアルゴリズム
この論文では Cuckoo フィルターに使用される Cuckoo ハッシュテーブルの基本単位をエントリと呼ぶ。各エントリには 1 つのフィンガープリントが保存される。ハッシュテーブルはバケットの配列で構成され、バケットには複数のエントリを含めることができる。
このセクションでは Cuckoo フィルターがどのように Insert, Lookup, Delete 操作を行うかを説明する。セクション 3.1 では Cuckoo フィルターが動的に新しい要素を挿入できるようにする標準的な Cuckoo ハッシングの変種である部分キー Cuckoo ハッシュについて説明する。この手法は以前の研究 [11] で初めて紹介されたが、そこでは完全なキーが格納されている通常の Cuckoo ハッシュテーブルの検索および挿入の性能を向上させることが目的であった。この論文では対照的にフィンガープリントのみで部分キー Cuckoo ハッシュを使用する際の空間効率の最適化と分析に焦点を当て、Cuckoo フィルターを Bloom フィルターと同等またはそれよりもさらにコンパクトなものにする。
 3.1 Insert
3.1 Insert
前述の通り、標準的な Cuckoo ハッシングで既存のハッシュテーブルに新しい要素を挿入するには、新しい要素のための空間を確保するために必要に応じてそれらをどこに再配置するかを決定するために、元の既存の要素にアクセスする何らかの手段が必要である (セクション 2.2)。しかし Cuckoo フィルターはフィンガープリントのみを保存するため元のキーを復元して再ハッシュしその代替の位置を見つける方法がない。この制約を克服するために部分キー Cuckoo ハッシングと呼ばれる技術を利用してフィンガープリントに基づいて要素の代替の位置を導出する。要素 \(x\) に対し我々のハッシュスキームは次のように 2 つの候補バケットのインデックスを計算する: \[ \begin{equation} \begin{aligned} h_1(x) & = \text{hash}(x), \\ h_2(x) & = h_1(x) \oplus \text{hash}(\mbox{$x$'s fingerprint}). \end{aligned} \label{hash} \end{equation} \]
式 (\(\ref{hash}\)) の XOR 演算は重要な特性を保証している。\(h_1(x)\) は同じ式を使用して \(h_2(x)\) とフィンガープリントから計算することもできる。言い換えると、元々バケット \(i\) にあったキーを置き換えるには、(\(i\) が \(h_1(x)\) であろうと \(h_2(x)\) であろうと) 現在のバケットインデックス \(i\) とそのバケットに保存されているフィンガープリントから \[ \begin{equation} j = i \oplus \text{hash}(\mbox{fingerprint}) \label{relocate} \end{equation} \] でその代替バケット \(j\) を直接計算する。したがって挿入ではテーブル内の情報のみが使用され、元の要素 \(x\) を取得する必要はない。
さらにフィンガープリントはテーブル内で要素を均一に分散できるように現在のバケットのインデックスと XOR 演算される前にハッシュ化される。もし代替の場所がフィンガープリントをハッシュせずに "\(i \oplus \text{fingerprint}\)" で計算された場合、フィンガープリントのサイズがテーブルのサイズと比較して小さいときに近くのバケットから追い出された要素がテーブル内で互いに近くに配置されることになる。たとえば 8 ビットのフィンガープリントを使用した場合、XOR 演算によりバケットインデックスの下位 8 ビットが変更される一方で高位ビットは変更されないため、バケット \(i\) から追い出された要素はバケット \(i\) から最大 256 離れたバケットに再配置される。フィンガープリントをハッシュするとこれらの要素をハッシュテーブルの全く別の場所にあるバケットに再配置できるようになり、ハッシュの衝突が減ってテーブルの使用率が向上する。
部分キー Cuckoo ハッシングを使い、Cockoo フィルターはアルゴリズム 1 に示すプロセスによって新しい要素を動的に追加する。これらのフィンガープリントは \(h_1\) や \(h_2\) のサイズよりかなり短くすることができるため 2 つの結果が生じる。第一に、式 (\(\ref{hash}\)) で計算される \((h_1,h_2)\) の可能な選択肢の総数は、標準的な Cuckoo ハッシングのような完全なハッシュを使用して \(h_1\) と \(h_2\) を導出するよりもはるかに小さくなる可能性がある。これにより多くの衝突を引き起こす可能性があり、特に ([10, 13] のような) Cuckoo ハッシングに関する以前の分析は成り立たない。部分キー Cuckoo ハッシングの完全な解析はまだ未解決のままである (この論文の範囲を超えている)。セクション 4 ではこの問題についての詳細な議論を行い実用的なワークロードに対して高い占有率を達成する方法について考察する。
第二に、同じフィンガープリントを持つ 2 つの異なる要素 \(x\) と \(y\) を挿入することは問題がない。同じフィンガープリントがバケット内に複数回出現することができる。ただし、Cuckoo フィルターは同じ要素を \(2b\) 回 (\(b\) はバケットサイズ) を超えて挿入するアプリケーションには向いていない。これはこのような重複した要素の 2 つのバケットが過負荷になるためである。このようなシナリオにはいくつかの解決策がある。まずテーブルが削除をサポートする必要がない場合は各フィンガープリントのコピーは一つしか保存する必要がないためこの問題は発生しない。次に、ある程度の空間コストでカウンターをバケットに関連付けそれらを適切にインクリメント/デクリメントすることができる。最後に、元のキーがどこかに (おそらくより低速な外部ストレージに) 保存されている場合、テーブルがバケットとフィンガープリントと一致する (偽陽性) エントリを既に含んでいるときに挿入を遅くするという代償を払って、そのレコードを参照して重複挿入を完全に防ぐことができる。同様の要件が従来の Bloom フィルターと \(d\)-left カウンティングフィルターにも当てはまる。
 3.2 Lookup
3.2 Lookup
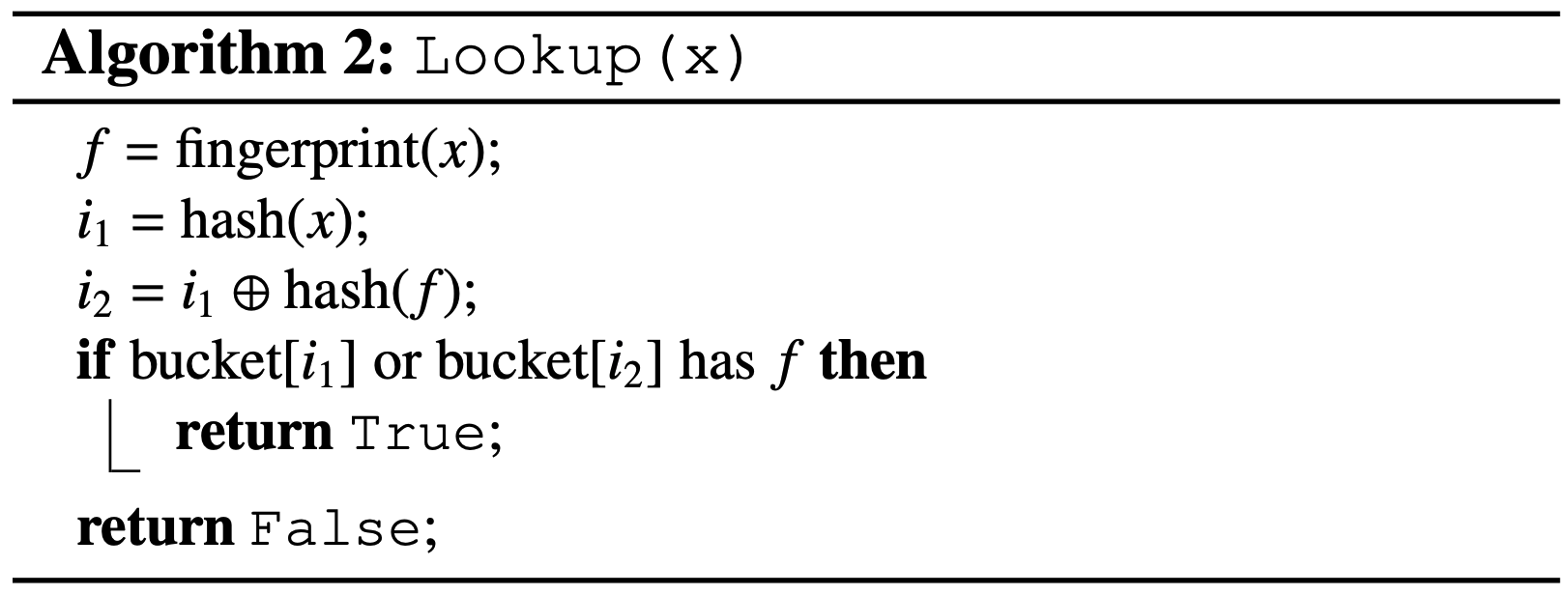
Cuckoo フィルターの検索処理はアルゴリズム 2 に示すように単純である。要素 \(x\) が与えられると、アルゴリズムはまず式 (\(\ref{hash}\)) に従って \(x\) のフィンガープリントと 2 つの候補バケットを算出する。そしてこれら 2 つのバケットが読み取られる。どちらかのバケット内の既存のフィンガープリントが一致すれば Cuckoo フィルターは true を返し、そうでなければ false を返す。バケットのオーバーフローが起きない限り偽陽性は発生しないことに注意。
 3.3 Delete
3.3 Delete
標準的な Bloom フィルターは削除ができないため 1 つの要素を削除するためにフィルター全体を再構築する必要がある一方で、カウンティング Bloom フィルターはかなりの空間を必要とする。Cuckoo フィルターはカウンティング Bloom フィルターと似ていて、削除時にハッシュテーブルから対応するフィンガープリントを削除することで挿入されている要素を削除することができる。同様の削除プロセスを持つ他のフィルターは Cuckoo フィルターよりも複雑であることが分かる。例えば \(d\)-left カウンティング Bloom フィルターはフィンガープリントの衝突による "偽削除" (false deletion) 問題を防ぐために追加のカウンターを使用しなければならず1、Quotient フィルターは削除後の "空の" エントリーを埋めるためにフィンガープリントのシーケンスをシフトし "バケット構造" を維持しなければならない2。
アルゴリズム 3 で示されている Cuckoo フィルターの削除プロセスははるかに簡単である。特定の要素について両方の候補バケットをチェックし、どちらかのバケット内でフィンガープリントが一致すると、その一致したフィンガープリントのコピーがそのバケットから削除される。
削除では要素を削除した後にエントリーをクリーンアップする必要はない。また 2 つの要素が 1 つの候補バケットを共有し同じフィンガープリントを持つ場合の "偽削除" 問題も回避できる。例えば要素 \(x\) と \(y\) の両方がバケット \(i_1\) に存在し、フィンガープリント \(f\) 上で衝突する場合、部分キー Cuckoo ハッシュは \(i_2 = i_1 \oplus \text{hash}(f)\) であるため、両者がバケット \(i_2\) にも存在できることを保証する。\(x\) を削除するとき、\(x\) または \(y\) の挿入時に追加された \(f\) のコピーがプロセスによって削除されてもかまわない。\(x\) が削除された後もバケット \(i_1\) と \(i_2\) のどちらかに対応するフィンガープリントが残っているため \(y\) は依然として集合のメンバーとして認識されている。この重要な結果はフィルターの偽陽性の振る舞いが削除後も変わらないということである。(上記の例では \(y\) がテーブル内にあると定義上 \(x\) の検索に対して偽陽性を引き起こす。これは同じバケットとフィンガープリントを共有しているためである。) これは近似集合メンバーシップデータ構造の期待される偽陽性であり、その確率は \(\epsilon\) で境界を保ったままである。
要素 \(x\) を安全に削除するには、その要素が事前に挿入されていなければならないことに注意。さもなければ、挿入されていない要素を削除すると、たまたま同じフィンガープリントを共有する実際には異なる要素が意図せず削除される可能性がある。この要件は他のすべての削除をサポートするフィルターにも当てはまる。
- 1\(d\)-left カウンティング Bloom フィルターの単純な実装には "偽削除" 問題がある。\(d\)-left カウティング Bloom フィルターは各要素をテーブルのパーティションからの \(d\) 個の候補バケットにマッピングし、その \(d\) 個のバケットを一つにフィンガープリントを保存する。2 つの異なる要素が 1 つのバケットのみを共有し、それらが同じフィンガープリントを持つ場合 (フィンガープリントが小さい場合に起きやすい)、この特定のバケットからフィンガープリントを直接削除すると間違った要素が削除される可能性がある。この問題に対処するために \(d\)-left カウンティング Bloom フィルターは各テーブルエントリに追加のカウンターと追加の間接関数 (indirection) を使用する [5]。
- 2Quotient フィルターでは同じ商 (quotient) (すなはち \(q\) 個の最上位ビット) を持つすべてのフィンガープリントはその数値の順序に従って連続したエントリに格納されなければならない。従ってフィンガープリントのクラスタから 1 つのフィンガープリントを削除するには、穴の後のすべてのフィンガープリントを 1 スロット分シフトさせ、またそれらのメタデータのビットも変更する必要がある [2]。
 4. 漸近的な挙動
4. 漸近的な挙動
ここで我々は部分キー Cuckoo ハッシュを使用して Cuckoo フィルターにフィンガープリントを保存すると、フィルターサイズに応じてゆっくりと増加するフィンガープリントサイズの下限が得られることを示す。これはフィンガープリントのサイズが望ましい偽陽性率のみに依存する他のアプローチ (以前に取り上げた静的 Bloom フィルターのフィンガープリントや完全ハッシュなど) とは対照的である。これは否定的に見えるかもしれないが、実際にはその影響は重要ではないように思われる。経験的に、各バケットが 6 ビット以上の 4 つのフィンガープリントを保持している場合、最大 40 億の要素を含むフィルターはハッシュテーブルを 95% の負荷で効率的に埋めることができる。
このセクションと次のセクションでの分析に使用される表記は以下の通り:
| \(\epsilon\) | 目標の偽陽性率 |
| \(f\) | フィンガープリントのビット長 |
| \(\alpha\) | 負荷係数 (\(1 \le \alpha \le 1\)) |
| \(b\) | バケットあたりのエントリ数 |
| \(m\) | バケット数 |
| \(n\) | 要素数 |
| \(C\) | 要素ごとの平均ビット数 |
最小フィンガープリントサイズ: 我々の提案する部分キー Cuckoo ハッシングは与えられた要素の現在の位置とフィンガープリントに基づいて候補バケットを導出する (セクション 3)。その結果として各要素の候補バケットは独立ではない。例えば要素がバケット \(i_1\) または \(i_2\) に配置できるとする。式 (\(\ref{hash}\)) より、\(f\)-ビットのフィンガープリントを使用すると \(i_2\) の可能な値の数は最大で \(2^f\) 個である。1 バイトのフィンガープリントでは \(i_1\) が与えられたときの \(i_2\) の可能な値の数は最大 \(2^f=256\) 個しかない。\(m\) 個のバケットを持つテーブルでは \(2^f \lt m\) (または同等の \(f \lt \log_2 m\) ビット) のとき \(i_2\) の選択はハッシュテーブル全体の \(m\) 個のバケットすべての部分集合に過ぎない。
直感的には、フィンガープリントが十分に長ければ部分キー Cuckoo ハッシングは標準の Cuckoo ハッシングに十分近似できる可能性がある。しかしハッシュテーブルが非常に大きく、比較的短いフィンガープリントを格納する場合、ハッシュの衝突により挿入が失敗する可能性が高まり、テーブルの占有率が減少する可能性がある。このような状況は、Cuckoo フィルターが多数の要素をターゲットにしているものの偽陽性率が適度に低い場合に発生することがある。以下では挿入失敗の確率の下限を解析的に求める。
まず与えられた \(q\) 個の要素が同じ 2 つのバケットで衝突する確率を導出する。最初の要素 \(x\) が最初のバケット \(i_1\) とフィンガープリント \(t_x\) を持つと仮定する。他の \(q-1\) 個の要素がこの要素 \(x\) と同じ 2 つのバケットを持つ場合、それらは3 (1) 同じフィンガープリントを持たなければならず、それは確率 \(1/2^f\) で起き、(2) その最初のバケットは \(i_1\) か \(i_1 \oplus h(t_x)\) のどちらかでなければならずこれは同じ確率 \(2/m\) で起きる。したがって、このような \(q\) 個の要素が同じ 2 つのバケットを共有する確率は \(\left(2/m \cdot 1/2^f \right)^{q-1}\) となる。
ここで定数 \(c\) および定数バケットサイズ \(b\) で \(m=cn\) 個のバケットで構成される空のテーブルに \(n\) 個のランダムな要素を挿入する構築プロセスについて考える。同じ 2 つのバケットに \(q=2b+1\) 個の要素がマッピングされている場合、挿入は失敗する。この確率は失敗の下限を与えている (そして我々はこれがこの構築プロセスの失敗確率を支配していると信じているが、これは証明しないし下限を得るために証明する必要もない)。\(n\) 個の要素のうち \(2b+1\) 要素の取り得る集合は合計で \(\binom{n}{2b+1}\) 通りあるため、構築過程で衝突する \(2b+1\) 個の要素のグループの予想数は \[ \begin{equation} \binom{n}{2b+1} \left(\frac{2}{2^f\cdot m}\right)^{2b} = \binom{n}{2b+1} \left(\frac{2}{2^f\cdot cn}\right)^{2b} = \Omega \left(\frac{n}{4^{bf}}\right) \label{eq3} \end{equation} \] となる。
我々は重大な失敗確率を回避するには \(4^{bf}\) は \(\Omega(n)\) でなければならないと結論づける。そうでなければこの期待値は \(\Omega(1)\) となる。したがってフィンガープリントのサイズは \(f = \Omega(\log n/b)\) ビットでなければならない。
Bloom フィルターは要素ごとに定数 (約 \(\ln(1/\epsilon)\) ビット) を使用することを思い出すと、フィンガープリントに必要なビット数が \(\Omega(\log n)\) であることから、この結果はやや残念に思える。したがってこのアプローチのスケーラビリティについて懸念があるかもしれない。しかし次に示すように適切なサイズのバケットを使用している限り、フィンガープリントのサイズは小さいままであり、Cuckoo フィルターの実際の適用は下限の分母の \(b\) 係数によって節約される。
経験的評価: Figure 2 はフィンガープリントサイズ \(f\)、バケットサイズ \(b\)、テーブルのバケット数 \(m\) を変化させたときに部分キー Cuckoo ハッシングで達成される負荷係数を示している。実験ではフィンガープリントのサイズ \(f\) を 1 から 20 ビットまで変化させた。ランダムな 64 ビットのキーが空のフィルターに挿入され、1 回の挿入で空のエントリを見つけるために既存のフィンガープリントが 500 回以上再配置されたところで (我々の "満杯" 条件) 停止し、達成された負荷係数 \(\alpha\) を測定する。我々はこの実験を \(m=2^{15},\) \(2^{20},\) \(2^{25},\) \(2^{30}\) 個のバケットを持つフィルターに対して 10 回実行し、10 回の試行に渡る最小の負荷を計測した。テストベッドマシンのメモリ制約により大きなテーブルは使用しなかった。
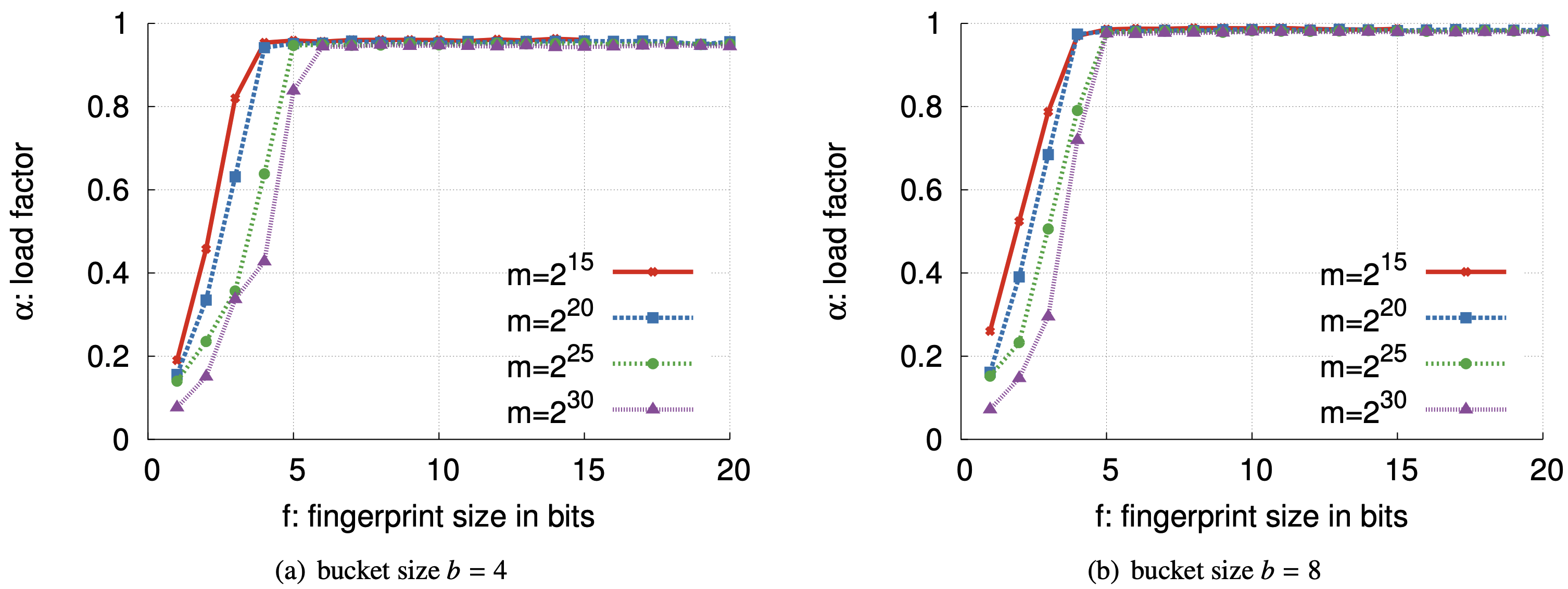
Figure 2 に示すように、さまざまな構成において十分に長いフィンガープリントでは \(b=4\) のフィルターでは占有率 95% まで充填でき、\(b=8\) のフィルターは 98% まで充填できた。その後はフィンガープリントのサイズを増やしても負荷率を改善するという点でほとんど効果はなかった (ただし当然ながら偽陽性率は減少する)。理論が示唆するように、フィルターが大きくなるにつれて最適に近い占有率を達成するために必要な最小 \(f\) は増加する。また Figure 2(a) と Figure 2(b) を比較すると、理論も示唆するようにバケットサイズ \(b\) が大きくなると高占有率のため最小 \(f\) が減少する。全体として、現実的なサイズの要素の集合には短いフィンガープリントで十分であると考えられる。\(b=4\) と \(m=2^{30}\) の場合でもテーブルに最大 40 億の要素を含めることができ、フィンガープリントが 6 ビットを超えると \(\alpha\) は 2 つの完全に独立したハッシュ関数を使用した実験で得られる "最適な負荷係数" に近づく。
洞察: 式 (\(\ref{eq3}\)) で導き出されたフィンガープリントのサイズの下限は Figure 2 に示されている経験的結果と併せて Cuckoo フィルターに重要な洞察を与える。理論的には Cuckoo フィルターの空間コストは Bloom フィルターより "悪い" が (\(\Omega(\log n)\) 対定数)、この設定において定数項は非常に重要である。Bloom フィルターで \(\epsilon=1\%\) を達成するには、保存される要素が 1,000個、100万超、10億個のいずれであっても 1 要素あたりおよそ 10 ビットを必要とする。対照的に Cuckoo フィルターはそのハッシュテーブルの同じ高い空間効率を維持するためにより長いフィンガープリントを必要とするが、それに応じてより低い偽陽性率が達成される。理論でも予測されるように、バケットサイズ \(b\) が十分に大きければフィンガープリントあたりの \(\Omega(\log n)\) ビットはゆっくりと増加する。我々は、実用的な目的ではそれは実装のために妥当なサイズの定数として扱うことができることを発見した。Figure 2 は数十億の要素をターゲットとする Cuckoo フィルターの場合、6 ビットのフィンガープリントはハッシュテーブルの非常に高い使用率を確保するのに十分であることを示している。
セクション 7 で説明するようにヒューリスティックな部分キー Cuckoo ハッシングは非常に効率的である。しかしながら、新しい要素を挿入するコストの限界の証明や、ハッシュ関数にどれだけの独立性が要求されるかの研究など、この手法に関するいくつかの理論的な問題は将来の研究のために未解決のままである。
- 3ここではフィンガープリントのハッシュ (つまり \(t_x \to h(t_x)\)) に衝突がないと仮定する。実際には \(t_x\) は数ビットであり \(h(t_x)\) はもっと長いからである。
 5. 空間の最適化
5. 空間の最適化
セクション 3 で示した Cuckoo フィルター操作の Insert, Lookup, Delete の基本アルゴリズムはハッシュテーブルの構成 (例えば各バケットがいくつのエントリーを持つかなど) とは独立している。ただし Cuckoo フィルターのパラメータを適切に選択することは空間効率に大きな影響を与える可能性がある。このセクションではパラメータの選択と追加のメカニズムを通じて Cuckoo フィルターの空間効率を最適化することに焦点を当てる。
空間効率は満杯状態のフィルターの各要素を表す平均ビット数によって測定され、テーブルサイズをフィルターが効率的に格納できる要素の総数で割ることで導出される。ハッシュテーブルの各エントリーには 1 つのフィンガープリントが格納されるが、すべてのエントリーが占有されているわけではないのは前述の通り。その結果、各要素の保存コストは実質的にフィンガープリントよりも高くなる。各フィンガープリントが \(f\) ビットで、ハッシュテーブルの負荷係数が \(\alpha\) の場合、各要素の償却空間コスト \(C\) は \[ \begin{equation} C = \frac{\text{table size}}{\text{# of items}} = \frac{f\cdot (\text{# of entries})}{\alpha\cdot(\text{# of entries})} = \frac{f}{\alpha} \text{bits} \label{eq4} \end{equation} \] となる。後に示すように \(f\) と \(\alpha\) の両方はバケットサイズ \(b\) に関連している。次のセクションでは最適なバケットサイズ \(b\) を選択することにより目標とする偽陽性率を与えて式 (\(\ref{eq4}\)) を (近似的に) 最小化する方法を検討する。
 5.1 最適バケットサイズ
5.1 最適バケットサイズ
Cuckoo フィルターの総サイズを一定に保ちながらバケットサイズを変更すると次の 2 つの結果が得られる:
バケットを大きくするとテーブルの占有率が向上する (つまり \(b\) を大きくする \(\to\) \(\alpha\) が大きくなる)。\(k=2\) のハッシュ関数ではバケットサイズ \(b=1\) (つまりハッシュテーブルが直接マッピングされる) ときの負荷率 \(\alpha\) は 50% だが、バケットサイズ \(b=2,\) \(4,\) \(8\) を使用するとそれぞれ 84%, 95%, 98% に増加する。
より大きなバケットは同じ偽陽性率を維持するためにより長いフィンガープリントを必要とする (つまり \(b\) を大きくする \(\to\) \(f\) が大きくなる。より大きなバケットでは、各検索でより多くのエントリーがチェックされるためフィンガープリントの衝突が発生する可能性が高くなる。存在しない要素を検索する最悪ケースでは、クエリーはバケットごとに \(b\) 個のエントリーを持ち得る 2 つのバケットを探す必要がある。(これらのバケットがすべて埋まっているとは限らないが、ここではバケットが埋まっている最悪ケースを分析する。これにより 95% が満たされているテーブルについてかなり正確な推定値が得られる。) 各エントリーにおいて、クエリーが 1 つの保存されたフィンガープリントとマッチし偽陽性のマッチに成功する確率は最大でも \(1/2^f\) である。このような比較を \(2b\) 回行った後、偽フィンガープリントがヒットする確率の合計の上限は \[ \begin{equation} 1 - (1 - 1/2^f)^{2b} \approx 2b/2f \label{eq5} \end{equation} \] となり、これはバケットサイズ \(b\) に比例する。目標とする偽陽性率 \(\epsilon\) を維持するためにフィルターは \(2b/2^f \le \epsilon\) を保証し、したがって必要とされる最小フィンガープリントのサイズはおよそ: \[ \begin{equation} f \ge \lceil \log_2(2b/\epsilon)\rceil = \lceil \log_2(1/\epsilon)+\log_2(2b)\rceil \text{ bits} \label{eq6} \end{equation} \] となる。
空間コストの上限: 既に示したように \(f\) も \(\alpha\) もバケットサイズ \(b\) に依存する。式 (\(\ref{eq4}\)) による平均空間コスト \(C\) は \(\alpha\) が \(b\) とともに増加する: \[ \begin{equation} C \le \lceil \log_2(1/\epsilon) + \log_2(2b)\rceil / \alpha \label{eq7} \end{equation} \] によって制限される。例えば \(b=4\) で \(1/\alpha \approx 1.05\) のとき、式 (\(\ref{eq7}\)) は各要素に \(1.44 \log_2(1/\epsilon)\) ビット以上を必要とする Bloom フィルターよりも Cuckoo フィルターの方が漸近的に (定数係数で) 優れていることを示している。
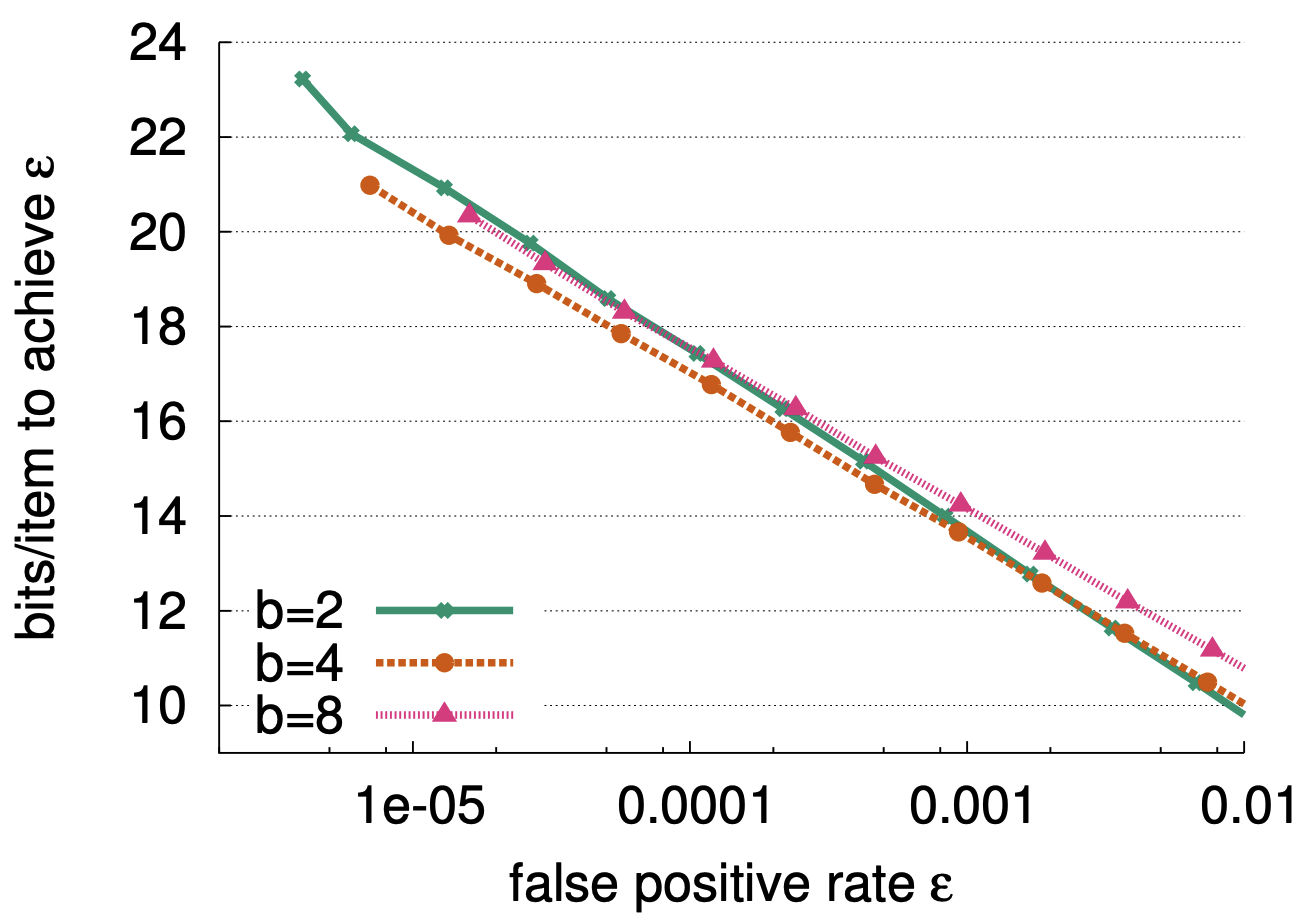
最適バケットサイズ \(b\): 異なるバケットサイズ \(b\) を使用して空間効率を比較するために、まず異なるフィンガープリントサイズで部分キー Cuckoo ハッシングにより Cuckoo ハッシュテーブルを構築し、要素ごとの償却空間コストとその達成された偽陽性率を測定する。Figure 3 に示すように、空間的に最適なバケットサイズは目標とする偽陽性率 \(\epsilon\) に依存する。\(\epsilon \gt 0.002\) の場合、バケットごとに 2 つの要素を持つ方がバケットごとに 4 つの要素を持つよりもわずかに良い結果をもたらす。\(\epsilon\) が \(0.00001 \lt \epsilon \le 0.002\) に減少した場合、バケットあたり 4 つのエントリーが空間を最小化する。
要約すると、我々は \((2,4)\)-Cuckoo フィルター (つまり各要素には 2 つの候補バケットがあり、各バケットには最大 4 つのフィンガープリントがある) をデフォルト構成として選択する。これは、ほとんどの実用的なアプリケーション [6] が関心を持つであろう偽陽性率に関して最高または最高に近い空間効率を達成するためである。以下では各バケットをエンコードすることで \(b=4\) の Cuckoo フィルターの空間をさらに節約する手法を紹介する。
 5.2 空間節約のための半ソートバケット
5.2 空間節約のための半ソートバケット
このサブセクションでは、バケットごとに \(b=4\) のエントリーを持つ Cuckoo フィルターに対して要素ごとに 1 ビットを節約する技法について説明する。この最適化はバケット内のフィンガープリントの順序はクエリーに影響しないという事実に基づいている。この観察に基づいてまずフィンガープリントをソートし、次にソートされたフィンガープリントのシーケンスをエンコードすることで各バケットを圧縮することができる。このスキームは [5] で使用されている "半ソートバケット" (semi-sorting buckets) 最適化と類似している。
以下の例は圧縮がどのように空間を節約するかを示している。各バケットが \(b=4\) のフィンガープリントを含み、各フィンガープリントは \(f=4\) ビットと仮定する (より一般的なケースについては後述する)。圧縮されていないバケットは \(4\times 4=16\) ビットを占有する。ただし、このバケットに保存されている 4 つの 4 ビットフィンガープリントをすべてソートすると (空のエントリは値 "0" のフィンガープリントを格納する者として扱われる)、可能な結果は全部で 3876 (置換を含む一意の組み合わせの数) しかない。これらの 3876 個の可能なバケット値を事前に計算して追加のテーブルに保存し、元のバケットをこの事前計算されたテーブルのインデックスに置き換えると、元の各バケットは 16 ビットではなく 12 ビットのインデックス (\(2^{12}=4096 \gt 3876\)) で表すことができフィンガープリントごとに 1 ビットを節約することができる4。
この順列ベースのエンコード (つまり考え得るすべての結果のインデックス付け) では各検索で追加のエンコード/デコードテーブルの間接参照が必要になることに注意。したがって高い検索性能を達成するにはエンコード/デコードテーブルをキャッシュに納まる程度に小さくすることが重要である。結果として我々の "半ソート" 最適化はこの手法を 4 つのエントリーのバケットを持つテーブルのにも適用する。またフィンガープリントが 4 ビットより大きい場合、各フィンガープリントの最上位 4 ビットのみがエンコードされ残りは直接個別に保存される。
- 4Cuckoo フィルターが削除をサポートする必要がない場合、フィンガープリントリストの重複エントリを無視することができ、エントリごとに追加のビットの一部を節約できる可能性が生じる。
 6. Bloom フィルターとの比較
6. Bloom フィルターとの比較
Table 2 に示す指標といくつかの追加要素を用いて Bloom フィルターと Cuckoo フィルターを比較する。

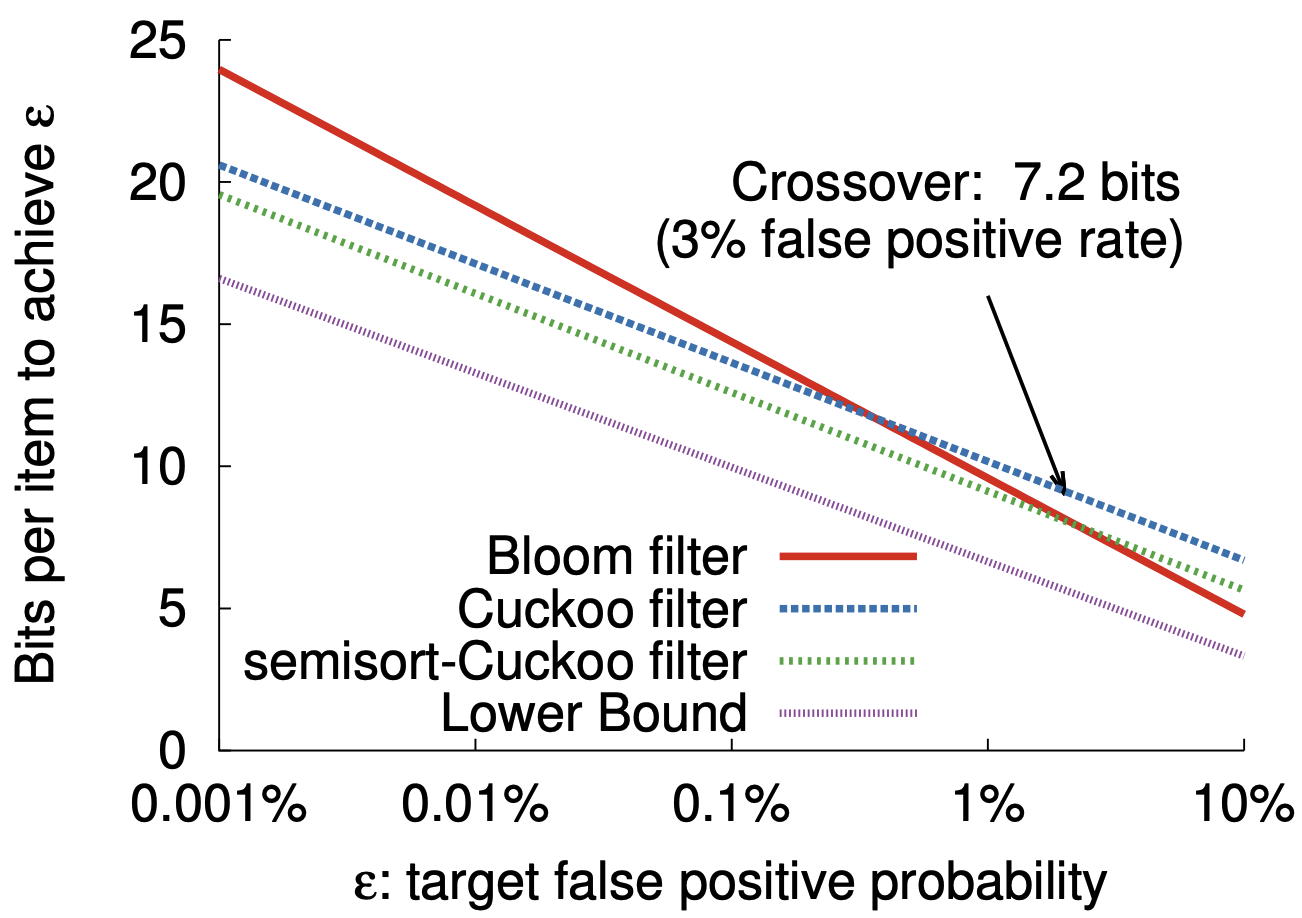
空間効率性: Table 2 は空間最適化された Bloom フィルターと Cuckoo フィルターを半ソートありとなしで比較している。Figure 4 は \(\epsilon\) が 0.001% から 10% まで変換する場合にこれらのスキームで 1 つの要素を表現するのに必要なビット数を示している。情報理論的な境界では各要素に \(\log_2(1/\epsilon)\) ビットが必要であり、最適な Bloom フィルターは 1 要素あたり \(1.44\log_2(1/\epsilon)\) ビットを使用し 44% のオーバーヘッドとなる。したがって半ソートを用いた Cuckoo フィルターは \(\epsilon \lt 3\%\) であれば Bloom フィルターより空間効率が良い。
メモリアクセス数: \(k\) 個のハッシュ関数を持つ Bloom フィルターの場合、ポジティブクエリーはビット配列から \(k\) ビットを読み取る必要がある。\(k=\log_2(1/\epsilon)\) を必要とする空間最適化された Bloom フィルターの場合、\(\epsilon\) が小さくなるにつれてポジティブクエリーはより多くのビットを検査しなければならず、各ビットの読み取り時にキャッシュラインミスが発生する可能性が高くなる。例えば \(\epsilon=25\%\) の場合は \(k=2\) だが、\(\epsilon=1\%\) の場合は \(k\) は 7 になる。空間最適化された Bloom フィルターへのネガティブクエリーは、ビットの半分が設定されているため返される前に平均 2 ビットを読み取る。Cuckoo フィルターへのクエリーはポジティブかネガティブかを問わず常に固定数のバケットを読み取り、(最大で) 2 回のキャッシュラインミスが発生する。
値の関連付け: Cuckoo フィルターはマッチした各フィンガープリントに対して (フィルターの外部に保存されている) 関連する値を返すように拡張することもできる。Cuckoo フィルターのこの特性は近似テーブル検索メカニズムを提供し、これは (偽陽性のヒットにより複数のフィンガープリントとマッチする可能性があるため) 既存の要素については平均して \(1+\epsilon\)、存在しない要素については平均して \(\epsilon\) の値を返す。標準の Bloom フィルターにはこの機能はない。Bloomier フィルターのような変種は Bloom フィルターを一般化して関数を表現できるが、これらの構造はより複雑で Cuckoo フィルターよりも多くの空間を必要とする [7]。
最大容量: Cuckoo フィルターには負荷しきい値がある。実現可能な最大負荷率に達すると挿入は自明ではなくなり、失敗する可能性が高くなるためより多くの要素を格納するためにハッシュテーブルを拡張しなければならない。対照的に Bloom フィルターには新しい要素を挿入し続けることができるが、同じ目標偽陽性率を維持するためには Bloom フィルターでも拡張する必要がある。
重複の制限: Cuckoo フィルターが削除をサポートする場合、同じ要素の複数のコピーを保存する必要がある。同じ項目を \(kb+1\) 回挿入すると挿入は失敗する。これは重複挿入がカウンターのオーバーフローを引き起こすカウンティング Bloom フィルターと似ている。しかし Bloom フィルターや削除不可能な Cuckoo フィルターに同じ項目を複数回挿入しても効果はない。
 7. 評価
7. 評価
我々の実装5は標準的な Cuckoo フィルターのための約 500 行の C++ コードとセクション 5.2 で説明されている "半ソート" 最適化のサポートのための約 500 行のコードで構成されている。以下では基本的な Cuckoo フィルターを "CF"、半ソート機能を持つ Cuckoo フィルターを "ss-CF" と表記する。Cockoo フィルターに加えて比較のために他の 4 つのフィルターを実装した:
標準 Bloom フィルター (BF) [3]: 我々は標準 Bloom フィルターをベースラインとして評価した。すべての実験においてハッシュ関数の数 \(k\) はフィルターサイズと要素の総数に基づいて最小の偽陽性率を達成するように構成されている。さらにより少ないハッシュ処理で検索と挿入を高速化するパフォーマンス最適化が適用されている [16]。各挿入または検索には 2 つのハッシュ関数 \(h_1(x)\) と \(h_2(x)\) のみが必要で、これら 2 つの関数を使用して追加の \(k-2\) 個のハッシュ関数を \[ g_i(x) = h_1(x) + i \cdot h_2(x) \] の形式でシミュレートする。
Blocked Bloom フィルター (blk-BF) [22]: 各フィルターはブロックの配列で構成され、各ブロックは小さな Bloom フィルターである。各ブロックのサイズはテストベッドの CPU キャッシュラインと一致する 64 バイトである。小さな Bloom フィルターごとに標準的な Bloom フィルターと同様に複数のハッシュ関数をシミュレートする最適化も適用している。
Quotient フィルター (QF) [2]: 我々は Quotient フィルターの独自実装を評価した6。このフィルターは、要素ごとに 3 ビットを検索に有用な追加のメタデータとして保存する。Quotient フィルターのパフォーマンスは負荷が大きくなるにつれて低下するため [2] で評価したように最大負荷係数を 90% に設定する。
\(d\)-left カウンティング Bloom フィルター (dl-CBF) [5]:このフィルターは \(d=4\) のハッシュテーブルを持つように構成されている。すべてのハッシュテーブルは同じ数のバケットを持ち、各バケットは 4 つのエントリーを持つ。
標準 Bloom フィルターと Blocked Bloom フィルターは削除をサポートしていないため、ベースラインとして比較されることを強調しておく。
実験のセットアップ: 挿入する要素はすべて事前に乱数生成器で生成された 64 ビット整数である。重複する可能性は非常に低いため重複要素は削除しなかった。
各クエリーでは、すべてのフィルターが最初に CityHash [1] を使用して要素の 64 ビットハッシュを生成する。次に各フィルターはハッシュの 64 ビットを必要に応じて分割する。例えば Bloom フィルターは上位 32 ビットと下位 32 ビットをそれぞれ最初の 2 つの独立したハッシュとして扱い、これら 2 つの 32 ビット値を使って他の \(k-2\) ハッシュを算出する。64 ビットハッシュを計算する時間 (我々のテストベッドでは 1 要素あたり約 20 ナノ秒) は測定に含まれている。すべての実験では 2 つの Intel Xeon プロセッサ (L5640@2.27GHz, 12MB L3 キャッシュ) と 32GB DRAM を搭載したマシンを使用している。
メトリクス: さまざまなフィルターが機能、空間、性能のトレードオフをどのように実現するかを完全に理解するために以下の指標によって上記のフィルターを比較する:
空間効率性: ビット単位のフィルターサイズを満杯のフィルターに含まれる要素数で割った値で測定する。
達成偽陽性率: 存在しない項目でフィルターにクエリーを行いポジティブの返値の割合をカウントすることで測定する。
構築率: 満杯のフィルターに含まれる要素数を、この満杯のフィルターを空から構築する時間で割った値で測定する。
検索、挿入、削除スループット: フィルターが 1 病患に実行できる操作の平均数で測定する。この値はワークロードとフィルターの占有率によって異なる。
 7.1 達成偽陽性率
7.1 達成偽陽性率
まず空間効率と偽陽性率を評価する。各実行ではすべてのフィルターが同じサイズ (192MB) になるように構成されている。Bloom フィルターは 9 個のハッシュ関数を使用するように設定され、1 要素あたり 13 ビットで偽陽性を最小化する。Cuckoo フィルターの場合、ハッシュテーブルには \(m=2^{25}\) 個のバケットがあり、それぞれが 4 つの 12 ビットエントリで構成される。\(d\)-left カウンティング Bloom フィルターは同じ数のハッシュテーブルエントリーを持つが \(d=4\) のパーティションに分割されている。Quotient フィルターも \(2^{27}\) エントリがあり、各エントリは 3 ビットのメタデータと 9 ビットの余剰が格納されている。
各フィルターは初期状態で空であり、フィルターで挿入エラー (CF および dl-CBF) が検出されるか、目標容量制限 (BF, blk-BF, QF) に達するまで要素が配置される。さまざまなフィルターの構築率と偽陽性率を Table 3 に示す。

すべてのフィルターの中で ss-CF は最も低い偽陽性率を達成している。ほぼ同じ量の空間 (12.60 bit/item) を使用して半ソートを有効にすることで各要素のフィンガープリントに 1 ビット多くエンコードできるため、偽陽性率は 0.19% から 0.09% に半減する。一方、半ソートでは各バケットにアクセスする際にエンコードとでコードを必要とするため構築率が 1 秒あたり 500 万件から 313 万件に低下する。
BF と blk-BF はともに \(k=9\) のハッシュ関数で要素あたり 13.00 ビットを使用するが、Blocked フィルターの偽陽性率は BF の 2 倍、最良の CF の 4 倍高くなる。この違いは、blk-BF がハッシュによって各要素を単一のブロックに割り当てるためであり、不均衡なマッピングは平均よりも多くの要素を提供する "ホット" ブロックと、あまり利用されない "コールド" ブロックを作り出すためである。残念ながらこのような不均衡な割り当ては強力なハッシュ関数が使用されている場合でもブロック間で発生し [18] 全体的な偽陽性率を増加させる。一方、blk-BF はどのようなクエリーに対しても単一のキャッシュラインで動作することで最高の構築率を達成する。
QF は BF や CF に比べて要素ごとに多くのビットを消費し、2 番目に優れた偽陽性率を達成している。各バケットのエンコードとデコードにコストがかかるため QF の構築率は最も低い。
最後に、dl-CBF はテーブル全体が約 78% 埋まると挿入の失敗を認識し構築を停止するため保存される項目はさらに少なくなる。各検索で 16 個のエントリをチェックする必要があるためハッシュ衝突の可能性が高くなり、達成される偽陽性率は他のフィルターよりはるかに悪くなる。
 7.2 検索パフォーマンス
7.2 検索パフォーマンス
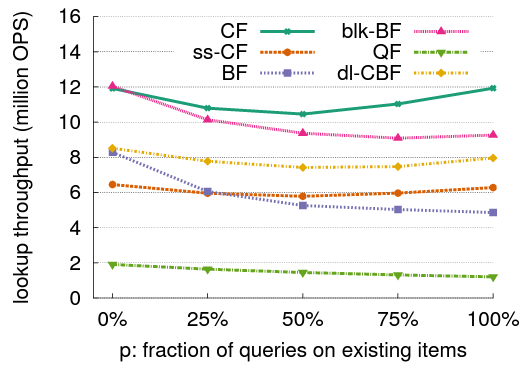
様々なワークロード: 次に、フィルターが満たされた後の検索性能のベンチマークを行う。このセクションでは様々なワークロードでの検索のスループットと遅延を比較する。ワークロードは検索速度に影響を与える可能性があるポジティブクエリー (つまりテーブル内の要素) とネガティブクエリー (つまりテーブルにない要素) の割合によって特徴付けられる。入力ワークロード中のポジティブクエリーの割合 \(p\) を 0% (すべてのクエリーがネガティブ) から 100% (すべてのクエリーがポジティブ) まで変化させる。
検索スループットのベンチマーク結果を Figure 5 に示す。各フィルターは 192MB を占有し、テストベッドの L3 キャッシュ (20MB) よりはるかに大きい。
blk-BF は、各検索が最初の "0" ビットをフェッチした直後に戻ることができるため、あらゆるクエリーはポジティブの場合に良好な性能を発揮する。しかしポジティブなクエリーが増えると検索の一部として追加のビットを読み取る必要があるためパフォーマンスは低下する。BF のスループットは \(p\) が増加すると同様に変化するが約 4 MOPS 遅くなる。これは BF では 1 回の検索を完了するために複数のキャッシュミスが発生する可能性があるのに対し、Blocked バージョンは常に 1 つのキャッシュラインで動作し、検索ごとのキャッシュミスは最大でも 1 回であるためである。
対照的に、CF は常に 2 つのバケット7をフェッチするためクエリーが 100% ポジティブでも 100% ネガティブでも同様の高い性能を達成する。\(p=50\%\) の場合、CPU の分岐予測の精度が最も低いためパフォーマンスが僅かに低下する (マッチするかしないかの確率がちょうど 1/2)。半ソートではポジティブクエリーの割合が増加すると CF のスループットと同様の傾向を示すが、各バケットを読み取る時に余分なデコードオーバーヘッドが発生するためスループットは低い。その代わりに半ソート版は標準的な Cuckoo フィルターと比較して偽陽性率が 1/2 に減少する。しかしクエリーの 25% 以上がポジティブである場合、ss-CF は依然として BF よりもパフォーマンスが優れている。
QF はすべてのフィルターの中で最も性能が悪い。QF が 90% 埋まっている場合、検索ではテーブルエントリの長いチェーンを検索し、それぞれをデコードして目的の要素を見つけなければならない。
dl-CBF は ss-CF よりも優れているが BF より 30% 遅い。また各検索で一定数のエントリのみが検索されるためすべてのネガティブクエリーとすべてのポジティブクエリーを処理するときにほぼ同じパフォーマンスが維持される。
異なる占有率: この実験では、これらのフィルターが異なる占有率で満たされた場合の検索スループットを測定する。各フィルターの負荷計数 \(\alpha\) を 0 (空) から最大占有率まで変化させる。Figure 6 はすべてのクエリーがネガティブ (つまり存在しない要素) の場合とすべてのクエリーがポジティブ (つまり存在する要素) である場合の平均瞬間検索スループット (the average instantaneous lookup throughput) を示している。
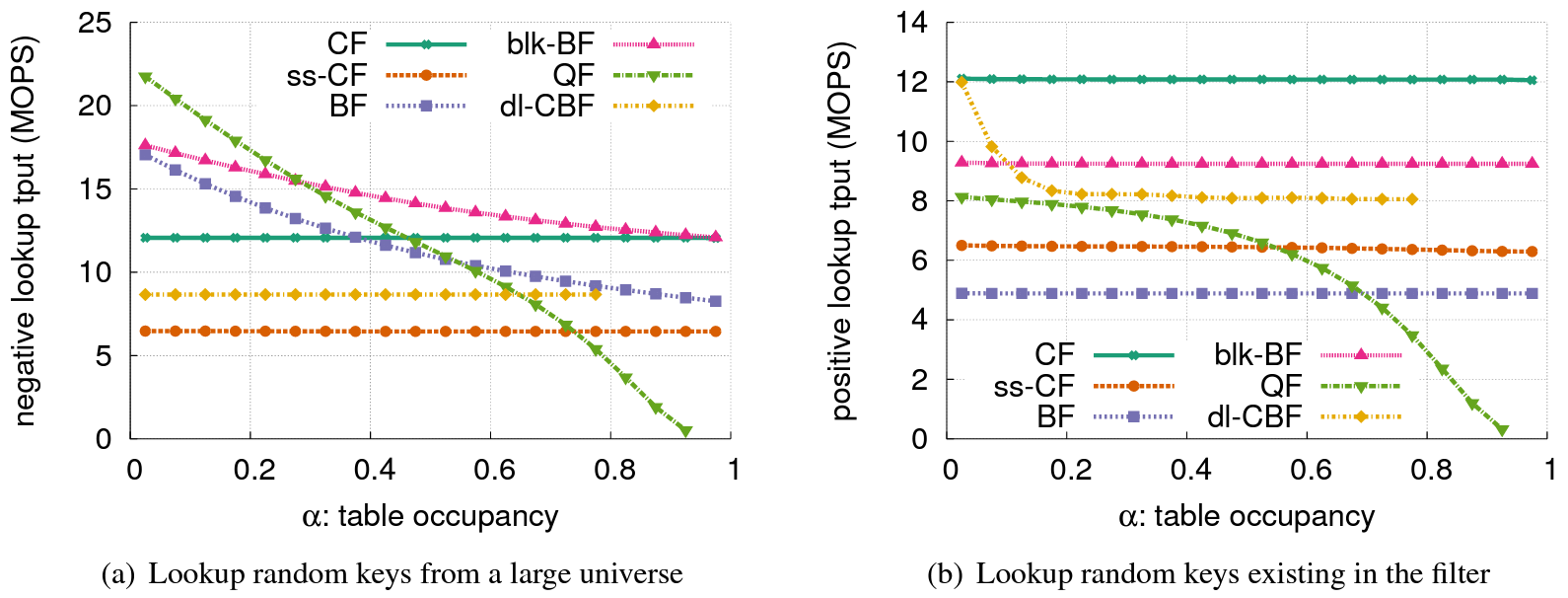
CF と ss-CF のスループットはネガティブクエリーとポジティブクエリーの両方において、様々な負荷計数レベルに渡ってほぼ安定している。これはより多くの要素が挿入されても読み取りと比較を行うエントリの総数が一定であるためである。
対照的に QF のスループットは負荷が増加すると大幅に低下する。このフィルターは負荷率が大きくなるにつれて目的の要素のより長いエントリのチェーンを検索する。
BF と blk-BF の両方はネガティブクエリーとポジティブクエリーを処理する際に異なる動作をする。ポジティブクエリーの場合、挿入された要素数に関係なく常に合計 \(k\) ビットのチェックをする必要があるため一定の検索スループットが提供される。一方、ネガティブクエリーではフィルターの負荷が低い場合に設定されるビットが少なくなり "0" が見つかった場合に検索が早く戻ることがある。
dl-CBF は BF とは異なる動作をする。すべての検索がネガティブの場合、このフィルターに含まれる要素数に関係なく 4 つのバケットから合計 16 のエントリを検索する必要があるため、CF と同様に一定のスループットが保証される。ポジティブクエリーの場合、挿入される要素が少なければ 4 つのバケットがすべてチェックされる前に検索が早く返される可能性がある。ただし dl-CBF が約 20% 充填された後はこの差は無視できる程度になる。
 7.3 挿入パフォーマンス
7.3 挿入パフォーマンス
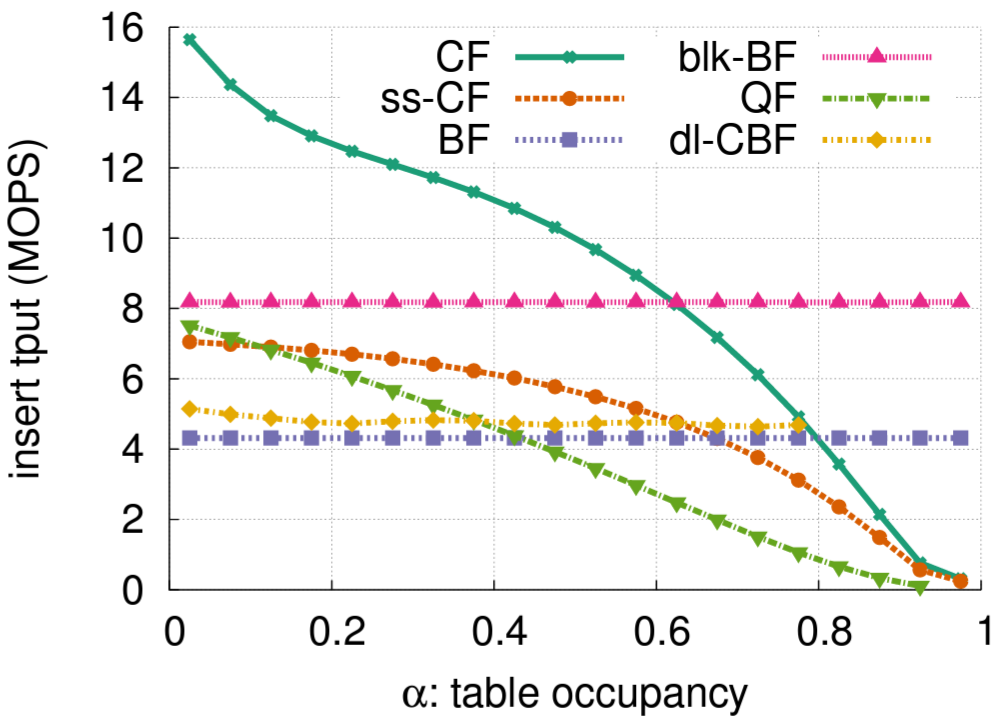
満杯のフィルターに含まれる要素の総数と、これらの要素を挿入する総時間に基づいて測定された全体の構築速度を Table 3 に示す。また構築プロセス全体にわたる瞬間的な挿入スループットも調査する。つまり Figure 7 に示すように異なるフィルターが負荷係数のレベルにあるときの挿入スループットを測定する。
Figure 6 に示す検索スループットとは対照的に、どちらのタイプの CF も (全体的な構築速度は依然として高いものの) 充填量が多くなると挿入スループットが低下する。一方で BF と blk-BF はどちらもほぼ一定の挿入スループットを保証する。CF は新しい要素の挿入に成功する前に既存のキーの劣を再帰的に移動させなければならない場合があり、このプロセスは負荷係数が高くなるとより高価になる。対照的に、両方の Bloom フィルターは負荷係数に関係なく常に \(k\) ビットを設定する。
また QF は新しい要素を挿入する前に要素のシーケンスをシフトする必要があり、テーブルが一杯になるとこのシーケンスが長くなるため挿入スループットも低下する。
dl-CBF は一定のスループットを維持する。各挿入では最大 4 つのバケット内で空のエントリのみを検索する必要がある。そのようなエントリが見つからない場合、Cuckoo ハッシングのように既存の要素を再配置せずに挿入が停止する。最大負荷係数が 80% に満たないのもこのためである。
 7.4 削除パフォーマンス
7.4 削除パフォーマンス
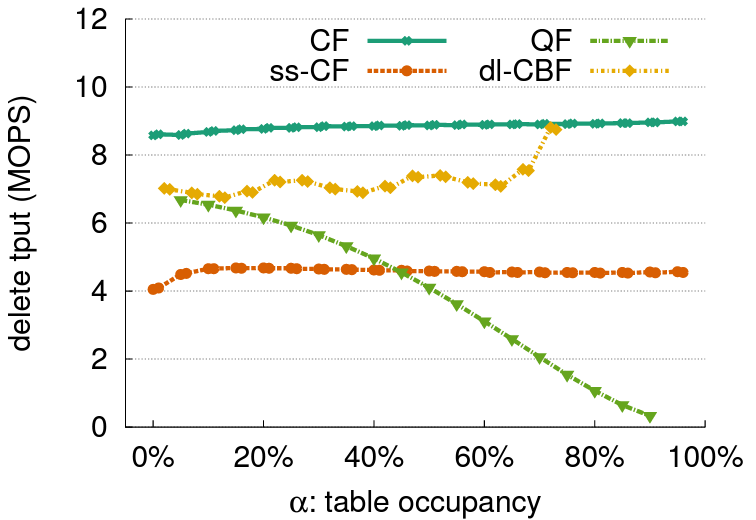
Figure 8 は削除をサポートするフィルター間の削除パフォーマンスを比較している。実験では、最初は満杯のフィルターから空になるまでキーを削除する。CF が最も高いスループットを達成した。CF と ss-CF はどちらもプロセス全体を通じて安定したパフォーマンスを提供する。dl-CBF はすべてのフィルターの中で 2 番目に性能が良い。QF は満杯に近い状態では最も遅いが、空に近い状態では ss-CF より速い。
評価のまとめ: CF は様々なワークロードや占有レベルにおいて高く安定した検索性能を保証する。挿入スループットはフィルターの充填が進むにつれて低下するが、全体的な構築速度は依然として blk-BF を除く他のフィルタよりも高速である。半ソートを有効にすると Cuckoo フィルターは空間最適化された BF よりも空間効率が良くなる。また検索、挿入、削除も遅くなるが、それでも従来の BF より高速である。
- 5https://github.com/efficient/cuckoofilter
- 6オリジナルの作成者からのソースコードはライセンスの問題により比較のために公開されていない。
 8. 結論
8. 結論
Cuckoo フィルターは近似集合メンバーシップクエリーのための新しいデータ構造で、これまで Bloom フィルターを使用して解決されていた多くのネットワーク問題に利用できる。Cuckoo フィルターは次の 3 つの方法で Bloom フィルターを改良している: (1) 要素の動的削除のサポート、(2) 検索性能の向上、(3) 低い偽陽性率 (\(\epsilon \lt 3\%\)) を必要とするアプリケーションのための空間効率の向上。Cuckoo フィルターは Cuckoo ハッシングに基づいて要素集合のフィンガープリントを保存するため高い空間占有率を達成する。さらなる重要な貢献として、我々は部分キー Cuckoo ハッシングを適用した。これにより保存されたフィンガープリントのみに基づく再配置を可能にすることで Cuckoo フィルターを大幅に効率化した。我々の構成探索ではサイズ 4 のバケットを使用する Cuckoo フィルターが幅広いアプリケーションで適切に機能することが示唆されているが、魅力的な Cuckoo フィルターのパラメータはアプリケーション依存の調整のために簡単に変更することができる。
我々は、Cuckoo フィルターがさらなる拡張と最適化が可能であり、その利用をさらに推進するものと期待しているが、説明したデータ構造はすでにネットワークと分散システムの実用的な要求に十分適した高速で効率的な構成要素である。
 9. ACKNOWLEDGEMENTS
9. ACKNOWLEDGEMENTS
This work is supported by funding from Intel via the Intel Science and Technology Center for Cloud Computing (ISTC-CC), and National Science Foundation under awards CCF-0964474, CNS-1040801, CCF-1320231, CNS-1228598, and IIS-0964473. We gratefully acknowledge the CoNEXT reviewers for their feedback and suggestions; Rasmus Pagh for discussions on analyzing space usage of cuckoo filters that led to many of the insights about the asymptotic behavior; Hyeontaek Lim for code optimizations; and Iulian Moraru, Andrew Pavlo, Peter Steenkiste for comments on writing.
 10. REFERENCES
10. REFERENCES
- CityHash. https://code.google.com/p/cityhash/.
- M. A. Bender, M. Farach-Colton, R. Johnson, R. Kraner, B. C. Kuszmaul, D. Medjedovic, P. Montes, P. Shetty, R. P. Spillane, and E. Zadok. Don’t thrash: How to cache your hash on flash. PVLDB, 5(11):1627–1637, 2012.
- B. H. Bloom. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM, 13(7):422–426, 1970.
- F. Bonomi, M. Mitzenmacher, and R. Panigrahy. Beyond Bloom filters: From approximate membership checks to approximate state machines. In Proc. ACM SIGCOMM, Pisa, Italy, Aug. 2006.
- F. Bonomi, M. Mitzenmacher, R. Panigrahy, S. Singh, and G. Varghese. An improved construction for counting bloom filters. In 14th Annual European Symposium on Algorithms, LNCS 4168, pages 684–695, 2006.
- A. Broder, M. Mitzenmacher, and A. Broder. Network Applications of Bloom Filters: A Survey. In Internet Mathematics, volume 1, pages 636–646, 2002.
- B. Chazelle, J. Kilian, R. Rubinfeld, A. Tal, and O. Boy. The Bloomier filter: An efficient data structure for static support lookup tables. In Proceedings of SODA, pages 30–39, 2004.
- J. G. Cleary. Compact Hash Tables Using Bidirectional Linear Probing. IEEE Transactions on Computer, C-33(9), Sept. 1984.
- S. Dharmapurikar, P. Krishnamurthy, and D. E. Taylor. Longest prefix matching using Bloom filters. In Proc. ACM SIGCOMM, Karlsruhe, Germany, Aug. 2003.
- M. Dietzfelbinger and C. Weidling. Balanced allocation and dictionaries with tightly packed constant size bins. Theoretical Computer Science, 380(1):47–68, 2007.
- B. Fan, D. G. Andersen, and M. Kaminsky. MemC3: Compact and concurrent memcache with dumber caching and smarter hashing. In Proc. 10th USENIX NSDI, Lombard, IL, Apr. 2013.
- L. Fan, P. Cao, J. Almeida, and A. Z. Broder. Summary cache: A scalable wide-area Web cache sharing protocol. In Proc. ACM SIGCOMM, Vancouver, BC, Canada, Sept. 1998.
- N. Fountoulakis, M. Khosla, and K. Panagiotou. The multipleorientability thresholds for random hypergraphs. In Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms, pages 1222–1236. SIAM, 2011.
- N. Hua, H. C. Zhao, B. Lin, and J. J. Xu. Rank-Indexed Hashing: A Compact Construction of Bloom Filters and Variants. In Proc. of IEEE Int’l Conf. on Network Protocols (ICNP) 2008, Orlando, Florida, USA, Oct. 2008.
- P. Jokela, A. Zahemszky, C. Esteve Rothenberg, S. Arianfar, and P. Nikander. Lipsin: Line speed publish/subscribe inter-networking. In Proc. ACM SIGCOMM, Barcelona, Spain, Aug. 2009.
- A. Kirsch and M. Mitzenmacher. Less hashing, same performance: Building a better Bloom filter. Random Structures & Algorithms, 33(2):187–218, 2008.
- H. Lim, B. Fan, D. G. Andersen, and M. Kaminsky. SILT: A memory-efficient, high-performance key-value store. In Proc. 23rd ACM Symposium on Operating Systems Principles (SOSP), Cascais, Portugal, Oct. 2011.
- M. Mitzenmacher, A. W. Richa, and R. Sitaraman. The power of two random choices: A survey of techniques and results. In Handbook of Randomized Computing, pages 255–312. Kluwer, 2000.
- M. Mitzenmacher and B. Vocking. The asymptotics of selecting the shortest of two, improved. In Proc. the Annual Allerton Conference on Communication Control and Computing, volume 37, pages 326–327, 1999.
- A. Pagh, R. Pagh, and S. S. Rao. An optimal bloom filter replacement. In Proc. ASM-SIAM Symposium on Discrete Algorithms, SODA, 2005.
- R. Pagh and F. Rodler. Cuckoo hashing. Journal of Algorithms, 51(2):122–144, May 2004.
- F. Putze, P. Sanders, and S. Johannes. Cache-, hash- and space-efficient bloom filters. In Experimental Algorithms, pages 108–121. Springer Berlin / Heidelberg, 2007.
- D. Sanchez, L. Yen, M. D. Hill, and K. Sankaralingam. Implementing signatures for transactional memory. In Proc. the 40th Annual IEEE/ACM International Symposium on Microarchitecture, pages 123–133, Washington, DC, USA, 2007.
- H. Song, S. Dharmapurikar, J. Turner, and J. Lockwood. Fast hash table lookup using extended bloom filter: An aid to network processing. In Proc. ACM SIGCOMM, pages 181–192, Philadelphia, PA, Aug. 2005.
- M. Yu, A. Fabrikant, and J. Rexford. BUFFALO: Bloom f ilter forwarding architecture for large organizations. In Proc. CoNEXT, Dec. 2009.
- D. Zhou, B. Fan, H. Lim, D. G. Andersen, and M. Kaminsky. Scalable, High Performance Ethernet Forwarding with CuckooSwitch. In Proc. 9th International Conference on emerging Networking EXperiments and Technologies (CoNEXT), Dec. 2013.
翻訳抄
要素が集合に含まれているかを効率的に判断するための確率的データ構造である Bloom フィルターの変種で、削除操作において Bloom フィルターより高い性能を示す Cuckoo フィルターに関する 2014 年の論文。Cuckoo ハッシュテーブルに基づいている。要素を格納する 2 つの位置を決めるのに部分キー Cuckoo ハッシングを導入したことで、元の要素を参照しなくても位置を移動できるようにしている。部分キー Cuckoo フィルターは、\(f=h(x)\), \(h_1(x)=f\), \(h_2(x)=f\oplus h(f)\) ということだが、\(f\) の上位半分を第一テーブル、下位半分を台にテーブルのインデックスとし、双方ともインデックスが \(f\) の半分を表しているため残りの半分のみをバケットに保存すれば良い。これで空間を半分にできるのではないか。
- FAN, Bin, et al. Cuckoo Filter: Practically Better Than Bloom. In: Proceedings of the 10th ACM International on Conference on emerging Networking Experiments and Technologies. 2014. p. 75-88.