有向非巡回グラフ
 概要
概要
DAG (directed acyclic graph; 有向非巡回グラフ) は有向グラフの中でも閉路をもたない (つまり一度通過した頂点にふたたび戻ることはない) 構造を持つグラフ。ソフトウェアの分野ではジョブ管理システムやビルドシステム、ネットワーク問題で扱う。
 git のハッシュ付き DAG 構造
git のハッシュ付き DAG 構造
バージョン管理システムである git はファイルの変更とコミットの単位を DAG を用いて表している。それぞれのノードにはハッシュ値が割り当てられており、親のノードは子のノードのハッシュ値に基づいたハッシュ値が割り当てらているという点で Merkle Tree と類似している※1。
Fig 1 は git でいくつかのコミットを行った時に構築される DAG を表している。Blob がファイル、Tree がディレクトリのハッシュを持つノードに相当する。
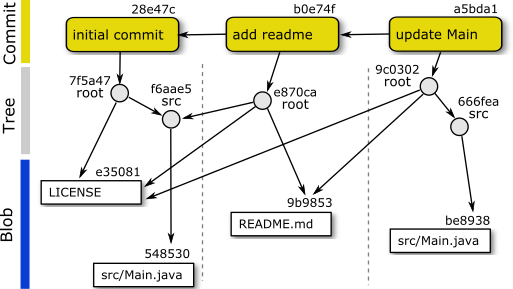
- リポジトリ直下の
LICENSEとsrcディレクトリ下のMain.javaを含めた最初のコミット。 - リポジトリ直下に
README.mdを追加してコミット。 src/Main.javaを修正してコミット。
重複をバランスする必要がなく葉でないノードもデータを持っている。Git は Blob (ファイル)、Tree (ディレクトリ)、Commit の 3 つの不変なオブジェクトブランチやタグは不変オブジェクトへの参照であり、rebase は参照先を変更するだけである。
- ※1 IPFS ではこのようなハッシュ付き DAG 構造を Merkle DAG と呼んでいるが、これは暗号理論に基づいたデータの検証というより重複したオブジェクトを効率的に排除する目的で導入されていることから、Merkle Tree の発展版のような印象をもたせる呼称はあまり適切ではないと感じる。
