論文翻訳: Cuckoo hashing
Rasmus Pagha,*,1 and Flemming Friche Rodlerb,2
Received 23 January 2002
 概要
概要
我々は Dietzfelbinger ら [SIAM J.Comput. 23 (4) (1994) 738-761] の古典的な動的完全ハッシュ方式の理論的性能に匹敵する、最悪ケースで一定の検索時間を備えた単純な辞書を提示する。空間使用量は二分探索木と同様である。最悪ケースでも検索時間が一定である従来の動的辞書よりも概念的にはるかに単純であることに加えて、我々のデータ構造は完全なハッシュを使用せず、キーをプローブ配列の中で遡ることができるオープンアドレッシングの変種を使用するという点で興味深いものである。我々のアルゴリズムに触発されたより弱いハッシュ関数を用いた実装は非常に実用的であることが分かった。この実装は検索時間に関して平均的なケース (ただし自明ではない最悪ケース) を保証する最もよく知られた辞書と競合する。
Keywords: Data structure; Dictionaries; Information retrieval; Searching; Hashing; Experiments
Table of Contents
- 概要
- 1. 導入
- 2. Cuckoo ハッシング
- 3. 線形空間辞書の背景と関連研究
- 4. 実験
- 5. 結論
- Acknowledgements
- Appendix A. ユニバーサルハッシュ関数の構成と性質
- 10. REFERENCES
- 翻訳抄
- aIT University of Copenhagen, Rued Langgaardsvej 7, 2300 København S, Denmark
- bON-AIR A/S, Digtervejen 9, 9200 Aalborg SV, Denmark
- *Corresponding author. E-mail addresses: pagh@itu.dk (R. Pagh), ffr@onair-dk.com (F.F. Rodler)
- 1Partially supported by the Future and Emerging Technologies program of the EU under contract number IST1999-14186 (ALCOM-FT). This work was initiated while visiting Stanford University, and the draft manuscript completed at Aarhus University.
- 2This work was done while staying at Aarhus University.
 1. 導入
1. 導入
辞書データ構造はコンピュータサイエンスの世界に広く普及している。辞書はユニバース \(U\) からの要素 (キーと呼ばれる) の挿入と削除の下で集合 \(S\) を維持するために使用される。メンバーシップクエリー ("\(x \in S?\)") はデータへの可参照性を提供する。肯定的な応答の場合、辞書は \(x\) が挿入されたときに関連付けられたサテライトデータ (satellite data) の一部も提供する。以下では \(|S|\) を \(n\) とする。
理論上も実際上も、最も効率的な辞書はハッシュ技術に基づいている。主な性能パラメータはもちろん検索時間、更新時間、空間である。この一定の要因は多くのアプリケーションにとって非常に重要である。特に検索時間は重要なパラメータである。十分に疎 (sparse) なハッシュテーブルが使用されている場合、単純なユニバーサルハッシュ関数を使用することですべての辞書操作に対するメモリプローブの期待回数を任意に 1 に近づけることができることがよく知られている。したがって速度と合理的な空間使用量を両立させることが課題となる。我々は特に \(O(n)\) ワードの空間を使用する方式のみを考慮する。セクション 3 ではそのような辞書に関する文献を調査する。
この論文の貢献は Cuckoo Hashing と呼ばれる新しいハッシュスキームである。このスキームは Dietzfelbinger ら [10] の古典的な辞書と同じ理論的特性を持つがはるかに単純である。このスキームは検索時間において最悪ケースで一定であり、更新時間は償却想定定数時間 (amortized expected constant time) である。さらに空間使用量はおよそ \(2n\) ワードであり、[10] で使用された \(35n\) ワードと比較すべきである。これは空間使用量が碑文探索木の使用量と同等であることを意味する。我々の検索手順の特別な特徴は (漸近的に小さなハッシュ関数記述へのアクセスを無視すると) メモリアクセスが 2 つだけであり、これらは独立していることからハードウェアがサポートしていれば並列に実行できることである。
我々の分析に必要なハッシュ関数より弱いハッシュ関数を使用するため Cuckoo Hashing は非常に簡単に実装ができる。セクション 4 ではそのような実装について説明し、検索時間に対して自明ではない最悪ケースの保証を持たない最も一般的に使用されているハッシュスキームでの実験と比較を報告する。このような最新のマルチレベルメモリアーキテクチャ上で行われた実験はこれまでの文献に記載されていなかったようである。我々の実験では、特に辞書がキャッシュに収まるほど小さい場合に Cuckoo Hashing が非常に競争力があることが分った。したがって検索の最悪ケース保証が必要な場合、Cockoo Hashing は実用上魅力的であると考えられる。対照的に [10] のハッシュスキームは高い定数係数を示すことが知られている。効率的なデータ構造とアルゴリズムの LEDA ライブラリ [25] は、現在我々のものに基づく Cuckoo Hashing の実装を組み込んでいる。
 1.1. 前置き
1.1. 前置き
ハッシュに関する他の多くの理論的研究と同様に、ここではキーが \(U=\{0,1\}^w\) のビット列であり、\(w\) がコンピュータのワード長である場合を考える (理論上の目的としては RAM としてモデル化されている)。キーが長い場合は 2 つの点を変更する必要がある。
キーはハッシュテーブルの外に格納され、ハッシュテーブルのセルにはキーへのポインタが含まれている必要がある。
長いキーのハッシュは付録 A で完全を期すために説明されている標準的な手法を使用して処理する必要がある。
常にではないが、メンバーシップが決定された後に関連情報をどのように返すかは通常は明確である。例えばこの論文で説明するハッシュテーブルに基づく手法では \(x \in S\) の関連情報は \(x\) とともにハッシュテーブルに格納することができる。したがって我々は関連情報の処理に使用される時間と空間は無視し、\(S\) を維持する問題に集中する。
我々のアルゴリズムはユニバーサル族のハッシュ関数を使用する。我々は Carter と Wegman [7] の元の概念の以下のよく知られた一般化を使用する。
定義 1. 任意の \(k\) 個の異なる要素 \(x_1,\) \(\ldots,\) \(x_k\) \(\in\) \(U\)、任意の \(y_1,\) \(\ldots,\) \(y_k\) \(\in\) \(R\)、一様にランダムな \(i\) \(\in\) \(I\), \({\rm Pr}[h_i(x_1)=\) \(y1,\) \(\ldots,\) \(h_i(x_k)\) \(=\) \(y_k]\) \(\leq\) \(c/|R|^k\) に対して、族 \(\{h_i\}_{i \in I}\), \(h_i : U \to R\) は \((c,k)\)-ユニバーサルである。
 2. Cuckoo ハッシング
2. Cuckoo ハッシング
Cuckoo Hashing は [26] で説明されている静的辞書の動的かである。この辞書はそれぞれ \(r\) 個の単語で構成される 2 つのハッシュテーブル \(T_1\) と \(T_2\) と、2 つのハッシュ関数 \(h_1,h_2:U \to \{0,\ldots,r-1\}\) を使用する。各キー \(x \in S\) は \(T_1\) のセル \(h_1(x)\) または \(T_2\) のセル \(h_2(x)\) のいずれかに格納されるが、両方に格納されることはない。我々の検索関数は
| 1. | \( {\it function} \ \text{lookup}(x) \) | |
| 2. | \( \hspace{12pt}{\it return} \ (T_1[h_1(x)] = x) \lor (T_2[h_2(x)] = x) \) | |
| 3. | \( {\it end} \) | |
である。実際、検索のための 2 つのテーブルアクセスは特殊な場合を除いて線形空間を使用するすべての辞書の中で最適である ([26] 参照)。
[26] では、ある定数 \(\epsilon \gt 0\) に対して \(r \geq (1+\epsilon)n\) (つまりテーブルが半分より少し少ない) で、\(h_1\) と \(h_2\) が \((O(1),O(\log n))\)-ユニバーサル族から一様にランダムに選ばれた場合、\(h_1\) と \(h_2\) に従って \(S\) のキーを再配置する方法がない確率は \(O(1/n)\) であることが示されている。キーの適切な配置は 2-SAT に短縮することで期待される線形時間で計算可能であることが [26] で示されている。
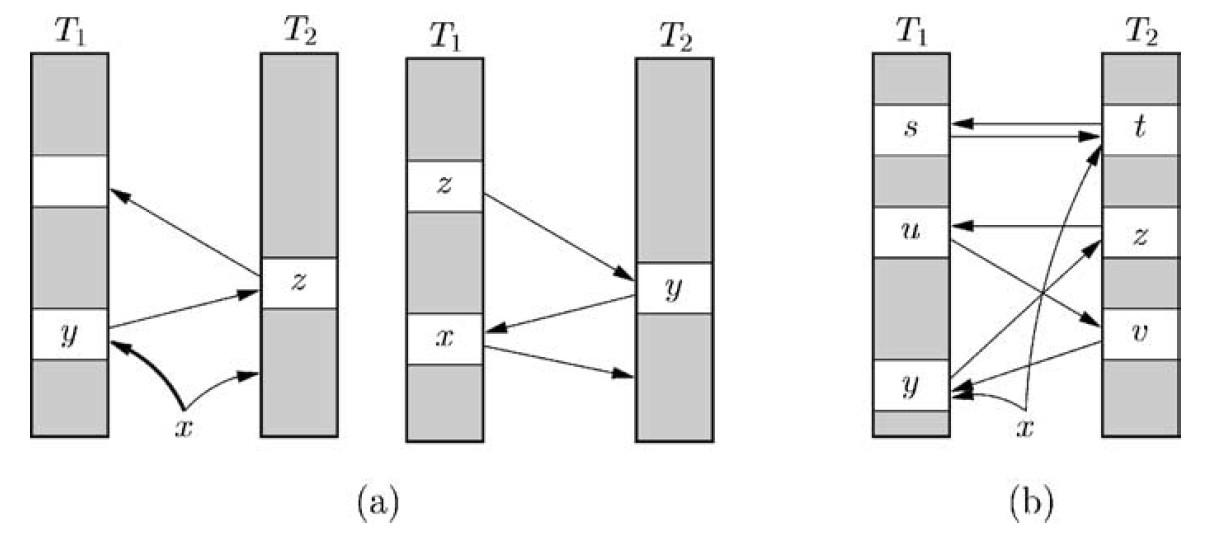
ここである定数 \(\epsilon \gt 0\) に対して \(r \geq (1+\epsilon)n\) を仮定したまま上記の単純な動的化を検討する。もちろん削除は定数時間で簡単に実行できるが、テーブルがまばらになりすぎた場合にテーブルを縮小することで発生する可能性のあるコストは考慮されない。挿入に関しては、すべてのキーが自分の "巣" (nest) を持つまで他のキーをキックしてゆく "カッコウアプローチ" (cuckoo approach) が非常にうまく行くことがわかった。具体的には \(x\) を挿入するとき、まず \(T_1\) のセル \(h_1(x)\) が占有されているかを確認する。占有されていなければ完了である。そうでなければ、とにかく \(T_1[h_1(x)] \leftarrow x\) を設定し以前の占有者 "巣なし" (nestless) とする。次にそのキーは同じ方法で \(T_2\) に挿入され、以下同様に繰り返し挿入される (Fig. 1(a) 参照)。
Fig. 1(b) に示すようにこの処理がループすることもある。そのため反復回数はセクション 2.3 で指定する値 "MaxLoop" に制限される。この反復回数に達した場合、新しいハッシュ関数を使用してテーブル内のキーを再ハッシュ (rehash) し、巣なしキーに対応するためにもう一度試行する。再ハッシュのために新しいテーブルを割り当てる必要はない。単にテーブルを走査して削除し、テーブルの意図した位置にないことが判明したすべてのキーに対して通常の挿入手順を実行するだけで良い。(意図した位置にないキーをキックすることは、単にこのキーの新たな挿入を開始することに相当することに注意)。
変数 \(x\) と \(y\) の値が入れ替わることを表現するために \(x \leftrightarrow y\) という表記を使い、挿入手順を以下のコードにまとめる。
| 1. | \( {\it procedure} \ {\rm insert}(x) \) | |
| 2. | \( \hspace{12pt}{\it if} \ {\rm lookup}(x) \ {\it then} \ {\it return} \) | |
| 3. | \( \hspace{12pt}{\it loop} \ {\rm MaxLoop} \ {\it times} \) | |
| 4. | \( \hspace{24pt}x \leftrightarrow T_1[h_1(x)] \) | |
| 5. | \( \hspace{24pt}{\it if} \ x = \perp \ {\it then} \ {\it return} \) | |
| 6. | \( \hspace{24pt}x \leftrightarrow T_2[h_2(x)] \) | |
| 7. | \( \hspace{24pt}{\it if} \ x = \perp \ {\it then} \ {\it return} \) | |
| 8. | \( \hspace{12pt}{\it end} \ {\it loop} \) | |
| 9. | \( \hspace{12pt}{\rm rehash}(); {\rm insert}(x) \) | |
| 10. | \( {\it end} \) | |
この手続きは各テーブルが \((1+\epsilon)n\) セルより大きいままであると想定している。そのような境界が不明な場合はより大きなテーブルへの再ハッシュがいつ必要かを見つけるためにテストを行わなければならない。テーブルのサイズ変更は通常 doubling/halving 手法 ([10] 参照) により更新ごとに償却想定定数時間で行うことができる。
ハッシュテーブルのサイズが \(r\) の場合、ハッシュ関数を変更せずに \(r^2\) を超える挿入は実行されないように強制する。より具体的には、最後の再ハッシュの開始から \(r^2\) 回の挿入が実行された場合、新しい再ハッシュを強制する。
 2.1. ハッシュ関数
2.1. ハッシュ関数
Siegel [35] の結果 (付録 A で詳述) により、\(r^2\) 個のキーの任意の集合に減退した場合に、ある定数 \(\delta \gt 0\) 対して確率 \(1-O(1/n^2)\) で \((1,n^\delta)\)-ユニバーサルとなるハッシュ関数族を構築できる。また評価時間が一定で \(o(n)\) 個のワードを記述するランダム関数 \(h_1\) と \(h_2\) もその中から選ぶことができる。特定のハッシュ関数の組を用いて挿入されるキーは最大でも \(r^2\) であるため、これは次のことを意味する:
確率 \(O(1/n^2)\) でハッシュ関数は何かしらの不特定の動作をする (つまり考えられる最悪の事態を想定する必要がある)。
そうでなければ、ハッシュ関数は \((1,n^\delta)\)-ユニバーサル族から選ばれたかのように正確に振る舞う。
\(n\) がある定数より大きい場合、\({\rm MaxLoop} \lt n^\delta\) となり族は高い確率で \((1,{\rm MaxLoop})\)-ユニバーサルとなるだろう。これは \(h_1\) と \(h_2\) が、挿入ループ中に処理されるどのキー集合に対しても真にランダムな関数のように動作することを意味する。
 2.2. 変種
2.2. 変種
挿入するキーが既に辞書に存在する場合、挿入ループの前の検索呼び出しにより堅牢性が保証される。これが発生しないことが分っている場合は実装を若干高速化できる。
挿入手順は \(T_1\) へのキー挿入に偏っていることに注意。セクション 4 で説明するように、これにより \(T_1\) でより多くのキーが見つかるため検索の成功が高速になる。この効果は \(T_1\) が \(T_2\) よりも大きい非対称スキームを使用する場合にさらに顕著になる。どちらの場合も挿入時間は完全に対称な実装より僅かに悪化するだけである。
もう一つの変種は、両方のハッシュ関数にサイズ \(2r\) の単一テーブル \(T\) を使用することである。この場合の結果と分析はここで説明した 2 テーブル方式と同様である。この場合に John Tromp [38] による次のトリックを使うと各キーが配置されるハッシュ関数の追跡を回避することができる: キー \(x\) の可能な位置を \(h_1(x)\) と \((h_2(x) - h_1(x))\bmod 2r\) に変更すると、マップ \(i \mapsto (h_2(x)-i)\bmod 2r\) を用いて \(x\) の一つの位置から別の位置にジャンプできる。
以下では対象 2 テーブル方式のみを検討する。
 2.3. 分析
2.3. 分析
他のランダムかハッシュスキームの分析と同様に、我々は忘却敵対者モデル (oblivious adversary model) を仮定する。つまり挿入されたキーがアルゴリズムによって行われたランダムな選択から独立していると仮定する。
挿入手順の分析は 3 つの主要な部分で構成される。
まず、挿入手順の動作のいくつかの有用な特徴を示す。
次に、挿入手順が少なくとも \(t\) 回の反復を行う確率の境界を導出する。
最後に、この手順が償却期待定数時間を使用していることを論証する。
 挿入手続きの動作
挿入手続きの動作
挿入手続きの最も単純な動作はハッシュテーブルのセルに複数回アクセスしない場合である。この場合、挿入手続きは単純に繰り返しのない巣のないキー \(x_1,x_2,\ldots\) のシーケンスを実行し、\(x_1\) を \(T_1\) に挿入し、シーケンスの残りのキーを一方のテーブルから他方のテーブルに移動する。
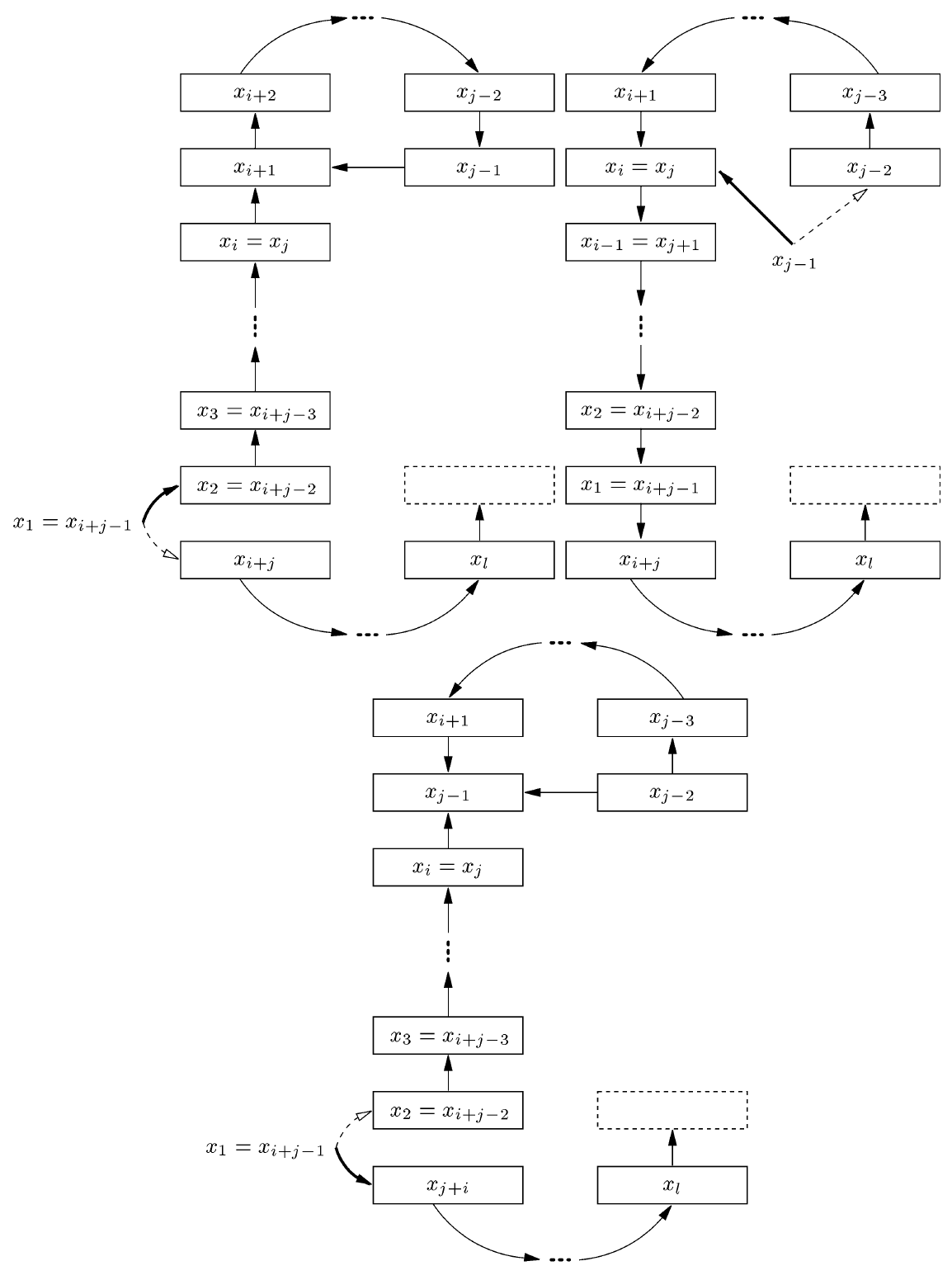
ある時点で、挿入手順が以前に訪れたセルに戻る場合は Fig. 2 に示すようにより複雑な動作となる。最初に訪れたセルのキー \(x_1\) 2 回目に巣となり (シーケンス中の \(i\) と \(j \gt i\) の位置で発生) 元のセルに戻される。その後すべてのキー \(x_{i-1},\ldots,x_2\) が挿入開始時の位置に戻される (最大反復回数に達していないと仮定)。これは \(x_1\) が再び巣なしになることを意味し、手続きはそれを 2 番目のテーブルに配置しようとする。この後のある時点で、空のセルまたは以前に訪問したセルに移動される巣なしキー \(x_l\) が現われる (これも最大反復回数に達していないと仮定する)。前者の場合、手続きは終了する。後者の場合、\(l-i+1\) 個のキーが \(l-i\) 個のセルにのみハッシュする "閉ループ" (closed loop) があるため再ハッシュしなければならない。つまりループ馬最大反復回数まで実行され、その後に再ハッシュが行われることを意味する。
補題 1. 挿入手順が閉ループに入らないと仮定する。このとき巣なしキーのシーケンスの任意の接頭辞 \(x_1,x_2,\ldots,x_p\) について、キー \(x_1\)、つまり挿入される始まりのキーの出現から始まる、繰り返しのない少なくとも \(p/3\) 個の連続したキーの部分列が存在しなければならない。
証明. 挿入手順が以前に訪問したセルに戻らない場合、接頭辞自体は \(x_1\) で始まる \(p\) 個の個別の巣なしキーのシーケンスとなる。そうでなければ、巣なしキーのシーケンスは Fig. 2 のようになる。\(p \lt i + j\) の場合、最初の \(j-1 \geq (i+j-1)/2 \geq p/2\) の巣なしキーが目的のシーケンスを形成する。\(p \geq i+j\) の場合、シーケンス \(x_1,\ldots,x_{j-1}\) と \(x_{i+j-1},\ldots,x_p\) のいずれかの長さは少なくとも \(p/3\) でなければならない。∎
 確率の境界
確率の境界
次に挿入ループが少なくとも \(t\) 回繰り返される可能性を考える。\(t \gt {\rm MaxLoop}\) であればもちろん確率は 0 である。そうでない場合、上記の分析を用いると反復回数 \(t\) は 3 つの (相互排他的でない) 状況で実行される可能性がある:
使用されるハッシュ関数族が (挿入されるキーを含む) 辞書内のキーの集合に制限される場合、\((1,{\rm MaxLoop})\)-ユニバーサルではない。
挿入手順が "閉ループ" に入った。つまり Fig. 2 の \(x_l\) が \(l \leq 2t\) の間に以前に訪れたセルに移動した。
挿入手順が、新しく挿入されたキーから始まる少なくとも \((2t-1)/3\) 個の連続する巣なしキーのシーケンスを処理した。
我々は最初の状況が確率 \(O(1/n^2)\) で発生するようなハッシュ関数族を選択した。最初の状況が発生しないという条件の下で後の 2 つの状況の確率を求める。
2 つ目の状況では \(v \leq l\) が個別の巣なしキーの数を表すものとする。閉ループが形成される可能性の数は \(v^3r^{v-1}n^{v-1}\) 未満である (\(i\) と \(j\) の取り得る値は \(v^2\)、\(x_l\) の取り得る位置は \(v\)、セルの取り得る選択肢は \(r^{v-1}\)、\(x_1\) 以外のキーのとりうる選択肢は \(n^{v-1}\))。\(v \leq {\rm MaxLoop}\) であるためハッシュ関数は \((1,v)\)-ユニバーサルである。これは、各可能性が最大でも \(r^{-2v}\) の確率で発生することを意味する。\(v\) のすべての可能な値を合計し、\(r/n \gt 1+\epsilon\) を使用すると、状況 1 の確率は最大でも次のようになる: \[ \sum_{v=3}^l v^3 r^{v-1} n^{v-1} r^{-2v} \leq \frac{1}{rn} \sum_{v=3}^\infty v^3 (n/r)^v = O(1/n^2) \] 上記の導出は Sanders と Vöcking [32] の提案に従ったものであり、この論文の会議版 [27] における \(O(1/n)\) の限界を改善している。
3 つ目の状況では、\(b_1\) が挿入されるキーで \((\beta_1,\beta_2)=(1,2)\) または \((\beta_1,\beta_2)=(2,1)\) のいずれかとなるような \(v=\lceil(2t-1)/3\rceil\) 個の異なる巣なしキー \(b_1,\ldots,b_v\) のシーケンスが存在する: \[ \begin{equation} h_{\beta_1}(b_1) = h_{\beta_1}(b_2), \ \ h_{\beta_2}(b_2) = h_{\beta_2}(b_3), \ \ h_{\beta_1}(b_3) = h_{\beta_1}(b_4), \ \ \ldots \label{eq1} \end{equation} \] \(b_1\) が与えられたとき、\(v\) 個の異なるキーの並びは最大で \(n^{v-1}\) 通りある。このようなシーケンスと \((\beta_1,\beta_2)\) の 2 つの選択肢のいずれについても、ハッシュ関数は \((1,{\rm MaxLoop})\)-ユニバーサル族から選択されているため、(\(\ref{eq1}\)) の \(b-1\) 個の式が成り立つ確率は \(r^{-(v-1)}\) に愛しい。したがって (\(\ref{eq1}\)) を満たす長さ \(v\) の任意のシーケンスが存在する確率、つまり状況 2 の確率は \[ \begin{equation} 2(n/r)^{v-1} \leq 2(1+\epsilon)^{-(2t-1)/3+1} \label{eq2} \end{equation} \] に束縛される。
 分析の結論
分析の結論
前のセクションから、挿入ループの予想される反復回数は \[ \begin{eqnarray} 1 & + & \ \sum_{t=2}^{\rm MaxLoop} \left( 2(1+\epsilon)^{-(2t-1)/3+1} + O(1/n^2) \right) \nonumber \\ & \leq & 1 + O\left(\frac{\rm MaxLoop}{n^2}\right) + 2 \sum_{t=0}^\infty \left((1+\epsilon)^{-2/3}\right)^t \nonumber \\ & = & O\left( 1 + \frac{1}{1 - (1 + \epsilon)^{-2/3}} \right) \nonumber \\ & = & O(1 + 1/\epsilon) \label{eq3} \end{eqnarray} \] によって制限されていることがわかる。
最後に再ハッシュのコストを考える。まず挿入の失敗によって引き起こされる強制的な再ハッシュのみを考慮する。これは挿入ループが \(t={\rm MaxLoop}\) 反復で実行されたときに起きる。前のセクションによると、閉ループに入ったりハッシュ関数族が \((1,{\rm MaxLoop})\)-ユニバーサルにならないためにこれが発生する確率は \(O(1/n^2)\) である。\({\rm MaxLoop}=\lceil 3\log_{1+\epsilon}r\rceil\) とすると、(\(\ref{eq2}\)) より、閉ループに入らず再ハッシュする確率は \[ 2(1+\epsilon)^{-(2 {\rm MaxLoop} - 1)/3+1} = O(1/n^2) \] となる。
まとめると特定の挿入によって再ハッシュが発生する確率は \(O(1/n^2)\) である。特に再ハッシュ中に実行された \(n\) 回の挿入はすべて確率 \(1-O(1/n)\) で成功する (つまりそれ以上の再ハッシュは発生しない)。1 回の挿入に要する期待時間の合計は \(O(1)\) であるため、すべてのキー挿入を試行する期待合計時間は \(O(n)\) である。再ハッシュ中に挿入が失敗した場合、再帰的な再ハッシュが開始される。これは単にすべてのキーを再ハッシュしてもう一度やり直すことに相当する。新しいハッシュ関数で最初からやり直す確率は 1 より小さいため、再ハッシュにかかる期待時間の合計は \(O(n)\) となる。したがってどのような挿入でも強制的な再ハッシュに使われる想定時間は \(O(1/n)\) となる。
挿入に失敗せずに \(r^2\) 回の挿入が行われた場合にも再ハッシュが発生する。再ハッシュの期待コストは \(O(n)\) であるため、このような再ハッシュの挿入当たりの償却期待コストは \(O(1/n)\) である。
まとめると、挿入にかかる償却期待時間は定数で制限されることを示した。再ハッシュの確率が小さいことは、(\({\ref{eq2}\)) と合わせて、実際に挿入時間の分散 (variance) も一定であることを意味している。
 3. 線形空間辞書の背景と関連研究
3. 線形空間辞書の背景と関連研究
ハッシュは Dumey [13] によってハアジメテ公開文献に記述され、1950 年代に疎テーブルの情報を高速に検索するための空間効率の良いヒューリスティックとして登場した。Knuth は [20, Section 6.4] で最も重要な古典的ハッシュ法を調査している。最も著名で、セクション 4 の実験の基礎となるものは、Chained Hashing (個別のチェーンを使用)、Linear Probing、Double Hashing である。アルゴリズムに関する主要な教書から判断すると Knuth のアルゴリズムの選択は汎用辞書の実装に関する現在の実践と一致している。特に Linear Probing の優れたキャッシュ使用率は細心のアーキテクチャで有力な選択肢となっている。また Two-Way Chaining [2] と呼ばれる細心の方式も調査する予定である。すべての方式はセクション 4 で簡単に説明する。
 3.1. 初期のハッシュ方式の分析
3.1. 初期のハッシュ方式の分析
初期のハッシュスキームの理論的解析は、ハッシュ関数の値が一様にランダムで独立であるという仮定の下で行われた。前述のスキームの平均および期待される最悪ケースの動作の正確な分析が行われている。例えば [16, 20] を参照。ここでは漸近的に消失する項を無視していくつかの事実についてのみ言及する。一部の数値は実装の詳細に依存することに注意。以下はセクション 4 で説明する実装に当てはまる。
まずテーブルの \(\alpha\) 分の 1 (\(0 \lt \alpha \lt 1\)) がキーで占められているハッシュテーブルにキーを挿入するために、2 つの "オープンアドレッシング" スキームで必要となるメモリプローブの期待数を検討する。Linear Probing の場合、挿入時に期待されるプローブ数は \((1+1/(1/\alpha)^2)/2\) である。これは検索に失敗した場合に期待されるプローブ数と一致し、その後に削除がない場合にキーを検索するのに必要なプローブ数と一致する。削除は、削除されたキーが挿入されなかった場合の構成にキーを並べる。Double Hashing では挿入の期待コストは \(1/(1-\alpha)\) である。キーが移動することは決してないため、これはキーの検索とキーの削除に必要なプローブ数と一致する。最後の再ハッシュ以降にキーがハッシュテーブルに保存されていない場合、(失敗して) キーを検索する期待コストは \(1/(1-\beta)\) である。ここで \(\beta\) はテーブルに含まれる "削除済み" マーカーとキーの割合である。テーブル内のキーにまだ "削除済み" マーカーが残っている場合、失敗した検索の期待コストは 1 回のプローブ増加となる。
ハッシュテーブルサイズ \(n/\alpha\) の Chained Hashing の場合、検索に失敗したときに走査されるリストの期待長は \(\alpha\) である。これは新しいキーを挿入するために必要なプローブの予想数が \(1+\alpha\) であることを意味し、その後にキーを検索するために必要なプローブ数でもある (ポインターへのプローブはカウントされないことに注意)。削除するとキーが一度も挿入されなかった場合と同じデータ構造となる。
期待されるプローブ数の観点から、上記は任意の \(\alpha\) に対して Chained hashing が Double Hashing よりも優れており、また Linear Probing よりも優れていることを意味している。ただし Chained Hashing が使用する空間は同じ \(\alpha\) に対してオープンアドレッシング方式で使用される空間よりも大きいことに注意すべきである。その違いはキーとポインタの相対的なサイズによって異なる。
\(\alpha \lt 1\) を定数とする。Linear Probing における最長のプローブシーケンスは期待長 \(\Omega(\log n)\) である。Double Hashing では成功した最長プローブシーケンスの長さは \(\Omega(\log n)\) であると期待され、失敗した最長の検索の長さが線形である確率はゼロではない。Chaining Hashing で期待される最大チェーン長は \(\Theta(\log n/\log\log n)\) である。
上記の結果は実際の結果と一致しているように見えるが、分析に使用されたランダム性の仮定はアプリケーションにおいて疑わしいものである。Carter と Wegman [7] はユニバーサルハッシュ関数族の概念を導入し Chain Hashing の分析からそのような仮定を取り除くことに成功した。Carter と Wegman のユニバーサル族のランダム関数で実装すると、Chained Hashing は辞書操作当たりの規定時間が一定となる (さらにテーブルのサイズを変更するための償却期待定数コストがかかる)。この論文でも使用されている Seigel のハッシュ関数族 [35] を使用すると、Linear Probing と Double Hashing が上記のパフォーマンス限界を満たしていることが証明されている [33, 34]。
 3.2. キー再配置スキーム
3.2. キー再配置スキーム
いくつかの (オープンアドレッシング) ハッシュスキームが提案されているが、これらは Cuckoo Hashing と重要な機能、つまり挿入中にキーが移動するという点を共有している [4, 17, 21, 22, 31]。これらのスキームの主な焦点は (ほぼ) 満杯なテーブルからキーを見つけるために必要なプローブの平均数を標準のオープンアドレッシングで示される平均 \(O(\log n)\) から定数に減らすことである。これはプローブシーケンス内でキーを時々前方に移動させることによって行われる。
我々の新しいアルゴリズムは最悪ケースでプローブ数を一定に減らすためにキーを再配置する。そのために必要な条件はハッシュ関数値の再利用、つまりキーがプローブシーケンス内でキーを後方に移動させることである。後方への移動はこれまでの再配置スキームでは使用されていなかったが、これはキーを後方に移動しても新鮮な "ランダムな" 配置が得られないという難点があるためであろう。我々は満杯のハッシュテーブルを扱うのではなく、一定の割合の空きセルを持つハッシュテーブルを扱うため、最悪の場合でも検索に定数時間を使用することができる。(この分析ではハッシュテーブルが十分に疎である必要があり、ハッシュ関数が真にランダムであると仮定している。) これは挿入と削除のたびに小さな割り当て問題を解決する辞書を示唆している。
最悪ケースの検索コストを最適化する鍵の配置は、実際は Rivest によって既に [31] で検討されている。Rivest はプローブシーケンスが与えられていると仮定し、成功した最長探索の長さを最小化するシーケンスを見つけるための多項式時間アルゴリズムを提示している。またキーセットを更新した場合、新たに最適配置を達成するために移動させる必要があるキーの数が一定であること示している。[26] とこの論文から、同じパフォーマンスとランダム性を仮定したアルゴリズムが Aho と Lee [1] によって公開される 8 年前に、Rivest の辞書が最悪ケースの定数検索時間と償却想定定数の更新時間を達成したことがわかる。さらに、分析には Siegel のハッシュ関数で十分である。しかし Cuckoo Hashing の挿入アルゴリズムは Rivest が提案したものよりはるかに単純で効率的である。
Cuckoo Hashing と類似したもう一つの重要なキー再配置スキームは Last-Come-First-Served Hashing [29] であり、探索時間の分散が少ないことが主な特徴である。キーの移動にこの論文で使用されているのと同じ貪欲な戦略 (greedy strategy) を使用するがハッシュ関数の値は再利用されない。
 3.3. 最悪ケースの検索を保証するハッシュスキーム
3.3. 最悪ケースの検索を保証するハッシュスキーム
Two-Way Chaining [2] は Chained Hashing に変わるものであり、高確率で \(O(\log\log n)\) の最大検索時間を提供する (真にランダムなハッシュ関数を仮定)。このスキームはキーが 2 つの場所 (この場合はリンクリスト) のどちらかに格納されるという Cuckoo Hashing と共通する機能を持つ。我々が検討する実装はサイズ \(O(\log\log n)\) の固定サイズ配列でリストを表現する (より長いチェーンが必要であれば再ハッシュを行う)。空間使用量を線形にするためにはサイズ \(O(n/\log\log n)\) のハッシュテーブルを使用する必要があり、平均チェーン長が \(\Omega(\log\log n)\) となる [3]。(キーを 2 つの場所のうちの 1 つに保存するというアイディアは Karp, Luby, Meyer auf der Heide [18] によって PRAM シミュレーションの文脈でさらに以前から使用されていたことに注意。)
この最悪ケースを保証するもう一つのスキームは、Multilevel Adaptive Hashing [5] である。しかし \(O(\log\log n)\) 回のハッシュ関数評価、メモリプローブ、比較が並列に可能であれば検索は \(O(1)\) の最悪ケース時間で実行できる。これは Cuckoo Hashing に似ているが、後者はたった 2 回のハッシュ関数評価、メモリプローブ、比較を使用するのみである。
最悪ケースの定数検索時間を持つ辞書は Fredman, Komlós, Szemerédi [15] によって最初に作られたが、それは静的であり、つまり更新をサポートしていなかった。その後 Dietzfelbinger ら [10] によって償却期待定数時間で挿入と削除ができるように拡張された。Dietzfelbinger と Meyer auf der Heide [11] は、操作が高確率で定数時間内で実行される辞書、すなはち少なくとも \(1-n^{-c}\) (\(c\) は我々が選択した任意の定数) で実行される辞書を提示することで更新性能を向上させた。後に同じ特性を持つより単純な辞書が開発された [8]。\(n=|U|^{1-o(1)}\) のとき、\(O(n)\) ワードの空間使用量は情報理論的な最小値 \(B=\log\binom{|U|}{n}\) ビットの定数係数以内にはならない。Raman と Rao の辞書 [30] は [10] と同じ性能を提供しすべてのケースで \(B+o(B)\) ビットを使用する。ただしキーに関連付けられた情報はサポートしていない。
ごく最近、Fotakis ら [14] は各キーの \(d\) 個の可能な位置を使用して Cuckoo Hashing の一般化を分析し、この場合、挿入の期待時間が一定で \(1-2^{-\Omega(d)}\) の空間使用率が達成できることを示した。
 4. 実験
4. 実験
Cuckoo Hashing の実用性を検証するために [20, Section 6.4] で説明されている 3 つのよく知られたハッシュスキーム、Chained Hashing (個別のチェーンを使用)、Linear Probing、および Double Hashing と実験的に比較する。また Two-Way Chaining [2] も考慮する。
最初の 3 つの方法はすべてハッシュテーブルの位置 \(h(x)\) にキー \(x\) を格納しようとするものである。これらは衝突の解決方法、つまり 2 つ以上のキーが同じ場所にハッシュされたときに何が起こるかが異なる。
Chained Hashing. 特定の場所にハッシュ化されたすべてのキーを保存するためにリンクリストを使用する。
Liner Probing. キーは次の空のエントリに格納される。キー \(x\) の検索は \(h(x)\) から始まり \(x\) または空のテーブルエントリが見つかったときに終了するテーブルスキャンによって行われる。削除の場合、検索シーケンスの穴を埋めるために一部のキーを元に戻さなければならないかもしれない。詳細は [20, Algorithm R] を参照。
Double Hashing. 挿入と検索は Linear Probing に似ているが、一度に 1 ステップずつ次の位置を検索するのではなく、2 番目のハッシュ関数値を使用してステップサイズを決定する。削除は、削除されたキーのセルに特別な "削除済み" マーカーを置くことによって行われる。検索では削除されたセルをスキップするが、挿入では上書きする。
4 番目の方法である Two-Way Chaining は Chained Hashing の 2 つのインスタントして説明できる。キーは 2 つのハッシュテーブルの一つ、つまり短いチェーンにハッシュされるテーブルに挿入される。最近 [6] で提案されているようなキャッシュに適した実装は、単純に各リンクリストを短い固定サイズの配列にすることである。より長いリストが必要な場合は再ハッシュを実行しなければならない。
 4.1. これまでの実験結果
4.1. これまでの実験結果
セクション 3 で調査した検索が最悪ケースの定数検索時間を伴う辞書には理論的な観点から改善の余地がほとんどないが、大きな定数係数と複雑な実装が直接の実用化を妨げている。例えば [10] の "Dynamic Perfect Hashing" スキームでは空間の上限は \(35n\) ワードである。[10] の著者らはより実用的な Wenzel による変形を参照しており、これは二分探索木に匹敵する空間を使用する。
[19] によれば、[39] で説明されている LEDA ライブラリ [25] でのこの変種の実装は平均挿入時間が \(n \le 2^{17}\) で AVL 木よりも大きく、Chained Hashing での挿入よりも 4 倍以上遅い。(Intel® Pentium® 120MHz プロセッサを搭載した Linux PC 上で。) [25, Table 5.2] にリストされている実験結果は、Chained Hashing と Dynamic Perfect Hashing の更新性能の間に 6 倍以上の開きがあり、検索では 2 倍以上の開きがあることを示している。(300MHz Sun ULTRA SPARC 上で。)
Silverstein [36] は、[10] の動的完全ハッシュスキームの空間上限は DIMACS 辞書テスト [24] のサブセットで実行した場合に観測されるものと比べてかなり悲観的であると報告している。彼はさらに時間だけでなく空間も改善する方法を模索し、観測される時間と空間の両方をおよそ 3 倍改善している。それでも、改良されたスキームでは 1 回の操作にかかる時間を同程度にするために Linear Probing の実装よりも 2~3 倍の空間が必要である。Silverstein はハッシュテーブルのパック表現を使用したデータ構造のバージョンも検討している。この設定では Dynamic Perfect Hashing スキームは Liner Probing とほぼ同じ量の空間を使用し 50% 以上遅くなった。
(最悪ケースの定数検索時間がない) "古典的な" 辞書に関する最近の実験的研究はかなり限られているようである。[19] ではメモリ使用量と速度の両方において Chained Hashing が Dynamic Perfect Hashing の実装よりも優れていると報告されている。
 4.2. データ構造の設計と実装
4.2. データ構造の設計と実装
正の 32 ビット符号付き整数をキーとし、0 を \(\perp\) とする。データ構造は、集合内に既に存在する要素を挿入しようとする試みや、集合内にない要素を削除しようとする試みを正しく処理できるという点で堅牢である。再ハッシュ中にはこのようなことは起きないことが知られており、挿入手順の僅かに高速なバージョンが使用される。
我々は空間使用量が合理的でなければならないという制約の下で、辞書操作の時間を最小限に抑えることに重点を置いている。辞書の負荷計数によって使用されるメモリに対する集合のサイズを理解する。(Chained Hashing での負荷計数の概念は伝統的にリンクリストに使用される空間を無視するが、我々はメモリ使用量が等しいことを意味するために負荷係数が等しいことを望む。) [20, Fig. 44] に見られるように Linear Probing と Double Hashing の速度は負荷係数が 1/2 を超えると急速に劣化するが、負荷係数が 1/4 以下ではどの方法もあまり改善されない。Cuckoo Hashing は各テーブルのサイズが集合のサイズより大きい場合にのみ機能するため、負荷係数が 1/2 未満の下での比較しかできない。テーブルサイズの倍と半分を考慮して負荷係数を 1/5 と 1/2 の間で変化させ、特に "標準的な" 負荷係数である 1/3 に注目する。Cuckoo Hashing と Two-Way Chaining では挿入が失敗し "強制再ハッシュ" が発生する可能性がある。負荷係数が特定のしきい値 (やや恣意的に 5/12 に設定) よりも大きい場合、テーブルサイズを 2 倍にする機会を利用する。我々の実験によるとこれは平均負荷係数を僅かに減少させるだけである。
Chained Hashin を除けば、検討されたスキームは現在のところ実現不可能なランダム性の仮定の下でしか分析されていないという点で共通している。しかし経験上、むしろ単純で効率的なハッシュ関数族は、より強力なランダム性仮定の下で予想される性能に近いパフォーマンスをもたらす。我々は [9] より正の整数 \(q\) に対して範囲 \(\{0,1\}^q\) を持つ関数族を使用する。すべての奇数 \(a\), \(0 \lt a \lt 2^w\) に対してこの族は関数 \(h_a(x)=(ax \bmod 2^w) \div 2^{w-q}\) を含む。評価は 32 ビットの乗算とシフトによって非常に効率的に実行できることに注意。ただしこのハッシュ関数の選択はハッシュテーブルのサイズが 2 の累乗であることを要求する。族のランダム関数 (C の rand 関数を使用して選択) は Cuckoo Hashing を除くすべてのスキームで正常に動作するようである。Cuckoo Hashing では、様々なハッシュ関数を試したところハッシュ関数の選択にかなり敏感であることがわかった。[9] の族から独立して選ばれた 3 つの関数の排他的論理和は高速で問題なく動作しているようだ。この現象に対する良い説明はない。すべてのスキームについて様々な代替ハッシュ族を試行したが性能は低下した。
すべてのメソッドは C で実装されている。我々は各スキームを可能な限り高速で実行できるように努めた。参考文献と異なる具体的な選択と詳細は次の通り:
Chained Hashing. C の malloc 関数と free 関数が性能のボトルネックになることが判明したため、単純な "フリーリスト" メモリ割り当てスキームを使用している。割り当てられたメモリの半分はハッシュテーブルに、もう半分はリスト要素に使用される。データ構造の空きリスト要素がなくなるとそのサイズは 2 倍になる。多くの場合にキャッシュミスを 1 回節約できるため、各リンクリストの先頭のキーをハッシュテーブルに直接保存する。ハッシュテーブルに最初のキーを格納すると期待されるメモリ使用率も僅かに向上する。これは空ではないすべてのリンクリストが 1 要素短くなるためと、ここで考慮される負荷係数ではハッシュテーブルのセルの半分以上が連結リストを含むと予想されるためである。
Double Hashing. 削除されたセルでテーブルが詰まって検索に失敗した場合のパフォーマンスが低下することを防ぐため、ハッシュテーブルの 2/3 がキーと "削除済み" マーカーで占められるとすべてのキーが再ハッシュされる。2/3 という割合は挿入時間と検索失敗時間のトレードオフを適切に取ることがわかった。
Linear Probing. [36] の実装と同様に、我々の最初の実装は削除マーカーを使用した。しかし [20, Algorithm R] で説明された削除方法を使用した方が必要な再ハッシュが遙かに少なくなりかなり高速であることがわかった。
Two-Way Chaining. 各バケットには 4 つのキーを入れる。これは [6] の結果によれば数十万のキーに対応して強制再ハッシュの確率を低く抑えるのには十分である。より大きなキーのコレクションに対しては各バケットにもっと多くの鍵を入れるべきでありその結果全体的なパフォーマンスが低下する。
Cuckoo Hashing. 我々が実験したアーキテクチャでは検索における 2 つのメモリアクセスを並列化できなかった。したがって最初のメモリ検索が失敗した後にのみ 2 番目のハッシュ関数を評価する。
すべてのスキームで、再ハッシュは新しく割り当てられたハッシュテーブルにすべてのキーを繰り返し挿入することで実装された。効率性を高めるために、キーがすでに挿入されているかをチェックしない特別な挿入手順を使用した。
Cuckoo Hashin の変種をしようしていくつかの実験を行った。特に、第一のテーブルサイズが第二のテーブルの 2 倍である Asymmetric Cuckoo を検討した。これにより最初のテーブルにさらに多くのキーが存在することになり、成功した検索の平均性能が僅かに向上する。例えば負荷計数 1/3 で挿入と削除の交互の長いシーケンスのあと、要素の 76% が Asymmetric Cuckoo の第一テーブルに存在するのに対し、Cuckoo Hashing では 63% であった。他の操作では大幅な速度の低下はなかった。Asymmetric Cuckoo の結果が Cuckoo Hashing の結果と大きく異なる場合の結果について述べる。
 4.3. セットアップ
4.3. セットアップ
実験は 800MHz Intel Pentium III プロセッサと 256MB メモリ (PC100 RAM) を搭載した Linux (カーネル 2.2) を実行する PC で行った。このプロセッサには 16kB のレベル 1 データきゃっスト 256kB のレベル 2 "アドバンスト転送" キャッシュが搭載されている。我々の結果はキャッシュミスのコストと "ランダムな" 位置への予想されるプローブ数によってパラメータ化された単純なモデルにうまく適合した (詳細は技術報告書 [28] を参照)。したがって、これらの結果は他のハードウェア構成においても重要であると考えられる。Pentium プロセッサをタイミング実験に使用する利点はクロックサイクル単位で時間を測定できる rdtsc 命令である。これによりアルゴリズムの動作に関する非常に正確なデータにアクセスできるようになり、Cuckoo Hashing データ構造への呼び出しを発行するプログラムによって使用された時間をは破棄できるようになる。我々の場合、ハードウェアデバイスやプロセススケジューラからの割り込みによって著しく乱された測定値を破棄する方法も提供している。これらの測定値は他のすべてのタイミングから大幅に分離された小さなタイミンググループとして表示されるためである。プログラムは gcc コンパイラバージョン 2.95.2 を使用し、最適化フラグ -O9 -DCPU=586 -march=i586 -fomit-frame-pointer -finline-functions -fforce-mem -funrollloops -fno-rtti を使用してコンパイルした。前述のように操作の時間を計るためにグローバルクロックサイクルカウンターを使用する。辞書操作に費やされたクロックサイクル数が 5000 を超え、再ハッシュが行われなかった場合、呼び出しが中断されたと判断し結果を無視する (経験的に 2000~5000 クロックサイクルを要した操作は存在しないことが確認されている)。再ハッシュが行われたときに割り込みに費やされた時間をフィルタリングする方法はない。しかし、すべてのテストは無関係なユーザが存在しないマシンで行われたため混乱は最小限に抑えられているはずである。我々のマシンでは rdtsc 命令を呼び出すのに 32 クロックサイクルかかった。これらのクロックサイクルは結果から差し引かれている。
 4.4. 結果
4.4. 結果
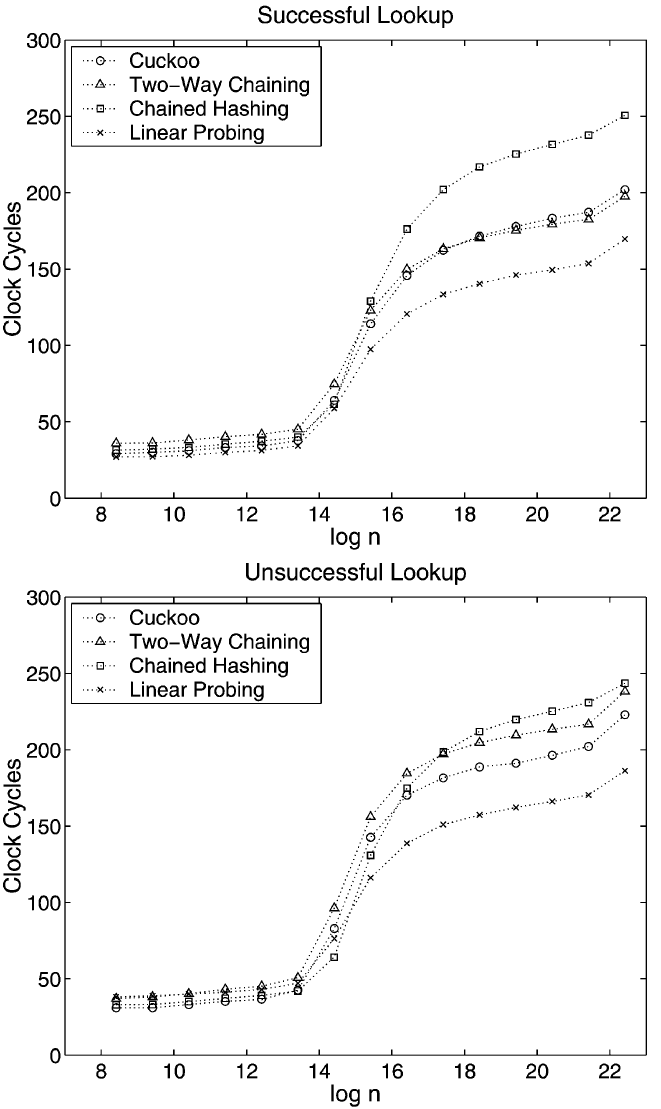
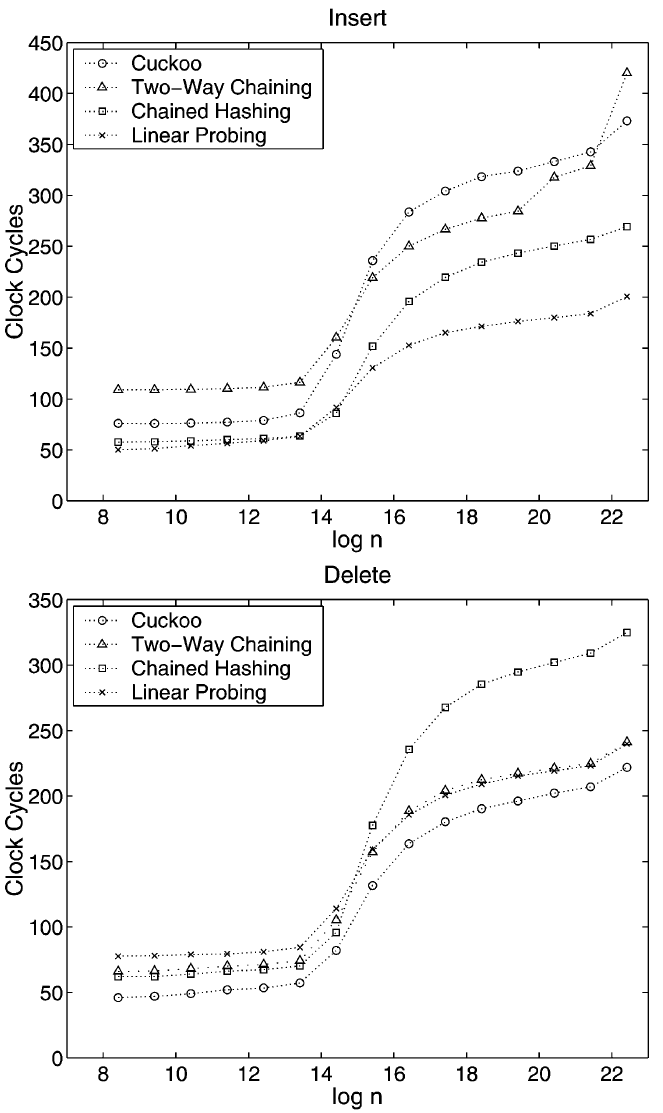
我々の主な実験は辞書のサイズがあまり変化しない状況をモデル化するように設計された。ランダムに生成された一連の混合操作を考慮する。我々はインターネット上で公開されている高品質のランダムビットのコレクションからテスト操作シーケンスを構築した [23]。このシーケンスは \(n\) 個の異なるランダムなキー操作から始まり、その後ランダムに失敗した検索、ランダムに成功した検索、ランダムに削除、ランダムに挿入という 4 つの操作を \(3n\) 回実行する。我々は要素数が安定している "平衡状態" で操作を測定した。負荷計数 1/3 の結果は Fig. 3 と Fig. 4 に示すとおりで、10 回の実行に渡る平均を示している。最大 \(2^{24}/3\) 個のキーでこの実験を行った。Linear Probing は Double Hasing よりも一貫して高速であったため、プロットではこれを唯一のオープンアドレッシングスキームとして選択した。強制再ハッシュの時間は挿入時間に追加した。サイズ \(2^{12}\) から \(2^{16}\) の集合では 10 回の実行に渡って結果に大きなばらつきがあった。この範囲の外では、極端な値は平均値から約 7% 未満しか離れていない。データ構造がレベル 2 キャッシュを満たし始めると大きなばらつきが始まる。これはテストプログラムがディスクからデータを読み取り、その結果データ構造の一部がキャッシュから時々削除されることが原因であると考えられる。
見てわかるように、データ構造全体がレベル 2 キャッシュに収まる限り、つまり \(n \lt 2^{16}/3\) の間、検索にかかる時間はどのスキームでもほぼ同じである。この後、ランダムメモリセルへの平均アクセス回数 (キャッシュミスの確率が 1 に近づく) が表示される。曲線の形状はランダムメモリセルへのアクセスにおけるキャッシュミスの確率の増加を反映している (詳細は技術報告書 [28] のセクション 5 を参照)。これにより Linear Probing が平均的な勝者となり、Cuckoo Hashing と Tow-Way Chaining が約 40 クロックサイクル遅れて続く。挿入の場合、ランダムメモリセルへのアクセス数は大規模な集合で再び優位を占めるが、小さな集合ではキャッシュ内のアクセス数と計算量が増えるため Cuckoo Hashing と特に Two-Way Chaining が遅くなる。Two-Way Chaining では 100 万要素以上の集合で強制再ハッシュのコストが発生し、その時点ではバケットサイズを大きくすることでより良い結果が得られた可能性がある。削除については Chained Hashing はリスト要素を開放するときにランダムなメモリセルにアクセスするため大きな集合では遅れるが、Cuckoo Hashin は単純であるため最速のスキームとなる。キャッシュに収まる辞書の場合、挿入と削除の合計時間が 4 つのスキーム野中で Cuckoo Hashing が最も小さいことに注意。
この時点で我々は、Linear Probing と Two-Way Chaining がうまくキャッシュを利用できるかはキャッシュラインがキー (およびキーと一緒に置かれる関連情報) よりもかなり大きいかどうかにかかっていることに言及する必要がある。そうでない場合、キャッシュミスの数が大幅に増加する。ここで取り上げた他のスキームではこのような劣化は見られない。
 DIMACS テスト
DIMACS テスト
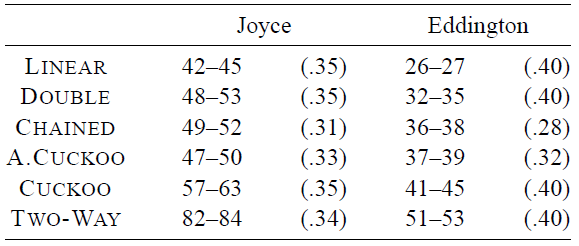
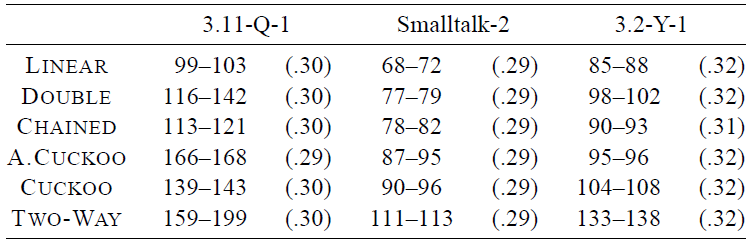
実際には辞書内のデータにランダムにアクセスすることはほとんどない。特に、同じキーの繰り返し検索や、寿命の短いキーの削除などにより、キャッシュは上記のランダムテストよりも有用に機能する。経験則として、このような操作にかかる時間はすべてのデータ構造がキャッシュにある場合の時間とほぼ同じとなる。より現実的なデータに対して辞書の実際のテストを実行するために、第 5 回 DIMACS 実装チャレンジ [24] の辞書テストの代表的なサブセットを選択した。付録 A で説明するように、文字列キーを含むテストは文字列を 32 ビット整数にハッシュすることで前処理した。これにより高い確率でキーへのアクセスパターンが保持される。各テストについて、前処理に要した時間を除いた 1 回あたりの平均時間を記録した。6 回の実行の最小値と最大値を Fig. 5 と Fig. 6 に示した。またこれらには平均負荷係数も記載している。Linear Probing がやはり高速だが、ほとんどの場合 Cuckoo スキームより 20~30% 速いだけである。
 挿入時のキャッシュミス数
挿入時のキャッシュミス数
ランダムメモリセルへのアクセス (つまりキャシュミス) の階数がハッシュスキームの性能に重要であることを見てきた。(適切なランダム性の仮定の下で) 古典的なスキームのプローブ動作は非常に正確な理解があるのに対し、セクション 2.3 での挿入にかかる期待時間の分析はかなり粗雑であり、一定の上限が確立されているだけである。我々の計算があまり厳密な境界を示さない理由の一つは、辞書に新しい要素を入れるために必要なキーの移動数について悲観的な見積もりを使用しているためである。多くの場合、別のセルが占有している可能性がある (could) 場合でも空きセルは見つかる。またキーの移動の大部分が第一テーブルに新しいキーを配置する試みの失敗からのバックトラックに費やされるだろうと悲観的に想定している。
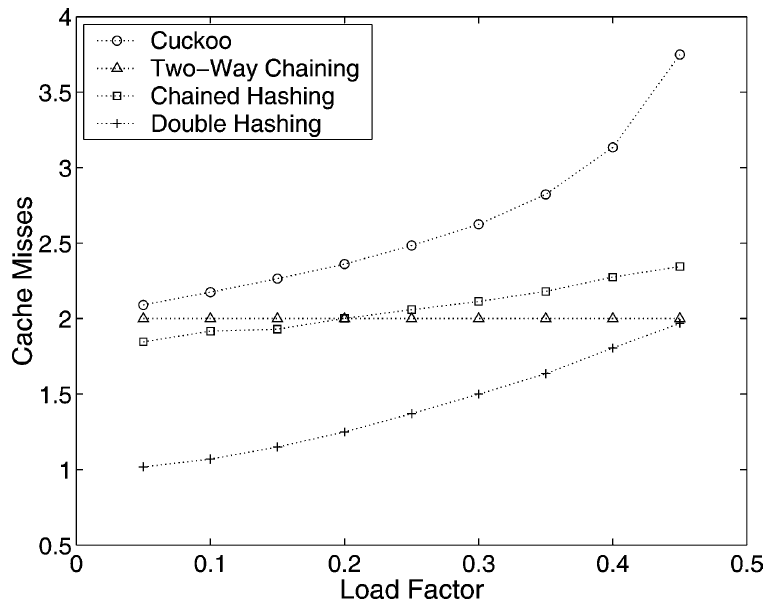
Fig. 7 は様々なスキームと 1/2 未満の負荷係数について挿入時のプローブ平均数を実験的に求めた値である。キャッシュ内にあることがわかっている場所への読み取りと書き込み、および再ハッシュのコストは無視した。測定はサイズ \(2^{15}\) のテーブルと真にランダムなハッシュ関数値を使用し \(10^5\) 回の挿入と削除の後の "平衡状態" で行った。この曲線はテーブルの (消失項までの) サイズとは無関係であると考えられる。非キャッシュメモリアクセス回数はキャッシュアーキテクチャ (キャッシュラインの長さ) に依存するため、Linear Probing の曲線は現われないが、通常は 1 に非常に近い値である。Cuckoo Hashing の曲線は \(2+1/(4+8\alpha) \approx 2+1/(4\epsilon)\) のようである。これはセクション 2.3 の分析 (\(\ref{eq3}\)) とよく一致している。Two-Way Chaining の可能な最大負荷係数は \(O(1/\log\log n)\) である。
セクション 2 で述べたように Cuckoo Hashing の挿入アルゴリズムは \(T_1\) へのキー挿入に偏っている。\(T_1\) で挿入を開始する代わりに開始テーブルをランダムに選択すると挿入時のキャッシュミス数は僅かに減少する。これは負荷バランスが均等になるにつれて \(T_1\) の空きセル数が増えるためである。しかしこれは検索時間が僅かに増加することも意味する。また挿入では要素が既に挿入されているかもチェックするため、Cuckoo Hashing は少なくとも 2 回のキャッシュミスが発生することにも注意。セル \(T_1[h_1(x)]\) または \(T_2[h_2(x)]\) のどちらかが空いているときにすぐ挿入することで、最初の検索を使用して挿入の性能を僅かに向上させることができる。負荷係数 1/3 の場合、新しく挿入されたキーの約 10% が \(T_2\) に配置される。この割合が比較的低いことが、我々の実装で追加のチェックを行う利点がないと判断した理由である。
検索は Chained Hashing における挿入と非常に似ているため、この 2 つの操作に対するキャッシュミスの数は等しいと考えることもできる。ただし我々の実装ではフリーリストから空きセルを取得することで余分なキャッシュミスが発生する可能性がある。これが図の Chained Hashing の曲線が Knuth [20, Fig. 44] の同様のプロットと異なる理由である。
 5. 結論
5. 結論
我々は最悪ケースの検索時間が定数となる新しい辞書を提示した。実装は非常に簡単であり、平均的な性能はこれまでの最良の辞書に匹敵する。最悪ケースで検索時間を定数にする以前スキームは実装がより複雑で平均ケースでの性能も劣っていた。いくつかの課題が残っている。まず第一に、このスキームに適していることが証明されている明示的で真に実用的なハッシュ関数族はまだ見つかっていない。この方向への第一歩は最近 Dietzfelbinger と Wolfel [12] によって講じられたが、彼らのハッシュ関数は依然として比較的大量の空間を必要とする。第二に、なぜこのスキームが低い定数係数を示すかについての正確な理解が不足している。特に Fig. 7 の曲線について説明する必要がある。
 Acknowledgements
Acknowledgements
The authors thank Andrei Broder, Martin Dietzfelbinger, Rolf Fagerberg, Peter Sanders, John Tromp, and Berthold Vöcking for useful comments and discussions on this paper and Cuckoo Hashing in general.
 Appendix A. ユニバーサルハッシュ関数の構成と性質
Appendix A. ユニバーサルハッシュ関数の構成と性質
 A.1. ユニバーサルハッシュ関数族
A.1. ユニバーサルハッシュ関数族
ユニバーサル族の簡単な例として \(U\) からあるコドメインへのすべての関数の族は \((1,|U|)\)-ユニバーサルである。ただし実装目的ではより簡潔なメモリ表現を持つ族が必要である。範囲 \(R=\{0,\ldots,r-1\}\) と素数 \(p \gt \max(2^w,r)\) の \((2,k)\)-ユニバーサル族の標準的な構成は \[ \begin{equation} \left\{ x \mapsto \left( \left( \sum_{l=0}^{k-1} a_l x^l \right) \bmod p \right) \bmod r \mid 0 \leq a_0,a_1,\ldots,a_{k-1} \lt p \right\} \label{eqa1} \end{equation} \] である。
この論文では評価時間が一定である (ただし定数は小さくない) Seigel [35] によるハッシュ関数の構造を用いる。このハッシュ関数の性質は以下の定理で捉えることができる。この定理は後述するように Seigel の論文からユニバーサル折りたたみ関数 (universal collapse function) を用いて導くことができる。
定理 1 (Seigel). \(\gamma\) と \(\delta \gt 0\) を定数とし任意の集合 \(X \subseteq U\) を取る。空間と初期化時間 \(O(|X|^\delta)\) を使用すると、ある定数 \(\delta' \gt 0\) に対して次のような関数族を構成することができる:
少なくとも \(1-|X|^{-\gamma}\) の確率で、\(X\) に限定すると族は \((1,|X|^{\delta'})\)-ユニバーサルである。
さらに、族からの関数は定数時間で評価でき、時間と空間 \(O(|X|^\delta)\) を使用してランダム関数を選択できる。
 A.2. ユニバーサルの折りたたみ
A.2. ユニバーサルの折りたたみ
キーが単一のワードであるという制限は、ユニバースを折りたたみする標準的な手法を使用して長いキーを処理できるため深刻なものではない。具体的には \((O(1),2)\)-ユニバーサル族からのランダム関数 \(\rho\) を適用することで長いキーを \(O(1)\) ワードのキーにマッピングすることができる。このような関数はキー内のワード数に線形な時間で評価できる [7]。これはキーの各ワードに対して \((O(1),2)\)-ユニバーサル族の関数をキーの各ワードで評価し、関数値のビットごとの排他的論理和を計算することで機能する。(効率的な実装については [37] を参照。) 範囲 \(\{0,1\}^{2\log(n)+c}\) を持つこのような関数 \(\rho\) は確率 \(1-O(2^{-c})\) で \(S\) 上の単射となる。実際、初期サイズ \(n\) の辞書にある \(\Omega(2^{c/2}n)\) 個の連続する集合のシーケンスでは、\(\rho\) は一定の確率で単射となる ([10] 参照)。\(S\) の 2 つの要素間の \(\rho\) の衝突が辞書内で検出されるとすべてが再ハッシュされる。つまり \(\rho\) が新たに選択されデータ構造全体が再構築される。もし再ハッシュが期待値 \(O(n)\) で実行できるなら、その償却期待コストは挿入ごとに \(O(2^{-c/2})\) となる。このようにしてユニバースのサイズを効果的に \(O(n^2)\) に減らすことができるが、メンバーシップを決定するために完全なキーを保存する必要がある。
 10. REFERENCES
10. REFERENCES
- A.V. Aho, D. Lee, Storing a dynamic sparse table, in: Proceedings of the 27th Annual Symposium on Foundations of Computer Science (FOCS ’86), IEEE Comput. Soc. Press, 1986, pp. 55–60.
- Y. Azar, A.Z. Broder, A.R. Karlin, E. Upfal, Balanced allocations, SIAM J. Comput. 29 (1) (1999) 180–200.
- P. Berenbrink, A. Czumaj, A. Steger, B. Vöcking, Balanced allocations: the heavily loaded case, in: Proceedings of the 32nd Annual ACM Symposium on Theory of Computing (STOC ’00), ACM Press, 2000, pp. 745–754.
- R.P. Brent, Reducing the retrieval time of scatter storage techniques, Commun. ACM 16 (2) (1973) 105–109.
- A.Z. Broder, A.R. Karlin, Multilevel adaptive hashing, in: Proceedings of the 1st Annual ACM–SIAM Symposium on Discrete Algorithms (SODA ’90), ACM Press, 1990, pp. 43–53.
- A.Z. Broder, M. Mitzenmacher, Using multiple hash functions to improve IP lookups, in: Proceedings of the 20th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2001), vol. 3, IEEE Comput. Soc. Press, 2001, pp. 1454–1463.
- J.L. Carter, M.N. Wegman, Universal classes of hash functions, J. Comput. System Sci. 18 (2) (1979) 143–154.
- M. Dietzfelbinger, J. Gil, Y. Matias, N. Pippenger, Polynomial hash functions are reliable (extended abstract), in: Proceedings of the 19th International Colloquium on Automata, Languages and Programming (ICALP ’92), in: Lecture Notes in Comput. Sci., vol. 623, Springer-Verlag, 1992, pp. 235–246.
- M. Dietzfelbinger, T. Hagerup, J. Katajainen, M. Penttonen, A reliable randomized algorithm for the closest-pair problem, J. Algorithms 25 (1) (1997) 19–51.
- M. Dietzfelbinger, A. Karlin, K. Mehlhorn, F. Meyer auf der Heide, H. Rohnert, R.E. Tarjan, Dynamic perfect hashing: upper and lower bounds, SIAM J. Comput. 23 (4) (1994) 738–761.
- M. Dietzfelbinger, F. Meyer auf der Heide, A new universal class of hash functions and dynamic hashing in real time, in: Proceedings of the 17th International Colloquium on Automata, Languages and Programming (ICALP ’90), in: Lecture Notes in Comput. Sci., vol. 443, Springer-Verlag, 1990, pp. 6–19.
- M. Dietzfelbinger, P. Woelfel, Almost random graphs with simple hash functions, in: Proceedings of the 35th Annual ACM Symposium on Theory of Computing (STOC ’03), 2003, pp. 629–638.
- A.I. Dumey, Indexing for rapid random access memory systems, Computers and Automation 5 (12) (1956) 6–9.
- D. Fotakis, R. Pagh, P. Sanders, P. Spirakis, Space efficient hash tables with worst case constant access time, in: Proceedings of the 20th Symposium on Theoretical Aspects of Computer Science (STACS ’03), in: Lecture Notes in Comput. Sci., vol. 2607, Springer-Verlag, 2003, pp. 271–282.
- M.L. Fredman, J. Komlós, E. Szemerédi, Storing a sparse table with O(1) worst case access time, J. Assoc. Comput. Mach. 31 (3) (1984) 538–544.
- G. Gonnet, Handbook of Algorithms and Data Structures, Addison–Wesley, 1984.
- G.H. Gonnet, J.I. Munro, Efficient ordering of hash tables, SIAM J. Comput. 8 (3) (1979) 463–478.
- R.M. Karp, M. Luby, F. Meyer auf der Heide, Efficient PRAM simulation on a distributed memory machine, Algorithmica 16 (4–5) (1996) 517–542.
- J. Katajainen, M. Lykke, Experiments with universal hashing, Technical Report DIKU, Technical Report 96/8, University of Copenhagen, 1996.
- D.E. Knuth, Sorting and Searching, in: The Art of Computer Programming, vol. 3, 2nd ed., Addison–Wesley, Reading, MA, 1998.
- J.A.T. Maddison, Fast lookup in hash tables with direct rehashing, The Computer Journal 23 (2) (1980) 188–189.
- E.G. Mallach, Scatter storage techniques: a uniform viewpoint and a method for reducing retrieval times, The Computer Journal 20 (2) (1977) 137–140.
- G. Marsaglia, The Marsaglia random number CDROM including the diehard battery of tests of randomness, http://stat.fsu.edu/pub/diehard/.
- C.C. McGeoch, The fifth DIMACS challenge dictionaries, http://cs.amherst.edu/~ccm/challenge5/dicto/.
- K. Mehlhorn, S. Näher, LEDA: A Platform for Combinatorial and Geometric Computing, Cambridge University Press, 1999.
- R. Pagh, On the cell probe complexity of membership and perfect hashing, in: Proceedings of the 33rd Annual ACM Symposium on Theory of Computing (STOC ’01), ACM Press, 2001, pp. 425–432.
- R. Pagh, F.F. Rodler, Cuckoo hashing, in: Proceedings of the 9th European Symposium on Algorithms (ESA ’01), in: Lecture Notes in Comput. Sci., vol. 2161, Springer-Verlag, 2001, pp. 121–133.
- R. Pagh, F.F. Rodler, Cuckoo hashing, Research Series RS-01-32, BRICS, Department of Computer Science, University of Aarhus, August 2001, 21 pp.
- P.V. Poblete, J.I. Munro, Last-come-first-served hashing, J. Algorithms 10 (2) (1989) 228–248.
- R. Raman, S.S. Rao, Succinct dynamic dictionaries and trees, in: Proceedings of the 30th International Colloquium on Automata, Languages and Programming (ICALP ’03), in: Lecture Notes in Comput. Sci., vol. 2719, Springer-Verlag, 2003, pp. 345–356.
- R.L. Rivest, Optimal arrangement of keys in a hash table, J. Assoc. Comput. Mach. 25 (2) (1978) 200–209.
- P. Sanders, B. Vöcking, personal communication, 2001.
- J.P. Schmidt, A. Siegel, On aspects of universality and performance for closed hashing (extended abstract), in: Proceedings of the 21st Annual ACM Symposium on Theory of Computing (STOC ’89), ACM Press, 1989, pp. 355–366.
- J.P. Schmidt, A. Siegel, The analysis of closed hashing under limited randomness (extended abstract), in: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing (STOC ’90), ACM Press, 1990, pp. 224–234.
- A. Siegel, On universal classes of fast high performance hash functions, their time–space tradeoff, and their applications, in: Proceedings of the 30th Annual Symposium on Foundations of Computer Science (FOCS ’89), IEEE Comput. Soc. Press, 1989, pp. 20–25.
- C. Silverstein, A practical perfect hashing algorithm, in: Data Structures, Near Neighbor Searches, and Methodology: Fifth and Sixth DIMACS Implementation Challenges, in: DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 59, American Mathematical Society, 2002, pp. 23–48.
- M. Thorup, Even strongly universal hashing is pretty fast, in: Proceedings of the 11th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA ’00), ACM Press, 2000, pp. 496–497.
- J. Tromp, personal communication, 2003.
- M. Wenzel, Wörterbücher für ein beschränktes Universum, Diplomarbeit, Fachbereich Informatik, Universität des Saarlandes, 1992.
翻訳抄
衝突時に他の位置へ要素を「追い出す」ことで高速な検索、挿入、削除が可能なハッシュテーブルの一種である Cuckoo Hashing に関する 2014 年の論文。
- PAGH, Rasmus; RODLER, Flemming Friche. Cuckoo hashing. Journal of Algorithms, 2004, 51.2: 122-144.