論文翻訳: Hopscotch Hashing

概要

我々はユニプロセッサとマルチコアマシンの両方を対象とするリサイズ可能な新しい逐次および並行ハッシュマップアルゴリズムを提示する。このアルゴリズムは、チェーン法、カッコウハッシュ法、線形プローブ法の要素をすべて備えつつ、それら従来のアプローチの制限とオーバーヘッドを回避した新しい Hopscotch 多段階プロービングと変位手法にもどついている。結果として得られるアルゴリズムは同期オーバーヘッドが非常に低くキャッシュヒット率が高いテーブルを提供する。

最先端の 64-way Niagara II マルチコアマシンでの一連のベンチマークにおいて、この新しいアルゴリズムの並行バージョンは非常にスケーラブルであることが証明された。場合によっては現在最もスケーラブルである Lea の java.concurr.util. の ConcurrentHashMap の 2 倍、あるいは 3 倍のスループットを実現している。さらに Intel および Sun 製のユニプロセッサマシンでのテストでは、このアルゴリズムの逐次バージョンはカッコウハッシュ法や境界線形プローブ法などの最も効果的な逐次ハッシュテーブルアルゴリズムを常に上回る性能を示した。

新しい Hopscotch アルゴリズムの最も興味深い特徴は、テーブルが 90% 以上埋まっている場合でも優れたパフォーマンスを発揮し続けて、テーブル密度が高くなるにつれて他のアルゴリズムに対する優位性が増すことである。

Table of Contents

1. 概要
2. 1. 導入
   1. 1.1 背景
3. 2. 新しい HOPSCOTCH アルゴリズム
4. 3. 複雑性
5. 4. パフォーマンス評価
   1. 4.1 全体的なベンチマークの設定
   2. 4.2 マルチコアでの並行ハッシュマップ
   3. 4.3 並行ベンチマークの結果
   4. 4.4 ユニプロセッサ上の逐次ハッシュマップ
   5. 4.5 逐次のセットアップ
   6. 4.6 逐次ベンチマークの結果
6. 5. 結論と今後の研究
7. 6. ACKNOWLEDGEMENTS
8. REFERENCES
9. APPENDIX
   1. A. CONCURRENT HOPSCOTCH HASHING
   2. B. CORRECTNESS OF THE CONCURRENT HOPSCOTCH ALGORITHM
      1. B.1 Correct Set Semantics
      2. B.2 Progress
10. 翻訳抄

1. 導入

ハッシュテーブルはコンピュータサイエンスにおいて最も広く使用されているデータ構造の一つである。またハッシュテーブルはパフォーマンスの向上が何百万ものアプリケーションやシステムにメリットをもたらす可能性があることから最も徹底的に研究されているデータ構造の一つでもある。

典型的なサイズ変更可能なハッシュテーブルは一定数の要素を保持するバケットの連続的にサイズ変更される配列であり、そのため add(), remove(), contains() メソッドの呼び出しには期待される定数時間が必要である [1]。ハッシュテーブルの一般的な使用パターンでは contains() の呼び出しが圧倒的に多いため [7]、この操作の最適化が多くのハッシュテーブルアルゴリズムの目標となっている。

この論文では hopscotch ハッシュ法を紹介する。これはキャッシュに敏感なマシンを対象とした新しいタイプのオープンアドレス型リサイズ可能ハッシュテーブルで、最先端の湯にプロセッサとマルチコアマシンのほとんど (すべてではないにしても) が含まれる。このようなマシンでは決定論的な定数時間で実行される contains() メソッドが提供され、実際には 2 回のキャッシュロードが必要となる (補題 3.3)。

1.1 背景

チェーンハッシュ法 (chained hashing) [5] は、各バケットがアイテムのリンクリストを保持する配列で構成されるクローズドアドレスハッシュテーブル方式である。クローズドアドレス方式はアイテム検索に要する時間の点で他のアプローチよりも優れているが、動的メモリ割り当てと間接参照を使用するためキャッシュのパフォーマンスが低下する [8]。通常、並列環境では動的メモリ割り当てにスレッドセーフなメモリマネージャやガーベッジコレクターが必要でオーバーヘッドが追加されるためさらに魅力が薄れる。

線形プローブ法 (linear probing) [5] アイテムが連続した配列に保持されるオープンアドレスハッシュ方式である。各エントリは 1 つのアイテムのバケットとなる。新しいアイテムは配列上のバケットにハッシュされ、そのバケットから空のバケットが見つかるまで順に走査することによって挿入される。配列が順次アクセスされることから、各キャッシュラインが複数の配列エントリを保持するため、キャッシュの局所性は良好である。残念ながら線形プローブ法には固有の制限がある。各 contains() 呼び出しはキーを線形に検索するためテーブルがいっぱいになるとパフォーマンスが低下する (テーブルが 90% いっぱいになると、秋が見つかるまでに探索される場所の予想数は約 50 になる [5])。また、キーのクラスタ化によってパフォーマンスに大きなばらつきが生じる可能性もある。一定期間使用すると、削除されたアイテムによって引き起こされる汚染 (contamination) [2] と呼ばれる現象が発生し、失敗する contains() の呼び出し効率が低下する。

カッコウハッシュ法 (cuckoo hashing) [8] は線形プローブ法とは異なり、アイテムの位置を特定するために決定論的な定数ステップのみを必要とするオープンアドレスハッシュ手法である。カッコウハッシュ法では 2 つのハッシュ関数を使用する。新しいアイテム \(x\) は、アイテムを 2 つの配列インデックスにハッシュすることによって挿入される。いずれかのスロットが空であれば \(x\) はそこに追加される。両方が満杯の場合、どちらかの占有アイテムが新しいアイテムに置き換えられる。置き換えられたアイテムは、もう一方のハッシュ関数を使用して再挿入され、場合によっては別のアイテムを置き換える。置き換えの連鎖が長くなりすぎるとテーブルがリサイズされる。カッコウハッシュ法の欠点は異なるキャッシュライン上の無関係な場所のシーケンスにアクセスする必要があることである。さらに大きな欠点は、テーブルが 50% 以上埋まっている場合、置換シーケンスが長くなりすぎてテーブルのサイズ変更が必要になるため、カッコウハッシュ法のパフォーマンスが低下する傾向があることである。

Java™ 並行パッケージ java.util.concurrent の Lea のアルゴリズム [6] はおそらく最も効率的な並行でリサイズ可能なハッシュアルゴリズムとして知られている。これはバケット事のロックでは無く、小数の高レベルロックを使用するクローズドアドレスハッシュアルゴリズムである。Shalev と Shavit [10] はロックフリーのクローズドアドレスでリサイズが可能な別の高性能な方式を提示している。Purcell と Harris [9] は線形プローブに基づくリサイズ不可能なオープンアドレスの並行ハッシュテーブルを最初に提案した。カッコウハッシュ法の並行バージョンは [3] に記載されている。

2. 新しい HOPSCOTCH アルゴリズム

Hopscotch ハッシュ法はこれら 3 つのアプローチの利点を次のように組み合わせる。一つのハッシュ関数 \(h\) がある。あるエントリにハッシュされたアイテムは、常にそのエントリか、次の \(H-1\) エントリのいずかに存在する。ここで \(H\) は定数である (我々の実装では \(H\) は標準的なマシンワードサイズの 32 である)。言い換えると "仮想" バケットは固定サイズで、次の \(H-1\) バケットと重なっている。各エントリにはホップ情報ワード (hop-information word) を含んでいる。これは \(H\) ビットのビットマップで、現在のエントリの仮想バケットにハッシュされたアイテムが続く \(H-1\) エントリのどれに含まれているかを示す。このようにして、どのエントリがそのバケットに属するかをワードで確認し、定数のエントリを読み込むことでアイテムを素早く見つけることができる (ほとんどのマシンではこれに最大でも 2 回のキャッシュラインのロードが必要である)。

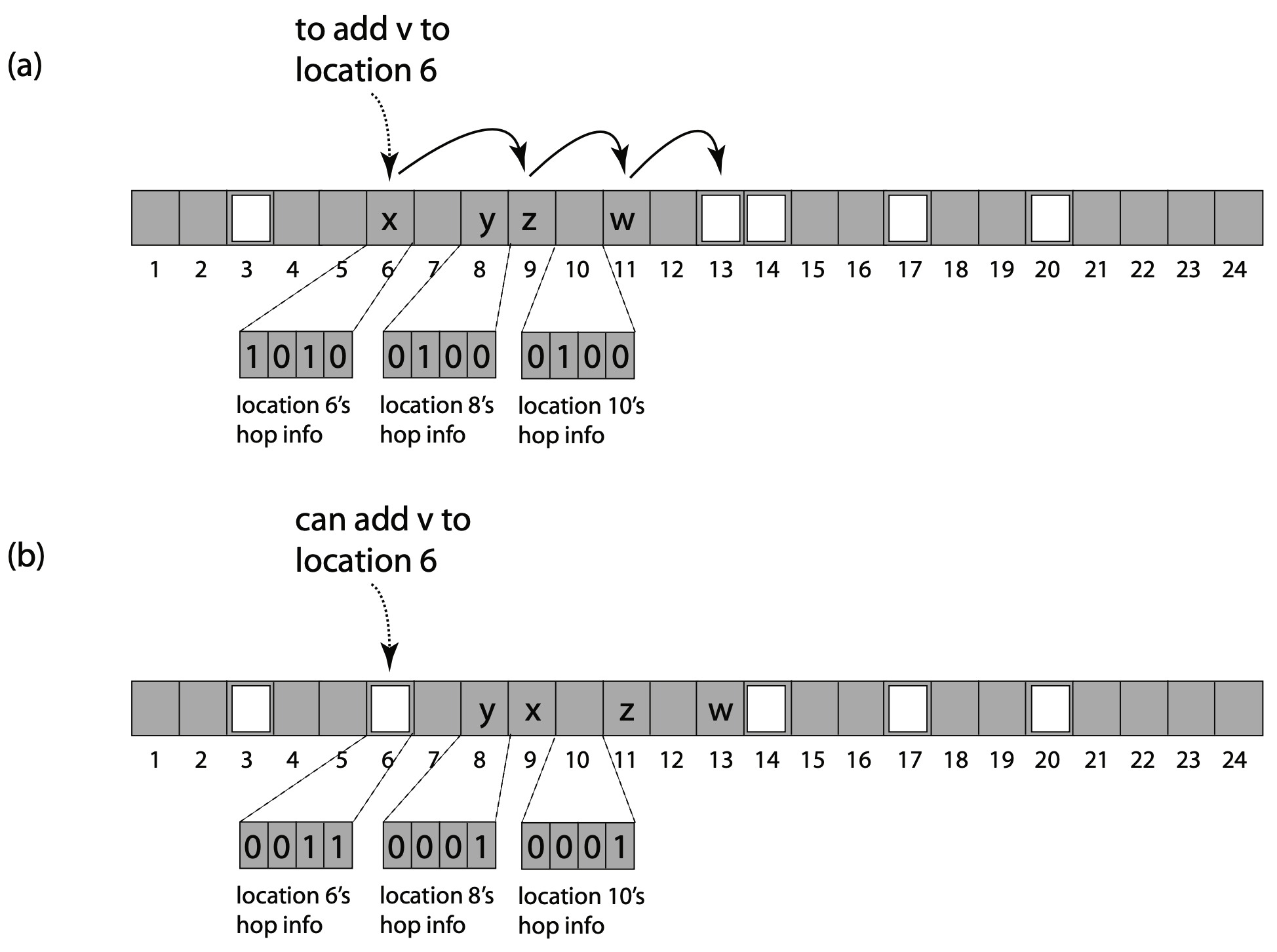
\(h(x)=i\) の場合にアイテム \(x\) を追加する方法は次の通り。

• \(i\) から開始し、線形プローブ法を使用してインデックス \(j\) の空のエントリを見つける。

• 空のエントリのインデックス \(j\) が \(i\) の \(H-1\) 範囲にある場合、\(x\) をそこに格納して戻る。

• そうでない場合 \(j\) は \(i\) から離れすぎている。\(i\) に近い空のエントリを作成するには、\(i\) と \(j\) の間にあるが \(j\) から \(H-1\) の範囲内にあるハッシュ値を持ち、エントリが \(j\) より下に (below) あるアイテム \(y\) を見つける。\(y\) を \(j\) に移動すると \(i\) により近い新しい空きスロットが生成される。これを繰り返す。そのようなアイテムが存在しない場合、またはバケットに既に \(H\) 個のアイテムが含まれている場合、テーブルのサイズを変更してハッシュし直す。

つまりこのアイディアは、線形プローブ法のように空のスロットを元の場所に残したり、カッコウハッシュ法のように目的のバケットからアイテムを移動してから新しい場所を探したりするのではなく、"空のスロットを目的のバケットに向かって移動する" という考え方である。カッコウハッシュ法の変位シーケンスは循環的になる可能性があるため、変位の連鎖が長くなりすぎると通常の実装では中断してサイズを変更する。その結果、カッコウハッシュ法ではテーブルが 50% 未満の時に最も効率よく機能する。一方、Hopscotch ハッシュ法では変位のシーケンスが循環的になることはない。つまり、空のスロットが新しいアイテムのハッシュ値に近づくか、あるいはそのような移動が不可能かのどちらかである。その結果 Hopscotch ハッシュ法は遙かに高い負荷をサポートできる (セクション 4 を参照)。さらにカッコウハッシュ法とは異なり変位が成功する確率はハッシュ関数 \(h\) に依存しないため、ハッシュ関数 \(h\) は普遍性が示される単純な関数を利用できる。

Hopscotch には複数のアイテムを格納できるバケットという利点があるが、チェーンとは異なり隣接するメモリロケーションに配置されるため局所性が非常に高い。また線形プローブ法と同様に一定の予想時間でアイテムを挿入するがクラスタ化は発生せず、Hopscotch の変位方式によりアイテムは常にバケット内で決定論的定数時間で見つかることが保証される。

最後に、定数を超えるアイテムが \(h\) によって特定のバケットにハッシュされた場合、テーブルのサイズを変更する必要があることに注意が必要である。幸いにも、我々が示すように、ユニバーサルハッシュ関数 \(h\) では \(H=32\) の場合にこの種のリサイズが発生する確率は \(1/32!\) である¹。実際には、ホップ情報、32 個のキー、およびそれらのデータへのポインタはすべて 2 つのキャッシュラインに収まるため contains() が引き起こすキャッシュ無効化 (cacche invalidation) は最大でも 2 回である。Fig 1 はアルゴリズムの実行例を示している。

Hotscotch アルゴリズムの並行バージョンではバケットを各ロックにマッピングする。このロックはそのバケットのアイテムを保持するすべてのテーブルエントリへのアクセスを制御する。contains() 呼び出しは待ち時間なし (wait-free) で実行され、ロックを無視して単にホップ情報とバケット内のキーを走査する。一方、add() と remove() はデータに変更を適用する前にバケットのロックを取得する。紙面の都合上、詳細な説明とコードは付録に記載し、比較的単純な resize() メソッドの説明は論文の完成版まで保留する。

3. 複雑性

我々は Hopscotch アルゴリズムの逐次バージョンと並行バージョンに共通する複雑性特性を分析する。並行実行に必要な Safety と Liveness の証明の概要は委員会の判断により付録に記載されている。

ハッシュテーブルの最も重要な特性は期待される定数時間性能である。以下のすべての補題においてハッシュ関数 \(h\) がユニバーサルであると仮定し、ハッシュ関数をキーの均一分布としてモデル化するという標準的な慣例 [1] に従うと仮定する。前述の通り、\(H\) はバケットが保持できるキーの最大数であり実装上は定数である。\(n\) はテーブル内のキー数、\(m\) はテーブルのサイズ、\(\alpha=n/m\) はテーブルの密度または負荷である。

バケットサイズの \(H\) はあらかじめ定義された定数であるため、コードから次のことが導かれる:

補題 3.1. contains() と remove() メソッドは定数時間 (決定論的) で完了する。

バケットのオーバーフローによって resize() が繰り返し呼び出されないようにするには、この定数をどの程度大きくする必要があるだろうか?

補題 3.2. バケット内のアイテム数の期待値は \[ f(m,n) = 1 + \frac{1}{4} \left( \left( 1 + \frac{2}{m} \right)^m - 2 \frac{n}{m} \right) \approx 1 + \frac{e^{2\alpha} - 1 - 2 \alpha}{4} \]

証明. Hopscotch バケットのアイテム数の期待値はチェーンハッシュ法バケットのアイテム数の期待値と同じである。この結果は [5] の Chapter 6.4 の定理 15 から得られる。∎

チェーンハッシュ法と同様に、Hopscotch ハッシュ法でも一般的なケースではバケット内のアイテムが非常に少ないことを以下に示す。

補題 3.3. バケット内のアイテムの最大期待値は一定である。

証明. 再び [5] に従うと、関数 \(f(n,m)\) は増加し、アイテム数である \(n\) の最大値は \(m\) であるため、関数が評価する値はおよそ 2.1 となる。∎

これは、バケット内のアイテムを検索するときには、通常は実行すべき作業が非常に少ないことを意味する。

ユニバーサルハッシュ関数を使用する場合でもバケット内のアイテムの最悪ケースの数が一定で無いことが知られている [5]。ではオーバーフローによる resize() が発生する可能性はどの程度だろうか? その可能性は低いことが分かっている。

補題 3.4. バケットに \(H\) を超えるキーが存在する確率は \(1/H!\) である。

証明. バケットに \(H\) 個のキーが含まれる確率は、チェーンハッシュ法における長さ \(H\) のチェーンが含まれる確率と等しい。[2] の Section 3.3.10 より、\[ {\rm Pr}\{\text{$H$ items in bucket}\} = \binom{n}{H} \frac{(m-1)^{n-H}}{m^n} = \\ \frac{n!}{H! (n-H)!} \frac{(m-1)^{n-H}}{m^n} = \frac{1}{H} n (n-1) \ldots (n-H+1) \frac{(m-1)^{n-H}}{m^{n-H} m^H} \le \frac{1}{H!} \] となる。

\(m\) は最大値であり関数は単調に増加することから、最後の不等式は \(n\) を \(m\) に置き換えることで得られる。∎

したがって、一様ハッシングではバケットに \(H=32\) 以上の項目があるために resize() メソッドが呼び出される確率は \(1/32!\) となる。

以下に示すことが残っている:

補題 3.5. add() メソッドは期待される定数時間で完了する。

証明. [5] より、\(\alpha = n/m \lt 1\) で満たされたオープンアドレスハッシュテーブルが与えられた場合、空いているスロットが見つかるまでのエントリの期待値は最大で \(1/2(1+(1/(1-\alpha))^2)\) であり、これは定数である。したがって、空いているスロットが見つかるまでにテストされるエントリの数によって制限される変位の期待値は最大でも定数である。∎

例えば、ハッシュテーブルの 50% が使用されている場合、空きスロットが見つかるまでにテストされるエントリの期待値は最大で \(1/2(1+(1/(1-0.5))^2)=2.5\) となり、90% 使用されている場合にテストされるエントリの期待値は \(1/2(1+(1/(1-0.9))^2)=50\) となる。

この完成版の論文では以下を証明する:

補題 3.6. resize() メソッドは \(O(n)\) 時間で完了する。

4. パフォーマンス評価

このセクションでは、Hopscotch ハッシュ法の性能を並行 (マルチコア) と逐次 (ユニプロセッサ) の両方の設定で最も効率的な従来のアルゴリズムと経験的に比較する。将来的には実際のアプリケーションのコンテキストで我々のアルゴリズムを評価できれば良いが、ここでは文献で採用されている標準的なアプローチを使用する。このアプローチではこの分野の最近の論文 [8; 10] で使用されているものと同様のマイクロベンチマークを使用するが、テーブル密度ははるかに高くなっている (最大 90%)。

4.1 全体的なベンチマークの設定

ベンチマークでは各テストポイントを 10 回サンプリングして平均をプロットした。テーブルがキャッシュラインに収まらないようにし、データ構造の動作に関するすべての側面が明らかになるようにテーブルサイズは約 \(2^{23}\) アイテムとした。各テストではすべてのハッシュマップに同じキーセットを使用した。すべてのテスト対象のハッシュマップは C++ で実装され、同じコンパイラと設定を使用してコンパイルされた。線形プローブ法のようなオープンアドレスのハッシュと対照的に、クローズドアドレスのハッシュマップはチェーンハッシュ法のようにリストノードを動的に割り当てる。メモリ管理スキームがパフォーマンスに影響を与えることを回避するため、クローズドタイプのハッシュマップの結果は、メモリ割り当てライブラリを使用した場合とメモリ事前割当ライブラリを使用した場合の両方 (mtmalloc ライブラリ、マルチスレッド malloc ライブラリ) で示している。

すべてのアルゴリズムのベンチマークでは各バケットにキーとデータへのポインタのペア (サテライトキーとデータ) が存在した。このスキームは一般的なハッシュマップである。

4.2 マルチコアでの並行ハッシュマップ

まず Hopscotch 法の並行バージョンと、マルチコアマシンの文献で最も高いパフォーマンスを誇る 2 つのリサイズ可能な並行ハッシュテーブルアルゴリズムとの比較を示す。

• ロックベースのチェーン法: これは Lea [6] によるアルゴリズムである。

• ロックフリーのチェーン法: Shalev と Shavit [10] によるロックフリー分割順序 (split-ordered) ハッシュテーブルである。(最終的な論文にはこのベンチマークが含まれる予定である)

• 新しい Hopscotch: バケットのホップ情報の表現でアルゴリズムの並行バージョンを使用した。

最後に、ロックの選択による影響を排除するために、すべてのロックベースの並行アルゴリズムで同じタイプのロックとロック構造 (メモリセグメントごとに 1 つのロック) を使用した。

我々は 64-way Sun UltraSPARC T2™ で一連のベンチマークを実行した。これは 8 つのコアを持ちそれぞれが 8 つの多重化されたハードウェアスレッドをサポートしている、Niagara アーキテクチャに基づくマルチコアマシンである。

4.3 並行ベンチマークの結果

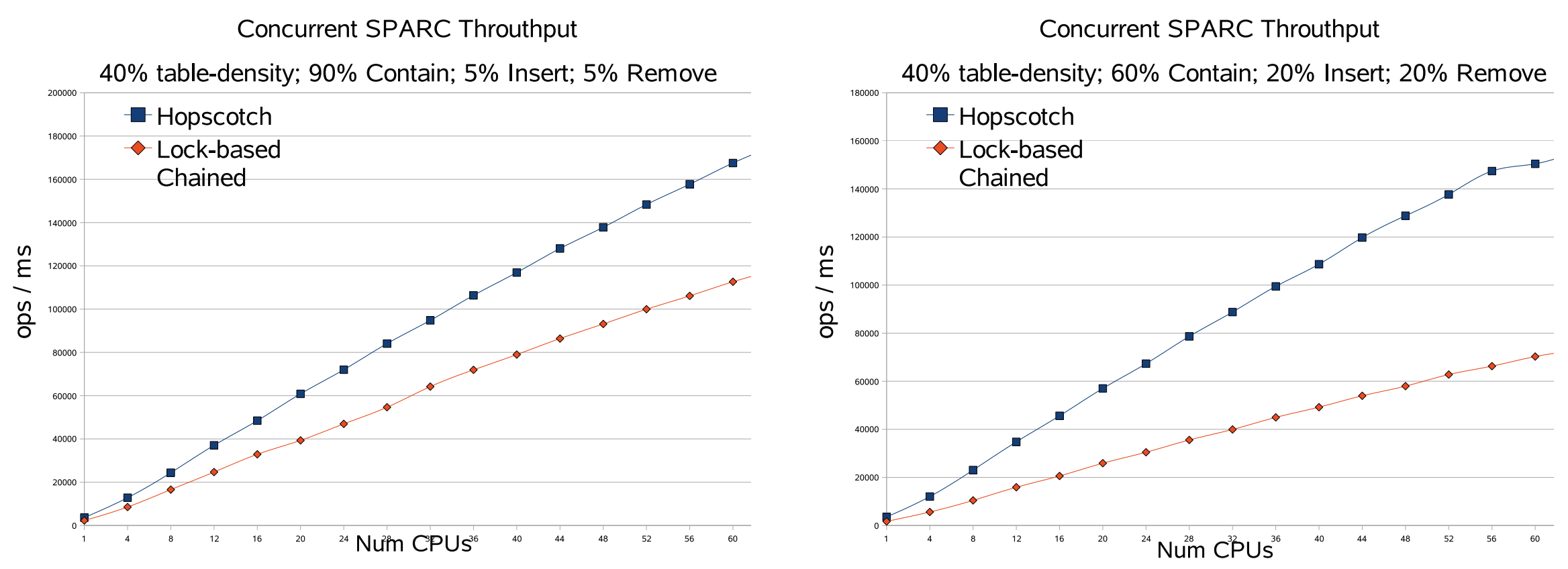
Fig 2 では一般的に見られるアクションの配分 (90% の contains(), 5% の add(), 5% の remove()) と、それほど一般的ではない配分 (60% の contains(), 20% の add(), 20% の remove()) の一般的なスループットを分析した。テーブル密度は 40% で、並行数をマシンがサポートするハードウェアの最大スレッド数である 64 スレッドまで増やした。見ての通り、新しい Hopscotch アルゴリズムのスループットはよりスケーラブルで Lea のチェーン法アルゴリズムの約 2 倍のスループットがある。メモリ管理を排除し、動的メモリアルゴリズムに必要なすべてのスペースを事前に割り当てた場合でも、アルゴリズムの間にはまだ大きなギャップがある。ロックが同じでメモリ管理の影響が排除されていることを考えると、グラフに見られるのは Hopscotch アプローチの純粋な優位性である。この優位性の理由は Hopscotch の法がキャッシュの動作が優れているためである。アイテムを見つけるのに 2 回のキャッシュミスが必要であることは補題 3.3 で証明されている。

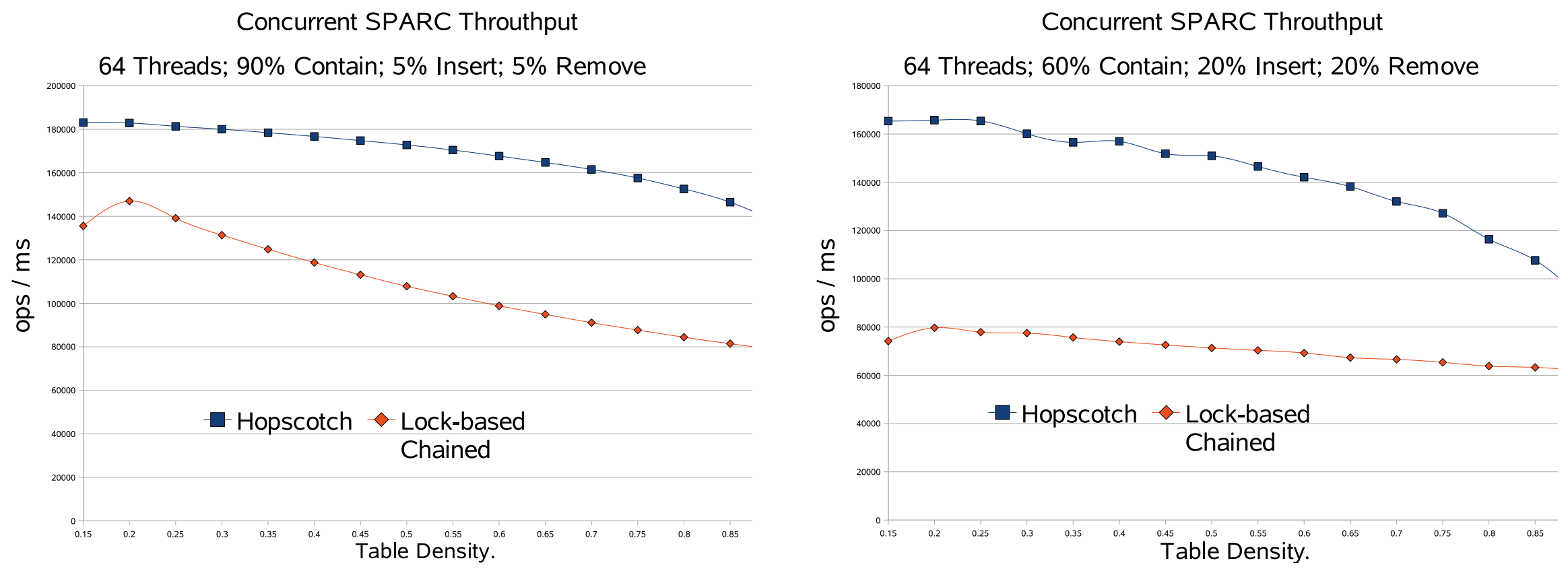
Fig 3 では、64 スレッドという並行性 (実質的にマシン上のハードウェアスレッドの数) においてテーブル密度の関数としてスループットの変化を分析している。各サンプリングポイントでは所定のレベルでテーブル密度を安定させた。見ての通り、Hopscotch はすべての密度で大幅に優れたパフォーマンスを発揮している。密度が増加すると Hopscotch は (訳注: ドラフトのためここで切れている)

4.4 ユニプロセッサ上の逐次ハッシュマップ

我々は最も効果的な既知の逐次ハッシュマップを選択した。

• 線形プローブ法: 各バケットに最大プローブ長を格納する最適化バージョン [5] を使用した。

• チェーン法: 各リンクリストの先頭の要素を直接ハッシュテーブルに格納する [5] の最適化版を使用した。

• 新しい Hopscotch: 逐次バージョンと、リストのようなホップ情報表現を使用し、99% までのテーブル密度で性能をテストできるようにした。

4.5 逐次のセットアップ

SPARC アーキテクチャ: 1.20GHz で動作する Sun UltraSPARC T1™ マルチコア CPU の単一コアと、INTEL アーキテクチャ: Xeon™ CPU 3.00GHz の基本的に異なる 2 つのユニプロセッサアーキテクチャで一連のベンチマークを実行した。

4.6 逐次ベンチマークの結果

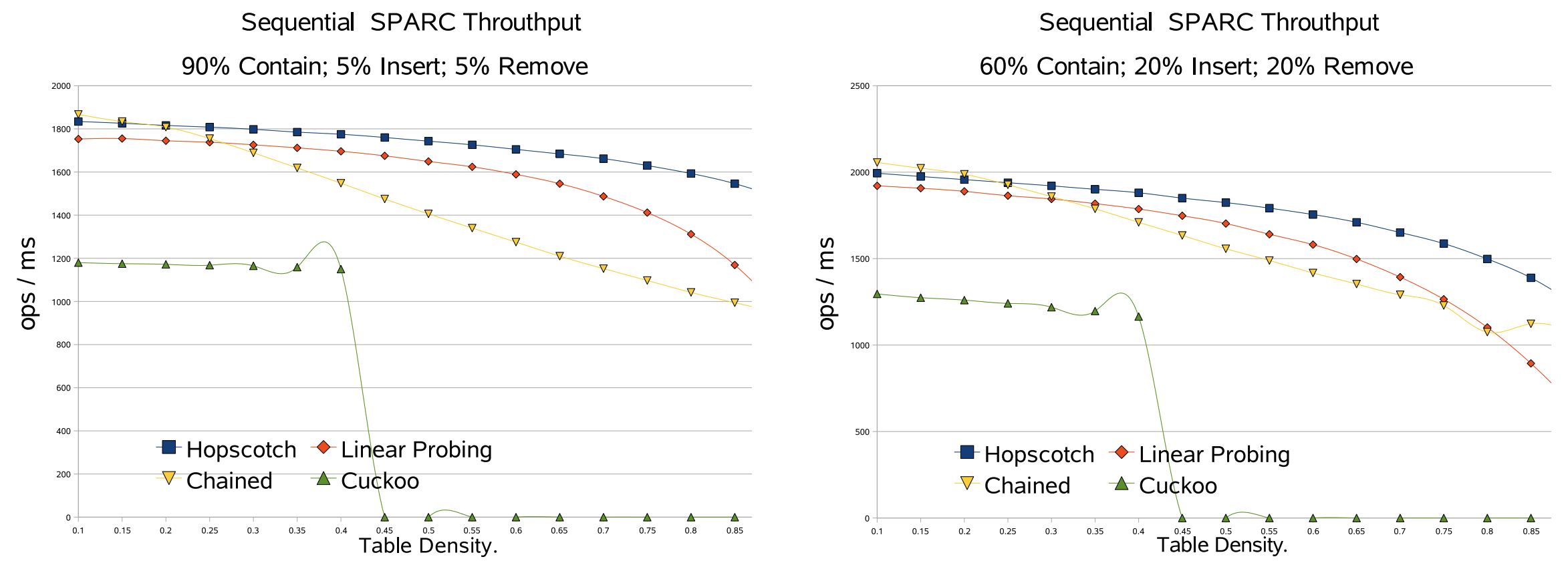
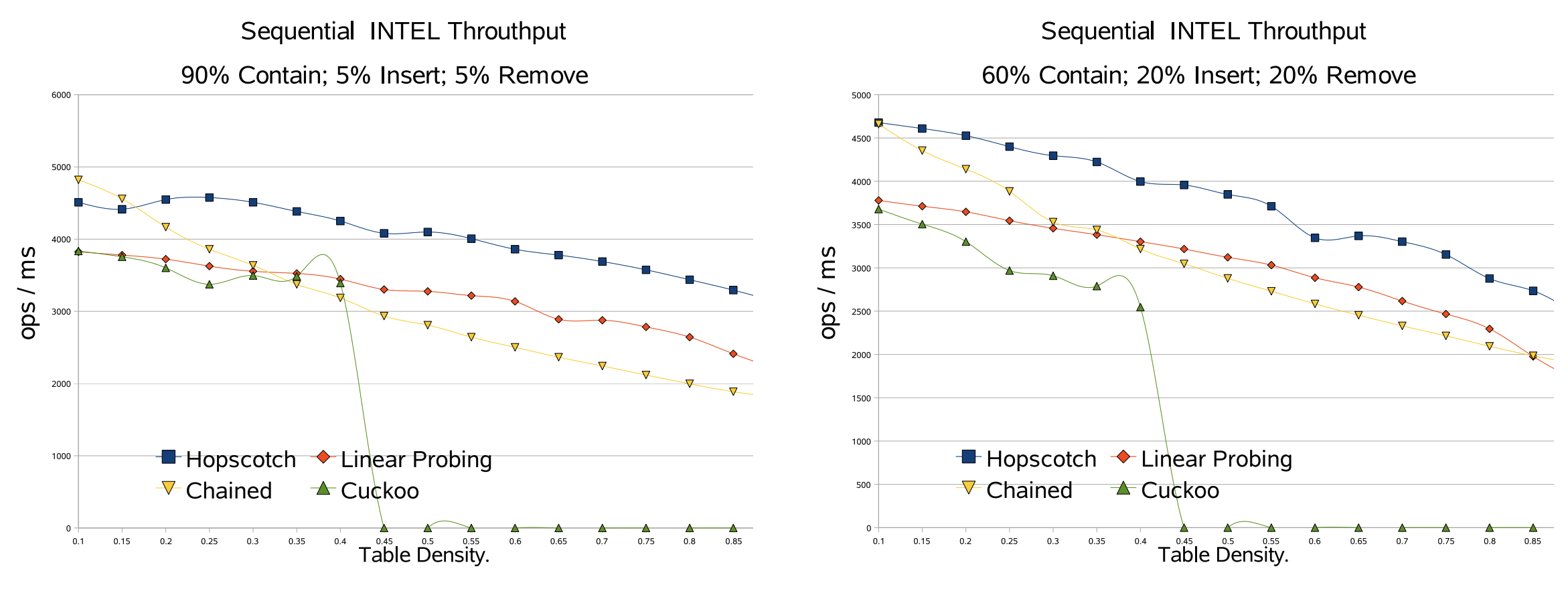
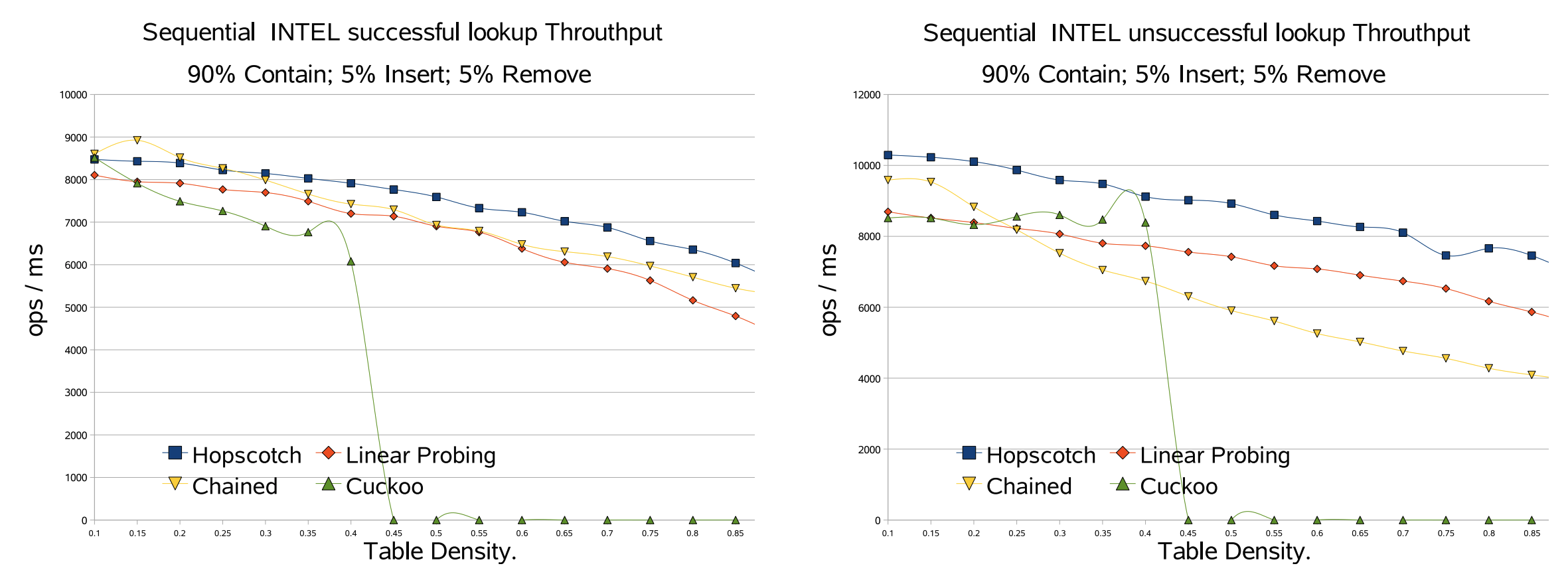
以下のグラフは平均テーブル密度の関数としてスループットの変化を示している。Fig 3 ではさまざまなアクションが混在した場合の一般的なスループットを示している。これらのテストの密度範囲は 10〜90% である。見ての通り新しい Hopscotch アルゴリズムは他のハッシュマップよりも優れているが、重要な点はテーブル密度の増加に対する耐性が高いことである。我々は動的メモリアルゴリズムのすべてのメモリを事前に割り当て中和 (neutralized) したバージョンを使用してすべてのメモリを事前割り当てしている。したがって、ここで見られるのは Hopscotch アプローチの純粋な利点である。この利点の理由はキャッシュ動作が優れていることである。アイテムを見つけるには 2 回のキャッシュミスが必要であり、これはテーブルがほぼいっぱいの場合でも同様である。これは線形プローブ法の場合とは異なり、テーブルがいっぱいになるにつれアイテムは元のバケットからどんどん離れてゆく。カッコウハッシュ法の理論的な分析ではテーブル密度が 50% を超えると挿入時に新しいキーを導入できる有効な配置を見つけられないことが示されている。

まとめると、Hopscotch ハッシュ法は並行でも逐次でも優れた性能を発揮し、時にはかなり大きなパフォーマンスを発揮する。これはその優れたキャッシュ動作によるものである。

5. 結論と今後の研究

我々は Hopscotch アルゴリズムを紹介し、逐次および並行の両方の既知のアルゴリズムすべてに対する優位性を示した。Hopscotch ハッシュ法の resize() メソッドは [6] と同じスタイルで並行化できることに注目し、今後の研究でそうする予定である。また実際のアプリケーションでアルゴリズムの性能を評価しキャッシュミスベンチマークを実行することも興味深い。最後に、テーブル密度が高い場合に Hopscotch が非常に優れたパフォーマンスを発揮する理由を正式に分析することも興味深い。これはテーブルがいっぱいの時でも、ある任意のバケット \(i\) から \(H\) 未満離れた位置で始まるすべてのハッシュテーブルバケット (空であると判明したものなど) には、\(h\) によってこのバケットにハッシュされたアイテムが少なくとも 1 つある (したがって \(i\) に移動できる) 確率を示すことになる。

6. ACKNOWLEDGEMENTS

We thank Dave Dice for helping us with the execution of our algorithm on the N2 machine at Sun Labs. And Doug Lea for his guidance and insight.

REFERENCES

1. Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. Introduction to Algorithms, Second Edition. MIT Press, Cambridge, Massachusetts, 2001.
2. Gonnet, G. H., and Baeza-Yates, R. Handbook of algorithms and data structures: in Pascal and C (2nd ed.). Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA, 1991.
3. Herlihy, M., and Shavit, N. The Art of Multiprocessor Programming. Morgan Kaufmann, NY, USA, 2008.
4. Herlihy, M. P., and Wing, J. M. Linearizability: a correctness condition for concurrent objects. ACM Transactions on Programming Languages and Systems (TOPLAS) 12, 3 (1990), 463–492.
5. Knuth, D. E. The art of computer programming, volume 1 (3rd ed.): fundamental algorithms. Addison Wesley Longman Publishing Co., Inc., Redwood City, CA, USA, 1997.
6. Lea, D. Hash table util.concurrent.concurrenthashmap in java.util.concurrent the Java Concurrency Package. http://gee.cs.oswego.edu/cgi-bin/viewcvs.cgi/jsr166/src/main/java/util/concurrent/.
7. Lea, D. Personal communication, Jan. 2003.
8. Pagh, R., and Rodler, F. F. Cuckoo hashing. Journal of Algorithms 51, 2 (2004), 122–144.
9. Purcell, C., and Harris, T. Non-blocking hashtables with open addressing. In Lecture Notes in Computer Science, Distributed Computing, Springer Berlin / Heidelberg 3724/2005 (October 2005), 108–121.
10. Shalev, O., and Shavit, N. Split-ordered lists: Lock-free extensible hash tables. Journal of the ACM 53, 3 (2006), 379–405.

APPENDIX

A. CONCURRENT HOPSCOTCH HASHING

……

B. CORRECTNESS OF THE CONCURRENT HOPSCOTCH ALGORITHM

B.1 Correct Set Semantics

B.2 Progress

翻訳抄

既知のハッシュテーブルアルゴリズムより逐次/並行の両面でパフォーマンスに優れている Hopscotch ハッシュ法に関する 2008 年の論文 (ドラフト)。

1. HERLIHY, Maurice; SHAVIT, Nir; TZAFRIR, Moran. Hopscotch hashing. In: Distributed Computing: 22nd International Symposium, DISC 2008, Arcachon, France, September 22-24, 2008. Proceedings 22. Springer Berlin Heidelberg, 2008. p. 350-364.