論文翻訳: HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm
 概要
概要
この Extended Abstract は、非常に大きなデータアンサンブルの一意な (distinct) 要素の数 (カーディナリティ (cardinality)) を推定することに特化した、ほぼ最適な確率的アルゴリズムである HyperLogLog を詳述し分析する。HyperLogLog は \(m\) 単位 (通常は "小さいバイト数") の補助メモリを使用し、データを一度走査して相対精度 (標準誤差) が通常約 \(1.04/\sqrt{m}\) となるようにカーディナリティ推定値を生成する。これは既知のカーディナリ推定アルゴリズムである LogLog を改善するものであり、元のメモリの 64% しか消費せずに達成できる。具体的には、この新しいアルゴリズムではわずか 1.5 キロバイトのメモリを使用するだけで、典型的な精度 2% で \(10^9\) をはるかに超えるカーディナリ推定が可能になる。このアルゴリズムは適切に並列化され、スライディングウィンドウモデルに適応する。
Table of Contents
 導入
導入
このノートの目的は大規模データセットアンサンブル ─ ここでは多重集合 (multiset) と呼び、通常は大規模なストリーム (読み取り 1 回限りのシーケンス) ─ のカーディナリティとして知られる一意の要素の数 (number of distinct elements) を推定する効率的なアルゴリズムを提示し分析することである。この問題は過去 20 年間で大きな注目を集めており、ワームの伝播、ネットワーク攻撃 (Denial of Service など)、Web 上のリンクベースのスパム [3] など、ネットワークとトラフィックの監視におけるアプリケーションがますます増えている。例えば、ネットワーク上のデータストリームはパケットのシーケンスで構成され、各パケットにはアドレスのペア (送信元と送信先) を含むヘッダがあり、その後に特定のデータのボディが続いている。さまざまなタイムスライスにおける異なるヘッダペアの数 (多重集合のカーディナリティ) は個別のアクティブフローの数を記録するため、攻撃を検出しトラフィックを監視するための重要な指標になる。実際、ワームやウイルスは通常多数の異なる接続を開くことで伝播し、膨大なトラフィックの中で気づかれずに通過することもあるが、カーディナリティが計測されるとその活動が明らかとなる ([11] の Estan と Varghese による明快な説明を参照)。カーディナリティ推定器の他の応用例としては、自然言語テキスト [4, 5]、生物学的データ [17, 18]、非常に大規模な構造化データベース、インターネットのグラフなど、膨大なデータセットのデータマイニングがある。[22] の著者は確率的カーディナリティ推定器によって 500 倍以上の計算効率が達成されたと報告している。
明らかに、多重集合のカーディナリティはその要素数に本質的に比例する記憶複雑度で正確に決定できる。しかし、ほとんどのアプリケーションでは処理される多重集合はコアメモリに保持するには大きすぎる。そこで重要なアイディアは、カーディナリティの値 \(n\) を正確に計算すると言う制約を緩和し、\(n\) を近似的に推定する確率的アルゴリズムを開発することである。(多くの実用的なアプリケーションでは数パーセントの誤差は許容範囲である。) 線形以下のメモリのみを使用するアルゴリズム [2, 6, 10, 11, 15, 16]、または最悪でも線形メモリだが小さな暗黙定数を必要とするアルゴリズム [24] が開発されている。
既知の効率的なカーディナリティ推定器はすべてランダム化に依存しており、これはハッシュ関数の使用によって保証されている。特定のデータドメイン \(\mathcal{D}\) に属するカウント対象の要素についてハッシュ関数 \(h: \mathcal{D} \to \{0,1\}^\infty\) が与えられていると仮定する。つまりハッシュ値を \(\{0,1\}^\infty\) の無限バイナリ列、または等価的に単位区間の実数と同様と同じと見なす。(実際には 32 ビットのハッシュで \(10^9\) を超えるカーディナリティを推定できる; 詳細はセクション 4 を参照。) ハッシュ関数は、ハッシュ値がランダム性の均一モデルに極めて類似するように設計されていると仮定する。つまり、ハッシュ値のビットは独立しており、それぞれ発生する確率は \(\frac{1}{2}\) であると想定している。この仮定を証明する実用的な方法は、巡回冗長検査 (CRC)、モジュラー算術、またはブール代数の簡略化された暗号化の使用 (sha1 など) に基づいて知られている [20]。
最もよく知られたカーディナリティ推定器は、入力となる多重集合 \(\mathcal{M}\) のハッシュ値 \(h(\mathcal{M})\) に対して適切かつ簡潔な観測を行い、未知のカーディナリティ \(n\) の妥当な推定値を推測することに依存している。\(\{0,1\}^\infty\) 列 (または等価的に実数 \([0,1]\)) の多重集合 \(S \equiv h(\mathcal{M})\) の観測可能量 (observable) を、\(S\) の基礎となる集合のみに依存する関数、つまり複製に依存しない量として定義する。そしてカーディナリティ観測可能量には 2 つの大きなカテゴリがある。
ビットパターン観測可能量: これらは (バイナリ) \(S\)-値の先頭で発生する特定のビットパターンに基づいている。例えばストリーム \(S\) の先頭の列でビットパターン \(0^{\rho-1}1\) を観測したということは、\(S\) のカーディナリティ \(n\) が少なくとも \(2 \rho\) であることを示している可能性が高い。Flajolet-Martin [15] による確率的カウント (Probabilistic Counting) として知られているアルゴリズムと、より最近の Durand-Flajolet [10] の LogLog はこのカテゴリに属する。
順序統計観測可能量: これらは \(S\) に現われる最小の (実数) 値などの順序統計に基づいている。例えば \(X=\min(S)\) の場合、期待値に関しては \(\mathbb{E}(X)=1/(n+1)\) となるため、\(n\) はおよそ \(1/X\) のオーダーであると期待できる。Bar-Yossef ら [2] や Giroire の MinCount [16, 18] はこのタイプである。
上で述べたような観測可能量は 1 つまたは少数のレジスタで維持することができる。しかしながらこの場合、\(\log_2 n\) または \(1/n\) によって、求められるカーディナリティ \(n\) の大まかな指標を提供するのみである。一つの難点は、変動性がかなり高いことから 1 つの変数の維持に対応する 1 つの観測では正確な予想を得るのには十分でないことである。すぐに思いつくのは、いくつかの試行を並行して行うことである。\(m\) 個の確率変数の集合がそれぞれ標準偏差 \(\sigma\) を持つ場合、それらの算術平均は標準偏差 \(\sigma/\sqrt{m}\) を持ち、これは \(m\) を増やすことでいくらでも小さくすることができる。しかしこの単純な戦略には 2 つの大きな欠点がある。まず計算時間の面でコストがかかり (走査された要素ごとに \(m\) 個のハッシュ値を計算する必要がある)、さらに悪いことに、独立したハッシュ関数の大規模な集合が必要になるが、そのような構築法は知られていない [1]。
[15] において確率的平均化 (stochastic averaging) という名前で紹介された解決策は、1 つのハッシュ関数で \(m\) 回の試行の効果をエミュレートすることである。大雑把に言えば、入力ストリーム \(h(\mathcal{M})\) を \(m\) 個のサブストリームに分割する。これは、ハッシュ値の単位区間を \([0,\frac{1}{m}[\), \([\frac{1}{m},\frac{2}{m}[\), \(\ldots\), \([\frac{m-1}{m},1]\) に分割することに対応する (訳注: \([a,b[\) は右半開区間)。そして \(m\) 個のサブストリームに対応する \(m\) 個の観測可能量 \(O_1\), \(\ldots\), \(O_m\) を保持する。\(\{O_j\}\) の適切な平均は、平均化効果によって \(m\) が増加するにつれて \(1/\sqrt{m}\) に比例して品質が向上するカーディナリティの推定値を生成することが期待される。このアプローチの利点は、(\(m\) に比例する量ではなく) 多重集合 \(\mathcal{M}\) の要素ごとに一定数の基本操作のみが必要であり、ただ一つのハッシュ関数のみを必要とすることである。
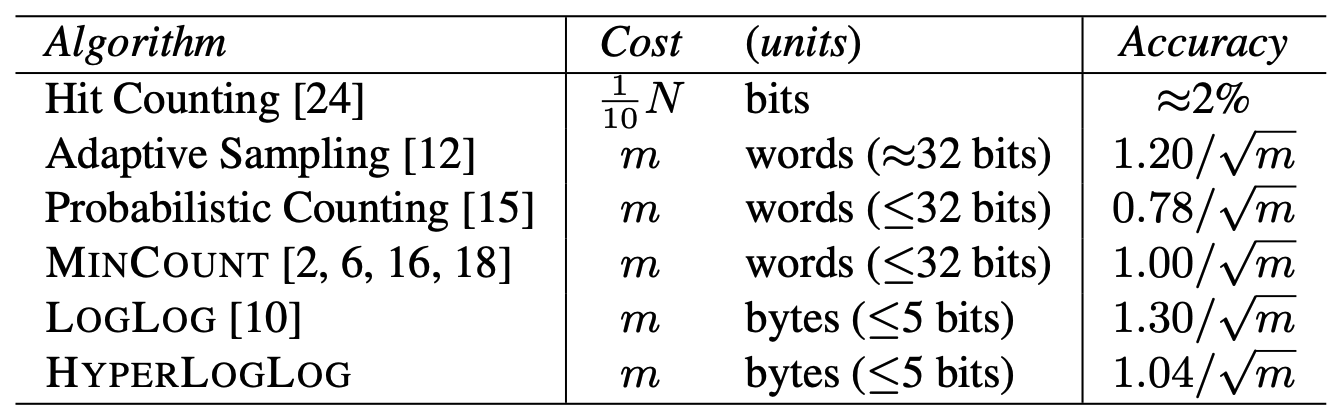
いくつかのアルゴリズムの性能は Fig 1 で比較されている。レビューについては [13] も参照。次のセクションで詳しく説明する HyperLogLog は、LogLog と同じ観測可能量、すなはち得られる最大の \(\rho\) 値に基づいている。ここで \(\rho(x)\) はバイナリ列 \(x\) の最も左にあるビット 1 の位置である。前述の意味で確率的平均化が採用されている。しかし我々のアルゴリズムは評価関数が標準的な LogLog とは異なる。標準のアルゴリズムが幾何平均1 (geometric mean) に相当するものを使用するのに対し、我々のアルゴリズムは調和平均 (harmonic means) 基づいている。調和平均を使うというアイディアは元々 Chassaing と Gérin [6] の洞察に満ちたノートから着想を得たものである。このような平均は右側の裾がゆっくりと減衰する確率分布を抑える効果があり、ここでは分散削減装置として機能し、それによって推定の質を大幅に向上させる。後述する定理 1 は HyperLogLog の相対誤差 (厳密には標準誤差) が \(\beta_\infty/\sqrt{m}\) に数値的に近いという主な結論を要約したものである。ここで \(\beta_\infty=\sqrt{3 \log 2 - 1} \doteq 1.03896 \) である。このアルゴリズムはカーディナリティ \(\le N\) を推定する必要があるとき、各レジスタは最大で \(\log_2 \log_2 N + O(1)\) ビットのレジスタのコレクションを維持する必要がある。特に HyperLogLog は対応するメモリの 64% しか消費することなく標準的な LogLog に匹敵する精度を達成する。結果として、\(m=2048\)、32 ビットのハッシュ、各 5 ビット長の短いバイトを使用することで、1.5kB (キロバイト) のストレージを使用して \(N=10^9\) を超えるカーディナリティまでを典型的に 2% の精度で推定できる。
その証明はポアソン化 (poassonization)、メリン変換 (Mellin transforms)、鞍点デポアソン化 (saddle-point depoissonization) など、現在ではアルゴリズムの解析において標準的な手法に基づいている。しかし、調和平均の特殊な非線形特性によりいくつかの非標準的な問題が存在し、解析のいくつかの要素が完全にルーチン化されているわけではない。
- 1論文 [10] では極端なデータを打ち切ることで分散の提言を試みる SuperLogLog という別の手法も紹介されている。しかしバイアスや標準誤差に関して分析に容易に応じられないという欠点がある。
 1 HyperLogLog アルゴリズム
1 HyperLogLog アルゴリズム
| 1. | \( {\it Let} \ h : \mathcal{D} \to [0,1] \equiv \{0,1\}^\infty \) | // ドメイン \(\mathcal{D}\) から二進ドメインへのハッシュデータ |
| 2. | \( {\it Let} \ \rho(s) \) | // \(s \in \{0,1\}^\infty\) に対して左端の 1 ビットの位置 (\(\rho({\tt 0001}\ldots) = 4\)) |
| 3. | \( {\bf Algorithm} \ {\sf HyperLogLog}({\bf input} \ \mathcal{M}: \text{multiset of items from domain $\mathcal{D}$}) \) | |
| 4. | \( {\bf assume} \ m=2^b \ {\rm with} \ b \in \mathbb{Z}_{\gt 0}; \) | |
| 5. | \( {\bf initialize} \ \text{a collection of $m$ registers}, M[1],\ldots\,M[m],\ \text{to} \ -\infty; \) | |
| 6. | \( {\bf for} \ v \in \mathcal{M} \ {\bf do} \) | |
| 7. | \( \hspace{12pt}{\bf set} \ x := h(v); \) | |
| 8. | \( \hspace{12pt}{\bf set} \ j = 1 + \langle x_1 x_2 \cdots x_b \rangle_2; \) | // \(x\) の最初の \(b\) ビットによって決定されるバイナリアドレス |
| 9. | \( \hspace{12pt}{\bf set} \ w := x_{b+1} x_{b+2} \cdots; \ \ {\bf set} \ M[j] := \max(M[j], \rho(w)); \) | |
| 10. | \( {\bf compute} \ Z := \left( \sum_{j=1}^m 2^{-M[j]} \right)^{-1}; \) | // "indicator" 関数 |
| 11. | \( {\bf return} \ E := \alpha_m m^2 Z \) | // \(\alpha_m\) は式 (\(\ref{eq3}\)) で与えられる |
HyperLogLog アルゴリズムは Fig 2 で完全に示されている。対応するプログラムについては後ほどセクション 4 で説明する。入力はデータ項目の多重集合 \(\mathcal{M}\)、つまり要素が順次読み込まれるストリームである。出力は \(\mathcal{M}\) 内の異なる要素の数として定義されるカーディナリティの推定値である。適切なハッシュ関数 \(h\) は固定されている。このアルゴリズムは確率的平均化と併せて特定のビットパターン観測可能値に依存する。列 \(s \in \{0,1\}^\infty\) が与えられたとき、\(\rho(s)\) は左端の 1 の位置 (つまり先頭の 0 の連続の長さに 1 を加えたもの) を表すものとする。ストリーム \(\mathcal{M}\) は項目のハッシュ値2の最初の \(b\) ビットに基づいてサブストリーム \(\mathcal{M}_1,\ldots,\mathcal{M}_m\) に分割される。ここで \(m=2^b\) であり、各サブストリームは独立して処理される。\(\mathcal{N}\equiv\mathcal{M}_j\) のようなサブストリーム (先頭の \(b\) ビットが取り除いたハッシュ値で構成されていると見なされる) では、対応する観測可能値は \[ \begin{equation} {\rm Max}(\mathcal{N}) := \max_{x \in \mathcal{N}} \rho(x) \label{eq1} \end{equation} \] となり、\({\rm Max}(\emptyset)=-\infty\) という規則に従う。アルゴリズムは \(j=1,\ldots,m\) について \({\rm Max}(\mathcal{M}_j)\) の値 \(\mathcal{M}^{(j)}\) をその場 (on the fly) で (レジスタ \(M[j]\) に) 収集する。すべての要素が走査されると、アルゴリズムは指標 (indicator) \[ \begin{equation} Z := \left( \sum_{j=1}^m 2^{-M^{(j)}} \right)^{-1} \label{eq2} \end{equation} \] を計算する。そして \(2^{M^{(j)}}\) の調和平均の正規化されたバージョンを \[ \begin{equation} E := \frac{\alpha_m m^2}{\sum_{j=1}^m 2^{-M^{(j)}}}, \text{ with } \alpha_m := \left( m \int_0^\infty \left( \log_2 \left(\frac{2+u}{1+u}\right) \right)^m du \right)^{-1} \label{eq3} \end{equation} \] の形式で返す。
以下にアルゴリズムの基礎となる直感を説明する。\(\mathcal{M}\) の未知のカーディナリティを \(n\) とする。各サブストリームはおよそ \(n/m\) 個の要素で構成される。その場合、その \({\rm Max}\)-パラメータは \(\log_2 (n/m)\) に近いはずである。\(2^{\rm Max}\) の調和平均 (我々の表記では \(mZ\)) はおそらく \(n/m\) のオーダーである。従って \(m^2Z\) は \(n\) のオーダーであるはずである。後続の分析で導かれる定数 \(\alpha_m\) を最終的に導入することで \(m^2Z\) に存在する体系的な乗法バイアスを補正する。
我々の主要な主張である以下の定理 1 は理想的多重集合 (ideal multiset) の状況を扱うものである。
定義 1. カーディナリティ \(n\) の理想的多重集合は、実数区間 \([0,1]\) 上の \(n\) 個の均一かつ同一に分布するランダム変数に任意の複製と置換を適用して得られるシーケンスである。
この論文の分析部分 (セクション 2 と 3) では、アルゴリズムが処理するハッシュ値の集合 \(h(\mathcal{M})\) が理想的多重集合を構成すると仮定している。この仮定は、適切に設計されたハッシュ関数の結果をモデル化する自然な方法である。このような理想的多重集合の異なる要素の数は確率 1 で \(n\) に等しいことに注意。以降、このモデルにおける期待値と分散の演算子を \(\mathbb{E}_n\) と \(\mathbb{V}_n\) とする。
定理 1. Fig 2 の HyperLogLog を (未知の) カーディナリティ \(n\) の理想的多重集合に適用し、結果として得られるカーディナリティ推定値を \(E\) とする。
推定値 \(E\) は \[ \frac{1}{n} \mathbb{E}_n(E) \underset{n\to\infty}{=} 1 + \delta_1(n) + o(1) \] という意味で漸近的にほぼ偏りがない。ここで \(m \ge 16\) であれば \(|\delta_1(n)| \lt 5 \cdot 10^{-5}\) である。
\(\frac{1}{n}\sqrt{\mathbb{V}_n(E)}\) として定義されてる標準誤差は、\(n\to\infty\) のとき \[ \frac{1}{n} \sqrt{\mathbb{V}_n(E)} \underset{n\to\infty}{=} \frac{\beta_m}{\sqrt{m}} + \delta_2(n) + o(1) \] を満たす。ここで \(m\ge 16\) であれば \(|\delta_2(n)|\lt 5\cdot 10^{-4}\) である。
定数 \(\beta_m\) は \(\beta_{16}\doteq 1.106\), \(\beta_{32}\doteq 1.070\), \(\beta_{64}\doteq 1.054\), \(\beta_{128}\doteq 1.048\), \(\beta_\infty=\sqrt{3\log(2)-1}\doteq 1.03896\) で上限が定まる。
標準誤差は、観測される典型的な誤差を相対的に測定する (平均二乗の意味で)。関数 \(\delta_1(n)\) と \(\delta_2(n)\) はごくわずかな振幅の振動関数を表し、計算可能であり、その影響は理論的に少なくとも部分的に補正できる。いずれにしても実用的な目的のためには安全に無視できる。
論文の計画. 論文の大部分は定理 1 の証明に費やされている。我々は \(Z\) が指標 \(1/\sum 2^{M^{(j)}}\) である場合の \(\mathbb{E}_n(Z)\) と \(\mathbb{V}_n(Z)\) の漸近的挙動を決定する。\(E\) を漸近的にほぼ無偏推定量とする式 (\(\ref{eq3}\)) の値 \(\alpha_m\) はこの解析から標準誤差の値と同様に導出される。平均の分析はセクション 2 の主題である。実際、\(\mathbb{E}_n(Z)\) の正確な表現は扱いにくいため、まず問題を "ポアソン化" (ppoissonize) して \(\mathbb{E}_{\rho(\lambda)}(Z)\) を調べる。これは、要素の総数が固定されておらず、パラメータ \(\lambda\) のポアソン法則に従う場合の指標 \(Z\) の期待値を表す。次に、\(\lambda := n\) を選択した場合に \(\mathbb{E}_n(Z)\) と \(\mathbb{E}_{\rho(\lambda)}(Z)\) の挙動が漸近的に近いことを証明する。これがデポアソン化ステップ (depoissonization step) である。指標 \(Z\) つまり標準誤差の分散分析はセクション 3 で概説されており、平均値分析と完全に並行している。最後に、セクション 4 では HyperLogLog アルゴリズムを実際のコンテキストで実装する方法を検討し、シミュレーションと最適性に関する問題について検討する。
- 2このアルゴリズムは、いくつかの算術演算を追加する代償として \(m\ge 3\) の任意の積分値に対処するために適応することができる。
 2 平均値分析
2 平均値分析
我々の出発点は (\(\ref{eq2}\)) で定義された確率変数 \(Z\) ("指標") である。ここで \(\mathbb{E}_n(Z)\) は (未知の) カーディナリティ \(n\) が固定された理想的多重集合モデルでの期待値であることは前に述べた。分析は命題 1 の \(\mathbb{E}_n(Z)\) の厳密な表現から始まり、命題 2 で要約される対応するポアソン期待値の漸近分析に続き命題 3 のデポアソン化の議論で終わる。
 2.1 Exact expressions
2.1 Exact expressions
……
命題 1. 固定のカーディナリティ \(n\) の理想的多重集合から得られる指標 \(Z\) の期待値は \(v,k\ge 1\) と \(\gamma_{0,k}=0\) の場合 \[ \begin{equation} \mathbb{E}_n(Z) = \sum_{k_1,\ldots,k_m \ge 1} \frac{1}{\sum_{j=1}^m 2^{-k_j}} \sum_{n_1+\ldots+n_m=n}\left( \begin{array}{c} n \\ n_1,\ldots,n_m\end{array} \right) \frac{1}{m^n} \prod_{j=1}^m \gamma_{n_j,k_j} \label{eq4} \end{equation} \] を満たす。ここで \(\gamma_{v,k}=(1-\frac{1}{2^k})^v-(1-\frac{1}{2^{k-1}})^v\) である。
…… \[ \begin{equation} \mathbb{E}_{\rho(\lambda)}(Z) = \sum_{k_1,\ldots,k_m\ge 1} \frac{1}{\sum_{j=1}^m 2^{-k_j}} \prod_{j=1}^m g\left(\frac{\lambda}{m2^{k_j}}\right) \label{eq5} \end{equation} \] ここで \(g(x)=e^{-x}-e^{-2x}\) である。
……
 2.2 Asymptotic analysis under the Poisson model
2.2 Asymptotic analysis under the Poisson model
……
命題 2. \(\alpha_m\) が (\(\ref{eq3}\)) のとき、ポアソン期待値 \(\mathbb{E}_{\rho(\lambda)}(Z)\) は \[ \begin{equation} \mathbb{E}_{\rho(\lambda)}(Z) \underset{\lambda\to\infty}{=} \frac{\lambda}{m} \left( \frac{1}{m\alpha_m} + \epsilon_m \left(\frac{\lambda}{m}\right) + o(1) \right) \label{eq6} \end{equation} \] を満たす。ここで \(m\ge 16\) のとき \(|\epsilon_m(t)| \lt 5\cdot 10^{-5}/m\) である。
……
 2.3 Analysis under the fixed-size model (depoissonization)
2.3 Analysis under the fixed-size model (depoissonization)
……
定理 (解析的デポアソン化). \(f(z) = e^{-z} \sum f_k z^k/k!\) を列 \((f_k)\) のポアソン生成関数とする。\(f(z)\) が全体であるとする。また、ある \(\theta \lt \frac{\pi}{2}\) および実数 \(\alpha \lt 1\) に対して円錐 \(S_\theta = \{z/z= re^{i\phi}, |\phi| \le \theta\}\) が存在し、\(|z|\to\infty\) として次の 2 つの条件が満たされると仮定する:
\(C_1\): \(z \in S_\theta\) に対して \(|f(z)|=O(|z|) が成り立つ。
\(C_2\): \(z \not\in S_\theta\) に対して \(|f(z)e^z| = O(e^{\alpha|z|})\) が成り立つ。
このとき \(f_n = f(n) + O(1)\) である。
この定理の使用は、ポアソン率 \(\lambda\equiv z\) が複素平面で変化することを許容した場合、ポアソン平均 (量 \(f(z)\)) を推定することと等しく、その場合、漸近的に固定サイズの推定量 (シーケンス \(f_n\)) に戻る方法が提供される。Mellin 手法は、このような方法を使用できるほど十分に堅牢であることが分かった。
命題 3. 固定のカーディナリティ \(n\) の多重集合に適用される HyperLogLog 指標 \(Z\) の平均値の期待値は、\(n\to\infty\) のとき漸近的に \[ \mathbb{E}_n(Z) = \mathbb{E}_{\rho(n)}(Z) + O(1) \] を満たす。
証明. ……
 3 Variance and other stories
3 Variance and other stories
 3.1 Valiance analysis
3.1 Valiance analysis
 3.2 Constants
3.2 Constants
 4 議論
4 議論
ここでは HyperLogLog アルゴリズム (Fig 3, Fig 4, Fig 5) の実装に関する最終的な考察と、それに伴う複雑さに関する考慮事項を示す。
| 1. | \( {\it Let} \ h : \mathcal{D} \to \{{\tt 0},{\tt 1}\}^{32} \) | // \(\mathcal{D}\) から 2 進数 32-bit ワードへのハッシュデータ |
| 2. | \( {\it Let} \ \rho(s) \) | // \(s\) の左端の 1-bit の位置: \(\rho({\tt 1}\cdots)=1\), \(\rho({\tt 0001}\cdots)=4\), \(\rho({\tt 0}^K)=K+1\) |
| 3. | \( {\bf define} \ \alpha_{16}=0.673; \alpha_{32}=0.697; \alpha_{64}=0.709; \alpha_m=0.7213/(1+1.079/m) \text{ for $m\gt 128$} \) | |
| 4. | \( {\bf Program} \ {\sf HyperLogLog}({\bf input} \ \mathcal{M}: \text{multiset of items from domain $\mathcal{D}$}) \) | |
| 5. | \( {\bf assume} \ m=2^b \text{ with } b \in [4..16] \) | |
| 6. | \( {\bf initialize} \text{ a collection of $m$ registers, $M[1],\ldots,M[m]$, to 0} \) | |
| 7. | \( {\bf for} \ v \in \mathcal{M} \ {\bf do} \) | |
| 8. | \( \hspace{12pt}{\bf set} \ x := h(x) \) | |
| 9. | \( \hspace{12pt}{\bf set} \ j = 1 + \langle x_1 x_2 \cdots x_b \rangle_2 \) | // \(x\) の最初の \(b\) ビットで決まる 2 進数アドレス |
| 10. | \( \hspace{12pt}{\bf set} \ w := x_{b+1} x_{b+2} \cdots \) | |
| 11. | \( \hspace{12pt}{\bf set} \ M[j] := \max(M[j], \rho(w)) \) | |
| 12. | \( {\bf compute} \ E := \alpha_m m^2 \cdot \left( \sum_{j=1}^m 2^{-M[j]} \right)^{-1} \) | // "生の" HyperLogLog 推定値 |
| 13. | \( {\bf if} \ E \le \frac{5}{2} m \ {\bf then} \) | |
| 14. | \( \hspace{12pt}{\bf let} \ \text{$V$ be the number of registers equal to $0$} \) | |
| 15. | \( \hspace{12pt}{\bf if} \ V \ne 0 \ {\bf then \ set} \ E^* := m \log(m/V) \ {\bf else \ set} \ E^* := E \) | // 小範囲補正 |
| 16. | \( {\bf if} \ E \le \frac{1}{30}2^{32} \ {\bf then} \) | |
| 17. | \( \hspace{12pt}{\bf set} \ E^* := E \) | // 中範囲 - 補正なし |
| 18. | \( {\bf if} \ E \gt \frac{1}{30} 2^{32} \ {\bf then} \) | |
| 19. | \( \hspace{12pt}{\bf set} \ E^* := -2^{32} \log(1 - E/2^{32}) \) | // 大範囲補正 |
| 20. | \( {\bf return} \ \text{典型的な相対誤差 $\pm1.04/\sqrt{m}$ でのカーディナリティ推定値 $E^*$} \) | |
HyperLogLog プログラム. ほとんどの実用的な使用条件に対応するためのプログラムを Fig 3 に示す。Fig 2 のアルゴリズムと比較して、初期化に関する 1 つの修正と、推定値に関する 2 つの最終的な補正が導入されている。
レジスタの初期化. Fig 2 のアルゴリズムではレジスタは \(-\infty\) で初期化される。これにより平均的なケースの表現が比較的単純になるという利点がある。式 (\(\ref{eq4}\)) と (\(\ref{eq5}\)) を参照。しかしその結果、アルゴリズムによって返される推定値 \(E\) はレジスタの 1 つが未処理のままになった時点で、つまり \(m\) 個のサブストリームが空になった時点で、値 0 を想定する。クーポンコレクター問題 (coupon collector problem) に関する既知の事実を踏まえると、これは \(n \ll m\log m\) のときに \(E=0\) となることが予想されることを意味し、アルゴリズムは小さなカーディナリティに対して大きな誤差を伴うことを意味する。Fig 3 のプログラムではレジスタの初期化を 0 に変更している。定理 1 の結論、すなはち推定値が漸近的に無偏の性質を持つという結論は、\(n \gg m\log m\) に達するとすべてのサブストリームが圧倒的確率で空ではなくなるため、このプログラムに依然として適用できる。この変更の利点は \(n\) が \(m\) の小さな倍数であっても使用可能な推定値を得られるようになったことである (この事実はポアソン近似によってさらに確認できる)。次に説明するように、\(n\) が非常に小さい値 (例えば \(n\) が定数または \(n=m\)) の場合にプログラムが提供する推定値は効率的に修正ができる。
小範囲補正. HyperLogLog プログラム (レジスタの初期化に関する上記 i の補正を含む) については、広範なシミュレーションにより、\(m\ge 16\) のときカーディナリティ値 \(n=\frac{5}{2}m\) のときに漸近状態が実質的に達成されることが実証されている (公称誤差 \(1.04/\sqrt{m}\) に本質的に影響を与えること無く検出可能なバイアスもない)。これに対して \(n\lt\frac{5}{2}m\) の場合に非線形なゆがみが生じ始める。極端な例としてレジスタを 0 に初期化した生のアルゴリズムでは、\(n=0\) の場合、常に推定値 \(\alpha_m m \doteq 0.7m\) が返される(!)。したがって \(E\) (つまり \(n\)) が \(m\) に対して比較的小さい場合は推定値に補正を加える必要がある。
この解決策は Whang ら [24] の Hit Counting アルゴリズムで既に利用されているランダムな割り当ての確率的な性質から得られる。このアルゴリズムの分析は [9, Sec. 4.3] で議論されている。\(n\) 個のボールが \(m\) 個のビンにランダムに投げ入れられたとする。よく知られているように空のビンの数は約 \(me^{-\mu}\) であり、\(\mu\) は \(n/m\) である。したがって合計 \(m\) 個のビンの中に \(V\) 個の空のビンが観測された場合、\(\mu\) は \(\log(m/V)\) に近いことが正当に予想される。(この推定値の品質は \(V\) の平均、分散、分布について正確な形式と漸近的な形式が分かっているため正確に分析することができる。[21] などを参照。) ここでビンは \(m\) 個の "部分多重集合" に関連するものであり、ビン \(j\) が空であることは対応するレジスタ \(M[j]\) が初期値 0 を保持しているということから分かる。この修正は Fig 3 のプログラムに組み込まれている。
大範囲補正. 範囲 \(1..N\) のカーディナリティで \(N\) が \(10^9\) のオーダーの場合、少なくとも \(L=32\) ビットでハッシュ化を行うべきである (\(2^{32}\doteq 4\cdot 10^9\))。しかしカーディナリティ \(n\) が \(2^L\) に近づく (またはそれを超える) とハッシュ衝突が起こりやすくなる。ランダムに選択されたハッシュ関数の場合、この効果は前の段で説明したタイプのボールとビンのモデルによってモデル化できる。この場合 \(m\) を \(2^L\) に置き換える。つまり HyperLogLog の量 \(E\) は異なるハッシュ値の数を推定するものであり、高い確率で \(2^L(1-e^{-\Lambda})\) である。ここで \(\Lambda=n/2^L\) である。この関係を反転すると近似式 \(n=-2^L \log(1-E/2^L)\) が得られ、これがプログラムで使用されている式である。
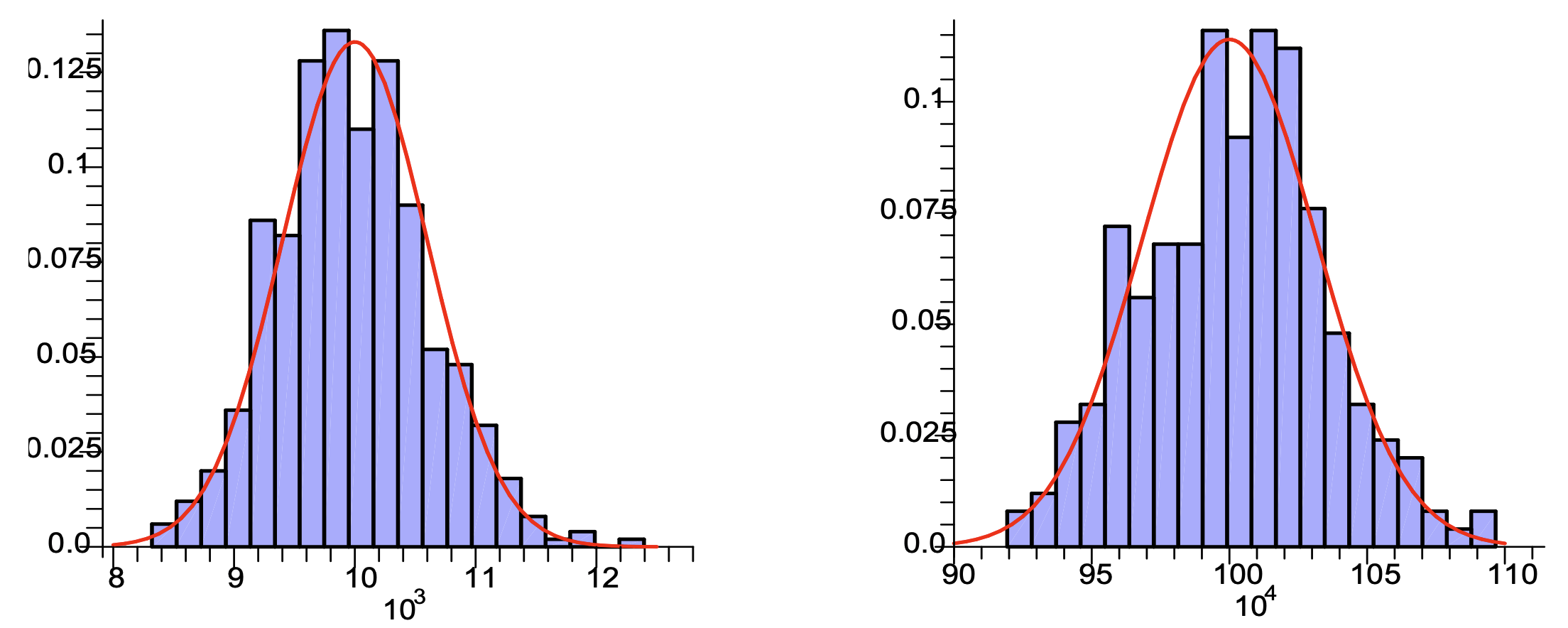
レジスタに関しては、その値は先験的に \(0..L+1-\log_2 m\) の範囲にある。32 ビットのハッシュ値でレジスタを格納するには 5 ビット ("ショートバイト") で十分である (もちろん一部の実装では標準の 8 ビットバイトを使用することもできる)。返される結果の品質については、平均化効果と中央極限定理により推定値はおおよそガウス分布に従うと予想される。この特性は Fig 4 (下) のシミュレーションによって十分に裏付けられている。したがって:
\(\sigma \approx 1.04/\sqrt{m}\) を標準誤差とする。HyperLogLog によって提供される推定値は、すべてのケースのそれぞれ 65%, 95%, 99% において、正確なカウント値の \(\sigma\), \(2\sigma\), \(3\sigma\) の範囲内に収まることが予想される。
実際には HyperLogLog プログラムは非常に効率的である。[10] の標準的な LogLog や [16] の MinCount と同様に、その実行時間はハッシュ関数の計算によって支配されているため、データの単純な走査 (例えば Unix コマンドの "wc -l" による単純な行末のカウント) よりも 3〜4 倍遅いだけである。
最適性の考察. 我々のタイトルで表現されている near-optimality は 2 つの事実の組み合わせによるものである。
明らかに、\(N\) の範囲まで \(\epsilon\)-近似カウントを維持するには \(\Omega(\log\log N)\) ビットが必要である。実際、カーディナリティは指数スケール \[ 1, (1+\epsilon), (1+\epsilon)^2, \cdots, (1+\epsilon)^L = N \] に配置する必要がありこれは \(\log_{(1+\epsilon)} N\) 区間で構成され、少なくとも \(\log_2 \log_{(1+\epsilon)}N\) ビットの情報量で表現する必要がある。
Chassing と Gérin [6] は順序統計に基づく幅広いアルゴリズムについて、達成可能な最高の精度は \(1/\sqrt{m}\) に近い値で下限が制限されることを示している。この結果に基づくと、おおよそ順序統計3を維持していると見なせる我々のアルゴリズムは、Chassaing-Gérin クラスの情報理論的最適値からわずか 4% 程度しか外れておらず、通常 3〜5 倍短いメモリユニットを使用している。
最後にまとめると、このアルゴリズムはコーディングが容易で効率的であり、特定の基準ではほぼ最適であることが証明されている。"現実の" データでは理論分析と非常に良く一致しているように見える。これは Pranav Kashyap が実施した広範なテスト (サンプルについては Fig 5 参照) によって最近確認された事実であり、同氏の貢献にここで感謝の意を表したい。このプログラムは非常に多様なデータコレクションに適用でき ("良好な" ハッシュ関数のみが必要)、適切な修正が加えられれば非常に小さいものから非常に大きいものまで、幅広いカーディナリティにもスムーズに対応できる。さらに、最適な並列化や分散化4が可能であり "スライディングウィンドウ" の使用 [7] にも適用できる。
全体として HyperLogLog は非常に実用的で多用途であり、分析予測にうまく適合している。
- 3実際には \([0,1]\)-数値の多重集合 \(S\) の対して、\(2^{-\max_S(\rho(x))}\) は最大でも 2 の係数までの \(\min(S)\) の近似値である。
- 4元もファイルを任意の部分ファイルに分割した場合、レジス立ちを収集し、コンポーネント事に最大値を求める演算を適用すれば十分である。
HyperLogLog プログラムによって生成された推定値の相対誤差の理想的多重集合上の変化を示す典型的な 4 つの実行のトレース。\(n \le N\) と \(\langle N,m\rangle\) のさまざまな値について: (左上) \(\langle 10^4,256\rangle\); (右上) \(\langle 10^8,1024\rangle\); (左下) \(\langle 10^8,1024\rangle\); (右下) \(\langle 10^7,65536\rangle\)。\(n\) の値は対数スケールでプロットされている。
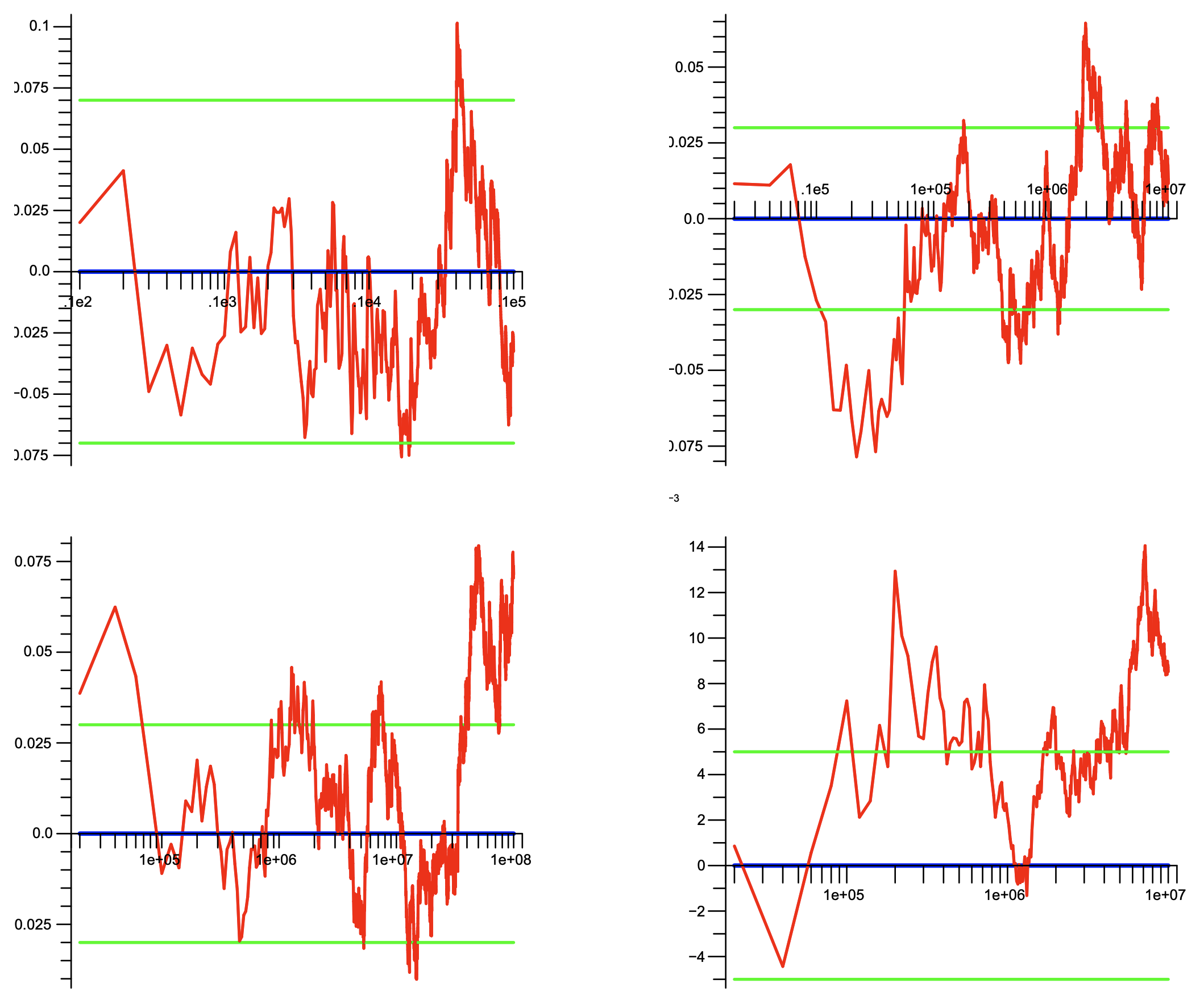
(上部と下部の水平線は予想される標準誤差を表しており、\(m=256\) に対して ±7%、\(m=1024\) の場合は ±3%、\(m=65535\) の場合は ±0.5% である。)
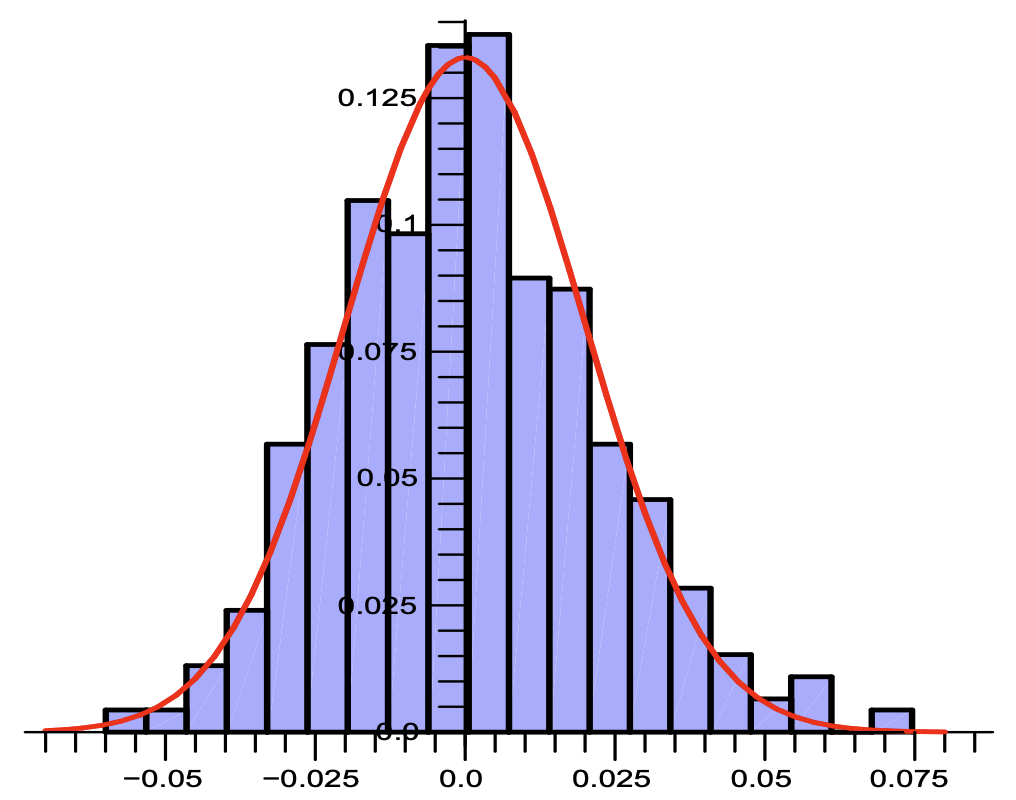
アルゴリズムによって生成された推定値の経験的ヒストグラム (それぞれ 500 回と 250 回のシミュレーションに基づく)と、ガウス曲線に基づく左図 \((n,m)=(10^4,256)\) または右図 \((n,m)=(10^6,1024)\) の近似適合。
 References
References
- ALON, N., MATIAS, Y., AND SZEGEDY, M. The space complexity of approximating the frequency moments. Journal of Computer and System Sciences 58, 1 (1999), 137–147.
- BAR-YOSSEF, Z., JAYRAM, T. S., KUMAR, R., SIVAKUMAR, D., AND TREVISAN, L. Counting distinct elements in a data stream. In Randomization and Approximation Techniques (RANDOM) (2002), J. D. P. Rolim and S. P. Vadhan, Eds., vol. 2483 of Lecture Notes in Computer Science, Springer, pp. 1–10. 6th International Workshop, RANDOM 2002, Cambridge, MA, USA, September 13-15, 2002, Proceedings.
- BECCHETTI, L., CASTILLO, C., DONATO, D., LEONARDI, S., AND BAEZA-YATES, R. Using rank propagation and probabilistic counting for link-based spam detection. In Proceedings of the Workshop on Web Mining and Web Usage Analysis (WebKDD) (2006), ACM Press.
- BRODER, A. Z. On the resemblance and containment of documents. In Compression and Complexity of Sequences (1997), IEEE Computer Society, pp. 21–29.
- BRODER, A. Z. Identifying and filtering near-duplicate documents. In Proceedings of Combinatorial Pattern Matching: 11th Annual Symposium, CPM 2000, Montreal, Canada (2000), R. Giancarlo and D. Sankoff, Eds., vol. 1848 of Lecture Notes in Computer Science, pp. 1–10.
- CHASSAING, P., AND GÉRIN, L. Efficient estimation of the cardinality of large data sets. In Proceedings of the 4th Colloquium on Mathematics and Computer Science, Nancy (2006), vol. AG of Discrete Mathematics & Theoretical Computer Science Proceedings, pp. 419–422. Full paper available at http://arxiv.org/abs/math.ST/0701347.
- DATAR, M., GIONIS, A., INDYK, P., AND MOTWANI, R. Maintaining stream statistics over sliding windows. SIAM Journal on Computing 31, 6 (2002), 1794–1813.
- DE BRUIJN, N. G. Asymptotic Methods in Analysis. Dover, 1981. A reprint of the third North Holland edition, 1970 (first edition, 1958).
- DURAND, M. Combinatoire analytique et algorithmique des ensembles de données. PhD thesis, École Polytechnique, France, 2004.
- DURAND, M., AND FLAJOLET, P. LOGLOG counting of large cardinalities. In Annual European Symposium on Algorithms (ESA03) (2003), G. Di Battista and U. Zwick, Eds., vol. 2832 of Lecture Notes in Computer Science, pp. 605–617.
- ESTAN, C., VARGHESE, G., AND FISK, M. Bitmap algorithms for counting active flows on high speed links. Technical Report CS2003-0738, UCSD, Mar. 2003. Available electronically. Summary in ACM SIGCOMM Computer Communication Review Volume 32 , Issue 3 (July 2002), p. 10.
- FLAJOLET, P. On adaptive sampling. xComputing 34 (1990), 391–400.
- FLAJOLET, P. Counting by coin tossings. In Proceedings of ASIAN’04 (Ninth Asian Computing Science Conference) (2004), M. Maher, Ed., vol. 3321 of Lecture Notes in Computer Science, pp. 1–12. (Text of Opening Keynote Address.).
- FLAJOLET, P., GOURDON, X., AND DUMAS, P. Mellin transforms and asymptotics: Harmonic sums. Theoretical Computer Science 144, 1–2 (June 1995), 3–58.
- FLAJOLET, P., AND MARTIN, G. N. Probabilistic counting algorithms for data base applications. Journal of Computer and System Sciences 31, 2 (Oct. 1985), 182–209.
- GIROIRE, F. Order statistics and estimating cardinalities of massive data sets. In 2005 International Conference on Analysis of Algorithms (2005), C. Martínez, Ed., vol. AD of Discrete Mathematics and Theoretical Computer Science Proceedings, pp. 157–166.
- GIROIRE, F. Directions to use probabilistic algorithms for cardinality for DNA analysis. Journées Ouvertes Biologie Informatique Mathématiques (JOBIM’06), 2006.
- GIROIRE, F. Réseaux, algorithmique et analyse combinatoire de grands ensembles. PhD thesis, Université Paris VI, 2006.
- JACQUET, P., AND SZPANKOWSKI, W. Analytical de-Poissonization and its applications. Theoretical Computer Science 201, 1-2 (1998), 1–62.
- KNUTH, D. E. The Art of Computer Programming, 2nd ed., vol. 3: Sorting and Searching. Addison-Wesley, 1998.
- KOLCHIN, V. F., SEVASTYANOV, B. A., AND CHISTYAKOV, V. P. Random Allocations. John Wiley and Sons, New York, 1978. Translated from the Russian original Slǔcajnye Razmeščeniya.
- PALMER, C., GIBBONS, P., AND FALOUTSOS, C. Data mining on large graphs. In Proceedings of the ACM International Conference on SIGKDD (2002), pp. 81–90.
- SZPANKOWSKI, W. Average-Case Analysis of Algorithms on Sequences. John Wiley, New York, 2001.
- WHANG, K.-Y., VANDER-ZANDEN, B., AND TAYLOR, H. A linear-time probabilistic counting algorithm for database applications. ACM Transactions on Database Systems 15, 2 (1990), 208–229.
翻訳抄
大規模データセットから要素のカーディナリティを推定するアルゴリズムである HyperLogLog に関する 2007 年の論文。HyperLogLog におけるカーディナリティとは distinct つまり「異なりの数」であり、集合論の文脈において「濃度」を意味するカーディナリティとは異なる点に注意。例えば多重集合 \(\{a,a,b,c,c,c\}\) の濃度 (集合論での cardinality) は 6 だが異なりの数 (HyperLogLog での cardinality) は 3 である。
- Philippe Flajolet, Éric Fusy, Olivier Gandouet, Frédéric Meunier. HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm. AofA: Analysis of Algorithms, Jun 2007, Juan les Pins, France. pp.137-156, ⟨10.46298/dmtcs.3545⟩. ⟨hal-00406166v2⟩