構造的アルゴリズム

論文翻訳: The Log-Structured Merge-Tree (LSM-Tree)

Takami Torao 1996年の論文 #LSMTree
  • このエントリーをはてなブックマークに追加
Patrick O'Neil 1 , Edward Cheng 2
Dieter Gawlick 3 , Elizabeth O'Neil 1
To be published: Acta Informatica

Abstract

高性能なトランザクションシステムアプリケーションは、通常、アクティビティトレースを提供するために履歴テーブルに行を挿入し、同時にトランザクションシステムはシステム回復のためのログレコードを生成する。どちらのタイプの情報生成も効率的なインデックス生成の恩恵を受けることができる。よく知られている例としては、特定のアカウントのアカウントアクティビティに関する履歴の効率的なクエリーをサポートするように変更した TPC-A ベンチマークアプリケーションがある。これには急速に拡大する履歴テーブルにアカウント ID によるインデックスを必要とする。しかし残念ながら B-Tree のような標準的なディスクベースのインデックス構造では、リアルタイムでこのようなインデックスを維持するためにトランザクションの I/O を実質的に 2 倍にし、システム全体のコストを最大 50% まで増加させる。リアルタイムインデックスを低コストで維持する方法が望ましいことは明らかである。LSM-Tree (Log-Structured Merge-Tree) は長期間にわたってレコードの挿入 (および削除) が頻繁に行われるファイルに対して、低コストのインデックスを提供するために設計されたディスクベースのデータ構造である。LSM-Tree はインデックス変更を延期しバッチ処理するアルゴリズムを使用して、マージソートを彷彿とさせる効率的な方法でメモリベースのコンポーネントから 1 つ以上のディスクコンポーネントにカスケードする。このプロセスの間、すべてのインデックス値はメモリコンポーネントまたはディスクコンポーネントのいずれかを介して (非常に短いロック期間を除き) 継続的に検索アクセスすることができる。このアルゴリズムは B-Tree のような従来のアクセス方法と比較し、ディスクアームを移動を大幅に削減し、従来のアクセス方法による挿入のためのディスクアームコストがストレージメディアコストを圧倒するような領域でのコストパフォーマンスを改善する。LSM-Tree のアプローチは挿入と削除の操作以外にも一般化される。しかし即時応答を必要とするインデックス検索では場合によって I/O 効率を低下させるため、エントリを取得する検索よりもインデックス挿入の方が一般的なアプリケーションでは LSM-Tree が最も有用である。セクション 6 の結論では、LSM-Tree アクセス方式におけるメモリとディスクコンポーネントのハイブリッド利用と、一般に理解されているディスクページをメモリにバッファリングするハイブリッド方式の利点を比較している。

Table of Contents

  1. Abstract
  2. 1. 導入
    1. 5 分ルール
  3. 2. 2-コンポーネント LSM-Tree アルゴリズム
    1. 2.1 2-コンポーネント LSM-Tree の成長過程
    2. 2.2 Find in the LSM-tree Index
    3. 2.3 Deletes, Updates and Long-Latency Finds in the LSM-tree
  4. 3. Cost-Performance and the Multi-Component LSM-Tree
    1. 3.1 The Disk Model
      1. Muti-page block I/O Advantage
    2. 3.2 Comparison of LSM-tree and B-tree I/O costs
      1. B-tree Insert Cost Formula.
      2. LSM-tree Insert Cost Formula.
      3. A Comparison of LSM-tree and B-tree Insert Costs
    3. 3.3 Multi-Component LSM-trees
    4. 3.4 SLM-trees: Component Sizes
      1. Minimizing Total Cost
  5. 4. Consistency and Recovery in the LSM-tree
    1. 4.1 Concurrency in the LSM-tree
    2. 4.2 Recover in the LSM-tree
  6. 5. Cost-Performance Comparison with Other Access Methods
    1. Time-Split B-tree
    2. MD/OD R-Tree
    3. Differential File
    4. Selective Deferred Text Index Updates
  7. 6. Conclusions and Suggested Extensions
    1. 6.1 Extensions of LSM-tree Application
  8. Acknowledgements
  9. References
  10. 翻訳抄
  1. 1Dept. of Math & C.S, UMass/Boston, Boston, MA 02125-3393, {poneil | eoneil}@cs.umb.edu
  2. 2Digital Equipment Corporation, Palo Alto, CA 94301, edwardc@pa.dec.com
  3. 3Oracle Corporation, Redwood Shores, CA, dgawlick@us.oracle.com

1. 導入

アクティビティフロー管理システムにおける長寿命トランザクションが商用利用可能になるにつれ ([10], [11], [12], [20], [24], [27]) トランザクションログ記録へのインデックス付きアクセスを提供する必要性が高まるだろう。従来のトランザクションログは中断と回復に重点を置いており、回復はバッチ化されたシーケンシャルリードで実行され、システムは時折トランザクションロールバックが発生する通常の処理において、比較的短期間の履歴を参照する必要があった。しかしシステムがより複雑なアクティビティを担当するようになると 1 つの長期的なアクティビティを構成するイベントの期間と数が増加し、何が完了したかをユーザに思い出させるために過去のトランザクションステップをリアルタイムで確認する必要性が生じることがある。同時に、システムが認識するアクティブなイベントの総数は、メモリコストの継続的な低下が予想されるにもかかわらず、現在アクティブなログを追跡するために使用されているメモリ常駐データ構造がもはや現実不可能なレベルまで増加する。膨大な数の過去のアクティビティログに関するクエリーに応答する必要性は、インデックス化されたログアクセスがますます重要となることを意味する。現在のトランザクションシステムにおいても総乳量の多い履歴テーブルに対するクエリーをサポートするためにインデックスを提供することには明らかな価値がある。ネットワーク、電子メール、およびその他のほぼトランザクショナルなシステムは、多くの場合、ホストシステムに悪影響を与える膨大なログを生成する。具体的でよく知られた例から始めるために次の例 1.1 および 1.2 で TPC-A ベンチマークを改良したものを検討する。この文書で提示する例は説明を簡単にするために特定の数値パラメータ値を扱っていることに注意。履歴テーブルとログの両方に時系列データが含まれるが、LSM-Tree のインデックスエントリは時間的なキー順序が同一であるとは想定されていないことにも注意。効率を向上するための唯一の前提は、検索レートに比べて更新レートが高いことである。

5 分ルール

次の 2 つの例はどちらも 5 分ルール [13] に基づいている。この基本的な結果は、ページ参照頻度が約 60 秒に 1 回を超える場合、メモリバッファ領域を購入してページをメモリに保持しディスク I/O を回復することでシステムコストを削減できるというものである。60 秒という時間は、1 秒あたり 1 回の I/O を提供するディスクアームの償却コストと、1 秒で償却される 4kB のディスクページをバッファリングするためのメモリコストの比率である。セクション 3 の表記法では、この比率は COSTP / COSTM をメガバイト単位のページサイズで割ったものである。ここでは単にディスクアクセスとメモリバッファをトレードオフしているだけだが、メモリ価格はディスク価格より早く低下することから、60 秒の時間幅は年々大きくなることが予想されることに注意。1987 年に 5 分と定義されたときよりも 1995 年の現在の方が短くなっている理由は、一部には技術的な理由 (バッファリングの想定が異なる) であり、一部はその後に非常に安価な大量生産ディスクが導入されたことに依るものである。

例 1.1. TPC-A ベンチマーク [26] で想定される、1 秒あたり 1000 県のトランザクションを実行するマルチユーザアプリケーションを考える (このレートはスケール可能だが以下は 1000TPS のみを考える)。各トランザクションは、任意に選択された 100 バイトの行 Balance カラムから金額 Delta を引くことでカラムを更新し、次に 1000 行の Branch テーブル、10,000 行の Teller テーブル、100,000,000 行の Account テーブルの 3 つのテーブルそれぞれから行を選ぶ。トランザクションは次に Account-ID, Branch-ID, Teller-ID, Delta, Timestamp を含む 50 バイトの行を History テーブルに書き込んでからコミットする。

ディスクとメモリのコストを予測する一般的な計算の結果、Account テーブルのページは今後数年間はメモリに常駐することは無く (参考文献 [6] 参照)、一方で Branch テーブルと Teller テーブルは現時点で完全にメモリ常駐になるはずである。与えられた仮定の下では Account テーブルの同一ディスクページへの繰り返し参照は約 2,500 秒間隔で行われ、5 分ルールによるバッファ常駐を正当化するために必要な頻度を遙かに下回る。ここで各トランザクションは約 2 回のディスク I/O を必要とし、1 回は目的の Account レコードを読み込むため (アクセスしたページが既にバッファ内にあるという希なケースは重要で無いと見なす)、もう 1 回はバッファに読み込み用のスペースを確保するために以前のダーティな Account ページを書き出すため (定常の動作に必要) である。従って 1000 TPS は毎秒約 2000 回の I/O に相当する。これは [13] で想定されているディスクアーム 1 秒あたり 25 I/O の公称レート 80 個のディスクアーム (アクチュエータ) を必要とする。それ以降の 8 年間 (1987 年から 1995 年まで) で速度は年間 10% 未満の割合で上昇し、公称レートは現在 1 秒あたり約 40 I/O、つまり 1 秒あたり 2000 I/O に対して 50 ディスクアームとなっている。TPC アプリケーションのディスクコストは [6] ではシステムの総コストの約半分と計算されているが IBM のメインフレームシステムではいくらか低くなる。しかしメモリと CPU のコストはディスクよりも急速に低下するため、I/O をサポートするためのコストは明らかにシステムの総コストの増加要因となっている。

例 1.2. 次に、挿入量の多い History テーブルのインデックスを検討し、このようなインデックスによって TPC アプリケーションのディスクコストが実質的に 2 倍になることを示す。History の「Timestamp と連結された Account-ID」(Acct-ID || Timestamp) のインデックスは、次のような最近のアカウントアクティビティに対する効率的なクエリーをサポートするために非常に重要である:

(1.1) Select * from History
    where History.Acct-ID = %custacctid
    and History.Timestamp > %custdatetime;

Acct-ID || Timestamp がインデックスが存在しない場合、このようなクエリーでは History テーブルのすべての行を直接検索する必要があるため現実的ではない。Acct-ID のインデックスのみでもほとんどの利点が得られるが Timestamp が省略されても後に続くコストの考慮は変わらないため、ここではより有用な連結インデックスを仮定する。このようなセカンダリ B-Tree インデックスをリアルタイムで維持するにはどのようなリソースが必要だろうか。B-Tree のエントリは毎秒 1000 件生成され、20 日間の累積機関、1 日 8 時間、16 バイトのインデックスエントリを想定すると、9.2GB のディスクに 576,000,000 エントリ、またインデックスリーフページで約 230 万ページが必要となる。トランザクションの Acct-ID 値はランダムに選択されるため、各トランザクションではこのインデックスから少なくとも 1 ページを読み込む必要があり、定常状態ではページの書き込みも必要となる。5 分ルールではこれらのインデックスページはバッファに常駐しない (ディスクページは約 2300 秒間隔で読み取られる) ため、すべての I/O はディスクに対して行われる。既にアカウントテーブルの更新に必要な 2000 I/O に加えてこの毎秒 2000 の I/O を追加するには、さらに 50 本のディスクアームを追加購入する必要がありディスク要件は 2 倍になる。この考えは、ログファイルのインデックスを 20 日間だけ維持するために必要な削除は、利用が少ない時間帯にバッチジョブとして実行できると楽観的に想定している。

履歴ファイルの Acct-ID || Timestamp インデックスに B-Tree を考慮したのは、それが商用システムで使用される最も一般的なディスクスペースのアクセス方法であり、実際、古典的では一貫して優れた I/O コスト・性能が得られるディスクインデックス構造は無いためである。この結論に至った考察についてはセクション 5 で述べる。

この論文で紹介する LSM-Tree のアクセス方法は、ディスクアームの使用を大幅に減らして Account-ID || Timestamp インデックスの頻繁な頻繁なインデックス挿入を実行できるためコストが桁違いに低くなる。LSM-Tree はインデックス変更を延期 (defer) しバッチ処理 (batch) するアルゴリズムを使用する、マージソートを彷彿とさせる特に効率的な方法で変更をディスクに移行する。セクション 5 で説明するように、インデックスエントリの配置を最終的なディスク位置まで延期する機能は基本的に重要であり、一般的な LSM-Tree ではこのような延期された配置がカスケード状に連続している。LSM-Tree 構造は削除、更新、および長い待ち時間 (long latency) の検索操作など、インデックス作成の他の操作も同じ遅延効率でサポートする。即時の応答を必要とする検索のみが比較的コストの高いままである。LSM-Tree が効率的に使用される主な領域は、例 1.2 のような検索が挿入よりもはるかに少ない頻度で行われるアプリケーションである (ほとんどの人は、小切手を書いたり預金をしたりするのと同じくらいの頻度で最近のアカウントアクティビティを尋ねることはない)。このような状況ではインデックス挿入のコストを削減することが最も重要である。同時に、すべてのレコードを逐次検索することは問題外であるため、頻繁な検索アクセスを行うために何らかのインデックスを維持する必要がある。

この論文の計画は次の通り。セクション 2 では 2-コンポーネント LSM-Tree アルゴリズムを紹介する。セクション 3 では LSM-Tree の性能を分析し、マルチコンポーネント LSM-Tree の動機づけを説明する。セクション 4 では LSM-Tree の平行性と回復性の概念を概説する。セクション 5 では競合するアクセス方法とその性能について検討する。セクション 6 の結論では LSM-Tree のいくつかの意味を評価し拡張のための多くの提案を示す。

2. 2-コンポーネント LSM-Tree アルゴリズム

LSM-Tree は 2 つ以上のツリー状のコンポーネントデータ構造で構成される。このセクションでは単純な 2 つのコンポーネントでのケースを扱う。以下では例 1.2 のように LSM-Tree が History テーブルの行をインデックス付けしていると仮定する。以下の Figure 2.1 参照。

2-コンポーネント LSM-Tree には C0 ツリー (または C0 コンポーネント) と呼ばれる完全にメモリ常駐の小さなコンポーネントと、C1 ツリー (または C1 コンポーネント) と呼ばれるディスク常駐の大きなコンポーネントがある。C1 コンポーネントはディスク常駐だが、C1 内の頻繁に参照されるページノードは通常通りメモリバッファに残る (バッファは図示されていない) ため、C1 の人気上位ディレクトリノードはメモリ常駐であることが期待できる。

Figure 2.1. 2-コンポーネント LSM-Tree の概略図。

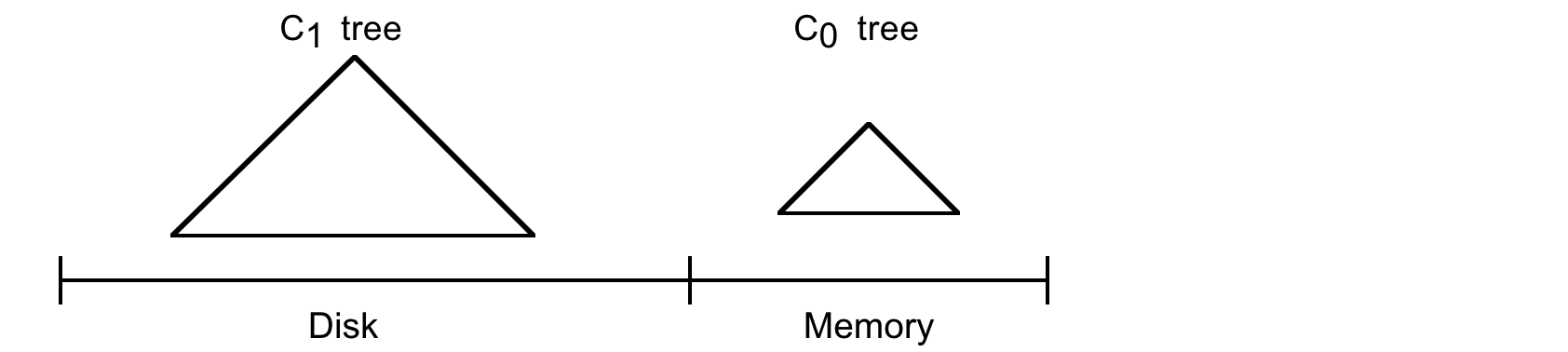
新しい History 行が生成されるたびに、まず、この挿入を回復するためのログレコードが通常の方法で逐次ログファイルに書き込まれる。次に History 行のインデックスエントリがメモリ常駐の C0 ツリーに挿入され、その後にディスク上の C1 ツリーに移行する。インデックスエントリの検索は、最初に C0 で検索して次に C1 で検索する。C0 ツリーのエントリがディスク常駐の C1 `ツリーに移行するまでにはある程度の待ち時間 (遅延) があり、これはクラッシュ前にディスクに書き込まれなかったインデックスエントリの回復の必要性を示唆している。回復についてはセクション 4 で説明するが、ここでは History 行の新規挿入を回復できるログレコードを論理ログとして扱うことだけを述べておく。回復中は、挿入された History 行を再構築し、同時に C0 の失われた内容を取り戻すためにこれらの行のインデックスに必要なエントリを再作成することができる。

インデックスエントリをメモリ常駐の C0 ツリーに挿入する操作には I/O コストがかからない。ただし C0 コンポーネントを格納するメモリ容量のコストはディスクに比べて高く、このためサイズが制限される。エントリを低コストのディスクメディアにある C1 ツリーに移行する効率的な方法が必要である。これを実現するには、挿入の結果として C0 ツリーが割り当てられた最大値に近いしきい値サイズに達するたび、継続的なローリングマージ (rolling merge) プロセスが C0 ツリーからエントリの連続セグメントを削除してディスク上の C1 ツリーにマージする。Figure 2.2 にローリングマージプロセスの概念図を示す。

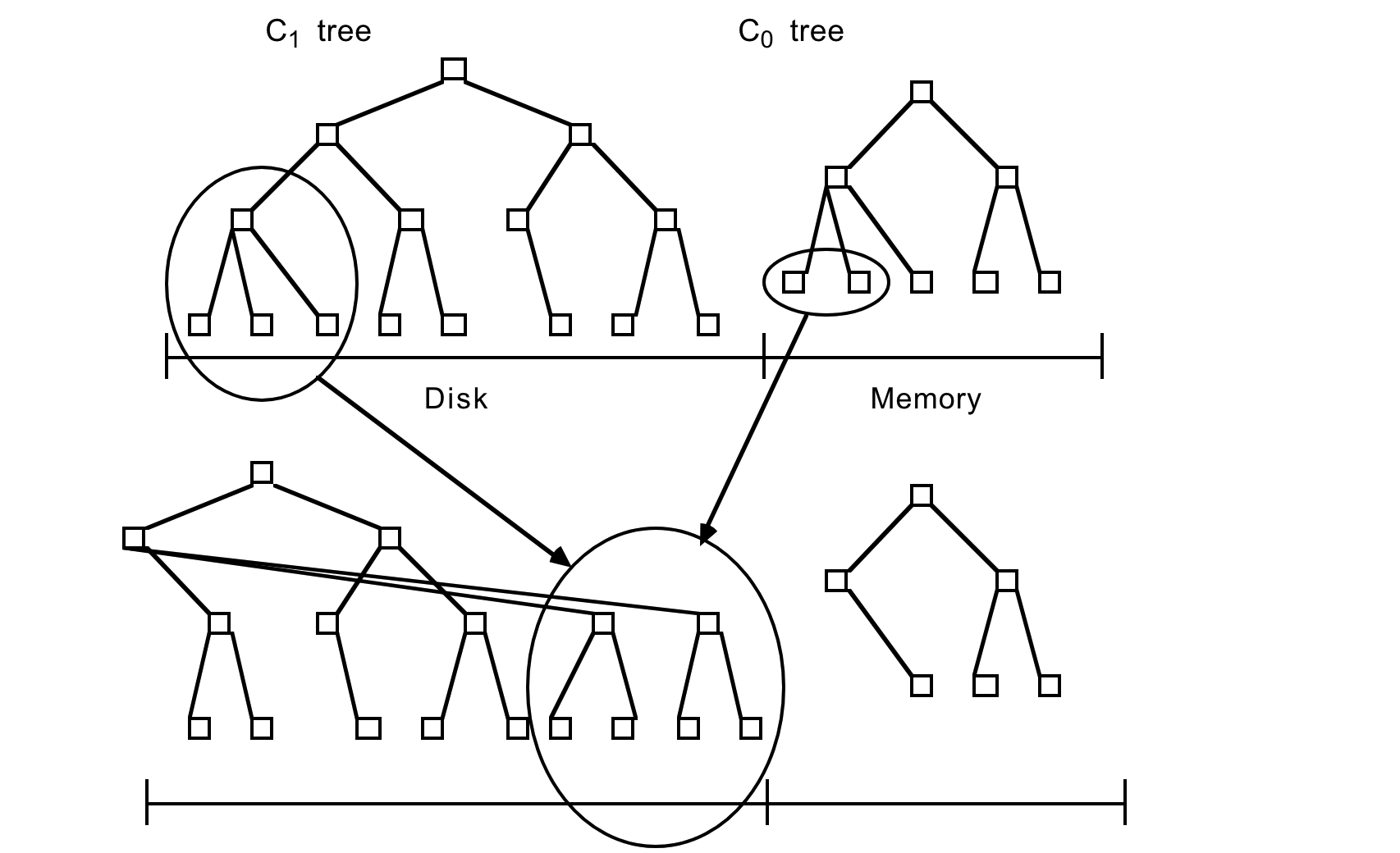
Figure 2.2. 結果をディスクに書き戻すローリングマージステップの概念図

C1 ツリーは B-Tree と同様のディレクトリ構造を持つが、シーケンシャルディスクアクセスに最適化されており、ノードは 100% 満たされ、ルート以下の各レベルのシングルページノードのシーケンスは効率的なアーム使用のために連続した複数ページディスクブロックにまとめられている。この最適化は SB-Tree [21] でも使用されている。複数ページブロック I/O はローリングマージ中と長距離 (long range) 検索に使用され、単一ページノードはバッファリング要件を最小化するためにインデックス付き検索のマッチングに使用される。256kB の複数ページブロックサイズはルート以下のノードを含むように想定されている。ルートノードは定義により常に 1 ページである。

ローリングマージは一連のマージステップで実行される。C1 ツリーのリーフノードを含む複数ページのブロックを読み取ると C1 バッファ内のエントリの範囲が常駐する。その後、各マージステップでは、このブロックにバッファされている C1 ツリーのディスクページサイズのリーフノードを読み取り、リーフノードのエントリを C0 ツリーのリーフレベルから取得したエントリとマージすることで C0 のサイズを縮小し、C1 ツリーの新しくマージされたリーフノードを作成する。

マージ前の古い C1 ツリーノードを含むバッファリングされたマルチページブロックは空ブロック (emptying block) と呼ばれ、新しいリーフノードは充填ブロック (filling block) と呼ばれる別のバッファリングされたマルチページブロックに書き込まれる。この充填ブロックが C1 の新しくマージされたリーフノートでいっぱいになると、ブロックは新しい空き領域に書き込まれる。Figure 2.2 では、マージされた結果を含む新しいマルチページブロックは以前のノードの右側にあるように示されている。後続のマージステップでは C0 および C1 コンポーネントの増加するインデックス値セグメントをまとめ、最大値に達するとローリングマージが最小値から再び開始される。

新しくマージされたブロックは新しいディスク位置に書き込まれるため、古いブロックは上書きされずクラッシュした場合のリカバリに利用できる。メモリにバッファリングされた C1 の親ディレクトリノードもこの新しいリーフ構造を反映するように更新されるが、通常は I/O を最小限に抑えるためにバッファ内に長時間残る。C1 コンポーネントの古いリーフノードはマージステップの完了後に無効化され C1 ディレクトリから削除される。一般に、古いリーフノードが空になったタイミングでマージステップによって新しいノードが生成される可能性は低いため、各マージステップの後にはマージされた C1 コンポーネントのリーフレベルエントリが残る。一般に、充填ブロックが新しくマージされたノードでいっぱいになると、縮小ブロックにエントリを含む多数のノードが存在するため、同じ考慮点はマルチページのブロックにも当てはまる。これらの残りのエントリは更新されたディレクトリノード情報と同様にディスクに書き込まれることなくしばらくブロックメモリバッファに残る。マージステップ中の並行性と、クラッシュ時に失われたメモリからのリカバリについてはセクション 4 で詳しく説明する。リカバリ時の再構築時間を短縮するために、マージプロセスのチェックポイントが定期的に作成され、バッファリングされたすべての情報がディスクに強制的に書き込まれる。

2.1 2-コンポーネント LSM-Tree の成長過程

LSM-Tree の成長初期からその変容をたどるために、まずメモリ上の C0 ツリーコンポーネントへの最初の挿入から始めよう。C1 ツリーとは異なり C0 ツリーは B ツリーのような構造を持つことは想定されていない。まず、ノードは任意のサイズにすることができる。C0 ツリーはディスク上に置かれることがないため、ディスクページサイズのノードにこだわる必要はなく、深さを最小限に抑えるために CPU 効率を犠牲にする必要はない。したがって (2-3) ツリーや AVL ツリー (例えば [1] などで説明されている) は C0 ツリーの代替構造として考えられる。成長中の C0 ツリーがしきい値サイズに達すると、左端のエントリシーケンスが C0 ツリーから削除され (これは一度に 1 つのエントリでは無く、効率的なバッチ方式で行う必要がある)、100% フルパックされた C1 ツリーのリーフノードに再編成される。連続するリーフノードは、ブロックがいっぱいになるまでバッファ常駐の複数ページブロックの初期ページに左から右に配置される。その後、このブロックはディスクに書き出され、C1 ツリーのディスク常駐リーフレベルの最初の部分になる。連続するリーフノードが追加されるにつれて、C1 ツリーのディレクトリノード構造がメモリバッファに作成される。詳細は以下で説明する。

C0 のしきい値サイズがしきい値を超えないように、C1 ツリーのリーフレベルの連続する複数ページブロックは、増え続けるキーシーケンスの順序でディスクに書き出される。上位レベルの C1 ツリーのディレクトリノードは、合計メモリとディスクアームコストの観点からより適切な個別の複数ページブロックバッファに保持されるか単一ページバッファに保持される。これらのディレクトリノードのエントリには B ツリーのように下位の個々の単一ページノードへのアクセスを導くセパレータが含まれる。その目的は、単一ページインデックスノードのパスに沿ってリーフレベルまで効率的な完全一致アクセスを提供し、そのような場合には複数ページブロックの読み取りを回避して、メモリバッファ要件を最小限に抑えることである。したがって、ローリングマージまたは長距離検索の場合は複数ページブロックの読み取りと書き込みを行い、インデックス検索 (完全一致) アクセスの場合は単一ページノードの読み取りと書き込みを行う。このような二項対立をサポートするやや異なるアーキテクチャが [21] で紹介されている。C1 ディレクトリノードの部分的にいっぱいになった複数ページブロックは、通常、一連のリーフノードブロックが書き出される間、バッファに残すことができる。C1 ディレクトリノードは次の場合にディスク上の新しい位置に強制的に移動される:

  • ディレクトリノードを含む複数ページブロックバッファがいっぱいになる

  • ルートノードが分割され、C1 ツリーの深さが増加する (深さが 2 を超える)

  • チェックポイントが実行される

最初のケースではいっぱいになった 1 つの複数ページブロックがディスクに書き出される。後の 2 つのケースでは、すべての複数ページブロックバッファとディレクトリノードバッファがディスクにフラッシュされる。

C0 ツリーの右端の葉エントリが初めて C1 ツリーに書き出されたあと、2 つのツリーの左端から処理が最初からやり直される。ただし、この時点とそれ以降のパスでは C1 ツリーの複数ページにわたる葉レベルブロックをバッファに読み込み、C0 ツリーのエントリとマージする必要がある。これにより C1 の新しい複数ページのはブロックが生成されディスクに書き込まれる。

マージが開始すると状況はより複雑になる。2 つのコンポーネントから成る LSM-tree におけるローリングマージプロセスは、概念的なカーソルが C0 ツリーと C1 ツリーの等しいキー値を量子化されたステップでゆっくりと循環し、インデックスデータを C0 ツリーからディスク上の C1 ツリーに描画してゆくものと考えることができる。ローリングマージカーソルは C1 ツリーの葉レベルと、各上位ディレクトリレベルとに位置する。各レベルでは、C1 ツリーの現在マージ中のすべてのマルチページブロックは一般的に 2 つのブロックに分割される。

2.2 Find in the LSM-tree Index

2.3 Deletes, Updates and Long-Latency Finds in the LSM-tree

3. Cost-Performance and the Multi-Component LSM-Tree

3.1 The Disk Model

Muti-page block I/O Advantage

3.2 Comparison of LSM-tree and B-tree I/O costs

B-tree Insert Cost Formula.

LSM-tree Insert Cost Formula.

A Comparison of LSM-tree and B-tree Insert Costs

3.3 Multi-Component LSM-trees

3.4 SLM-trees: Component Sizes

Minimizing Total Cost

4. Consistency and Recovery in the LSM-tree

4.1 Concurrency in the LSM-tree

4.2 Recover in the LSM-tree

5. Cost-Performance Comparison with Other Access Methods

Time-Split B-tree

MD/OD R-Tree

Differential File

Selective Deferred Text Index Updates

6. Conclusions and Suggested Extensions

6.1 Extensions of LSM-tree Application

Acknowledgements

References

  1. Alfred V. Aho, John E. Hopcroft, and Jeffrey D. Ullman, "The Design and Analysis of Computer Algorithms", Addison-Wesley.
  2. Anon et al., "A Measure of Transaction Processing Power", Readings in Database Systems, edited by Michael Stonebraker, pp 300-312, Morgan Kaufmann, 1988.
  3. R. Bayer and M Schkolnick, "Concurrency of Operations on B-Trees", Readings in Database Systems, edited by Michael Stonebraker, pp 129-139, Morgan Kaufmann 1988.
  4. P. A. Bernstein, V. Hadzilacos, and N. Goodman, "Concurrency Control and Recovery in Database Systems", Addison-Wesley, 1987.
  5. D. Comer, "The Ubiquitous B-tree", Comput. Surv. 11, (1979), pp 121-137.
  6. George Copeland, Tom Keller, and Marc Smith, "Database Buffer and Disk Configuring and the Battle of the Bottlenecks", Proc. 4th International Workshop on High Performance Transaction Systems, September 1991.
  7. P. Dadam, V. Lum, U. Praedel, G. Shlageter, "Selective Deferred Index Maintenance &Concurrency Control in Integrated Information Systems," Proceedings of the Eleventh International VLDB Conference, August 1985, pp. 142-150.
  8. Dean S. Daniels, Alfred Z. Spector and Dean S. Thompson, "Distributed Logging for Transaction Processing", ACM SIGMOD Transactions, 1987, pp. 82-96.
  9. R. Fagin, J. Nievergelt, N. Pippenger and H.R. Strong, Extendible Hashing — A Fast Access Method for Dynamic Files, ACM Trans. on Database Systems, V 4, N 3 (1979), pp 315-344
  10. H. Garcia-Molina, D. Gawlick, J. Klein, K. Kleissner and K. Salem, "Coordinating MultiTransactional Activities", Princeton University Report, CS-TR-247-90, February 1990.
  11. Hector Garcia-Molina and Kenneth Salem, "Sagas", ACM SIGMOD Transactions, May 1987, pp. 249-259.
  12. Hector Garcia-Molina, "Modelling Long-Running Activities as Nested Sagas", IEEE Data Engineering, v 14, No 1 (March 1991), pp. 14-18.
  13. Jim Gray and Franco Putzolu, "The Five Minute Rule for Trading Memory for Disk Accesses and The 10 Byte Rule for Trading Memory for CPU Time", Proceedings of the 1987 ACM SIGMOD Conference, pp 395-398.
  14. Jim Gray and Andreas Reuter, "Transaction Processing, Concepts and Techniques", Morgan Kaufmann 1992.
  15. Curtis P. Kolovson and Michael Stonebraker, "Indexing Techniques for Historical Databases", Proceedings of the 1989 IEEE Data Engineering Conference, pp 138-147.
  16. Lomet, D.B.: A Simple Bounded Disorder File Organization with Good Performance, ACM Trans. on Database Systems, V 13, N 4 (1988), pp 525-551
  17. David Lomet and Betty Salzberg, "Access Methods for Multiversion Data", Proceedings of the 1989 ACM SIGMOD Conference, pp 315-323.
  18. David Lomet and Betty Salzberg, "The Performance of a Multiversion Access Method", Proceedings of the 1990 ACM SIGMOD Conference, pp 353-363.
  19. Patrick O'Neil, Edward Cheng, Dieter Gawlick, and Elizabeth O'Neil, "The Log-Structured Merge-Tree (LSM-tree)", UMass/Boston Math & CS Dept Technical Report, 91-6, November, 1991.
  20. Patrick E. O'Neil, "The Escrow Transactional Method", TODS, v 11, No 4 (December 1986), pp. 405-430.
  21. Patrick E. O'Neil, "The SB-tree: An index-sequential structure for high-performance sequential access", Acta Informatica 29, 241-265 (1992).
  22. Patrick O'Neil and Gerhard Weikum, "A Log-Structured History Data Access Method (LHAM)," Presented at the Fifth International Workshop on High-Performance Transaction Systems, September 1993.
  23. Mendel Rosenblum and John K. Ousterhout, "The Design and Implementation of a Log Structured File System", ACM Trans. on Comp. Sys., v 10, no 1 (February 1992), pp 26-52.
  24. A. Reuter, "Contracts: A Means for Controlling System Activities Beyond Transactional Boundaries", Proc. 3rd International Workshop on High Performance Transaction Systems, September 1989.
  25. Dennis G. Severance and Guy M. Lohman, "Differential Files: Their Application to the Maintenance of Large Databases", ACM Trans. on Database Systems, V 1, N 3 (Sept. 1976), pp 256-267.
  26. Transaction Processing Performance Council (TPC), "TPC BENCHMARK A Standard Specification", The Performance Handbook: for Database and Transaction Processing Systems, Morgan Kauffman 1991.
  27. Helmut Wächter, "ConTracts: A Means for Improving Reliability in Distributed Computing", IEEE Spring CompCon 91.
  28. Gerhard Weikum, "Principles and Realization Strategies for Multilevel Transaction Management", ACM Trans. on Database Systems, V 16, N 1 (March 1991), pp 132-180.
  29. Wodnicki, J.M. and Kurtz, S.C.: GPD Performance Evaluation Lab Database 2 Version 2 Utility Analysis, IBM Document Number GG09-1031-0, September 28, 1989.

翻訳抄

メモリ内のデータを定期的にストレージ上の大規模構造にマージすることで高い書き込みスループットと効率的なクエリー処理を実現するデータ構造である LSM-Tree に関する 1996 年の論文。

  1. O’NEIL, Patrick, Edward Cheng, Dieter Gawlick, Elizabeth O'Neil. The log-structured merge-tree (LSM-tree). Acta Informatica, 1996, 33: 351-385.