Slate: Stratified Hash Tree
A machine-translated English version is available.
 前書き
前書き
Slate (Stratified Hash Tree) は非対称の Merkle ツリーを持つ追加専用のログ構造 (列構造) データストアです。データセットが短時間で大きく増加することが予想され、最近追加されたデータへ頻繁にアクセスがあり、2 つのログの差異 (分岐点) を素早く見つける必要のあるアプリケーションで役に立ちます。このデータ構造の設計における核心的要件は以下の 3 点です:
時間的局所性の原理に基づき、最近アクセスされたデータに対する I/O 操作を効率化する構造を持つ。
分散環境におけるトランザクションログのような複数のデータ列を比較し、その差異や分岐位置を高速に特定できる。
永続的データ構造として過去のすべてのバージョンを維持する。
この構造の本質はデータの追加が可能なハッシュツリー (Merkle ツリー) であり、一般的なハッシュツリーと同様に小さなデータ片を用いてデータの破損や改ざんを検証することができます。
この文書の内容は、該当するアルゴリズムに関する論文や書籍が見つけられなかったため、今のところ個人的な研究です。要素の追加によりノードの積層が成長してゆく構造的特徴から、この構造を Stratified Hash Tree (層様のハッシュツリー) と名付けています。
具体的な実装は https://github.com/torao/slate を参照してください。
Table of Contents
- 前書き
- 概要
- 1. 導入
- 2. 関連研究
- 3. 予備知識と定義
- 4. Slate データ構造
- 5. 操作とアルゴリズム
- 6. 複雑性の解析
- 7. 実装上の考慮
- 8. 実験的評価
- 9. アプリケーション
- 10. 議論
- 11. 結論
- References
 概要
概要
1.  導入
導入
Slate または Stratified Hash Tree (層様ハッシュツリー) は現実的な二次記憶装置に対して追記効率の良い構造を持つ部分的永続性データ構造 (partial persistent data structure) のハッシュツリー (Merkle ツリー) である。分散トランザクションログやブロックチェーンのように単一のシーケンス値 \(i\) によってデータを特定する、差異検出や分岐検出といった検証機能が必要なリスト構造に向いている。このデータ構造の直列化形式は非常にシンプルであり、SSD のような二次記憶装置上のファイル (ブロックデバイス) で効率的に表現することができる。データの追加操作はファイルへの単一の追記のみで完結するため非常に高速でありながら、木構造の永続性により読み取り操作とは競合しない。
Slate は葉ノードの追加により木構造が内包する完全二分木の部分構造を連結することによって成長する。したがって、Slate は常に完全二分木1 (perfect binary tree) ではないが、大半のノードが完全二分木に含まれており、木構造全体が完全二分木に近い特性を持っている。Figure 1 に示す図は Slate に 1 から 16 までのデータを追加するときの概念上の木構造の成長と、その直列化された形式を示している。
Figure 1 が示すように、Slate の直列化表現は追加のみの操作であることからファイル操作に対して高速である。また、任意の時点の木構造を完全な履歴として保持していることから、過去のある時点を基準としたデータ要求であっても正しいハッシュツリーで応答することができ、またロールバック操作と末尾置換操作も容易である。これらの操作をサポートする場合、Slate は純粋な append-only ではなくなるが、操作の大部分が追記であることを前提に設計されている。この意味で「追記最適化」という表現を用いる。
Slate が取り組む目的は「追記可能な大規模データ列に対する接頭辞マッチングと修復」である。この目的を達成するために Slate は以下の特徴を持つ。
Persistent append-based growth list with verifiable hash tree. Slate はハッシュツリーとして管理されるデータ構造である。時系列データのように高頻度の追加が行われる用途に最適化されており、データ構造レベルで部分的永続性 (partial persistent) である。通常のハッシュツリーと同様に、データの差異や破損、改ざんの有無を検出したり、またその位置や履歴分岐点を特定するために使用できる。
Append-optimized serialization with history revision support. ファイルのようなブロックデバイスに対する直列化形式をサポートし、特に追記に最適化されている。また、あるバージョンへのロールバック (切り詰め; truncate) と、それ以降を新しく追加する後方置換 (suffix replacement) 操作をサポートする (データ構造は永続的だが直列化形式はこのような変更の可能性がある点に注意)。
Multi-versioned data structure. この木構造は永続的であり、過去の構造の完全な履歴が保存されている。このためデータの追加によってツリーが成長したとしても過去の任意の時点の木構造を再現することができる。必要に応じて過去の特定のバージョンへの巻き戻し、そこから再開することができる。
Assign efficiency to more recent data. Slate の直列化形式は、より最近追加されたデータのアクセス効率が高くなるような局所性を持つように設計されている。最も最新のデータは \(O(1)\) の I/O 操作 (seek + read) でアクセスでき、最も古いデータ、つまり最悪ケースであっても \(O(\log n)\) の I/O 操作でアクセスできる。これは、最近追加されたデータの方が古いデータより頻繁にアクセスされるという現実的な特性に適合している。
Strength of safety over time. 認証パスのレベル (ルートノードからの距離) を安全性の強度と考えたとき、ハッシュツリーとしての安全性は長期間存在する要素と新しく追加された要素とで非対称的である。ある要素の強度は、別の要素が追加されるたびに対数で増加し、全体が完全二分木となったときすべての要素が通常のハッシュ木と同等の信頼性を持る。これはブロックの追加によって過去のブロックの信頼性 (確定性) が増すブロックチェーンと類似した特性である。
Slate の基本的な操作は追加 (append) と取得 (get) である。拡張として範囲取得 (scan) がある。これらの操作のみに限り直列化形式も永続的で並行読み取りが容易に実装できる。オプションとして truncate と suffix replacement が可能である。delete はハッシュ値のみを残して論理削除を行うことができるが、そのハッシュ値の信憑を検証する手段が失われる。
- 1この文書での完全二分木とは、すべての中間ノードがちょうど 2 つの子を持ち、すべての葉ノードがルートノードから等しい距離を持つ木構造を意味する。
2.  関連研究
関連研究
Slate は複数の確立された研究領域の概念を統合した新しいデータ構造である。これは、基盤領域として、永続データ構造、ハッシュベースの完全性検証、層様データの局所性を引用し、その応用領域として分散バージョン管理システムは実用的な同期要件と解決手法を明らかにしている。
本セクションでは、これらの各研究領域における Slate の理論的位置付けを明確にし、既存手法との比較を通じて本研究の独自性と貢献を示す。
2.1.  ハッシュベースの改ざん証跡可能な追記型ログシステム
ハッシュベースの改ざん証跡可能な追記型ログシステム
ハッシュ関数と木構造を用いたデータの完全性の保証は Merkle [6] によって公開鍵暗号システムのプロトコルとして最初に提案された。これは Merkle ツリーと呼ばれ、葉ノードにデータのハッシュ値を配置し、中間ノードに子ノードのハッシュ値を再帰的に格納することで、効率的な完全性検証を可能にする。この基本構造は、後にデジタル署名システム [7] や様々な分散システムで広く採用されることとなった。
Haber と Stornetta によるデジタル文書タイムスタンプの研究 [Haber 1990] では、文書のハッシュ値を時系列で連鎖させることで文書の存在時刻を証明可能にした。この手法は Bayer ら [Bayer 1992] によってハッシュツリーベースの改良が加えられ、複数文書の効率的なタイムスタンプが実現された。
改ざん証跡可能な追記型ログシステムとしては Crosby と Wallach が効率的な増分と所属を証明する追記型の Merkle ツリーである History Tree [Crosby 2009] を提案した。History Tree は時間的順序付けされた append-only 木構造として優れており、実際、その変種である Google の Certificate Transparency (CT) [CT 2013] は History Tree をベースに現在 Web PKI において広く実用化されている公開監査可能な証明書ログを実現している。特に、CT の木構造とその成長過程は本文書で提案する Slate とよく似た構造を持つ。両者は左から右へ葉ノードを順次追加し、一過性ノードによる完全二分木の連結を通じて上位レベルのノードを段階的に構築するという共通の木成長パターンを採用している。しかし、CT が証明書発行の監視と検証に焦点を当てているのに対し、本文書の Slate は分散システムにおける効率的な追記操作と差分検出という異なる問題に取り組んでいる。具体的には、異なる更新頻度を持つ複数のデータ列間での効率的な差分検出や、ツリーの直列化表現とデータ局所性、時間的最適化については議論されていない。
ハッシュツリーは分散システムや P2P 環境でレプリカのアンチエントロピーのためにも使われている。改ざん証跡可能な追記型ログシステムはブロックチェーン技術の発達と共に注目を集め、Ethereum の Merkle Patricia Tree [Wood 2014]、IPFS の Merkle DAG [Benet 2014] など、用途に適合する様々な変種が開発された。Boodman と Weinstein が Noms データベースプロジェクトで導入した Prolly Tree [PT 2015] は git のような分散バージョン管理システムとしての機能を持った Key-Value ストアである。これはローリングハッシュ関数を使用して B-Tree に似た確率的平衡構造の多分岐ハッシュツリーを生成する。BlueSky の AT Protocol で使用されている Merkle Search Tree [MST 2019] (MST) は Prolly Tree と類似しており、大規模ネットワークや分散 P2P 環境に焦点を当て、キーと値のペアを保存できる B-Tree に似た多分岐構造を持つハッシュツリーである。MST は、木構造のバランスとキーの順序の両方を維持しながら、同じデータセットに対して挿入/削除の順序に依存せず同一のツリーを生成するという決定論的な構築を実現している。これらのデータ構造と Slate は共に状態の差異を検出する目的でハッシュツリーを利用しているが、その設計目的は大きく異なっている。Prolly Tree と MST は分散 CRDT の効率的な同期に重点を置き、因果一貫性または結果整合性に基づいた状態の複製と共有に焦点を当てているのに対し、Slate は時間局所性を持つ追記ワークロードに最適化されており、最近のエントリで高速なアクセスを必要とするトランザクションログや変更履歴のような時系列データに特に適している。
本文書で提案する Slate は、これらの既存手法の利点を継承し、分散トランザクションログ同期に有利な最適化を導入している。具体的には、時間的局所性を活用した階層構造により最近のデータへの高速アクセスを実現し、append-only 特性を保持しながら効率的な差分検出を可能にしている。また、不規則な更新パターンに対応するために適応的な階層管理機能を提供し、既存の Merkle ツリーや History Tree では実現困難であった実用的な分散同期性能を達成している。
2.2.  永続性とバージョン付けされたデータ構造
永続性とバージョン付けされたデータ構造
関数型プログラミングの文脈での永続的データ構造の理論は、データ構造が変換する過程で構造の複数バージョンへの効率的なアクセスを可能にする。永続的データ構造は Driscoll ら [5] によって体系的に研究された。この論文では、変更時に履歴を失う一過性 (ephemeral) 構造と、その後のアクセスのために維持される永続的 (persistent) 構造を区別している。彼らの研究は、任意のデータ構造に対する汎用的な永続化手法に焦点を当てたもので、ファットノード方式とノードコピー方式の 2 つの基本的な手法を導入した。
一方で、我々の Slate は、部分的永続性の特徴を提供する木構造上の追記にのみ注目している。また、バージョンスタンプや複数のポインタを注意深く管理する必要がある一般的なノードコピー方式とは異なり、Slate は各エントリ \(e_i\) が更新操作 \(i\) の間に作成されたすべてのノードを含む階層構造によってシンプルに永続性を実現する。この設計上の選択により、我々の Slate からは複雑なポインタ管理の必要性が排除されている。さらに、Slate の追記のみという特性は、分散トラザクションログやブロックチェーンのような不変性と効率的な検証が重要となる最近のアプリケーションによく適合している。Driscoll らの手法のように明示的なバージョンポインタを保持するのではなく、Slate はその層様構造によってバージョン情報を暗黙的にエンコードし、時間的局所性を空間的局所性として自然に保持する。
2.3.  層様データ構造
層様データ構造
層化 (stratification) による最適化は、データの特性や使用パターンに応じて複数の階層を設けることで、全体的な性能向上を図る設計手法である。この概念は、メモリ階層の原理に基づき、アクセス頻度や時間的局所性の違いを活用してシステム効率を改善する。
階層型ストレージ管理 (hierarchical storage management) の概念は、ストレージシステムにおいてデータのアクセス頻度や重要度に応じて異なる性能特性を持つストレージ階層にデータを配置する手法である。高速だが高コストで容量の小さい SSD から、低速だが低コストで大容量の HDD やテープストレージまで、複数の階層を組み合わせてコスト効率と才能のバランスを最適化する。この階層化の原理は、時間的局所性と空間的局所性を活用し、頻繁にアクセスされるデータを高速階層に、アーカイブデータを低速階層に配置することで全体効率を向上させる。
Stratified B-Tree は 2011 年に Twigg らによって提案された、バージョン付けされた辞書のためのデータ構造である [Twigg et al., 2011]。これは Copy-on-Write B-Tree の非効率性を解決することを目的として開発された。Stratified B-Tree は Key-Value ペアを配列の層に配置することで、更新と範囲クエリー時のシーケンシャル I/O を可能にし、同時に不要な重複を避けるための密度を維持する。積層するデータ構造という意味で本文書の Stratified Hash Table と類似しているが、両者は層化の軸が根本的に異なる。Stratified B-Tree が独立して管理されるバージョン空間として層を使用するのに対し、我々の Stratified Hash Tree は時間的順序を分離し、時間的局所性を持つ単位として層を使用する。ただし、Stratified Hash Tree においても層はバージョンとして利用できる点で概念的類似性がある。
LSM-Tree (Log-Structured Merge Tree) [1] は、書き込み集約的なワークロードに最適化された層様データ構造である。LSM-Tree は、メモリ上の構造 (memtable) とディスク上の複数のレベルの構造 (SSTable) を組み合わせて書き込み操作を効率化する。新しいデータは最初メモリ内構造に追加され、一定のサイズに達するとディスク上の下位レベルにフラッシュされる。定期的なコンパクション処理により、複数のレベル間でデータがマージされ、重複の除去と空間効率の最適化が行われる。この階層化アプローチは、Cassandra, HBase, RocksDB などの現代の NoSQL データベースで広く採用されている。LSM-Tree の層の概念は、本文書の Slate とは書き込み最適化と層管理という点で共通するが、LSM-Tree が主にストレージ効率と書き込み性能に焦点を当てているのに対し、Slate はそれらに加えて差分検出と同期効率に最適化されている。
これらの既存の層様データ構造は、いずれも階層化による効率化という共通の設計思想を持つが、それぞれ異なる問題領域に特化している。Stratified B-Tree はバージョン管理辞書、LSM-Tree は書き込み集約型ストレージ、階層型ストレージはコスト効率的な大容量ストレージを主な対象とする。本文書の Slate は、これらの階層化概念を時間的局所性が空間的局所性となるように転換し、append-only 環境で最近のデータのアクセス効率を向上する最適化を提供している。
2.4.  トランザクションログと分散バージョン管理の同期
トランザクションログと分散バージョン管理の同期
分散環境における効率的なデータ同期と一貫性保証は、現代の分散システムにおける根本的な課題である。この分野では、コンセンサスアルゴリズム、分散バージョン管理、差分同期技術、そして分散台帳技術が相互に関連し合いながら発展してきた。
Raft は分散システムにおけるコンセンサスをを実現するためのアルゴリズムとして Paxos アルゴリズムの代替として設計された [Raft 2014]。これは複雑性の排除によって Paxos より理解しやすく設計されており、形式的に安全性が証明されている。Raft はリーダーアプローチによってコンセンサスを実装し、クラスタで選出された唯一のリーダーが他のサーバとのログレプリケーションを管理する責任を負っている。TiDB や YugabyteDB のような現代的な分散 SQL データベースでは、各データ単位は Raft を使用して他のノードにレプリケートされる。リーダー選出、ログレプリケーション、コミット処理という一連のプロセスにより、ノード障害やネットワーク分断下でもデータの一貫性が保証される。
Raft でリーダー交替が起きたとき、フォロワーのログが新しいリーダーのログとどこまで同期しているかを知るために、ログの末尾から 1 つずつ比較する。この手法は簡単だが、最悪ケースで \(O(n)\) となるログ全体の線形操作が必要となる場合があり、大規模なログでは性能の問題となる可能性がある。
Git は分散バージョン管理システムの実用的な実装例である。Git では、リポジトリの履歴が DAG (Directed Acyclic Graph) 構造として表現され、各コミットが親コミットへのポインタを持つ。ブランチをコミットのデータ列としたとき、差分の検出はブランチの分岐点を検出することと同じである。これは git merge-base アルゴリズムによって実現されており、2 つのブランチの共通祖先 (最低共通祖先: LCA) を特定する。これは、たとえば rebase 操作時に 2 つのブランチの共通祖先を見つけ、一方のブランチの各コミットからの変更をもう一方のブランチの上に適用するときに使用される。しかし、この手法はブランチ後方からの線形探索で分岐点を検出する。双方のブランチの後方から順にコミットをマークし、共通するコミットが存在するかを検出する。したがって、2 つのブランチに含まれるコミット数をそれぞれ \(N\), \(M\) としたとき、最悪ケースでは \(O(N+M)\) の計算量を必要とする。
Dolt は git のようなバージョン管理をサポートし、複数のブランチを構築できる SQL データベースである。ブランチの分岐点検出は最悪ケースで git merge-base と同じ \(O(N+M)\) となる。
差分同期 (Delta Synchronization) の代表例である rsync アルゴリズムは効率的な差分転送の基盤技術である [Tridgell, 1999]。rsync はファイル内で変更された部分のみを同期することでネットワーク帯域幅の占有を最小化する。これは、クライアントとリモートサーバの両方でファイルをチャンクに分割し、それらのチェックサム交換することで差分のみの転送を行うことができる。このアプローチは効率的だが、ファイル単位での処理に限定され、構造化されたデータの階層的な差分検出には適していない。
ブロックチェーンの軽量クライアントはハッシュベース検証がもたらす軽量化の重要な例である。Bitcoin の Simplified Payment Verification (SPV) では、クライアントはすべてのブロックではなくブロックヘッダのみをダウンロードし、Merkle 証明に依存してトランザクションを検証する。SPV クライアントがトランザクションを必要としたとき、フルノードから取得した特定のトランザクションがブロックに含まれていることを証明するために Merkle 証明を要求ル。これらの値をハッシュ化し、ブロックヘッダ内の Merkle ルートと比較することでトランザクションがブロックの一部であることを確認でキス。しかし、SPV は主に包含の証明に特化しており、複数のノード間での効率的な差分同期機能は提供されていない。
これらの既存手法は、それぞれ特定の同期要件や検証要件に対して解決策を提供しているが、分散トランザクションログの効率的な差分検出という共通の観点を持ちながら限界がある。Raft や Git の線形探索は直感的だが、大きな履歴に対して非効率になる可能性がある。rsync のファイルレベル同期はブロックデバイスに特化されており構造化データには適していない。ブロックチェーンの軽量クライアントの検証は単発的で、継続的な差分追跡には最適化されていない。
本文書で提案する Stratified Hash Tree はこれらの制約を解決する可能性を持っている。時間的局所性を活用した階層構造により、Raft のログ同期や Git の分岐点検出では最悪ケースで \(O(\log n)\) の効率化が期待できる。また rsync では階層的差分検出により従来のブロックレベル同期を超えた精度を実現し、ブロックチェーン環境では連続的なブロック検証における計算量の削減が見込まれる。これらの改善により、既存手法と比較した性能向上が期待される。
トランザクションログやコミットグラフ上の分岐点検出は、表面的には最小共通祖先 (LCA) 問題と類似している。しかし、従来の LCA アルゴリズム [Harel & Tarjan 1984, Schieber & Vishkin 1988, Binary Lifting] はグラフ構造が明らな状況でインデックスを構築し、各ノードの構造的関係を高速に検索することを目的としている。一方で、分散システムにおける実際の問題は、異なるマシン上で作成したデータ系列の整合性を検証しながら双方の分岐点を遠隔で特定することである。Slate は、このような分散かつ動的特性を持つ環境に特化して設計されている。これは、従来の LCA 研究が扱う共通祖先問題とは根本的に異なる問題設定であるため、本文書では追記最適化ハッシュツリーとしての独自の貢献に焦点を当てる。
3.  予備知識と定義
予備知識と定義
このセクションでは Slate 説明する上で必要な前提知識を説明する。
3.1.  ログ構造
ログ構造
本文書では、ログ構造を次のように定義する。
\(\mathbb{N}\) を自然数全体の集合 \(\{1,2,\ldots\}\)、\(\mathbb{N}_0\) を非負値 \(\mathbb{N}\cup\{0\}\) とする。離散インデックス集合 \(i \in \mathbb{N}\) と値集合 \(V\) に対し、ログ (log) は長さ \(n \in \mathbb{N}_0\) を持つ有限列 (\(\ref{log}\)) として定義する。\[ \begin{equation} L = \langle x_1, x_2, \ldots, x_n \rangle, \quad x_i \in V \quad (i = 1, 2, \ldots, n) \label{log} \end{equation} \] ここで要素 \(x_i\) の論理インデックスは \(i\) である。インデックスは対応する要素が存在する期間は不変である。
3.1.1.  ログの基本操作
ログの基本操作
ログの基本操作は次の 3 つである。
\(\textrm{size}(L) \to \mathbb{N}_0\): ログ \(L\) の長さ \(n\) を参照する操作。
\(\textrm{get}(L, i) \to V\): \(1 \le i \le n\) のとき、ログ \(L\) のインデックス \(i\) に対応する要素 \(x_i\) を参照する操作。そうでない場合は未定義 \(\bot\) を返す。
\(\mathrm{append}(L,v) \to L'\): ログ \(L\) の末尾に要素 \(v \in V\) を追加し、新しいログ \(L'\) を生成する操作。
接頭辞安定性: \({\mathrm{append}\) 操作は既存のログの接頭辞を変化させない。すなわち、任意の \(i \lt n\) について \(L'[i] = L[i]\) が成り立つ。
3.1.2.  ログの拡張操作
ログの拡張操作
拡張操作として次の操作を定義する。
\(\textrm{truncate}(L, m) \to L'\): あるしきい値 \(m\) より後の接尾辞を削除してログの長さを \(m\) に短縮する操作。これはログ複製システムでのロールバックに相当する。\(m\) 以降の要素はログから消滅し、再利用されることはない。\[ \mathrm{truncate}(L,m) \to L' = \langle x_1, x_2, \ldots, x_m \rangle \quad (m \le n) \] この操作をサポートする場合、\(u \gt m\) で並行して参照している処理と競合するため、ロックなどで排他制御を行う必要があることに注意。
切り詰めをサポートする場合、追記との組み合わせによって接尾辞置換を行うことができる。この操作は \(\mathrm{truncate}(L, m)\) と \(\mathrm{append}(L, v)\) を直列に一括実行することと等価である。
実運用では、切り詰めや置換が発生しない保護境界としてコミット指標 \(c\) (安定接頭辞の長さ) を導入することができる。これにより、\(u \le c\) となるようなスナップショット \(L^{(u)}\) での参照操作が切り詰め操作と排他制御することなく並行実行することができる。
3.1.3.  ログ上の並行実行モデル
ログ上の並行実行モデル
本文書ではログに対する並行実行モデルを SWMR (single-write, multi-read) と想定する。読み取りはスナップショット一貫性を満たす。
各読み取りは、操作を開始するときに対象とする \(L\) の長さ \(u\) を固定し、一連の読み取りの中で \(u\) を境界とするスナップショット \(L^{(u)} = \langle x_1, x_2, \ldots, x_u \rangle\) のみを観測する。すなわち、読み取り操作 \(\textrm{get}(L, i)\) は並行する追記や他の読み取り操作の影響を受けず、\(i \le u\) であれば常に同一値を観測する。
3.2.  ハッシュツリー
ハッシュツリー
ハッシュツリー (hash tree) またはマークルツリー (Merkle tree) は 1979 年に Ralph Merkle によって提案された認証可能なデータ構造である [Merkle 1979]。これは大規模なデータセットの完全性を効率的に検証できる二分木構造であり、葉ノードに暗号学的ハッシュ関数から算出したデータブロックのハッシュ値を格納し、各中間ノードはその 2 つの子ノードのハッシュ値を連結したものを再帰的にハッシュ化して得たハッシュ値を保持する。
3.2.1.  ハッシュツリーの基本構造
ハッシュツリーの基本構造
ハッシュツリーの構築は以下の手順で行われる。
葉ノード: \(n\) 個のデータブロック \(d_1, d_2, \ldots, d_n\) に対して、各ブロックのハッシュ値 \(h_i = H(d_i)\) を計算し、これらを葉ノード \(b_i\) とする。ここで \(H\) は暗号学的ハッシュ関数である。
中間ノード: 2 つの子ノード \(v_{\ell}\) と \(v_r\) を持つ中間ノード \(v\) のハッシュ値は \(h_v = H(h_{v_{\ell}}\,||\,h_{v_r})\) として計算される。ここで \(||\) は連結演算子である。
ルートハッシュ: 木構造の頂点に位置するルートノードのハッシュ値は、データセット全体の暗号学的な要約として機能する。
3.2.2.  認証パス
認証パス
ハッシュツリーの重要な特徴の一つは、特定のデータブロック \(d_i\) の所属証明 (木構造に含まれていること) が \(O(\log n)\) サイズの認証パス (authentication path) で可能な点である。認証パス \(\pi_i\) は、葉ノードからルートノードまでの経路上にある各ノードの兄弟ノードのハッシュ値の列である。この列を用いることで、対象のデータブロックのハッシュ値からルートハッシュまでを再帰的に計算し、ルートハッシュと一致するかを検証することができる。
データブロック \(d_i\) の検証には以下の情報が必要となる:
データブロック \(d_i\) 自体。
認証パス \(\pi_i = [h_{s_1}, h_{s_2}, \ldots, h_{s_k}]\)、ここで \(h_{s_j}\) は経路上の各ノードの兄弟ノードのハッシュ値。
各レベルでの左右の位置情報 (左子ノードか右子ノードか)。
認証者は、これらの情報からルートハッシュを再計算し、認証者が持つ信頼できるルートハッシュと比較することでデータの完全性と所属を検証できる。
3.2.3.  ハッシュツリーの性能特性
ハッシュツリーの性能特性
標準的なハッシュツリーは以下の計算複雑性を持つ:
構築: \(O(n)\) - 各データブロックのハッシュ計算に \(O(1)\)、各中間ノードのハッシュ計算に \(O(1)\) がかかり、中間ノードは \(n-1\) 個存在するため、合計で \(O(n)\) となる。
検証: \(O(\log n)\) - 認証パスに含まれるハッシュ値の数、つまり木の高さに比例する。
更新: (部分的) \(O(\log n)\) - 単一のデータブロックの更新は、その葉ノードからルートノードまでの経路上のノードのハッシュ値を再計算する必要があり、これも木の高さに比例する。
3.2.4.  Slate におけるハッシュツリーの応用
Slate におけるハッシュツリーの応用
Slate は標準的なハッシュツリーに対して以下の拡張を行う:
累積的な成長: 新しいデータの追加時に、既存の完全二分木構造を維持しながら木構造を成長させる。これにより、過去の任意の時点の木構造を再現可能である。
層様配置: データの追加順序に基づいて層 (stratum) を形成し、同一世代のノードを同じエントリに格納して I/O の単位とする。これにより、時間的局所性を活用した I/O 効率の向上を実現する。
非対称アクセス効率: 右枝方向 (より新しいデータ) への探索が同一エントリ内で完結するため、最新データへのアクセスが効率化される。
3.3.  数学的表現と実装の効率性
数学的表現と実装の効率性
Slate の構造は二分木に基づいており、その数学的な表現において 2 のべき乗や 2 の余剰が頻繁に現われる。これらの多くは汎用プログラミング言語における単純な四則演算とビット演算を用いて高速に算出することができる。以下に、Slate の実装で頻繁に使用される数学的表現と、それに対応する効率的なビット演算を示す。ここで \({\tt <<}\) をビット左シフト、\({\tt >>}\) をビット右シフト、\({\tt \&}\) をビット論理積、\({\tt \hat{}}\) をビット反転の演算子とする。
| \(2^j\) | \({\tt 1 << j}\) |
|---|---|
| \(i \bmod 2^j\) | \({\tt i \ \& \ ((1 << j) - 1)}\) |
| \(i - (i \bmod 2^j)\) | \({\tt i \ \& \ \hat{}((1 << j) - 1)} = {\tt (i >> j) << j }\) |
| \(\left\lfloor \frac{i}{2^j} \right\rfloor\) | \({\tt i >> j}\) |
| \(\left\lceil \frac{i}{2^j} \right\rceil\) | \({\tt (1 + (1 << j) - 1) >> j}\) |
| \(\left\lfloor \log_2 x \right\rfloor\) | \(x\) の 2 進数表現で最も左にある 1 の位置 [Warren 2012]。Rust の ilog2()。 |
| \(\left\lceil \log_2 x \right\rceil\) | \(x-1\) の 2 進数表現で最も左にある 1 の位置 [Warren 2012]。 |
| \({\rm popcount}(x)\) | \(x\) のビット内に存在する 1 の個数 [Warren 2012]、つまり \(\sum_{k=0} ( \lfloor x/2^k\rfloor \bmod 2 )\)。主要な CPU 命令セットには POPCNT 相当の命令があり、いくつかのプログラミング言語でも利用可能。 |
| \({\rm trailing\_zeros}(x)\) | \(x\) の最右ビットから連続する 0 の個数 (count tailing zeros) [Warren 2012]。主要な CPU 命令セットには CTZ 相当の命令があり、いくつかのプログラミング言語でも利用可能。 |
| \({\rm clz}(x) = \begin{cases} n - 1 - \lfloor \log_2(x) \rfloor & \text{if } x > 0 \\ n & \text{if } x = 0 \end{cases}\) | \(x\) の最左ビットから連続する 0 の個数 (count leading zeros) [Warren 2012]、つまり \(x\) を \(n\) ビット整数としたときの \(\max\{k: k\lt 2^{n-k}\}\)。主要な CPU 命令セットには CLZ 相当の命令があり、いくつかのプログラミング言語でも利用可能。 |
| \({\rm clo}(x)\) | \(x\) の最左ビットから連続する 1 の個数 (count leading ones) [Warren 2012]、つまり \({\rm clz}({}^\lnot x)\)。主要な CPU 命令セットには CLO 相当の命令があり、いくつかのプログラミング言語でも利用可能。 |
実際の演算においては、\(|I|\) をインデックス型 \(I\) のビット幅としたとき、特に \(j = |I|\) の境界条件でのオーバーフローを起こす可能性があることに注意。整数型のビット幅以上の左右ビットシフト演算は、例えば C 言語では未定義動作とされており [C23 2024]、また Rust では program error とされている [Rust RFC560]。このため実際には境界チェックのために if(j < 64) のような条件分岐を追加する必要があるが、幸い、実用的なデータサイズでは j < 64 は実質的に常に true となり、これは CPU の分岐予測と投機実行に高い予測成功率を達成させるため、このこのような境界チェックの追加によるオーバーヘッドはほぼ無視できるだろう。
3.4.  左枝への移動回数を得る方法
左枝への移動回数を得る方法
Slate の探索では左枝方向の移動回数が性能特性に大きく影響する重要なコストパラメータとなる。ここで、完全二分木のルートノードから葉ノードまでの経路において左枝方向または右枝方向へ移動する回数を求める。この方法は [Knuth 1997; EXERCISES 2.3.1-5] で紹介されている二分木の各ノードにインデックスを付ける手法から導くことができる。
高さが \(h\) で、葉ノードが左から順に \(x \in \{0,1,\ldots,2^h-1\}\) とインデックス付けされている完全二分木について考える。この \(x\) の 2 進数表現は、経路上の左右の選択を 1 (右枝を選択) と 0 (左枝を選択) の並びで符号化したものと一致する。したがって、\(x\) の 2 進数表現における 1 の個数は右枝方向に進んだ回数であり、0 の個数は左枝方向に進んだ回数である。これらは前述の \({\rm popcount}(x)\) で簡単に求めることができる。
情報理論の観点では、木構造におけるルートから葉までの経路は符号語であり、\(x\) の 2 進数表現における 1 の個数とは \(0\) と \(x\) のハミング距離 (Hamming distance)、0 の個数は \(2^h-1\) と \(x\) のハミング距離として統計的特徴量 (特定の選択の頻度) を表している。
我々の興味はルートから葉までの経路上で左枝方向に進む回数だが、この符号化により、その問題を \(x\) の 2 進数表現に含まれる 0 の個数を数える問題に置き換えることができる。ここで \(x\) の \(h\) 桁 2 進数表現に含まれる 0 の個数、つまり \(x\) と \(2^h-1\) のハミング距離を式 (\(\ref{io_cost}\)) のように表す。\[ \begin{eqnarray} c(x) & = & {\rm hamming\_distance}(x,2^h-1) \nonumber \\ & = & {\rm popcount}(x \oplus 2^h-1) \nonumber \\ & = & h - {\rm popcount}(x) \label{io_cost} \end{eqnarray} \] ここで \(\oplus\) はビット XOR (排他的論理和) 演算子である。この \(c(x)\) は単調的ではなく Figure 2 のように離散的に分布する。
ある数値 \(x\) の \(h\) 桁の 2 進数表現において、最も左の位置から連続する 1 の各ビットは、それ以降の \(x' \ge x\) において少なくとも 0 になることはない。この文書では、\(x\) の最も左に位置する 1 の連続の長さ \({\rm clo}(x)\) を、\(x\) における \({\rm popcount}(x)\) の下限とし、それから \(c(x)\) の上限を定義する。
定義 1: すべての \(x' \ge x\) における \(c(x')\) の最大値を \(c(x)\) の上限 (upper bound) \(c_u(x)\) と定義する。\[ \begin{eqnarray} c_u(x) & = & \max\{c(x') : x \le x' \lt 2^h\} \nonumber \\ & = & h - {\rm clo}(x) \nonumber \\ & = & \left\lfloor \log_2(2^h - x) \right\rfloor \label{hul} \end{eqnarray} \]
同様に、ある数値 \(x\) の最左ビットから続く 0 は、それ以前の \(x' \le x\) において少なくとも 1 になることはない。また、\(x=2^k-1\) となるような \(k\le h\) が存在しなければ、追加で少なくとも 1 つの 0 を持つはずである。これは \(h+1\) ビット整数における \({\rm clz}(x+1)\) と等しい。
定義 2: すべての \(x' \le x\) における \(c(x')\) の最小値を \(c(x)\) の下限 (lower bound) \(c_l(x)\) と定義する。\[ \begin{eqnarray} c_l(x) & = & \min\{c(x') : 0 \le x' \le x\} \nonumber \\ & = &\left\lceil \log_2 \frac{2^h}{x+1} \right\rceil = h - \left\lfloor \log_2 (x+1) \right\rfloor \label{hll} \end{eqnarray} \]
Figure 2 は \(h=11\) の設定で算出した実際の \(c(x)\) の分布と、式 (\(\ref{hul}\)) と (\(\ref{hll}\)) による上限/下限を図示している。
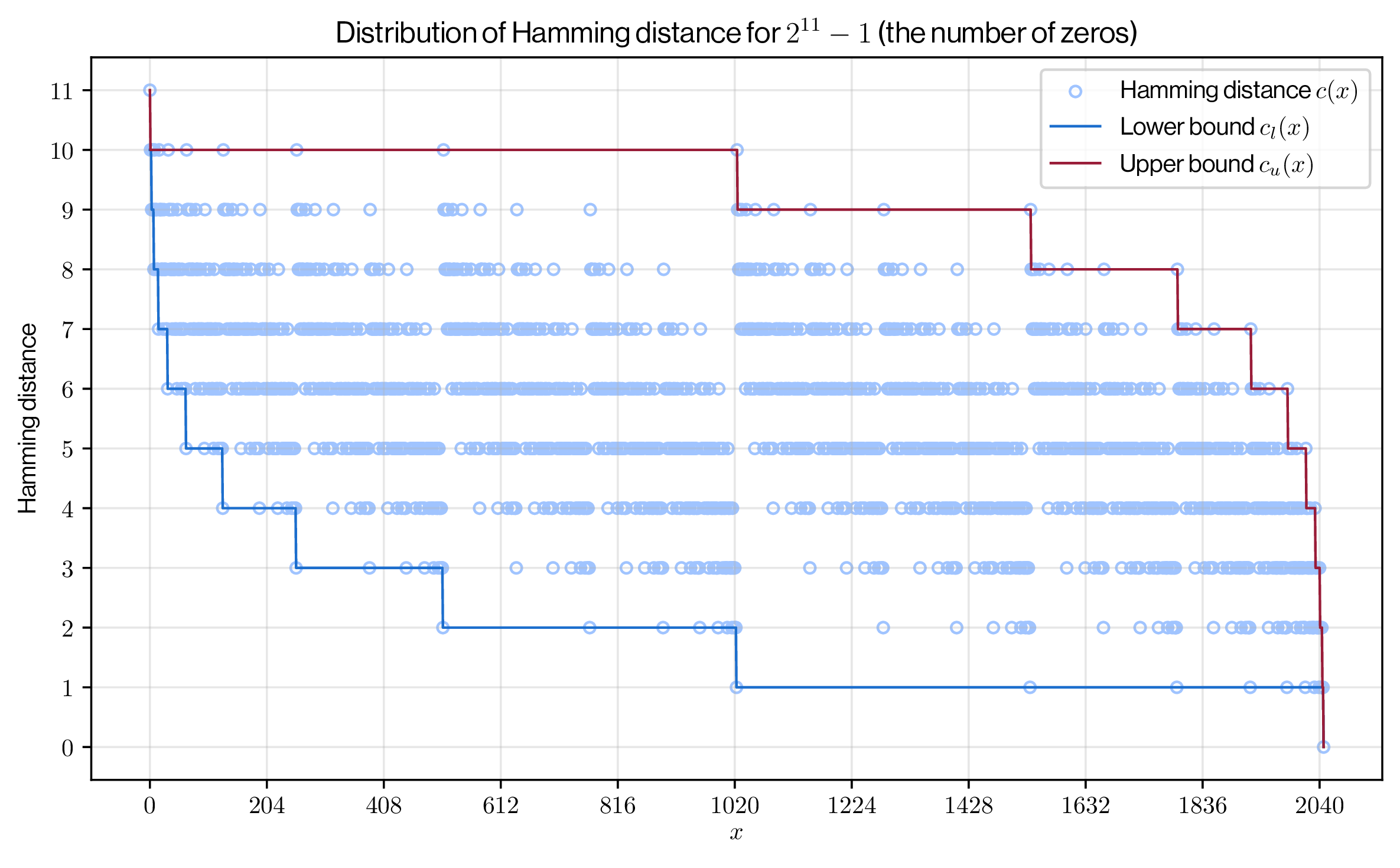
境界は共に \(c_u(0) = c_l(0) = h\) で最大値を取り、\(c_u(2^h-1) = c_l(2^h-1) = 0\) で最小値を取る単調減少関数である。ただし、上限は横反転対数、下限は縦反転対数という違いがある。これは、\(2^h-1\) の近傍では \(c(x)\) の上限が低く抑えられ、反対に 0 の近傍では下限が高く伸びるという特徴をもたらしている。
4.  Slate データ構造
Slate データ構造
このセクションでは Slate データ構造の基本的な性質とその数学的な定義を説明する。
Slate はその多くの領域を完全二分木が占める二分木である。本文書では \(n\) 個のユーザデータ (葉ノード) を含む Slate の木構造全体を \(T_n\)、あるノード \(b\) が木構造 \(T\) に含まれていることを便宜的に \(b \in T\)、\(T_1\) が \(T_2\) の部分木であることを \(T_1 \subseteq T_2\) と表記する。また、特に \(T_n\) の成長過程に注目するとき \(n\)-th 世代と表現する。
Slate は部分構造として含まれている一つ以上の完全二分木を統合しながら成長する。また木構造の大半が完全二分木であることから、完全二分木に近い特性を持つ。したがって Slate の特徴を活用するには木構造全体から完全二分木を判定する方法が重要である。ここでは Slate 構造の現実的な操作に必要な数学的背景を記述する。
4.1.  木構造の構築
木構造の構築
Slate は独立した (互いに部分構造ではない) 完全二分木を一世代限りの一過性ノードで接続する木構造である。この木構造は決定論的であり、その大部分が完全二分木によって構成されていることから Slate は完全二分木に近い特性を持つ。
高さ \(h\) を持つ完全二分木は \(2^h\) の葉ノードを含んでいる。\(n\) 個の葉ノードを含む (\(n\)-th 世代の) 木構造 \(T_n\) に含まれている独立した完全二分木は、\(n\) を \(2^h\) の和で表現することで得られる。\[ \begin{equation} n = \sum_{h\ge 0} b_h 2^h \quad (b_h \in \{0,1\}) \label{n_expansion} \end{equation} \] 式 (\(\ref{n_expansion}\)) は \(n\) の 2 進数展開である。つまり、木に含まれるノード数 \(n\) は完全二分木を大きさごとに 2 進数で符号化したものと見なすことができる。また、木に含まれる独立した完全二分木が \(m={\rm popcount}(n)\) 個となることは明らかである。
例 1: \(n=22\) での木構造 \(T_{22}\) の構築スケッチを Figure 3 に示す。\(22\) の 2 進数表現 \(10110_2\) のビット 1 の位置から、\(T_{22}\) には \(h\in\{4,2,1\}\) となる \(m=3\) つの完全二分木を部分木として含んでおり、それらのルートノードを接続する 2 つの一過性ノードが存在する。それぞれの完全二分木の葉ノードの合計は \(2^4+2^2+2^1=22\) で \(n\) と一致する。
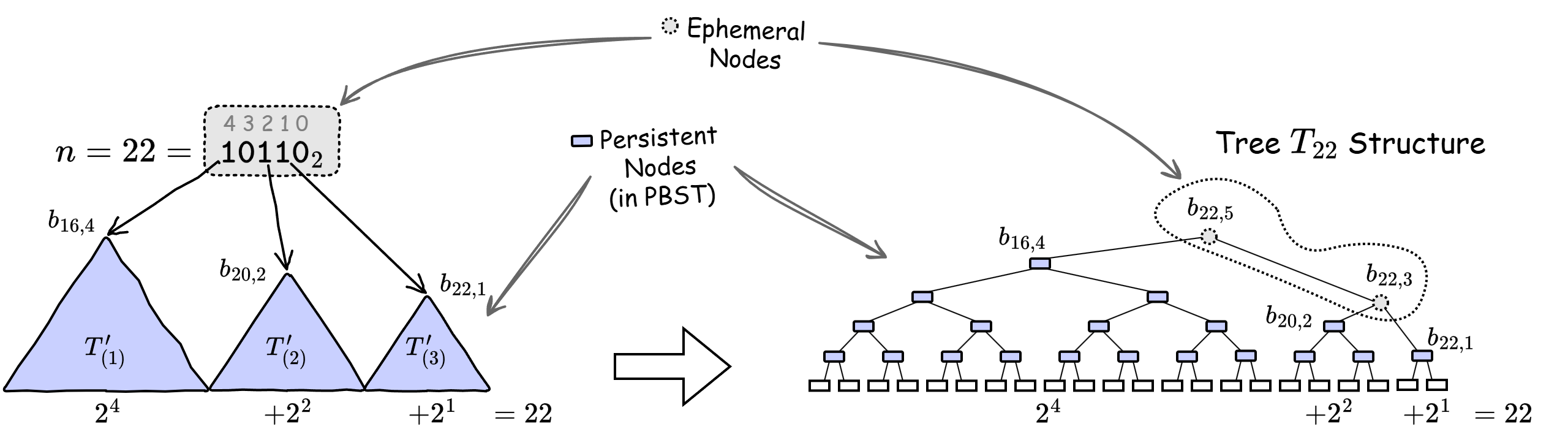
Figure 3. \(T_{22}\) 構造のスケッチ。\(n=22\) で符号化された完全二分木を構築し、それらのルートノードを一過性ノードで接続することで Slate の木構造は決定論的に構築することができる。
4.2.  ノード
ノード
ユーザデータは Slate の葉ノードに格納される。ここで \(i \in \{1,2,\ldots\}\) をユーザデータのインデックスとし、Slate に \(i\) 番目に追加された葉ノードを \(b_i\) と表す。
既存の木構造 \(T_{i-1}\) に \(i\) 番目の葉ノード \(b_i\) を追加するときに発生する中間ノードを \(b_{i,j}\) と表記する。ここで \(j \in \{1,2,\ldots\}\) は、\(b_{i,j}\) をルートノードとする部分木を考えたときに最も遠い葉ノードまでの距離 (高さまたは深さ) を表している。したがって木構造全体で最も大きい \(j\) を持つノードは常にルートノードであり、その \(j\) 木の高さを表している。また、任意の \(b_{i,j}\) をルートノードとする部分木において \(j\) が最も大きくなるケースはその部分木が完全二分木のときであることから、ルートノードの取る \(j\) の最大値は \(\lceil \log_2 i \rceil\) である。ここで \(j=0\) を持つ単一の葉ノードも部分木とみなすことに注意。\[ \begin{equation} i \in \{1,2,\ldots\}: 0 \le j \le \lceil \log_2 i \rceil \label{ij} \end{equation} \]
式 (\(\ref{ij}\)) は、現実的な実装において \(i\) の定義域を 64-bit 整数としても \(j\) の取りうる最大値は高々 64 であることを意味している。
Figure 1 ですみれ色と薄いグレーで示しているように、中間ノードには 2 つの種類がある。一つはそのノードをルートとする部分木が完全二分木のケースで、これは永続性 (persistent) を持ち、\(i\)-th 世代以降のすべての木構造でも顕在する。もう一つは完全二分木でないケースで、これは他の完全二分木の部分木を接続するために設置された \(i\)-th 世代でのみ現れる一過性 (ephemeral) の中間ノードである。一過性の中間ノードは、説明を簡略化するために Figure 1 では消去しているが、直列化形式の中では常に存在しており、その木構造はいつでも復元することができる。
ある中間ノード \(b_{i,j}\) が左枝に \(b_{i_\ell,j_\ell}\)、右枝に \(b_{i_r,j_r}\) を接続していることを示すために \(\underset{(i_\ell,j_\ell)(i_r,j_r)}{b_{i,j}}\) と表記する。\(\underset{(i_\ell,j_\ell)(i_r,j_r)}{b_{i,j}}\) と表記する。
4.2.1.  永続性ノード
永続性ノード
Algorithm 1 は式 (\(\ref{n_expansion}\)) に基づいてビット 1 の位置から完全二分木を列挙する擬似コードである。これで得られる \(m\) 個の完全二分木のルートノード集合を \(\mathcal{B}'_n=(b'_{i_1,j_1},\ldots,b'_{i_m,j_m})\) とする。これらは配置上の左から順序付けられているため \(i_1 \lt \ldots \lt i_m\) である。また左に位置する完全二分木がより高いという性質を持つことから \(j_1 \gt \ldots \gt j_m\) である。
| 1. | \( {\bf function} \ {\rm pbst\_roots}(n:{\it Int}) \to {\it Sequence}[{\it Node}] \) | |
| 2. | \( \hspace{12pt}r := n \) | |
| 3. | \( \hspace{12pt}\mathcal{B}'_n := \emptyset \) | |
| 4. | \( \hspace{12pt}{\bf while} \ r \ne 0 \) | |
| 5. | \( \hspace{24pt}j = \lfloor \log_2 r \rfloor \) | |
| 6. | \( \hspace{24pt}i = n - r + 2^j \) | |
| 7. | \( \hspace{24pt}\mathcal{B}'_n := \mathcal{B}'_n \, \cup \, \{b'_{i,j}\} \) | // \(b'_{i,j}\) は完全二分木となる部分構造のルート |
| 8. | \( \hspace{24pt}r := r - 2^j \) | |
| 9. | \( \hspace{12pt}{\bf return} \ \mathcal{B}'_n \) | |
4.2.2.  一過性ノード
一過性ノード
Slate における一過性の中間ノードは、\(T_n\) の部分木である独立した完全二分木のルートノード \(\mathcal{B}'_n\) を右から接続したものである。したがって独立した完全二分木を列挙することで一過性の中間ノードも列挙することができる。
定義 1: 一過性ノード (ephemeral node): 木構造 \(T_n\) を構成する独立した完全二分木のルートノード集合 \(\mathcal{B}'_n\) を右から接続することで得られる、\(n\)-th 世代でのみ現れる中間ノードを一過性ノードと呼ぶ。ここで \(n\) 世代の木構造に現われる一過性ノードの集合を \(\mathcal{B}_n\) と表す。
命題 1: 木構造 \(T_n\) に含まれる一過性ノードの数は式 (\(\ref{ephemeral_count}\)) のように表される。\[ \begin{equation} |\mathcal{B}_n| = \begin{cases} {\rm popcount}(n) - 1 & \text{if $n \ge 1$}\\ 0 & \text{if $n = 0$ is necessary to consider} \end{cases} \label{ephemeral_count} \end{equation} \]
Proof. 木構造 \(T_n\) に含まれる独立した完全二分木の数は \(m={\rm popcount}(n)\) であり、それらのルートノードを接続するためには \(m-1\) 個の一過性ノードが必要であることから、式 (\(\ref{ephemeral_count}\)) が成り立つ。∎
Algorithm 1 より得られる \(m\) 個の完全二分木のルートノード集合 \(\mathcal{B}'_n\) に対して、それらを接続する一過性の中間ノードは \(\mathcal{B}_n=(b_{n,j_1+1},\ldots,b_{n,j_{m-1}+1})\) となる。ここで、左から \(k\) 番目に位置する任意の一過性中間ノードは式 (\(\ref{ephemeral_node}\)) のように表される。\[ \begin{equation} \left\{ \begin{array}{ll} \underset{(i_k,j_k)(n,j_{k+1}+1)}{b_{n,j_k+1}} \ \ & (k \lt m - 1) \\ \underset{(i_k,j_k)(i_m,j_m)}{b_{n,j_k+1}} \ \ & (k = m - 1) \end{array} \right. \label{ephemeral_node} \end{equation} \] 式 (\(\ref{ephemeral_node}\)) で表される一過性中間ノードは、左枝に完全二分木の \(b'_{i_k,j_k}\)、右枝に一過性ノード \(b_{n,j_{k+1}+1}\) または右端の完全二分木 \(b'_{i_m,j_m}\) を接続し、\(n\)-th 世代で一過性の中間ノードであるため \(i=n\)、右枝に接続する二分木より左枝に接続する二分木の方が必ず高いため \(j=j_k+1\) となることを意味している。Algorithm 2 は一過性の中間ノードを生成するアルゴリズムである。
| 1. | \( {\bf function} \ {\rm ephemeral\_nodes}(n:{\it Int}) \to {\it Sequence}[{\it Node}] \) | |
| 2. | \( \hspace{12pt}\mathcal{B}'_n := {\rm pbst\_roots}(n) \) | // Algorithm 1 |
| 3. | \( \hspace{12pt}\mathcal{B}_n := \emptyset \) | |
| 4. | \( \hspace{12pt}{\bf for} \ x := {\rm size}(\mathcal{B}'_n)-1 \ {\bf to} \ 1 \) | |
| 5. | \( \hspace{24pt}i = n, \) | |
| 6. | \( \hspace{24pt}j = \mathcal{B}'_n[x].j+1 \) | |
| 7. | \( \hspace{24pt}left = \mathcal{B}'_n[x-1] \) | |
| 8. | \( \hspace{24pt}right = \mathcal{B}_n[0] \ {\bf if} \ x \ne {\rm size}(\mathcal{B}'_n)-1 \ {\bf else} \ \mathcal{B}'_n[x] \) | |
| 9. | \( \hspace{24pt}\mathcal{B}_n := b \{i, j, left, right\} \ \mid\mid \ \mathcal{B}_n \) | |
| 10. | \( \hspace{12pt}{\bf return} \ \mathcal{B}_n \) | |
この木構造の構築手順から、任意のノード \(b_{i,j} \in T_n\) の左右の枝に接続されているノード \(b_{i_l,j_l}\) と \(b_{i_r,j_r}\) は以下の自明な性質を持っている。
性質 1: 任意のノード \(b_{i,j} \in T_n\) の左枝に接続されているノード \(b'_{i_l,j_l}\) を頂点とする部分木は完全二分木である。また、右枝に接続されているノード \(b_{i_r,j_r}\) を頂点とする部分木は、\(i\ne n\) のとき完全二分木であり、\(i=n\) のとき完全二分木の可能性がある。
性質 2: 任意のノード \(b_{i,j} \in T_n\) の左枝に接続されているノード \(b_{i_l,j_l}\) の高さは \(j_l = j - 1\) である。
性質 3: 任意のノード \(b_{i,j} \in T_n\) の右枝に接続されているノード \(b_{i_r,j_r}\) のインデックスは \(i_r = i\) である。またこの性質を再帰的に考慮すると、任意のノードの右枝を葉ノードまでたどる一連のノードは同じ \(i\) の値を持つ。
4.2.3.  エントリ
エントリ
木構造が \(T_{i-1}\) から \(T_i\) へ移行するときに追加されるノードの集合をエントリ (entry) と呼び \(e_i\) と表す。
定義 1: エントリ \(e_i\) は、1) 葉ノード \(b_i\)、2) 永続ノードの集合 \(\{b'_{i,j}: 1 \le j \le {\rm tailing\_zeros}(i)\}\)、3) 一過性ノードの集合 \(\mathcal{B}_i\) の和集合で構成される。\[ \begin{equation} e_i = \{b_{i}\} \cup \{b'_{i,j} : 1 \le j \le {\rm tailing\_zeros}(i)\} \cup \mathcal{B}_i \label{entry} \end{equation} \]
本文書ではエントリを直列化形式の追記と読み出しの I/O 単位と仮定する。定義 1 より、エントリ \(e_i\) に含まれるノード数は命題 2 のように表すことができる。
命題 2: エントリ \(e_i\) に含まれるノードの総数は式 (\(\ref{esize}\)) で表される。\[ \begin{eqnarray} |e_i| & = & 1 + {\rm tailing\_zeros}(i) + \left({\rm popcount}(i) - 1\right) \nonumber \\ & = & {\rm tailing\_zeros}(i) + {\rm popcount}(i) \label{esize} \end{eqnarray} \]
Proof. エントリ \(e_i\) に含まれる永続性ノードは、\(T_i\) で最も右に配置されている独立した完全二分木と重なる部分のノードである。最も右に位置する完全二分木は、\(i\) の 2 進数表現で最も右に位置するビット 1 に対応する高さを持つことから、\(e_i\) に含まれる (葉ノードを除く) 永続性ノードの数は \(i\) の 2 進数表現における末尾の 0 の個数 \({\rm tailing\_zeros}(i)\) と一致する。
エントリ \(e_i\) に含まれる一過性ノードは、木構造 \(T_i\) に含まれる独立した完全二分木を連結する。独立した完全二分木は \(i\) の 2 進数表現における 1 の個数と一致することから、\(e_i\) に含まれる一過性ノードの数は \({\rm popcount}(i)-1\) となる。∎
命題 2 より、\(n\) 個のエントリを含む Slate 構造 \(T_n\) の直列化表現の空間複雑性は \(\Theta(n \log n)\) であり、したがって 1 エントリあたりの平均の空間複雑性は \(\Theta(\log n)\) である。
4.3.  完全二分木の判定
完全二分木の判定
木構造 \(T_n\) に含まれる任意のノード \(b_{i,j}\) をルートとする (葉ノードまでを含む) 部分木を \(T_{i,j} \subseteq T_n\) とする。\(i,j\) に対して式 (\(\ref{pbt}\)) が成り立つような整数 \(q\) が存在するならば、この部分木 \(T_{i,j}\) は完全二分木 (perfect binary tree) である。\[ \begin{equation} i = q \times 2^j \label{pbt} \end{equation} \] ここで \(q \ge 1\) は同一の高さ \(j\) を持つ完全二分木 \(T_{*,j} \subseteq T_n\) の中で先頭から何番目の部分木かを意味している。\(T_{i,j}\) が完全二分木であることを意図しているとき \('\) (prime) を付けて \(T'_{i,j}\) と表記し、同様に完全二分木となる部分木のルートノードを意図しているとき \(b'_{i,j}\) と表記する。また式中では完全二分木となる部分木を \({\rm PBST}\) (perfect binary subtree) と表記する。
完全二分木となった部分木構造はそれ以降の世代でも残り続ける。このため、\(T_{i,j}\) が完全二分木の場合、ノード \(b'_{i,j}\) は永続的であり、そうでない場合、ノード \(b_{i,j}\) は一過性である。
実装では式 (\(\ref{pbt}\)) から導かれる式 (\(\ref{pbst}\)) を使って添字のビット演算のみで \(T_{i,j}\) が完全二分木かを判断することができる。\[ \begin{equation} \begin{cases} i \equiv 0 \pmod{2^j} & \quad \text{If $T_{i,j}$ is a PBST} \\ i \not\equiv 0 \pmod{2^j} & \quad \text{Otherwise} \end{cases} \label{pbst} \end{equation} \] なお、\(j=0\) の時に式 (\(\ref{pbst}\)) は必ず true となることは明らかであるから、任意の葉ノード \(b_i = b'_{i,0}\) は完全二分木であり、永続的である。
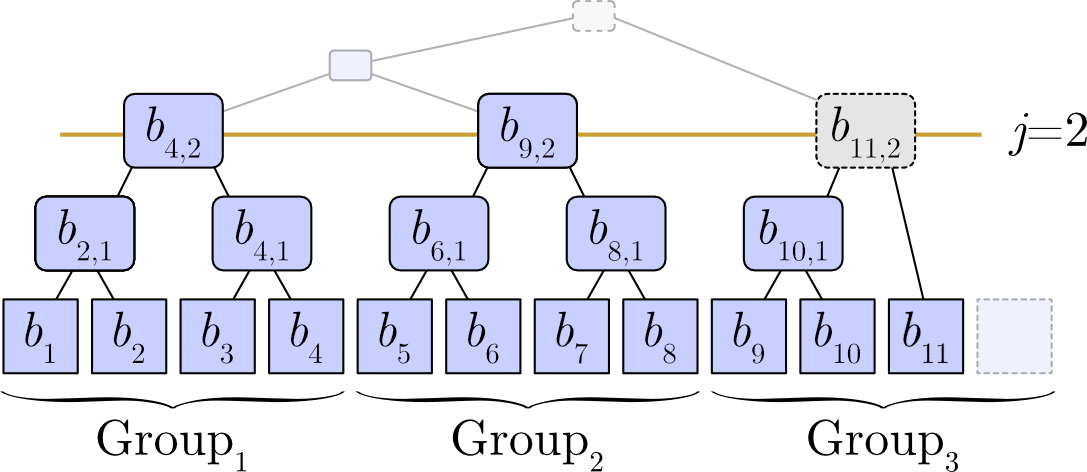
Slate はデータを \(2^j\) ずつのグループに分割する階層構造の性質がある。世代 \(n\) において完全に埋まっているグループは、対応する部分木が完全二分木であることを意味する。例えば、高さ \(j=2\) では容量 4 のグループとなり、\(n=11\) に対して 2 つのグループが完全に埋まり 1 つのグループが埋まっていない。\[ \begin{array}{lll} {\rm Group}_1 & = & (1, 2, 3, 4) & \quad \text{completely filled (PBST)} \\ {\rm Group}_2 & = & (5, 6, 7, 8) & \quad \text{completely filled (PBST)} \\ {\rm Group}_3 & = & (9, 10, 11, \_) & \quad \text{not completely filled (not PBST)} \end{array} \] これを木構造で表すと Figure 4 のようになる。
4.4.  任意の部分木に含まれる葉ノード数
任意の部分木に含まれる葉ノード数
任意のノード \(b_{i,j}\) を頂点とする部分木 \(T_{i,j}\) に含まれる葉ノードの数 \(r_{i,j}\) を求める。まず、部分木が完全二分木の場合は \(r'_{i,j}=2^j\) であることは明らかである。次に、部分木が完全二分木ではない場合、木は高さ \(j\) の部分木の中で \(\lfloor \frac{i}{2^j}\rfloor\) 番目のグループに対応しており、その前には \(\lfloor\frac{i}{2^j}\rfloor\) 個の満杯のグループが存在している。したがって、葉ノードの数は式 (\(\ref{r_cases}\)) のように表される。\[ \begin{equation} \begin{cases} r'_{i,j} & = & 2^j & \quad i \equiv 0 \pmod{2^j} \\ r_{i,j} & = & i - \left\lfloor\frac{i}{2^j}\right\rfloor \times 2^j & \quad i \not\equiv 0 \pmod{2^j} \end{cases} \label{r_cases} \end{equation} \]
完全二分木 \(i \equiv 0 \pmod{2^j}\) のケースでは、式 (\(\ref{pbt}\)) が成り立つ整数 \(q \ge 1\) が存在する。\(q-1\) は一つ前のグループの番号であるため \(q-1=\lfloor \frac{i-1}{2^j} \rfloor\) と表すことができる。したがって \(r'_{i,j}\) は式 (\(\ref{r_pbst}\)) のように変形できる。\[ \begin{eqnarray} r'_{i,j} & = & 2^j = q \times 2^j - (q - 1) \times 2^j \nonumber \\ & = & i - \left\lfloor\frac{i-1}{2^j}\right\rfloor \times 2^j \label{r_pbst} \end{eqnarray} \] 一方、完全二分木でない \(i \not\equiv 0 \pmod{2^j}\) のケースでは、\(\lfloor\frac{i}{2^j}\rfloor = \lfloor\frac{i-1}{2^j}\rfloor\) であるため、\(r_{i,j}\) も式 (\(\ref{r_ephemeral}\)) のように変形できる。\[ \begin{eqnarray} r_{i,j} & = & i - \left\lfloor \frac{i}{2^j} \right\rfloor \times 2^j \nonumber \\ & = & i - \left\lfloor \frac{i-1}{2^j} \right\rfloor \times 2^j \label{r_ephemeral} \end{eqnarray} \] これにより、式 (\(\ref{r_cases}\)) におけるケース分岐は式 (\(\ref{r_pbst}\), \(\ref{r_ephemeral}\)) に統合することができる。ここで \(\lfloor\frac{i-1}{2^j}\rfloor\) は \(T_{i,j}\) より前に存在するグループの個数を表している。
一般に、任意の整数 \(a\), \(b\) (\(b\gt 0\)) に対して \(a = \lfloor\frac{a}{b}\rfloor \times b + (a \bmod b)\) であることから、\(a=(i-1)\) を適用すると式 (\(\ref{r}\)) が得られる。\[ \begin{eqnarray} r_{i,j} & = & i - \left\lfloor \frac{i-1}{2^j} \right\rfloor \times 2^j \nonumber \\ & = & ((i - 1) \bmod 2^j) + 1 \label{r} \end{eqnarray} \] この式 (\(\ref{r}\)) により、任意のノード \(b_{i,j}\) に含まれる葉ノードの数 \(r_{i,j}\) は、完全二分木か一過性ノードかにかかわらず統一的に計算できる。
4.5.  部分木のカバー範囲
部分木のカバー範囲
任意の部分木 \(T_{i,j} \subseteq T_n\) に含まれている葉ノードのインデックス範囲 \([i_{\rm min}, i_{\rm max}]\) について考える。性質 3 より、最大のインデックスが \(i_{\rm max} = i\) であることは明らかであるため、最小のインデックス \(i_{\rm min}\) に注目する。
高さ \(j\) を持つ部分木 \(T_{i,j}\) より前には、\(T_{i,j}\) が完全二分木かどうかにかかわらず、同じ高さ \(j\) を持つ部分木 (完全二分木) \(T'_{i',j}\)、\(i' \lt i\) が \(\lfloor\frac{i-1}{2^j}\rfloor\) 個存在する。高さ \(j\) の完全二分木は \(2^j\) 個の葉ノードを含んでいることから、\(T_{i,j}\) の最小のインデックス \(i_{\rm min}\) は \(T_{i,j}\) より前に存在する葉ノードの総数 + 1 と考えることができる。\[ \begin{equation} \left\{ \begin{array}{lcl} i_{\rm min} & = & \left\lfloor \frac{i-1}{2^j} \right\rfloor \times 2^j + 1 = i - ((i-1)\bmod 2^j) \\ i_{\rm max} & = & i \end{array} \right. \label{subtree_range} \end{equation} \] 式 (\(\ref{subtree_range}\)) より、\(T_{i,j}\) に含まれる葉ノードの数は \(i_{\rm max}-i_{\rm min}+1=r\) で式 (\(\ref{r}\)) と一致する。また \(T_{i,j}\) に隣接する「左隣りの部分木の最大の葉ノード」と「右隣りの部分木の最小の葉ノード」も算出することができる。この考え方は中間ノードの接続の説明で使用する。
定義 2: (最小共通祖先 (LCA: Lowest Common Ancestor)) 2 つの葉ノード \(b_x,b_y \in T_n\), \(x \lt y\) の共通祖先を \({\rm LCA}(b_x,b_y)\) と表記し、その高さを \(j^*(x,y)\) とする。
定義 3: (部分木の所属) \(b_x \in T_{i,j}\) のとき、式 (\(\ref{subtree_range}\)) より式 (\(\ref{leaf_belonging}\)) が成り立つ。\[ \begin{equation} b_x \in T_{i,j} \Longleftrightarrow \left\lfloor\frac{x-1}{2^j}\right\rfloor = \left\lfloor\frac{i-1}{2^j}\right\rfloor \label{leaf_belonging} \end{equation} \]
命題 3: (共通祖先の高さ) 任意の 2 つの葉ノード \(b_x,b_y \in T_n\), \(1 \le x \lt y \le n\) の最小共通祖先の高さ \(j^*(x,y)\) は式 (\(\ref{lca_height}\)) で与えられる。\[ \begin{equation} j^*(x,y) = \min\left\{ j \in \mathbb{N}: j \ge 1 + \left\lfloor \log_2 \left( (x-1) \oplus (y-1) \right) \right\rfloor \land \left\lfloor\frac{x-1}{2^j}\right\rfloor = \left\lfloor\frac{i-1}{2^j}\right\rfloor \right\} \label{lca_height} \end{equation} \]
Proof. 証明を 2 つに分ける。\(b_x\) と \(b_y\) が高さ \(h\) の同一の PBST \(T'_{\alpha\cdot 2^h,h}\) に含まれる場合、\(\alpha-1)\times 2^h \lt x \le y \le \alpha\times 2^h\) が成り立つ。\(x\) と \(y\) の PBST 内での相対位置を 0 基準で表すと、\(x' = x-1-(\alpha-1)\times 2^h\), \(y' = y-1-(\alpha-1)\times 2^h\) であり、完全二分木の性質により 2 つのノードの共通祖先の高さはその相対位置の二進表現が最初に異なるビット位置に対応する。すなはち \(j^*(x,y)=1+\lfloor\log_2(x'\oplus y')\rfloor\) である。ここで同一の定数 \((\alpha-1)\times 2^h\) を両者から引いても XOR 結果は変化しないため、\(x'\oplus y'=(x-1)\oplus(y-1)\) となる。したがって、同一の PBST 内では: \[ j^*(x,y) = 1+\lfloor\log_2((x-1)\oplus(y-1))\rfloor \]
\(b_x\) と \(b_y\) が異なる PBST に含まれる場合、
4.6.  左右の子ノードのインデックス
左右の子ノードのインデックス
任意のノード \(b_{i,j} \in T_n\) の左右の枝に接続されているノード \(b_{i_\ell,j_\ell}\) と \(b_{i_r,j_r}\) を求める。性質 2 と性質 3 から \(j_\ell = j-1\) と \(i_r=i\) は明らかであるため、残りの \(i_\ell\) と \(j_r\) を求める。
まず \(i_\ell\) は以下のような考えで求めることができる。これは \(b_{i,j}\) の左枝に接続されているノードであるため完全二分木であることに注意。
\(T_{i_\ell,j-1}\) は \(T_{i,j}\) と最も左側の葉ノードを共有している。つまり、\(T_{i_\ell,j-1}\) より前にある葉ノード数は \(T_{i,j}\) より前にある葉ノード数と同じであり、その個数は式 (\(\ref{subtree_range}\)) より \(i_{\rm min}-1=\lfloor\frac{i-1}{2^j}\rfloor\times 2^j\) である。
性質 1 より、\(T_{i_\ell,j-1}\) は高さ \(j-1\) の完全二分木である。したがって、\(T_{i_\ell,j-1}\) は \(2^{j-1}\) 個の葉ノードを内包している。
したがって、\(T_{i_\ell,j-1}\) の最も右側に位置する葉ノードは \(i_\ell = \lfloor\frac{i-1}{2^j}\rfloor\times 2^j + 2^{j-1}\) である。
次に、\(T_{i,j_r}\) に含まれる葉ノードの数が \(i-i_\ell\) であることから、\(T_{i,j_r}\) の高さは \(j_r=\lceil\log_2(i-i_\ell)\rceil\) と算出できる。結果的に、任意のノード \(b_{i,j} \in T_n\) における左右のノード \(b_{i_l,j_l}\), \(b_{i_r,j_r}\) は式 (\(\ref{lr_index}\)) のように表すことができる。\[ \begin{equation} \begin{cases} (i_\ell, j_\ell) & = & \left(\left\lfloor \frac{i-1}{2^j} \right\rfloor \times 2^j + 2^{j-1}, j-1 \right) \\ & = & ((i-1)-((i-1) \bmod 2^j) + 2^{j-1}, j-1) \\ (i_r, j_r) & = & (i, \left\lceil \log_2(i-i_l) \right\rceil) \end{cases} \label{lr_index} \end{equation} \]
4.7.  特定のエントリまでの距離
特定のエントリまでの距離
\(n\) 個のデータを持つ木構造 \(T_n\) において、最新のエントリ \(e_n\) から特定のエントリ \(e_k\) までの距離について考える。これは、性質 2 と性質 3 より、\(T_n\) のルートノードから \(b_k\) までの経路上で左枝方向へ移動する回数と等価であり、\(b_k\) を含む完全二分木構造を特定した後はセクション 3.4 の方法を適用できる。
\(T_n\) の部分木で葉ノード \(b_k \in e_k\) を含む完全二分木 \(T'_{i,j}\) を特定する。これは Algorithm 1 で列挙した完全二分木のルートノードのそれぞれに対して式 (\(\ref{subtree_range}\)) を適用し、その範囲内に \(b_k\) を含むかを判定することで行うことができる。ここで \(b_k, e_k \in T'_{i,j} \subseteq T_n\) とする。
完全二分木 \(T'_{i,j}\) のルートノード \(b'_{i,j}\) から葉ノード \(b_k\) への経路で左枝方向へ移動する回数をセクション 3.4 で紹介した方法で算出する。完全二分木 \(T'_{i,j}\) の再左端の葉ノード \(i_{\rm min}\) は 1. で使用した式 (\(\ref{subtree_range}\)) において算出済みであることに注意。
\(T'_{i,j} \ne T_n\) の場合、つまり \(n \ne i\) の場合、\(T'_{i,j}\) は \(e_n\) に含まれる一過性ノードの左枝に接続されていることを意味するため、その距離 1 を加算する。
任意の葉ノード \(b_k\) を内包する完全二分木 \(T'_{i,j}\) は Algorithm 1 を適用して列挙した完全二分木のそれぞれで \(b_k\) を含むかどうかを判断することで特定できる。
Slate の設計はエントリを移動するたびに 1 回の I/O Read が発生する。したがって \(e_n\) から \(e_k\) に到達するまでの距離は、\(e_k\) に含まれる任意のノード \(b_{k,*}\) にアクセスするときに発生する I/O Read 回数と等しい。これは Slate の検索性能的特徴を表す重要な指標である。
前述のように Slate の直列化形式においてはある世代で追加されるすべてのノードが同一のエントリに含まれている。言い換えると、任意の中間ノード \(b_{i,x}\) の右枝側のノード \(b_{i,y}\) は \(b_{i,x}\) と同じエントリに含まれており、従って右枝側への探索はストレージ上の 1 回の seek + read で済むことを意味している。従って最悪ケースはルートノードを起点にすべての移動が左枝側となるようなケース、つまり最も古いデータを検索する場合である。このような最悪ケースで最古のエントリを読み出すための seek + read 回数は \(O(log_2 N)\) となる。
具体例を挙げると、最新のエントリのみをメモリ上にキャッシュしている場合、\(T_{16}\) の木構造に含まれている各ノードに到達するまでの seek + read 回数は Figure 5 のようになる。

命題 4: 完全二分木における距離の分布は二項分布となる。
4.8.  直列化表現
直列化表現
Slate に \(i\) 番目の値 \(b_i\) を追加するとき、一つの葉ノード \(b_i\) と 0 以上の中間ノード \(b_{i,j}\) が発生する。これらのノード情報をまとめ、Slate の直列化表現 \(S\) に \(i\) 番目に追加される要素をエントリ \(e_i\) と表す。これらは Figure 1 の Serialized Layout のように配置される。ここで、\(S\) の最も右に配置されているノードは常に Slate のルートノードである。
エントリ \(e_i\) には同一の世代を持つ全てのノード \(b_{i,*}\) が含まれている。加えて、中間ノードの右枝に接続しているノードは同一の世代であることから、ノードを右枝側に探索するケースは一回のエントリ読み込みで完了することができる。言い換えると、Slate はより最近のユーザデータへのアクセスがより効率的となる特性を持つ。
5.  操作とアルゴリズム
操作とアルゴリズム
Slate の直列化表現であるリスト構造を \(S\) とし、\(S[x]\) を \(S\) の \(x\) 番目に格納されているノードとする。特に \(S[{\rm last}]\) という表記は \(S\) の最末尾のノードを表している。
5.1.  追加操作
追加操作
\(S\) に新しい葉ノード \(b_i\) を追加する操作は Algorithm 1 と Algorithm 2 を用いてエントリ \(e_i\) を構築し \(S\) に連結する。
- 以下のノード集合を用いて \(e_i\) を構築する。ここですべてのノードは \(j\) で降順ソートされるものとする。
- 葉ノード \(b_i\)
- Algorithm 1 で得た順序集合 \(\mathcal{B}'_i\) に含まれる \(b'_{i,*}\) である中間ノード
- Algorithm 2 で得た順序集合 \(\mathcal{B}_i\) のすべての中間ノード
- \(e_i\) を \(S\) に連結する。
この手順により作成される \(e_i\) は、先頭のノードに葉ノード \(b_i\)、末尾のノードに木構造のルートノードを配置している。
Figure 6 は \(T_{13}\) に \(b_{14}\) を追加するために上記の操作を行った結果として構築される木構造である。「新しく追加された \(b_i\) を含む最大の部分木」と「その部分木の左隣りに位置する最も大きな完全二分木」とを中間ノードが接続し木構造全体が接続されることが分かる。

5.1.1.  \({\rm append}(e:{\it Node})\) 関数
\({\rm append}(e:{\it Node})\) 関数
Algorithm 4 は既存の木構造の直列化表現に新しい葉ノード \(b_n\) を追加する操作を表している。
| 1. | \( {\bf function} \ {\rm append}(b_n:Node) \) | |
| 2. | \( \hspace{12pt}\mathcal{B}'_n = {\rm pbst\_roots}(n) \) | // Algorithm 1 |
| 3. | \( \hspace{12pt}\mathcal{B}_n = {\rm ephemeral\_nodes}(n) \) | // Algorithm 2 |
| 4. | \( \hspace{12pt}e_n = {\rm sort} \ (\{b_n\} \cup \{b_{i,*} \in \mathcal{B}'_n \mid i=n\} \cup \mathcal{B}_n) \ {\rm by} \ j \) | // \(j\) で降順ソートされた順序集合となるように |
| 5. | \( \hspace{12pt}S := S \mid\mid e_i \) | |
5.2.  検索操作
検索操作
Slate の検索は通常の二分木検索と同じである。木構造全体が完全二分木となる特殊なケースではすべての葉ノードへは \(O(\log_2 N)\) で均等に到達できるが、そうでない場合、最近追加された葉ノードが比較的レベルの低い部分木に属するという偏りを持つことから、最新のデータがより速く検索できる特徴を持つ。ただしその場合、一過性の中間ノードが存在することにより +1 ステップの操作が必要であるため、検索に対する一般化した計算複雑性は \(O(\lceil \log_2 N \rceil)\) である。
5.2.1.  単一検索操作
単一検索操作
5.2.1.1.  \({\rm contains}(b_{i,j}:{\it Node},k:{\it Int})\) 関数
\({\rm contains}(b_{i,j}:{\it Node},k:{\it Int})\) 関数
二分木の探索で左右の枝のどちらに検索対象の葉ノードが含まれているかは式 (\(\ref{subtree_range}\)) を使用することができる。あるノード \(b_{i,j}\) をルートとする部分木に葉ノード \(b_k\) が含まれるかを判定することで中間ノードの左右の枝のどちらに検索対象の葉ノードが含まれているかを判断することができる。
| 1. | // \(b_{i,j}\) をルートとする部分木構造に葉ノード \(b_k\) が含まれているかを判定 | |
| 2. | \( {\bf function} \ {\rm contains}(b_{i,j}:{\it Node}, k:{\it Int}) \to {\it Boolean} \) | |
| 3. | \( \hspace{12pt}i_{\rm min}, i_{\rm max} = {\rm range}(b_{i,j}) \) | |
| 4. | \( \hspace{12pt}{\bf return} \ i_{\rm min} \le k \ {\bf and} \ k \le i_{\rm max} \) | |
5.2.1.2.  \({\rm retrieve}(e:{\it Node},i:{\it Int})\) 関数
\({\rm retrieve}(e:{\it Node},i:{\it Int})\) 関数
マルチスレッド/マルチプロセス環境で追加と検索の操作を並行処理で行っている場合、追加操作の途中で実行されると \(S[{\rm last}]\) が Slate のルートノードでない可能性があることに注意。
| 1. | \( b_i := {\rm retrieve}(S[{\rm last}], i) \) | |
| 2. | \( {\bf function} \ {\rm retrieve}(b_{i,j}:{\it Node}, k:{\it Int}) \to {\it Node} \) | |
| 3. | \( \hspace{12pt}{\bf if} \ j = 0 \ {\bf then} \) | |
| 4. | \( \hspace{24pt}{\bf return} \ {\bf if} \ i = k \ {\bf then} \ b_{i,j} \ {\bf else} \ {\it None} \) | |
| 5. | \( \hspace{12pt}{\bf else \ if} \ {\rm contains}(b_{i,j}.{\rm left}, k) \ {\bf then} \) | |
| 6. | \( \hspace{24pt}{\bf return} \ {\rm retrieve}(b_{i,j}.{\rm left}, k) \) | |
| 7. | \( \hspace{12pt}{\bf else} \) | |
| 8. | \( \hspace{24pt}{\bf return} \ {\rm retrieve}(b_{i,j}.{\rm right}, k) \) | |
5.2.2.  範囲検索操作
範囲検索操作
すべての要素は \(S\) 上で直列化されているため範囲検索は容易である。\(t_0\) から \(t_1\) までの要素を取得するには、まず \(S\) 上の \(b_{t_0}\) の位置を検索し、そこから \(S\) を右方向に \(b_{t_1}\) を検出するまで読み込むだけで良い。
読み込み位置を \(i\) とすると 1 要素あたり 1 から \(\log_2 i\) 個の中間ノードの読み込みまたはスキップ (seek) が発生するが、中間ノード自体はそれほど大きくなく、連続した領域であることから I/O バッファが有効に機能して大きな影響はないと考えられる。
| 1. | \( {\bf function} \ {\rm range\_scan}(b_{i,j}:{\it Node}, i_{\rm min}:{\it Int}, i_{\rm max}:{\it Int}) \to \) | |
5.2.2.1.  \({\rm range}(b_{i,j}:{\it Node})\) 関数
\({\rm range}(b_{i,j}:{\it Node})\) 関数
| 1. | \( {\bf function} \ {\rm range}(b_{i,j}:{\it Node}) \to ({\it Int}, {\it Int}) \) | |
| 2. | \( \hspace{12pt}i_{\rm max} = i \) | |
| 3. | \( \hspace{12pt}i_{\rm min} = (\lfloor 1/2^j \rfloor - (1 \ {\bf if} \ i \bmod 2^j = 0 \ {\bf else} \ 0)) \times 2^j + 1 \) | |
| 4. | \( \hspace{12pt}{\bf return} \ (i_{\rm min}, i_{\rm max}) \) | |
\(j\) の範囲が \(0..\lceil \log_2 i \rceil\) であることから、\(i\) の定義域を 64-bit とすると \(2^j\) は 65-bit の値域を取りうることに注意。
5.2.3.  ハッシュ付き検索操作
ハッシュ付き検索操作
ハッシュツリーとして要素を検索する場合、要素そのものだけではなく経路から分岐する中間ノードのハッシュ値も取得しなければならない。\(T_n\) を \(b_{n,\ell}\) をルートとする木構造とし、任意のノード \(b_{i,j} \in T_n\) に属するすべての葉ノード (ユーザデータ) を取得するときに必要となる中間ノードついて考える。
5.2.3.1.  \({\rm level}(b_{n,\ell}:{\it Node}, b_{i,j}:{\it Node})\) 関数
\({\rm level}(b_{n,\ell}:{\it Node}, b_{i,j}:{\it Node})\) 関数
ハッシュ付き検索の結果に必要な中間ノードの個数は \(b_{i,j}\) のレベル (\(b_{i,j}\) から目的のルートノード \(b_{n,\ell}\) までの祖先の数) に等しい。もし \(T_n\) が完全二分木であれば \(\ell - j\) であることは明らかだが、そうでない場合、\(b_{i,j}\) を含む完全二分木までの距離をヒューリスティックに求める必要がある。
| 1. | \( {\bf function} \ {\rm level}(b_{n,\ell}:{\it Node}, b_{i,j}:{\it Node}) \to Int \) | |
| 2. | \( \hspace{12pt}{\bf if} \ {\bf not} \ {\rm contains}(b_{n,\ell}, i) \ {\bf then} \) | |
| 3. | \( \hspace{24pt}{\bf return} \ {\it None} \) | |
| 4. | \( \hspace{12pt}b := b_{n,\ell} \) | |
| 5. | \( \hspace{12pt}{\rm step} := 0 \) | |
| 6. | \( \hspace{12pt}{\bf while} \ b \ne b_{i,j} \ {\bf and} \ b.i \bmod 2^{b.j} \ne 0 \) | |
| 7. | \( \hspace{24pt}b := b.{\rm left} \ {\bf if} \ {\rm contains}(b.{\rm left}, i) \ {\bf else} \ b.{\rm right} \) | |
| 8. | \( \hspace{24pt}{\rm step} = {\rm step} + 1 \) | |
| 9. | \( \hspace{12pt}{\bf return} \ b.j - j + {\rm step} \) | |
この関数はサーバ応答に正しい数の中間ノード (ハッシュ値) が含まれていることをクライアント側で検証するために使うことができる。
5.2.3.2.  \({\rm retrieve\_with\_hashes}()\) 関数
\({\rm retrieve\_with\_hashes}()\) 関数
| 1. | \( {\bf function} \ {\rm retrieve\_with\_hashes}(b_{n,\ell}:{\it Node}, b_{i,j}:{\it Node}) \to ({\it Set}[{\it Node}], {\it Sequence}[{\it Node}]) \) | |
| 2. | \( \hspace{12pt}{\bf if} \ {\bf not} \ {\rm contains}(b_{n,\ell}, i) \ {\bf then} \) | |
| 3. | \( \hspace{24pt}{\bf return} \ {\it None} \) | |
| 4. | \( \hspace{12pt}b := b_{n,\ell} \) | |
| 5. | \( \hspace{12pt}{\rm branches} := \emptyset \) | |
| 6. | \( \hspace{12pt}{\bf while} \ b \ne b_{i,j} \) | |
| 7. | \( \hspace{24pt}{\bf if} \ {\rm contains}(b.{\rm left}, i) \ {\bf then} \) | |
| 8. | \( \hspace{36pt}b := b.{\rm left} \) | |
| 9. | \( \hspace{36pt}{\rm branches} := {\rm branches} \mid\mid b.{\rm right} \) | |
| 10. | \( \hspace{24pt}{\bf else} \) | |
| 11. | \( \hspace{36pt}b := b.{\rm right} \) | |
| 12. | \( \hspace{36pt}{\rm branches} := {\rm branches} \mid\mid b.{\rm left} \) | |
| 13. | \( \hspace{12pt}i_{\rm min}, i_{\rm max} = {\rm range}(b) \) | |
| 14. | \( \hspace{12pt}{\rm values} := {\rm range\_scan}(b, i_{\rm min}, i_{\rm max}) \) | |
| 15. | \( \hspace{12pt}{\bf return} \ ({\rm branches}, {\rm values}) \) | |
5.2.4.  分岐ノードの算出
分岐ノードの算出
ある \(T_n\) のルートノードから任意の \(b_{i,j} \in T_n\) までを結ぶ距離を求める。Algorithm 1 によって求めた完全二分木の部分構造のルートノードの中で \(b_{i,j}\) を含む部分木を \(b'_{i',\log_2 i'}\) とする。
- 対象のノード \(b_{i,j}\) を含む完全二分木のルートノードを取得し、\(T_n\) のルートノードからの距離を得る。
- 完全二分木のルートノードを \(b'_{i',j'}\) としたとき、\(b'_{i',j'}\) からの距離 \(j' - j\) を計算する。
| 1. | \( {\bf function} \ {\rm nodes\_at\_branches}(n:{\it Int}, i:{\it Int}, j:{\it Int}) \to {\it Int} \) | |
| 2. | \( \hspace{12pt}\mathcal{B}'_n = {\rm Algorithm1}(n) \) | |
| 3. | \( \hspace{12pt}b := {\rm root \ of \ } T_n \) | |
| 4. | \( \hspace{12pt}{\bf for} \ b'_{i',j'} \ {\bf in} \ \mathcal{B}'_n \) | |
| 5. | \( \hspace{24pt}{\bf if} \ {\rm contains}(b'_{i',j'}, i, j) \) | |
5.3.  補助的操作
補助的操作
5.3.1.  起動時の初期動作
起動時の初期動作
すべての操作は木構造のルートノードを含むエントリ \(S[{\rm last}]\) に頻繁にアクセスするため、効率的な動作のために起動時に \(S[{\rm last}]\) の内容を読み込んでメモリ上で保持すべきである。しかし、先頭の \(S[1]\) から逐次読み込んでいては \(S\) が大きくなったときに時間がかかることから、ファイルの末尾から \(S[{\rm last}]\) を取得できるようにすべきである。これは次のように実装できるだろう:
ファイルの末尾から固定長の seek で \(S[{\rm last}]\) の先頭位置が分かる情報を入れておく。
\(S[{\rm last}]\) からその情報までが正しい情報であることを確認するためのチェックサムを入れておく。
ノードとしては正しいがすべての中間ノードが書き込まれていない状況を検知するため、読み込んだ \(S[{\rm last}]\) が木構造全体を表していることを確認する。
\(S[{\rm last}]\) の破損を検出した場合、\(S[1]\) から最後に正しく読み込みができた要素 \(b_i\) を \(S[{\rm last}]\) として
5.3.2.  ロールバックと末尾置換操作
ロールバックと末尾置換操作
ロールバック操作は直列化されたストレージをある世代の位置まで truncate するだけである。
6.  複雑性の解析
複雑性の解析
6.1.  時間複雑性
時間複雑性
6.2.  空間複雑性
空間複雑性
6.3.  I/O 複雑性
I/O 複雑性
現実的なコンピュータシステムでは、メインメモリと HDD や SSD などの二次記憶装置の間に数桁の性能差が存在し、メモリ階層の性能特性はアルゴリズム設計の重要な制約となる。Slate のようなディスク指向のデータ構造においては、メモリ上での \(O(\log N)\) 程度の木構造操作に要する計算コストは単一の I/O 操作によって完全に償却される可能性が高い。したがって、ディスク指向データ構造の実際の性能特性は I/O アクセスパターンに大きく依存することとなり、現実的な性能要因は I/O 複雑性が支配的となる。
Slate における I/O アクセスパターンは 2 つある。一つ目は追記操作で、これは常に \(O(1)\) の Seek なし I/O Write 操作で完了する。二つ目は読み取り操作で、検索対象データの時間的位置により I/O 複雑性が変化する。このセクションでは、データ読み取りに対する Seek 操作を伴う I/O Read の複雑性について論議する。
6.3.1.  読み取り操作時の I/O パターン
読み取り操作時の I/O パターン
Slate における読み取り操作の I/O 操作はエントリ単位での Seek + Read として発生し、各 I/O 操作は二次記憶装置上の異なる位置への物理的なランダムアクセスとなる。
6.3.1.1.  I/O Read 回数の算出
I/O Read 回数の算出
木構造 \(T_n\) における位置 \(i\) のデータを参照するために発生する正確な I/O 回数は、木構造のルートノードから \(b_i\) への探索経路上で遭遇するエントリ数として定義される。これは Algorithm 3 の実行によって求めることができる。
Slate の構造的特性により、右枝方向への移動は同一エントリ内で完結するため追加の I/O を伴わない。一方、左枝方向への移動は異なるエントリへのアクセスを要求することから新たな I/O が発生する。したがって、位置 \(i\) への I/O 回数は、ルートノードから \(b_i\) への探索経路における左枝移動回数 (場合によって +1) として算出される。
6.3.1.2.  I/O Read 回数の分布と上限/下限
I/O Read 回数の分布と上限/下限
Slate の構造上、任意のエントリ \(e_i\) に到達するまでに要する I/O 回数の分布は一様ではない。この分布を単純な数学的表現で記述することは困難だが、ここでは以下の境界特性によってその上限と下限を決定することができる。
まず、木構造が完全二分木であると仮定した場合の分布について考える。セクション 3.4 で述べたように、これはルートノードからの経路で左枝方向へ移動した回数と一致するため、最新の値 \(b_n\) から \(b_i\) の距離のハミング重みの分布となる。
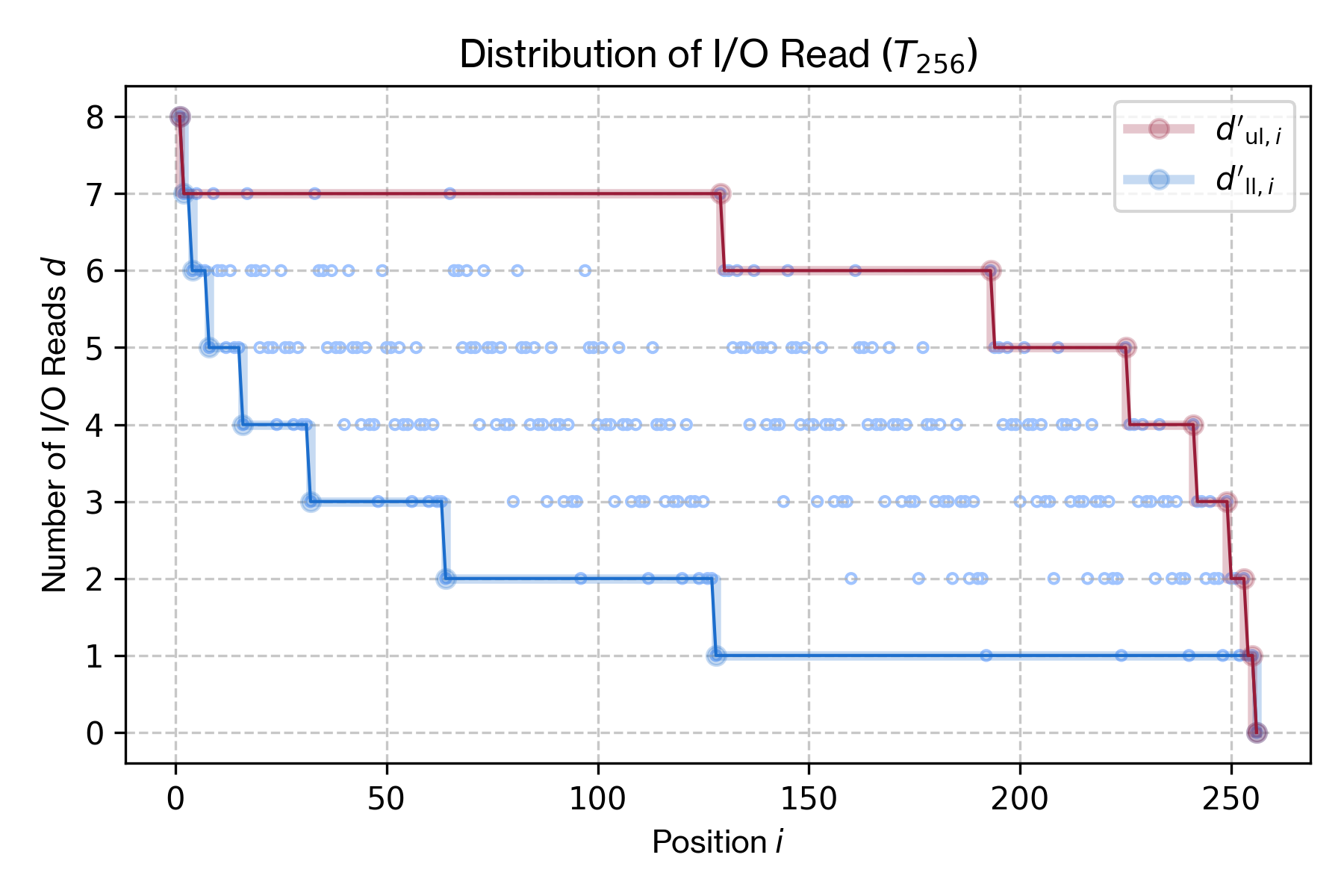
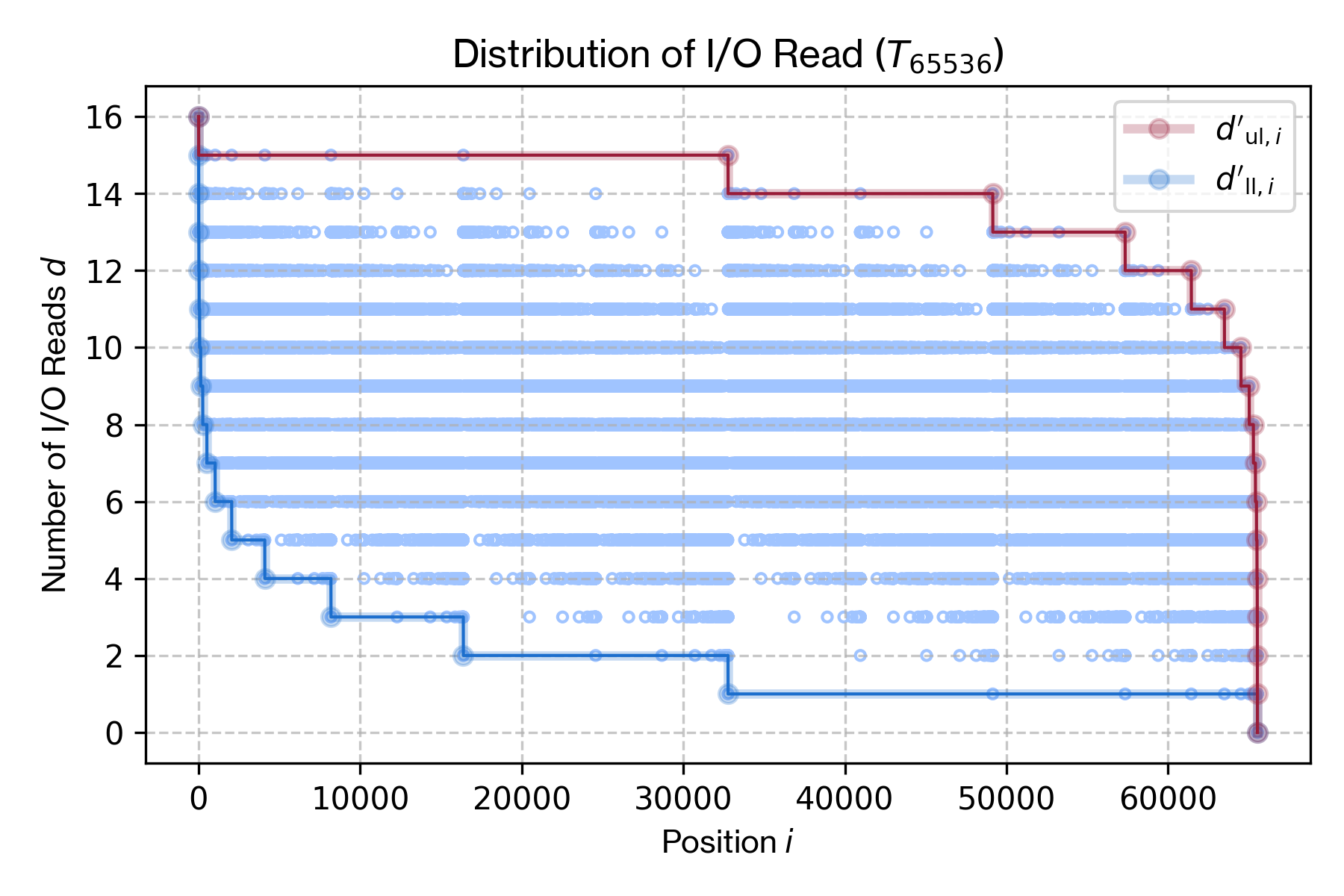
\(n=2^h\) 個のデータを含む完全二分木構造 \(T'_n\) において、最新のエントリ \(e_n\) から任意の位置のエントリ \(e_i\) に到達するまでに必要な I/O Read 回数 \(d\) の上限 \(d'_{u,i}\) と下限 \(d'_l\) はそれぞれ式 (\(\ref{io_read_worst}\)) のように表すことができる。\[ \begin{equation} \left\{ \begin{array}{ll} d'_u & = \left\lfloor \log_2 (n - i + 1) \right\rfloor \\ d'_l & = \left\lceil \log_2 \frac{n}{i} \right\rceil = h - \left\lfloor \log_2 i \right\rfloor \end{array} \right. \label{io_read_worst} \end{equation} \] \(i\) について展開すると I/O Read 回数 \(d\) の上限と下限に対応する範囲が得られる。\[ \begin{equation} \left\{ \begin{array}{l} i \le n + 1 - 2^{d'_u} \\ i \ge 2^{h-d'_l} \end{array} \right. \label{io_read_range} \end{equation} \] 上限 \(d'_{u,i}\) と下限 \(d'_{l,i}\) は双方とも単調減少の関数である。その最大値は上限における \(i=1\) のケース、最小値は下限における \(i=n\) のケースである。\[ \begin{equation} \left\{ \begin{array}{ll} d'_{\rm max} & = \left\lfloor \log_2 n \right\rfloor = h \\ d'_{\rm min} & = \left\lceil \log_2 1 \right\rceil = 0 \end{array} \right. \label{io_read_minmax} \end{equation} \]
Figure 7 は実際に Algorithm 3 を用いて算出した \(T_{256}\) と \(T_{65536}\) に対して各位置 \(i\) の I/O Read 回数と上限、下限を描画したものである。上限と下限は点対称の対数曲線となっていることが分かる。
次に、\(T_n\) が完全二分木ではない場合について考える。この場合、木構造が内包する複数の完全二分木を一過性ノードが連結するという構成である。各完全二分木の上限、下限、最大、最小は式 (\(\ref{io_read_worst}\)) と (\(\ref{io_read_minmax}\)) に従うが、最も右に位置する完全二分木以外は一過性ノードからの +1 ステップが追加される。
このスケッチを Figure 8 に表す。これは \(n=352=2^8+2^6+2^5\) の木構造を表しており、高さがそれぞれ 8, 6, 5 の 3 つの完全二分木を内包している。各完全二分木はそれぞれ式 (\(\ref{io_read_worst}\)) にしたがう上限/下限の特性を持ち、最も右の完全二分木以外は I/O Read 回数が +1 加算されている。
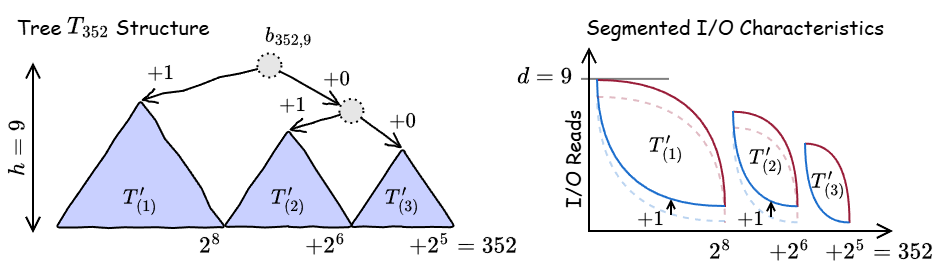
Figure 9 は Algorithm 3 を用いて \(n=352\) での I/O Read 分布をプロットしたものである。3 つの完全二分木に対応する分布が存在し、それぞれ (\(\ref{io_read_worst}\)) にしたがう上限/下限が存在していることが分かる。
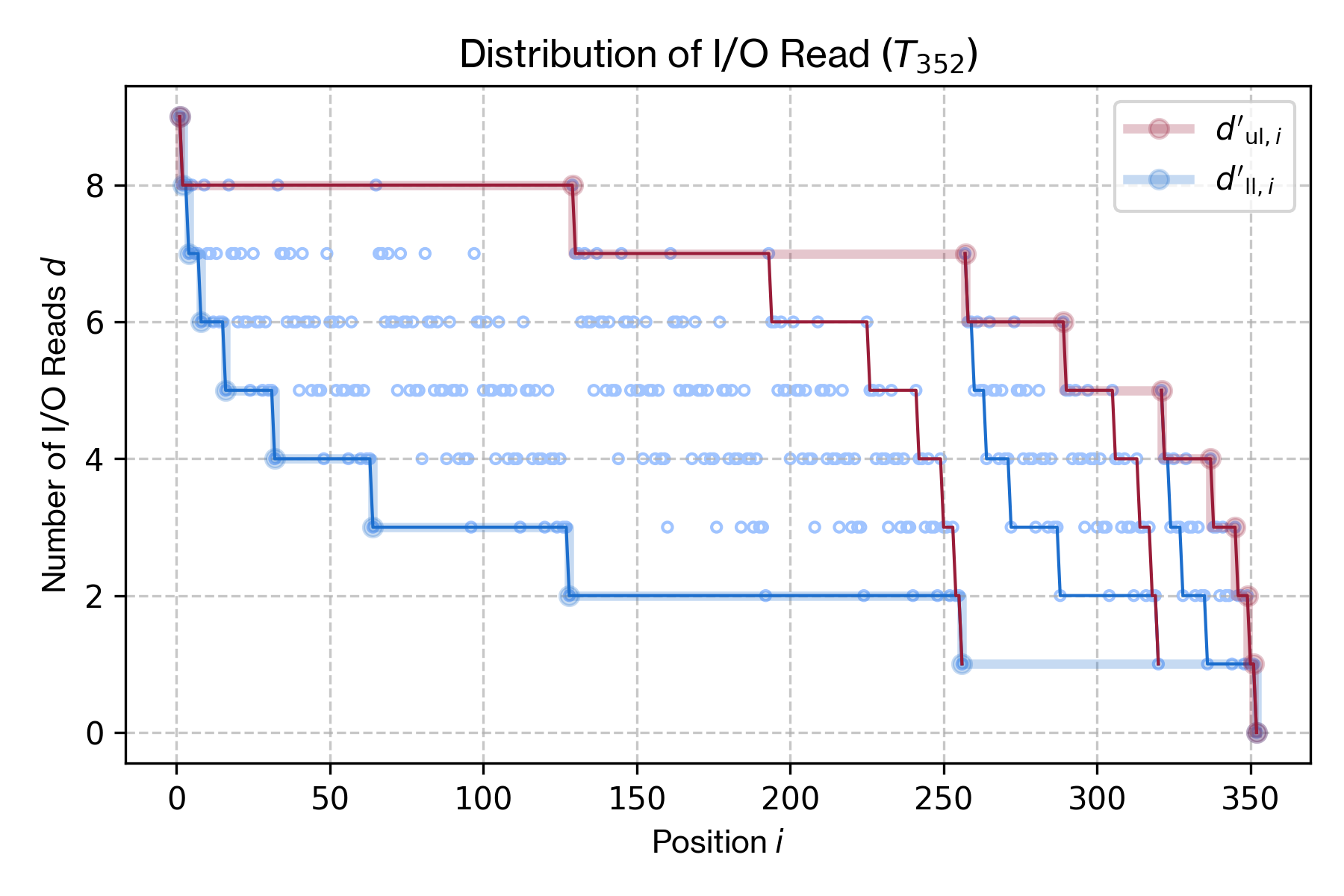
完全二分木が内包する完全二分木に対して再帰的に同様の操作を行うことでより詳細な I/O Read 回数を表現することができるかもしれないが (これは最終的に Algorithm 3 に到達するだろう)、本文書の主題とは異なるため「第一層」のみにとどめる。
上限. 単純な数式表現は困難だが、各完全二分木において右の完全二分木のもっとも大きい \(d'_u\) を自身の \(d'_u\) へ順に接続することで求めることができる。これは、異なる対数減少を段階的に接続した形となるため、正確な対数ではないものの対数減少と似た性質を持つ曲線となる。
下限. 最右端のノードで \(d=0\) となる以外は最も左に位置する完全二分木の下限が全体に適用される。
Slate におけるデータアクセスは \(O(\log (n-i))\) の I/O Read 回数を上限とする。これはより新しいデータ (つまり \(n\) に近い位置のデータ) ほど少ない I/O Read しか必要としないことを意味する。また、最悪ケース、つまり最新のデータから最も離れた \(i=1\) へのアクセスであっても I/O Read 回数は \(O(\log n)\) であり、これは一般的な二分木で各ノードごとに I/O が発生するケースと同程度である。
この I/O 分布の非対称性は Slate の時間的局所性最適化の特徴である。結論として、Slate は新しいデータほどアクセス効率が良いという傾向を持ち、これは現実的な時系列データやログ構造における典型的なアクセスパターンと整合する。
7.  実装上の考慮
実装上の考慮
7.1.  キャッシュ設計
キャッシュ設計
Slate での追加操作と検索操作を効率的に実行するためには、木構造の特定のノードを戦略的にキャッシュする必要がある。このセクションでは Slate の構造的特徴を考慮したキャッシュ設計について記述する。
7.1.1.  キャッシュ忘却特性
キャッシュ忘却特性
Slate が厳密な意味でのキャッシュ忘却アルゴリズム (Cache-Oblivious Algorithm) とは断言できないが、以下の特性からキャッシュ忘却に近い特性を持つと予想する。
直列化レイアウトでの局所性: 同一世代のノード \(b_{i,*}\) がすべて同一エントリ \(e_i\) に格納され、右枝方向への探索が単一のメモリブロック内で完結する。この特性は、キャッシュラインサイズやページサイズに依存せずに局所性の恩恵を受ける。
再帰的な完全二分木構造: Slate が内包する完全二分木 \(T'_{i,j}\) はそれぞれ独立した部分構造として扱うことができる。これは一般的な木構造と同様の階層的アクセスパターンと言える。これにより、キャッシュ階層の深さにかかわらず、自然に階層的な局所性を活用できる。
アクセスパターンの偏り: Slate は新しいデータほど浅い位置に配置される構造的特徴を持つ。これは、時系列データの「最近のデータほどアクセス頻度が高い」という性質と整合する。この偏りはキャッシュサイズにかかわらず有効に機能する。
Slate が内包する完全二分木では標準的な二分探索木と同等のキャッシュ忘却性を持ち、最悪ケース (最古のデータへのアクセス) であっても、各レベルでたかだか 1 回のキャッシュに抑えられることから、次の予想が成り立つと考える。
予想: メモリ階層のパラメータ (キャッシュサイズ \(M\)、ブロックサイズ \(B\)) を知らない状態であっても、\(n\) 個の要素を持つ Slate における検索操作のキャッシュミス回数は \(O(\log_B n)\) となる。
このようなキャッシュ忘却の特性により、Slate は様々なハードウェア環境において明示的なキャッシュ管理を実装しなくても効率的な性能を発揮することが期待される。ただし、この特性は理論上の予測であり、厳密な証明は今後の課題である。
7.1.2.  段階的なキャッシュ戦略
段階的なキャッシュ戦略
Slate におけるキャッシュ忘却特性は主にデータの局所性に由来する特徴で、ディスク I/O の削減や CPU キャッシュの有効活用に関連している。一方で、現実の実装では計算の削減を目的として明示的なキャッシュが推奨される。
Slate の優れた構造設計により、最新エントリ \(e_n\) には木構造の操作を開始するために必要な以下の情報がすべて含まれている。
現世代のルートノード \(b_{n,\lceil \log n \rceil}\): これはすべての操作の起点となる。
完全二分木のルートノードへの参照: 追加操作において新しく発生するノードとの接続先として (実データではなく位置のみが) 参照される。また検索操作では I/O なしに完全二分木のルートの位置を特定できる。
一過性ノード集合 \(\mathcal{B}_n\): 現世代の木構造を形成する。
この特性により、キャッシュを全く使用しない場合であっても、直列化表現 \(S_n\) の末尾のエントリ \(e_n\) の 1 回の読み込みで木構造の操作を開始できる。
言い換えると、最新のエントリ \(e_n\) をメモリ上にキャッシュするだけでも、すべての主要な操作において最初の 1 回の読み込みを削減できる。\(e_n\) のキャッシュに必要な空間計算量は \(O(\log n)\) と極めて小さく、その効果はあらゆる操作で一律 1 回の I/O 削減として現われる。この費用対効果の高さから、最新エントリのキャッシュは強く推奨される。
加えて、読み込み中心のワークロードでは、キャッシュの範囲を木構造の下に向かって段階的に拡張することでさらなる性能向上が可能である。ここで、上で述べた最新エントリ \(e_n\) のキャッシュをレベル 0 (基本キャッシュ) とする。レベル \(k\) のキャッシュは完全二分木のルートから深さ \(k\) までのノードを含むエントリをキャッシュする。空間計算量は \(O(2^k \times (\log n)^2)\) となるが、\(k\) の上限は木の高さ \(\log_2 n\) に制限される。
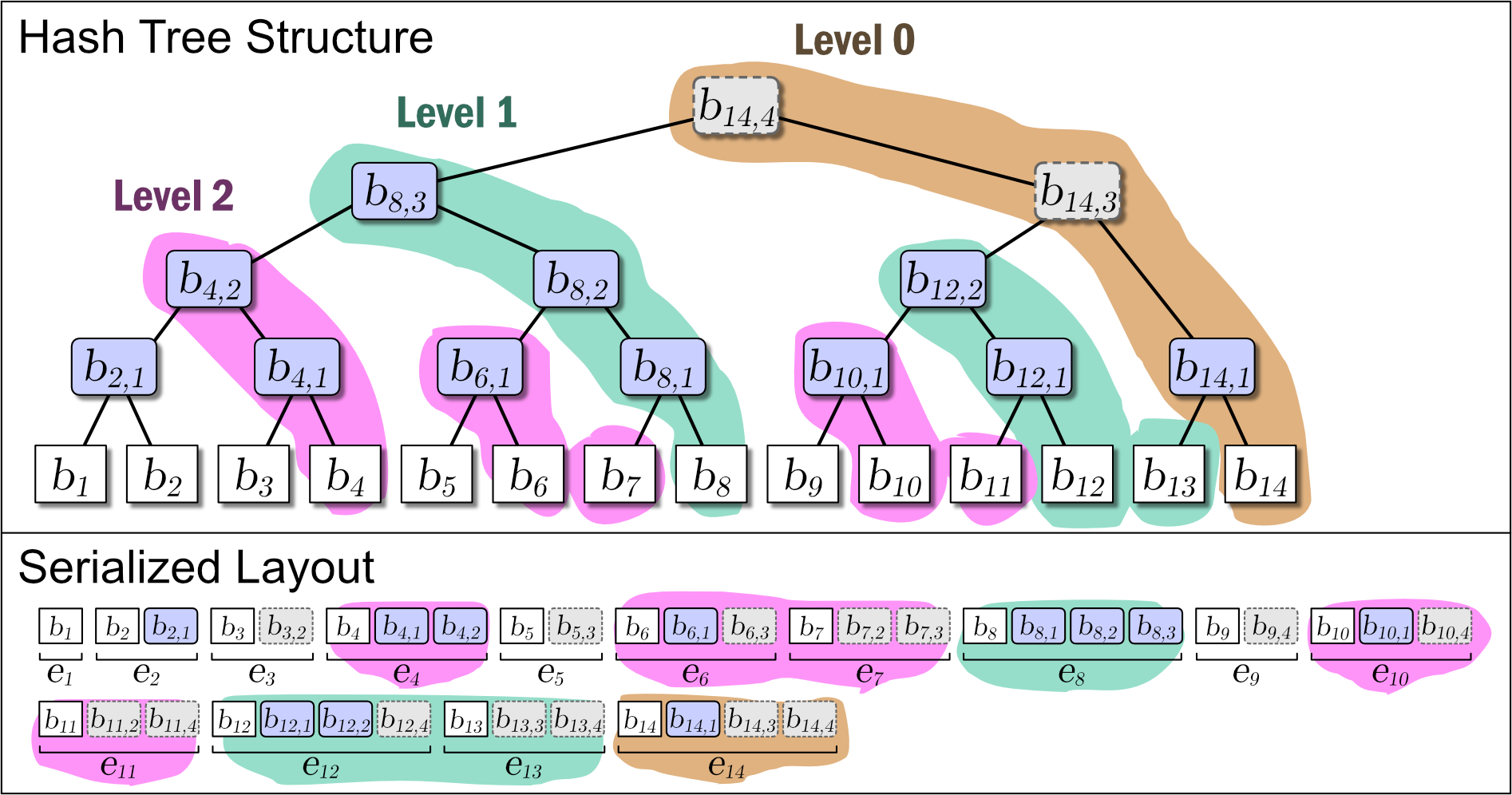
例えば、レベル 1 は \(T_n\) が内包する各完全二分木のルートノード \(b'_{i,j} \in \mathcal{B}'_n\) を含んでいる各エントリ \(e_i\) をキャッシュする。これにより、完全二分木の探索を I/O なしに開始することが可能となり、追加で 1 回の READ が削減される。空間計算量は \(O((\log n)^2)\) となる。さらにレベル 2 では、各完全二分木のルートノードの左枝の子ノードを含む各エントリをキャッシュする。完全二分木内の最初の分岐までがカーバされるようになり、さらに 1 回の READ が削減される。このようにして、検索のワークロードに対して適応的に段階化されたキャッシュを使用することができる。
7.1.3.  実装上の推奨事項
実装上の推奨事項
Slate の段階的キャッシュは 1 レベルの追加で全範囲のデータに渡って 1 回の I/O Read 削減できる。一方で、多くのアプリケーションではレベル 0 の基本キャッシュのみでも十分な効果があるだろう。追記中心のワークロードではキャッシュレベルの追加は世代移行の負荷が増加する。特に、最近のデータへのアクセスが多い時系列データ処理では、キャッシュレベルの追加は空間量と計算量を過度に消費するだけで実効的な効果をもたらさない可能性がある。
一方、全データ範囲にわたる均等なアクセスパターンを持つアプリケーションでは、キャッシュレベルの追加によってよって古いデータへのアクセスも効果を期待できる。キャッシュが占有する空間はレベル \(L\) に対して \(O(L^2 \log n)\) で増加するため、レベル 2 以上は追記頻度が低く低レイテンシーのアクセスが要求される用途でのみ考慮されるべきである。
このように、Slate のキャッシュ設計は、最小限のメモリ使用量で効果を得られる基本戦略と、アクセスパターンに応じた段階的な拡張オプションを提供する。構造自体が局所性を持つことにより、キャッシュなしでも実用的な性能を持ちながら、単純なキャッシュ戦略で有効な性能向上を実現できる。
従来の検索木におけるキャッシュ最適化では探索経路の重複排除が重要であるが、ハッシュツリーにおいては認証パス生成や差分検出のために兄弟ノードのハッシュ値も必要となるため、単純な経路最適化では不十分である。SLATEにおけるキャッシュ戦略は、探索効率よりもハッシュ値の検証処理に必要なノード集合の局所性を重視する必要がある。
追加の選択肢として、最近アクセスしたエントリ (LRU などで) や頻繁にアクセスのあることが分っている世代のノード集合をヒューリスティックにキャッシュすることが考えられるが、その有効性はアプリーションのアクセスパターンに依存するためここでは省略する。
7.2.  並行処理
並行処理
実用的なシステムでは複数のプロセスやスレッドからの並行したアクセスが前提となる。特にトランザクションログやブロックチェーンの用途では並行性が必須となる。Slate の構造的特性は並行処理の環境で特に有利に機能する。確定済みとなり、書き込まれたすべてのノードとその関連する木構造が永続的となった部分木には、複数のプロセスが並行してデータにアクセスできる。
7.2.1.  読み取りの安全性
読み取りの安全性
\(n\) 世代までが確定している (truncate や replace が起きない) のであれば、木構造 \(T_n\) も直列化表現 \(S_n\) も値や構造が変わることはない。したがって、追記操作とは完全に独立して読み取り操作が可能である。
確定済みエントリの安定性: 一度書き込まれたエントリは変更されない。
Slate に書き込まれた要素および関連するツリー構造が永続的であることは並行処理に有利に機能する。直列化表現 \(S\) への要素や中間ノードの追加は単一プロセスで行う必要があるが、検索については検索開始時点の確定済み木構造を基準に行うことで、追加処理や他の検索処理が進行中であっても安全に行うことができる。
7.2.2.  書き込み競合の回避
書き込み競合の回避
Slate への新しい世代の追加は、木構造の一貫性とファイルの整合性を保つために単一のプロセスまたはスレッドで行う必要がある。これは、新しいエントリの構築と直列化表現の書き込みが青とミックに行われることを保証するためである。
複数のプロセスまたはスレッドが Slate を共有するケースにおいて、整合性を保証する最も簡単な方法は、書き込み操作に対して排他制御を適用することである。追加操作を実行するプロセスは、まず書き込みロックを獲得し、新しいエントリの構築とファイルへの書き込みを完了した後、ロックを解放する。この方法は単純で確実だが、書き込み頻度が高い場合にはロック競合により各プロセスのスループットが低下する可能性がある。
より高度な設計として、書き込み操作を専用のプロセスまたはスレッドに委譲する方法がある。この設計では、追加要求をジョブキューに投入し、専用の書き込みプロセスがそれを逐次処理する。これにより書き込み操作の直列化が自然に実現され、ロック機構が不要になる。ただし、キューの管理やプロセス間通信 (終了の通知など) のオーバーヘッドが発生することからシステム全体の構造が複雑化する。
追加操作の頻度がそれほど高くないシステムでは、楽観的ロックを使用することで CPU リソースの効率的な利用が期待できる。この方式では、各プロセスは以下の手順で追加を試みる:
まず、現在の確定済み世代 \(x\) のエントリを参照し、それに基づいてメモリ上で新しい世代 \(x+1\) のエントリを作成する。世代 \(x\) のエントリは immutable であり、エントリの構築はローカルな操作であるため、他に同じ処理を行おうとしているプロセスと競合することなく実行できる。
次に Compare-and-Swap (CAS) 操作を用いて世代番号の更新を試みる。世代 \(x\) から \(x+1\) への更新に成功した場合、現在のルートを新しいエントリのルートに更新し、ファイルへの追記を実行する。もし他のプロセスが先に世代を更新していた場合、構築したエントリを破棄し、最新の状態を参照して最初からやり直す。
7.2.3.  楽観的ロックを使った並行書き込み
楽観的ロックを使った並行書き込み
要素の追加頻度がそれほど高くないシステムにおいては、追記操作において楽観的ロックを使うことで CPU リソースの効率化を期待することができる。
一つの方法は、確定済みの高さを表すアトミック更新が可能な変数 \(x_1\) と、追加処理が進行中の高さを表す CAS (Compare and Swap) が可能な変数 \(x_2\) を使用する。追加処理を開始したプロセス \(P\) はまず \(x_1\) から最新の確定済み高さを参照し (仮にその値を \(n\) とする) 木構造 \(T_n\) に基づいて要素や中間ノードの直列化表現をメモリ上で準備する。次に、実際に書き込みを行う直前に \(x_2\) に対して \(n \to n+1\) の更新を試みる。\(x_2\) の更新に成功した場合、実際に書き込みを行い、最後に \(x_1\) を \(n+1\) に更新する。\(x_2\) の更新に失敗した場合は自身が基準にした木構造 \(T_n\) が最新ではないため最初からやり直す。ただし、この方法は \(x_2\) の更新に成功したプロセスが \(x_1\) を更新する前に (外部からのシグナルや disk full などで) 停止してしまうケースである。この場合、ある一定期間 \(x_1 \ne x_2\) かつ書き込みが進行していなければ、書き込み中のプロセスが使用している I/O リソースをクローズし、書き込み位置を \(x_1\) の最後まで戻し、最後に \(x_2\) を \(x_1\) と等しくなるように戻すといったタイマー監視の処理が必要になるかもしれない。
7.3.  障害耐性と回復
障害耐性と回復
Slate では直列化された個々のノードが (ハッシュツリーのハッシュ値はと別に) チェックサムを持つことでデータの破損を検出可能にしている。
要素の追加操作中にシステムが異常終了した場合、次に起動したときに \(S[{\rm last}]\) が破損している可能性がある。それぞれのノードはチェックサムを追加することによって破損を検出できるようにしている。
最後のエントリがすべてのデータとツリー構造を要約していることから、完成した Slate の最後のエントリに対する署名を追加することで、第三者が検証可能なように "封印" することができるだろう。
7.4.  コンパクション
コンパクション
Slate に格納されるデータ列 \(D = \{d_1,d_2,\ldots,d_n\}\) に対して、任意の部分範囲 \(D^*\) で畳み込み関数 \(f: D^* \to C\) が定義でき、畳み込み結果のマージ関数 \(m: C \times C \to C\) が定義できる場合、Slate 上で LSM-Tree のようなコンパクションを実装することができるだろう。
まず、完全二分木 \(T'_{i,j} \in T_n\) がある条件を満たしたときに、その \(2^j\) 個の葉ノードを畳み込みを行う。取り得る条件の一つは、\(j\) があるしきい値 \(\theta\) を超えたときである。典型的には \(\theta = \alpha \log n\) であり、\(\alpha\) は調整可能なパラメータ、\(n\) は期待データサイズである。また、最新のデータからの差が \(\delta\) を超えたことを条件としても良い。ここで、ハッシュツリー上は畳み込み済みの完全二分木のルートに相当するハッシュまでを保持する。次に、2 つの畳み込み済み完全二分木が一つの完全二分木に統合されるとき、それらの畳み込み済み状態をマージする。木構造が成長するにしたがってこの操作を繰り返すことで、古いデータを圧縮することができる。
差分の検出は畳み込み済みの完全二分木のルートまでとする。その位置のハッシュ値が異なる場合、畳み込み結果の中に差分が含まれていることから、その畳み込み結果を同期する必要があることがわかる。
Slate の永続的データ構造により、この畳み込みやマージは追記操作や他の参照操作と競合せずに行うことができる。このコンパクション機構は、Slate に時間的局所性を保ちながら空間効率を大きく改善する可能性がある。
8.  実験的評価
実験的評価
このセクションでは、実際に Slate の実装を使用して行ったベンチマークの結果を示し、現実の性能特性がこの文書で説明した理論的挙動と一致しているかについて議論する。また、同じ Slate の構造だがストレージタイプが異なる実装や、Slate と類似した別のデータ構造と比較する。
8.1.  ベンチマーク環境
ベンチマーク環境
まずベンチマークの計測に使用した環境やパラメータの詳細と、その選定理由などを記述する。
8.1.1.  比較対象のデータストア実装の選定
比較対象のデータストア実装の選定
残念ながら、私の知る限り Slate と類似した目的を持ち直接的な比較対象となるような実装は存在しない。一つの可能な選択肢はバージョン管理機能を持つ検証可能な Key-Value ストアである。そのようなコンポーネントはブロックチェーンで必須の機能であり、いくつかの実装が現実適用されている。ただし、これらはデータストアの改ざん検出やデータの包含判定 (メンバーシップ検証) といった旧来の Merkle Tree としての機能に特化しており、目的の異なる Slate と比較することはあまり意味がないことかもしれない。また、多くはそのブロックチェーン実装に強く依存しており、Slate と比較可能な機能だけを切り離すことが困難である。
このセクションでは、このような選択の困難がありながら、以下のデータストア実装を比較対象として選定した。ただし、すべてのワークロードですべての実装と比較できたわけではない点に注意。
Slate (file): 単一のファイル上に構築した Slate 実装。この文書で議論の対象としている実装である。
Slate (rocksdb): Slate のデータ構造を持ち、ストレージ層 (バックエンド) を RocksDB に置き換えたバージョン。Slate のストレージ層はいくつかの規約を実装できれば差し替え可能である。RocksDB は LSM-Tree 構造を持ち、一般に広く使われている埋め込み型 Key-Value ストアに対して、単一ファイルでの追記優位性や参照性能の比較を意図している。
Slate (memkvs): Slate のデータ構造を持ち、ストレージ層をメモリ上の HashMap に置き換えたバージョン。ノードの直列化や I/O のコストが存在しないケースのベースラインを大まかに知ることを意図している。
Unindexed Sequence File: 単一ファイルに固定長データを単純に追記するだけの実装である。追記において、Slate のノード操作に関連する時間および空間複雑性が存在しない場合のベースラインを大まかに知ることを意図している。また参照では後方からのナイーブな逐次検索を行うケースとする。
Binary Tree (file): 単一ファイル上に保存された完全二分木構造の単純な Hash Tree。ストレージ層は Slate (file) と同じ実装である。時間的局所性を持たない構造として比較することを意図している。
IAVL+: Cosmos (Tendermint) において StateDB をバージョン管理するための Merkle Tree に基づく Key-Value ストア。
DoltDB: git に似たバージョン管理が可能な Key-Value ストア。
また、以下の実装はこの計測での比較対象からは除外した。
Merkle Patricia Trie: Ethereum で使用されている、疎なデータ集合に最適化された Merkle Tree (Trie 木)。ただし Ethereum の State DB に大きく依存した実装となっており、Slate と比較可能な機能のみを切り離すことが可能かが疑わしかったため、比較対象から除外している。
8.1.2.  計測するワークロード
計測するワークロード
append: 対象とするデータストアにデータを順番に追加してゆき、特定のデータ数に到達するまでの時間と、その時点でのストレージ消費量を計測する。
get: 特定のデータ数 \(n\) が保存されたデータストアに対し、様々な位置 \(i\) に対してデータを参照する時間を計測する。これは比較対象のデータストアでの位置に対する参照性能の特性を調べることを目的としている。
biased get: アクセス頻度が位置の Zipf 分布に従うワークロードでデータを参照する時間を計測する。最新に近いデータがアクセスされやすい環境で参照コストがどのように変化するかを調査し、この文書で主張する時間的局所性が有効に機能することを示す。
cached get: キャッシュレベルの変化に対するデータ参照時間の推移を計測し、キャッシュによる I/O 回数の削減が参照性能に与える影響を示す。
branch detection: ある位置で分岐したデータ列が保存されている 2 つのデータストアにおいて、分岐した位置を特定するまでの時間を計測する。
ロールバック操作 (truncate) や末尾置換操作 (suffix replacement) は get と append の組み合わせであるため、この計測からは省略している。
8.1.3.  計測パラメータと環境のプロビジョニング
計測パラメータと環境のプロビジョニング
ベンチマークはパブリッククラウドである AWS 環境で行った。この理由は、追試が必要なときに同等の環境を準備することが容易であることに加えて、パブリッククラウドで広く利用されている構成は商用的な意味での「現代の一般的なコンピューティング性能」基準を示唆していると考えられるためである。また、特定の実装に有利/不利なハードウェアが意図せず配備されている可能性を排除することも意図している。このベンチマーク環境の詳細を Table 1 に示す。
| Date | 2025-09-18 |
|---|---|
| Platform | AWS EC2 c5.2xlarge (8vCPU Intel Xeon Platinum 8124M 3.00GHz, 16 GiB memory) |
| Operating System | Ubuntu 24.04.3 LTS, Linux kernel 6.14.0-1012-aws |
| Storage used | EBS gp3, 2.0 TB NVMe (ext4); SeqWrite 149.0 MiB/s, SeqRead 131.0 MiB/s, RandWrite 1699 IOPS, RandRead 1699 IOPS |
ストレージの EBS はベースラインスループットの 125 MiB/s に制限されていることに注意。これは SATA 接続の HDD と同程度のスループットである。したがって、以下に示す実測値は HDD 程度のスループットにおける性能であることを想定すべきである。
現実的な計測では利用可能なリソースやコストが限られており、与えられたリソース上でなるべく広範囲をカバーする計測を行うべきである。Table 1 のプラットフォーム上で何度かの予備計測を行い、以下の 2 つの方針で計測することにした。
異なるデータストア実装の性能特性を比較するための計測。このベンチマークでは \(n = 8{\rm Mi} = 8 \times 1024^2\) エントリで行う。この数は 1) 16 GiB のメモリで単一の memkvs Slate を展開可能なエントリ数と、2) 2.0 TiB のストレージで単一の rocksdb Slate を展開可能なエントリ数に基づく。
ファイル実装の Slate にフォーカスして Slate の性能特性を知るための計測。このベンチマークでは \(n = 2{\rm Gi} = 2 \times 1024^3\) エントリで行う。この数は 2.0 TiB のストレージで分岐検出のために複数の file Slate を展開可能なエントリ数に基づく。
各データストア実装に実際に保存するデータは、データの位置 \(i\) を SplitMix64 で乱数化した値 \(v_i = {\rm splitmix64}(i)\) を保存する。\(v_i\) は 64-bit 整数であり、ストレージ上は \(|v_i|=8\) バイト固定長のリトルエンディアン表現で保存される。
8.2.  性能比較
性能比較
このセクションでは、対象とするデータストア実装に対して、上記のワークロードで計測した結果を示し、議論する。
8.2.1.  append 性能比較
append 性能比較
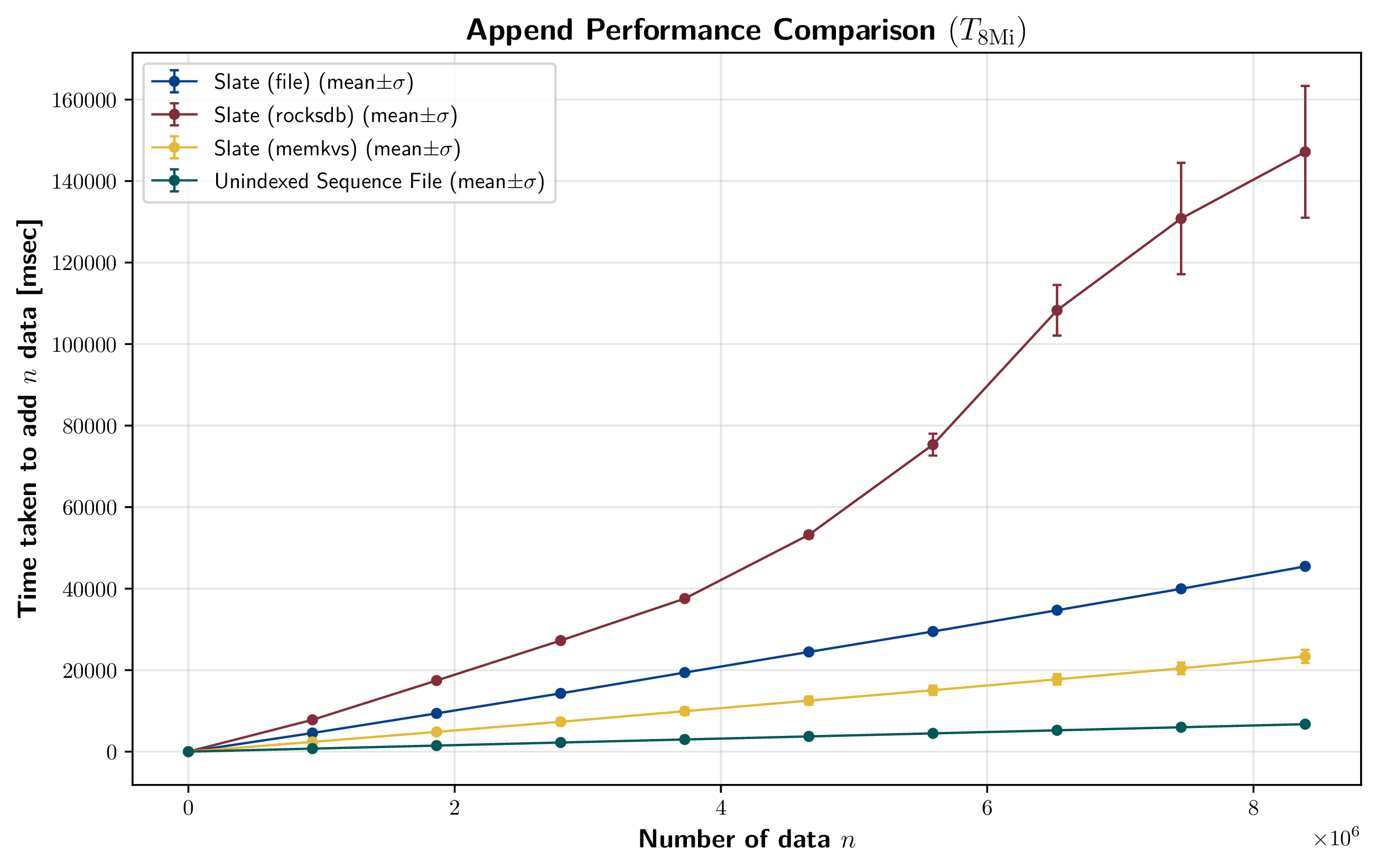
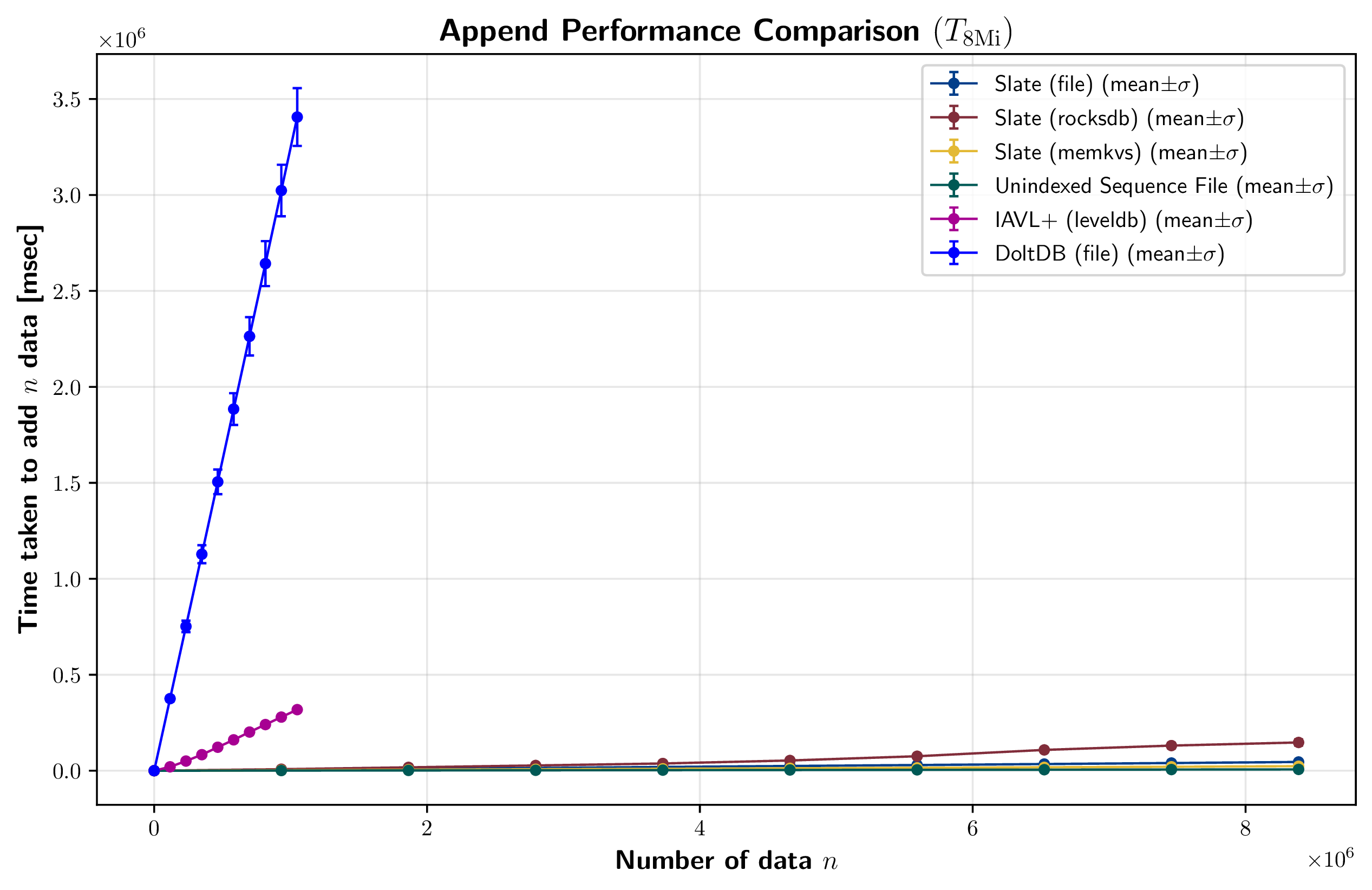
いくつかの実装で append の性能を計測した結果を Figure 11 に示す。これは各実装において \(n\) 個のエントリを追加するまでにかかった時間の推移を表している。
それぞれの実装について、\(x\) 個のエントリを追加するまでにかかった時間を \(y=\alpha x\) として線形回帰で得た \(\alpha\) 値、つまり 1 回の append にかかった時間の想定値を Table 2 に示す。
| Implementation | append processing time |
|---|---|
| Slate (file) | 0.005325 [msec] |
| Slate (rocksdb) | 0.015516 [msec] |
| Slate (memkvs) | 0.002728 [msec] |
| Unindexed Sequence File | 0.000802 [msec] |
| IAVL+ | 0.290724 [msec] |
| DoltDB | 3.241283 [msec] |
Slate (memkvs) はメモリ上の HashMap をストレージ層に持つ Slate 実装である。また、Unindexed Sequence File はシーケンシャルファイルに対して単純に 8 バイト固定長のデータを目的のデータ数まで書き込む処理である。これらはデータ永続性やインデックス機構を持つ他の実装の性能上限を示す参考として記載している。
シーケンシャルファイルを使用する Slate (file) 実装は \(n=8{\rm Mi}\) の計測範囲の終わりまで直線的な性能を示している。これは、1 回の append で想定される \(O(\log n)\) 程度のノード構築の時間的複雑性が I/O コスト \(O(1)\) に比べて非常に小さく、結果的にメモリ上の操作が相殺されていることを示唆している。
またこの結果は、ストレージ層に RocksDB を使用する Slate (rocksdb) 実装は全体的に Slate (file) より遅いことを示している。これは、RocksDB の LSM-Tree 構造における書き込みコストが単純なシーケンシャルファイルに比べて大きいためと考えられる。興味深いことに、\(n=4{\rm Mi}\) エントリあたりまでは直線的に推移したあと、1 回の append にかかる時間が徐々に増加している。
IAVL+ と DoltDB は Slate と比較して 1 桁以上遅いため Figure 11 (右) に分離している。Slate との対比のために 1 データの append ごとに commit やバージョン付けを行ったが、この粒度の高い操作がこれらの DB で想定しないワークロードかもしれない。
8.2.2.  get 性能比較
get 性能比較
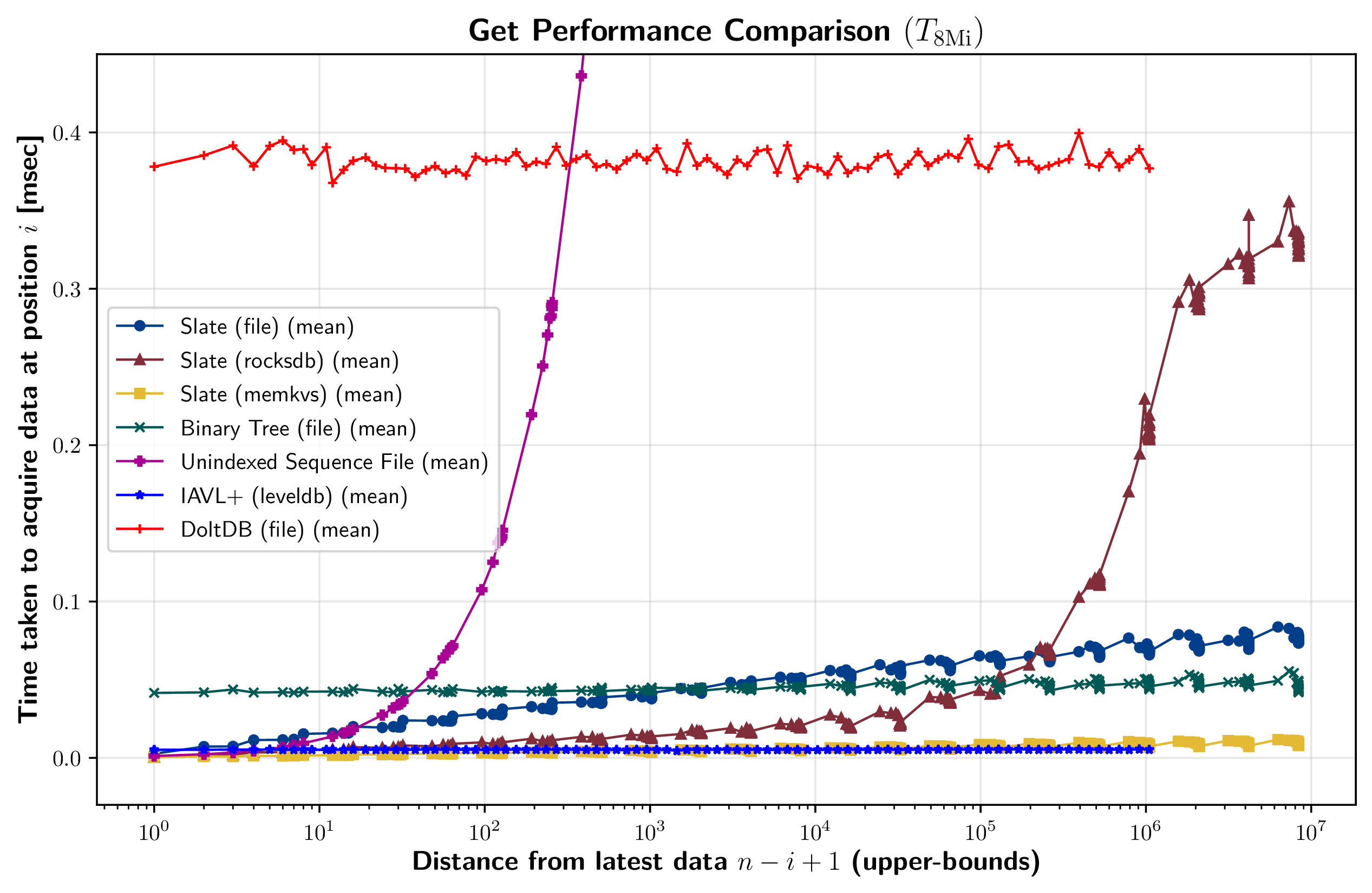
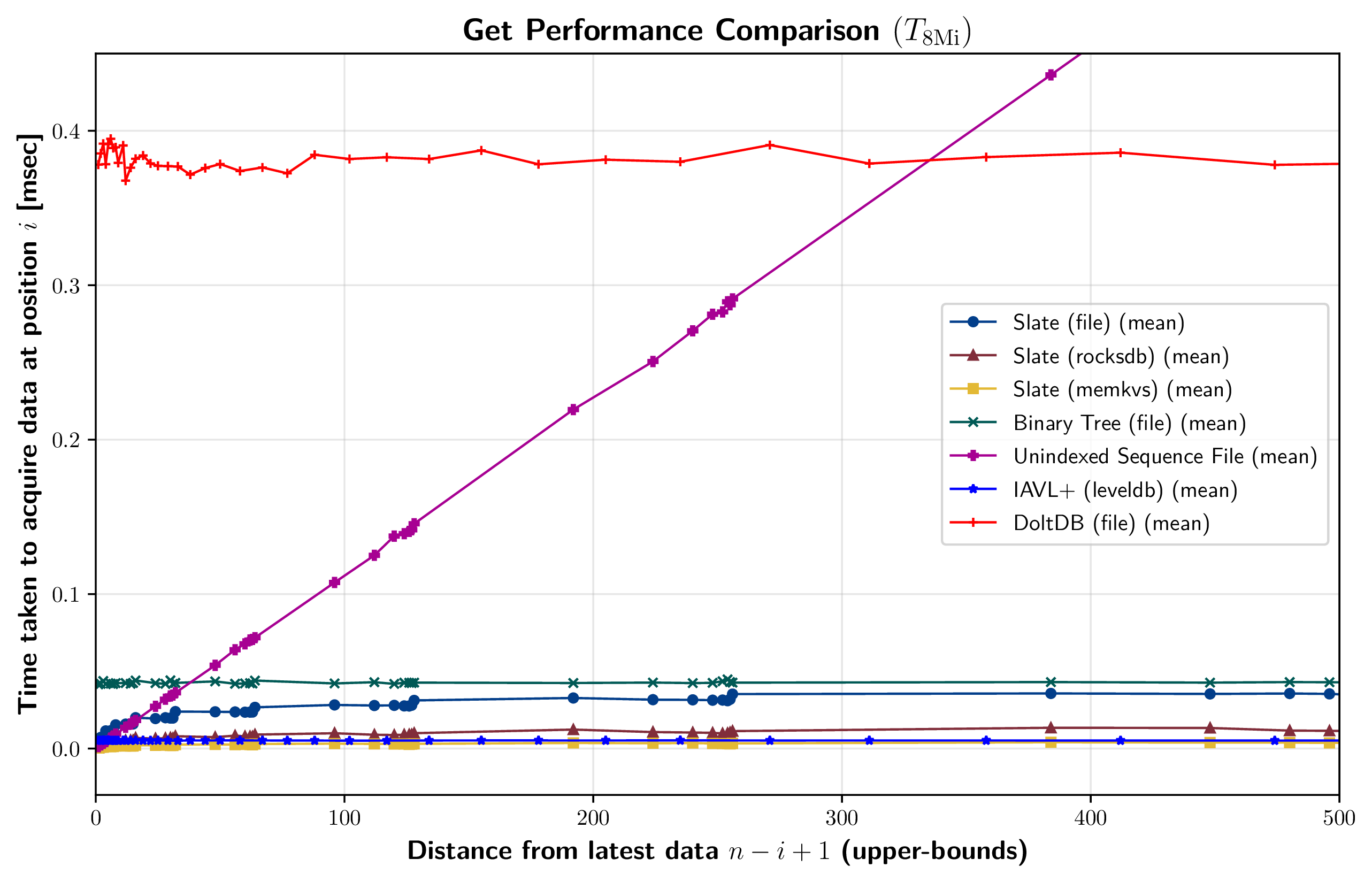
いくつかの実装で get の性能を計測した結果を Figure 12 に示す。これは各実装において \(n = 8{\rm Mi}\) 個のエントリが保存されたデータストアに対して、位置 \(i\) のデータを参照するまでにかかった時間を表している。
Slate (file) の計測結果では、get コストが最新データに近い位置 (グラフ左側) から遠い位置 (グラフ右側) に向けて対数的な増加を示している。これは、get の時間複雑性が最新データからの位置に対する I/O 回数に依存するという予想と一致する。右下のグラフは Slate (file) のデータ数を \(n=2{\rm Gi}\) に増やしたケースで同様の計測を行った結果である。\(n=8{\rm Mi}\) のケースと同様に対数増加の傾向を示しているが、距離が離れるにつれて振動している。
Slate (rocksdb) の計測結果は、最新データに近い位置で Slate (file) よりも良いが、遠い位置になると get 時間が対数の傾向を超えて大幅に増加する。これは、RocksDB の LSM-Tree 構造においてレベルが深くなると、単純なシーケンシャルファイルに比べて読み込みコストが大きくなるためと考えられる。
Binary Tree (file) の計測結果は、位置に依存しないほぼ一定の get コストを示している。これは、完全二分木構造がデータの位置に関係なく \(O(\log n)\) の I/O 回数でデータにアクセスする構造的特徴と一致している。
Unindexed Sequence File に対する get は、ファイルの後方から逐次読み出して位置 \(i\) に到達するまでの時間を計測している。これは最新データからの距離に対して直線的な get コストの増加を示しており、この傾向は逐次読み出し回数に比例する予想と一致している。
IAVL+ と DoltDB は位置に依存せず一定の get コストを示している。ただし、それらの速度には大きな違いがあり、IAVL+ は Slate (memkvs) と同程度の高速な結果となった。これは、総データ量が \(8{\rm Mi} \times 8{\rm B} = 64{\rm MiB}\) 程度であるため、すべてのデータが IAVL+ か LevelDB のメモリ上に保存されている可能性がある。逆に DoltDB については Slate と比較して非常に遅い結果となった。
8.2.3.  Zipf 分布に従うアクセス頻度の get 性能分布
Zipf 分布に従うアクセス頻度の get 性能分布
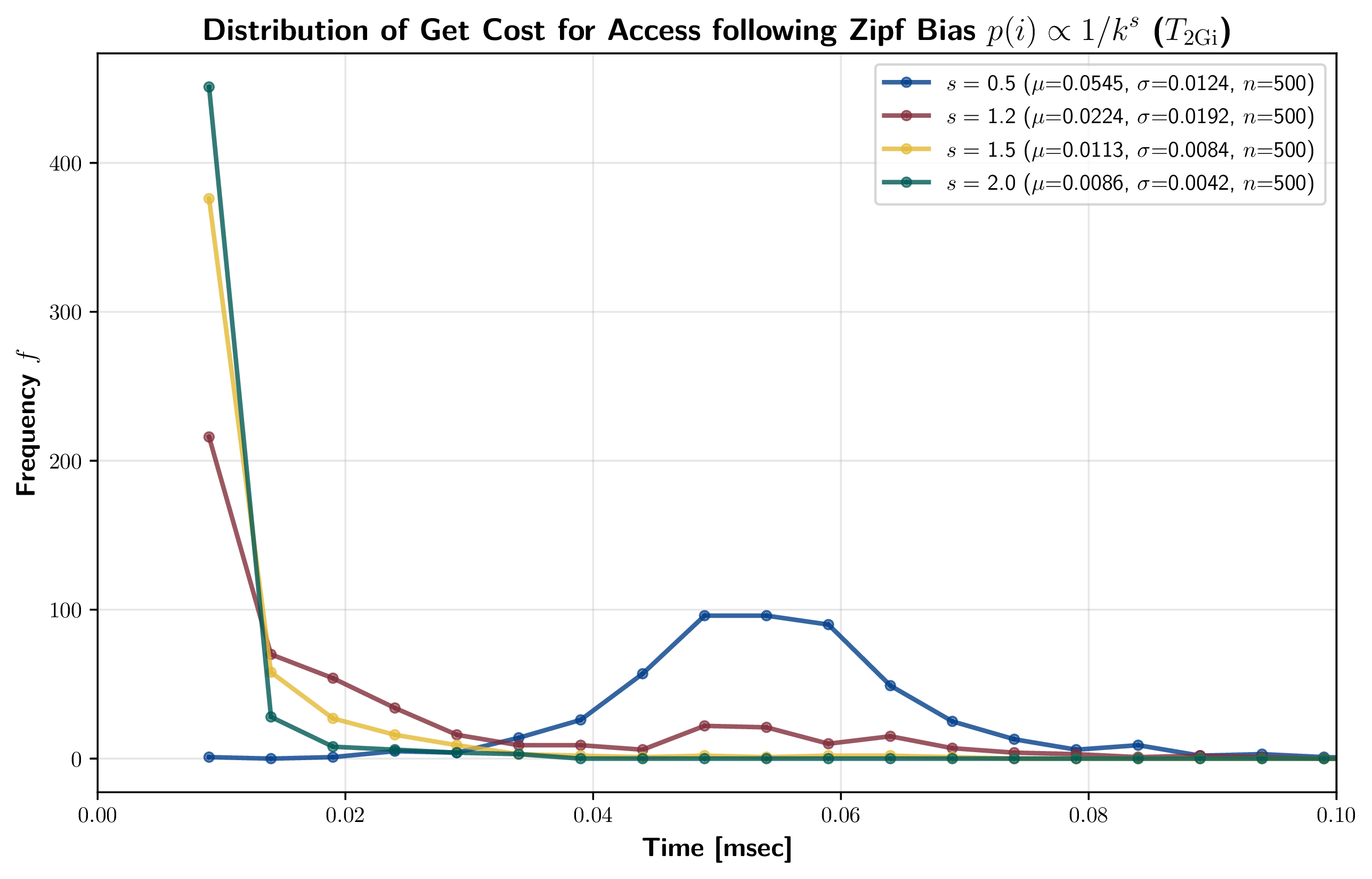
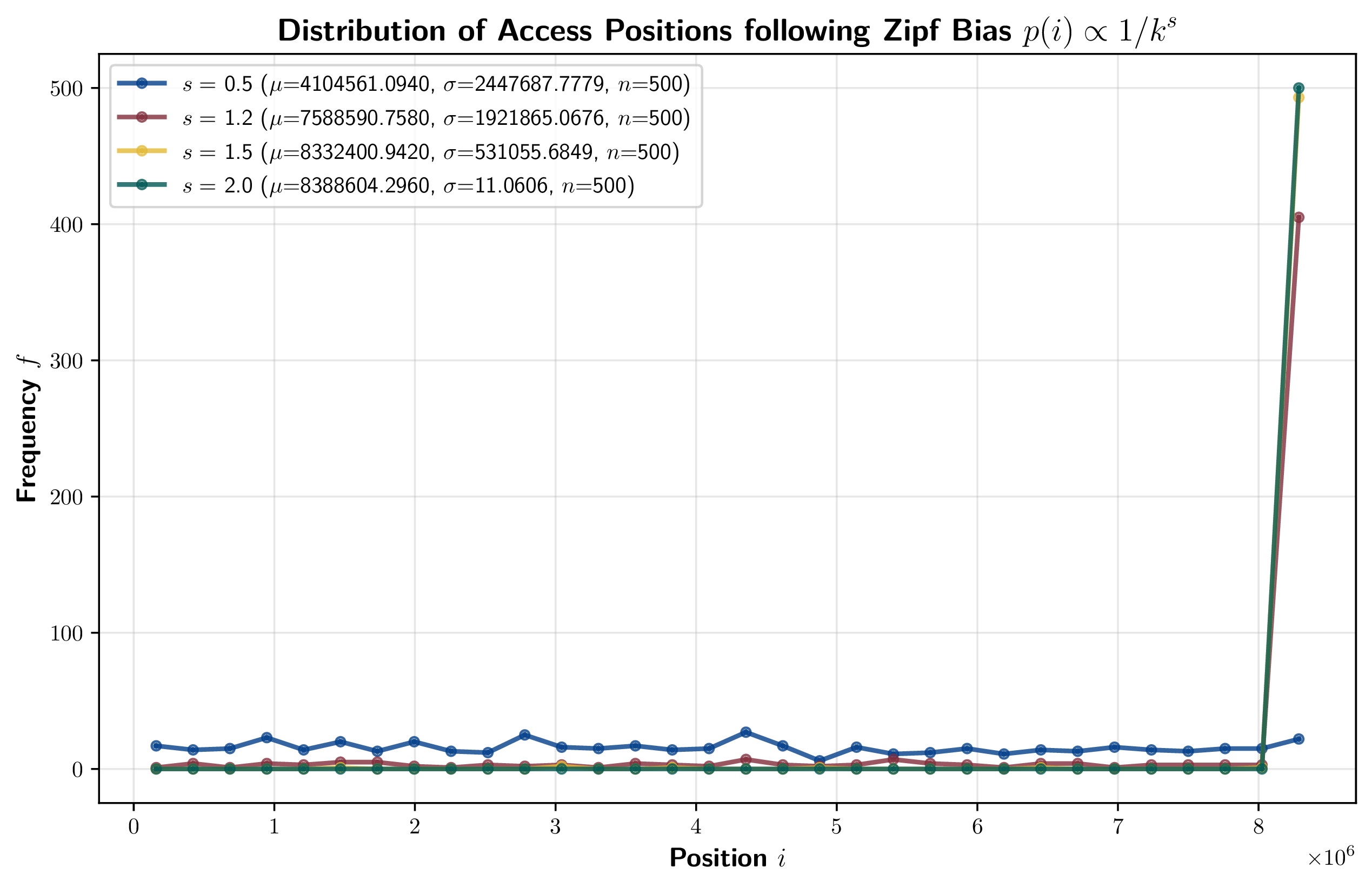
時間局所性を持つアクセスに対して Slate が有利に機能するという本文書の主張を示すために、アクセス頻度が最新データからの距離の Zipf 分布に従うワークロードでの get 性能を計測した。位置 \(i\) の最新データからの距離を \(r_i=n-i+1\) としたとき、その位置の重みを \(w_i = 1/r_i^s\) とする。ここで \(s \ge 0\) は分布の傾きを決定するパラメータである。このとき、位置 \(i\) のデータが参照される確率は \(p_i = \frac{w_i}{\sum_{x=1}^{n} w_x}\) とする。この分布に従う乱数をアクセス位置とし、\(n = 8{\rm Mi}\) 個のエントリが保存された Slate (file) 実装に対して 500 回の get を行い、その時間を計測した。この get 時間の分布を Figure 13 に示す。
この計測では分布の傾きを決定するパラメータ \(s\) を 0.5, 1.2, 1.5, 2.0 と変化させた。\(s=0.5\) はかなり平坦に近い分布であり、\(s=2.0\) はほとんどが最新データに近い位置に集中する分布である。計測結果からは \(s\) が大きい方が get 時間の平均値 \(\mu\) とその分散 \(\sigma\) が小さくなる傾向が見られた。したがって、この計測結果は、Slate が時間的局所性を持つアクセス傾向に対して有利に機能するという主張を支持していると考えられる。
8.2.4.  分岐の検出性能
分岐の検出性能
分岐の検出性能は、ある位置 \(i\) のデータのみが異なる Slate (file) を 2 つ用意し、認証パスを用いてその位置を特定するまでの時間を計測する。ここでそれぞれの Slate には \(n = 8{\rm Gi}\) 個のエントリが保存されており、差異の位置 \(i\) は I/O 回数の理論的上限となる、式 (\(\ref{io_read_worst}\)) の \(d'_u\) に基づく 277 個の位置を選択した。
この計測結果を Figure 14 に示す。x 軸は最新データからの距離 \(n-i+1\) を対数スケールで示している。
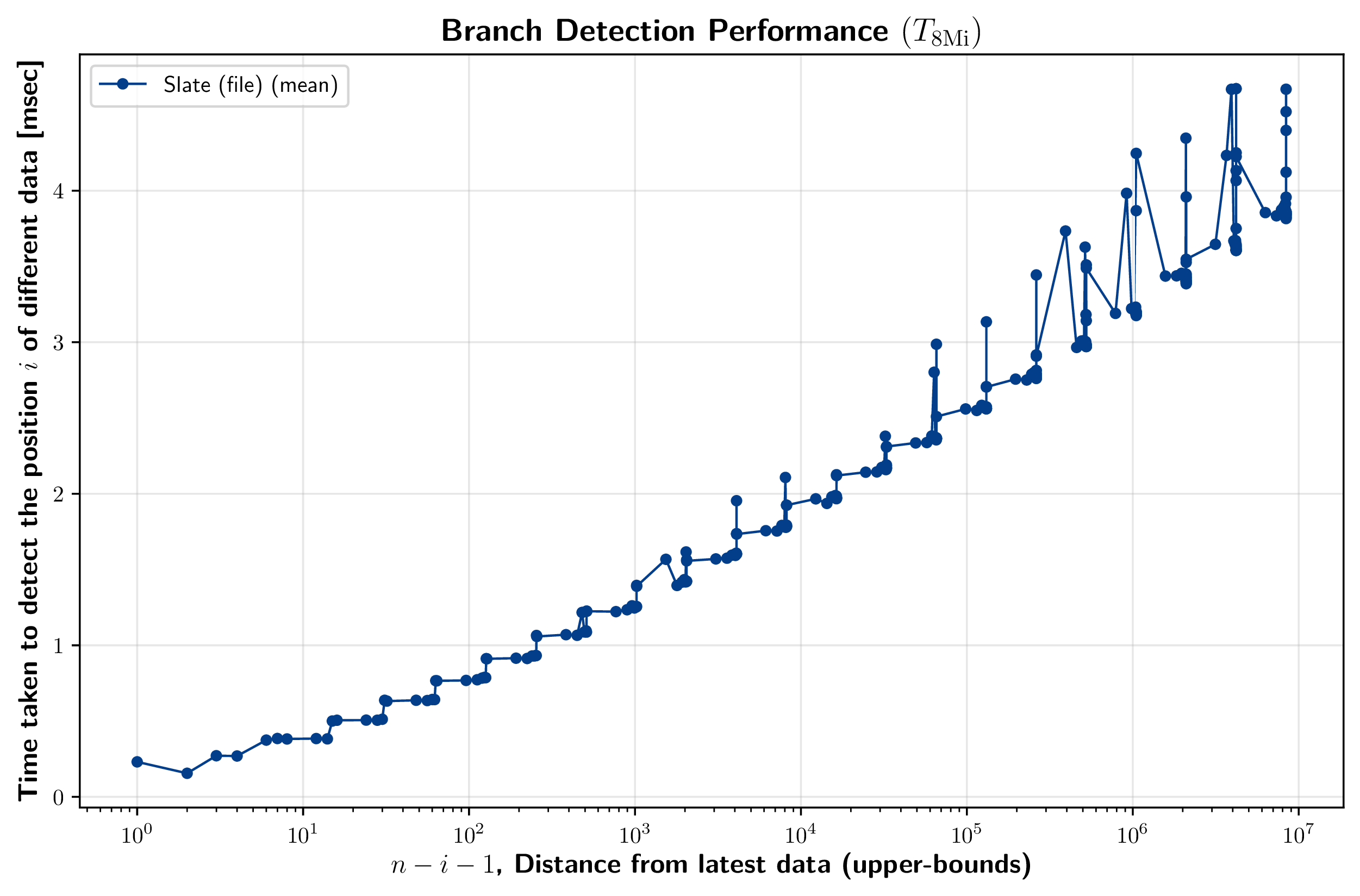
8.2.5.  キャッシュ性能比較
キャッシュ性能比較
Slate (file) 実装において、キャッシュレベルを変化させた場合の get 性能を計測した結果を Figure 15 に示す。これは \(n = 8{\rm Mi}\) 個のエントリが保存されたデータストアに対して、位置 \(i\) のデータを参照するまでにかかった時間を表している。
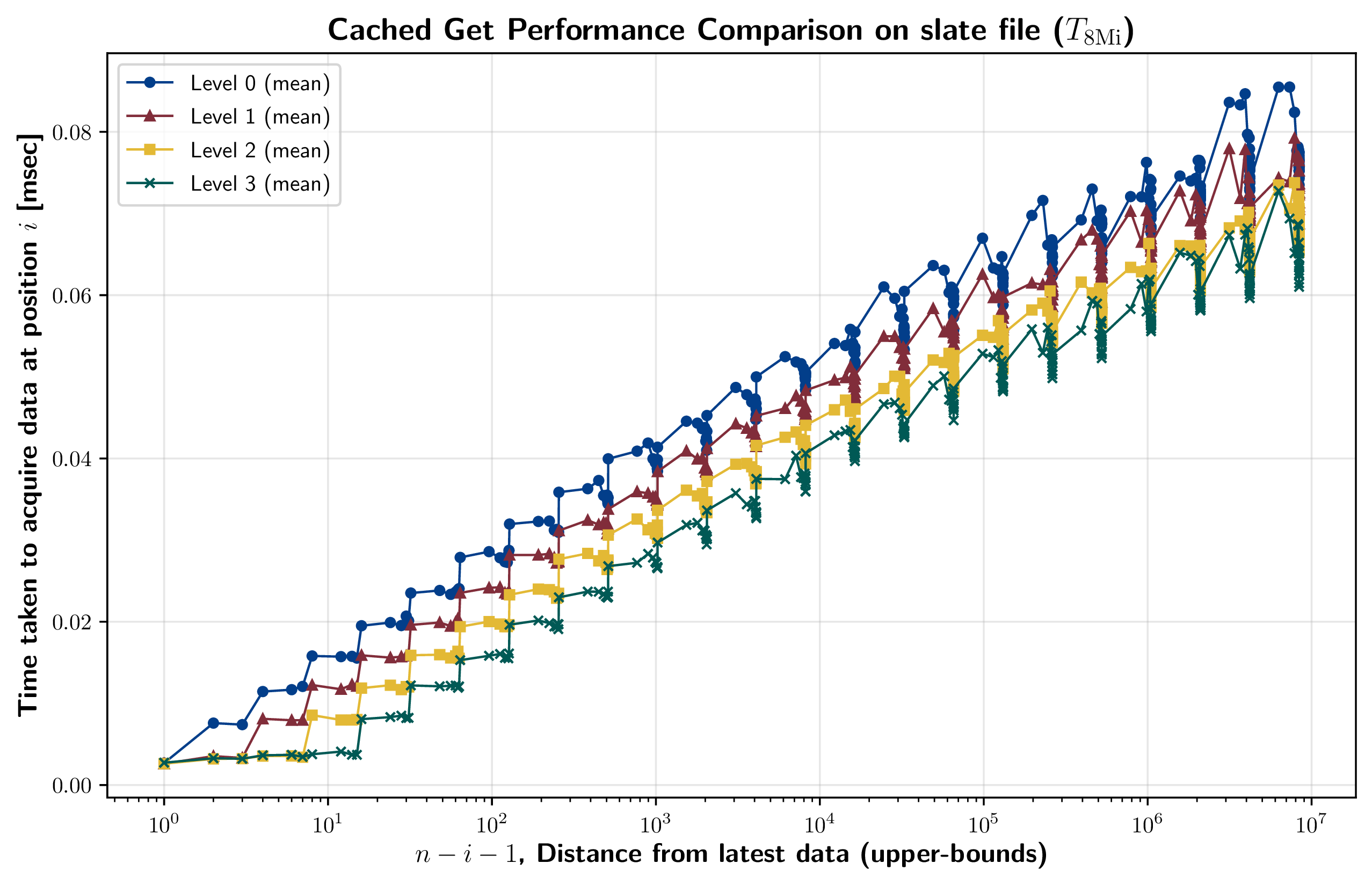
Slate のノードはセクション 7.1.2 で説明したようにキャッシュレベルに応じてメモリ上に保持される。この計測結果から、キャッシュレベルを一つあげると、全体を通して I/O Read 1 回分の get コストが減少していることが現われている。
9.  アプリケーション
アプリケーション
9.1.  分散トランザクションログの修復と一貫性の維持
分散トランザクションログの修復と一貫性の維持
分散コンセンサスアルゴリズムの Raft においてリーダーが交代したとき、新しいリーダーと各フォロワー間でログの一貫性を保証するプロセスがある。これは、双方のログ (トランザクションログ) がどこまで一致しているかを検出して、それ以降のログをリーダーのログで上書きする。このプロセスにおいて、Raft ではリーダーのログを後方から送信する。
9.2.  ハッシュグラフとバージョン管理システム
ハッシュグラフとバージョン管理システム
分散バージョン管理システムの git における merge-base コマンドでは、2 つのブランチの分岐点を見つけるために、双方のコミットを起点に親を遡って共通の祖先を探すアルゴリズムを使用している。これは平均ケースで \(O(\log n)\)、最悪ケースで \(O(n)\) の計算量となる。
木構造の特定の世代を基準に別のハッシュ木を枝として分岐させることができるだろう。これは git のブランチシステムに似ている。
9.3.  ブロックチェーンシステム
ブロックチェーンシステム
ブロックチェーンのチェーン状の連鎖を Slate に置き換えることで、概念が簡素化され、light client での利用も自然に統合できる。
ブロックチェーンは、追記型のチェーン状のデータ構造を持ち、特に Bitcoin などのフォークが発生するタイプについては一貫性を維持するために修復機構を備えている。つまり、ブロックチェーンはビザンチン障害耐性を持つ分散トランザクションログと見なすことができる。このため、ブロックチェーンにおいてもブロックの検証や、効率的な分岐点の検出のために Slate を使用することができる。
一般的なブロックチェーンは、あるブロックに前のブロックのハッシュ値を埋め込むことで概念的にチェーン状のデータ構造を構築する。ただし、この構造は、あるブロックの正当性を確認するために、その直前の検証済みブロックを持っていなければならない。これは、帰納的に、あるブロックのみを入手しても、その検証のために、それより前のすべてのブロックを入手する必要があることを意味する。
ブロックチェーンには、light client と呼ばれる、自身が必要な一部のデータのみを追跡するノードが存在する。このノードは、自身が持っていないブロックが必要になったときに、それを full node に問い合わせて入手するが、そのブロックが改ざんされていないことを確認するために、一般にハッシュツリーを使用する。
light client はブロックチェーンネットワークから最新のブロックを取得してハッシュツリーを計算し、そのルートハッシュを追跡する。light client は、あるブロックが必要になったとき、full node にそのブロックを問い合わせ、ブロックをハッシュツリーの最小限の枝も含めて取得する。light client は、ブロックのハッシュ値から枝を遡って算出したルートハッシュが、自身の追跡しているルートハッシュと一致していれば、そのブロックが改ざんされていないことを保証できる (暗号論的ハッシュ関数を使用していれば意図したハッシュ値に衝突させるような改ざんを行うことは不可能である)。
つまり、light client を想定するブロックチェーンはすでにハッシュツリーを計算する実装を行っている。あるブロックに前のブロックのハッシュ値を埋め込む代わりに、Slate 構造化したルートハッシュを埋め込むことができる。つまり、ブロックチェーンの現状は「チェーン状に連結されたブロック」と「ハッシュツリー状に連結されたブロック」の 2 つの観点を持ち、局面によって概念を切り替えている状態である。これは実装面で余分な複雑さをもたらしている。Slate の構造に基づく概念に統一することで観点が簡素化される。
ブロックチェーンには、あるブロックが追加されて世代が進むにつれてそのブロックの改ざん耐性が高くなるという特性がある。これは、ハッシュの衝突を想定したとしても、チェーンが長くなるにつれて過去のブロックを遡って改ざんするすることが難しくなることを意味している。Slate でも古いデータはルートノードからの深さが高くなるため、オーダーは異なるものの同様の性質を考慮できる。
10.  議論
議論
10.1.  トレードオフ
トレードオフ
10.2.  セキュリティ考察
セキュリティ考察
ハッシュツリーには Certificate Transparency [RFC 9162] は葉ノードと中間ノードとでハッシュファミリーのドメインを分離することで第二原像耐性を追加している。
10.3.  将来的な拡張
将来的な拡張
Slate の中間ノードに単調増加する属性の範囲を持たせることによって、位置 \(i\) ではなくその属性値によって検索することができるだろう。例えば時系列データにおいてデータが \(i\) に伴って単調増加するタイムスタンプを持つとする。各中間ノードは、自身が含む葉ノードのタイムスタンプの範囲を保持することで、左右どちらの枝に該当する時刻のデータが含まれているかを判断できる。これは B-Tree などの一般的な検索木と同じアイディアである。Merkle Search Tree [MST 2019] で、各中間ノードに属性を付けることで、ハッシュ木に簡易的な検索をサポートする。この手法は Slate にも応用できるだろう。
11.  結論
結論
 References
References
- O’Neil, P., Cheng, E., Gawlick, D. et al. The log-structured merge-tree (LSM-tree). Acta Informatica 33, 351–385 (1996). https://doi.org/10.1007/s002360050048
- [Haber 1990] Haber, S., Stornetta, W.S. How to time-stamp a digital document. J. Cryptology 3, 99–111 (1991). https://doi.org/10.1007/BF00196791
- Buldas, A., Saarepera, M. (2004). On Provably Secure Time-Stamping Schemes. In: Lee, P.J. (eds) Advances in Cryptology - ASIACRYPT 2004. ASIACRYPT 2004. Lecture Notes in Computer Science, vol 3329. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-30539-2_35
- Hash Calendar実装の特許: US Patent 8,719,576 B2: "Document verification with distributed calendar infrastructure" (2014). Inventors: Ahto Buldas, Märt Saarepera
- Driscoll, J. R., Sarnak, N., Sleator, D. D., Tarjan, R. E.: Making data structures persistent. In J. Hartmanis, editor, Proceedings of the 18th Annual ACM Symposium on Theory of Computing, May 28-30, 1986, Berkeley, California, USA, pages 109–121. ACM, (1986)
- R. C. Merkle. Protocols for public key cryptosystems, in Secure communications and asymmetric cryptosystems, pp. 73–104, Routledge, 2019.
- Merkle, R.C. (1987) A Digital Signature Based on a Conventional Encryption Function. Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, 16-20 August 1987, 369-378. https://doi.org/10.1007/3-540-48184-2_32
- [Crosby 2009] Crosby, Scott A., and Dan S. Wallach. Efficient Data Structures for Tamper-Evident Logging. USENIX security symposium. 2009.
- [Bayer 1992] Bayer, Dave; Stuart A., Haber; Wakefield Scott, Stornetta (1992). "Improving the Efficiency And Reliability of Digital Time-Stamping”. Sequences II: Methods in Communication, Security and Computer Science. Springer-Verlag: 329–334. CiteSeerX 10.1.1.46.5923.
- [CT 2013] LAURIE, Ben. Certificate transparency. Communications of the ACM, 2014, 57.10: 40-46.
- [Raft 2014] ONGARO, Diego; OUSTERHOUT, John. In Search of an Understandable Consensus Algorithm (Extended Version). In: 2014 USENIX annual technical conference (USENIX ATC 14). 2014. p. 305-319.
- [C23 2024] According to ISO/IEC 9899:2024, §6.5.7/3, “If the value of the right operand is negative or is greater than or equal to the width of the promoted left operand, the behavior is undefined.” ISO9899:2024
- [Rust RFC560] Rust Language Team. RFC 560: Integer Overflow. 2015, Describes the semantics of integer overflow and shift operations in Rust.
- [Knuth 1997] KNUTH, Donald E. 1997. The Art of Computer Programming: Fundamental Algorithms, Volume 1. Addison-Wesley Professional.
- [Warren 2012] Henry S. Warren. 2012. Hacker's Delight (2nd. ed.). Addison-Wesley Professional.
- [PT 2015] Aaron Boodman and Rafael Weinstein. 2015. Noms: The versioned, forkable, syncable database. Technical documentation. Attic Labs. Retrieved Aug 31, 2025 from https://github.com/attic-labs/noms/blob/master/doc/intro.md.
- [MST 2019] Alex Auvolat, François Taïani. Merkle Search Trees: Efficient State-Based CRDTs in Open Networks. SRDS 2019 - 38th IEEE International Symposium on Reliable Distributed Systems, Oct 2019, Lyon, France. pp.1-10, ff10.1109/SRDS.2019.00032ff. ffhal-02303490f
- [Merkle 1979] Merkle, R.C. (1990). A Certified Digital Signature. In: Brassard, G. (eds) Advances in Cryptology — CRYPTO’ 89 Proceedings. CRYPTO 1989. Lecture Notes in Computer Science, vol 435. Springer, New York, NY. https://doi.org/10.1007/0-387-34805-0_21
- [RFC 9162] LAURIE, Ben; MESSERI, E.; STRADLING, R. RFC 9162: Certificate Transparency Version 2.0. 2021.