構造的アルゴリズム
\( \def\vector#1{\boldsymbol{#1}} \)

論文翻訳: The Priority R-Tree: A Practically Efficient and Worst-Case Optimal R-Tree

Takami Torao 2004年の論文 #RTree
  • このエントリーをはてなブックマークに追加

概要

我々はウィンドウクエリーを常に \(O((\frac{N}{B})^{1-\frac{1}{d}} + \frac{T}{B})\) の I/O で応答する最初の R-Tree 変種である Priority R-Tree、または PR-Tree を提示する。ここで \(N\) は R-Tree に格納されている \(d\) 次元の (ハイパー) 矩形の数、\(B\) はディスクブロックサイズ、\(T\) は出力サイズである。これは漸近的に最適であり、\(T=0\) であっても、クエリーがツリー内の全ての \(\frac{N}{B}\) 葉を検査する可能性のある他の R-Tree 変種より大幅に優れている。また PR-Tree の実用的な性能について現実のデータと人工のデータの両方を使用して広範な実験的研究を行った。この研究において PR-Tree は現実のよく配分されたデータにおいて最も知られている R-Tree 変種と同等となり、より極端に偏ったデータでははっきりと優れていることを示している。

Table of Contents

  1. 概要
  2. 1. INTRODUCTION [under construction]
    1. 1.1 Background and previous results
    2. 1.2 Our results
  3. 2. THE PRIORITY R-TREE
    1. 2.1 二次元疑似 PR-Tree
      1. 2.1.1 構造
      2. 2.1.2 クエリーの複雑度
      3. 2.1.3 Efficient construction algorithm
    2. 2.2 Two-dimensional PR-tree
    3. 2.3 Multi-dimensional PR-tree
    4. 2.4 Lower bound for heuristic R-tree
  4. 3. EXPERIMENTS
    1. 3.1 Experimental setup
    2. 3.2 Datasets
      1. 3.2.1 Real-life data
      2. 3.2.2 Synthetic data
    3. 3.3 Experimental results
      1. 3.3.1 Bulk-loading performance
      2. 3.3.2 Query performance
    4. 3.4 Conclusions of the experiments
  5. 4. CONCLUDING REMARKS
  6. 5. REFERENCES
  7. 翻訳抄

1. INTRODUCTION

1.1 Background and previous results

1.2 Our results

2. THE PRIORITY R-TREE

この章では PR-Tree について説明する。単純化のためにまず我々は 2.1 節で 2 次元疑似 PR-Tree を説明する。疑似 PR-Tree はウィンドウクエリーに対して効率的に応答するが、全ての葉が同じレベルではないため実際の R-Tree ではない。2.2 節では疑似 PR-Tree から実際の 2 次元 PR-Tree を得る方法を示し、2.3 節では PR-Tree を \(d\) 次元に拡張する方法を論じる。最後に 2.4 節では \(T=0\) であっても Packed Hilbert R-Tree、4 次元 Hilbert R-Tree、TGS R-Tree に対するクエリーが全ての葉を検査することを強制させられることができることを示す。

2.1 二次元疑似 PR-Tree

この章では 2 次元疑似 PR-Tree について説明する。疑似 PR-Tree は R-Tree のように葉に入力矩形を持ち、各内部ノード \(v\) はその子 \(v_c\) のそれぞれに最小境界ボックスを持っている。ただし R-Tree とは異なり、すべての葉がツリーの同じレベルにあるわけではなく、内部ノードは次数 6 (\(\Theta(B)\) ではなく) しか持たない。

疑似 PR-Tree の基本的な考え方は、入力矩形 \(((x_{\rm min}, y_{\rm min}), (x_{\rm max}, y_{\rm max}))\) を 4 次元の点 \((x_{\rm min}, y_{\rm min}, x_{\rm max}, y_{\rm max})\) として見る (4 次元 Hilbert R-Tree に似ている)。基本的に疑似 PR-Tree は \(N\) 個の入力矩形に対する \(N\) 個の点の \(k\) 次元 Tree であるが、各内部ノードの下には 4 個の余分な葉が追加されている。直感的には、これらのいわゆる優先葉 (priority leaves) には 4 つの次元のそれぞれの端に位置する \(B\) 点 (矩形) が含まれている。4 次元の \(k\) 次元 Tree は、各 \(k\) 次元 Tree ノード \(\nu\) の分割値を、\(\nu\) を根とするサブツリーに格納されている入力矩形の最小境界ボックスに置き換えるだけで R-Tree のような構造に容易にマッピングできる。優先葉を使用するという考えは Agarwal ら [2] による最近の構造に導入された。彼らは \(B\) ではなく 1 の優先葉を使用している。2.1.1 項では疑似 PR-Tree の正確な定義を与え、2.1.2 項では \(O(\frac{N}{B} + \frac{T}{B})\) の I/O でウィンドウクエリーに応答するために利用できることを示している。

2.1.1 構造

\(S = \{R_1, R_2, \ldots, R_N\}\) を平面内の \(N\) 個の矩形集合とし、簡単のため矩形が定義している座標のどのような 2 つも等しくないと仮定する。\[R_i^* = (x_{\rm min}(R_i), y_{\rm min}(R_i), x_{\rm max}(R_i), y_{\rm max}(R_i))\] を \[R_i = ((x_{\rm min}(R_i), y_{\rm min}(R_i)), (x_{\rm max}(R_i), y_{\rm max}(R_i)))\] の 4 次元の点への写像と定義し、\(S^*\) を \(S\) に対応する \(N\) 個の点と定義する。

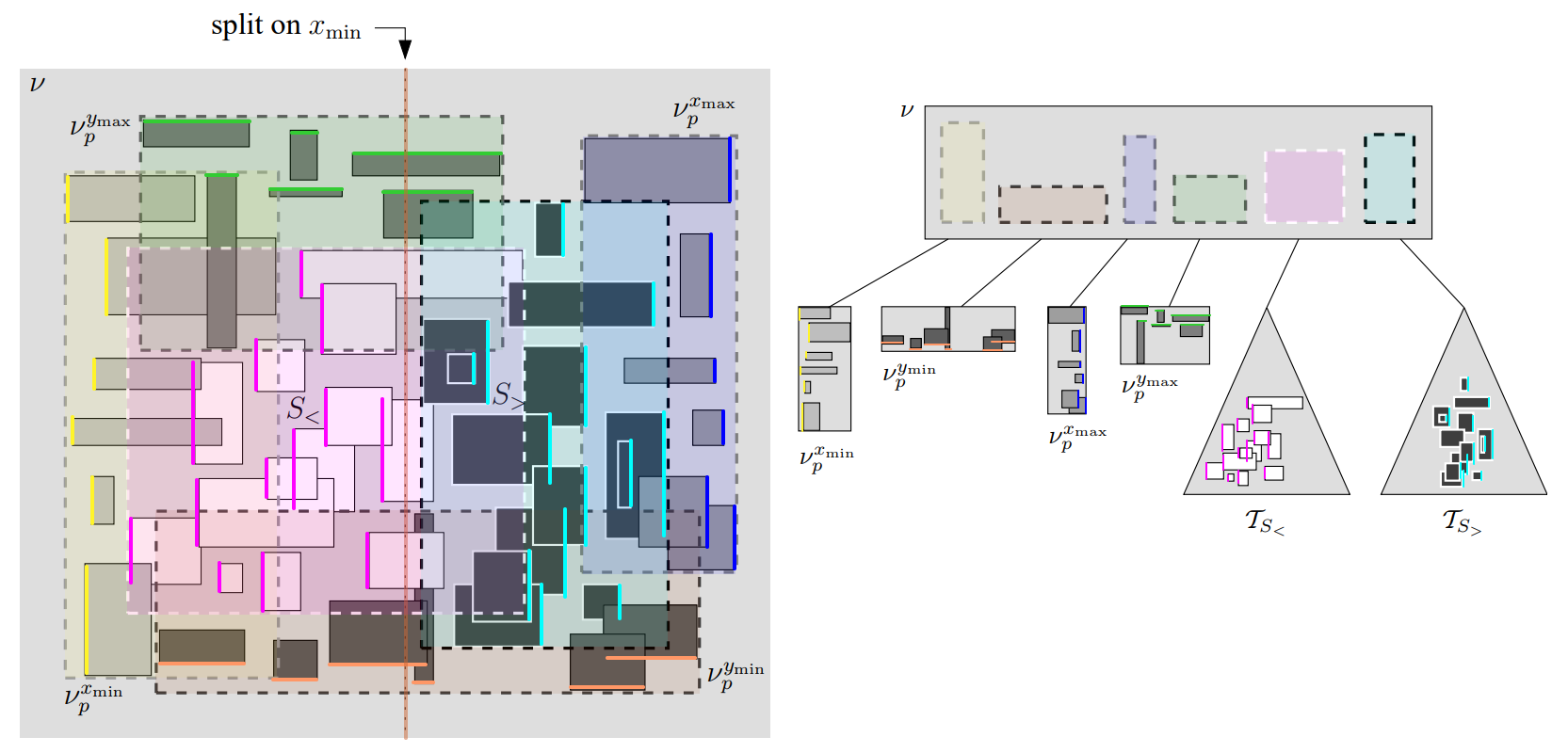
\(S\) 上の疑似 PR-Tree \(T_S\) は再帰的に定義される: もし \(B\) より小さい個数の矩形を含む場合、\(T_S\) は単一の葉からなる。それ以外の場合、\(T_S\) は 6 つの子、すなはち 4 つの優先葉と 2 つの再帰的疑似 PR-Tree というノード \(\nu\) からなる。それぞれの子 \(\nu_c\) に対して \(\nu\) をルートとするサブツリーに格納されている全ての入力矩形の最小境界ボックスを \(\nu\) に格納する。ノード \(\nu\) とそれより下に位置する優先葉は次のように構成される: 最初の優先葉 \(\nu_p^{x_{\rm min}}\) は \(S\) 内で \(x_{\rm min}\) 座標の最小値をもつ \(B\) 個の矩形を、2 番目の優先葉 \(\nu_p^{y_{\rm min}}\) は残りの矩形から最小 \(y_{\rm min}\) 座標を有する \(B\) 個の矩形を、3 番目の優先葉 \(\nu_p^{x_{\rm max}}\) は残りの矩形から最大 \(x_{\rm max}\) 座標を有する \(B\) 個の矩形を、最後の優先葉 \(\nu_p^{y_{\rm max}}\) は残りの矩形から最大 \(y_{\rm max}\) 座標を有する \(B\) 個の矩形を入れる。このため優先葉には \(S\) 上の「端に位置する」矩形、すなはち最左端に左辺、最右端の右辺、最上端の上辺、最下端の下辺をもつ矩形が含まれる2。

Figure 1: 疑似 PR-Tree での内部ノードの構築 (色付は訳者による)

優先葉を構築した後、残りの矩形 (もしあれば) の集合 \(S_r\) を同じサイズの 2 つのサブセット \(S_\gt\) と \(S_\lt\) に分割し、疑似 PR-Tree \(T_{S_\gt}\) と \(T_{S_\lt}\) を再帰的に構築する。この分割は \(S_r^*\) で 4 次元の \(k\) 次元 Tree を構築したのと同様に、ラウンドロビン方式で \(x_{\rm min}\), \(y_{\rm min}\), \(x_{\rm max}\) または \(y_{\rm max}\) 座標を使用して実行される。つまり \(T_S\) の根を構築する時に、我々は \(x_{\rm min}\) に基づいて、次の再帰のレベルは \(y_{\rm min}\) 値に基づいて、次に \(x_{\rm max}\) 値、\(y_{\rm max}\) 値等々と分割する。例として Figure 1 を参照。例えば \(x_{\rm min}\) に対応する分割とは、\(S_r\) に含まれる矩形の半分が左辺を \(\ell\) の左に持ち、もう半分が左辺を \(\ell\) の右に持つような垂直線 \(\ell\) に基づいて分割することである。

\(T_S\) の各ノードおよび葉を \(O(1)\) ディスクブロックに格納し、6 つの葉のうち少なくとも 4 つが \(\Theta(B)\) 個の矩形を含んでいることから、我々は以下を得る (2.1.3 項ではほとんど全ての葉がいっぱいとなることを保証する方法について論議する)。

補題1: 平面上の \(N\) 個の矩形の集合による疑似 PR-Tree は \(O(\frac{N}{B})\) ディスクブロックを専有する。

2. \(S\) は 4 つの優先葉のそれぞれに \(B\) 個を入れるだけの矩形を含んでいないかもしれない。この場合、個数が \(B\) より小さければ単一の葉を構築できることから、それぞれに少なくとも \(\frac{B}{4}\) 個を置くことができると仮定しても良い。

2.1.2 クエリーの複雑度

我々はウィンドウクエリー \(Q\) と交差する最小境界ボックスを有する全てのノードを再帰的に検査することによって R-Tree と同様に擬似 PR-Tree 上の \(Q\) に応答する。ただし、既知の R-Tree 変種とは異なり、疑似 PR-Tree においてはこの手順で実行される I/O 回数が自明ではない (事実、最適である) ことを証明できる。

補題2: 平面上の \(N\) 個の矩形からなる疑似 PR-Tree へのウィンドウクエリーは、最悪 \(O(\frac{N}{B} + \frac{T}{B})\) 回の I/O を使用する。

証明: \(T_S\) を平面上の \(N\) 個の矩形の集合 \(S\) からなる疑似 PR-Tree とする。制限されたクエリーを証明するために、「\(k\) 次元ノード」すなはち優先葉ではなく、矩形範囲 \(Q\) を有するクエリーに応答するために検査される \(T_S\) のノードの数に制限する; 検査される葉の総数は最大でも 4 倍の大きさである。

最初の \(O(\frac{T}{B})\) は検査されるノード \(\nu\) の数の上限であり、\(\nu\) の親より低い優先度のノードの少なくとも 1 つの全ての矩形が報告される。従って、検査される \(k\) 次元ノードの数を制限する必要がある。

\(\mu\) をノード \(\nu\) の親とする。\(\mu\) の優先葉のいずれも完全に報告されない、つまり \(\mu\) の各優先葉 \(\mu_p\) は \(Q\) と交差していない少なくとも 1 つの矩形を含む。このような矩形 \(E\) のそれぞれは \(Q\) の 1 つの側面を含む先によって \(Q\) から分離することができる ─ Figure 2 参照。

2.1.3 Efficient construction algorithm

2.2 Two-dimensional PR-tree

2.3 Multi-dimensional PR-tree

2.4 Lower bound for heuristic R-tree

3. EXPERIMENTS

3.1 Experimental setup

3.2 Datasets

3.2.1 Real-life data

3.2.2 Synthetic data

3.3 Experimental results

3.3.1 Bulk-loading performance

3.3.2 Query performance

3.4 Conclusions of the experiments

4. CONCLUDING REMARKS

5. REFERENCES

  1. P. K. Agarwal, L. Arge, O. Procopiuc, and J. S. Vitter. A framework for index bulk loading and dynamization. In Proc. International Colloquium on Automata, Languages, and Programming, pages 115–127, 2001.
  2. P. K. Agarwal, M. de Berg, J. Gudmundsson, M. Hammar, and H. J. Haverkort. Box-trees and R-trees with near-optimal query time. Discrete and Computational Geometry, 28(3):291–312, 2002.
  3. L. Arge, O. Procopiuc, and J. S. Vitter. Implementing I/O-efficient data structures using TPIE. In Proc. European Symposium on Algorithms, pages 88–100, 2002.
  4. L. Arge and J. Vahrenhold. I/O-efficient dynamic planar point location. International Journal of Computational Geometry & Applications, 2003. To appear.
  5. R. Bayer and E. McCreight. Organization and maintenance of large ordered indexes. Acta Informatica, 1:173–189, 1972.
  6. N. Beckmann, H.-P. Kriegel, R. Schneider, and B. Seeger. The R*-tree: An efficient and robust access method for points and rectangles. In Proc. SIGMOD International Conference on Management of Data, pages 322–331, 1990.
  7. S. Berchtold, C. Böhm, and H.-P. Kriegel. Improving the query performance of high-dimensional index structures by bulk load operations. In Proc. Conference on Extending Database Technology, LNCS 1377, pages 216–230, 1998.
  8. B. Chazelle. The Discrepancy Method: Randomness and Complexity. Cambridge University Press, New York, 2001.
  9. D. Comer. The ubiquitous B-tree. ACM Computing Surveys, 11(2):121–137, 1979.
  10. D. J. DeWitt, N. Kabra, J. Luo, J. M. Patel, and J.-B. Yu. Client-server paradise. In Proc. International Conference on Very Large Databases, pages 558–569, 1994.
  11. V. Gaede and O. Günther. Multidimensional access methods. ACM Computing Surveys, 30(2):170–231, 1998.
  12. Y. J. García, M. A. López, and S. T. Leutenegger. A greedy algorithm for bulk loading R-trees. In Proc. 6th ACM Symposium on Advances in GIS, pages 163–164, 1998.
  13. A. Guttman. R-trees: A dynamic index structure for spatial searching. In Proc. SIGMOD International Conference on Management of Data, pages 47–57, 1984.
  14. H. J. Haverkort, M. de Berg, and J. Gudmundsson. Box-trees for collision checking in industrial installations. In Proc. ACM Symposium on Computational Geometry, pages 53–62, 2002.
  15. I. Kamel and C. Faloutsos. On packing R-trees. In Proc. International Conference on Information and Knowledge Management, pages 490–499, 1993.
  16. I. Kamel and C. Faloutsos. Hilbert R-tree: An improved R-tree using fractals. In Proc. International Conference on Very Large Databases, pages 500–509, 1994.
  17. K. V. R. Kanth and A. K. Singh. Optimal dynamic range searching in non-replicating index structures. In Proc. International Conference on Database Theory, LNCS 1540, pages 257–276, 1999.
  18. S. T. Leutenegger, M. A. López, and J. Edgington. STR: A simple and efficient algorithm for R-tree packing. In Proc. IEEE International Conference on Data Engineering, pages 497–506, 1996.
  19. Y. Manolopoulos, A. Nanopoulos, A. N. Papadopoulos, and Y. Theodoridis. R-trees have grown everywhere. Technical Report available at http://www.rtreeportal.org/, 2003
  20. O. Procopiuc, P. K. Agarwal, L. Arge, and J. S. Vitter. Bkd-tree: A dynamic scalable kd-tree. In Proc. International Symposium on Spatial and Temporal Databases, 2003.
  21. J. Robinson. The K-D-B tree: A search structure for large multidimensional dynamic indexes. In Proc. SIGMOD International Conference on Management of Data, pages 10–18, 1981.
  22. N. Roussopoulos and D. Leifker. Direct spatial search on pictorial databases using packed R-trees. In Proc. SIGMOD International Conference on Management of Data, pages 17–31, 1985.
  23. T. Sellis, N. Roussopoulos, and C. Faloutsos. The R+-tree: A dynamic index for multi-dimensional objects. In Proc. International Conference on Very Large Databases, pages 507–518, 1987.
  24. TIGER/Line™ Files, 1997 Technical Documentation. Washington, DC, September 1998. http://www.census.gov/geo/tiger/TIGER97D.pdf

翻訳抄

空間インデックス (spatial index) のためのアルゴリズム Priority R-Tree (2004) に関する論文。

  1. 原文: The Priority R-Tree: A Practically Efficient and Worst-Case Optimal R-Tree
  2. Priority R-tree (Wikipedia)