Quotient フィルター
 概要
概要
Quotient フィルター [3] または商フィルターは大規模データセットに対する近似メンバーシップクエリー (AMQ; approximately membership query) を行うための確率的データ構造である。Bloom フィルターと似ているが空間とキャッシュをより効率的に利用できる構造を持つ上、テーブルサイズの変更や要素の削除をサポートすることができる。
Quotient フィルターは Donald Knuth の The Art of Computer Programming, Vol. 3 [2] セクション 6.4 の演習問題 13 に基づいている。
The Art of Computer Programming, Vol. 3, Section 6.4 Exercises 13
13. [24] (Abbreviated keys.) Let \(h(K)\) be a hash function, and let \(q(K)\) be a function of \(K\) such that \(K\) can be determined once \(h(K)\) and \(q(K)\) are given. For example, in division hashing we may let \(h(K) = K \bmod M\) and \(q(K) = \lfloor K / M \rfloor\); in multiplicative hashing we may let \(h(K)\) be the leading bits of \((AK/w) \bmod 1\), and \(q(K)\) can be the other bits.
Show that when chaining is used without overlapping lists, we need only store \(q(K)\) instead of K in each record. (This almost saves the space needed for the link fields.) Modify Algorithm C so that it allows such abbreviated keys by avoiding overlapping lists, yet uses no auxiliary storage locations for overflow records.
Table of Contents
 アルゴリズム
アルゴリズム
Quotient フィルターの基本的な設計は線形プローブ法のハッシュテーブルと似ている。ただし、テーブルには要素ではなく要素のフィンガープリント (ハッシュ値) のみを格納する。Quotient フィルターは異なる要素に対して同一のフィンガープリントが生成されるハード衝突 (hard collision)を許容しているため、決定的なメンバーシップ判定のできるハッシュテーブルとは性質が異なる。Quotient フィルターの偽陽性はハード衝突が発生したときに起きる。
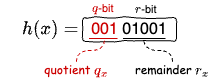
要素 \(x\) のフィンガープリントは上位 \(q\)-bit の商 (quotient) \(q_x\) と下位 \(r\)-bit の余剰 (remainder) \(r_x\) に分割される (Fig 1 左)。Quotient フィルターのテーブルは \(m=2^q\) 個のバケットで構成されている (Fig 1 右)。フィンガープリントの商はバケットのインデックとして使用され、余剰は (衝突がなければ) そのバケットに格納される。
ある要素 \(x\) が商 \(q_x\) を持つとき、インデックス \(q_x\) のバケットを \(x\) の正規スロット (canonical slot) と呼ぶ。
Quotient フィルターのバケットインデックスはオープンアドレス法のハッシュテーブルと同様に循環している。したがって \(i\) の次を示す \({\rm incr}(i)\) や前を示す \({\rm decr}(i)\) は次のように表すことができる。\[ \begin{eqnarray*} {\rm incr}(i) & = & (i + 1) \bmod 2^q & \text{ (i.e., if } i = 2^q-1 \text{ then } 0 \text{ else } i+1 \text{)} \\ {\rm decr}(i) & = & (i - 1) \bmod 2^q & \text{ (i.e., if } i = 0 \text{ then } 2^q-1 \text{ else } i-1 \text{)} \end{eqnarray*} \]
 衝突の解決方法
衝突の解決方法
異なる要素が同じフィンガープリントとなるハード衝突に対して、異なるフィンガープリントが同一の商を持つことをソフト衝突 (soft collision) と呼ぶ。Quotient フィルターではソフト衝突したフィンガープリントは昇順ソートされたひとかたまりの並びになるように配置される。その並びをラン (run) または連続部分と呼ぶ。
Fig 2 はチェーン法のハッシュテーブルと、それと同じ要素を格納している Quotient フィルターの比較である。ハッシュテーブルでは衝突が発生した要素はチェーン状のリスト構造に格納するのに対して、Quotient フィルターではそのチェーンを直列に並べた状態で格納する。
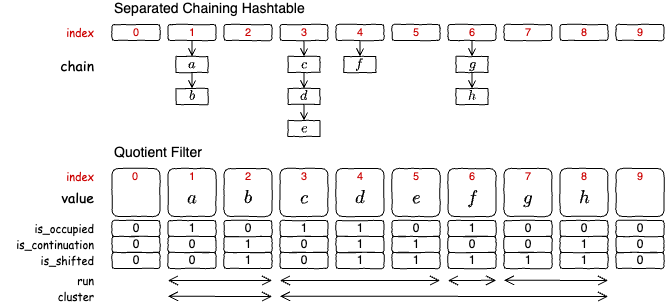
各バケットは衝突を認識するために後で説明するような is_occupied, is_continued, is_shifted という 3 つのフラグを持つ。
正規スロットから開始し、衝突や追い出しによって位置をずらされた値が格納されているひとかたまりの並びをクラスタ (cluster) と呼ぶ。言い換えると、クラスタの先頭のバケットの値は必ず正規スロットに格納されている。たとえば Fig 2 では 1 から始まるクラスタと 3 から始まるクラスタの 2 つが存在する。クラスタは 1 つ以上のランの連続で構成されており、クラスタ内のフィンガープリントは昇順ソートされているように配置されている。
衝突や追い出しによってクラスタが伸張するこによって、前後のクラスタが統合されることがある。
 挿入操作
挿入操作
Quotient フィルターの挿入操作は次の通りである。
- フィンガープリントの正規スロットが空の場合、単純にその正規スロットに剰余を格納する。
- フィンガープリントの正規スロットが空ではない場合、正規スロットを含むクラスタ内で、商に対応するランの開始位置を探索する。
- 対応するランが存在しない場合、商に対応するランが昇順で並ぶ位置にフィンガープリントの剰余を挿入する。
- 対応するランが存在する場合、剰余の昇順でラン内にフィンガープリントの剰余を挿入する。
ハード衝突が発生した場合、対応するランは同じ剰余を持つ複数のバケットを持つ。ただし、フィルターが削除をサポートしないのであれば各フィンガープリントのコピーは一つしか保存する必要がない。
 正規スロットが空いているケース
正規スロットが空いているケース
挿入しようとしているフィンガープリントに対応する正規スロットに値が設定されていなければ、挿入操作は単純にそのバケットへ剰余を格納して is_occupied を 1 に設定するだけである。
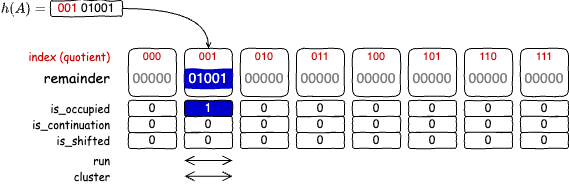
Quotient フィルターはフィンガープリントが衝突が発生していなくても前方の衝突によってその正規スロットに値が設定されている可能性がある点に注意。
 正規スロットが埋まっているケース
正規スロットが埋まっているケース
フィンガープリントの衝突が発生していたり、他の衝突による位置のシフトで正規スロットが埋まっていた場合、その正規スロットを含んでいるクラスタから商に対応するランを検索し、ラン内で昇順ソートされた位置にフィンガープリントの剰余を挿入する。
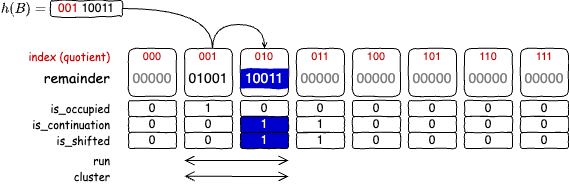
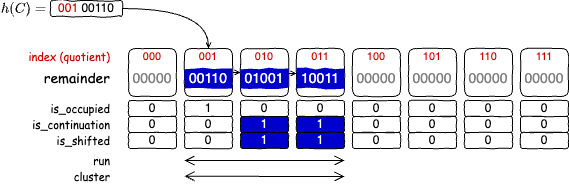
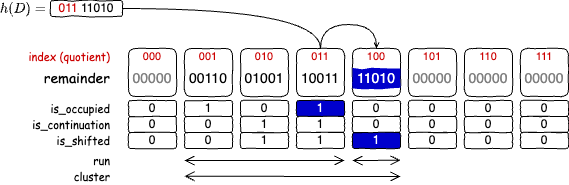
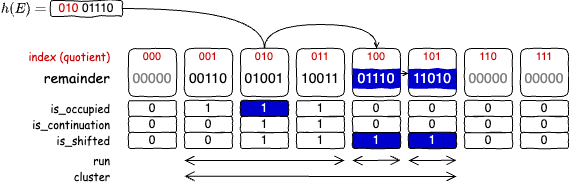
他の衝突の影響で、衝突が発生していないにもかかわらず正規スロットが埋まっている場合も同様である。この場合、フィンガープリントの挿入に加えて正規スロットの is_occupied フラグを 1 に設定する操作が必要である。
 各フラグの意味
各フラグの意味
バケットに付属する 3 つのフラグは、最終的にランやクラスタを認識したり、衝突して位置を動かされたフィンガープリントの商を決定するために使用される。
is_occupied: このフラグが 1 のとき、そのバケットが属するクラスタ内にこの商を持つフィンガープリントが含まれていることを意味している。つまり、クラスタ内で何番目の is_occupied かと、クラスタ内で何番目のランかをマッピングすることで、そのランの商を決定することができる。値ではなくバケットに結びつけられたフラグである。
is_continuation: このフラグが 1 のとき、そのバケットは直前のバケットに格納されているフィンガープリントと同じ商を持つ (衝突している) ことを意味する。つまり、is_continuation において 0 の後に 1 が続く並びのひとかたまりは 1 つの「ラン」を表している。
is_shifted: このフラグが 1 のとき、そのバケットに格納されている値は衝突や追い出しによって正規スロットではない位置に格納されていることを意味する。つまり、is_shifted において 0 の後に 1 が続く並びのひとかたまりは 1 つの「クラスタ」を表している。
空のバケットはすべてのビットが 0 に設定されている。クラスタの開始を示すバケットは is_occupied が 1 でそれ以外の 2 つが 0 に設定されている。したがってクラスタの開始位置は前方に向かって is_occupied=1, is_continuation=is_shifted=0 のフラグを持つバケットを探索することになる。
 検索操作
検索操作
ある要素 \(x\) が Quotient フィルターに含まれるかを検査することを考える。まず \(x\) のフィンガープリントの商 \(q_x\) のバケットが is_occupied=0 であれば \(x\) は含まれていない。そうでなければ、(1) \(q_x\) の属するスラスタの先頭を見つけ、(2) \(q_x\) に対応するランを見つけ、(3) ランの中に剰余 \(r_x\) が存在するかを確認する、という手順を取る。
 \(q_x\) に対応するランの探索
\(q_x\) に対応するランの探索
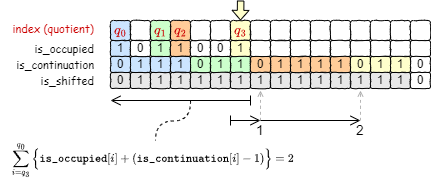
\(q_x\) が属するクラスタの開始位置 \(q'\) は \(q_x\) 以前に存在する is_shifted=0 のバケットである。まず \(q_x\) の位置から \(q'\) 検索し、その間に含まれるフラグから式 (\(\ref{k}\)) に示す \(k\) を算出する。\[ \begin{equation} k = \sum_{i=q_x}^{q'} \Big\{ {\tt is\_occupied}[i] + ({\tt is\_continuation}[i] - 1) \Big\} \label{k} \end{equation} \] この \(k\) は「クラスタ内で \(q_x\) 以前に存在する正規スロットの合計 - クラスタ内で \(q_x\) 以前に存在するランの合計」を表しており、つまり「\(q_x\) 以後のランの位置」を表している。したがって \(q_x\) から開始して \(k\) 番目に存在するランが \(q_x\) に対応するランである。
Fig 6 は \(q_x\) に対応するランの開始位置 \(i\) を探すための擬似コードである。このルーチンを実行した後に \(i\) は \(q_x\) に対応するランの開始位置を示している。
| 1. | \( i := q_x \) | |
| 2. | \( k := 0 \) | |
| 3. | \( {\bf while} \ \ {\tt is\_shifted}[i] \ne 0 \ {\bf do} \) | |
| 4. | \( \hspace{12pt} \)// if(is_occupied[i]==1){ k++; } if(is_continuation[i]==0){ k--; } | |
| 5. | \( \hspace{12pt}k := k + {\tt is\_occupied}[i] + ({\tt is\_continuation}[i] - 1) \) | |
| 6. | \( \hspace{12pt}i := {\rm decr}(i) \) | |
| 7. | \( {\bf done} \) | |
| 8. | \( i := q_x \) | |
| 9. | \( {\bf if} \ \ k \gt 0 \ {\bf then} \) | |
| 10. | \( \hspace{12pt}{\bf do} \) | |
| 11. | \( \hspace{24pt}i := {\rm incr}(i) \) | |
| 12. | \( \hspace{24pt} \)// if(is_continuation[i]==0){ k--; } | |
| 13. | \( \hspace{24pt}k := k + ({\tt is\_continuation}[i] - 1) \) | |
| 14. | \( \hspace{12pt}{\bf while} \ \ k \gt 0 \) | |
| 15. | \( {\bf end} \) | |
Fig 7 は商 \(q_3\) に対応するランの位置を検索する例である。
 剰余 \(r_x\) の探索
剰余 \(r_x\) の探索
\(q_x\) に対応するランを見つけたらその開始位置から剰余 \(r_x\) を逐次探索を行う。ランの剰余は昇順にソートされていることから、ランの先頭から順に \(r_i \gt r_x\) を検出するか、is_continuation[i]=0 を検出したときに「非存在」として探索を終了することができる。
| 1. | \( {\bf do} \) | |
| 2. | \( \hspace{12pt}{\bf if} \ \ {\tt bucket}[i] = r_x \ \ {\bf then} \ {\bf return} \ \text{$x$ probably exist.} \) | |
| 3. | \( \hspace{12pt}{\bf if} \ \ {\tt bucket}[i] \gt r_x \ \ {\bf then} \ {\bf break} \) | |
| 4. | \( \hspace{12pt}i := {\rm incr}(i) \) | |
| 5. | \( {\bf while} \ \ {\tt is\_continuation}=1 \) | |
| 6. | \( {\bf return} \ \text{$x$ doesn't exist.} \) | |
 削除操作
削除操作
Quotient フィルターの基本的な構造はフィンガープリントの線形プローブ法ハッシュテーブルである。したがってその仕組みは削除をサポートしている。ただし、フィルターに存在しない要素の削除でハード衝突が起きた場合、意図しないフィンガープリントが削除され致命的な偽陰性が発生する可能性がある。このため、Counting Bloom Filter と同様に、Quotient フィルターがサポートする削除は「確実にこのフィルターが含んでいる要素」に対してのみである。この要件は他のすべての削除をサポートするフィルターにも当てはまる [4]。
削除でクラスタ内に格納されたフィンガープリントをシフトさせる代わりに、4 つ目の墓石 (tombstone) フラグを追加しても良い。この場合、ラン内の最後の 1 つを削除したときに is_occupied フラグを 0 に戻す必要がある。
 フィルターサイズの変更
フィルターサイズの変更
Quotient フィルターはバケットの位置とそこに格納されている値でフィンガープリントを完全に復元して列挙できる (フィンガープリントから要素を復元できないだけである)。このためフィルターをより効率的なサイズに変更することができる。
Quotient フィルターのサイズを 2 倍、つまり商を \(q+1\)、剰余を \(r-1\) とした新しいテーブルを作成し、現在のテーブルに格納されているすべてのフィンガープリントを移動することでフィルターの拡張が可能である。
リサイズではフィンガープリントを昇順で取り出せるため、通常の挿入と異なり、ソートのための挿入位置の探索やシフトの処理は省略できる。
 カスケードフィルター
カスケードフィルター
カスケードフィルター (cascade filter) [3] は Quotient フィルターの応用である。第一層の Quotient フィルターをメモリ上、第二層以下の Quotient フィルターをストレージ上に配置することで Bloom フィルターより大規模なフィルターを構築することができる。
 参考文献
参考文献
- Dzejla Medjedovic, Emin Tahirovic, Ines Dedovic. 大規模データセットのためのアルゴリズムとデータ構造. マイナビ出版 (2024)
- Donald Knuth. The Art of Computer Programming: Sorting and Searching, volume 3. アスキー (2006)
- Michael A Bender, Martin Farach-Colton, Rob Johnson, Russell Kraner, Bradley C Kuszmaul, Dzejla Medjedovic, Pablo Montes, Pradeep Shetty, Richard P Spillane, and Erez Zadok. Don’t thrash: How to cache your hash on flash. Proceedings of the VLDB Endowment, 5(11), 2012.
- FAN, Bin, et al. Cuckoo Filter: Practically Better Than Bloom. In: Proceedings of the 10th ACM International on Conference on emerging Networking Experiments and Technologies. 2014. p. 75-88.