構造化アルゴリズム

論文翻訳: An Introduction to Bε-trees and Write-Optimization

Takami Torao 2015年の記事 #BTree #BεTree
  • このエントリーをはてなブックマークに追加

Michael A. Bender, Martin Farach-Colton, William Jannen, Rob Johnson, Bradley C. Kuszmaul, Donald E. Porter, Jun Yuan, and Yang Zhan

Abstract

Bε-Tree は書き込みに最適化されたデータ構造の一例であり、データベースやファイルシステムなどのアプリケーションのディスク上のストレージを整理するために使用することができる。Bε-Tree は B-Tree に似た Key-Value API を提供するが、特に挿入、範囲クエリー、および Key-Value の更新パフォーマンスが優れている。この記事では Bε-Tree について説明し、B-Tree や Log-Structured Merge Tree (LSM ツリー) との漸近的なパフォーマンスを比較し、実際の性能測定結果を示す。この記事を読み終えた読者は Bε-Tree の仕組み、性能特性、他の Key-Value ストアとの比較、Bε-Tree から最大のパフォーマンスを引き出すアプリケーション設計方法についての基本的な理解が得られるはずである。

Table of Contents

  1. Abstract
  2. 1 Bε-Tree
    1. 1.1 性能分析
    2. 1.2 ノードサイズ (\(B\)) が性能に与える影響
    3. 1.3 ε の役割
    4. 1.4 Bε-Tree を使用してアプリケーションを高速化する方法
    5. 1.5 Log-Structured Merge Tree
  3. 2 パフォーマンス比較
  4. 3 結論
  5. Acknowledgements
  6. References
  7. 翻訳抄

1 Bε-Tree

Bε-Tree は B-Tree [2] とバッファ付きリポジトリツリー [3] の間の漸近的なパフォーマンストレードオフ曲線を示す方法として Brodal と Fagerberg [1] によって提案された。どちらのデータ構造も同じ操作をサポートするが、B-Tree はクエリーを優先し、バッファ付きリポジトリツリーは挿入を優先する。

この記事を含む研究者らは、Bε-Tree がこの曲線の "中間点" を占めるように構成された場合に B-Tree に匹敵するクエリ性能を実現しながら B-Tree よりも桁違いに高速な挿入性能を実現する実用的な有用性があることを認識している。それ以来 Bε-Tree は高性能な商用 TokuDB [4] と BetrFS research file system [5] の両方で使用されている。興味のある読者のために Bε-Tree の簡単なリファレンス実装を作成した。https://github.com/oscarlab/Be-Tree.

まず Bε-Tree に対する基本的な操作がどのように行われるかを説明する。次に、これらの設計上の選択の背景にある動機を示し、これらの選択が漸近解析にどのように影響するかを説明する。

API と基本構造. Bε-Tree は Figure 1 に示すようにディスク上のデータを整理するための B-Tree のような検索ツリーである。B-Tree も Bε-Tree も Key-Value ストアの API をエクスポートする:

  • \({\tt insert}(k,v)\)

  • \({\tt delete}(k)\)

  • \(v = {\tt query}(k)\)

  • \([v_1,v_2,\ldots] = {\tt range\mbox{-}query}(k_1,k_2)\)

B-Tree と同様に、Bε-Tree のノードサイズは基礎となるストレージデバイスのブロックサイズの倍数となるように選択される。一般的な Bε-Tree のノードサイズは数百キロバイトから数メガバイトの範囲である。B-Tree も Bε-Tree も内部ノードはピボットキーと子ポインタを格納し、葉はキーでソートされたキーと値を格納する。説明を簡単にするために、各キーと値またはピボットとポインタのペアを単位サイズと考えるものとするが、実際には B-Tree も Bε-Tree も異なるサイズのキーと値を格納できる。したがって、サイズ \(B\) の葉には \(B\) 個の (以降ではアイテムと呼ぶ) Key-Value ペアを保持する。

Bε-Tree の特徴は、Figure 1 に示すように内部ノードにもバッファ用のいくらかの空間が割り当てられることである。各内部ノードのバッファは、最終的にこのノードの下のリーフに適用される更新をエンコードするメッセージを格納するために使用される。このバッファはメモリ内のデータ構造ではなくノードの一部であり、ノードがディスクに書き込まれたりメモリから退避されるときには常にそれが行われる。ε の値は 0 から 1 の間でなければならず、内部ノードがピボットに使用する空間量 (\(\approx B^\epsilon\)) とバッファとして使用する空間量 (\(\approx B - B^\epsilon\)) を選択する調整パラメータである。

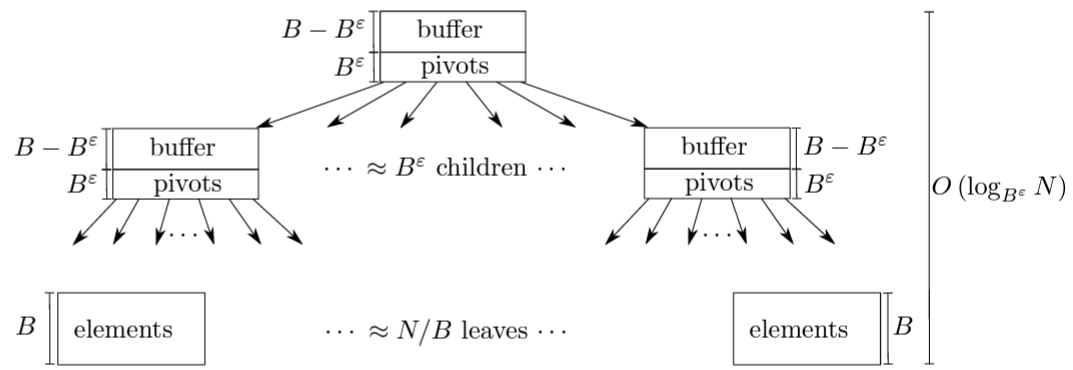
Figure 1. Bε-Tree。各ノードのサイズはおおよそ \(B\) で、\(\epsilon\) は内部ノードの空間のピボットに使用される量 (\(B^\epsilon\)) と保留中の更新のバッファリングに使用される量 (\(B-B^\epsilon\)) を制御する。B-Tree と同様にアイテムは葉に格納され、ツリーの高さは分岐計数 (ここでは \(B^\epsilon\)) に基づいてアイテムの総数 (\(N\)) の対数となる。

挿入と削除. 挿入は "挿入メッセージ" としてエンコードされ、特定のキーに当ててツリーのルートノードのバッファに追加される。十分なメッセージがノードに追加されてバッファがいっぱいになると、メッセージのバッチがノードの子ノードのいずれかにフラッシュされる。通常、保留中のメッセージが最も多い子ノードが選択される。フラッシュの過程で、各メッセージは最終的に適切な葉ノードに配信され、新しいキーと値が葉に追加される。葉ノードがいっぱいになると B-Tree のように分割される。B-Tree と同様に、内部ノードに子ノードが増えすぎると、そのノードは分割され、バッファ内のメッセージは 2 つの新しいノードに分散される。

バッチでツリーの下にメッセージを移動させることが Bε-Tree の挿入パフォーマンスの鍵となる。Bε-Tree は新しく挿入されたメッセージをルート近くのバッファに格納することで、要素を目的の場所に配置するためにディスク上を探し回ることを回避することができる。Bε-Tree はサブツリーに十分なメッセージが蓄積し I/O コストを償却できる場合にのみメッセージをサブツリーに移動する。これは同じデータを複数回書き換えることになるが、次のセクションでの分析で示すようにより小規模でランダムな挿入のパフォーマンスを向上させることができる。

Bε-Tree はツリーに "墓石メッセージ" を挿入することでアイテムを削除する。これらの墓石メッセージは葉に到達するまでツリーを下ってフラッシュされる。墓石メッセージが葉にフラッシュされると、Bε-Tree は削除されたアイテムと墓石メッセージの両方を破棄する。したがって、削除されたアイテムまたは葉ノード全体は墓石メッセージが葉に到達するまで存在し続けることができる。削除はメッセージとしてエンコードされるため、削除はアルゴリズム的には挿入と非常に似ている。

高性能な Bε-Tree は大量のメッセージがすべて 1 つの葉に向かうケースを検出して最適化する必要がある。1 つの葉を完全に埋め尽くすような一連のキーが挿入されたとする。これらのメッセージを内部ノードに書き込んで、ルートからリーフへの経路上の各ノードにすぐに書き換えるのではなく、これらのメッセージはその葉の他の保留中のメッセージと共に葉にフラッシュすべきである。TokuDB と BetrFS の Bε-Tree 実装には一連のメッセージがすべて 1 つの子に送られる場合に中間ノードへの書き込みを回避するためのヒューリスチックがいくつか含まれている。

ポイントクエリーと範囲クエリー. キー \(k\) 宛てのメッセージは、キー \(k\) に向かう root-to-leaf 経路に沿った \(k\) の葉またはバッファに適用されることが保証される。この不変条件により Bε-Tree のポイントクエリーと範囲クエリーの I/O コストは B-Tree と同等になることが保証される。

B-Tree でも Bε-Tree でも、ポイントクエリーはルートから正しい葉までの各ノードを訪問する。ただし Bε-Tree では、クエリーに応答するということは、この経路上のノードのバッファでメッセージを確認し、クエリーの結果を返す前に関連メッセージを適用することも意味する。たとえばキー \(k\) のクエリーで葉にエントリ \((k,v)\) が見つかり、内部ノードに \(k\) に対する墓石メッセージが見つかった場合、キー \(k\) のエントリはツリーから論理的に削除されているため、クエリーは "NOT FOUND" を返す。この場合、クエリーは葉を更新する必要がないことに注意。墓石メッセージが葉にフラッシュされると葉は最終的に更新される。範囲クエリーはポイントクエリーに似ているが、適切なサブツリーを走査する際にキーの全範囲のメッセージをチェックし適用しなければならない点が異なる。

バッファの検索と挿入を効率的に行うために、通常各ノード内のメッセージバッファは赤黒木のような均衡のとれた二分探索木に編成されている。バッファ内のメッセージはターゲットキーとタイムスタンプの順にソートされる。タイムスタンプによってメッセージが正しい順序で適用される。したがってバッファへのメッセージの挿入、バッファ内の検索、および 1 つのバッファから別のバッファへのフラッシュはすべて高速である。

1.1 性能分析

この記事では B-Tree, Bε-Tree, LSM-Tree の動作を I/O の観点から分析する。我々の主な監視は RAM に収まらないほど大きなデータセットである。したがってパフォーマンスにもっとも大きく影響するのは、各操作を完了するために何回の I/O 要求を発光しなければならないかである。アルゴリズムの文献では、これはディスクアクセスマシン (DAM) モデル、外部メモリモデル、または I/O モデルとして知られている。

パフォーマンスモデル. B-Tree と Bε-Tree を単一のフレームワークで比較するためにいくつかの単純化された家庭を置く。すべての Key-Value ペアは同じサイズであり、ツリー内の各ノードは \(B\) 個の Key-Value ペアを保持できると仮定する。ツリー全体は \(N\) 個の key-Value ペアが格納される。また各ノードは単一の I/O トランザクションでアクセスできると仮定する。つまり回転ディスク上ではノードは連続して格納され、1 回のランダムシークのみが必要である。

このモデルはハードドライブや SSD などのブロックストレージデバイスの主要な性能特性に焦点を当てている。たとえばハードドライブの場合はこのモデルはノードを読み取るためにランダムシークのレイテンシーをキャプチャする。SSD の場合、このモデルは I/O 帯域幅コスト、つまり操作ごとにデバイスから読み取りまたは書き込みする必要のあるブロック数をキャプチャする。デバイスが帯域幅またはレイテンシのどちらに束縛されているかに関係なく、特定のノードサイズ \(B\) の場合、アクセスされるノードの数を最小化することで帯域幅とレイテンシの両方のコストを最小化できる。いるかに関係なく、所与のノードサイズBの場合、アクセスされるノード数を最小化することで、帯域幅と待ち時間の両方のコストを最小化できます。

Bε-Tree の I/O パフォーマンス. Table 1 は B-Tree と Bε-Tree の各処理の漸近的な複雑性を示している。アップサート (upsert) とイプシロン (\(\epsilon\))、およびそれらが性能にどのように影響するかについては記事の後半で説明する。\(\epsilon\) は 0 から 1 の間のチューニングパラメータであることに注意。\(\epsilon\) は通常、設計時に設定され分析では定数となる。

B-Tree と Bε-Tree のポイントクエリーの複雑性はどちらもアイテム数の対数 (\(O(\log_B N)\)) であり、Bε-Tree では一定のオーバーヘッド \(1/\epsilon\) が追加される。同じノードサイズの B-Tree と比較すると、Bε-Tree では \(B\) から \(B^\epsilon\) のファンアウトが削減されツリーの高さが \(1/\epsilon\) 倍となる。したがって、たとえば \(\epsilon=1/2\) となるような Bε-Tree をクエリーすると最大で 2 倍の I/O が必要になる。

範囲クエリーでは最初のキーに対して対数の検索コストが発生する。また範囲のサイズと、範囲がいくつのブロックデバイスにまたがって分散しているかに比例したコストが発生する。スキャンコストは読み取られたキーの数 (\(k\)) をブロックサイズ (\(B\)) で割った値とほぼ同じである。範囲クエリーの総コストは \(O(k/B+\log_B N)\) 回の I/O である。B-Tree と比較すると、メッセージのバッチ処理は挿入コストをバッチサイズ (\(B^{1-\epsilon}\)) で割ることになる。例えば \(B=1024\)、\(\epsilon=1/2\) の場合、Bε-Tree は B-Tree より \(\approx \epsilon B^{1-\epsilon} = \frac{1}{2}\sqrt{1024} = 16\) 倍速く挿入を実行できる。

Table 1. 重要な操作の漸近的 I/O コスト。Bε-Tree は効率的な挿入、ポイントクエリー (アップサートが存在する場合でも)、範囲クエリーを同時にサポートする。これらの複雑度は \(0 \lt \epsilon \le 1\) の場合に適用される。\(\epsilon\) は設計時定数であることに注意。一般的な \(\epsilon\) に対する複雑度を示し、\(\epsilon\) を典型的な値である 1/2 に設定した場合の複雑度を評価する。\(1/\epsilon\) 因子は漸近分析で消失する定数に評価される。

書き込みの最適化. Bε-Tree や LSM-Tree のような書き込み最適化データ構造 (WODS; write-optimized data structures)) では小さなランダム挿入をバッチ処理することが不可欠である。WODS は、メッセージがツリーを移動するときに小さな書き込みを複数回発行する可能性があるが、I/O コストが大きなバッチで分割されると、挿入や削除の 1 回当たりのコストは操作ごとに 1 回の I/O よりも遙かに小さくなる。対照的に B-Tree へのランダム挿入のワークロードでは、新しい要素をターゲットの葉に書き込むために、挿入ごとに少なくとも一回の I/O が必要である。

Bε-Tree のフラッシュ戦略は常に大きなバッチで要素を移動できるように設計されている。ノードのバッファがいっぱいになり、\(B-B^\epsilon\approx B\) 個のメッセージが含まれている場合にのみ子ノードにメッセージがフラッシュされる。バッファがフラッシュされるときに必ずすべてのメッセージがフラッシュされるわけではない。親ノードと子ノードを書き換えるコストを相殺するのに十分な保留メッセージがある場合にのみ子ノードにメッセージがフラッシュされる。具体的には、少なくとも \((B-B^\epsilon)/B^\epsilon \approx B\) 個のメッセージがフラッシュのたびに親のバッファから子のバッファに移動される。その結果、Bε-Tree 内のどのノードも、ノードの十分な部分が変更される場合にのみ書き換えられる。

キャッシュ. ほとんどのシステムはツリーのサブセットを RAM にキャッシュする。LRU 置換ポリシーではツリーの最上部へのアクセスはキャッシュにヒットする可能性が高いが、葉や "下位ノード" へのアクセスはミスすることが多くなる。したがって、キャッシュがウォーム状態の場合、検索にかかる実際のコストは \(O(\log_B N)\) 回の I/O よりはるかに少なくなる可能性がある。B-Tree と Bε-Tree の両方で、葉のみがキャッシュの外にある場合、ポイントクエリーと更新には 1 回の I/O のみが必要だが、範囲クエリーの I/O コストは読み取る葉の数に比例する。

1.2 ノードサイズ (\(B\)) が性能に与える影響

B-Tree は挿入と範囲クエリーのコストのバランスを取るための小さなノードを持つ. B-Tree の実装では更新と範囲クエリーの性能のトレードオフに直面する。ノードサイズ \(B\) が大きいほど範囲クエリーが有利になり、ノードサイズが小さいほど挿入と削除が有利になる。ノードを大きくすると、シークなどの I/O コストをより多くのデータで償却できるため範囲クエリーのパフォーマンスが向上する。しかしノードが大きいほどインデックスに新しい項目が追加されるたびに葉と場合によって内部ノードを完全に書き換える必要があり、書き換える量が増えるため更新のコストが高くなる。

そのため多くの B-Tree 実装では小さなノード (数十から数百KB) が使用され、その結果、範囲クエリーのパフォーマンスが最適ではなくなる。ディスク上の空き領域が断片化されると B-Tree ノードもディスク上に散在する可能性がある。これはエージング (aging) と呼ばれることもある。これにより範囲クエリーはスキャンでそれぞれの葉をシークしなければならず帯域幅の使用率が悪化する。

例えばシーク時間が 5ms で帯域幅が 100MB/s のディスクに 4KB のノードが格納されている場合、1 つのキーを更新しても 4KB を書き換えるだけである。しかｓ範囲クエリーでは 4KB の葉ノードごとにシークを実行する必要があるため、ネット帯域幅は 800KB/s となり、ディスク本来の帯域幅の 1% 未満となる。

Bε-Tree はノードが大きい場合でも更新と範囲クエリーが効率的. 対照的に Bε-Tree でのバッチ処理では、\(B\) を B-Tree よりも Bε-Tree で大幅に大きくすることができる。Bε-Tree では挿入あたりの帯域幅コストが \(O(\frac{B^\epsilon \log_B N}{\epsilon})\) であり、\(B\) が大きくなるにつれて増加は遙かに緩やかになる。その結果 Bε-Tree では数百キロバイトから数メガバイトのノードサイズが使用される。

大きな \(B\) を使うことで Bε-Tree はディスク帯域幅に近い範囲クエリーを実行できる。例えば 4MB のノードを使用する Bε-Tree は、4MB のデータを返すごとに 1 回のシークを実行するだけでよく、上記と同じディスクで 88MB/s を超える正味の帯域幅が得られる。

上記の挿入複雑度の比較では、\(\epsilon=1/2\) の Bε-Tree はバッファ空間のためにファンアウトが犠牲になるため B-Tree の 2 倍の深さになると述べた。これはノードサイズが同じ場合にのみ当てはまる。Bε-Tree は実際にはより大きなノードを使用できるため、Bε-Tree は B-Tree とほぼ同じファンアウトと高さを持つ。

1.3 ε の役割

元々、Bε-Tree のパラメータ \(\epsilon\) は挿入とポイントクエリーのパフォーマンスの間に適切なトレードオフ曲線があることを示すために設計された。パラメータ \(\epsilon\) の範囲は 0 から 1 である。このセクションの残りの部分で説明するように、\(\epsilon\) を指数にすることで漸近的分析が暗黙的に行われて興味深いトレードオフ曲線が生まれる。

直感的に、パラメータ \(\epsilon\) とのトレードオフはノード内でピボットと子ポインタの格納に使われる空間の量 (\(\approx B^\epsilon\)) と、メッセージバッファに使われる空間の量 (\(\approx B-B^\epsilon\)) である。\(\epsilon\) が増加すると分岐計数 (\(B^\epsilon\)) も増加し、ツリーの深さが減少して検索が高速に実行される。\(\epsilon\) が減少するとバッファが大きくなり、フラッシュごとにより多くの挿入がバッチ処理され、全体的な挿入パフォーマンスが向上する。

極端な例として、\(\epsilon=1\) の場合、Bε-Tree は内部ノードにピボットキーと子ポインタのみが含まれるため、単なる B-Tree となる。一方 \(\epsilon=0\) の場合、Bε-Tree は各ノードに大きなバッファを持つバイナリ探索木となり、バッファ付きリポジトリツリー [3] と呼ばれる。

最も興味深い構成は \(\epsilon=1/2\) のように \(\epsilon\) を厳密に 0 と 1 の間に置くことである。このような構成では、Bε-Tree は B-Tree と同じ漸近的なポイントクエリーの性能を持つが、挿入パフォーマンスは漸近的に優れている。

挿入の場合、\(\epsilon=1/2\) に設定するとコストがノードサイズの平方根で割り算される。正式なコストは \(O(\frac{\log_B N}{\epsilon B^{1-\epsilon}}) = O(\frac{\log_B N}{\sqrt{B}})\) である。挿入コストは \(\sqrt{B}\) で割られるため、より大きなノードを選択する (\(B\) を増加させる) ことで挿入パフォーマンスが劇的に向上する。

他のすべてのパラメータが同じであると仮定すると、\(\epsilon\) を減少させるとポイントクエリーの速度が定数 \(1/\epsilon\) だけ低下する。\(\epsilon=1/2\) の場合のクエリーパフォーマンスを確認するには Table 1 のポイントクエリーコストを評価する: \(O(\frac{\log_B N}{\epsilon}) = O(\frac{\log_B N}{1/2}) = O(2 \log_B N)\) で I/O の数が 2 倍になる。\(\epsilon\) を 1/2 から 1/4 に変更するとこの値は 4 倍になる。このコストは \(B\) を増やすことで相殺でき、上で指摘したように挿入パフォーマンスも向上する。

上記の分析では、すべてのキーが単位サイズであり、ノードが \(B\) 個のキーを保持できると仮定している。実際のシステムでは可変サイズのキーを扱わなければならないため、\(B\)、ひいては \(\epsilon\) は固定ではないし事前に知ることもできない。それでも、内部ノードにアイテムをバッファリングしそれらをツリーの下位にバッチでフラッシュすることで挿入を高速化できるという Bε-Tree の洞察はこの設定にも当てはまる。

実際には、Bε-Tree の実装では固定の物理ノードサイズとファンアウト (\(B^\epsilon\)) を選択する。TokuDB と BetrFS の実装では、ノードは約 4MB、分岐計数は 4 から 16 の範囲である。その結果、フラクタルツリーは常に少なくとも 256KB のバッチでデータをフラッシュできる。

1.4 Bε-Tree を使用してアプリケーションを高速化する方法

上記の分析の実用的な結果は、Bε-Tree はポイントクエリーよりも更新を桁違いに高速化できると言うことである。この検索と挿入の非対称性は Bε-Tree 状のアプリケーションを設計する上で 2 つの意味を持つ。

パフォーマンスルール. 可能な限り更新前のクエリー (query-before-update) を避ける。

検索と挿入の非対称のため、一般的な読み取り-変更-書き込み (read-modify-write) (または読み取り-変更-挿入) パターンはクエリーの速度に束縛されるが、Bε-Tree が B-Tree より速くなることはない。

アップサート. Bε-Tree はこのような性能の非対称を埋めるのに役に立つ新しいアップサート (upsert) 操作をサポートしている。アップサートはキーの値を知らなくても発行できるコールバック関数を使用して更新をエンコードするメッセージの一種である。

アップサートは、キー、古い値、およびアップサートメッセージと一緒に格納できる補助データにのみ依存する変更を非同期でエンコードできる。墓石はアップサートの特殊なケースである。アップサートは、カウンターをインクリメント、ファイルのアクセス時間の更新、引き出し後のユーザの口座残高の更新、その他多くの操作にも使用できる。

アプリケーションはアップサートを使用してツリーに "アップサートメッセージ" \((k,(f,\Delta))\) を挿入することで、Bε-Tree のキー \(k\) に関連付けられた値を更新できる。ここで \(f\) はコールバック関数、\(\Delta\) は実行する更新を指定する補助データである。このアップサートメッセージはクエリーの後に挿入を実行することと意味的に等価である: \[ v \leftarrow {\tt query}(k); \ \ \ {\tt insert}(k, f(v,\Delta)) \] ただし、アップサートではこれらの操作は実行されない。代わりに、挿入メッセージや墓石メッセージのように、メッセージ \((k,(f,\Delta))\) がツリーに挿入される。

アップサートメッセージ \((k,(f,\Delta))\) が葉にフラッシュされると、葉内の \(k\) に関連付けられた値 \(v\) は \(f(v,\Delta)\) に置き換えられ、アップサートメッセージは破棄される。アップサートメッセージが葉に到達する前にアプリケーションが \(k\) をクエリーすると、クエリーが返される前にアップサートメッセージが \(v\) に適用される。

挿入メッセージや削除メッセージと同様に、ルートと葉の間で同じキーに対して複数のアップサートをバッファリングできる。複数のアップサートが保留中の状態でキーがクエリーされた場合、各アップサートはルートから葉へのパスで収集され、ツリーに挿入された順序でキーに適用されなければならない。

キー \(k\) のアップサートメッセージは常に Bε-Tree のルートから \(k\) を含む葉までの検索パス上にあるため、アップサートメカニズムは検索 I/O パフォーマンスに影響を与えない。したがって、アップサートメカニズムはクエリーの速度を低下させることなく更新を 1～2 桁高速化できる。

パフォーマンスルール. 適切なインデックスを維持することで、挿入パフォーマンスを使用してクエリーパフォーマンスを向上する。

セカンダリインデックス. データベースではセカンダリインデックスによってクエリー大幅に高速化することができる。たとえば \(k_1\), \(k_2\), \(k_3\) の 3 つの列を持つデータベーステーブルと、時々 \(k_1\) を使用してクエリーを実行し、時々 \(k_2\) を使用してクエリーを実行するアプリケーションについて考える。テーブルが \(k_1\) でソートされた B-Tree として実装されている場合、\(k_1\) を使用したクエリーは非常に高速だが、\(k_2\) を使用したクエリーは非常に低速になる。つまりデータベース全体をスキャンしなければならないかもしれない。この問題を解決するために、\(k_1\) でソートされたインデックスと \(k_2\) でソートされたインデックスの 2 つを保持sルウようにテーブルを構成することができる。これによりクエリーはクエリーの種類に基づいて適切なインデックスを使用できる。

B-Tree で複数のインデックスを保持する場合、各インデックスの更新には追加の挿入を必要とする。挿入はポイントクエリーと同じくらい高価であるため、各列にインデックスを維持することは現実的ではないことが多い。したがって、テーブル設計者は予想されるクエリーの種類やキーの分布などの要因を注意深く分析し、どの列にインデックスを設定するかを決定する必要がある。

Bε-Tree はこれらの問題を根本的に解決する。インデックスの維持コストは低い。ポイントクエリーは基本的に高価である ─ Bε-Tree のポイントクエリーは B-Tree よりも高速ではない。したがって Bε-Tree アプリケーションはクエリーを効率的に実行するために必要なインデックスを維持する必要がある。

適切な Bε-Tree インデックスを設計するために 3 つのルールがある。

まず、データベースのクエリーに使用するキーでソートされたインデックスを管理する。たとえば上記の例では、データベースは 2 つの Bε-Tree を維持する必要がある (1 つは \(k_1\) でソートされたもの、もう 1 つは \(k_2\) でソートされたもの)。

第二に、意図したクエリーに応答するために必要なすべての情報が各インデックスに含まれているようにする。例えばアプリケーションが \(k_2\) のキーを使って \(k_3\) の値を検索する場合、\(k_2\) でソートされたインデックスには各エントリに対応する \(k_3\) 値が格納されているべきである。多くのデータベースでは、セカンダリインデックスにはプライマリインデックスのキーのみを含んでいる。したがって、たとえば \(k_2\) に対するクエリーはプライマリキー値 \(k_1\) を返す。\(k_3\) を取得するには、アプリケーションはセカンダリインデックスから取得した \(k_1\) 値を使用してプライマリインデックスで別のクエリーを実行する必要がある。あるクエリーに関連するすべての情報を含むインデックスを、そのクエリーに対するカバー (covering) インデックスと呼ぶ。

最後に、アプリケーションが可能な限り範囲クエリーを実行できるようにインデックスを設計する。例えばアプリケーションが \(a \le k_1 \le b\) かつ \(k_2\) が述語 (predicate) を満たすすべてのエントリ \((k_1,k_2,k_3)\) を検索する場合、アプリケーションは \(k_2\) が述語に一致するエントリのみを含む、\(k_1\) でソートされたセカンダリインデックスを維持すべきである。

1.5 Log-Structured Merge Tree

Log-Structured Merge Tree (LSM-Tree) [7] は多くのバリエーションを持つ WODS である [8, 9]。通常、LSM-Tree 指数関数的に増加するサイズの B-Tree の対数で構成される。あるレベルのインデックスがいっぱいになると、次のインデックスにマージして空にする。各レベルが増加する係数は Bε-Tree の分岐計数 (\(B^\epsilon\)) に匹敵する調整可能なパラメータである。比較を容易にするために、Table 1 に増加計数 \(B^\epsilon\) を持つ LSM-Tree での操作の I/O 複雑度を示す。

LSM-Tree は Bε-Tree と同じ挿入複雑度を持つように調整できるが、ナイーブに実装された LSM-Tree での問い合わせはクエリーを \(O(\log_B N)\) の B-Tree で返す必要があるため、\(O(\frac{\log_B^2 N}{\epsilon})\) 回の I/O を必要とする場合がある。ほとんどの LSM-Tree 実装ではブルームフィルタを使用して、1 つの B-Tree を除くすべての B-Tree でのクエリーを回避し、ポイントクエリーのパフォーマンスを \(O(\frac{\log_B N}{\epsilon})\) 回の I/O に向上させる。

LSM-Tree の問題の一つは、ブルームフィルタの利点が範囲クエリーにまで及ばないことである。ブルームフィルターはポイントクエリーを改善するためだけに設計されており範囲クエリーはサポートしていない。そのため LSM-Tree のすべてのレベルで範囲クエリーを実行する必要がある。これにより、Table 1 の検索オーバーヘッドが 2 乗され、Bε-Tree や B-Tree よりも明らかに劣る漸近的パフォーマンスが得られる。

LSM-Tree に対する Bε-Tree の 2 つ目の利点は、Bε-Tree ではアップサートを効率的に利用できることである。LSM-Tree でアップサートを使用すると、ブルームフィルタを追加することによるパフォーマンス上の利点が損なわれる。上述したように、アップサートは LSM-Tree を含むすべての WODS に共通する検索と挿入の非対称性に対処するものである。アプリケーションがアップサートを使用する場合、そのキーに対する保留中のメッセージを含むツリーのすべてのレベルにそのキーのメッセージが存在する可能性がある。そのため、後続のポイントクエリーでは、ツリーのすべてのレベルを問い合わせしなければならずブルームフィルタを追加する意味がなくなる。LSM-Tree のすべてのレベルを問い合わせると、Bε-Tree や B-Tree と比較してオーバーヘッドが 2 乗され、Bε-Tree のルートから葉までの経路をたどるよりもコストがかかることに注意。

要約すると、ブルームフィルタで強化された LSM-Tree は一部のワークロードで Bε-Tree の性能に匹敵するが、すべてのワークロードでそうはならない。Bε-Tree は LSM-Tree の性能を漸近的に上回る。特に、Bε-Tree はアップサートを多用するワークロードでの小さな範囲クエリーやポイントクエリーにおいて LSM-Tree より漸近的に高速である。

2 パフォーマンス比較

Bε-Tree がどのように機能するかを知るために、Bε-Tree をベースとしたカーネル内の研究用ファイルシステムである BetrFS のデータをいくつか紹介する。BetrFS を B-Tree で構築された btrfs など他のファイルシステムと比較する。より詳細な評価は最近の FAST 論文 [5] に掲載されている。

すべての実験結果は 4 コア 3.40 GHz Intel Core i7 CPU、4 GB RAM、250GB 7200 RPM ATA ディスクを搭載した Dell Optiplex 790 で収集した。各ファイルシステムは 4096 バイトのブロックサイズを使用した。システムは Linux カーネルバージョン 3.11.10 の 64 ビット Ubuntu 13.10 で実行された。核実験は BTRFS、ext4、XFS、ZFS などを含む複数の汎用ファイルシステムと比較した。エラーバーと±の範囲は 95% 信用区間を示す。特に明記されていない限りベンチマークはコールドキャッシュテストである。

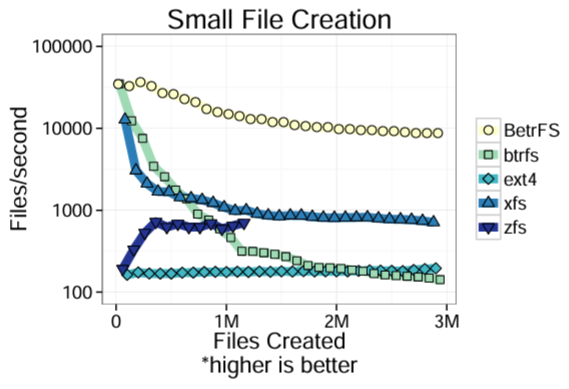
小さな書き込み. 我々は TokuDB ベンチマーク [10] を使って 4 つのスレッド (1 CPU につき 1 スレッド) を使用し、ファンアウトが 128 の平衡ディレクトリツリー (balanced directory tree) に 200 バイトのファイルを 300 万個作成した。BetrFS では、ファイルの作成は Bε-Tree への挿入として実装され、小さなファイルの書き込みはアップサートとして実装されるため、このベンチマークはこれら 2 つの操作における Bε-Tree のパフォーマンスを示している。Figure 2 は各ファイルシステムでのファイル作成時の持続レート (sustained rate) を示している (対数スケールに注意)。ZFS の場合、ベンチマークを完了する前にファイルシステムがクラッシュしたため、実験を 5 回再実行し最も実行時間の長い反復のデータを使用した。BetrFS は最初から最も高速なファイルシステムの 1 つであり、実験中も良好なパフォーマンスを維持した。BetrFS の定常状態の性能は他のファイルシステムよりも桁違いに高速である。

この性能差は書き込み総数が少なく、バイトあたりのシーク数が少ないこと、つまり小さな書き込みの集約が優れていることの両方に起因する。blktrace のプロファイリングに基づくと、大きな違いの 1 つは書き込みバイト数である。BetrFS がディスクに書き込むそう MB は 4-10 倍少なく、書き込み要求の総数も 1 桁少なくなっている。他のファイルシステムでは ext4、XFS、ZFS がほぼ同じ量のデータを書き込んだが、基本的な書き込みスループットは大きく異なっていた。

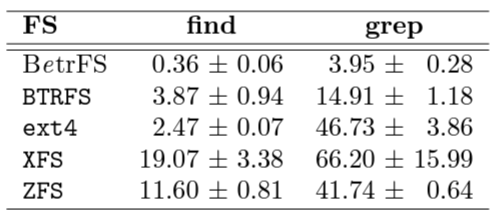
Figure 2. 4 スレッドを使用し 200 バイトのファイルを 300 万個作成した場合の持続的なファイル作成速度。高い方が優れている。

局所性とディレクトリ操作. BetrFS では高速な範囲クエリーは高速な大規模ディレクトリスキャンに変換される。Table 2 は Linux 3.11.10 ソースツリー上でコールドキャッシュから find と grep -r を実行するのにかかった時間を示している。grep テストはファイルの内容を再帰的に検索し "cpu_to_be64" という文字列を探し、find テストは "wait.c" という名前のファイルを検索する。

find と grep の両ベンチマークでは、ファイルシステムのデータとメタデータが大きなノードに保存され、フルパスによって辞書式にソートされているため良好な結果が得られる。したがって関連するファイルはディスク上で互いに近くに保存される。BetrFS もメタデータのみを含む第 2 のインデックスも保持するため、メタデータのスキャンを範囲クエリーとして実装することができる。その結果、BetrFS は他のファイルシステムよりもディレクトリのメタデータとファイルデータの検索を 1～2 桁高速に行うことができる。

Table 2. ディレクトリ操作のベンチマーク。秒単位で計測されている。低いほど優れている。

制限事項. BetrFS はまだ研究段階のプロトタイプであり、現在のところ大規模なディレクトリのリネーム、大規模な削除、大規模なシーケンシャル書き込みの 3 つの主要なケースにおいて他のファイルシステムよりもかなりパフォーマンスが悪いことに注意 (詳細は [5] にある)。BetrFS は名前の変更と削除を Bε-Tree 操作に直接マッピングしないため速度が低下する。シーケンシャル書き込みが遅い主な理由は、基礎となるフラクタルツリーにおいてすべてのデータをログに追加してからツリーに挿入するため、すべてのデータが少なくとも 2 回ディスクに書き込まれるためである。これらの問題は進行中の研究開発の取り組みで解決できると考えている。漸近分析によって裏付けられた我々の目標は、BetrFS がすべてのワークロードで他のファイルシステムに匹敵するかそれを上回ることである。

3 結論

Bε-Tree の実装は B-Tree の検索性能に匹敵し、挿入と削除を桁違いに高速化し、ディスク帯域幅に近い範囲クエリーを実行できる。Bε-Tree の設計と実装は、更新と範囲クエリのコストのトレードオフを、小さな更新と大きなノードをバッチ処理することで相互に有益な相乗効果に変換される。BetrFS を使った我々の結果は Bε-Tree の漸近的な改良により、Bε-Tree の性能特性に合わせて設計されたアプリケーションの実用的な性能向上をもたらすことを示している。

Acknowledgements

This work was supported in part by NSF grants CNS-1409238, CNS-1408782, CNS-1408695, CNS1405641, CNS-1149229, CNS-1161541, CNS-1228839, CNS-1408782, IIS-1247750, CCF-1314547, Sandia National Laboratories, and the Office of the Vice President for Research at Stony Brook University.

References

  1. G. S. Brodal and R. Fagerberg, “Lower bounds for external memory dictionaries,” in Proceedings of the 14th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 546–554, 2003.
  2. D. Comer, “The ubiquitous B-tree,” ACM Computing Surveys, vol. 11, pp. 121–137, June 1979.
  3. A. L. Buchsbaum, M. Goldwasser, S. Venkatasubramanian, and J. R. Westbrook, “On external memory graph traversal,” in Proceedings of the 11th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 859–860, 2000.
  4. Tokutek, Inc., “TokuDB: MySQL Performance, MariaDB Performance.” http://www.tokutek.com/products/tokudbfor-mysql/, 2013.
  5. W. Jannen, J. Yuan, Y. Zhan, A. Akshintala, J. Esmet, Y. Jiao, A. Mittal, P. Pandey, P. Reddy, L. Walsh, M. Bender, M. Farach-Colton, R. Johnson, B. C. Kuszmaul, and D. E. Porter, “BetrFS: A right-optimized write-optimized file system,” in Proceedings of the USENIX Conference on File and Storage Technologies (FAST), pp. 301–315, 2015.
  6. A. Aggarwal and J. S. Vitter, “The input/output complexity of sorting and related problems,” Communications of the ACM, vol. 31, pp. 1116–1127, Sept. 1988.
  7. P. O’Neil, E. Cheng, D. Gawlic, and E. O’Neil, “The log-structured merge-tree (LSM-tree),” Acta Informatica, vol. 33, no. 4, pp. 351–385, 1996.
  8. R. Sears and R. Ramakrishnan, “bLSM: a general purpose log structured merge tree,” in Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data, pp. 217–228, 2012.
  9. P. Shetty, R. P. Spillane, R. Malpani, B. Andrews, J. Seyster, and E. Zadok, “Building workload-independent storage with VT-trees,” in Proceedings of the USENIX Conference on File and Storage Technologies (FAST), pp. 17–30, 2013.
  10. J. Esmet, M. A. Bender, M. Farach-Colton, and B. C. Kuszmaul, “The TokuFS streaming file system,” in Proceedings of the 4th USENIX Workshop on Hot Topics in Storage (HotStorage), June 2012.

翻訳抄

B-Tree と似た構造を持ち、更新と挿入で高い性能を持つ Bε-Tree に関する 2015 年の記事。

  1. BENDER, Michael A., et al. An Introduction to B-trees and Write-Optimization, login; magazine, 2015, 40.5.
  2. Ori Bernstein on An Introduction to Bε-trees and Write-Optimization [PWL NYC]