構造的アルゴリズム

B-Tree

Takami Torao #BTree
  • このエントリーをはてなブックマークに追加

概要

B-Tree または B 木は自己平衡型の多分木データ構造である。各ノードがソート済みの複数のキーと子ノードへの参照を持つことで、二分木より高さの低いツリー構造を形成することができる。このため検索や挿入、削除操作の効率が良く、特にディスクや SSD のようなストレージドライブに対する I/O を最適化するように設計できることから、大量のデータを効率的に管理するようなデータベースやファイルシステムなどで広く使用されている。

Table of Contents

  1. 概要
  2. アルゴリズム
    1. 検索操作
    2. 挿入操作
    3. 削除操作
  3. 参照

アルゴリズム

B-Tree における葉ノード (leaf node) またはリーフノードはツリー構造の最下層に位置し子ノードを持たないノードである。また内部ノード (internal node) は葉ノード以外の全てのノードで、少なくとも 3 つの子ノードへの参照 (ピボット) を持っている。B-Tree では内部ノードと葉ノードの両方がキーを持ち、更新操作に対してツリー全体がバランスを保ちながら効率的なデータアクセスを行える構造を維持する。

B-Tree においてルートを除くすべてのノードは少なくとも \(S\) 個、最大で \(2S\) 個のソートされたキー (およびそれに付随するデータ) を持つ。ここで \(S \ge 1\) は B-Tree ごとの定数である。加えて内部ノードはキーよりも 1 個多い子ノードへの参照を持っている。つまり内部ノードは \(S \le n \le 2S\) となるような \(n\) 個のキーと \(n+1\) 個の子ノードへの参照を持っている。B-Tree の次数 (order) は書籍や論文によって異なることがあるが、Knuth [1] では \(2S+1\) を次数としている。

ルートノードは例外的な扱いである。ルートが葉ノードの場合はそのキー数 \(n\) が \(0 \le n \le 2S\) の範囲を取る。またルートが内部ノードの場合のキー数 \(n\) は \(1 \le n \le 2S\) であり、少なくとも 1 つのキーと 2 つの子ノードへの参照を持つ必要がある。

内部ノードのピボットはしばしば \(i\) 番目のキー \(k_i\) の左右に子ノードへの参照 \(p_i\) と \(p_{i+1}\) が配置されているように表現される。\(k_i\) の左の \(p_i\) が指すノードをルートとする部分ツリーに含まれるすべてのキーは \(k_i\) より小さく、\(k_i\) の右の \(p_{i+1}\) が指す部分ツリーに含まれるすべてのキーは \(k_i\) より大きい。したがって、キー \(k_i\) は左右の部分ツリーを隔てる境界やセパレータと見なすことができる。また内部ノードのキー値はその子の部分ツリーのキー値を束縛しているとも言える。

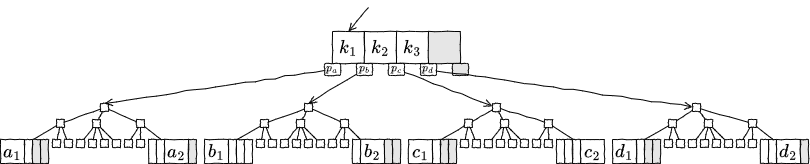
各ノードのキーはソートされていることから、帰納的に、部分ツリーの葉ノードの最も左に配置されているキーはその部分ツリー内で最も小さいキーであり、反対に最も右に配置されているキーは最も大きいキーである。Fig 1 に B-Tree 上のあるノードとそれを頂点とする部分ツリーを示す。ここで \(\{a_1 \lt \ldots \lt a_2\}\) \(\lt\) \(k_1\) \(\lt\) \(\{b_1 \lt \ldots \lt b_2\}\) \(\lt\) \(k_2\) \(\lt\) \(\{c_1 \lt \ldots \lt c_2\}\) \(\lt\) \(k_3\) \(\lt\) \(\{d_1 \lt \ldots \lt d_2\}\) である。

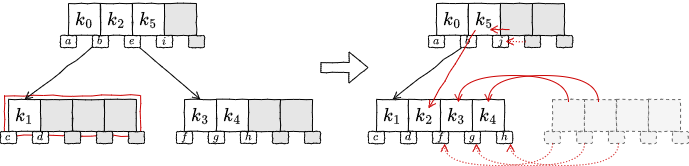
Fig 1. \(S=2\) の B-Tree 上のノードの概念図。中間ノードは 3 個のソートされたキーと、4 個の子ノードへの参照を持つ。

B-Tree は挿入や削除のときにノードの分割やマージを行い、ツリーのバランスを保つことでツリー全体の高さ、つまり操作の最悪時間計算量を \(O(\log_S N)\) で維持する。ルートからそれぞれの葉ノードまでの経路はすべて同じ長さとなる。

検索操作

B-Tree の検索はバイナリツリーの検索と似ている。基本的な方針は、ノードを評価して検索対象のキー \(K\) と一致するものが存在しなければ再帰的に子ノードを探索する操作を繰り返す。このため検索の最悪計算量は B-Tree の木の高さと等しく \(O(\log_S N)\) となる。

  1. ルートノードからキー \(K\) の探索を開始する。

  2. キー \(K\) とノード内のキーを比較し、検索対象のキーが位置すべきインデックスを得る。ここでノード内のキーがソートされていることから二分探索を適用することができる。

  3. 二分探索で得たインデックスにキーが存在し、かつ、それが検索対象のキー \(K\) と等しい場合 (\(i \lt k.length \land k[i]=K\)):

    1. キーが見つかったという結果で検索を終了する。

  4. 二分探索で得たインデックスにキーが存在しない、または、それが検索対象のキー \(K\) と異なる場合:

    1. ノードが葉ノードの場合:

      1. キーが存在しなかったという結果で検索を終了する。

    2. ノードが内部ノードの場合:

      1. 二分探索で得たインデックスの子ノードに移動する。

      2. 移動先の子ノードで再帰的に検索処理を実行する。

この B-Tree の検索と二分探索のアルゴリズムは次の擬似コードで表すことができる。

1. \( {\bf function} \ {\rm lookup}(node, key) \)
2. \( \hspace{12pt}i = {\rm bsearch}(node.keys, key) \)
3. \( \hspace{12pt}{\bf if} \ i \lt node.keys.length \land node.keys[i] = key \)
4. \( \hspace{24pt}{\bf return} \ node.values[i] \)
5. \( \hspace{12pt}{\bf if} \ {\rm is\_leaf}(node) \)
6. \( \hspace{24pt}{\bf return} \ {\rm NOT\_FOUND} \)
7. \( \hspace{12pt}{\bf return} \ {\rm lookup}(node.children[i], key) \)
1. \( {\bf function} \ {\rm bsearch}(keys, key) \)
2. \( \hspace{12pt}left = 0 \)
3. \( \hspace{12pt}right = keys.length - 1 \)
4. \( \hspace{12pt}{\bf while} \ left \le right \)
5. \( \hspace{24pt}mid = \lfloor (left + right) / 2 \rfloor \)
6. \( \hspace{24pt}{\bf if} \ keys[mid] = key \)
7. \( \hspace{36pt}{\bf return} \ mid \)
8. \( \hspace{24pt}{\bf else \ if} \ keys[mid] \lt key \)
9. \( \hspace{36pt}left = mid + 1 \)
10. \( \hspace{24pt}{\bf else} \)
11. \( \hspace{36pt}right = mid - 1 \)
12. \( \hspace{12pt}{\bf return} \ left \)

\(S\) が小さい場合は、条件分岐の多い二分探索より逐次検索を行った方が現実的に速い可能性がある。

挿入操作

B-Tree での挿入操作はアップサート (upsert) つまり「あれば更新、なければ挿入」として実装されることが多い。挿入操作はまず挿入位置を見つける処理がルートから葉ノードの方向に伝播し、その後に分割 (split) がツリーの上方向に向かって伝播する。このため最悪計算量は木の高さに依存し \(O(\log_S N)\) となる。

  1. 検索と同じ方法でキーが挿入されるべき葉ノードまで移動し、その適切な位置のインデックスを得る。

  2. 移動中のノードに挿入するキーと同じキーが存在する場合:

    • アップサート操作: そのキーに関連するデータを更新して終了する。

    • 厳密な挿入操作: 既に同じキーが存在するという結果で終了する。

  3. 葉ノード上の適切なインデックスにキーを挿入する。

  4. ノードに含まれているキー数が \(2S\) 個以下の場合:

    1. 挿入操作を終了する。

  5. 分割: ノードに含まれているキー数が \(2S+1\) 個になっている場合:

    1. ノードを \(S\) 個, \(1\) 個, \(S\) 個の 3 つのパートに分割する。

    2. 上位の内部ノードが存在する場合 (分割したノードがルートでない場合):

      1. 中央値の 1 個のキーを上位の内部ノードに挿入する。このとき、そのキーの右に配置する子ノードへの参照は後方の \(S\) 個のノードを指す。

      2. 上位ノードのキー数が \(2S+1\) 個になっている場合:

        1. 上位ノードに対して再帰的に分割処理を実行する。

      3. 挿入操作を終了する。

    3. 上位のノードが存在しない場合 (分割したノードがルートの場合):

      1. 新しいノードを作成し、中央の 1 個のキーを新しいノードに挿入し、その両側の子への参照を分割した左右のノードに向ける。

      2. B-Tree のルートを新しいノードに設定する。

      3. 挿入操作を終了する。

削除操作

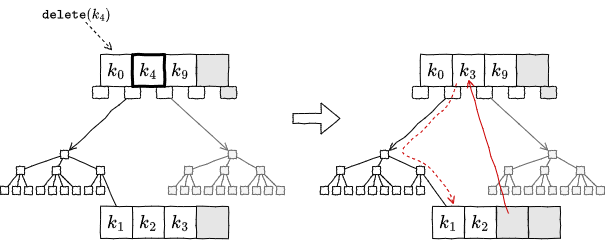
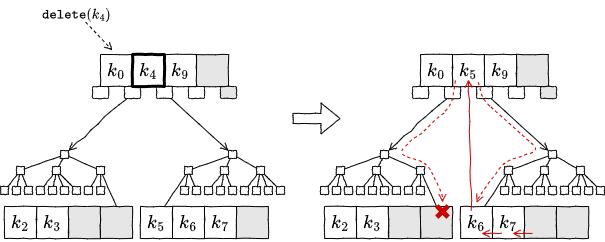
B-Tree の削除はやや複雑である (このため書籍ではしばしば省略される)。削除操作では、キーが存在するノードが葉ノードか内部ノードかによって処理が異なる。また削除後にノードのキー数が \(S\) 未満になった場合、B-Tree のすべてのノードがキー数の制約を満たし、全体のバランスが維持されるように、兄弟ノードとのキーの再分配やノードのマージといったリバランス (再構成) が必要になる。

  1. 検索と同じ方法で削除対象のキーが含まれているノードを見つける。

  2. 削除対象のキーが葉ノードに存在する場合:

    1. 葉ノードに含まれているキーを削除する。

    2. 葉ノードに対してリバランスを実行する。

    3. 削除処理を終了する。

  3. 削除対象のキーが内部ノードに存在する場合:

    1. 削除対象のキーの左の部分ツリーに属している最も右の葉ノードを検索する。

    2. その葉ノードのキー数が \(S+1\) 以上の場合:

      1. その葉ノードの最も右のキー (最も大きいキー)、つまり削除対象のキーの一つ前のキー (predecessor) を、削除対象のキーの位置に移動する。

      2. 削除処理を終了する。

    3. 削除対象のキーの右の部分ツリーに属している最も左の葉ノードを検索する。

    4. その葉ノードのキー数が \(S+1\) 以上の場合:

      1. その葉ノードの最も左のキー (最も小さいキー)、つまり削除対象のキーの一つ後ろのキー (successor) を、削除対象のキーの位置に移動する。

      2. 削除処理を終了する。

    5. 削除対象のキーの左の部分ツリーの最右の葉ノードも、右の部分ツリーの最左の葉ノードも、キーの数が \(S+1\) に満たない場合:

      1. predecessor または successor のどちらかのキーを削除対象のキーの位置に移動する。

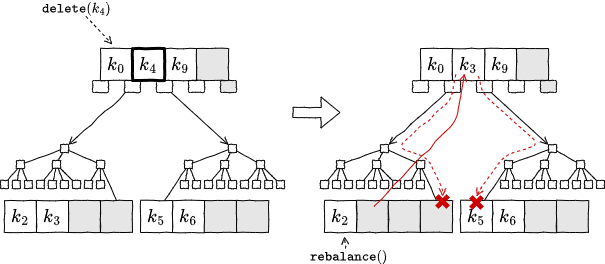
      2. キー数の減った葉ノードに対してリバランスを実行する。

      3. 削除処理を終了する。

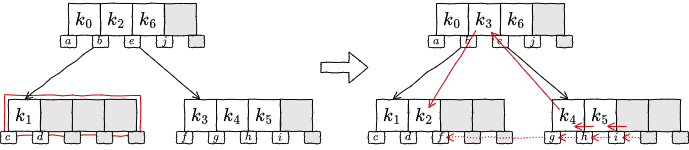
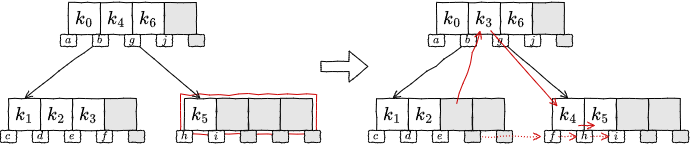
リバランス (rebalance) はキーの削除によって一時的に不変条件を満たさなくなった (キー数が \(S\) 個未満となったノードを持つ) B-Tree に対して、不変条件を満たすようにキーを移動してツリーを再構築する操作である。この操作は下位ノードから上位ノードの方向に遡及的に影響を及ぼす。

あるノード (葉ノードまたは内部ノード) について:

  1. ノードに含まれているキー数が \(S\) 個以上の場合:

    1. リバランス処理を終了する。

  2. ノードがルートの場合:

    1. ノードが内部ノードで、かつ、ノードに含まれているキー数が 0 個の場合 (つまり、ただ 1 つの子ノードへの参照を持つ場合):

      1. ノードを破棄して、子ノードを B-Tree の新しいルートとする。

    2. リバランス処理を終了する。

  3. ルートではなく、かつ、ノードに含まれているキー数が \(S\) 未満の場合:

    1. 再配分: 右に兄弟ノードが存在し、右の兄弟ノードに含まれているキー数が \(S+1\) 個以上の場合:

      1. 上位ノードのキーを移動し、右の兄弟ノードの最も左のキー (最も小さいキー) を上位ノードに移動する。内部ノードの場合は関連する子ノードの参照を移動する。

      2. リバランス処理を終了する。

    2. 再配分: 左に兄弟ノードが存在し、左の兄弟ノードに含まれているキー数が \(S+1\) 個以上の場合:

      1. 上位ノードのキーを移動し、左の兄弟ノードの最も右のキー (最も大きいキー) を上位ノードに移動する。内部ノードの場合は関連する子ノードの参照を移動する。

      2. リバランス処理を終了する。

    3. マージ: 左右のどちらの兄弟ノードもキー数が \(S+1\) 個以上でなかった場合:

      1. 上位ノードのキーを移動し、右の兄弟ノードのキーをすべて移動して右の兄弟ノードを破棄する。内部ノードの場合は関連する子ノードの参照を移動する。

        右の兄弟ノードが存在しない場合は左の兄弟ノードに対して同様の処理を行う。また左右のどちらにマージしても良い。

      2. キー数の減った上位ノードに対してリバランス処理を再帰的に実行する。

      3. リバランス処理を終了する。

参照

  1. Donald E.Knuth. The Art of Computer Programming Volume 3 Sorting and Searching Second Edition 日本語版. KADOKAWA (2015)
  2. Dzejla Medjedovic, Emin Tahirovic, Ines Dedovic. 大規模データセットのためのアルゴリズムとデータ構造. マイナビ出版 (2024)
  3. Alex Petrov. 詳説データベース ―ストレージエンジンと分散データシステムの仕組み. O'REILLY Japan (2021)