論文翻訳: The Log-Structured Merge-Tree (LSM-Tree)
Dieter Gawlick 3 , Elizabeth O'Neil 1
To be published: Acta Informatica
 Abstract
Abstract
高性能なトランザクションシステムアプリケーションは、通常、アクティビティトレースを提供するために履歴テーブルに行を挿入し、同時にトランザクションシステムはシステム回復のためのログレコードを生成する。どちらのタイプの情報生成も効率的なインデックス生成の恩恵を受けることができる。よく知られている例としては、特定のアカウントのアカウントアクティビティに関する履歴の効率的なクエリーをサポートするように変更した TPC-A ベンチマークアプリケーションがある。これには急速に拡大する履歴テーブルにアカウント ID によるインデックスを必要とする。しかし残念ながら B-Tree のような標準的なディスクベースのインデックス構造では、リアルタイムでこのようなインデックスを維持するためにトランザクションの I/O を実質的に 2 倍にし、システム全体のコストを最大 50% まで増加させる。リアルタイムインデックスを低コストで維持する方法が望ましいことは明らかである。LSM-Tree (Log-Structured Merge-Tree) は長期間にわたってレコードの挿入 (および削除) が頻繁に行われるファイルに対して、低コストのインデックスを提供するために設計されたディスクベースのデータ構造である。LSM-Tree はインデックス変更を延期しバッチ処理するアルゴリズムを使用して、マージソートを彷彿とさせる効率的な方法でメモリベースのコンポーネントから 1 つ以上のディスクコンポーネントにカスケードする。このプロセスの間、すべてのインデックス値はメモリコンポーネントまたはディスクコンポーネントのいずれかを介して (非常に短いロック期間を除き) 継続的に検索アクセスすることができる。このアルゴリズムは B-Tree のような従来のアクセス方法と比較し、ディスクアームを移動を大幅に削減し、従来のアクセス方法による挿入のためのディスクアームコストがストレージメディアコストを圧倒するような領域でのコストパフォーマンスを改善する。LSM-Tree のアプローチは挿入と削除の操作以外にも一般化される。しかし即時応答を必要とするインデックス検索では場合によって I/O 効率を低下させるため、エントリを取得する検索よりもインデックス挿入の方が一般的なアプリケーションでは LSM-Tree が最も有用である。セクション 6 の結論では、LSM-Tree アクセス方式におけるメモリとディスクコンポーネントのハイブリッド利用と、一般に理解されているディスクページをメモリにバッファリングするハイブリッド方式の利点を比較している。
Table of Contents
- Abstract
- 1. 導入
- 2. 2-コンポーネント LSM-Tree アルゴリズム
- 3. コストパフォーマンスと複数コンポーネントの LSM-Tree
- 4. LSM-Tree における並行性と回復性
- 5. 他のアクセス方法とのコストパフォーマンス比較
- 6. 結論と拡張の提案
- Acknowledgements
- References
- 翻訳抄
- 1Dept. of Math & C.S, UMass/Boston, Boston, MA 02125-3393, {poneil | eoneil}@cs.umb.edu
- 2Digital Equipment Corporation, Palo Alto, CA 94301, edwardc@pa.dec.com
- 3Oracle Corporation, Redwood Shores, CA, dgawlick@us.oracle.com
 1. 導入
1. 導入
アクティビティフロー管理システムにおける長寿命トランザクションが商用利用可能になるにつれ ([10], [11], [12], [20], [24], [27]) トランザクションログ記録へのインデックス付きアクセスを提供する必要性が高まるだろう。従来のトランザクションログは中断と回復に重点を置いており、回復はバッチ化されたシーケンシャルリードで実行され、システムは時折トランザクションロールバックが発生する通常の処理において、比較的短期間の履歴を参照する必要があった。しかしシステムがより複雑なアクティビティを担当するようになると 1 つの長期的なアクティビティを構成するイベントの期間と数が増加し、何が完了したかをユーザに思い出させるために過去のトランザクションステップをリアルタイムで確認する必要性が生じることがある。同時に、システムが認識するアクティブなイベントの総数は、メモリコストの継続的な低下が予想されるにもかかわらず、現在アクティブなログを追跡するために使用されているメモリ常駐データ構造がもはや現実不可能なレベルまで増加する。膨大な数の過去のアクティビティログに関するクエリーに応答する必要性は、インデックス化されたログアクセスがますます重要となることを意味する。現在のトランザクションシステムにおいても総乳量の多い履歴テーブルに対するクエリーをサポートするためにインデックスを提供することには明らかな価値がある。ネットワーク、電子メール、およびその他のほぼトランザクショナルなシステムは、多くの場合、ホストシステムに悪影響を与える膨大なログを生成する。具体的でよく知られた例から始めるために次の例 1.1 および 1.2 で TPC-A ベンチマークを改良したものを検討する。この文書で提示する例は説明を簡単にするために特定の数値パラメータ値を扱っていることに注意。履歴テーブルとログの両方に時系列データが含まれるが、LSM-Tree のインデックスエントリは時間的なキー順序が同一であるとは想定されていないことにも注意。効率を向上するための唯一の前提は、検索レートに比べて更新レートが高いことである。
 5 分ルール
5 分ルール
次の 2 つの例はどちらも 5 分ルール [13] に基づいている。この基本的な結果は、ページ参照頻度が約 60 秒に 1 回を超える場合、メモリバッファ領域を購入してページをメモリに保持しディスク I/O を回復することでシステムコストを削減できるというものである。60 秒という時間は、1 秒あたり 1 回の I/O を提供するディスクアームの償却コストと、1 秒で償却される 4kB のディスクページをバッファリングするためのメモリコストの比率である。セクション 3 の表記法では、この比率は COSTP / COSTM をメガバイト単位のページサイズで割ったものである。ここでは単にディスクアクセスとメモリバッファをトレードオフしているだけだが、メモリ価格はディスク価格より早く低下することから、60 秒の時間幅は年々大きくなることが予想されることに注意。1987 年に 5 分と定義されたときよりも 1995 年の現在の方が短くなっている理由は、一部には技術的な理由 (バッファリングの想定が異なる) であり、一部はその後に非常に安価な大量生産ディスクが導入されたことに依るものである。
例 1.1. TPC-A ベンチマーク [26] で想定される、1 秒あたり 1000 県のトランザクションを実行するマルチユーザアプリケーションを考える (このレートはスケール可能だが以下は 1000TPS のみを考える)。各トランザクションは、任意に選択された 100 バイトの行 Balance カラムから金額 Delta を引くことでカラムを更新し、次に 1000 行の Branch テーブル、10,000 行の Teller テーブル、100,000,000 行の Account テーブルの 3 つのテーブルそれぞれから行を選ぶ。トランザクションは次に Account-ID, Branch-ID, Teller-ID, Delta, Timestamp を含む 50 バイトの行を History テーブルに書き込んでからコミットする。
ディスクとメモリのコストを予測する一般的な計算の結果、Account テーブルのページは今後数年間はメモリに常駐することは無く (参考文献 [6] 参照)、一方で Branch テーブルと Teller テーブルは現時点で完全にメモリ常駐になるはずである。与えられた仮定の下では Account テーブルの同一ディスクページへの繰り返し参照は約 2,500 秒間隔で行われ、5 分ルールによるバッファ常駐を正当化するために必要な頻度を遙かに下回る。ここで各トランザクションは約 2 回のディスク I/O を必要とし、1 回は目的の Account レコードを読み込むため (アクセスしたページが既にバッファ内にあるという希なケースは重要で無いと見なす)、もう 1 回はバッファに読み込み用のスペースを確保するために以前のダーティな Account ページを書き出すため (定常の動作に必要) である。従って 1000 TPS は毎秒約 2000 回の I/O に相当する。これは [13] で想定されているディスクアーム 1 秒あたり 25 I/O の公称レート 80 個のディスクアーム (アクチュエータ) を必要とする。それ以降の 8 年間 (1987 年から 1995 年まで) で速度は年間 10% 未満の割合で上昇し、公称レートは現在 1 秒あたり約 40 I/O、つまり 1 秒あたり 2000 I/O に対して 50 ディスクアームとなっている。TPC アプリケーションのディスクコストは [6] ではシステムの総コストの約半分と計算されているが IBM のメインフレームシステムではいくらか低くなる。しかしメモリと CPU のコストはディスクよりも急速に低下するため、I/O をサポートするためのコストは明らかにシステムの総コストの増加要因となっている。
例 1.2. 次に、挿入量の多い History テーブルのインデックスを検討し、このようなインデックスによって TPC アプリケーションのディスクコストが実質的に 2 倍になることを示す。History の「Timestamp と連結された Account-ID」(Acct-ID || Timestamp) のインデックスは、次のような最近のアカウントアクティビティに対する効率的なクエリーをサポートするために非常に重要である:
(1.1) Select * from History
where History.Acct-ID = %custacctid
and History.Timestamp > %custdatetime;
Acct-ID || Timestamp がインデックスが存在しない場合、このようなクエリーでは History テーブルのすべての行を直接検索する必要があるため現実的ではない。Acct-ID のインデックスのみでもほとんどの利点が得られるが Timestamp が省略されても後に続くコストの考慮は変わらないため、ここではより有用な連結インデックスを仮定する。このようなセカンダリ B-Tree インデックスをリアルタイムで維持するにはどのようなリソースが必要だろうか。B-Tree のエントリは毎秒 1000 件生成され、20 日間の累積機関、1 日 8 時間、16 バイトのインデックスエントリを想定すると、9.2GB のディスクに 576,000,000 エントリ、またインデックスリーフページで約 230 万ページが必要となる。トランザクションの Acct-ID 値はランダムに選択されるため、各トランザクションではこのインデックスから少なくとも 1 ページを読み込む必要があり、定常状態ではページの書き込みも必要となる。5 分ルールではこれらのインデックスページはバッファに常駐しない (ディスクページは約 2300 秒間隔で読み取られる) ため、すべての I/O はディスクに対して行われる。既にアカウントテーブルの更新に必要な 2000 I/O に加えてこの毎秒 2000 の I/O を追加するには、さらに 50 本のディスクアームを追加購入する必要がありディスク要件は 2 倍になる。この考えは、ログファイルのインデックスを 20 日間だけ維持するために必要な削除は、利用が少ない時間帯にバッチジョブとして実行できると楽観的に想定している。
履歴ファイルの Acct-ID || Timestamp インデックスに B-Tree を考慮したのは、それが商用システムで使用される最も一般的なディスクスペースのアクセス方法であり、実際、古典的では一貫して優れた I/O コスト・性能が得られるディスクインデックス構造は無いためである。この結論に至った考察についてはセクション 5 で述べる。
この論文で紹介する LSM-Tree のアクセス方法は、ディスクアームの使用を大幅に減らして Account-ID || Timestamp インデックスの頻繁な頻繁なインデックス挿入を実行できるためコストが桁違いに低くなる。LSM-Tree はインデックス変更を延期 (defer) しバッチ処理 (batch) するアルゴリズムを使用する、マージソートを彷彿とさせる特に効率的な方法で変更をディスクに移行する。セクション 5 で説明するように、インデックスエントリの配置を最終的なディスク位置まで延期する機能は基本的に重要であり、一般的な LSM-Tree ではこのような延期された配置がカスケード状に連続している。LSM-Tree 構造は削除、更新、および長い待ち時間 (long latency) の検索操作など、インデックス作成の他の操作も同じ遅延効率でサポートする。即時の応答を必要とする検索のみが比較的コストの高いままである。LSM-Tree が効率的に使用される主な領域は、例 1.2 のような検索が挿入よりもはるかに少ない頻度で行われるアプリケーションである (ほとんどの人は、小切手を書いたり預金をしたりするのと同じくらいの頻度で最近のアカウントアクティビティを尋ねることはない)。このような状況ではインデックス挿入のコストを削減することが最も重要である。同時に、すべてのレコードを逐次検索することは問題外であるため、頻繁な検索アクセスを行うために何らかのインデックスを維持する必要がある。
この論文の計画は次の通り。セクション 2 では 2-コンポーネント LSM-Tree アルゴリズムを紹介する。セクション 3 では LSM-Tree の性能を分析し、マルチコンポーネント LSM-Tree の動機づけを説明する。セクション 4 では LSM-Tree の平行性と回復性の概念を概説する。セクション 5 では競合するアクセス方法とその性能について検討する。セクション 6 の結論では LSM-Tree のいくつかの意味を評価し拡張のための多くの提案を示す。
 2. 2-コンポーネント LSM-Tree アルゴリズム
2. 2-コンポーネント LSM-Tree アルゴリズム
LSM-Tree は 2 つ以上のツリー状のコンポーネントデータ構造で構成される。このセクションでは単純な 2 つのコンポーネントでのケースを扱う。以下では例 1.2 のように LSM-Tree が History テーブルの行をインデックス付けしていると仮定する。以下の Figure 2.1 参照。
2-コンポーネント LSM-Tree には C0 ツリー (または C0 コンポーネント) と呼ばれる完全にメモリ常駐の小さなコンポーネントと、C1 ツリー (または C1 コンポーネント) と呼ばれるディスク常駐の大きなコンポーネントがある。C1 コンポーネントはディスク常駐だが、C1 内の頻繁に参照されるページノードは通常通りメモリバッファに残る (バッファは図示されていない) ため、C1 の人気上位ディレクトリノードはメモリ常駐であることが期待できる。
新しい History 行が生成されるたびに、まず、この挿入を回復するためのログレコードが通常の方法で逐次ログファイルに書き込まれる。次に History 行のインデックスエントリがメモリ常駐の C0 ツリーに挿入され、その後にディスク上の C1 ツリーに移行する。インデックスエントリの検索は、最初に C0 で検索して次に C1 で検索する。C0 ツリーのエントリがディスク常駐の C1 `ツリーに移行するまでにはある程度の待ち時間 (遅延) があり、これはクラッシュ前にディスクに書き込まれなかったインデックスエントリの回復の必要性を示唆している。回復についてはセクション 4 で説明するが、ここでは History 行の新規挿入を回復できるログレコードを論理ログとして扱うことだけを述べておく。回復中は、挿入された History 行を再構築し、同時に C0 の失われた内容を取り戻すためにこれらの行のインデックスに必要なエントリを再作成することができる。
インデックスエントリをメモリ常駐の C0 ツリーに挿入する操作には I/O コストがかからない。ただし C0 コンポーネントを格納するメモリ容量のコストはディスクに比べて高く、このためサイズが制限される。エントリを低コストのディスクメディアにある C1 ツリーに移行する効率的な方法が必要である。これを実現するには、挿入の結果として C0 ツリーが割り当てられた最大値に近いしきい値サイズに達するたび、継続的なローリングマージ (rolling merge) プロセスが C0 ツリーからエントリの連続セグメントを削除してディスク上の C1 ツリーにマージする。Figure 2.2 にローリングマージプロセスの概念図を示す。
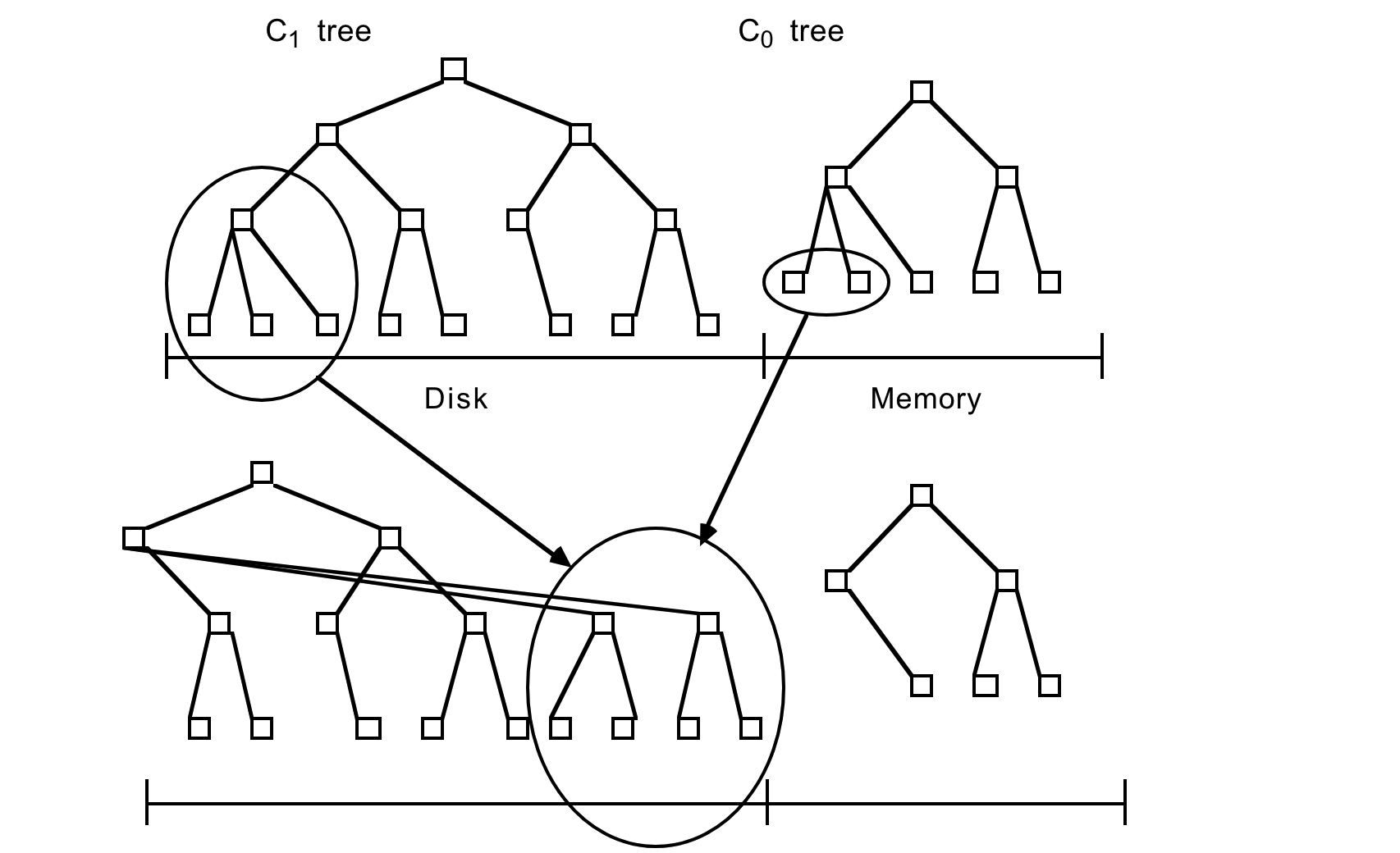
C1 ツリーは B-Tree と同様のディレクトリ構造を持つが、シーケンシャルディスクアクセスに最適化されており、ノードは 100% 満たされ、ルート以下の各レベルのシングルページノードのシーケンスは効率的なアーム使用のために連続した複数ページディスクブロックにまとめられている。この最適化は SB-Tree [21] でも使用されている。複数ページブロック I/O はローリングマージ中と長距離 (long range) 検索に使用され、単一ページノードはバッファリング要件を最小化するためにインデックス付き検索のマッチングに使用される。256kB の複数ページブロックサイズはルート以下のノードを含むように想定されている。ルートノードは定義により常に 1 ページである。
ローリングマージは一連のマージステップで実行される。C1 ツリーのリーフノードを含む複数ページのブロックを読み取ると C1 バッファ内のエントリの範囲が常駐する。その後、各マージステップでは、このブロックにバッファされている C1 ツリーのディスクページサイズのリーフノードを読み取り、リーフノードのエントリを C0 ツリーのリーフレベルから取得したエントリとマージすることで C0 のサイズを縮小し、C1 ツリーの新しくマージされたリーフノードを作成する。
マージ前の古い C1 ツリーノードを含むバッファリングされたマルチページブロックは空ブロック (emptying block) と呼ばれ、新しいリーフノードは充填ブロック (filling block) と呼ばれる別のバッファリングされたマルチページブロックに書き込まれる。この充填ブロックが C1 の新しくマージされたリーフノートでいっぱいになると、ブロックは新しい空き領域に書き込まれる。Figure 2.2 では、マージされた結果を含む新しいマルチページブロックは以前のノードの右側にあるように示されている。後続のマージステップでは C0 および C1 コンポーネントの増加するインデックス値セグメントをまとめ、最大値に達するとローリングマージが最小値から再び開始される。
新しくマージされたブロックは新しいディスク位置に書き込まれるため、古いブロックは上書きされずクラッシュした場合のリカバリに利用できる。メモリにバッファリングされた C1 の親ディレクトリノードもこの新しいリーフ構造を反映するように更新されるが、通常は I/O を最小限に抑えるためにバッファ内に長時間残る。C1 コンポーネントの古いリーフノードはマージステップの完了後に無効化され C1 ディレクトリから削除される。一般に、古いリーフノードが空になったタイミングでマージステップによって新しいノードが生成される可能性は低いため、各マージステップの後にはマージされた C1 コンポーネントのリーフレベルエントリが残る。一般に、充填ブロックが新しくマージされたノードでいっぱいになると、縮小ブロックにエントリを含む多数のノードが存在するため、同じ考慮点はマルチページのブロックにも当てはまる。これらの残りのエントリは更新されたディレクトリノード情報と同様にディスクに書き込まれることなくしばらくブロックメモリバッファに残る。マージステップ中の並行性と、クラッシュ時に失われたメモリからのリカバリについてはセクション 4 で詳しく説明する。リカバリ時の再構築時間を短縮するために、マージプロセスのチェックポイントが定期的に作成され、バッファリングされたすべての情報がディスクに強制的に書き込まれる。
 2.1 2-コンポーネント LSM-Tree の成長過程
2.1 2-コンポーネント LSM-Tree の成長過程
LSM-Tree の成長初期からその変容をたどるために、まずメモリ上の C0 ツリーコンポーネントへの最初の挿入から始めよう。C1 ツリーとは異なり C0 ツリーは B ツリーのような構造を持つことは想定されていない。まず、ノードは任意のサイズにすることができる。C0 ツリーはディスク上に置かれることがないため、ディスクページサイズのノードにこだわる必要はなく、深さを最小限に抑えるために CPU 効率を犠牲にする必要はない。したがって (2-3) ツリーや AVL ツリー (例えば [1] などで説明されている) は C0 ツリーの代替構造として考えられる。成長中の C0 ツリーがしきい値サイズに達すると、左端のエントリシーケンスが C0 ツリーから削除され (これは一度に 1 つのエントリでは無く、効率的なバッチ方式で行う必要がある)、100% フルパックされた C1 ツリーのリーフノードに再編成される。連続するリーフノードは、ブロックがいっぱいになるまでバッファ常駐の複数ページブロックの初期ページに左から右に配置される。その後、このブロックはディスクに書き出され、C1 ツリーのディスク常駐リーフレベルの最初の部分になる。連続するリーフノードが追加されるにつれて、C1 ツリーのディレクトリノード構造がメモリバッファに作成される。詳細は以下で説明する。
C0 のしきい値サイズがしきい値を超えないように、C1 ツリーのリーフレベルの連続する複数ページブロックは、増え続けるキーシーケンスの順序でディスクに書き出される。上位レベルの C1 ツリーのディレクトリノードは、合計メモリとディスクアームコストの観点からより適切な個別の複数ページブロックバッファに保持されるか単一ページバッファに保持される。これらのディレクトリノードのエントリには B ツリーのように下位の個々の単一ページノードへのアクセスを導くセパレータが含まれる。その目的は、単一ページインデックスノードのパスに沿ってリーフレベルまで効率的な完全一致アクセスを提供し、そのような場合には複数ページブロックの読み取りを回避して、メモリバッファ要件を最小限に抑えることである。したがって、ローリングマージまたは長距離検索の場合は複数ページブロックの読み取りと書き込みを行い、インデックス検索 (完全一致) アクセスの場合は単一ページノードの読み取りと書き込みを行う。このような二項対立をサポートするやや異なるアーキテクチャが [21] で紹介されている。C1 ディレクトリノードの部分的にいっぱいになった複数ページブロックは、通常、一連のリーフノードブロックが書き出される間、バッファに残すことができる。C1 ディレクトリノードは次の場合にディスク上の新しい位置に強制的に移動される:
ディレクトリノードを含む複数ページブロックバッファがいっぱいになる
ルートノードが分割され、C1 ツリーの深さが増加する (深さが 2 を超える)
チェックポイントが実行される
最初のケースではいっぱいになった 1 つの複数ページブロックがディスクに書き出される。後の 2 つのケースでは、すべての複数ページブロックバッファとディレクトリノードバッファがディスクにフラッシュされる。
C0 ツリーの右端の葉エントリが初めて C1 ツリーに書き出されたあと、2 つのツリーの左端から処理が最初からやり直される。ただし、この時点とそれ以降のパスでは C1 ツリーの複数ページにわたる葉レベルブロックをバッファに読み込み、C0 ツリーのエントリとマージする必要がある。これにより C1 の新しい複数ページのはブロックが生成されディスクに書き込まれる。
マージが開始すると状況はより複雑になる。2 つのコンポーネントから成る LSM-tree におけるローリングマージプロセスは、概念的なカーソルが C0 ツリーと C1 ツリーの等しいキー値を量子化されたステップでゆっくりと循環し、インデックスデータを C0 ツリーからディスク上の C1 ツリーに描画してゆくものと考えることができる。ローリングマージカーソルは C1 ツリーの葉レベルと、各上位ディレクトリレベルとに位置する。各レベルでは、C1 ツリーの現在マージ中のすべてのマルチページブロックは一般的に 2 つのブロックに分割される。これは、エントリが枯渇しているがマージカーソルがまだ到達していない情報を保持している "emptying" ブロックと、この時点までのマージの結果を反映する "filling" ブロックである。カーソルを定義する類似の "filling ノード" と "emptying ノード" が存在し、これらは確実にバッファ常駐となる。同時アクセスを目的として各レベルの emptying ブロックと filling ブロックには C1 ツリーのページサイズのノードが整数個含まれているが、これらはたまたまバッファ常駐となる。(個々のノードを再構築するマージステップの間、それらのノー土壌のエントリへの他のタイプの同時アクセスはブロックされている。) バッファリングされたすべてのノードをディスクに完全にフラッシュする必要がある場合、各レベルのバッファリングされたすべての情報をディスク上の新しい位置に書き込む必要がある (位置は上位ディレクトリ情報に反映され、回復のために順次ログエントリが作成される)。後になって C1 ツリーの特定のレベルのバッファ内の filling ブロックがいっぱいになり再度フラッシュする必要がある場合は新しい位置に書き込まれる。回復中に必要となる可能性のある古い情報がディスク上で上書きされることは決してなく、より最新の情報で新しい書き込みが成功したときにのみ無効化される。ローリングプロセスのより詳細な節目は、同時実行性と回復設計について検討するセクション 4 で示されている。
LSM-Tree の効率性に関する重要な考慮事項は、C1 の特定のレベルにおけるローリングマージプロセスが比較的高い割合でノードを通過するときに、すべての読み取りと書き込みが複数ページのブロックで行われることである。シーク時間と回転待ち時間を排除することで、通常の B-Tree エントリの挿入に伴うランダムページ I/O に比べて大きな利点が得られると期待されている。(この利点については以下のセクション 3.2 で分析する。) 常に新しい場所に複数ページブロックを書き込むというアイディアは Rosenblum と Ousterhout [23] が考案したログ構造ファイルシステム (Log-Structured File System) から着想を得たもので、ログ構造マージツリー (Log-Structured Merge-Tree) という名称もそこに由来している。新しいディスク領域を継続的に使用して新しい複数ページブロックを書き込むと、書き込まれているディスクが巻き戻され、古い破棄されたブロックを再利用しなければならないことに注意。この記録 (bookkeeping) はメモリテーブルで実行できる。古い複数ページのブロックは無効化され、単一のユニットとして再利用され、チェックポイントにより回復が保証される。ログ構造ファイルシステムでは古いブロックの再利用には大量の I/O が伴う。これは通常、ブロックは部分的にしか解放されないため、再利用にはブロックの読み取りと書き込みが必要になるためである。LSM-Tree ではローリングマージの終了時にブロックが完全に解放されるため余計な I/O は発生しない。
 2.2 LSM-Tree インデックスでの検索
2.2 LSM-Tree インデックスでの検索
LSM-Tree インデックスを使用して即時応答を必要とする完全一致検索 (exact-match find) または範囲検索 (range find) を実行する場合、最初に C0 ツリー、次に C1 ツリーで目的の値または値の集合を検索する。この場合、2 つのディレクトリを検索する必要があるため、B-Tree の場合と比較して若干の CPU オーバーヘッドが発生する可能性がある。2 つ以上のコンポーネントを持つ LSM-Tree では I/O のオーバーヘッドも発生する可能性もある。第三章を先取りすると、複数コンポーネント LSM-Tree をコンポーネント C0, C1, C2, ..., Ck-1, Ck を持つ、サイズが増加するインデックス付きツリー構造と定義する。C0 はメモリ常駐で、他のすべてのコンポーネントはディスク常駐である。すべてのコンポーネントペア (Ci-1, Ci) 間で非同期のローリングマージプロセスが逐次実行され、小さい方のコンポーネント Ci-1 がしきい値サイズを超過するたびに小さい方のコンポーネントから大きい方のコンポーネントにエントリが移動する。原則として、LSM-Tree 内のすべてのエントリが検査されたことを保証するには、完全一致検索または範囲検索がインデックス構造を通じて各コンポーネント Ci にアクセスする必要がある。しかし、この検索をコンポーネントの初期サブセットに限定できる最適化はいくつもある。
まず、タイムスタンプが一意であることが保証されているときのように、一意なインデックス値が生成のロジックによって保証されている場合、一致するインデックスによる検索は初期の Ci コンポーネントで目的の値を見つけることができれば完了となる。別の例として、検索基準が最近のタイムスタンプ値を使用する場合、検索対象とエントリがまだ最大のコンポーネントに移行していないように検索を制限することができる。マージカーソルが (Ci, Ci+1) ペアを循環するとき、最近 (最後の τi 秒) に挿入された Ci のエントリを保持する理由がしばしばあり、古いエントリのみが Ci+1 へ移動するようにする。最も頻繁に参照される検索結果が最近挿入された値である場合、多くの検索結果は C0 ツリーで完了できるため、C0 ツリーは貴重なメモリバッファリング機能を果たす。この点は [23] でも指摘されており、効率性に関する重要な考慮事項を表している。例えば、中断時にアクセスされる短期トランザクションの UNDO ログへのインデックスは、作成後の比較的短い期間でのアクセスの割合が大きく、これらのインデックスのほとんどがメモリに常駐したままであると予想される。各トランザクションの開始時間を追跡することで、例えば直近の τ0 秒に開始されたトランザクションのすべてのログが、ディスクコンポーネントに頼ることなくコンポーネント C0 にあることを保証できる。
 2.3 LSM-Tree における削除、更新、および長時間の遅延を伴う検索
2.3 LSM-Tree における削除、更新、および長時間の遅延を伴う検索
削除は挿入と同様に、遅延とバッチ処理という貴重な特性を共有できることに注意。インデックス付きの行が削除されるときに C0 ツリーの適切な位置にキー値エントリが見つからない場合、削除ノードエントリ (delete node entry) をその位置に配置できる。このエントリもキー値でインデックスが付けられるが、削除するエントリ Row ID (RID) が示される。実際の削除はローリングマージプロセス中に実際のインデックスエントリが検出された時点で行うことができる。つまり、削除ノードエントリはマージ中により大きなコンポーネントに移行 (migrate out) し、関連付けられたエントリに遭遇したときに消滅 (annihilate) する。その間に、検索リクエストは削除ノードエントリを介してフィルタリングされ、削除されたレコードへの参照が返されないようにする必要がある。このフィルタリングは関連するキー値の検索中に簡単に実行できる。これは削除ノードエントリはエントリ自体よりも前のコンポーネントの適切なキー値の位置に配置されるためである。そして多くの場合、このフィルタによりエントリが削除されたかどうかを判断するオーバーヘッドが削減される。インデックス付けされた値への変更を引き起こすレコードの更新は、どのような種類のアプリケーションでも珍しいものだが、そのような更新は更新と削除に続く挿入と見なせば LSM-Tree によって遅延された方式で処理できる。
効率的なインデックス更新のための別の種類の操作について概説する。述語削除 (predicate deletion) と呼ばれるプロセスは、述語をアサートする (asserting) だけでバッチ削除を実行する手段を提供する。例えば 20 日以上前のタイムスタンプを持つすべてのインデックス値を削除するという述語である。ローリングマージの通常の過程で、最も古い (最も大きい) コンポーネント内の影響を受けるエントリが常駐すると、このアサーションによりマージプロセス中にそれらのエントリが単純に削除される。さらに別の種類の操作である長い待ち時間の検索は、最も遅いカーソルの循環期間を問い合わせに応答する効率的な手段を提供する。検索ノートエントリ (find note entry) はコンポーネント C0 に挿入され、検索は実際には後のコンポーネントに移行するときに長時間かけて実行される。検索ノートエントリが LSM-Tree の最大の関連コンポーネントの適切な領域まで循環すると、長い待ち時間の検索のための RID の累積リストが完成する。
 3. コストパフォーマンスと複数コンポーネントの LSM-Tree
3. コストパフォーマンスと複数コンポーネントの LSM-Tree
このセクションでは 2 つのコンポーネントを持つ LSM-Tree のコストパフォーマンスを分析する。同じインデックス機能を提供する B-Tree との類推で LSM-Tree を分析し、大量の新規挿入処理に使用される I/O リソースを比較する。セクション 5 で説明するように、他のディスクベースのアクセス方法は新規インデックスエントリの挿入処理における I/O は B-Tree と同等である。ここで LSM-Tree と B-Tree を比較する最も重要な理由は、これら 2 つの構造が比較しやすいことである。どちらも葉のレベルで照合順序にインデックス付けされた各行のエントリを含み、ページサイズのノードのパスに沿ってアクセスを導く上位レベルのディレクトリ情報を持っている。LSM-Tree への新しいエントリの挿入における I/O の利点の分析は、効率は劣るもののよく理解されている B-Tree の動作の類似性によって効果的に説明される。
次のセクション 3.2 では I/O 挿入コストを比較し、2 コンポーネントの LSM-Tree と B-Tree のコストの比が小さいのは 2 つの要因の積であることを示す。最初の要因である COSTπ/COSTP はすべての I/O を複数ページブロックで実行することによって LSM-Tree で得られる利点に対応し、その結果、シークと回転待ち時間を大幅に節約することによってディスクアームをより効率的に利用する。COSπ 項は複数ページブロックの一部としてディスク上のページを読み書きするときのディスクアームコストを表し、COSP はページをランダムに読み書きするコストを表している。LSM-Tree と B-Tree の間の I/O コスト比を決定する台の要素は 1/M として与えられ、これはマージステップ中に得られるバッチ処理の効率を表す。M は C0 から C1 のページサイズ葉ノードにマージされるエントリの平均数である。葉ごとに複数のエントリを挿入することは、エントリが挿入されるたびにそのエントリが存在する葉ノードの読み書きするために通常 2 回の I/O を必要とする (大きな) B-Tree よりも有利である。5 分ルールにより、例 1.2 では B-Tree から読み込まれた葉ページがバッファに残っている短い時間の間に 2 回目の挿入のために再参照される可能性は低い。しがたって B-Tree インデックスにはバッチ処理の影響はなく、各葉ノードが読み込まれ、新しいエントリが挿入され、再び書き出される。しかし LSM-Tree では C0 コンポーネントが C1 コンポーネントと比較して十分に大きい限り重要なバッチ処理の影響が発生する。たとえば 16 バイトのインデックスエントリがある場合、完全にパックされた 4KB のノードには 250 エントリが期待できる。この 2 つの要因から LSM-Tree が B=Tree よりも効率的に優れていることは明らかであり、この優位性を得るには "ローリングマージ" が不可欠である。
複数ページブロックの効率と単一ページ I/O の効率の比率に対応する係数 COSTπ/COSTP は定数であり、LSM-Tree 構造でこれに影響を与えることはできない。しかしマージステップのバッチ処理効率 1/M は C0 コンポーネントと C1 コンポーネントのサイズ比に比例する。C1 コンポーネントに比べて C0 コンポーネントが大きいほどマージ効率が向上する。これは、ある時点まではより大きな C0 コンポーネントを使用することでディスクアームのコストをさらに節約できることを意味するが、これには C0 コンポーネントを格納するためのより大きなメモリコストを伴う。ディスクアームとメモリ容量の合計コストを最小限に抑えるには最適なサイズの組み合わせがあるが、大きな C0 を使用する場合、この解決策はメモリの面でかなり高価になる可能性がある。この考察が、セクション 3.3 で兼手王するマルチコンポーネント LSM-Tree の必要性を動機づけた。3-コンポーネント LSM-Tree はメモリ常駐コンポーネントの C0 とディスク常駐のコンポーネント C1 および C2 があり、コンポーネントのサイズは添え字が大きくなるにつれて大きくなる。C0 と C1 の間にはローリングマージプロセスが進行中であり、C1 と C2 の間にも別のローリングマージがあり、小さい方のコンポーネントがしきい値サイズを超えるたび、小さい方のコンポーネントから大きい方のコンポーネントにエントリが移動する。3-コンポーネント LSM-Tree の利点は、C0 と C1 の間、および C1 と C2 の間のサイズの合計比率を最適化するように C0 を選択することでバッチ処理の効率を幾何学的に改善できることである。その結果、C0 メモリコンポーネントのサイズを総インデックスに比例して大幅に小さくすることができ、コストが大幅に改善される。
セクション 3.4 では、メモリとディスクの総コストを最小化するためにマルチコンポーネント LSM-Tree のさまざまなコンポーネントの最適な相対サイズを導き出す数学的手法を導入する。
 3.1 ディスクモデル
3.1 ディスクモデル
B-Tree に対する LSM-Tree の利点は主に I/O コストの削減にある (ただし 100% フルなディスクコンポーネントは、他の既知の柔軟なディスク構造よりも容量超すとの点で有利である)。LSM-Tree のこの I/O コストの利点の 1 つは、ページ I/O が複数ページブロックの他の多くのページとともに償却できることである。
定義 3.1.1. I/O コストとデータ温度. 特定の種類のデータ、つまりテーブルの行やインデックスのエントリをディスクに保存する場合、保存するデータの量が増えるにつれて特定のアプリケーション環境での通常の使用時にディスクアームの使用率がますます高くなることがわかる。ディスクを購入するとき我々は 2 つのものにお金を払っている。1 つ目はディスク容量、2 つ目はディスク I/O レートである。通常、これら 2 つのうちの 1 つがあらゆる使用においても制限要因になる。容量が制限要因である場合、ディスクがいっぱいになり I/O を提供するディスクアームがアプリケーションによってほんの僅かしか利用されていないことがわかる。一方、データを追加するとディスクが部分的にしかいっぱいでないときにディスクアームが最大使用率に達することがある。これは I/O レートが制限要因であることを意味する。
ピーク使用時のランダムページ I/O には、ディスクアームの適正な使用量に基づくコスト COSTP がかかる。一方、大規模な複数ページブロック I/O の一部であるディスク I/O のコストは COSπ で表され、複数ページにわたるシーク時間と回転待ち時間を償却するためにこの量はかなり小さくなる。ストレージコストについては次の命名法を採用する:
- COSTd = 1 MByte のディスクストレージのコスト
- COSTm = 1 MByte のメモリストレージのコスト
- COSTP = 1 ページ/秒の I/O レートを提供するためのディスクアームコスト (ランダムページ用)
- COSTπ = 1 ページ/秒の I/O レートを提供するためのディスクアームコスト (複数ページブロック I/O の一部)
S MByte のストレージと 1 秒あたり H のランダムページ I/O 転送 (データはバッファリングされないと仮定) のデータ本体を参照するアプリケーションがあるとすると、ディスクアームの使用コストは S・COSTP、ディスクメディアの使用コストは S・COSTd で与えられる。どちらのコストが制限要因であるかによってもう一方のコストは無コストになるため、このディスク常駐データのアクセスにかかる計算コスト COST-D は次のように与えられる。\[ {\sf COST\mbox{-}D} = \max({\sf S}\cdot{\sf COST}_{\sf d}, {\sf H}\cdot{\sf COST}_{\sf P}) \] COST-D は、ディスクスペースがメモリにバッファリングされない当仮定の下で、このアプリケーションのデータアクセスをサポートするための総コスト COST-TOT でもある。この場合、総ストレージ要件 S が一定であっても、総コストはランダム I/O レート H に応じて直線的に増加する。ここでメモリバッファリングのポイントは、同じ合計ストレージ S に対して I/O レートが増加する特定の時点でディスク I/O をメモリバッファに置き換えることである。このような状況下でランダム I/O 要求をサポートするためにメモリバッファを事前に投入できると仮定すると、ディスクのコストはディスクメディアのみのコストまで低下するため、このバッファ常駐データにアクセスするための計算コスト COST-B は単純にメモリのコストとディスクメディアのコストを足したものになる: \[ {\sf COST\mbox{-}B} = {\sf S}\cdot{\sf COST}_{\sf m} + {\sf S}\cdot{\sf COST}_{\sf d} \] ここでこのアプリケーションのデータアクセスをサポートするための合計コストはこれら 2 つの計算コストの最小値となる: \[ {\sf COST\mbox{-}TOT} = \min( \max({\sf S}\cdot{\sf COST}_{\sf d}, {\sf H}\cdot{\sf COST}_{\sf P}), {\sf S}\cdot{\sf COST}_{\sf m} + {\sf S}\cdot{\sf COST}_{\sf d} ) \]
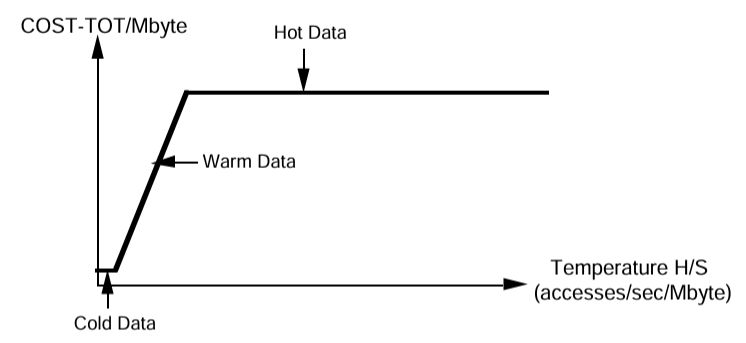
与えられたデータ S に対してページアクセスレート H が増加すると COST-TOT のグラフには 3 つのコスト状態が現われる。Figure 1.1 では COST-TOT/MByte と H/S (1 秒当たりのアクセス数/メガバイト) をグラフにしている。S が小さい場合、COST-TOT はディスクメディアのコスト S・COSTd によって制限され、これは S が固定されている場合は一定である。H/S が増加するにつれてコストはディスクアームの使用量 H・COSTP が支配的に形、S が固定されている場合は H/S の増加に比例する。最後に、5 分ルールによってメモリ常駐が決定される時点で S・COSTm + S・COSTd が支配的な要因になり、これは現在のコストのメモリ項 COSTm >> COSTd によって支配される。Copeland ら [6] に従いデータ本体の温度 (temperature) を H/S と定義し、これらの 3 つのコスト状態をコールド、ウォーム、ホットと名付ける。ホットデータはアクセスレート H が十分に高く、したがって H/S も高いためメモリバッファの常駐が正当化される ([6] 参照)。もう一方の極端な例では、コールドデータはディスク容量が制限される。つまり、コールドデータが占有するディスクボリュームには I/O レートを満たすのに十分なディスクアームが付属する。その中間にあるのがウォームデータで、そのアクセス要件は各ディスクアームで使用されるデータ容量を制限することによって満たされる必要があり、ディスクアームが使用限界となる。これらなお範囲は次のように分割される:
- Tf = COSTd/COSTP = コールドデータとウォームデータの温度分割点 ("freezing")
- Tb = COSTm/COSTP = ウォームデータとホットデータの温度分割点 ("boiling")
COSTπ を使用した複数ページブロックアクセスの場合にも同様に定義された範囲が存在する。ウォーム領域とホット領域の区分は 5 分ルール [13] の一般化である。
[6] で強調されているように、データベーステーブルが均一にアクセスされている場合にその温度を計算するのは簡単である。しかしこの温度の妥当性はアクセス方法に依存する。関連する温度には、論理挿入率 (バッチ化されたバッファ挿入を含む) ではなく、実際のディスクアクセス率が含まれる。LSM-Tree が達成することを表現する 1 つの方法は実際のディスクアクセスを減らしてインデックスデータの実効温度を下げることである。この考え方はセクション 6 の結論で再論される。
 複数ページブロック I/O の利点
複数ページブロック I/O の利点
複数ページブロック I/O によって得られる利点は Bounded Disorder ファイル [16]、SB-Tree [21]、Log Structured ファイル [23] などのいくつかの過去のアクセス方法の中心的なものである。IBM 3380 ディスク [29] での DB2 ユーティリティのパフォーマンスを分析した 1989 年の IBM の出版物では次のような分析が示されている: "... [単一ページの読み取り] を完了するのにかかる時間は約 20ms と推定される (シークに 10ms、回転遅延に 8.3ms、読み取りに 1.7ms を想定)。... [連続する 64 ページ] のシーケンシャルプリフェッチ読み取りを実行する時間は約 125ms (シーク 10ms、回転遅延 8.3ms、64 レコード[ページ]の読み取り 106.9ms と想定)、つまり 1 ページあたり約 2ms と推定される。" したがって、複数ページブロック I/O のページあたり 2ms とランダム I/O の 20ms の比率は、ディスクアームのレンタルコストの比率 COSTπ/COSTP が約 1/10 に等しいことを意味する。より最近の SCSI-2 ディスクの 4KByte ページの読み取りを分析すると、シーク 9ms、回転遅延 5.5ms、読み取り 1.2ms で合計 16ms になる。連続する 64 の 4KByte ページを読み取るには、シーク 9ms、回転遅延 5.5ms、64 ページの読み取り 80ms、つまり合計 95ms、1 ページあたり約 1.5ms が必要である。この場合も COSTπ/COSTP は約 1/10 に等しくなる。
我々は 1GB の容量を持ちピーク時の I/O レートを毎秒約 60~70 であるような SCSI-2 ディスクを搭載した約 1,000 ドルのワークステーションサーバシステムを分析する。長い I/O キューを回避するために使用できる公称 I/O レートはもっと低く毎秒約 40 I/O である。マルチブロック I/O の利点は顕著である。
1995 年の典型的なワークステーションコスト
COSTm = $100/MByte
COSTd = $1/MByte
COSTP = $25/(IOs/sec)
COSTπ = $2.5/(IOs/sec)
Tf = COSTd/COSTP = .04 IOs/(sec・MByte) ("freezing ポイント")
Tb = COSTm/COSTP = 4 IOs/(sec・MByte) ("boiling ポイント")
我々は Tb 値を使って 5 分ルールの基準間隔 τ を導出する。このルールは毎秒 1 ページの I/O レートを維持するデータには、そのデータを保持するために必要なメモリと同じコストがかかることを主張している。この一般的なコストは: \[ (1/\tau) \cdot {\sf COST}_{\sf P} = {\sf pagesize} \cdot {\sf COST}_{\sf m} \] τ について解くと τ = (1/pagesize)・(COSTP/COSTm) = 1/(pagesize・Tb) となり、上記の値ではページが 0.004MByte の場合、τ = 1/(.004・4) = 62.5 秒/IO となる。
例 3.1. 例 1.1 の TPC-A アプリケーションで 1000 TPS の速度を達成するには、Account テーブルに対して 1 秒あたり H = 2000 回の I/O が発生する。このテーブル自体は 100 バイトの 100,000,000 行で構成され、合計 S = 10 GB になる。ここでのディスクストレージコストは S・COSTd = $10,000 だが、ディスク I/O コストは H・COSTP = $50,000 である。温度 T = H/S = 2000/10,000 = 0.2 は freezing よりはるかに高い (5 分の 1) が boiling ポイントよりははるかに低い。このウォームデータはデータストレージにディスク容量の 1/5 しか使わない。我々はディスクアームに対価を払っているのであって容量に対して払っているのではない。例 1.2 の History テーブルに対する 20 日間の Acct-ID || Timestamp インデックスについて考える場合も同じ状況である。例 1.2 で計算したようにこのような B-Tree インデックスには約 9.2 GB の葉レベルエントリを必要とする。成長中のツリーが約 70% しか満たされていないことを考えるとツリー全体では 13.8 GB を必要とするが、これは Account テーブルと同じ I/O レート (挿入のみ) を持ち、温度が同等であることを意味する。
 3.2 LSM-Tree と B-Tree の I/O コスト比較
3.2 LSM-Tree と B-Tree の I/O コスト比較
ここでは、挿入、削除、更新、および長い待ち時間のかかる検索など、マージ可能 (mergeable) と呼ばれるインデックス操作の I/O コストについて検討する。以下の議論では LSM-Tree と B-Tree を比較する分析を示している。
 B-Tree 挿入コストの計算式
B-Tree 挿入コストの計算式
B-Tree の挿入を実行するためのディスクアームのレンタルコストについて考えてみよう。まずエントリを配置するツリーの位置にアクセスする必要があり、これにはツリーのノードを検索する必要がある。ツリーへの連続的な挿入は葉レベルのランダムな位置に行われると仮定し、アクセス経路のノードページは過去の挿入によって常にバッファに常駐していることはないとする。キーが常に増加する連続挿入、つまり insert-on-the-right の状況はこの想定に従わない比較的一般的なケースである。このような insert-on-the-right の状況は B-Tree が常に右に成長するので I/O がほとんどないため、B-Tree データ構造によってすでにかなり効率的に処理できることに注意。実際、これが B-Tree ロードが発生する基本的な状況である。増え続ける値によるログレコードのインデックスを扱うための構造は他にもいくつか提案されている [8]。
[21] では De で表される B-Tree の有効深 (effective depth) は B-Tree のディレクトリレベルをランダムに Key-Value 検索したときにバッファ内で見つからなかったページの平均数であると定義された。例 1.2 の Account-ID || Timestamp インデックス作成に使用されたサイズの B-Tree では De の値は通常約 2 である。
B-Tree への挿入を実行するには葉レベルページへの Key-Value 検索を実行し (De I/O)、それを更新し、(定常状態では) 対応するダーティ葉ページを書き出す (1 I/O)。比較的頻度の少ないノード分割は我々の分析に重要な影響を与えないことを示すことができるため無視する。このプロセスで読み書きされるページはすべてランダムアクセスでコストは COSTP である。したがって B-Tree での挿入の合計 I/O コスト COSTB-ins は次式で与えられる: \[ \begin{equation} {\sf COST_{B\mbox{-}ins}} = {\sf COST_P} \cdot ({\sf D_e} + 1) \tag{3.1} \label{eq31} \end{equation} \]
 LSM-Tree 挿入コストの計算式
LSM-Tree 挿入コストの計算式
LSM-Tree への挿入コストを評価するには複数の挿入の償却という観点から考える必要がある。これは、メモリコンポーネント C0 への単一の挿入ではまれにしか I/O の効果が発生しないためである。このセクションの冒頭で説明したように、LSM-Tree が B-Tree に対して持つ性能上の利点は 2 つの異なるバッチ効果に基づいている。1 つ目は既に述べたようにページ I/O のコスト COSTπ が削減されることである。2 つ目は新しく挿入されたエントリを C1 ツリーにマージする際の遅延により、通常は C0 に多数のエントリが蓄積される時間が生じ、したがってディスクからメモリへ、そしてメモリからディスクへの往復の間に複数のエントリが各 C1 ツリーの葉ページにマージされるという考えに基づいている。これに対して B-Tree の葉ページはメモリ上で参照される頻度が低すぎるため、複数のエントリが挿入されることはないものと想定している。
定義 3.2.1. バッチ-マージパラメータ M. この複数エントリの葉あたりのバッチ処理効果を定量化するために、ローリングマージ中に C1 ツリーの各単一ページ葉ノードに挿入される C0 ツリーのエントリの平均数として、与えられた LSM-Tree のパラメータ M を定義する。パラメータ M は LSM-Tree を特徴付ける比較的安定した値であると主張する。実際、M の値はインデックスエントリのサイズと C1 ツリーの葉レベルと C0 ツリーの葉レベルのサイズの比によって決まる。次の新しいサイズパラメータを定義する:
Se = エントリ (インデックスエントリ) サイズ (Bytes)
Sp = ページサイズ (Bytes)
S0 = C0 コンポーネント葉レベルのサイズ (MBytes)
S1 = C1 コンポーネント葉レベルのサイズ (MBytes)
このとき 1 ページのエントリ数はおよそ Sp/Se となり、コンポーネント C0 を占める LSM-Tree のエントリの割合は S0/(S0+S1) となるため、パラメータ M は次式で与えられる: \[ \begin{equation} {\sf M} = ({\sf S_p} / {\sf S_e}) \cdot ({\sf S_0} / ({\sf S_p} + {\sf S_1})) \tag{3.2} \label{eq32} \end{equation} \] コンポーネント C0 が C1 に比べて大きいほどパラメータ M も大きくなることに注意。一般的な実装では S1 = 40・S0 でディスクページあたりのエントリ数 Sp/Se が 200 であるため M = 5 となる。パラメータ M が与えられれば LSM-Tree へのエントリ挿入コスト COSTLSM-ins の大まかな式が得られる。C1 ツリー葉ノードをメモリに取り込んで再び書き出すまでの 1 ページ当たりのコスト 2・COSTπ を、この間に C1 ツリーの葉ノードにマージされる M 個の挿入に償却するだけである。\[ \begin{equation} {\sf COST_{LSM\mbox{-}ins}} = 2 \cdot {\sf COST_\pi} / {\sf M} \tag{3.3} \label{eq33} \end{equation} \] LSM-Tree と B-Tree の両方のケースで、インデックス更新の I/O に関連する比較的重要でないコストを無視していることに注意。
 LSM-Tree と B-Tree の挿入コスト比較
LSM-Tree と B-Tree の挿入コスト比較
2 つのデータ構造への挿入のコスト式 (\(\ref{eq31}\)) と (\(\ref{eq33}\)) を比べると次のような比率になる: \[ \begin{equation} {\sf COST_{LSM\mbox{-}ins}} / {\sf COST_{B\mbox{-}ins}} = {\sf K_1} \cdot ({\sf COST_\pi} / {\sf COST_P}) \cdot (1 / {\sf M}) \tag{3.4} \label{eq34} \end{equation} \] ここで K1 は (ほぼ) 定数の 2/(De+1) で、検討しているインデックスサイズでは約 0.67 となる。この式は、LSM-Tree への挿入と B-Tree への挿入のコスト比が、これまでに説明した 2 つのバッチ効果のそれぞれに直接比例していることを示している。COSTπ/COSTP は複数ページブロックのページ I/O とランダムページ I/O のコスト比に対応する小さな割合であり、1/M はローリングマージ中にページごとにバッチ処理されるエントリの数である。通常、2 つの比率の積はコスト比率をほぼ 2 桁改善する。当然、このような改善はインデックスが B-Tree として比較的高い温度を持つ領域でのみ可能であり、LSM-Tree インデックスに移行する際にディスク数を大幅に削減することが可能である。
例 3.2. 例 1.2 のようなインデックスが 1GB のディスクスペースを占有するが、必要なディスクアームアクセスレートを達成するためには 10GB の領域に保持する必要があると仮定すると、ディスクアームコストの節約には確かに改善の余地がある。式 (\(\ref{eq34}\)) で示される挿入コストの比率が 0.02 = 1/50 であるならば、インデックスとディスクコストを縮小することができる。しかし、より効率的な LSM-Tree ではコストをディスク容量に必要な量までしか削減できないことがわかる。必要なディスクアームサービスを受けるために 35GB に制限された 1GB の B-Tree から始めていた場合、1/50 のコスト改善の比率を完全に実現できる可能性がある。
 3.3 複数コンポーネント LSM-Tree
3.3 複数コンポーネント LSM-Tree
特定の LSM-Tree のパラメータ M は、ローリングマージ中に C1 ツリーの各単一ページの葉ノードに挿入される C0 ツリーのエントリの平均数として定義された。新しいエントリが挿入され C1 ツリーのノードにマージされる前に C0 ツリーに蓄積される遅延時間があるため、量 M は 1 より大きいと考えてきた。しかし、式 (\(\ref{eq32}\)) から明らかなように、C1 ツリーが C0 ツリーに比べて極端に大きかったり、エントリが極端に大きく 1 ページに収まる数が少ない場合は量 M が 1 未満になることがある。このような M の量は C0 ツリーからマージされるエントリごとに平均して 1 つ以上の C1 ツリーページをメモリに出し入れする必要があることを意味する。式 (\(\ref{eq34}\)) から見て M が非常に小さい場合、具体的には M < K1 ・COSTπ / COSTP の場合、複数ページのディスク読み取りのバッチ効果を打ち消す可能性さえあるため、挿入には LSM-Tree の代わりに通常の B-Tree を使用する方が良い。
M の値が小さくならないようにするには 2-コンポーネント LSM-Tree で C0 コンポーネントのサイズを C1 のサイズに対して増やすしかない。葉エントリの合計サイズが S (S = S0 + S1, ほぼ安定した値) である 2-コンポーネント LSM-Tree を考え、C0 への新しいエントリの挿入速度が 1 秒あたり R で一定であると仮定する。簡単のため C0 に挿入されたエントリは C1 コンポーネントに出力される前に削除されないと仮定する。これより C0 のサイズをしきい値サイズ近くに保つには、エントリは C0 に挿入される速度と同じ速度でローリングマージを通じて C1 コンポーネントに移行する必要がある (合計サイズ S がほぼ安定であることを考えると、これはまた C0 への挿入速度が (おそらく一連の述語削除 (predicate deletes) の連続を使用して) C1 から一定の削除速度によってバランスが取られる必要があることも意味する)。C0 のサイズを変えるとマージカーソルの循環速度に影響する。C1 へのバイト/秒での一定の移行速度は、ローリングマージカーソルが C0 のエントリをバイト/秒での一定の速度で移動する必要がある。したがって C0 のサイズが小さくなると C0 の最小インデックス値から最大インデックス値への循環速度が増加する。その結果、ローリングマージを実行するための C1 の複数ページブロックの I/O 速度も増加する必要がある。C0 のサイズを 1 エントリにすることが可能であれば、この概念乗の極端な時点で、新しく挿入されたエントリごとに C1 のすべての複数ページブロックを循環する必要があり、I/O に膨大な負荷がかかる。B-Tree で行われているように、新しく挿入されたエントリごとに C1 の関連ノードにアクセスするのではなく、C0 と C1 をマージするアプローチは我々にとって負担となるだろう。比較すると、C0 コンポーネントのサイズが大きいほどマージカーソルの循環が遅くなり、挿入の I/O コストが減少する。しかし、これによりメモリ常駐コンポーネント C0 のコストが増加する。
ここで、C0 の標準サイズは LSM-Tree の総コスト (C0 のメモリコスト、プラス、C1 コンポーネントのメディア/ディスクアームコスト) が最小になるポイントによって決まる。このバランスに到達するにはまず大きな C0 コンポーネントから始めて C1 コンポーネントをディスクメディアに密着させる。C0 コンポーネントが十分に大きければ C1 への I/O レートは非常に小さくなる。ここで、C1 を処理するための I/O レートが C1 コンポーネントのメディアの上に置かれたディスクアームがフルレートで動作するポイントまで高価なメモリを安価なディスクスペースと交換しながら C0 のサイズを縮小してゆくことができる。この時点で C0 のメモリコストをさらに削減すると、ディスクアームの負荷を軽減するために C1 コンポーネントを部分的にいっぱいになったディスクに分散する必要があるため、メディアコストが増加することになる。また C0 を縮小し続けるとある時点で最小コストポイントに到達する。ここで 2 つのコンポーネントからなる LSM-Tree では C0 について決定した標準サイズがメモリ使用の点で依然として高価になることが一般的である。代替案としては、3 つ以上のコンポーネントを持つ LSM-Tree の採用を検討することである。概念的には、C0 コンポーネントのサイズが非常に大きくメモリコストが重要な要因となる場合、2 つの極端なサイズの間に別の中間サイズのディスクベースのコンポーネントを作成することを検討する。これによりディスクアームのコストを抑えながら C0 コンポーネントのサイズを縮小できる。
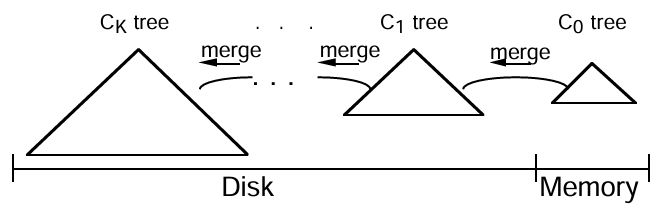
一般に、K+1 個のコンポーネントからなる LSM-Tree にはコンポーネント C0, C1, ..., CK-1, CK を持ち、これらはサイズが増加するインデックスツリー構造である。C0 コンポーネントツリーはメモリ常駐で、他のすべてのコンポーネントはディスク常駐である (ただしディスク常駐アクセスツリーと同様にアクセスの多いページはメモリにバッファリングされる)。挿入による圧力の下ですべてのコンポーネントペア (Ci-1, Ci) 間で非同期のローリングマージ処理が行われており、小さい方のコンポーネント Ci-1 がしきい値サイズを超えるたびに、絵小さい方のコンポーネントから大きい方のコンポーネントにエントリが移動する。LSM-Tree に挿入された長寿命エントリはその存続期間中に C0 ツリーから始まり一連の K 回の非同期ローリングマージステップを経て最終的に CK に移動する。
ここでは LSM-Tree が挿入を主とする環境に存在すると想定しているため挿入トラフィックでのパフォーマンスに焦点が当てられている。通常、3 つ以上のコンポーネントの LSM-Tree 検索ではディスクコンポーネントごとに 1 つの追加ページ I/O によりパフォーマンスが多少低下する。
 3.4 LSM-Tree: コンポーネントサイズ
3.4 LSM-Tree: コンポーネントサイズ
このセクションでは複数コンポーネントの LSM-Tree への挿入にかかる I/O コストの公式を導出し、さまざまなコンポーネントに最適なしきい値サイズを選択する方法を数学的に示す。拡張された例 3.3 は、B-Tree のシステムコスト、2-コンポーネントの LSM-Tree のシステムコストの改善、および 3 コンポーネントの LSM-Tree で得られる大きな節約を示している。
LSM-Tree のコンポーネントのサイズを S(Ci) を葉ノードに含まれるエントリのバイト数と定義する。コンポーネント Ci のサイズは Si と示し、S(Ci) = Si であり、すべての葉レベルのエントリの合計サイズを S = Σi Si と表す。ここで LSM-Tree のコンポーネント C0 にバイト/秒で比較的安定した挿入速度 R があると仮定し、簡単のため、新しく挿入されたすべてのエントリは一連のローリングマージステップによってコンポーネント CK に循環すると仮定する。また各コンポーネント C0, C1, ..., CK-1 のサイズ葉現在の分析で決定される最大しきい値サイズに近いと仮定する。コンポーネント CK はある一定の標準機関にわたって削除と挿入のバランスがとれているため、比較的安定したサイズであると仮定する。コンポーネント CK からの削除は、コンポーネント C0 への挿入速度 R に追加することなく行われると考えることができる。
固定の合計サイズ S とメモリコンポーネントのサイズ S0 を持つ K 個のコンポーネントの LSM-Tree が与えられたとき、ツリーは離船津するコンポーネントのペア間のサイズ比 ri, i = 1, ..., K によって完全に記述される。ここで ri = Si/Si-1 である。以下に記述するように、コンポーネントのペア (Ci-1, Ci) 間で進行中のすべてのマージ操作を実行するための合計ページ I/O レートは、R、C0 への挿入レート、および比率 ri の関数として表すことができる。使用率のバランスを取るために、さまざまなコンポーネントのブロックが異なるディスクアームに混在してストライピングされると想定しているため、H を最小化することはディスクアームの合計コストを最小化することと同じである (少なくとも、メディア容量ではなくディスクアームがゲーティングコスト (gating cost) を構成する範囲では)。与えられた R に対して総 I/O レート H を最小化する ri の値を見つけることは標準的な微積分の最小化問題である。合計サイズ S が固定されているという仮定は、ri 値の間にやや複雑な再帰関係を伴うかなり難しい問題に繋がることがわかる。しかし、定理 3.1 で示すように、最大コンポーネントサイズ SK が (メモリサイズ S0 と共に) 固定であるという同等の仮定を立てれば、すべての値 ri が単一の定数値 r に等しいときにこの最小化問題は解くことができる。定理 3.2 では全体のサイズ S が一定に保たれている場合の ri 値に関する少し正確な回を示し、ri の値 r を一定にすることで、実際に関心のあるすべての領域で同様の結果が得られることを論じる。すべて ri 因子についてこのような定数値 r を仮定すると Si = ri・S0 となる。したがって、合計サイズ S は個々のコンポーネントサイズの合計 S = S0 + r・S0 + r²・S0 + ... + rK・S0 によって与えられ、S と S0 に基づいて r を求めることができる。
したがって、定理 3.1 では SK, S0 および挿入率 R を固定した複数コンポーネント LSM-Tree の合計 I/O 率 H を最小化するには、最小と最大の幾何級数 (geometric progression) で中間コンポーネントのサイズを決定する必要があることを示す。2-コンポーネントの LSM-Tree の場合と同様に R と SK が一定のまま S0 を変化させ、H を S0 の関数として表すと、S0 が減少するにつれて H が増加することがわかる。これで S0 のサイズを変化させることで LSM-Tree の合計コスト (メモリとディスクアームのコスト) を最小化できる。特定のコンポーネント数に対して最適な合計コストに到達するための適切なプロセスを例 3.3 に示す。合計コストで唯一残っている自由変数はコンポーネント数 K+1 である。この値のトレードオフについてはこのセクションの最後で説明する。
定理 3.1. K+1 個のコンポーネントを持つ LSM-Tree があり、最大コンポーネントサイズ SK、挿入速度 R、およびメモリコンポーネントサイズ S0 が固定されている場合、すべてのマージを実行するための合計ページ I/O 速度 H は、比率 ri = Si/Si-1 がすべての共通値 r に等しいときに最小化される。したがって合計サイズ S は個々のコンポーネントサイズの合計で与えられ、\[ \begin{equation} {\sf S} = {\sf S_0} + {\sf r\cdot S_0} + {\sf r^2\cdot S_0} + \ldots {\sf r^K\cdot S_0} \tag{3.5} \label{eq35} \end{equation} \] となり、S と S0 に関して r を解くことができる。同様に、合計ページ I/O 速度 H は \[ \begin{equation} {\sf H} = (2 {\sf R/S_p}) \cdot ({\sf K} \cdot (1 + {\sf r}) - 1/2) \tag{3.6} \label{eq36} \end{equation} \] で与えられ、ここで Sp はページあたりのバイト数である。
Proof. ... (省略)
定理 3.2. 定理 3.1 の仮定を変更して、最大コンポーネントのサイズ SK ではなく合計サイズ S を固定する。この最小化問題ははるかに困難だがラグランジュ乗数を使って行うことができる。結果は、各 ri に対してより上位のインデックスを持つ ri に関する一連の積となる: \[ \begin{eqnarray*} {\sf r_{K-1}} & = & {\sf r_K} + 1 \\ {\sf r_{K-2}} & = & {\sf r_{K-1}} + 1/{\sf r_{K-1}} \\ {\sf r_{K-3}} & = & {\sf r_{K-2}} + 1/({\sf r_{K-1}} \cdot {\sf r_{K-2}}) \\ \ldots \end{eqnarray*} \]
証明は省略する。
後述するように ri の有効な値はかなり大きく、例えば 20 異常であるため、最大コンポーネントである SK のサイズが全体のサイズ S の大部分を支配する。したがって、定理 3.2 では、各 ri は通常、その上位の隣接 ri+1 からわずかな差しかないことに注意。以下では定理 3.1 の近似に基づいて例を示す。
 総コストの最小化
総コストの最小化
定理 3.1 から、R と SK を一定にしたまま S0 を変化させ、合計 I/O レート H を S0 の関数として表すと、式 (\(\ref{ex35}\)) により r は S0 の減少と共に増加し、式 (\(\ref{eq36}\)) により H は r に比例するため明らかに H は S0 の減少と共に増加することがわかる。ここで、高価なメモリと安価なディスクを交換することにより、2-コンポーネントの場合と同様に LSM-Tree の総コストを最小化できる。LSM-Tree を格納するために必要なディスクメディアと、これらのディスクアームをフルに利用し続ける総 I/O レート H を計算すると、これがコストを最小化する S0 のサイズを決定するための計算の出発点になる。この時点から C0 のサイズをさらに小さくすると、ディスクアームのコストが制限要因となる領域に入ったため、ディスクメディアのコストは反比例して増加する。以下の例 3.3 は 2-コンポーネントおよび 3-コンポーネントの LSM-Tree についてこのプロセスの数値に基づいて表したものである。この例の前に 2-コンポーネントの場合の解析的な導出を示す。
総コストはメモリコスト COSTm・S0 とディスクコストの合計である。ディスクコスト自体はディスクストレージと I/O コストの最大値であり、ここでは 1 秒あたりのページ数で表した複数ページブロックアクセスレート H に基づいている: \[ {\sf COST_{tot}} = {\sf COST_m} \cdot {\sf S_0} + \max [ {\sf COST_d} \cdot {\sf S_1}, {\sf COST_\pi} \cdot {\sf H}] \] 2-コンポーネントの場合について考えてみる。式 (\(\ref{eq36}\)) では K = 1, r = S1/S0 である。\[ \begin{eqnarray*} {\sf s} & = & ({\sf COST_m} \cdot {\sf S_0}) / ({\sf COST_d} \cdot {\sf S_1}) = \mbox{${\sf S_1}$データのストレージコストに対するメモリのコスト} \\ {\sf t} & = & 2 \cdot (({\sf R}/{\sf S_p})/{\sf S_1}) \cdot ({\sf COST_\pi}/{\sf COST_d}) ({\sf COST_m}/{\sf COST_d}) \\ {\sf C} & = & {\sf COST_{tot}}/({\sf COST_d}\cdot {\sf S_1}) = \mbox{${\sf S_1}$データのストレージコストに対する総コスト} \end{eqnarray*} \] 次に式 (\(\ref{eq36}\)) を代入して簡略化し、S0/S1 が小さいと仮定すると近似値が得られる: \[ {\sf C} \approx {\sf s} + \max(1, {\sf t}/{\sf s}) \] 相対コスト C は 2 つの変数 t と s の関数である。変数 t はアプリケーションが必要とする基本的な複数ページブロック I/O レートを測定する、一種の正規化された温度である。変数 s は LSM-Tree を実装するために使用するメモリの量を表す。S0 のサイズを決定するために最も単純なルールは C = s + 1 であり、ディスクストレージと I/O 容量が最大限に活用される s = t の線に従うことである。このルールは t <= 1 の時にコストが最小だが、t > 1 の場合、最小 C の軌跡は C = 2・t1/2 の曲線 s = t1/2 に従う。この結果を次元の形に戻すと、t >= 1 の場合は次のようになる: \[ \begin{equation} {\sf COST_{min}} = 2 [({\sf COST_m} \cdot {\sf S_1}) (2\cdot {\sf COST_\pi}\cdot {\sf R/S_p})]^{\sf 1/2} \tag{3.8} \label{eq38} \end{equation} \] したがって、LSM-Tree の総コスト (t ≧ 1 の場合) は LSM-Tree 内のすべてのデータを保持するのに十分な (非常に高い) メモリコストと、最も安価な方法でディスクに挿入データを書き込むために必要な複数ページブロック I/O をサポートするために必要な (非常に低い) ディスクコストの幾何平均の 2 倍であることがわかる。この合計コストの半分は S0 のメモリに使用され、残りの半分は S1 への I/O アクセス用のディスクに使用される。t >= 1 ではデータが十分に暖かくなり、最小点ではディスクストレージよりもディスク I/O が優位になるため、ディスクストレージのコストは表示されない。漸近的に B-Tree の R と比較してコストは R1/2 となり、R → ∞ となることに注意。
t <= 1 のより冷たいケースでは、最小コストは s = t に沿って発生し、ここで C = t + 1 < 2 である。つまり、この場合の合計コストは常に S1 をディスクに格納する基本コストの 2 倍未満となる。この場合、ディスクのサイズをストレージ要件に応じて決定し、次にその I/O 容量をすべて使用してメモリ使用量を最小化する。
例 3.3. 例 3.1 で詳述した Account-ID || Timestamp インデックスについて考える。以下の分析では、インデックスへの挿入速度 R を毎秒 16,000 バイト (オーバーヘッドを除く 1000 個の 16 バイトインデックスエントリ) で 20 日分のデータ、つまり 9.2 GB のデータに対して 5 億 7,600 万エントリのインデックスが生成される。
インデックスをサポートするために B-Tree を使用すると、例 3.1 で見たようにディスク I/O が制限要因となる。葉レベルのデータは warm である。葉レベルでランダムページを更新するには 1 秒あたり H = 2,000 のランダム I/O を提供するのに十分なディスク容量を使用する必要がある (すべてのディレクトリノードがメモリ常駐であると仮定)。セクション 3.1 の雹から典型的な COSTP = $25 を使用すると、I/O のコストは H・COSTP = $50,000 となる。上位レベルのノードをメモリにバッファリングするコストは次のように計算する。葉ノードが 70% フルであると仮定すると、葉ノードあたり 0.7・(4K/16) = 180 エントリであるため、葉の上位レベルには下位の葉を指す約 5.76 億 / 180 = 320 万のエントリが含まれる。このレベルのノードに 200 エントリを格納できるようにプレフィックス圧縮を許可すると、これは 1 ページ 4 KB のページが約 16,000 ページ、つまり 64 MB となり、メモリのコスト COSTm は 1 MB あたり $100、つまり $6,400 となる。これより上のレベルではノードバッファリングのコストは比較的小さいため無視し、B-Tree の合計コストはディスクの $50,000 とメモリの $6,400 ドル、つまり合計コストは $56,400 とする。
C0 と C1 の 2-コンポーネントからなる LSM-Tree では、エントリを格納するために 9.2 GB のディスク S1 が必要であり、そのコストは COSTd・S1 = $9,200 である。このデータをディスク密集させてパックし、複数ページブロック I/O を使用してディスクアームの等しいコストでサポートされる合計 I/O レート H を毎秒 H = 9200/COSTπ = 3700 ページとして計算する。ここで式 (\(\ref{eq36}\)) において総 I/O レート H を上記のように設定し、速度 R を 16,000 バイト/秒、Sp を 4K に設定して r を解く。結果として得られて比率 r = S1/S0 = 460 と S1 = 9.2 GB であることから、C0 のメモリは 20 MB でコストは $2,000 と計算される。これは総コストが $11,200 でディスク容量と I/O 機能が最大限に活用される、単純な s = t のソリューションである。t = .22 は 1 より小さいのでこれが最適なソリューションである。マージブロックを格納する 2 MB のメモリに 200 ドルを追加して合計コストは $11,400 となる。これは B-Tree のコストを大幅に改善したものである。
いかなソリューションの詳細な説明である。挿入速度 R = 16,000 バイト/秒は C0 から C1 にマージする必要がある 4 ページ/秒に変換される。C1 は C0 の 460 倍大きいため C0 からの新しいエントリは平均して C1 の 460 エントリ離れた位置にマージされる。したがって、C0 からページをマージするには、C1 の 460 ページ、合計 3,680 ページ/秒を読み書きする必要がある。しかし、これはまさに 9.2 ディスクが複数ブロック I/O 容量で提供するもので、各ディスクは 400 ページ/秒を提供し、これは公称ランダム I/O レート 40 ページ/秒の 10 倍である。
この例では 2-コンポーネントでディスクリソースを完全に利用しているため、ここでは 3-コンポーネントの LSM-Tree を検討する理由はない。より完全な分析を行うには、インデックスでどのように検索を実行しなければならないかを時々考慮し、より多くのディスクアームを利用することを検討することになる。次の例は純粋な挿入ワークロードに対して 3-コンポーネントでコストが改善されるケースを示している。
例 3.4. R を 10 倍に増やした例 3.3 を考えてみよう。B-Tree ソリューションでは I/O レート H = 20,000 I/O/秒をサポートするために 500 GB のディスクに $500,000 かかることに注意; このうちの 491 GB は未使用となる。しかし B-Tree のサイズは同じであり、ディレクトリをメモリにバッファリングするために $6,400 を支払う必要があるため合計コストは $506,400 となる。LSM-Tree 分析では、R が 10 倍に増えると言うことは t も同じ係数で 2.2 に増えることを意味する。この t は 1 より大きいため、最適な 2-コンポーネントソリューションではディスク容量がすべて利用されることはない。式 (\(\ref{eq38}\)) を用いて 2-コンポーネント LSM-Tree の最小コスト $27,000 を計算する。このコストの半分は 13.5 GB のディスクに、もう半分は 135 MB のメモリに充てられる。ここで 4.3 GB のディスクが未使用である。バッファ用のメモリが 2 MB の場合、合計コストは $27,200 となる。
以下は 2-コンポーネントソリューションの詳細な説明である。挿入速度 R = 160,000 バイト/秒は、C0 から C1 にマージする必要がある 40 ページ/秒に変換される。C1 は C0 の 68 倍大きいため、C0 からページをマージするには 68 ページの読み取りと C1 への 68 回の書き込みが必要で、合計 5450 ページ/秒となる。しかしこれは 13.5 ディスクが複数ブロック I/O 容量で提供するものと全く同じである。
R = 160,000 バイト/秒の場合の 3-コンポーネントからなる LSM-Tree では、最大のディスクコンポーネントのコストとコストバランスのとれた I/O レートは、2-コンポーネントの場合と同様に計算される。i = 1, 2 の場合、定理 3.1 により Si/Si-1 = r で、完全に占有されたディスクアームに対して r = 23、S0 = 17 MB (メモリコスト $1700) と計算される。小さい方のディスクコンポーネントのコストは大きい方のディスクコンポーネントの僅か 1/23 である。この時点でメモリサイズを増加させてもコスト効果は得られず、メモリサイズを小さくするとディスクコストが対応する係数である 2 乗で増加する。現在、ディスクコストはメモリコストよりもかなり高いため、メモリサイズを小さくしてもコスト効果は得られない。このように 3-コンポーネントの場合にも同様の s = t ソリューションが得られる。2 回のローリングマージ操作のためにバッファリング用に 4 MB のメモリを追加して $400 のコストがかかるとすると、3-コンポーネント LSM-Tree の合計コストはディスクに $9,200、メモリに $2,100、つまり合計 $11,300 となり、2-コンポーネント LSM-Tree のコストよりも大幅に改善される。
以下は 3-コンポーネントソリューションの詳細な説明である。メモリ内コンポーネント C0 は 17 MB、小さい方のディスクコンポーネント C1 はその 23 倍の 400 MB、C2 は C1 の 23 倍の 9.2 GB である。C0 から C1 にマージする必要がある 40 ページ/秒のデータの各ページには 23 ページの読み取りと 23 ページの書き込みが必要で、1 秒当たり 1840 ページとなる。同様に、40 ページ/秒が C1 から C2 にマージされ、各ページには C2 の 23 ページの読み取りと書き込みが必要である。2 つの I/O レートの合計は 3680 であり、これはちょうど 9.2 G のディスクの複数ブロック I/O 容量と全く同じである。
2 または 3-コンポーネントからなる LSM-Tree は単純な B-Tree 寄りも検索操作に多くの I/O を必要とする。どちらの場合でも最大のコンポーネントは対応する単純な B-Tree と非常によく似ているが、LSM-Tree の場合、インデックスの葉レベルのすぐ上のノードをバッファリングするためのメモリに$6,400 を払っていないない。ツリー内のさらに上位のノードは比較的少数で無視できるほどでありバッファリングされていると想定できる。エントリを検索するクエリーが十分に頻繁に行われてこのコストを正当化できる場合、すべてのディレクトリノードをバッファリングするために喜んでコストを払ってもいいことは明らかである。3-コンポーネントの場合は C1 コンポーネントも考慮する必要がある。これは最大コンポーネントの 23 分の 1 のサイズであるため、葉以外のノードをすべて簡単にバッファリングでき、このコストは分析的に追加する必要がある。C1 のバッファリングされていない葉へのアクセスは、C2 のエントリを検索している場合、検索のために別の追加の読み取りが必要となり、C2 のディレクトリをバッファリングするかどうかの決定が必要となる。したがって、3-コンポーネントのケースでは単純な B-Tree での検索に必要な 2 つの I/O に加えていくつかの追加のページ読み取りが発生する可能性がある (葉ノードのページ書き込みに対して 1 回の I/O をカウントする)。2-コンポーネントのケースでは追加の読み取りが 1 回発生する可能性がある。LSM-Tree コンポーネントの葉レベルより上のノードのバッファリング用にメモリを購入した場合、2-コンポーネントのケースでは B-Tree の速度を満たすことができ、3-コンポーねとのケースでは場合によっては 1 回の追加読み取りのみを支払うことができる。3-コンポーネントの場合にバッファリングを追加するための総コストは $17,700 となるが、それでも B-Tree より遙かに少ない。しかし、このお金を別の方法で使用した方が良い場合もある。完全な分析は、更新と検索の両方を含むワークロード全体の総コストを最小化するはずである。
我々は定理 3.1 の結果を用いてサイズ比 ri を変化させることにより、与えられた S0 でのマージ操作に必要な総 I/O を最小化し、次に、最適なディスクアームとメディアコストを達成するために S0 を選択して合計コストを最小化した。LSM-Tree で可能な残りの唯一のバリエーションは提供されるコンポーネントの総数 K+1 である。コンポーネントの数を増やすとコンポーネントサイズの比 r が値 e = 2.71... に達するまで、あるいはコールドデータ領域に達するまで S0 のサイズ葉現象し続けることがわかる。ただし、例 3.4 から、コンポーネント数が増加するにつれて S0 コンポーネントが徐々に小さくなっても、総コストに与える影響は小さくなって行くことがわかる。3-コンポーネントの LSM-Tree ではメモリサイズ S0 はすでに 17 MB に削減されている。さらに、コンポーネント数の増加に関連して、追加のローリングマージを実行するための CPU コストと、それらのマージのノードをバッファリングするためのメモリコスト (これは一般的なコスト領域では C0 のメモリコストを実際に圧倒する) などのコストが発生する。加えて、即時応答を必要とするインデックス付き検索では、すべてのコンポーネントツリーから検索を実行しなければならないことがある。このようなことを考慮すると、適切なコンポーネント数には強い制約が課せられ、実際には 3-コンポーネントが最大数になると思われる。
 4. LSM-Tree における並行性と回復性
4. LSM-Tree における並行性と回復性
このセクションでは LSM-Tree の並行性 (concurrency) と回復性 (recover) を実現するために使用するアプローチを調査する。これを達成するにはローリングマージプロセスの設計をより詳細に記述する必要がある。並列性と回復性のアルゴリズムの正しさの正式なデモンストレーションは今後の課題とし、ここでは提案された設計の動機付けを説明するだけとする。
 4.1 LSM-Tree での並行性
4.1 LSM-Tree での並行性
一般的に、サイズが増加する K+1 個のコンポーネント C0, C1, C2, ..., CK-1, CK の LSM-Tree が与えられる。ここで C0 コンポーネントツリーはメモリ常駐で他のすべてのコンポーネントはディスク常駐である。すべてのコンポーネントペア (Ci-1, Ci) 間では非同期のローリングマージプロセスが実行され、小さい方のコンポーネント Ci-1 がしきい値サイズを超えるたびに小さいコンポーネントから大きいコンポーネントにエントリが移動する。各ディスク常駐コンポーネントは B-Tree 型構造のページサイズのノードで構成されるが、ルートより下のすべてのレベルでキーシーケンス順の複数のノードが複数ページブロックに配置される。ツリー上位レベルのディレクトリ情報は単一ページノードを介してアクセスをチャネル化し、どのノードのシーケンスが複数ページブロック上に配置されるかも示す。こうすることで、このようなブロックの読み取りまたは書き込みを一括して実行できるようになる。ほとんどの状況では各複数ページブロックは単一ページのノードでいっぱいになるが、後述するようにそのようなブロックに存在するノードの数が少ない状況もいくつかある。その場合、LSM-Tree のアクティブなノードは複数ページブロックの連続したページセットに該当するが、必ずしもブロックの最初のページであるとは限らない。このような連続したページが複数ブロックの最初のページであるとは限らないという点を除いて、LSM-Tree コンポーネントの構造は [21] で提示されている SB-Tree の構造と同一である。詳細については参考文献を参照。
ディスクペースのコンポーネント Ci のノードは、等価一致検索が実行されるときのように、単一ページのメモリバッファに個別に常駐することも、それを含む複数ページのブロック内にメモリ常駐することもできる。複数ページのブロックは長距離検索の結果として、またはローリングマージカーソルが該当ブロックを高速で通過しているためにメモリにバッファリングされる。いずれにしても Ci コンポーネントのロックされていないすべてのノードは常にディレクトリ検索にアクセス可能であり、ディスクアクセスはローリングマージに参加している複数ページブロックの一部として存在する場合でもメモリ内の任意のノードを見つけるためにルックアサイド (lookaside) を実行する。これらの点を考慮すると、LSM-Tree における並行性アプローチでは 3 つの異なるタイプの物理的な競合を調停する必要がある。
検索操作は、ローリングマージを実行する別のプロセスがノードの内容を変更しているときにディスクベースコンポーネントのノードにアクセスすべきではない。
C0 コンポーネントへの検索または挿入は、別のプロセスが C1 へのローリングマージを実行するために同時に変更しているツリーの同じ部分にアクセスすべきではない。
Ci-1 から Ci へのローリングマージのカーソルは、Ci から Ci+1 へのローリングマージのカーソルを超えて移動する必要が生じる場合がある。これは、コンポーネント Ci-1 からの移動速度が常に Ci からの移動速度以上であるためであり、これはより小さなコンポーネント Ci-1 に付随するカーソルの循環速度が速いことを意味するためである。どのような並列実行方法を採用する場合でも 1 つのプロセス (Ci への移行) が交差するポイント (Ci からの移行) で他のプロセスにブロックされることなく、この通過を許可する必要がある。
ノードはディスクベースのコンポーネントへの同時アクセス中に物理的な競合を回避するために LSM-Tree で使用されるロックの単位である。ローリングマージによって更新されるノードは書き込みモードでロックされ、検索中に読み取られるノードは読み取りモードでロックされる。デッドロックを回避するためのディレクトリロックの方法は十分に知られている (たとえば [3])。C0 で採用されているロック方式は使用されるデータ構造に移動する。例えば (2-3)-Tree の場合、C1 のノードへのマージ中に影響を受ける範囲のすべてのエントリを含む単一の (2-3)-ディレクトリノード以下にあるサブツリーにロックを書き込むことができる。同時に、検索操作はアクセス経路上のすべての (2-3)-ノードを読み取りモードでロックし、1 種類のアクセスが他のアクセスを排除するようにする。我々は [28] の意味で複数レベルロックの最も低い物理レベルでの並行性のみを検討していることに注意。トランザクションの分離を維持し、ファントム更新の問題を回避するためのキー範囲ロックなどのより抽象的なロックの問題については他の人に任せる。議論については [4], [14] を参照。このように、読み取りロックは葉レベルで検索しているエントリがスキャンされるとすぐに解放される。カーソルの下にある (すべての) ノードの書き込みロックはより大きなコンポーネントからマージされた各ノードの後に解放される。これにより、長距離検索や、より高速なカーソルが比較的低速なカーソル位置を通過する機会が生まれ、上記のポイント (iii) に対処する。
ここで 2 つのディスクコンポーネント間でローリングマージを実行し、このローリングマージの内部コンポーネント (inner component) と呼ばれる Ci-1 から外部コンポーネント (outer component) と呼ばれる Ci にエントリを移行すると仮定する。カーソルは常に Ci-1 の葉レベルノード内の明確に定義された内部コンポーネントの位置を持ち、Ci へ移行しようとしている次のエントリを指し示し、同時に葉レベルノード位置へのアクセス経路に沿った Ci-1 の上位ディレクトリレベルのそれぞれの位置を持つ。カーソルはまた葉レベルとアクセス経路に沿った上位レベルの両方で、マージプロセスで検討しようとしているエントリに対応する Ci の外部コンポーネントの位置を持つ。マージカーソルが内部コンポーネントと外部コンポーネントの連続するエントリを通過して進むと、マージによって作成された Ci の新しい葉ノードは、新しいバッファ常駐複数ページブロックに左から右の順で直ちに配置される。したがって、現在のカーソル位置を囲む Ci コンポーネントのノードは、一般的に、メモリ内の 2 つの部分的に満たされている複数ページブロックバッファに分割される。kろえは、エントリが枯渇しているがまだマージカーソルが到達していない情報を保持する "emptying" ブロックと、この時点までのマージ結果を反映しているがディスクに書き込むにはまだ十分に満たされていない "filliing" ブロックである。並行アクセスの目的のために、emptying ブロックと filling ブロックの両方はバッファ常駐となる C1 ツリーのページサイズのノードを整数個含んでいる。個々のノードを再構築するマージステップ操作の間、関係するノードは書き込みモードでロックされ、エントリへの他のタイプの並行アクセスがブロックされる。
ローリングマージの最も一般的なアプローチでは、カーソルが通過するときにすべてのエントリを Ci に移行するのではなく、コンポーネント Ci-1 内の特定のエントリを保持したい場合がある。この場合、マージカーソルを囲む Ci-1 コンポーね都内のノードも 2 つのバッファ常駐複数ページブロックに分割される。1 つはマージカーソルがまだ到達していない Ci-1 のノードを含む "emptying" ブロック、もう一つはマージカーソルが最近通過してコンポーネント Ci-1 に保持されたエントリを含むノードが左から右に配置されている "filling" ブロックである。この最も一般的なケースではマージカーソルの位置は一度に 4 つの異なるノードに影響を与える。これは、マージが行われていようとしている emptying ブロックの内部と外部のコンポーネントノードと、カーソルが進むにつれて新しい情報が書き込まれている filling ブロック内の内部と外部のコンポーネントノードである。明らかに、これら 4 つのノードはどの瞬間にも完全にいっぱいになることはない。マージが実際にノード構造を変更している間、4 つのノードのすべてに対して書き込みロックをかけ、これらのロックを量子化された瞬間に解放して、カーソルがより速く通過できるようにする。これは、外部コンポーネントの emptying ブロック内のノードが完全に枯渇するたびにロックを解放することにしているが、他の 3 つのノードは一般的にその時点では満杯以下になっている。完全にいっぱいで葉内ノードを持つツリーや、ノードが完全にいっぱいではないブロックに対してすべてのアクセス操作を行うことができるため、これは問題ではない。1 つのカーソルが別のカーソルを通過する場合は特に慎重に検討する必要がある。これは、一般に、バイパスされるローリングマージのカーソル位置は、その内部コンポーネントで無効になり、カーソルの向きを再度変更するための準備が必要になるからである。上記のすべての注意事項はカーソルの移動によって変更が発生する両方のコンポーネントのさまざまなディレクトリレベルにも適用されることに注意。ただし高レベルのディレクトリノードは通常複数ページブロックバッファ内のメモリ常駐にしないため、多少異なるアルゴリズムを使用する必要があるが、それでもすべての瞬間に "filling" ノードと "emptying" ノードが存在する。このような複雑な考慮事項は LSM-Tree の実装によって追加の経験が得られた後の調査に譲る。
これまで我々はローリングマージが内部コンポーネント C0 から外部コンポーネント C1 に向かうという状況について特に考慮してこなかった。実際、これはディスクベースの内部コンポーネントと比較すると比較的単純な状況である。このようなすべてのマージステップと同様に 1 つの CPU をこのタスクを完全に専用し、他のアクセスが書き込みロックによって可能な限り短時間で排除されるようにする必要がある。マージされる C0 エントリの範囲は事前に計算され、既に説明した方法によってこのエントリ範囲に対する書き込みロックが事前に取得する必要がある。これに続いて、個々のエントリを削除するたびに再バランスを試みることなく、バッチ方式で C0 コンポーネントからエントリを削除することで CPU 時間を節約する。マージステップが完了した後に C0 ツリーを完全に再バランスすることができる。
 4.2 LSM-Tree での回復性
4.2 LSM-Tree での回復性
新しいエントリが LSM-Tree の C0 コンポーネントに挿入され、ローリングマージプロセスによってエントリ情報が順次大きなコンポーネントに移行されるとき、この作業はメモリバッファリングされた複数ページブロックで行われる。このようなメモリバッファリングされた変更と同様に、作業はディスクに書き込まれるまでシステム障害に対する耐性がない。クラッシュが発生してメモリが失われた後にメモリ内で行われた作業を再構築するという、典型的な回復問題に直面することになる。第二章の冒頭で述べたように、新しく作成されたレコードのインデックスエントリを回復するために特別なログを作成する必要はない。これらの新しいレコードのトランザクション挿入ログは、通常のイベントの過程でシーケンシャルログファイルに書き出される。これらの挿入ログ (都城、挿入されたレコードが配置されている RID とともにすべてのフィールド値を含む) を、インデックスエントリを再構築するための論理ベースとして扱うことは簡単である。インデックスを回復するこの新しいアプローチは、システム回復アルゴリズムに組み込む必要があり、このようなトランザクション履歴挿入ログのストレージ再利用が行われるまでの時間を延長する効果があるかもしれないが、これは些細な考慮事項である。
LSM-Tree インデックスの回復性を実証するためにはチェックポイントの形式を慎重に定義し、回復する必要のあるインデックスの更新を確定的に複製するためにはシーケンシャルログファイルのどこから開始しどのように連続したログを適用するかを知っていることを実証することが重要である。使用するスキームは次の通りである。時刻 T0 にチェックポイントが要求されると、ノードロックが解放されるようにすべての操作中のマージステップを完了させ、チェックポイントが完了するまで LSM-Tree への新しいエントリ挿入を延期する。この時点で、次のアクションで LSM-Tree のチェックポイントを作成する。
コンポーネント C0 の内容を既知のディスクの場所に書き込む。この後 C0 へのエントリの挿入は再開できるが、マージステップは引き続き延長される。
ディスクベースのコンポーネントのすべてのダーティメモリバッファリングノードをディスクにフラッシュする。
以下の情報を持つ特別なチェックポイントログを作成する:
- 時刻 T0 で最後に挿入されたインデックス付き行のログシーケンス番号 LSN0
- すべてのコンポーネントのルートディレクトリアドレス
- さまざまなコンポーネントのすべてのマージカーソルの位置
- 新しい複数ページブロックの動的割り当てのための現在の情報
このチェックポイント情報がディスク上に配置されると LSM-Tree の通常の操作を再開できる。クラッシュが発生してその後に再起動すると、このチェックポイントが見つかり、保存されたコンポーネント C0 がローリングマージの続行に必要な他のコンポーネントのバッファリングされたブロックと共にメモリにロードされる。次に LSN0 の後の最初の LSN から始まるログがメモリに読み込まれ、関連するインデックスエントリが LSM-Tree に入力される。チェックポイントの時点で、すべてのインデックス情報を含むすべてのディスクスペースのコンポーネントの位置がルートから始まるコンポーネントディレクトリに記録されている。この場所はチェックポイントのログからわかる。後続のチェックポイントによって古い複数ページブロックが不要になるまで常にディスク上の新しい場所に書き込まれるため、これらの情報は後の複数ページブロックの書き込みによって消去されることはない。インデクス付き行の挿入ログを回復すると C0 コンポーネントに新しいエントリが配置される。ここでローリングマージが再び開始され、チェックポイント以降に書き込まれた複数ページブロックは上書きされるが、最後に挿入された行のインデックスが作成されて回復が完了するまで、すべての新しいインデックスエントリが回復される。
この回復アプローチは明らかに機能しており、唯一の欠点はチェックポイント中にさまざまなディスク書き込みが行われる間におそらく大きな停止時間が発生することである。しかしこの停止時間は、C0 コンポーネントを短時間でディスクに書き込み、残りのディスク書き込みが完了するまでに C0 コンポーネントへの挿入を再開できるためそれほど重要ではない。これは単に C0 に新しく挿入されたインデックスエントリがより大きなディスクベースのコンポーネントにマージされない期間が通常よりも長くなるだけである。チェックポイントが完了するとローリングマージプロセスは見逃した作業に追いつくことができる。上記のチェックポイントログリストで言及されている最後の情報は、新しい複数ページブロックの動的割り当てに関する現在の情報であることに注意。クラッシュが発生した場合、動的ディスクストレージ割り当てアルゴリズムで利用可能な複数ページブロックを回復時に把握する必要がある。これは明らかに難しい問題ではない。実際、[23] ではこのようなブロックの断片化された情報をガーベッジコレクションするというより難しい問題を解決する必要があった。
回復のもう一つの少佐はディレクトリ情報に関係している。ローリングマージが進行するにつれて、複数ページブロックまたは上位レベルのディレクトリノードがディスクから取り込まれて空にされるたびに、空にされる前にチェックポイントが発生し、残りのバッファリングされた情報がディスクに強制的に書き出される必要がある場合に備えて、新しいディスク位置をすぐに割り当てる必要があることに注意。つまり、空になったノードを指すディレクトリエントリは新しいノードを指すように直ちに修正されなければならない。同様に、ツリー内のディレクトリエントリがディスク上の適切な位置を即座に指すことができるように、新しく作成されたノードのディスク位置を即座に割り当てる必要がある。すべての時点でローリングマージによってバッファリングされた下位レベルのノードへのポインタを含むディレクトリノードもバッファリングされるように注意する必要がある。こうすることでしか必要な変更をすべて迅速に行うことはできず、ディレクトリを修正するための I/O を待ってチェックポイントが停止することがなくなる。さらに、チェックポイントが発生し、複数ページブロックがメモリバッファに読み戻されてローリングマージが続行された後、関係するすべてのブロックを新しいディスク位置に割り当てる必要があるため、補助ノードへのすべてのディレクトリポインタを修正する必要がある。これは大変な作業に聞こえるかもしれないが、追加の I/O は必要なく、関係するポインタの数はバッファリングされた各ブロックに対しておそらく約 64 個だけであることを思い出すべきである。さらに、チェックポイントが回復時間が数分を超えないように十分な頻度で取得されると仮定すると、これらの変更は多数のマージされたノードに渡って償却されるはずである。これはチェックポイント間の I/O が数分であることを意味する。
 5. 他のアクセス方法とのコストパフォーマンス比較
5. 他のアクセス方法とのコストパフォーマンス比較
最初の例 1.2 では、商用システムで使用される最も一般的なディスクベースのアクセス方法でとなるように、History ファイルの Acct-ID || Timestamp インデックスに B-Tree を検討した。ここでは他のディスクインデックス構造では一貫して優れた I/O パフォーマンスが得られないと言うことを示したい。この主張の根拠として以下のように論じる。
任意のインデックス構造を扱っていると仮定する。Acct-ID || Timestamp インデックスのエントリ数は 1 日 8 時間の累積を 20 日間続ける間に毎秒 1000 エントリを生成しているとして仮定して計算したことを思い出しほしい。インデックスエントリの長さが 16 バイト (Acct-ID に 4 バイト、Timestamp に 8 バイト、History 行の RID が 4 バイト) とすると、無駄なスペースがないとしてもエントリ数は 9.2 GB、つまり 4 KB のインデックスページが約 230 万ページあることになる。これらの結論はインデックス方法の特定の選択によって変わることはない。B-Tree には上位レベルのディレクトリノードとともに一定量の無駄なスペースのある葉ノードが存在するが、拡張可能なハッシュテーブルにはディレクトリノードはないが多少異なる量の無駄なスペースがあり、どちらの構造にも上記の計算通り 9.2 GB のエントリが含まれていなければならない。さて、インデックス構造に新しいインデックスエントリを挿入するには、エントリを挿入するページを計算し、そのページがメモリに常駐していることを確認する必要がある。当然、次のような疑問が生じる: 新しく挿入されるエントリは、一般にすでに存在する 9.2 GB のインデックスエントリの任意の位置に配置されるのだろうか? ほとんどの従来のアクセス方法構造では、答えは Yes である。
定義 5.1. ディスクスペースのアクセス方法のインデックス構造は、新しく挿入されたインデックスエントリがインデックススキームによって他のすべてのエントリが既に存在する状態でキー値に基づいて最終的な照合順序で即座に配置される場合、連続構造 (continuum structure) という特性を持つと言う。
TPC ベンチマークアプリケーションの連続するトランザクションでは 100,000,000 通りの値からランダムに Acct-ID 値が生成される。定義 1.1 により、Acct-ID || Timestamp インデックスの各新規絵エントリ挿入は既存の 230 万ページのエントリの一つとしてほぼランダムな位置に配置される。例えば B-Tree では累積された 576,000,000 エントリには Acct-ID ごとに平均 5.76 のエントリが含まれる。したがって、新規エントリ挿入のそれぞれは同じ Acct-ID を持つすべてのエントリの右側に配置される。しかしそれでも 100,000,000 ポイントの挿入がランダムに選択されるため、各新規挿入が既存の 230 万ページのエントリの 1 つにランダムに配置される。これとは対照的に拡張可能なハッシュスキーム [9] では、新しいエントリは Acct-ID || Timestamp キー値からハッシュ値として計算された照合順序を持ち、新しいエントリが既存のすべてのエントリと同じ順序で配置される可能性は明らかに等しい。
連続構造の 9.2 GB のエントリを配置できる最小のページ数は 230 万ページでああり、毎秒 1,000 回の挿入があるとすると、このような構造の各ページは約 2,300 秒ごとに新しい挿入のためにアクセスされる。5 分ルールによりこれらすべてのページをバッファリングしておくのは不経済である。Bounded Disorder ファイル [16] のようにエントリを保持するノードを大きくすると、参照頻度は高くなるがノードをバッファリングするメモリコストも高くなり 2 つの効果が相殺されるため何の利点ももたらさない。一般的に、ページはエントリ挿入ためにメモリバッファに読み込まれ、後で他のページのための場所を作るためにバッファから削除する必要がある。バッファから削除する前にその場でディスクページを更新するトランザクションシステムでは、この更新によりインデックス挿入ごとに少なくとも 2 回の I/O が必要になる。したがって、更新を延期しない連続構造ではインデックス挿入ごとに少なくとも 2 回の I/O が必要であり、これは B-Tree とほぼ同等であると言える。
B-Tree [5] とその多数の変種である SB-Tree [21]、Bounded Disorder ファイル [16]、拡張ハッシュ [9] などのさまざまなタイプのハッシュスキーム、その他無数のものを含む既存のディスクベースのアクセス方法のほとんどは連続構造である。しかし Kolovson と Stonebraker の MD/OD R-Tree ([15]) や Lomet と Salzberg の Time-Split B-Tree ([17], [18]) のようにエントリを 1 つのセグメントから別のセグメントに移行するアクセス方法がいくつか存在する。また Differential File アプローチ [25] も小さなコンポーネントの変更を収集して後でフルサイズの構造に更新を実行する。これらの構造についてもう少し深く検討する。
まず、なぜ LSM-Tree が I/O 性能の点で連続構造よりも優れているか、つまり特定の状況でディスクアームの負荷を 2 桁も削減できる理由を正確に分析する必要がある。最も一般的な定式化では、LSM-Tree の利点は (1) コンポーネント C0 をメモリ常駐にしておく機能、(2) 慎重な遅延は位置の 2 つの要因からもたらされる。連続構造における新しいエントリの挿入は、エントリを配置する必要のあるインデックスのサイズを、経済的にメモリにバッファリングすることができないため、まさにこの理由で 2 回の I/O を必要とする。LSM-Tree 内のコンポーネント C0 の確実なメモリ常駐が保証されないとき、これが比較的小さなディスク常駐構造をバッファリングすることの単なる確率的な付随現象である場合、メモリ常駐特定が悪化する状況が発生する可能性があり、新しいエントリ挿入の割合が増加するにつれて追加の I/O が発生するため、LSM-Tree のパフォーマンスに深刻な悪化をもたらす。最初の挿入で I/O を引き起こさないことが保証されている場合、LSM-Tree の高性能を支える 2 つ目の要因であるインデックスの大きな連続体への慎重な遅延は位置は、コンポーネント C0 が高価なメモリメディアで制御なしに大きくならないことを保証するために重要である。実際、複数コンポーネント LSM-Tree では総コストを最小化するために一連の遅延配置が提供される。連続構造ではない特殊な構造を考慮すると、新しく挿入されるエントリの最終位置への遅延配置は提供される一方で、新しい挿入のための最初のコンポーネントがメモリ常駐のままであることを保証するために慎重に行われていないことがわかる。その代わりにこのコンポーネントは定義論文ではディスク常駐と見なされているが、大部分はメモリにバッファリングされる可能性がある。しかしこの要素は制御されていないため、コンポーネントは主にディスク常駐となり、B-Tree と同様に、新しい挿入ごとに少なくとも 2 回の I/O が必要になるまで I/O 性能が低下する。
 Time-Split B-Tree
Time-Split B-Tree
まず Lomet と Salzberg ([17], [18]) の Time-Split B-Tree または TSB-Tree について考える。TSB-Tree はタイムスタンプと Key-Value の次元でレコードを検索する 2 次元検索構造である。特定のキー値を持つレコードが挿入されるたびに古いレコードは時代遅れ (outmoded) になると想定される。ただし時代遅れかどうかにかかわらずすべてのレコードの永続的な履歴はインデックス化されて保持される。TSB-Tree の (現在の) ノードに新しいエントリが挿入され、それを受け入れる余地がない場合、状況に応じてノードを Key-Value または時間で分割することができる。ノードが時間 t で分割される場合、タイムスタンプ範囲が t 未満のすべてのエントリは分割の履歴ノードに移動し、タイムスタンプの範囲が t を超えるすべてのエントリは現在のノードに移動する。この目的は時代遅れになったレコードを安価な write-once ストレージ上の TSB-Tree の履歴コンポーネントに最終的に移行させることである。ツリー上にある現在のレコードと現在のノードはすべてディスク上にある。
TSB-Tree のモデルは我々のものと多少異なる。同じ Acct-ID を持つ新しい History 行が書き込まれたとき、古い History 行が時代遅れであることは想定しない。TSB-Tree の現在のノード集合が、より長期的なコンポーネントに更新を延期する別のコンポーネントを形成することは議論の余地がない。しかし LSM-Tree の C0 コンポーネントのように、この現在のツリーをメモリ内に保持する試みはない。実際、現在のツリーはディスク常駐し、履歴ツリーは write-once ストレージに常駐している。TSB-Tree が挿入性能を高速化するという主張はない。設計の意図はむしろ、時間の経過と共に生成されるすべてのレコードに対して履歴インデックスを提供することである。新しい挿入が実行されるメモリ常駐が保証されたコンポーネントがなければ各エントリの挿入に 2 回の I/O が必要な状況に戻る。
 MD/OD R-Tree
MD/OD R-Tree
Kolovson と Stonebraker の MD/OD R-Tree [15] は、タイムスタンプ範囲と Key-Value によって履歴レコードをクラスタリングしインデックスを作成するために 2 次元アクセス方法 (R-Tree) 変種を使用するという点で TSB-Tree と同等である。MD/OD R-Tree で導入された重要な R-Tree のバリエーションは磁気ディスク (MD) と光ディスク (OD) にまたがることを意図した構造である。TSB-Tree と同様に最終的な目的は安価な write-once 光ストレージに含まれる葉ページと適切なディレクトリページを含むアーカイブ R-Tree に時代遅れのレコードを最終的に移行することである。この移行はバキューム・クリーナー・プロセス (VCP; vacuum cleaner process) によって行われる。磁気ディスク上の R-Tree インデックスがしきい値のサイズに達すると、VCP は最も古い葉ページの一部を光ディスク上のアーカイブ R-Tree に移動する。この論文では、バキュームする割合と、アーカイブ R-Tree と現在の R-Tree が 1 構造か 2 構造かを含む、このプロセスの 2 つの異なるバリエーション (MD/OT-RT-1 と MD/OT-RT-2) について研究している。TSB-Tree と同様に現在のツリー (MD R-Tree) はディスク常駐として表現されるが、アーカイブツリー (OD R-Tree) は write-once ストレージ状に常駐する。MD/OT R-Tree が挿入パフォーマンスを高速化するという主張はない。OD ターゲットがローリングマージ手法を妨げることは明らかである。実際、[15] のシミュレーションで使用したレコード数が少ない場合でも、Figure 4 は、調査した 2 つのバリアント構造で挿入ごとに読み取られるページ数が 2 未満になることはないことを示している。MD/OD R-Tree をメモリ階層の 1 レベル上に昇格させてメモリとディスクを使用する場合、LSM-Tree と MD/OD R-Tree の間には大まかな対応関係があるが、3 つのメディアの機能の違いにより詳細のほとんどは同じではない。
 Differential ファイル
Differential ファイル
Differential ファイルアプローチ [25] は、長期間にわたって変更されていないメインデータファイルから始まり、新しく追加されたレコードが差分ファイル (differential file) と呼ばれる特定のオーバーフロー領域に配置される。将来のある時点で (厳密には指定されていないが) 変更はメインデータファイルと統合され新しい差分ファイルが開始されると想定されている。この論文の内容の多くは、動的領域がはるかに小さくなることの利点と、二重アクセスを回避する方法、最初に差分ファイルを (何らかのインデックスを介して) 探し次にメインデータファイルを (おそらく別のインデックスを介して) 調べる一意なレコード識別子による検索操作に関するものである。このような二重アクセスを回避する主なメカニズムとしてブルームフィルターの概念が提案されている。繰り返しになるが、上記で定義したアクセス方法と同様に差分ファイルでは差分ファイルのメモリを常駐させる規定はない。セクション 3.4 では差分ファイルがダンプされ、後でメインファイルに組み込まれる間、"差分-差分" ファイルをメモリキャッシュに保持してオンラインで再編成を可能にすることが提案されている。このアプローチについてはこれ以上分析していない。これは、C1 が C2 とマージされる間、C0 コンポーネントをメモリに保持するというアイディアに対応するが、セクション 3.2 で示されている 1 時間あたり 100 回の変更がある 10,000,000 レコードの例で確認できるように、差分-差分ファイルを常にメモリに常駐させる必要があるとは提案されておらず、挿入操作の I/O 節約についても言及されていない。
 選択的遅延テキストインデックス更新
選択的遅延テキストインデックス更新
Dadum, Lum, Praedel および Schlageter [7] のテキストインデックス保守方法も実際のディスク書き込みを遅延することでインデックス更新のシステム性能を向上させるように設計されている。インデックス更新は、クエリーとの衝突によって強制的に削除されるか、バックグラウンドタスクによって少しずつ削除されるまでメモリにキャッシュされる。これはテキストシステムであるため、ここでの衝突とは更新されるドキュメントに関連するキーワードをクエリーに関連するキーワードの間で発生する。更新後、クエリーはディスク上のインデックスから実行される。したがって LSM-Tree とは異なり、メモリキャッシュは権威インデックス (authoratative index) の一部ではない。遅延方法により、強制更新と少しずつ更新する両方のケースで、更新をある程度バッチ化することができる。ただし更新のパターンは依然として連続構造のようである。
 6. 結論と拡張の提案
6. 結論と拡張の提案
B-Tree は、メモリにバッファリングされた一般的なディレクトリノードを持つため実際にはハイブリッドデータ構造であり、大部分のデータに対するディスクメディアストレージの低コストと、最も人気のあるデータに対するメモリアクセスの高コストが組み合わされている。LSM-Tree はこの階層を複数のレベルに拡張し、複数ページのディスク読み取りを実行する際にマージ I/O の利点を取り入れている。
Figure 6.1 では Figure 1.1 を拡張し、B-Tree を介したデータアクセスと 2-コンポーネント、つまりディスクコンポーネントの数 K = 1 の LSM-Tree を介したデータアクセスについて、「MB あたりのアクセスコスト」と「MB あたりのアクセスレート」、つまりデータ温度をグラフ化している。最も低いアクセスレートから始めて "cold" データのコストはそれが配置されているディスクメディアに比例する。一般的なコストの数値で言えば 1 MB あたり毎秒 0.04 I/O の "freezing point" まではディスクアクセスのコストは 1 MB あたり $1 である。"warm data" 領域はディスクアームがアクセスの制限要因と形メディアが十分に利用されなくなる freezing point から始まる。例 3.3 で言えば 1 MB あたり毎秒 1 ページ I/O のコストは 1 MB あたり $25 である。最後に "hot data" だが、これはアクセス頻度が非常に高いため B-Tree でアクセスされたデータがメモリバッファ内に残すべき場合である。メモリが 1 MB あたり $100 の場合、このアクセスレートのコストは 1 MB あたり $100 になり、これは 1 MB あたり毎秒少なくとも 4 I/O のレート、つまり "boiling point" を意味する。
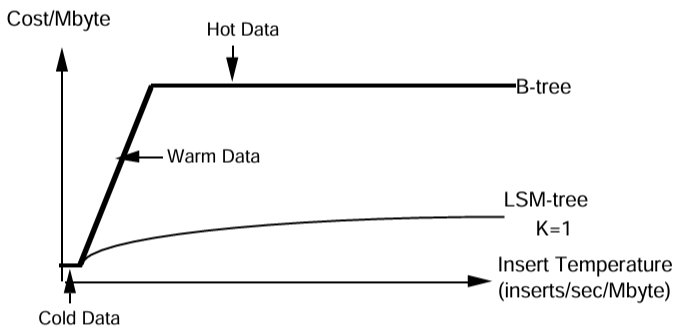
B-Tree におけるバッファリングの効果はアクセスレートがホットデータ領域に入るとグラフが平坦になることであり、よりアクセス頻度が高くなってもコストがこれまで以上に高くなることはなく、ウォームデータの上昇ラインの傾きが拡大する。少し考えれば LSM-Tree の効果は、挿入や削除のようなマージ可能な操作の現実的なアクセスレートでは、アクセスコストをコールドデータのコストに大幅に近づけることがわかる。さらに Figure 4.1 において「ホットデータ」とラベル付けされているような、B-Tree のメモリ常駐を示すアクセスレートの多くのケースは、LSM-Tree ではほとんどディスク上に収容することができる。このような場合、データは論理アクセスレート (挿入/秒) の点ではホットだが、LSM-Tree のバッチ効果により物理的なディスクアクセスレートではウォームに過ぎない。これはマージ可能な操作が非常に多いアプリケーションによって非常に大きな利点である。
 6.1 LSM-Tree アプリケーションの拡張
6.1 LSM-Tree アプリケーションの拡張
まず始めに LSM-Tree ツリーエントリ自体に、ディスク上の他の場所にあるレコードを指す RID ではなくレコードを含めることができることは明らかである。これはレコード自体を Key-Value によってクラスタ化できることを意味する。この代償は、エントリが大きくなり、それに伴って挿入速度 R (バイト/秒)、カーソルの移動、合計 I/O 速度 H が加速される。ただし例 3.3 で見たように、3-コンポーネントの LSM-Tree はレコードとインデックスを格納するディスクメディアのコストで必要な循環を提供できるはずである。そしていずれにしても行を非クラスタ化方式で格納するにはこのディスクメディアすべてが必要である。
クラスタリングの利点はパフォーマンスに非常に重要な影響を与える可能性がある。例えば Escrow トランザクション方式 [20] を考えてみよう。この方式は長期間の更新 (long-lived update) がノンブロッキングで行える性質を持つため、ワークフロー管理をサポートするのに適したレイヤーとして機能する。Escrow 方式では長期間トランザクション (long-lived transaction) によってさまざまな集計 Escrow フィールドに対する増分変更を多数生成できる。使用されるアプローチは、要求された増分量 (Escrow 量) を確保し、同時要求のために集計レコードのロックを解除することである。これらの Escrow 量のログを保持する必要があり、これらのログに対して、生成されたトランザクションのトランザクション ID (TID) と、Escrow 量が取得されたフィールドのフィールド ID (FID) の 2 つが考えられる。ログが古典的なログ構造のメモリに常駐しなくなるほどの長期間にわたって 1 つの TID を持つ Escrow ログが 20 個存在する可能性は十分にあり、トランザクションがコミットまたは中止を実行するまで TID によるクラスタリングが重要である。コミットまたは中止によってこれらのログの最終的な影響が決まる。コミットの場合、フィールドから取り出された量は永続的でありログは単に忘れ去られるだけであるが、中止の場合はログの FID で指定されたフィールドに量を戻そうとする。ある程度の速度が必要である。中止処理では中止されたトランザクションのログにアクセスし (TID によるクラスタリングは重要なり点である)、対応する FID を持つフィールドを修正すべきである。ただしフィールドがメモリに常駐していない場合、ログを含むレコードを読み取るのではなく、ログを FID でクラスタリングして再変換 (別の LSM-Tree に配置) することができる。次に Escrow フィールドがメモリに読み戻されると FID でクラスタ化された更新を実行すべき可能性のあるすべてのログにアクセスしようとする。ここでもアクセスされるログの数が多くなる可能性があり、これらのログを LSM-Tree にクラスタ化することは重要な節約となる。LSM-Tree を使用して、最初に TID で Escrow ログをクラスタ化し、次に関連するフィールドがメモリにない場合は FID でクラスタ化することで、長時間のトランザクションがコールドデータまたはウォームデータに大量の更新を行うときに多数の I/O を節約できる。このアプローチは [20] の "extended field" コンセプトを改良したものである。
セクション 2.2 の最後で述べた LSM-Tree アルゴリズムに対するもう一つの可能なバリエーションは、最近のエントリ (最後の τi 秒で生成されたもの) をコンポーネント Ci に保持し、Ci+1 に移行させないようにすることである。このアイディアからいくつかの代替案が提案される。1 つのバリエーションは、カーソルの循環中に TSB-Tree によって提供されるような時間-キーインデックスが生成されることを提案する。ローリングマージを使用すると新しいバージョンの挿入に非常に効率的に対応できる。また、複数コンポーネント構造ではアーカイブの時間-キーインデックスをうまく制御しながら、最終的なコンポーネントを write-once ストレージへの以降を提案する。このアプローチは明らかにさらなる研究に値するものであり、学会論文 [22] の主題となっている。
さらなる研究のための他のアイディアとしては以下のものがある。
定理 3.1 と例 3.3 のコスト分析アプローチを、I/O のバランスを取る目的で検索操作の一部とマージのバランスを取る必要がある状況に拡張する。ディスクの負荷が増加するためディスク I/O 容量のすべてをローリングマージ操作に割り当てて最適化することはできなくなる。ディスク容量のいくらかを検索操作の作業負荷のために確保しなければならない。コスト分析を拡張する他の方法は、コンポーネント CK への移行前に削除を許可し、(Ci-1, Ci) マージ中に内部コンポーネント Ci-1 内の最近のエントリの一部を保持することを検討することが挙げられる。
LSM-Tree を維持するために CPU 作業をオフロードできるため、ログレコードを生成する CPU でこれを実行する必要がないことは明らかである。ログを他の CPU に伝達し、後の検索要求も伝達するだけで済む。共有メモリがある場合はレイテンシを追加せずに検索を実行できる可能性がある。このような分散処理の設計は慎重に検討する必要がある。
 Acknowledgements
Acknowledgements
The authors would like to acknowledge the assistance of Jim Gray and Dave Lomet, both of whom read an early version of this paper and made valuable suggestions for improvement. In addition, the reviewers for this journal article made many valuable suggestions.
 References
References
- Alfred V. Aho, John E. Hopcroft, and Jeffrey D. Ullman, "The Design and Analysis of Computer Algorithms", Addison-Wesley.
- Anon et al., "A Measure of Transaction Processing Power", Readings in Database Systems, edited by Michael Stonebraker, pp 300-312, Morgan Kaufmann, 1988.
- R. Bayer and M Schkolnick, "Concurrency of Operations on B-Trees", Readings in Database Systems, edited by Michael Stonebraker, pp 129-139, Morgan Kaufmann 1988.
- P. A. Bernstein, V. Hadzilacos, and N. Goodman, "Concurrency Control and Recovery in Database Systems", Addison-Wesley, 1987.
- D. Comer, "The Ubiquitous B-tree", Comput. Surv. 11, (1979), pp 121-137.
- George Copeland, Tom Keller, and Marc Smith, "Database Buffer and Disk Configuring and the Battle of the Bottlenecks", Proc. 4th International Workshop on High Performance Transaction Systems, September 1991.
- P. Dadam, V. Lum, U. Praedel, G. Shlageter, "Selective Deferred Index Maintenance &Concurrency Control in Integrated Information Systems," Proceedings of the Eleventh International VLDB Conference, August 1985, pp. 142-150.
- Dean S. Daniels, Alfred Z. Spector and Dean S. Thompson, "Distributed Logging for Transaction Processing", ACM SIGMOD Transactions, 1987, pp. 82-96.
- R. Fagin, J. Nievergelt, N. Pippenger and H.R. Strong, Extendible Hashing — A Fast Access Method for Dynamic Files, ACM Trans. on Database Systems, V 4, N 3 (1979), pp 315-344
- H. Garcia-Molina, D. Gawlick, J. Klein, K. Kleissner and K. Salem, "Coordinating MultiTransactional Activities", Princeton University Report, CS-TR-247-90, February 1990.
- Hector Garcia-Molina and Kenneth Salem, "Sagas", ACM SIGMOD Transactions, May 1987, pp. 249-259.
- Hector Garcia-Molina, "Modelling Long-Running Activities as Nested Sagas", IEEE Data Engineering, v 14, No 1 (March 1991), pp. 14-18.
- Jim Gray and Franco Putzolu, "The Five Minute Rule for Trading Memory for Disk Accesses and The 10 Byte Rule for Trading Memory for CPU Time", Proceedings of the 1987 ACM SIGMOD Conference, pp 395-398.
- Jim Gray and Andreas Reuter, "Transaction Processing, Concepts and Techniques", Morgan Kaufmann 1992.
- Curtis P. Kolovson and Michael Stonebraker, "Indexing Techniques for Historical Databases", Proceedings of the 1989 IEEE Data Engineering Conference, pp 138-147.
- Lomet, D.B.: A Simple Bounded Disorder File Organization with Good Performance, ACM Trans. on Database Systems, V 13, N 4 (1988), pp 525-551
- David Lomet and Betty Salzberg, "Access Methods for Multiversion Data", Proceedings of the 1989 ACM SIGMOD Conference, pp 315-323.
- David Lomet and Betty Salzberg, "The Performance of a Multiversion Access Method", Proceedings of the 1990 ACM SIGMOD Conference, pp 353-363.
- Patrick O'Neil, Edward Cheng, Dieter Gawlick, and Elizabeth O'Neil, "The Log-Structured Merge-Tree (LSM-tree)", UMass/Boston Math & CS Dept Technical Report, 91-6, November, 1991.
- Patrick E. O'Neil, "The Escrow Transactional Method", TODS, v 11, No 4 (December 1986), pp. 405-430.
- Patrick E. O'Neil, "The SB-tree: An index-sequential structure for high-performance sequential access", Acta Informatica 29, 241-265 (1992).
- Patrick O'Neil and Gerhard Weikum, "A Log-Structured History Data Access Method (LHAM)," Presented at the Fifth International Workshop on High-Performance Transaction Systems, September 1993.
- Mendel Rosenblum and John K. Ousterhout, "The Design and Implementation of a Log Structured File System", ACM Trans. on Comp. Sys., v 10, no 1 (February 1992), pp 26-52.
- A. Reuter, "Contracts: A Means for Controlling System Activities Beyond Transactional Boundaries", Proc. 3rd International Workshop on High Performance Transaction Systems, September 1989.
- Dennis G. Severance and Guy M. Lohman, "Differential Files: Their Application to the Maintenance of Large Databases", ACM Trans. on Database Systems, V 1, N 3 (Sept. 1976), pp 256-267.
- Transaction Processing Performance Council (TPC), "TPC BENCHMARK A Standard Specification", The Performance Handbook: for Database and Transaction Processing Systems, Morgan Kauffman 1991.
- Helmut Wächter, "ConTracts: A Means for Improving Reliability in Distributed Computing", IEEE Spring CompCon 91.
- Gerhard Weikum, "Principles and Realization Strategies for Multilevel Transaction Management", ACM Trans. on Database Systems, V 16, N 1 (March 1991), pp 132-180.
- Wodnicki, J.M. and Kurtz, S.C.: GPD Performance Evaluation Lab Database 2 Version 2 Utility Analysis, IBM Document Number GG09-1031-0, September 28, 1989.
翻訳抄
メモリ内のデータを定期的にストレージ上の大規模構造にマージすることで高い書き込みスループットと効率的なクエリー処理を実現するデータ構造である LSM-Tree に関する 1996 年の論文。
- O’NEIL, Patrick, Edward Cheng, Dieter Gawlick, Elizabeth O'Neil. The log-structured merge-tree (LSM-tree). Acta Informatica, 1996, 33: 351-385.

