論文翻訳: PRESERVING ORDER IN A FOREST IN LESS THAN LOGARITHMIC TIME
P. van Emde Boas
Mathematical Centre, Amsterdam, Netherlands /
Mathematical Institute, University of Amsterdam
 ABSTRACT
ABSTRACT
我々は階層化二分木 (stratified binary tree) に基づくデータ構造を提示する。このデータ構造により、区間 \(1..n\) から優先度が選択される優先度付きキュー (priority queue) を、命令あたり平均・最悪ケースで \(O(\log \log n)\) の処理時間でオンラインで操作することができる。この構造は、ほぼ同程度に良好な良好な時間要件を持つマージ可能ヒープ (mergeable heap) を得るために使用される。
Table of Contents
- ABSTRACT
- 1. 導入
- 2. 一般的な背景
- 3. \(O(\log n)\) の処理時間を持つ "愚直な" 優先度付きキュー
- 4. 階層化木構造
- 5. 階層化木構造における操作
- 6. 階層化木の応用
- 7. 集合捜査問題間の帰着性
- ACKNOWLEDGEMENTS
- REFERENCES
- 翻訳抄
 1. 導入
1. 導入
集合操作のための効率的なアルゴリズム設計における主要な問題は、同時に実行したい異なる操作がもたらす矛盾した要求から生じる。集合内の要素の挿入、削除、あるいは要素の所属判定 (membership) を行う命令は、ランダムアクセスをサポートするデータ構造を必要とする。一方、最小要素や最大要素の値、あるいは特定の要素の後続要素や先行要素の値を計算する命令は、順序付けられた表現を必要とする。最後に、2 つの集合を結合する命令は、これまでのところツリー構造を用いてのみ効率的に実装されてきた。
これらの矛盾の 1 つを解決する効率的なアルゴリズムの例として、よく知られている union-find アルゴリズムが挙げられる。\(n\) 要素の全体集合 (universe) に対する \(O(n)\) 個の命令を実行する場合、命令あたりの最悪ケースの平均処理時間は \(A(n)\) のオーダーであることが示されている。ここで \(A\) はアッカーマン型の増大次数を持つ関数の逆関数である ([1, 9] 参照)。
順序アクセスとランダムアクセスという競合する要求を解決するためにこれまでに発表されてきたアルゴリズムは、いずれもオンラインで実行されなければならない \(n\) 要素の全体集合における \(O(n)\) 個の命令のプログラムにおいて、最悪ケースで命令あたり \(O(\log n)\) の処理時間を示している。明らかに、\(O(n)\) 個の命令を発効して \(n\) 個の実数をソートするできるようにする各命令レパートリーは、そのために平均命令あたり \(O(\log n)\) の処理時間を必要とすることを我々は忘れてはならない。しかし、全体集合が整数 \(1..n-1\) のみで構成されていると仮定すれば、ソートの複雑さに関する情報理論的な下限は適用されない。さらに、範囲 \(1..n\) の \(n\) 個の整数は線形時間でソートできることが知られている。
順序アクセスとランダムアクセスの競合を解決するために用いられてきたデータ構造には (とりわけ) バイナリヒープ、AVL 木、2-3 木がある。AHO, HOPCROFT & ULLMAN [1] では、命令レパートリー INSERT, DELETE, UNION, MIN をサポートするために 2-3 木が使用されており、最悪ケースで命令あたり \(O(\log n)\) オーダーの処理時間がかかる。著者らは (UNION を除く) 上記の操作をサポートする構造に対してマージ可能ヒープ (mergeable heap) (または優先度付きキュー (priority queue)) という名前を導入している。
優先度付きキューやマージ可能ヒープの操作にかかる \(O(\log n)\) の処理時間は、一部のアルゴリズムにおいてボトルネックとなることがある。例として、有向グラフにおける支配子 (dominator) を計算する TRAJAN の最近のアルゴリズム [10] を挙げる。したがって、マージ可能ヒープをより効率的に処理できれば、このアルゴリズムの計算量を削減できる。
別の例として、PERL, GAREY & EVEN によって最近発表された最適なプレフィックスコードを生成するための効率的なアルゴリズム [5] が挙げられる。最悪ケースの実行時間に表れる \(O(\log n)\) の係数は、優先度付きキューの実装にバイナリヒープを使用することに起因する。
本論文では、ランダムアクセスマシン上で命令あたり \(O(\log \log n)\) の最悪ケース処理時間を持つ優先度付きキューを表現するデータ構造について説明する。必要な記憶容量は \(O(n \log \log n)\) のオーダーである。この構造は、効率的な union-find アルゴリズムのツリー構造と組み合わせて使うことで、最悪ケースの計算量が \(O((\log \log n) \cdot A(n))\)、空間要件が \(O(n^2)\) となるマージ可能ヒープを生成できる。空間要件の改善の可能性は継続的な研究の対象である。
 1.1 論文の構成
1.1 論文の構成
セクション 2 では、効率的な union-find アルゴリズムの説明を含む、いくつかの表記法と背景情報を述べる。セクション 3 では、命令あたり \(O(\log n)\) の処理時間を持つ優先度付きキューの "愚直な" (silly) 実装を示す。この実装を再検討し、その効率を \(O(\log \log n)\) に改善する 2 つの方法を示す。
セクション 4 では、我々の階層化木とそれらの標準的な部分木への分解について説明する。次に、これらの木を用いて命令あたり最悪ケースおよび平均ケースの処理時間が \(O(\log \log n)\) となる優先度付きキューを記述津する方法を示す。セクション 5 では階層化木に対する基本的な操作を実行するアルゴリズムを提示して説明する。これらのアルゴリズムは、アムステルダム大学の R. KAAS & ZIJLSTRA によって書かれた我々の優先度付きキューの PASCAL 実装 [8] に基づいている。完全な階層化木が \(O(\log \log n)\) の時間でどのように初期化されるかについて説明する。セクション 6 では、複数の優先度付きキューを扱わなければならない場合にこの構造がどのように使用できるかについて説明する。後者の状況は、効率的なマージ可能ヒープを実装する場合に生じる。最後にセクション 7 では、他の集合操作問題との関係をいくつか示す。
セクション 4, 5, 6 を通して、この異なるフォントで記述された識別子は PASCAL 実装における同じ識別子の値と意味を表す。
 2. 一般的な背景
2. 一般的な背景
 2.1 命令
2.1 命令
\(n\) を固定の正の整数とする。我々の全体集合は集合 \(\{1,\ldots,n\}\) の部分集合から構成される。我々の全体集合における集合 \(S\) に対して、\(S\) に対して実行される以下の命令を考える:
| MIN | \(S\) の最小要素を計算 |
|---|---|
| MAX | \(S\) の最大要素を計算 |
| INSERT(j) | \(S := S \cup \{j\}\) |
| DELETE(j) | \(S := S \backslash \{j\}\) |
| MEMBER(j) | \(j \in S\) かどうかを計算 |
| EXTRACT MIN | \(S\) から最小要素を削除 |
| EXTRACT MAX | \(S\) から最大要素を削除 |
| PREDECESSOR(j) | \(s \lt j\) における最大要素を計算 |
| SUCCESSOR(j) | \(S \gt j\) における最小要素を計算 |
| NEIGHBOUR(j) | \(S\) における \(j\) の隣接要素 (neighbour) を計算 (後述の定義を参照) |
| ALL MIN(j) | \(S\) から \(e \le j\) のすべての要素 \(e\)を除去 |
| ALL MAX(j) | \(S\) から \(e \ge j\) のすべての要素 \(e\) を除去 |
(命令が正規に実行できない場合、例えば \(S=\emptyset\) の場合の MIN などは適切な処理が取られる)。
数 \(j \in \{1,\ldots,n\}\) の \(S\) における隣接要素とは、\(i-1\) の二進数展開において \(j-1\) と共通する最大の有効桁セグメントを持つ要素 \(i \in S\) である。もし \(S\) の複数の要素がこの記述に当てはまる場合、それらの中で通常の意味で \(j\) に最も近いものが選択される。
\(j\) の隣接は常に \(j\) の先行要素と後続要素 (predecessor and successor) から見つかるが、どちらになるかを事前に予測することは困難である。セクション 3 では、\(j\) の隣接が実際に \(S\) において \(j\) に最も近い要素であるという "幾何学的" 意味について説明する。現時点では以下の例を示す:
例: \(n=16\)、\(S=\{1,5,13,14\}\) とする。対応するに進数表現は 0000, 0100, 1100, 1101 である。4 (0011 に対応) の隣接は 1 であり、一方 15 (1110 に対応) の隣接は 14 である。14 は通常の意味で 13 よりも 15 に近い。
 2.2 優先度付きキュー
2.2 優先度付きキュー
優先度付きキューは単一の集合 \(S \subset \{1,\ldots,n\}\) を表現するデータ構造であり、この集合上で INSERT, DELETE, MIN 命令をオンライン (つまり任意の順序で、かつ各命令は次の命令を読む前に実行される) で実行できる。優先度付きキューが我々の主目的であるが、この時点で言及しておくと、実際には上記の命令レパートリーが我々のデータ構造上でサポートされており、最悪ケースおよび平均ケースの処理時間が命令あたり \(O(\log \log n)\) である (除去される要素あたり \(O(\log \log n)\) の処理時間である最後の二つの命令を除く)。
上記の完全な命令リストを以後拡張レパートリー (extended repertoire) と呼ぶ。
 2.3 Union-Find 問題
2.3 Union-Find 問題
\(\{1,\ldots,n\}\) の任意の分割 \(\Pi=\{A,B,\ldots\}\) について以下の命令を考える:
- FIND(i)
- \(i\) を含んでいる集合を計算する
- UNION(A,B,C)
- 集合 \(A\) と \(B\) の和集合を形成し、この和集合に \(C\) という名前を付ける
これらの 2 つの命令をサポートするデータ構造に特定の名前はない。このような構造を操作する問題は Union-Find 問題として知られている。
よく知られている効率的な Union-Find アルゴリズムは、木構造による集合の表現を使用する。木構造の各ノードは集合の要素に対応し、そのノードがその木の根である場合は集合の名前を指すポインタを持ち、そうでない場合は木構造内の親ノードを指すポインタを持つ。UNION 命令は、より小さい木の根をより大きい木の直接の子ノードにすることで実行される (平衡化; balancing)。FIND 命令を実行するには、要求された要素に対応するノードに直接アクセスし、そのポインタをたどってその木の根が見つかるまで探索する。この過程で遭遇するすべてのノードは根の直接の子孫となるため、それにより皇族の検索での処理時間が削減される。
上記のアルゴリズムがいかに効率的であるかは最近になってようやく確立された。その平均処理時間は当初 \(O(\log \log n)\) (FISHER [6]) や \(O(\log^* n)\) (HOPCROFT & ULLMAN [7] および独立に PATERSON (未発表)) と推定されていたが、最終的な上限と下限 \(O(A(n)\) が TARJAN [9] によって証明された。\(\log^* n\) は関数 \(2^{2^{⋰^{2}}}\) の逆関数、つまり \(\log^* n\) は \(n\) をゼロまで減らすのに必要な 2 を底とする対数の適用回数に等しいことに留意されたい。関数 \(A(n)\) は \(a(0,x)=2x\); \(a(i,0)=0\); \(i \ge 0\) に対して \(a(i,1)=2\); \(a(i+1,x+1)=a(i,a(i+1,x))\) のように定義されるアッカーマン型の関数の逆関数である。そして \(A(n)=\min\{j \,|\, a(j,j) \gt n\}\) である。(この定義は TARJAN の定義と本質的に異なる)。
 2.4 マージ可能ヒープ
2.4 マージ可能ヒープ
マージ可能ヒープとは、それ自体が結合および検索可能な集合で、INSERT, DELETE, MEMBER, MIN 命令をサポートするデータ構造である。すなわち UNION と FIND もサポートされている。マージ可能ヒープは、特定のノードの順序付けされていない子の集合を優先度付きキューで置き換えることによって Union-Find 構造から得ることができる。ここでノードの "値" は、そのノードとその子孫によって形成される集合内の最小要素に等しい。
このような表現では、命令は以下のように実行される:
- UNION
- 要素数が最も少ない構造の根優先度付きキューを、その最小要素に対応する位置でもう一方の構造の根優先度付きキューに挿入される。
- FIND
- まず要素自体から "上向き" に進み、その要素が属する構造の根優先度付きキューを見つける。次に、この根から要素まで戻りながら、経路に沿った優先度付きキューを削除操作によって切断する。その後、これらのキューは根優先度付きキューの (変更されている可能性のある) 最小要素の位置に挿入される。
- MIN
- 構造の根優先度付きキューで MIN 命令を実行するとその最小要素が判明する。この要素に対して FIND 命令を実行することで、その要素が格納されている場所にアクセスできるようになる。
- INSERT & DELETE
- これらの操作は、まず FIND 命令を実行することで優先度付きキューの挿入と削除に帰着される。MEMBER についても同様である。
このようにすることで、命令の平均処理時間は、使用されている優先度付きキュー命令の処理時間の \(A(n)\) 倍となる。後者の時間が \(O(\log n)\) 以下に削減されない限り、提案されているマージ可能ヒープの表現は非効率的と考えるべきである。なぜなら、マージ可能ヒープに対して \(O(\log n)\) の構造 (順序付けされていない葉を持つ 2-3 木 [1]) が知られているためである。我々の新しい効率的な優先度付きキューを使用することで、提案されたスキームは (時間に関して言えば) 従来の方法よりも効率的になる。空間要件についてはセクション 6 を参照。
 3. \(O(\log n)\) の処理時間を持つ "愚直な" 優先度付きキュー
3. \(O(\log n)\) の処理時間を持つ "愚直な" 優先度付きキュー
 3.1 構造
3.1 構造
このセクションで述べるスキームは、主に次のセクションで説明するより複雑な構造に対して実行される操作の背後にある考えを説明するために設計されている。
このセクションでは \(n=2^k\) と仮定する。高さ \(k\) の固定された二分木を考える。この木の \(2^k=n\) 個の葉は、左から右へ自然順序数で \(1..n\) を表現する。したがって、葉は集合 \(S\) の潜在的な要素を意味する。0 から \(n-1\) まで数えたとすると、この順序は数の二進数表現を根から葉への経路の符号として解釈したものに他ならない。二進桁は左から右へ読み取られ、0 は "左へ"、1 は "右へ" を意味する。
木内の各ノードに対して、その親ノードと、その左辺および右辺の子ノードをリンクする 3 つのポインタが関連付けられている。さらに、各ノードは 1 ビットのマークフィールドを持つ。
部分集合 \(S \subseteq [1..n]\) は、\(S\) の要素に対応するすべての葉と、これらの葉から木の根への経路上のすべてのノードをマークすることで表現される。Diagram 1 を参照。
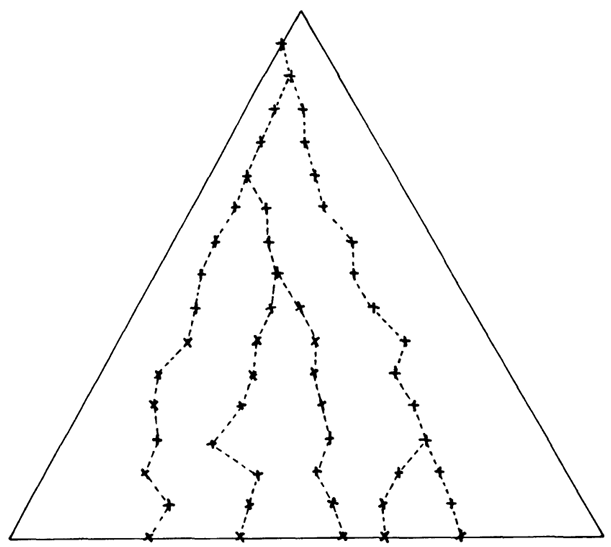
この表現を用いることで、セクション 2 にリストされている操作は、処理される各項目につき \(O(k)=O(\log n)\) の時間で実行できることが容易にわかる。(ALLMIN と ALLMAX 操作は複数の項目を削除する可能性があることに注意。)
我々は以下にアルゴリズムの概略を提示する:
- INSERT(i)
- 葉 \(i\) と、葉 \(i\) から根への経路上のすべてのノードを、既にマークされたノードに遭遇するまでマークする。
- DELETE(i)
- 葉 \(i\) と、葉 \(i\) から根への経路上のノードを、マークされた 2 つの子を持つ経路上の最下位ノードまで (ただしそれは含まない) マークを削除する。
- MEMBER(i)
- 葉 \(i\) がマークされているかどうかを検査する。
- MIN (MAX)
- 根から葉へ進み、常に最左端 (最右端) の存在する子を選択する。
- EXTRACT MIN (EXTRACT MAX)
- MIN (MAX) の後に DELETE を実行。
- ALLMIN(j)
- while MIN \(\le j\) do EXTRACTMIN od
- ALLMAX は同様に定義される。
- PREDECESSOR(j)
- 葉 \(j\) から根へ進み、\(j\) を右側子孫として持つノードで左側の子がマークされているものに遭遇するまで進む。この左側の子から葉へ進み、常に最右端の存在する子を取る。
- SUCCESSOR(j) は同様に定義される。
PREDECESSOR と SUCCESSOR 以外のすべての命令は、マークされていない葉から根への経路上の最も低いマークされたノード、またはマークされた葉から根への経路上の最も低い分岐点 (つまり両方の子がマークされているノード) を使用することに注意。最も低い "興味深い" ノードを超えて登らない類似の命令として以下の命令がある:
- HEIGHBOUR(j)
- 葉 \(j\) から進んで、このノードの "もう一方" の子がマークされている最下位のノードまで進む。このもう一方の子が左側の子である場合、このノードから葉へ進み、常に最右端のマークされた葉を選択する。そうでなければ、常に最左端のマークされた葉を選択する。
さらに、この集合を双方向連結リストを用いて表現し、マークされた各葉にリスト内の対応するエントリ (へのポインタ) を格納すると、NEIGHBOUR 命令の呼び出しに続いてリストを 1~2 ステップ実行するだけで PREDECESSOR や SUCCESSOR 命令の呼び出しを実行するのに十分である。
NEIGHBOUR 命令の説明から、ある数の隣接要素がどのような意味で \(j\) に "最も近い" 存在要素であるかは明らかである。つまり、隣接要素は可能な限り多くの共通祖先を持ち、この条件で隣接要素が明確に定義されない場合は、隣接要素は最下位共通祖先の他方の子孫であり、可能な限り \(j\) に近く発達したものである。
 3.2. 時間効率の改善
3.2. 時間効率の改善
上記の記述から、我々の "愚直な" 構造が命令あたり \(O(\log n)\) の処理時間で拡張レパートリーをサポートすることは明らかである。双方向連結リストを "追加の" 表現として使用すると、INSERT, DELETE, NEIGHBOUR は呼び出し時にツリーを操作する距離に比例した時間を要するが、一方 MIN と MAX は定数時間を要する。
残りの命令は "複合的" である。この観察は効率を向上させる道筋を開く。木を高く上向きに登らないことで節約された時間は、単一ノードでより多くの作業を実行するために使用できる。例えば、各ノードが固定数の代わりに存在する子の線形リストを使用することになれば、\(O(k)\) の処理時間を阻害することなく、根から葉へ向かって増加する分岐次数を持つ木を容易に実現できる。\(k! = n\) 個の葉を含む分岐次数 \(2,3,4,\ldots,k\) の木を使用することで、\(O(k)\) 時間で \(O(k!)\) サイズの優先度付きキューを維持できる。したがって上記の設定は \(O(\log n / \log \log n)\) の優先度付きキューをもたらし、これはすでに以前よりも優れている。
しかし改善の余地はまだ多い。単一ノードで実行したい操作自体が、優先付きキュー操作である。したがって、バイナリヒープを使用することで、分岐次数 \(2,4,8,\ldots,2^k\) に対応でき、これによりサイズ \(O(2^{k^2/2})\) の優先度付きキューが得られ、処理時間は \(O(\sqrt{\log n})\) に削減される。
どちらの変更においても空間要件は \(O(n)\) のままであることに注意。これは、§4 で述べる構造については当てはまらない。
"分割統治" 戦略によれば、各ノードで我々が説明しているのと同じ効率的な構造を使用すべきである。これは次のアプローチを示唆している。全体集合 \([1..n]\) をサイズ \(\sqrt{n}\) の \(\sqrt{n}\) 個のブロックに分割する。各ブロックはサイズ \(\sqrt{n}\) の優先度付きキューとされ、ブロック自体もこのサイズの別の優先度付きキューを形成する。INSERT を実行するには、まず挿入される要素を含むブロックがすでに存在要素を含んでいるかどうかを検査する。もし含まれていれば、新しい要素がブロックに挿入される。含まれていない場合、その要素がブロックの先頭要素として挿入され、ブロック全体が "ハイパーキュー" に挿入される。DELETE 命令も同様に実行できる。
ブロック内の最初の要素の挿入と最後の要素の削除がブロックのサイズと無関係に定数時間で実行できるような方法で上記のアイディアを実装できると仮定すると、上記の説明は実行時間に対して \(T(n) \le T(\sqrt{n}) + 1\) という型の漸化式をもたらし、これは \(T(n) \le O(\log \log n)\) という解を持つ。
この "愚直な" 表現を改善し、再び同じ効率をもたらす別の方法は以下のように考えられる。前述のように、"難しい" 命令は木を上向きに走査して最も低い "興味深い" ノード (例えば分岐点) まで到達し存在ノードの経路に沿って下向きに進むことで処理される。
これらの走査を "レベル上の二分探索" 戦略によって実行できれば、処理時間は \(O(k)\) から \(O(\log k) = O(\log \log n)\) に短縮される。同様の考え方は AHO, HOPCROFT & ULLMAN [2] によって提示された最下位共通祖先問題の特殊なケースの効率的な解法にも用いられている。
読者は、本論文の続きを読む際には両方のアプローチを念頭に置くべきである。
 4. 階層化木構造
4. 階層化木構造
 4.1. 清純部分木と静的情報
4.1. 清純部分木と静的情報
このセクションでは \(h\) を固定の正の整数とし、\(k=2^h\)、\(n=2^k\) とする。根 \(t\) を持ち \(n\) 個の葉を持つ高さ \(k\) の固定二分木 \(T\) を考える。
\(1 \ge j\) に対して \(2^d \, | \, j\) かつ \(2^{d+1} \, \not | \, j\) となるような最大の数 \(d\) を \({\rm RANK}(j\)) と定義する (訳注: \(a \, | \, b\) で「\(a\) は \(b\) を割り切る」という意味; \(2^d|j \Rightarrow j \bmod 2^d = 0\))。例えば \({\rm RANK}(12) = 2\)、\({\rm RANK}(17) = 0\) である。慣例により \({\rm RANK}(0) = h + 1\) とする。
\(j \gt 0\)、\({\rm RANK}(j)\) \(=\) \(d\)、\(j-2^d\) \(\gt\) \(0\) の場合、\({\rm RANK}(j)\) \(\lt\) \({\rm RANK}(j+2^d)\) かつ \({\rm RANK}(j)\) \(\lt\) \({\rm RANK}(j-2^d)\)、さらに \({\rm RANK}(j+2^d)\) \(\ne\) \({\rm RANK}(j-2^d)\) となることに注意。
\(T\) 内のノード \(v\) のレベルとは、\(T\) の葉から \(v\) までの経路の長さである。\(v\) のランクは \(v\) のレベルのランクである。葉のランクは \(h+1\) に等しく、頂点のランクは \(h\) に等しいことに注意。他のすべてのノードはより低いランクを持つ。葉の位置とは、その葉によって表される集合 \(\{1,\ldots,n\}\) 内の番号である。内部ノード \(v\) の位置は、その左側の子の最右端の子孫の葉の位置に等しい。この番号は、\(v\) から根までの経路に沿って木を分割することで生じる 2 つの部分の境界がどこにあるかを示す。
\(T\) の正準部分木 (CS; canonical subtree) とは、ランク \(\ge d\) のノードを根とする高さ \(2^d\) の二分部分木である。数値 \(d\) は CS のランクと呼ばれる。CS の根とそのすべての左側 (右側) の子孫から構成される CS の部分木は、左 (右) 正準部分木と呼ばれる。
完全木は明らかにランク \(h\) の正準部分木である。これは、ランク \(h-1\) の上位木と、同じランクの \(2^{k/2}\) (\(=\sqrt{n}\)) の下位木に分解される。これは前のセクションで提示した "サブキュー" の "ハイパーキュー" という "分割統治" アプローチに従っている。
\(T\) の任意のノード \(v\) に対して \(v\) の正準部分木と呼ばれる以下の部分木が関連付けられる。\(d={\rm RANK}(v)\) とする。
- UC(v)
- \(v\) を葉に持つランク \(d\) の唯一の正準部分木。
- LC(v)
- \(v\) を根に持つランク \(d\) の唯一の正準部分木。
\({\rm UC}(v)\) は \(v\) が根の場合には定義されず、\({\rm LC}(v)\) は \(v\) が \(T\) の葉の場合は定義されないことに注意。\(d=0\) のとき、\({\rm UC}(v)\) と \({\rm LC}(v)\) は 3 つのノードで構成される。さらに、\({\rm UC}(v)\) の根のランクと \({\rm LC}(v)\) の葉のランクは \(d\) より高いことにも注意。
\({\rm LC}(v)\) の左 (右) 正準部分木は \({\rm LLC}(v)\) (\({\rm RLC}(v)\)) と表記される。\({\rm LC}(v)\) と \({\rm UC}(v)\) のうち \(v\) を含む半分は一緒になって \(v\) の到達範囲 (reach) \({\rm R}(v)\) を形成する。\(v\) に格納される動的情報は、その到達範囲内で起こることにのみ依存する。頂点の到達範囲は完全な木であり、葉の到達範囲は葉の集合である。Diagram 2 に説明図を示す。
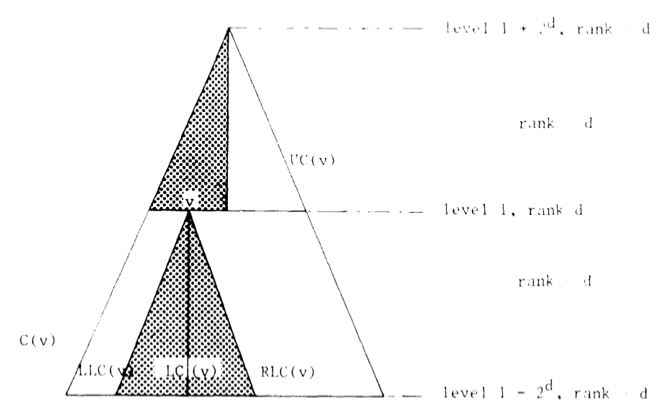
ランク \(d\) の内部ノード \(v\) の到達範囲は、明らかに \(C(v)\) と表記されるランク \(d+1\) の正準部分木の部分木である。\(v\) は \(C(v)\) の中心レベル (center-level) に位置すると言い、さらに、\(v\) はその到達範囲 \(R(v)\) の中心 (center) と呼ばれる。
ノード \(v\) と各 \(j \le h\) に対して、ランク \(ge j\) を持つ \(v\) の最も低い真の祖先を \({\rm FATHER}(v,j)\) と表記する。\({\rm FATHER}(v,h)\) は明らかに \(T\) の根 \(t\) に等しく、一方 \({\rm FATHER}(v,0)\) は \(v\ne t\) であれば) \(T\) 内の \(v\) の「真の」親である。各ノードには \(h\) 個のポインタ配列 father[0:h-1] があり、father[i] は \(v\) のランク \(i\) の親となる。\({\rm FATHER}(v,n)\) は常に木の根となるため、この要素は含める必要がない。これらのポインタにより、木内の経路に沿って \(O(h)\) ステップで所定のレベルまで移動することができる。さらに、正準部分木 \(U\) の根とその葉の一つが与えられれば、これら 2 つを含む最小範囲の中心まで 1 ステップで進むことができ、その範囲は \(U\) に完全に含まれることになる。
ノードの静的情報には、その位置だけでなく、内部ノードの場合はそのランクとレベルも含まれる。静的情報の割り当てと初期化は \(O(n \log \log n)\) 時間で実行できる。詳細は次のセクションで説明する。
 4.2. 動的情報
4.2. 動的情報
内部ノードの動的情報は 4 つのポインタ l_min, l_max, r_min, r_max と、plus, minus, undefined の値を取ることのできる指示フィールド ub を用いて格納される。葉における動的情報は 2 つのポインタ successor, predecessor, ブール値の present で構成される。
\(S \subset \{1,\ldots,n\}\) を我々の階層化木内で表現される集合とする。\(S\) のメンバーに対応する葉と、木内のそれらの祖先がすべてを present と呼ぶ。present ノードは我々の愚直な構造でマークされたノードと全く同じである。present ノードはアクティブになることができ、この場合その情報フィールドには意味のある情報が含まれる。非アクティブな内部ノードのこれらのフィールド値は、l_min = nil, l_max = nil, r_min = nil, r_max = nil, ub = undefined である。非アクティブな葉では、これらの値は predecessor = nil, successor = nil, present = false である。アクティブな葉 \(v\) の場合、これらのフィールドの意味は次のようになる:
predecessor- 存在する場合は \(S\) 内の \(v\) に対応する番号の先行要素に対する葉を指す。そうでない場合は
predecessor = nilとなる。 successo- 先行要素と同様
present-
= true
分岐点 (branchpoint) とは、2 つの present な子を持つ内部ノードであることを思い出されたい。
\(v\) を内部ノードとし、\(C(v)\) の頂点を \(t\) と表記する。\(v\) がアクティブな場合、その動的情報フィールドは以下の意味を持つ:
l_min- \({\rm LLC}(v)\) の最左端の present 葉を指す (そのようなノードが存在する場合)。存在しなければ
l_min = nil。 l_max- \({\rm LLC}(v)\) の最右端の present 葉を指す (同様)
r_min- \({\rm RLC}(v)\) の最左端の present 葉を指す (同様)
r_max- \({\rm RLC}(v)\) の最右端の present 葉を指す (同様)
ub- \(v\)t と \(t\) の間に分岐点が存在する場合は
plus、そうでない場合はminus。= plus
\(v\) がアクティブな内部ノードである場合、それは present であり、したがって \({\rm LC}(v)\) は少なくとも 1 つの present 葉を含む。これは、4 つのポインタがすべて nil に等しいアクティブな内部ノードを持つことが不可能であることを示している。
前のセクションで示唆されたように、最初の要素を挿入したり最後の要素を削除したりするために必要な時間は木のサイズに依存しないはずである。これは、そのアクティブ性が必要でない限り、present ノードがアクティブになることを防ぐことで実現される。これは以下のように表現される。
適正性条件 (properness condition): \(v\) を present な内部ノードとする。このとき、\(v\) がアクティブであるのは、\(v\) の到達範囲の内部に分岐点が存在する場合、かつその場合に限る (すなはち \(C(v)\) の頂点でも葉でもない \(R(v)\) 内の分岐点 \(u \in R(v)\) が存在する)。
葉がアクティブであるのは、それが present である場合、かつその場合に限る。根がアクティブであるためには集合が空でなければならない。
(実際には \(S=\emptyset\) の場合は退化的であり、いくつかのプログラミング上の問題を引き起こすが、実際には \(n\) を \(S\) の永続的なメンバーとして含めることで回避できた。)
内部ノード \(v\) が非アクティブだが present な場合、\(R(v)\) の頂点 \(t\) から \(R(v)\) に含まれる \(C(v)\) の唯一の present 葉 \(w\) へ至る present ノードの唯一の経路が存在する。我々のアプローチでは \(t\) から \(w\) へ、またはその逆方向へ、\(v\) を訪問することなく進むことができ、\(v\) に情報を格納することは無意味になる。
ある正準半木 (canonical half-tree) が 2 つの present 葉を持つ場合、その中心レベルにあるすべての present ノードはアクティブである。また、ランク \(d\) のノード \(v\) がアクティブの場合、\({\rm FATHER}(v,d)\) もアクティブである。これらの主張の検証は読者への演習として残しておく。
集合 \(S \subset \{1,\ldots,n\}\) は次のように表される。まず、\(S\) の要素に対応する葉とそのすべての祖先が present であると宣言される。次に、適正性条件を使用してどの present ノードがアクティブになるかを計算する。最後に、すべてのアクティブおよび非アクティブノードの動的フィールドにそれらの適切な値が与えられる。結果として得られる情報内容は集合 \(S\) の表現と呼ばれる。この表現が唯一であることは読者自身で確認することとして残しておく。
(我々の実際のプログラムでは、この構造は \(S=\{n\}\) で初期化され、他のすべての集合の表現は拡張レパートリーから命令シーケンスの実行結果となる。)
適正な情報のない例を Diagram 3 に示す (明らかな双方向連結リストデータは省略)。記号 \(\sim\) は nil または undefined を表す。
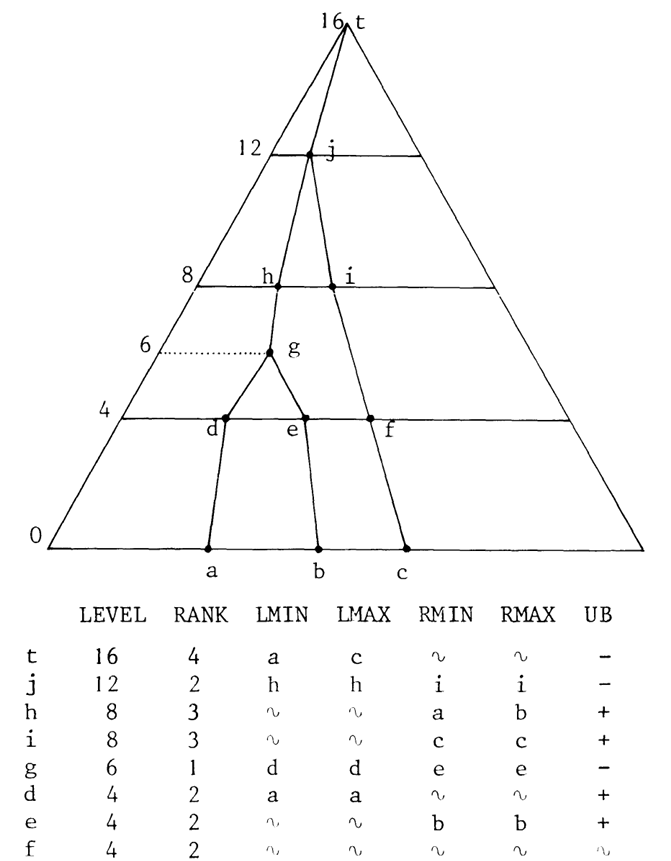
 5. 階層化木構造における操作
5. 階層化木構造における操作
階層化木内の特定のフィールドに値を割り当てることで集合 \(S\) の表現を記述したら、次のステップではセクション 1 で述べた集合操作が
処理時間 \(O(h) = O(\log \log n)\) が実現され;
表現の構造を維持、つまり適正性条件が有効なまま
であるように実行する方法を示す。
さらに、静的情報と動的情報の正当な初期状態が適切な時間と空間 (すなわちどちらも \(n \log \log n\) のオーダー) で作成できる方法を示さなければならない。
このセクションでは、木の葉によって形成される双方向連結リスト構造を操作するために必要な自明な操作については考慮しない。さらに常に \(n \in S\) と仮定する。ドライバは初期化時にこの要素を挿入し、この要素が \(S\) から削除されないように配慮する。
 5.1. 初期化
5.1. 初期化
初期化は、事前順序による単一の木の横断中に行われる。ノードが処理されるとき、その親ノードへのポインタと位置、そして内部ノードの場合はランクとレベルが適切なフィールドに格納される。必要な計算は以下の関係に基づいている:
頂点の親は
nilである。\({\rm RANK}(w)=d\) となるようなノード \(w\) の直系の子 \(v\) の親ノードは \[ \begin{eqnarray*} {\rm FATHER}(v,j) & = & w & \quad \text{for $j \le d$} \\ {\rm FATHER}(v,j) & = & {\rm FATHER}(w,j) & \quad \text{for $j \gt d$} \end{eqnarray*} \] を満たす。ノード \(w\) は、木横断処理を実行する再帰手続きのパラメータfathを使用することで、\(v\) の処理中にアクセス可能である。ノードのレベルは、その親ノードのレベルより 1 小さい。
レベル \(i \gt 0\) における最左端ノードの位置は \(2^{i-1}\) に等しく、レベル \(i\) における他の任意のノードの位置は \(2^i\) 前に処理されたレベル \(i\) における最後のノードの位置に等しい。葉はその位置の昇順で処理される。
ノードのランクはレベルのみに依存し、サイズ \(k=\log n\) の事前計算されたテーブルを使用して格納できる。
必要な 2 のべき乗を反復加算によって事前計算しておくと、上記の関係は、乗算やビット操作などの "非正当な" (illegitimate) 命令を使用せずに、処理されるノードあたり \(O(\log \log n)\) 時間で静的構造を初期化する方法を示している。\(2n-1\) 個のノードが存在するため、初期化には \(O(\log \log n)\) 時間がかかることが分かる。各ノードに必要な空間が \(O(\log \log n)\) であるため、空間は \(O(n \log \log n)\) となる。
加算のみを使用して \(O(\log n)\) 時間でランクを事前計算することは、読者への演習として残しておく。
 5.2. 操作
5.2. 操作
拡張命令レパートリーは (双方向連結リスト操作を除き)、insert, delete, neighbour という 3 つの基本演算で表現できる。これらの演算はそれぞれ線形再帰手続きで記述される。手続きはランク \(h\) の完全な木に対して呼び出される。正準部分木に対して呼び出された場合、手続きはランクに依存しない定数時間内で終了するか、ランクが 1 つ小さいトップまたはボトムの正準部分木を 1 回呼び出し、その前後にランクに依存しない定数時間の命令シーケンスを実行する。ランク 0 の部分木への呼び出しは、手続きのそれ以上の再帰呼び出しなしに終了する。前述の主張は手続き本体の検査によって検証できるが、そこから各手続きの実行時間が \(h = \log \log n\) のオーターであることが直接的に導かれる。正しい構造の維持に関しては、エラーなく動作する PASCAL 実装を参照する。さらに、アルゴリズムの正しさは再帰帰納法に基づくより非形式的なアプローチの一つを使用して証明できると感じているが、そのような証明はこれまで与えられていない。このアプローチは実装開発のデバッグ段階で成功裏に使用された。正しさの証明に関する研究を促進するために、上記の方針に従って私の手続きの正しさを説得力を持って証明した最初の人に 10 ドル (US $10.00) の賞金を授与する。
アルゴリズムの実行において、根 \(t\) と葉 \(v\) を持つ CS があり、\(v\) の方向で \(t\) のフィールド、すなわち \(v\) が \(t\) の左側の子孫である場合の \(t\) の左側のフィールドなどを調べたり変更したりしたいという状況が頻繁に生じる。\(t\) の特定の子孫が左側の部分木にあるか右側の部分木にあるかを判断するには、2 つのノードの位置を比較するだけで十分である。一般に以下が成り立つ:
\(t\) の子孫 \(v\) が左側の子孫である場合、\(v\) の位置は \(t\) 位置より大きくない場合のみである。
実際、ノードの位置は、子孫の方向性についてこの簡単なテストを容易にするために導入された。
挿入、削除、隣接は以下の基本操作を使用する。
myfields(v,t)- \(v\) 方向で \(t\) のフィールドへのポインタを返す。このポインタは
fieldptr型である。 mymin(v,t)- \(v\) の方向で \(t\) の \({\rm min}\) フィールド値を返す (これはたまたまポインタである)。
mymax(v,t)- \({\rm max}\) フィールドについて同様。
yourfileds(v,t),yourmin(v,t),yourmax(v,t)- 他の方向で \(t\) のフィールドの対応する値を返す。
minof(t)- \(t\) がアクティブの場合、\(t\) の 4 つの指示されたフィールドの最左端の値を返し、そうでなければ
nilを返す。 maxof- 最右端の値について同様。
型 ranktp は部分範囲 0..h である。
最後に、手続き clear は、その引数の動的フィールドに非アクティブ状態に対応する値を設定する。手続き内で言及される識別子はほとんどが "ノードへのポインタ" 型 (ptr) である。ここで "ノード" は前のセクションで言及されたフィールドを含むレコード型である。
 5.2.1.
5.2.1. insert 手続き
insert は、挿入されるノードの隣接ノードへのポインタ値を結果としてす関数手続きである。この隣接ノードは、その後にノードを双方向連結リストに挿入するために使用される。(完全木ではない CS の場合に隣接の意味を暗黙的に一般化していることをに注意)。
insert は値渡しで呼び出される 5 つのパラメータがある。その手続きのヘッダは次の通りである:
function insert (leaf, top, pres: ptr; no branchpoint: boolean; order: ranktp): ptr;パラメータの意味は次の通り:
order- 手続きが呼ばれた CS のランク
leaf- 挿入されるノード
top- 手続きが呼ばれた CS のルート
pres- トップの葉と同じ利便性を持つ、手続きが呼び出された CS の present 葉
nobranchpoint- 手続きが呼び出された CS の葉側に分岐ポイントが含まれていない場合にのみ true
一見するとパラメータ pres は myfields(leaf,top) から導出できるため不要に見える。しかし、対象とする CS が上位の CS のトップ CS である場合、top のフィールドは leaf のレベルよりはるかに下位のノードを参照するため、結果としてそれらの値が誤って解釈される可能性がある。この危険性 (我々のデータ構造の初期バージョン [3] では "動的アドレス変換" によって対処される) は、ノードアドレスに対するビット操作命令では解決できない。なぜなら、それらの実行時間は長さ \(\log n\) に応じて課金 (charge) されるべきであり、これは明らかに許容範囲を超える。実際にこの "間違い" が我々の構造の実装過程で発見された主要なバグの原因であった。
対象とする CS の leaf 側に present 葉が含まれていない場合 (pres = nil)、insert の呼び出しはそれ以上の再帰呼び出しを起こすことなく終了する。そうでなければ、ノード hl = FATHER(leaf,order-1) と hp = FATHER(pres,order-1) が計算される。nobranchpoint が true の場合、hp はアクティブではないもの present であり、この場合、特別な処理を実行する必要がある。この場合、hl は present であるのは hl = hp の場合のみであり、この等価性に応じて hp と hl の右 (right; 適切な?) フィールドを "アクティブ化" した後、ボトムコール
insert(leaf, hl, mymin (leaf, hl), true, order-1)またはトップコール
insert(hl, top, hp, true, order-1)が実行される。
この状況では、手続きは値として pres を返す。
nobranchpoint が false である場合、hl が present であるのは hl がアクティブである場合のみであり、アクティブかどうかは ub フィールドを調べることで判定される。hl がアクティブな場合、ボトムコール
insert (leaf, hl, mymin (leaf, hl), mymin (leaf, hl) = mymax (lef, hl), order-1)が実行され、その値が insert の結果として返される。そうでなければ nobranchpoint := (hp↑.ub = minus) を設定し、hl と hp のフィールドをアクティブ化した後、トップコール
insert (hl, top, hp, nobranchpoint, order-1)が実行される。この呼び出しは結果としてトップツリーの hl の隣接要素が nb で生成され、hl と nb の位置の比較結果に応じて、挿入の値は minof(nb) または maxof(nb) に等しくなる。
これらの処理の後、現在の呼び出しがボトム CS への呼び出しである場合、top ののフィールドを調整する必要があるかもしれない。これは、order が top のランクに等しい場合のみである。この観点から、完全な木はボトム CS を見なす必要があり、これは我々の構造に関する初期報告 [3, 4] で行われたようなレベルがリーフからトップに向かって逆順に番号付けされるのではなく、リーフからトップに向かって番号付けされる理由を説明している。
insert の初期呼び出しは次のようになる:
insert (pt, root, mymin (pt, root), mymin (pt, root) = mymax (pt, root), h)ここで root はアクティブであり、pt は present 葉ではないと仮定する。(これらの条件はドライバによって強制される。)
次に、insert の完全な PASCAL テキストを示す。
function insert(leaf, top, pres : ptr;
nonbranchpoint : boolean; order : ranktp) : ptr;
var hl, hp, nb : ptr; fptr : fieldptr;
begin if pres = nil then
begin fptr:= myfields(leaf, top);
with fptr↑ do
begin min:= leaf; max:= leaf end;
if leaf↑.position <= top↑.position then
insert:= top↑.right↑.min
else insert:= top↑.left↑.max
end else
begin hl:= leaf↑.fathers[order - 1];
hp:= pres↑.fathers[order - 1];
if nobranchpoint then
if hp <> hl then
begin fptr:= myfields(leaf, hl);
with fptr↑ do
begin min:= leaf; max:= leaf end;
fptr:= myfields(pres, hp);
with fptr↑ do
begin min:= pres; max:= pres end;
hl↑.ub:= plus; hp↑.ub:= plus;
nb:= insert(hl, top, hp, true, order - 1);
insert:= pres
end else
begin fptr:= myfields(pres, hp);
with fptr↑ do
begin min:= pres; max:= pres end;
hp↑.ub:= minus;
insert:= insert(leaf, hl, mymin(leaf, hl),
true, order - 1)
end
else if hl↑.ub <> undefined then
insert:= insert(leaf, hl, mymin(leaf, hl),
mymin(leaf, hl) = mymax(leaf, hl), order- 1)
else
begin fptr:= myfields(leaf, hl);
with fptr↑ do
begin min:= leaf: max:= leaf end;
nobranchpoint:= hp↑.ub = minus;
hl↑.ub:= plus; hp↑.ub:= plus;
nb:= insert(hl, top, hp,
nobranchpoint, order- 1);
if hl↑.position <= nb↑.position then
insert:= minof(nb) else insert:= maxof(nb);
end;
fptr:= myfields(leaf, top);
if top↑.rank = order then with fptr↑ do
if leaf↑.position < min↑.position
then min:= leaf else
if leaf↑.position > max↑. position
then max:= leaf
end;
end 5.2.2.
5.2.2. delete 手続き
手続き delete は値を返さない。6 個のパラメータを持ち、最初の 3 つは値渡しで、残りは参照渡しである (結果渡しでも同様だが、これは PASCAL では不可能である)。手続きのヘッダは以下の通り:
procedure delete (leaf, top: ptr; order : ranktp;
var pres 1, pres 2: ptr;
var nobranchpoint: boolean);値パラメータの意味は以下の通り:
leaf- 削除される葉
top- 対象となる CS のルート
order- 対象となる CS のランク
残りのパラメータは delete 呼び出し後に以下の意味を持つ。
pres 1, pres 2- 対象となる CS 内の present 葉であり、そのうち一つが
leafの隣接要素 (以下の説明を参照) nobranchpointtopからpres 1への経路上に分岐点が発生していない場合に限り true
delete の呼び出しは、leaf とその祖先を再開の分岐点まで非 present 状態にする必要があるが、その過程で異なる経路上にあるアクティブだった他のノードを非アクティブにする必要がある場合がある。この条件が満たされる限り、nobranchpoint は true のままである。
再開の分岐点のもう一つの子から可能な限り下方向に進むと隣接要素に到達する。しかし、常に最も遠い present ノードを選択すると、木内の leaf の極値要素 (extreme) と呼ばれるノードに到達する。極値は leaf の "二進近似" としては隣接要素と同等だが、通常の意味では限りなく遠いノードである。
削除呼び出し後、pres 1 と pres 2 は leaf の位置にしたがって順序付けされた隣接要素と極値要素である (つまり pros1↑.pos ≦ pres 2↑.pos)。最下位の分岐点が top と等しい場合、delete は内部呼びなしで終了する。この時点で pres 1 と pres 2 は yourmin(leaf, top) と yourmax(leaf, top) の値で初期化され、これら 2 つの値が等しい場合 nobranchpoint は true に設定される。
これらの値の更新は、終了した呼び出しがトップ呼び出しかボトム呼び出しか (delete の現在のバージョンでは認識されている) に応じて行われる。最後の呼び出しがトップ呼び出しだった場合、pres 1:= minof(pres 1); pres 2:= maxof(pres 2) となり、それらの等価性が再度テストされ、nobranchpoint を true のままにするかが決定される。true のままにする場合、以前に pres 1 が指していたノードは非アクティブ化される。
最後の呼び出しがボトム呼び出しだった場合、以前のトップでの ub フィールドと、このノードでの pres 1 から離れた位置へのポインタを調べて、このノードまたはその上位に分岐点が存在するかを判断する。分岐点が存在しない場合、以前のトップは非アクティブ化されます。
現在のトップのフィールドは、現在の呼び出しがボトム呼び出しの場合にのみ調整される。
delete の初期呼び出しは以下のようになる:
delete(pt, root, h, pres 1, pres 2, nobranchpoint);ドライバは pt が present 葉であり、かつ唯一の present 葉ではなことを確認する。delete の完全なテキストを以下に示す。
procedure delete(leaf, top : ptr; order : ranktp;
var pres1,pres2: ptr; var nobranchpoint : boolean);
var fptr : fieldptr; hl, hp : ptr;
begin fptr:= myfields(leaf, top);
with fptr↑ do if min = max then
begin min:= nil; max:= nil;
pres1:= yourmin(leaf, top);
pres2:= yourmax(leaf, top);
nobranchpoint:= pres1 = pres2
end else
begin hl:= leaf↑.fathers[order - 1];
if minof(hl) = maxof(hl) then
begin delete(hl, top, order - 1,
pres1, pres2, nobranchpoint);
clear(hl); hp:= pres1;
if nobranchpoint then hp↑.ub:= minus;
pres1:= minof(pres1); pres2:= maxof(pres2);
if nobranchpoint then
if (pres1 = pres2) then clear(hp)
else nobranchpoint:= false
end else
begin delete(leaf, hl, order - 1,
pres1, pres2, nobranchpoint);
if nobranchpoint then
if (hl↑.ub = minus)
and (yourmin(pres1, hl) = nil)
then clear(hl)
else nobranchpoint:= false
end;
if top↑.rank = order then
if min = leaf then min:= pres1 else
if max = leaf then max:= pres2
end
end; 5.2.3.
5.2.3. neighbour 手続き
関数 neighbour は値渡しで呼び出される 5 つ引数を持つ。これらの引数の意味は insert の引数とほぼ同じだが、、pres は pmin と pmax のペアに置き換えられる。
neighbour は present 葉と非 present 葉の両方に対して呼び出すことができる。これは、位置に関する高価なビット操作を行わない限り、近傍要素が与えられた引数の先行者か後続者かを判断できないという事実によって正当化される。
pmin と pmax は、対象とする CS の leaf 側における最左端と最右端の present 葉である。
neighbour は以下の場合に内部呼び出しなしに終了する:
pmin = nil;この場合、隣接要素は木の反対側にある。pmin = pmax = leaf;同様。leafがpmin - pmax区間の外にある; この場合、隣接要素は通常の意味で木の内部構造を調べることなく 2 つのうち最も近い方を返す。
ショートカット iii は手続き neighbour に固有である。これらの状況のいずれも発生しない場合、再帰呼び出しが実行される。この内部呼び出しは leaf と top の間の中心レベルのノード hl が present でない場合 (この状況では非アクティブと同等)、または leaf が hl の唯一の present 子孫である場合はトップ呼び出しとなる。それ以外の場合はボトム呼び出しが実行される。
neighbour の初期呼び出しは以下のように記述される。
neighbour(pt, root, mymin(pt, root), mymax(pt, root), h)空の木、または唯一の present 葉に対して呼び出された場合、neighbour はその結果として nil を返す。ドライバはこれらの退化的なケースが処理されるように配慮する。
neighbour のテキストを以下に示す:
function neighbour(leaf, top, pmin, pmax : ptr;
order : ranktp) : ptr;
var y, z, nb, hl : ptr; pos : 1..n;
begin pos:= leaf↑.position;
if (pmin = nil)
or ((pmin = pmax) and (pmin = leaf)) then
if pos <= top↑.position
then neighbour:= yourmin(leaf, top)
else neighbour:= yourmax(leaf, top)
else if pmin↑.position > pos then neighbour:= pmin
else if pmax↑.position < pos then neighbour:= pmax
else
begin hl:= leaf↑.fathers[order - 1];
y:= minof(hl); z:= maxof(hl);
if ((y = z) and (y = leaf))
or (hl↑.ub = undefined) then
begin nb:= neighbour(hl, top,
pmin↑.fathers[order -1], pmax↑.fathers[order -1],
order - 1);
if hl↑.position < nb↑.position
then neighbour:= minof(nb)
else neighbour:= maxof(nb)
end
else neighbour:= neighbour(leaf, hl,
mymin(leaf, hl), mymax(leaf, hl), order - 1)
end
end; 5.2.4. 手続きに関するいくつかの中期
5.2.4. 手続きに関するいくつかの中期
手続き
insert,delete,neighbourはすべてその内部呼び出しがボトム呼び出しであるという性質を持つ。この場合、完全な木も下位木であるとみなす。この観察は KAAS & ZIJLSTRA [8] によるものである。ランク \(d\) のノードでは、ランク \(d\) の親ポインタは手続きによって検査されることはない。これは、それらの値が内包する再帰呼び出しのローカル変数のスタックに保持されているという事実に起因する。特に、\(d\) 次の呼び出しでは対象とする CS 内に (
topを除く) すべてのノードの \(d\) 次ランクの親がパラメータtopに渡される。これらのポインタに必要な空間を省略することで、必要な記憶領域を定数倍削減できる可能性がある。
 6. 階層化木の応用
6. 階層化木の応用
このセクションでは、オフサイズ優先度付きキュー (すなわち \(n\) が \(2^{2^h}\) の形ではない) の表現と、多数の同じサイズの優先度付きキューを一度に操作する問題について論じる。後者の場合、\(O(\log \log n)\) の処理時間を損なうことなく記憶要件を削減する問題は未解決のまま残されている。
 6.1. オフサイズ優先度付きキュー
6.1. オフサイズ優先度付きキュー
\(n\) を任意の数とし、\(2^{2^{h-1}} \lt n \le 2^{2^h}\) となるように \(h\) を選択する。サイズ \(n\) の優先度付きキューを表現するためにランク \(h\) の階層化木を使用することは、そのサイズと初期化時間の両方が \(h\cdot 2^{2^h}\) のオーダーであり、\(n^2\cdot\log\log n\) 程度になる可能性があるため、現実的ではないと思われる。この空間の爆発的な増加を防ぐために、ランク \(h\) 木から会の部分木またはレベルを除去する方法がある。
 6.1.1. 下位部分木の除去
6.1.1. 下位部分木の除去
このアプローチでは、数 \(\le n\) に対応する歯を持たないランク \(h-1\) のすべての下位 CS は割り当ても初期化も行われない。実際には、これは \(n \le 2^{2^h}/2\) である限り、木の右側の部分が使用されないことを意味する。ドライバが退化性について配慮すれば、前のセクションの手続きは、木の大部分が物理的に存在しないことを通知することなく正しく動作する。時間と空間のオーバーヘッドは定数因子 3 によって制限される。
 6.1.2. レベルの除去
6.1.2. レベルの除去
\(k=\lceil\log n\rceil\) とする。高さ \(k\) の二分木は、高さ \(\lceil k/2\rceil\) の下位木に分割され、これらの木は同様に分割される。これにより、ランク 0 の特定のレベルが物理的に present ではない正準分解 (canonical decomposition) が実現される。各レベルにランクを割り当てる関数を事前計算した後 (これは \(O(\log n \dot \log \log n)\) 時間で解ける)、前のセクションのアルゴリズムを変更せずにそのまま使用できる。必要な時間と空間のオーバーヘッド係数は定数係数 2 で制限される。
 6.2. 多数の優先度付きキューの表現
6.2. 多数の優先度付きキューの表現
複数の優先度付きキューを表現しなければならない場合、ノード内の静的情報と動的情報を分離することが理にかなっている。静的情報は各キューについてほぼ同じである。より具体的には、ノードの位置をそのアドレスとして使用する "アドレス + 変異" 戦略を用いることで、位置が機知の各ノードにアクセスできる。すべてのノードは、下位からは親ポインタ、動的情報からは下向きポインタによってアクセスされるため、階層化ツリー内の静的情報の事前計算済みコピーを 1 つ用意するだけで十分である。アルゴリズムに関係する各キューには、ノードの位置から直接アクセスできる \(O(n)\) サイズのメモリブロックを動的情報用に割り当てるべきである。
上記の戦略を用いることで、導入部で約束された \(O(n\log\log n\times A(n))\) 時間、\(O(n^2)\) 空間のマージ可能ヒープツリーの表現に到達する。必要な空間の大部分は決して使用されないことは明らかであり、幸いなことに、初期化せずにこれだけ多くの空間を使用できるよく知られたトリック [1] がある。それでも、記憶要件をより合理的なレベルまで削減する動的な記憶域割り当てメカニズムを設計できるかどうかは当然の疑問である。
直接的なアプローチはノードがアクティブ化された時点でそのノードに記憶域を割り当てることである。しかしこの方法は間違っているように思われる。次のような質問に正しく答えることができなければならない: "ここで渡しは根 top といくつかの葉の pres と leaef を持つ特定の CS を考えており、pres は present だが leaf は present ではない。hl を中心レベルにおける leaf の祖先とする。hl がアクティブかどうか、そしてもしアクティブであればどこに割り当てられるかを判断する。" pres の中心レベルの祖先の検査は、pres が実際に leaf の隣接要素である場合にのみ正しい答えをもたらす。しかし、これは我々のアルゴリズムでは保証されていない。
最初に leaf の隣接要素を計算しようとした場合にも同じ問題が発生する。したがって、対象とする CS における hl の位置が分かっており、その場所にはその根からのアクセスがあることで、hl を格納するための特定の位置を確保することが必要であると思われる。
以下のアプローチは \(O(\log\log n)\) 時間を妨げるなく \(O(n\cdot\sqrt{n})\) でマージ可能ヒープ木の表現をもたらす。ランク \(d\) の木を考える。その左側または右側の部分木に複数の present 葉が含まれていない限り、すべての必要な情報は木の根に格納することができる。ある段階で同じ側に同じ側に 2 番目の葉を挿入する必要がある場合、上位木のための完全な記憶が連続セグメントとして割り当てられ、根のポインタがその初期アドレスを参照するようにする。特に、中心レベルのノードには根を介してアクセスできる固定アドレスが与えられる。中心レベルのノード自体は同様に扱われるランク \(d-1\) の下位木の根と見なされる。このように、insert の呼び出しは最大 \(O(\sqrt{n})\) のメモリセルを割り当てるが、一方で neighbour は追加のメモリを使用せず、delete は包含する CS の両側が単一の葉を除いて使い尽くされている場合に上位木のための空間を返す可能性がある。
現在の関連する記憶セグメントの初期アドレスは、すべての包含する呼び出しがボトム呼び出しでないかぎり、その値が内部呼び出しに渡される手続きへの新しいパラメータとして与えられる。
マージ可能ヒープアルゴリズムで使用されるメモリの上限 \(O(n\sqrt{n})\) は、各中間段階において入力内容が \(n\) 子以下の insert 命令を実行して得られる値と等しいことに注目することで得られる。
このセクションを完了するにあたり、レベルの 2 進分数を \(r \gt 2\) に対する \(r\) 進分割で置き換えることで記憶要件をさらに削減できることに注目する。これは各 \(\epsilon \gt 0\) に対して \(O(n\log\log n \cdot A(n))\) 時間、\(O(n^{1+\epsilon})\) 空間のマージ可能ヒープツリーの表現をもたらす可能性がある。
 7. 集合捜査問題間の帰着性
7. 集合捜査問題間の帰着性
優先度付きキューのオンライン操作 (オンライン insert-extract-min 問題とも呼ばれる) は、数多くの集合操作問題の一つである。これらの問題はそれぞれ、対応するオフライン変種も存在する。オフライン変種では命令の順序が事前に与えられ、それ絵に応じて返答の順序が生成されなければならず、プログラマは返答が与えられる順序を自由に選択できる。
明らかに、各オンラインアルゴリズムはオフライン変種を解くために使用できるが、その逆は成り立たない。
[3] では、insert-extract-min 問題、Union-Find 問題、insert-allmin 問題のオンライン変種とオフライン変種間の帰着性 (reducibility) を調査した。ここで、問題 A が問題 B に帰着可能であるとは、B のアルゴリズムを使用して同じ複雑さのオーダーを持つ A のアルゴリズムを設計できることを意味する。さらに、A と B が両方ともオフライン問題である場合、\(O(n)\) サイズの構造上の \(O(n)\) サイズの A 問題を、\(O(n)\) サイズの構造上の \(O(n)\) サイズの B 問題に、時間 \(O(n)\) で変換できるはずである。
HOPCROFT, AHO & ULLMAN はオフラインの insert-extract-min 問題がオンラインの Union-Find 問題に帰着可能であることを示した [2]。著者は、オフライン Union-Find 問題がオフライン insert-allmin 問題と等価であることを示した [3]。オンライン insert-allmin からオンライン insert-extract-min への "自然な" 帰着と合わせて、これらの帰着性が Diagram 4 に表現されている (接頭辞は議論されている問題を示している)。
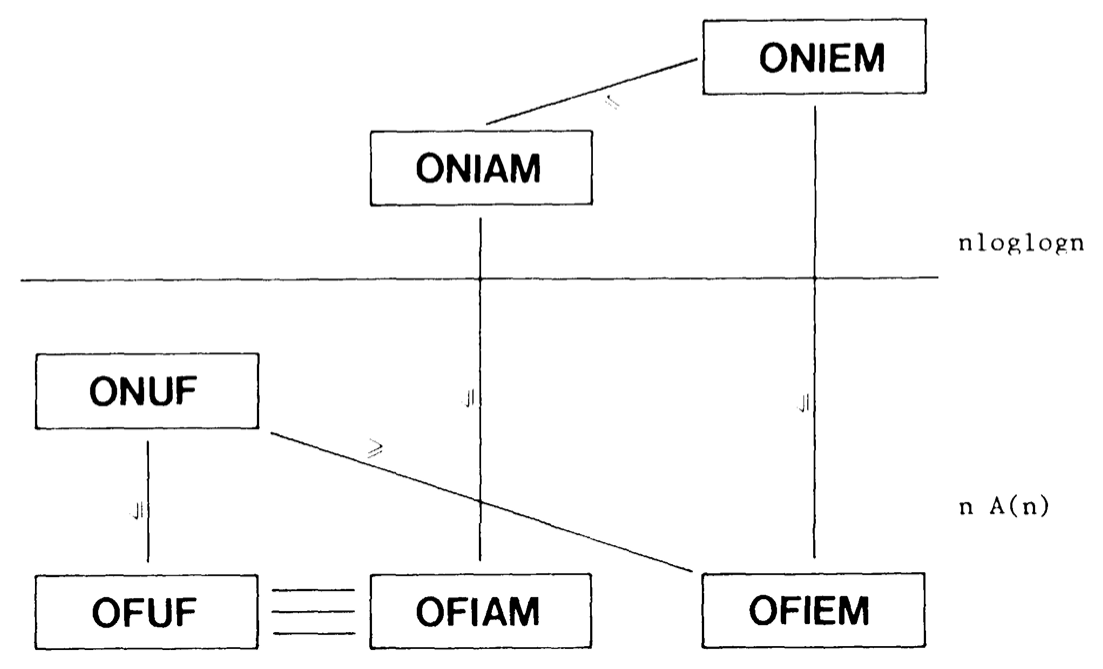
 ACKNOWLEDGEMENTS
ACKNOWLEDGEMENTS
I wish to thank J. Hopcroft for suggesting the problem and other useful suggestions. For the current state of the algorithms I am heavily indebted to R. Kaas and E. Zijlstra who, during the process of implementing the priority queue structure, discovered several hideous bugs in my earlier versions, and who contributed some nice and clever tricks; their use of a position field should be mentioned in particular. They also found the first recursive version of the delete procedure. Finally, T would like to thank R.E. Tarjan, Z. Galil and J. van Leeuwen for valuable ideas.
Author's addresses: Mathematical Institute, University of Amseterdam, Roetersstraat 15, Amsterdam; or Mathematical Centre, 2e Boerhaavestraat 49, Amsterdam
 REFERENCES
REFERENCES
- AHO, A.V., J.E. HOPCROFT & J.D. ULLMAN, The design and analysis of computer Algorithms, Addison Wesley, Reading, Mass. (1974).
- AHO, A.V., J.E. HOPCROFT & J.D. ULLMAN, On finding lowest common ancestors in trees, Proc. 5-th ACM symp. Theory of Computing (1973), 253-265.
- EMDE BOAS, P. VAN, An \(On \log \log n)\) On-Line Algorithm for the Insert-Extract Min Problem, Rep. TR 74-221 Dept. of Compo Sci., Cornell Univ., Ithaca 14853, N.Y.
- EMDE BOAS, P. VAN, The On-Line Insert-Extract Min Problem, Rep. 75-04, Math. Institute, Univ. of Amsterdam.
- EVEN, S., M.R. GAREY & Y. PERL, Efficient Generation of Optimal Prefix Code: Equiprobable Words Using Unequal Cost Letters, J. Assoc. Comput. Mach. 22 (1975), 202-214.
- FISHER, M.J., Efficiency of equivalence algorithms, in: R.E. MILLER & J.W. THATCHER (eds.), Complexity of Computer Computations~ Plenum Press, New York (1972), 158-168.
- HOPCROFT, J. & J.D. ULLMAN, Set-merging Algorithms, SIAM J. Comput. 2 (Dec. 1973), 294-303.
- KAAS, R. & E. ZIJLSTRA, A PASCAL implementation of an efficient priority queue, Rep. Math. Institute, Univ. of Amsterdam (to appear).
- TARJAN, R.E., Efficiency of a good but non linea set union algorithm, J. Assoc. Comput. Mach. 22 (1975), 215-224.
- TARJAN, R.E., Edge disjoint spanning trees, dominators and depth first search, Rep. CS~74-455 (Sept. 1974), Stanford.
- WIRTH, N., The Programming Language PASCAL (revised report), in K. JENSEN & N. WIRTH PASCAL User Manual and Report, Lecture Notes in Computer Science 18, Springer, Berlin (1974).
翻訳抄
現在は van Emde Boas Tree として知られている、整数の優先度付きキューにおいて従来の \(O(\log n)\) 時間を破る \(O(\log\log n)\) 時間での操作を可能にする階層化二分木 (stratified binary tree) データ構造を提案する 1975 年の論文。
- VAN EMDE BOAS, Peter. Preserving order in a forest in less than logarithmic time. In: 16th Annual Symposium on Foundations of Computer Science (sfcs 1975). IEEE, 1975. p. 75-84.

