論文翻訳: Authenticated Algorithms for Byzantine Agreement
[English]
 Abstract
Abstract
故障したプロセッサの存在する環境で合意に達することは信頼性の高いコンピュータシステムに対する分散システムの中心的な課題である。認証プロトコルを用いることで、隠れた故障プロセッサの振る舞いを、意図したターゲット全てへのメッセージ中継の失敗という単純な問題に限定することができる。この論文では、故障した振る舞いをこのように限定できるにもかかわらず、また、どのようなメッセージタイプやプロトコルが許可されているとしても、(ビザンチン) 合意に達するには少なくとも \(t+1\) フェーズまたはラウンドの情報交換が必要であることを示す。ここで \(t\) は故障プロセスの上限数である。我々は認証に基づく合意に達するためのアルゴリズムを提示する。このアルゴリズムは、正しく動作するプロセッサが送信するメッセージの総数 \(t\) とプロセッサ数 \(n\) の両方の多項式である。最良のアルゴリズムは \(t+1\) フェーズと \(O(nt)\) メッセージのみを使用する。
Key words. authentication, reliable distributed systems, Byzantine agreement, consistency, unanimity
Table of Contents
- Abstract
- 1. 導入
- 2. 履歴
- 3. 下限の結果
- 4. 認証を用いた多項式アルゴリズム
- 5 考察
- Acknowledgements
- References
- Transcription Note
 1. 導入
1. 導入
この論文では複数のプロセッサ間で合意を達成するためのアルゴリズムについて考察する。この合意は、信頼性の低いプロセッサのネットワークで、いくつかの同期した情報交換のフェーズを経て、ある情報の集合に全員が合意しなければならない、という文脈で行われる。ここでは簡単のために、この情報の集合はある値の集合 \(V\) からの単一の値で構成されていると仮定する。
我々の研究する合意は、ビザンチン合意 (LSP)、全会一致 (unanimity) (Db)、対話型整合性 (PSL) と呼ばれる。これは隠れた故障プロセッサが存在するときにすべての正しい (非故障) プロセッサがある値に合意するか、またはその値の生成者が故障していることで合意するかのどちらかで結論付ける。
- すべての正しいプロセッサが同じ値に合意する、かつ
- 送信者が正しい場合、すべての正しいプロセッサはその値に合意する。
I と II はすべてのプロセッサが同時に合意に達するという意味で暗に合意は同期的であるという考えを示している。言い換えると、各プロセッサが各々のアルゴリズム実行を完了する実時間が存在する必要があり、合意に達するためには事前にすべてのプロセッサがこの時間を認識し同意している必要がある。
我々の問題分析は故障プロセッサが予測不能で悪意を持つ可能性があるという最悪のケースを想定している。アルゴリズムは、正しいプロセッサが合意に達することを妨げるための共謀であっても、故障プロセッサによる任意の奇妙な動作に持ちこたえる必要がある。正しいプロセッサが故障プロセッサを識別できない場合でもビザンチン合意に達しなければならない。アルゴリズムは故障プロセッサに期待される動作に一切依存してはならない。
我々は情報交換に必要なフェーズ数の正確な下限を確立する。この下限 \((t+1)\) は認証されていないメッセージのみが好感される場合 (FL) には知られていた。我々は Lynch と Fischer によって与えられたこの証明を一般化し、あらゆる種類のメッセージに適用できるようにした。この下限の結果は我々の文脈ではやや驚くべきものである。これは、正しいプロセッサがあらゆる種類の検証可能な情報を交換することを許可したとしても、故障プロセッサの取り得る動作をただのメッセージ中継の失敗に限定したとしても、ビザンチン合意には \(t\) 以下のフェーズでは到達できないことを示している。なお十字軍合意 (crusader agreement) (Da) のように I を少し緩和すると 2 フェーズで合意を得ることができる。
検討したアルゴリズムは、単一のプロセッサが他のすべてのプロセッサに単一の値を送信するための方法を提供する。多くのプロセッサが互いに値を送信するケースへの一般化は明らかであろう。
我々は、任意の正しいプロセッサが他の正しいプロセッサにメッセージを送ることのできる何らかの信頼性の高い通信手段を想定する。例えば、この信頼性はネットワーク上の多数の経路でメッセージを何重にも送信することで達成できるかもしれない。いずれにせよ、この論文では特に明記しない限り完全に接続された完全に信頼できる通信ネットワークを想定し、送信されたメッセージの総数をカウントするときには通信媒体に特有の重複や繰り返しを無視する。また正しいプロセッサによって送信されたメッセージのみをカウントすることに注意。
認証を用いるアルゴリズムでは、任意のプロセッサが情報交換に新しい値やメッセージを挿入したり、他者から受信したと主張することを防ぐプロトコルを仮定する (DH) (RSA)。典型的な認証プロトコル (PSL) では送信者は送信するメッセージに署名を追加する。この署名にはメッセージが本物であり送信者によって送信されたものであることを受信者が確認できるようにエンコードされたメッセージのサンプル部分が含まれており、どのプロセッサも他者の署名を偽造することはできない。したがってどのプロセッサもメッセージの内容を秘密裏に変更することはできない。
ビザンチン合意を達成するこれまでのアルゴリズムはすべてメッセージ数が指数関数的である (\(O(n^t)\)、ここで \(n\) はプロセッサ数、\(t\) は検出されない故障プロセス数の上限)。今回示す新しい結果では交換するビット数に対して多項式となる認証を使用するアルゴリズムが含まれる。\(d\) をフェーズ数、\(m\) をメッセージ総数とすると、これまでのアルゴリズムは \(d=t+1\)、\(m=O(n^t)\) を使用していた。
Lynch と Fischer は \(d\) に対して \(t+1\) という下限を確立したが、その証明はあらゆる認証プロトコルを許可していないことに依存している。ここでは認証を許可する一般的な文脈で同じ下限を確立する。ただしこの我々の証明は特定の認証プロトコルに依存しないことに注意。実際、個の証明には認証やそのほかの特定のタイプのメッセージへの言及は含まれていない。
我々は \(d=t+1\) と \(m=O(n^2)\) のビザンチン合意アルゴリズムと \(d=t+2\) と \(m=O(nt)\) の修正版を示す。これらのアルゴリズムはまず完全なネットワークの文脈で示され、次に十分な接続性を持つ任意のネットワークに一般化する。メッセージの総数はネットワークのエッジ数のオーダーだが、より一般化されたネットワークではより多くのフェーズを必要とする。最後に、\(O(nt)\) メッセージのみでフェーズ数の下限 \(t+1\) を達成するアルゴリズムを示す。
 2. 履歴
2. 履歴
正しさを証明し、特に下限を確立するために、情報交換段階においてプロセッサ集合が行うメッセージ関連動作を、有向グラフのフェーズという一つのオブジェクトとして記述することにする。履歴の概念は、任意数の認証プロトコルや任意のメッセージタイプの交換を含む、同期的な情報交換動作を捉えることを目的としている。フェーズという概念を適切に一般化することによってセクション 3 の下限の結果を非同期アルゴリズムに拡張することができる。
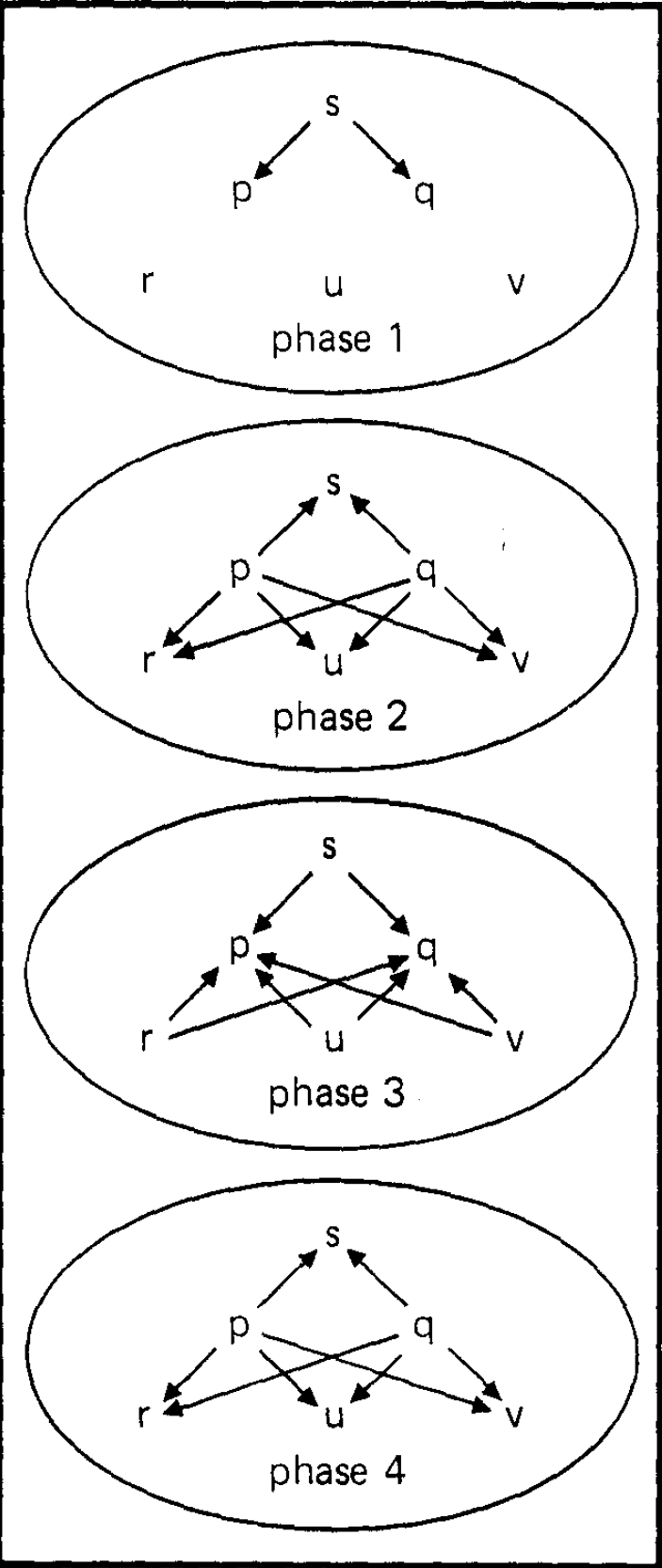
フェーズ (phase) は、プロセッサに対応するノードと、ラベル付きのエッジを持つ有向グラフである。ラベルは特定のフェーズであるプロセッサから別のプロセッサに送信される情報を表している。メッセージが送信されないときはエッジが存在しないと仮定する。\(n\) 個のプロセッサの履歴 (history) は、プロセッサの名前でラベル付けされたノードを持つ \(n\) 個のフェーズの有限列であり、フェーズ 0 と呼ばれる特別な初期フェーズがあり、フェーズ 0 には送信者 (sender) と呼ばれる 1 つのプロセッサへの単一の入力エッジのみが含まれている。(フェーズ 0 の入力エッジは送信者が送信すべき値を運ぶと仮定する。) Fig. 1 と Fig. 2 はラベルとフェーズ 0 を省略した履歴を示している。
履歴 \(H\) の部分履歴 (subhistory) は \(H\) からいくつかのエッジを取り除いたコピーである。各履歴 \(H\) とプロセッサ \(p\) から、ターゲットを \(p\) とするエッジのみで構成される \(p\) による部分履歴と呼ばれる一意の部分履歴 \(pH\) が存在する。したがって送信者による部分履歴は、何も送信しない場合であっても送信するはずの値を含むことになっている。
履歴のクラス \(C\) の合意アルゴリズムは正しさの規則 (\(p\) による部分履歴と、次のフェーズとして履歴に追加されるフェーズのエッジが与えられたときに、そのエッジに対して空かもしれないラベルを生成する関数) と決定関数 (\(C\) の履歴のプロセッサによる部分履歴から "送信者故障" を表す記号 0 を持つ \(V\) の和集合への関数) で構成される。ある正しさの規則に関して、フェーズ \(k\) での \(p\) からの各エッジが、前のフェーズ \(k-1\) の \(p\) による部分履歴上で作用する正しさの規則によって生成されたラベルを持つとき、プロセッサ \(p\) はフェーズ \(k\) で正しいと言われる。プロセッサ \(p\) は \(H\) の各フェーズで正しい場合、プロセッサ \(p\) は履歴 \(H\) に対して正しい。Fig. 1 と Fig. 2 の違いは、前者ではすべてのプロセッサが (何らかの適切な正しさの規則を仮定して) 正しく、後者では送信者が故障していることに注意。多くても履歴の \(t\) 個のプロセッサが正しくない場合、履歴を (正しさの規則に関して) \(t\)-faulty と呼ぶ。
実際には正しさの規則とは各プロセッサごとに 1 つずつあるかもしれない異なる正しさの規則の和集合である。同様に、決定関数は個々の決定関数の和集合である。
単純な正しさルールの例として、各プロセッサが前のフェーズの各受信メッセージを単純に署名し、他のすべてのプロセッサに (認証プロトコルに従って) 中継するというルールがある。
\(n\) 個のプロセッサ、(アルゴリズムの正しさの規則に関して) \(t\)-faulty、\(d\) フェーズ履歴のクラス \(C\) に対して、決定関数 \(F\) がビザンチン合意の規則に従うような合意アルゴリズムが存在する場合、ビザンチン合意は \(d\) フェーズ内で最大 \(t\) 個の故障を持つ \(n\) 個のプロセッサに対して達成できると言う:
\(p\) と \(q\) が \(C\) の \(H\) に対して正しいとき \(FpH = FqH\)、かつ
\(H\) の最初のフェーズで送信者が正しく、かつ \(p\) が \(C\) の \(H\) に対して正しいとき \(FpH = v\)。ここで \(v\) は送信者の値である。
我々は \(n \lt 3\) や \(t \gt n\) に対してビザンチン合意を定義しないことに注意。認証プロトコルの文脈では、履歴のクラス \(C\) は認証のセマンティクスと一致するものに限定されると仮定する。
 3. 下限の結果
3. 下限の結果
定理 1 (LSP). \(n \gt t+1\) と仮定すると、認証を伴うビザンチン合意は最大で \(t\) 個の故障を含む \(n\) 個のプロセッサに対して \(t+1\) フェーズで達成することができる。
証明. 正しさの規則のために、各ノードがフェーズ \(i\) で \(i\) 個の異なる署名を持つ受信メッセージに署名し、まだ署名していないプロセッサに正確に中継するようにする。メッセージは同じ値であっても異なる経路をたどってきたのであれば異なるものであることに注意。関数 \(F\) は部分履歴を操作し、正しさの規則に適合しないメッセージ (署名が繰り返されているものも含む) を削除し、残りのメッセージによって運ばれる \(V\) から (送信者によって) 認証されたすべての値を抽出する。もしちょうど 1 つの値 \(v\) が抽出された場合、\(F\) は出力として \(v\) を生成し、そうでなければ \(F\) は 0 を生成するだろう。
認証のセマンティクスと一致する、\(t+1\) フェーズを持つ \(t\)-faulty の履歴を \(H\) とする。フェーズ \(t\) の終わりには各メッセージは \(t\) 個の署名を運ぶ (現在の受信者の署名を除く)。したがって \(H\) の正しいメッセージに現れる各値は正しいプロセッサによって認識されたことになる。したがって、それぞれの正しいプロセッサは \(t+1\) フェーズ後に抽出された値の同じセットを持つことになる。∎
次の下限の結果はこのセクションの主要な結果である。これは定理 1 の結果がタイトであることを示すものである。
定理 2. \(n \gt t+1\) であれば、\(t\) 以下のフェーズで最大 \(t\) 個の故障を含む \(n\) 個のプロセッサではビザンチン合意を達成することはできない。
定理 2 の証明は Lynch と Fischer が認証のない限定的な場合について与えた証明 (FL) に触発されているが、それを自明でない形で一般化したものである。Lynch と Fischer は (PSL) の \(n \gt 3t\) の結果を用いてビザンチン合意の任意のアルゴリズムが均一 (uniform) でなければならないことを示した。均一性 (uniformity) を仮定して、彼らは \(t\)-faulty 履歴のバージョンに同値関係 (equivalence relation) を確立し、単一の同値クラスに含まれる履歴が多すぎることを示すことによって矛盾を得た。この同値性の彼らの証明は一度に 1 つのメッセージを変更しても同値性が保たれる性質に依存している。均一性の仮定を用いないこの性質の証明は、本質的に、次の帰納法における基本ケースの証明である。
定理 2 の証明. \(t\) フェーズ内のある \(n \gt t+1\) に対してビザンチン合意を達成できると仮定する。正しさの規則を \(R\) とし、\(\langle R,F\rangle\) が \(n\) 個のプロセッサ、深さ \(t\)、\(t\)-faulty 履歴上でビザンチン合意を達成できるような部分履歴上の決定関数を \(F\) とする。
Let \(C\) be the class of \(n\) processor, depth \(t\), \(t\)-faulty histories that have a critical sequence such that all incorrect processors appear on the sequence and any incorrect node appears at or after level corresponding to the order its label appears on the sequence. The class \(C\) contains histories that exhibit serial faultiness, in the sense that tha set of faulty processors is allowed to increase by at most one processor per phase, starting with no faults before phase 1, and once allowed in the set these faulty processors may exhibit their faultiness at any node corresponding to a phase at or after their entry. Note that any nodes corresponding to such a faulty processor may be correct.
Define an equivalence relation on histories in \(C\) by saying \(H\) is equivalent to \(H'\) if, whenever \(p\) is correct for \(H\) and \(q\) is correct for \(H'\), then \(FpH'=FpH\). Note that \(C\) includes histories in which all processors behave correctly. Since we assume \(V\) has more than one value, this means that there must be histories in \(C\) that are not equivalent. But, as we will show, \(C\) is a single equivalence class. Under an appropriate definition of \(\langle R,F\rangle\), both Fig. 1 and Fig. 2 could describe histories from the set \(C\). However, in Fig. 2 the result of the algorithm must be independent of any information from the sender since the sender sends nothing. This fact is the key idea behind the contradiction we obtain.
We say that a processor is hidden at phase \(k\) if it has not outedges at \(k\) or any later phase. We will also refer to the node at phase \(k\) as hidden if the processor is. In particular we will show by induction on the phase \(k\) that, if \(r\) is a node representing a processor at phase \(k\) of history \(H\) in \(C\), then:
- there is a history \(H'\) in \(C\), equivalent to \(H\), identical to \(H\) through phase \(k\) except for outedges of \(r\), with \(r\) correct and all processors correct after phase \(k\); and
- if all other nodes at phase \(k\) are correct, then there is a history \(H'\) in \(C\), equivalent to \(H\), identical to \(H\) through phase \(k\) except for outedges of \(r\), with \(r\) hidden and all other processors correct after phase \(k\).
Note that if a processor labels a hidden node, then changing the information on its inedge cannot affect the subhistory according to any other processor. In Fig. 2 the sender is hidden at phase 1.
In short we will show by induction that we can corect a node at any phase or hide a node if all other nodes at its phase are correct, and that the resulting history will be in \(C\) and equivalent to the one from which we started, while all changes will be to the outedges of the particular node and to edges at later phases. Thus we will have shown that every history in \(C\) is equivalent to any history in which the root is hidden and all other processors are correct.
Case 1. Let \(k=t\).
Let \(r\) be an incorrect node at phase \(k\) of history \(H\) in \(C\). If we correct the outedges of \(r\) one at a time, then for each individual change there is a processor correct for \(H\) that sees the same subhistory after the change as before. Thus each individual change preserves equivalence with \(H\). Since we cannot make any correct node incorrect, each individual change preserves membership in \(C\). Changes are only made to the outedges of \(r\). The final result \(H'\) has \(r\) correct and all processors trivially correct after \(k\).
Let \(r\) be a node at phase \(k\) in history \(H\) and \(C\) and let all other nodes at phase \(k\) be correct. Proceeding as in (a), we remove the outedges of \(r\), one at a time. Here we may change \(r\) from correct to incorrect but since there were no other incorrect nodes at phase \(k\) we could replace the \(k\)th entry in the critical sequence by the label of \(r\), preserving membership in \(C\). The rest of the argument is the same as that for (a).
Case 2. Assume the induction hypotheses (a) and (b) for all phases after \(k\).
Let \(r\) be an incorrect node at phase \(k\) of a history \(H\) in \(C\). The following steps will reserve membership in \(C\) and equivalence to \(H\) and change only outedges of \(r\) and edges at later phases.
- Correct all nodes after phase \(k\) (induction hypothesis (a)).
- While incorrect outedges of \(r\) remain,
- replace position \(k+1\) in the critical sequence by \(s\), a target of an incorrect outedge \(e\) from \(r\);
- hide \(s\) at phase \(k+1\) (induction hypothesis (b));
- correct \(e\) (some correct processor will see the same subhistories both before and after the change);
- correct all nodes at phase \(k+1\) (induction hypothesis (a)).
The final result \(H'\) will have \(r\) and all processors after phase \(k\) correct.
Assume all processos correct at phase \(k\) and let \(r\) be a node at phase \(k\). The following steps will preserve membership in \(C\) and equivalence to \(H\) and change only outedges of \(r\) and edges at later phases.
- Correct all nodes at phase \(k+1\) (induction hypothesis (a)).
- Replace the \(k\)th position in the critical sequence by the label of \(r\).
- While outedges of \(r\) remain,
- replace position \(k+1\) in the critical sequence by \(s\), a target of an outedge \(e\) from \(r\);
- hide \(s\) at phase \(k+1\) (induction hypothesis (b));
- remove \(e\) (some correct processor will see the same subhistories both before and after the change);
- correct all processors after phase \(k\) (induction hypothesis (a)).
- Hide the processor labelling \(r\) at phase \(k+1\) (induction hypothesis (b)). The final result \(H'\) will have \(r\) hidden at phase \(k\) and all other processors after phase \(k\) correct.
This completes the proof of Theorem 2. ∎
備考. これが定義されている場合は常に \(n\) 個のプロセッサに対して \(n-1\) フェーズでビザンチン合意を達成することができる。したがって定理 2 の下限には \(n \gt t+1\) という規定が必要である。
 4. 認証を用いた多項式アルゴリズム
4. 認証を用いた多項式アルゴリズム
導入で述べたように、故障しているプロセッサがメッセージの内容を検出できない方法で変更することを防ぐ何らかの認証技術が存在することを前提としている。
メッセージをカウントするために、フェーズと呼ばれる有向グラフのエッジのラベルに次の特定の構文を提供する。
値の集合 \(V\) はアトミックメッセージ (atomic message) の集合に含まれる。
ラベルはアトミックメッセージ (認証) またはラベル列である。
認証 (authentication) は \[ ({\rm label} \ a) p\] 形式のラベルである。ここで \(p\) はプロセッサ名であり \({\rm label}\ a\) はラベルである
ラベル列 (sequence of labels) は \[{\rm label}\ a, {\rm label}\ b\] 形式のラベルである。ここで \({\rm label} \ a\) と \({\rm label} \ b\) はラベルである。
\((a,b,c)p\) は \((a)p\), \(b(p)\) (訳注: \((b)p\) の誤記?), \((c)p\) と同じラベルではないことに注意。
ラベル \(a\) は次のいずれかの場合にラベル \(b\) の一部 (part) である:
- \(a=b\);
- ラベル \(c\) と、\(a\) が \(c\) の一部であり、\(b=(c)p\) であるようなプロセッサまたは \(p\) が存在する;
- \(b=c\) であり、\(d\) と \(a\) が \(c\) または \(d\) の一部であるようなラベル \(c\) と \(d\) が存在する。
メッセージはコンマのないラベルである。
したがって、前のフェーズで受信した認証付きメッセージを変更して前のフェーズで受信した認証付きメッセージとして次のフェーズで転送したり、受信していない認証付きメッセージを受信したことにしてそれを認証付きメッセージとして転送できないことを除いて、どのプロセッサも任意のフェーズで任意のメッセージを他のプロセッサに送信することができる。この論文の残りの部分では認証のセマンティクスと一致する履歴に注目する。特に \((a)q\) がプロセッサ \(p\) からのエッジのラベルの一部である場合、\(p=q\) または \((a)q\) のどちらかが前のフェーズの \(p\) への入力エッジ上のラベルの一部として現れる。
次の 2 つのアルゴリズムの背後にある基本的な考え方は、プロセッサがメッセージを中継しなければならないケースを制限することにより各エッジ上のメッセージ数を最小に抑えることである。定理 1 の証明では完全なグラフを想定しているため正しく認証された値が正しいプロセッサに公開されると次のフェーズですべての正しいプロセッサがその値を取得する。定理 3 ではプロセッサが情報を中継しなければならない値の数を制限する。定理 4 と定理 5 では正しいプロセッサが正しい認証付きの値を受信すると、他の正しいプロセッサもある一定のフェーズ数内でそれを受信するようにメッセージが移動する経路を制限している。最後に定理 6 では情報を中継するために必要なプロセッサの数を制限する。この場合、正しい中継プロセッサが正しい認証付きの値を受信すると他のプロセッサは 1 フェーズ後にそれを受信するが、中継プロセッサではない正しいプロセッサは他のプロセッサに知らされるよりずっと前にその値を受信する可能性がある。
我々のアルゴリズムがエッジに沿って何らかのメッセージを必要とするとき、正確に 2 つのプロセッサ間にエッジを持つ有向グラフのエッジ数を \(e\) とする。
定理 3. ビザンチン合意は、最大 \(t\) 個の故障がある \(n\) 個のプロセッサにおいて \(t+1\) フェーズ内で最大 \(O(e)=O(n^2)\) メッセージを用いて達成することができる。
Proof. Our correctness rule will be a restriction of that of the proof of Theorem 1 so that no processor relays more than two messages to any other, regardless of the number of messages received or the number of distinct paths incoming messages may have travelled. At the beginning of phase \(i+1\), each processor totally (lexicographically) orders all messages during the previous phase, discarding messages that are not of the form \((\cdots ((v)p_1)p_2 \cdots)p_i\) where \(v\) is a value not seen before, \(p_1\) is the signature of the sender, and all signatures are distinct. If a message carrying value \(v\) is not discarded, then the processor is said to extract \(v\). If the processor has not yet relayed any messages, then it relays the first two with distinct values (the first one if there are not two distinct values). If the processor has relayed only one message during all previous phases, then it relays the first of its messages. The relay process consists of signing the message and forwarding it to all those whose signatures do not already appear in the message. A processor relays a value only if it is either the first or the second diferent value extracted. Once a processor has relayed two distinct values, it stops processing messages for the algorithm and at the end it will decide "sender fault," i.e. the decision function \(F\) from the proof of Theorem 1 will produce 0 for this processor. If it gets through \(t+1\) phases without extracting any value, \(F\) will also produce 0; but if it has extracted exactly one value \(v\), then \(F\) will produce \(v\).
Each correct processor sends at most two messages over each edge. Thus, the total number of messages sent by correct processors is bounded by twice the number of edges, \(e\).
If the sender correctly sends \((v)s\) to each other processor, then authentication prevents faulty processors from importing more valeus, so \(F\) will produce \(v\) for each correct processor. If at phase \(t+1\) a correct processor receives and does not discard a message of the form \((\cdots ((v)p_1)p_2 \cdots)p_{t+1}\), then the first \(t\) processors on the list of signatures must be faulty, so the last one must be correct and all other correct processors have simultaneously received the same message. If, at the end of \(t+1\) phase, a correct processor has extracted only one value, then each correct processor has extracted only that value, and the decision function \(F\) will produce the same value for each correct processor. If any correct processor extracts more than one value, then all will. Consequently, although the sets of extracted values may not agree, they yield sufficient information to reach Byzantine agreement. ∎
送信可能なエッジを制限して有効なエッジ数を \(e=O(nt)\) に制限すればメッセージ数を減らすことができる。最初にこの削減を達成するために 1 つの追加フェーズを必要とする簡単な方法を示す。
定理 4. ビザンチン合意は、最大 \(t\) 個の故障がある \(n\) 個のプロセッサにおいて \(t+2\) フェーズ内で最大 \(O(nt)\) メッセージを用いて達成することができる。
Proof. We further restrict the correctness rule of the proof of Theorem 3 by arbitrarily choosing \(t+1\) processors to be relay processors and requiring any nonrelay processor to send messages only to relay processors (the sender is not a relay processor). Now the number of messages is \(O(nt)\). If a correct processor extracts a new value by phase \(t+2\), then some correct processor extracted that value by phase \(t\), some some correct relay processor extracted it by phase \(t+1\). Thus by phase \(t+2\) every correct processor must have extracted only that value. As in the proof of Theorem 3, although the sets of extracted values may not agree, they yield sufficient information to reach Byzantine agreement. ∎
定理 4 の証明で使用される制限付きネットワークでは \(t+1\) 個の接続グラフである。ビザンチン合意 (Da), (Db) に到達するには、グラフは少なくとも \(t+1\) の接続がなければならないことを示すのは簡単である。(LPS) では指数関数的な数のメッセージを使用して \(t+1\) 個の接続で十分であることが示された。
グラフの直径 (diameter) は頂点のペアを結ぶ最短経路の長さの最小上限であり、長さはエッジ数を意味する。グラフが \(k\) 接続であれば任意の頂点のペアの間に少なくとも \(k\) 個の最短頂点離散経路 (\(k\) vertex disjoint paths) が存在する。グラフの \(k\)-径は、頂点のペア間の \(k\) 個の最短頂点離散経路の長さの最小上限である。
定理 5. \(d\) を、最大 \(t\) 個の故障がある \(n\) 個のプロセッサの \((t+1)\)-接続ネットワークの \((t+1)\)-径とすると、ビザンチン合意は最大 \(O(e)\) メッセージを用いて \(t+d\) フェーズ以内に達成することができる。
Proof. We use the correctness rule and the decision function of Theorem 3, restricted of course so that only available edges of the graph are used for messages. If a processor extracts a new value at phase \(t+i\), then some correct processor has extracted a value by phase \(t\), so each correct processor will have extracted it (or two others) by phase \(t+d\). Again, each edge carries at most two messages, so the total number of messages is \(O(e)\). ∎
ここで完全なネットワークの過程に戻り、認証を使用したビザンチン合意の最適なアルゴリズムを示す。
定理 6. ビザンチン合意は、完全なネットワーク上で \(t+1\) フェーズ、\(O(nt)\) メッセージで達成することができる。
Proof. If \(n \gt 2t+1\) then \(O(n^2)=O(nt)\) so we are done by Theorem 3. Assume \(n \gt 2t\). We choose \(2t+1\) processors including the sender to play active relos and let all the others be passive. The correctness rule for the active processors is that of Theorem 3, except that they must ignore all messages signed by passive processors. The passive processors are not to send messages. The decision function for active processors is that of Theorem 3. Thus they reach Byzantine agreement among themselves by phase \(t+1\).
Passive processors modify the decision function so that it also counts the number of active processors that have sent more than one message, producing 0 if this number is at least \(t+1\). Passive processors discard the same messages as active processors, but they extract only values that have been signed (in the total collection of messages received) by at least \(t+1\) distinct active processors. Note that if a passive processor receives a message at phase \(t+1\) and does not discard it, then it will extract the value carried by that message because the \(t+1\) signature must occur in that message. However, if a message is received at an earlier phase and not discarded, its value may not be extracted until later confirming messages supply \(t+1\) distinct signatures.
If the correct active processors never extract a value, then the correct passive processors will never extract one because there are at most \(t\) faulty active processors. If any correct active processor extracts a new value then some correct active processor extracts that value by phase \(t\) and relays it to all. If a processor extracts a value at phase \(t\), then the message it relays will contain the signature of \(t+1\) active processors; otherwise, if it extracts the value by phase \(t-1\), then at least \(t\) other correct active processors will have extracts the value by phase \(t\). Thus if any correct active processor extracts onl one value, then each correct active processor extracts only that value and each correct passive processor will be able to extract that and only that value by phase \(t+1\).
If every correct active processor has extracted more than one value by phase \(t\), then the passive processors will have received more than one message from \(t+1\) active processors by phase \(t+1\).
The only difficult case is that in which each active processor extracts more than one value by phase \(t+1\), but some correct active processor has not extracted more than one value by the end of phase \(t\). It remains to show that in this case, the passive processors will be able to extract more than one value.
In this case, no correct active processor can extract more than one value by phase \(t-1\). At least two values are extracted by phase \(t\) (possibly by different processors). If the two values are extracted at phase \(t\), then the passive processors will extract them at phase \(t+1\). But at least one of them is extracted at phase \(t\). Moreover, if some correct active processor has extracted \(v\) by phase \(t-1\), then each correct active processor has extracted \(v\) or nothing by phase \(t-1\). Thus, if the first value is extracted at phase \(t\) or if all correct active processors extract that first value by \(t-1\), then the passive processors will be able to extract two values.
This leaves the case this \(v\) is extracted by some but not all correct active processors by phase \(t-1\). Each of the correct active processors that extracted \(v\) relays it to the passive processors by phase \(t\). If one of the processors that did not extracted \(v\) by phase \(t-1\) extracts two other values at phase \(t\), the passive processors can extract those two values. Otherwise, each of the processors that did not extract \(v\) by phase \(t-1\) will extract \(v\) at phase \(t\) and relay it to the passive processors. In any case the passive processors will extract at least two values. ∎
 5 考察
5 考察
認証を伴う \(t+1\) フェーズの下限はビザンチン合意を迅速に達成するために他の場所を探さなければならないことを意味する。実際、定理 2 の下限は送信するメッセージの種類に関係なく適用されるため、いくつかの要件を緩和する必要がある。個の証明は同期フェーズの文脈で行われているが、ビザンチン合意の非同期アルゴリズムと称されるものはその動作にフェーズを課すだけで同期フェーズの文脈に組み込むことができるのは確かである。
一つの可能性として、ビザンチン合意を達成する可能性のあるアルゴリズムに注目することが考えられる。確率論的な文脈では、可能な故障の数に現実的な上限 \(t\) が設定されている場合、正確に \(t\) 個の故障、正確に \(t-1\) 個の故障などの確率に関する情報も得られると思われる。
我々のアルゴリズムは必要なフェーズの最小数を減らすことはできないが、ビザンチン合意に必要なメッセージの総数を、プロセッサの数または正しいプロセッサによるビット交換数を指数関数から多項式に減らすことができる。可能な限り少数のフェーズで停止するアルゴリズムを見つけることは有用であろう。
最悪ケースで必要なメッセージ数の厳密な下限は確立していない。(DR) ではビザンチン合意を得るために交換しなければならないメッセージ数と署名数の下限が得られる。(DR) のアルゴリズムは我々のアルゴリズムより少ないメッセージ数で済むがより多くのフェーズを使用する。
 Acknowledgements
Acknowledgements
The authors thank Nancy Lynch for helpful suggestions about this manuscript. The proof of Theorem 6 uses suggestion of Lynch made in private correspondence with respect to a different problem. Subsequent to the completion of the proof of Theorem 2 in its present form, the authors received a private communication from Michael Merritt containing a somewhat similar proof of this result.
 References
References
- (DH) W. Diffie and M.Mellman, New direction in cryptography, IEEE Trans. Inform. Theory, IT-22 (1972), pp.644-654.
- (Da) D.Dolev, The Byzantine generals strike again, J. Algorithms, 3 (1982), pp.14-30.
- (Db) ─, Unanimity in an Unknown and unreliable environment, Proc. IEEE 22nd Symposium on Foundations of Computer Science, 1981, PP.159-168.
- (DR) D. Dolev and R. Reischuk, Bounds on information exchange for Byzantine agreement, Prof., ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing, Ottawa, Aug. 1982. See also IMB Research Report RJ3587 (1982).
- (FL) M. Fischer and N. Lynch, A lower bound for the time to assure interactive consistency, Inform. Proc. Letters, 14 (1982), pp. 183-186.
- (L) L. Lamport, using time instead of timeout for fault-tolerant distributed systems, Tech. Rep., Computer Science Laboratory, SRI International, June 1981.
- (LSP) L. Lamport, R. Shostak and M. Pease, The Byzantine generals problem, ACM Trans. Programming Languages and Systems, to appear.
- (PSL) M. Pease, R. Shostak and L. Lamport, Reaching agreement in the presence of faults, J. Assoc. Comput. Mach., 27 (1980), pp.228-234.
- (RSA) R. L. Rivest, A.Shamir and L. Adleman, A method for obtaining digital signatures and public-key cryptosystems, Comm. ACM, 21 (1978), pp.120-126.
Transcription Note
非同期ビザンチンアトミックブロードキャストに関する 1983 年の論文。
- DOLEV, D. STRONG H. R. Authenticated algorithms for Byzantine agreement. SIAM Journal on Computing, 1983, 12.4: 656-666.