$ \newcommand{\c}[1]{C\langle #1 \rangle} $ $ \newcommand{\ci}[2]{C_{#1}\langle #2 \rangle} $

論文翻訳: Time, Clocks, and the Ordering of Events in a Distributed System

2023年1月10日 1978年の論文 #LogicalClock #LamportTimestamp #CausalConsistency

Leslie Lamport
Massachusetts Computer Associates, Inc.

Abstract

分散システムにおいて、あるイベントが他のイベントより先に起こるという概念を検討し、イベントの部分順序付け (partial ordering) を定義することが示されている。分散アルゴリズムは全順序イベントに使用できる論理クロックの同期システムに対して与えられる。全順序の使用は同期問題の解決方法を用いて説明される。このアルゴリズムは物理クロックの同期に特化されており、クロックの同期がどの程度外れるかについての境界が導き出される。

Key Words and Phrases: distributed systems, computer networks, clock synchronization, multiprocess system
CR categories: 4.32, 5.29

Abstract
導入
部分順序
論理クロック
イベントの完全な順序付け
異常挙動
物理クロック
考察
付録
1. 定理の証明
Acknowledgements
References
翻訳抄

導入

時間という概念は我々の考え方の基本である。これはイベントの発生順序というより基本的な考え方から派生したものである。例えば時計が 3 時 15 分を示した後、3 時 16 分を指す前に何かが起こったとき、我々は 3 時 15 分に何かが起きたと言う。イベントの時制順序 (temporal ordering) という概念はシステムに関する我々の考え方に広く浸透している。例えば航空会社の予約システムでは、フライトが満席になる前に予約のリクエストが行われた場合、そのリクエストは許可されるべきであると規定されている。しかし、分散システムにおいてイベントを考える際にこの概念は慎重に再検討する必要があることがわかるだろう。

分散システムは、空間的に分離されメッセージを交換することによって相互に通信するプロセスの集まりで構成されている。ARPA ネットなどの相互接続されたコンピュータネットワークも分散システムである。また単一のコンピュータは中央制御装置、記憶装置、入出力チャネルが別々のプロセスである分散システムと見なすこともできる。メッセージの伝達遅延が単一プロセス内のイベント間の時間と比較して無視できない場合は分散システムである。

我々は主に空間的に分離されたコンピュータのシステムについて考察する。しかし我々の指摘の多くはより一般に適用できる。特に単一のコンピュータでのマルチプロセッシングシステムでは特定のイベントが発生する順序が予想できないため分散システムと同様の問題が発生する。

分散システムでは 2 つのイベントのどちらが先に起きたと言えないことがある。したがって "前に起きた" (happened before) という関係はシステム内のイベントの部分的な順序付けに過ぎない。人々がこの事実とその影響を完全に認識していないために問題が発生することがよくある。

この論文では "前に起きた" 関係によって定義される部分順序を議論し、それをすべてのイベントの一貫した全順序に拡張するための分散アルゴリズムを提供する。このアルゴリズムは分散システムを実装するために有用なメカニズムを提供することができる。同期問題を解決するための簡単な問題でその使用法を説明する。このアルゴリズムによって得られた順序がユーザが認識すると順序と異なる場合、予期せぬ異常挙動が発生する可能性がある。これは実際の物理クロックを導入することで回避することができる。我々はこれらのクロックを同期させる簡単な方法を説明し、それらがどの程度同期からずれるかの上限を導き出す。

部分順序

ほとんどの人々はイベント $a$ が $b$ よりも早い時間に起きたとき "$a$ は $b$ よりも前に起きた" と言うだろう。しかしシステムが仕様に正しく適合するには、その仕様がシステム内で観測可能なイベントの観点から与えられている必要がある。もし仕様が物理クロックに関するものならシステムには本物のクロックが含まれている必要がある。しかし、本物のクロックが含まれていたとしても、そのクロックの精度は完全ではなく正確な物理時間を刻むことができないという問題がある。このため我々は物理クロックを用いずに "前に起きた" 関係を定義する。

まずこのシステムをより正確に定義することから開始する。システムはプロセスの集合で構成されていると仮定する。各プロセスは一連のイベントで構成されている。アプリケーションによってはコンピュータ上でのサブプログラムの実行が 1 つのイベントであったり、1 つの機械語命令の実行がシーケンスの 1 つになるかもしれない。ここでプロセスのイベントはシーケンスを形成すると仮定しており、このシーケンスにおいて $a$ が $b$ の前に起きるなら $a$ は $b$ の前に発生する。つまり 1 つのプロセスはアプリオリな全順序を持つイベントの集合として定義される。これは一般的にプロセスが意味するところと考えられる¹。この定義を拡張してプロセスが個別のサブプロセスに分割できるようにすることは簡単だがここでそれを行うつもりはない。

ここではメッセージの送受信がプロセスにおける一つのイベントであると想定している。そして "$\to$" で示される "前に起きた" 関係は次のように定義できる。

定義. システムのイベント集合上の関係 "$\to$" は次の 3 つの条件を満たす最小の関係である: (1) $a$ と $b$ が同じプロセスのイベントであり $a$ が $b$ より先に起きるなら $a \to b$ である。(2) $a$ があるプロセスによるメッセージ送信であり、$b$ が他のプロセスによる同じメッセージの受信であれば $a \to b$ である。(3) $a \to b$ かつ $b \to c$ の場合、$a \to c$ である。2 つの異なるイベント $a$ と $b$ が $a \not\to b$ かつ $b \not\to a$ のとき並行 (concurrent) であると言う。

任意のイベント $a$ に対して $a \not\to a$ を仮定する。(あるイベントがそれ自身の前に起きうるシステムは物理的に意味がないように思われる。) これは $\to$ がシステム内のすべてのイベントの集合に対する無反射的な部分順序 (irreflexive partial ordering) であることを意味する。

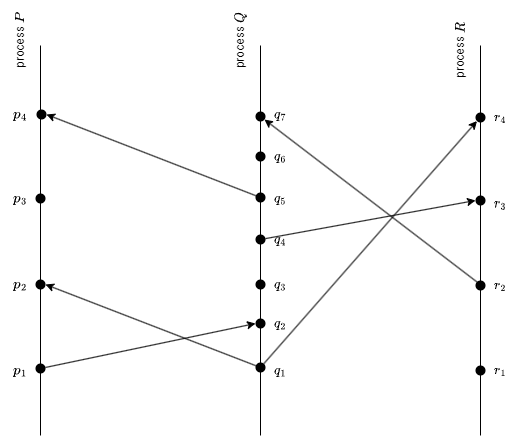
この定義は Fig 1 のような "時間-空間図" で見ると分かりやすい。横方向は空間、縦方向は時間を表し、遅い時間ほど上位に位置する。ドットはイベント、縦線はプロセス、横線 (原文は波線) はメッセージを表す²。$a \to b$ はプロセス線とメッセージ線に沿って時間を進めることで図中の $a$ から $b$ に行けることを意味することは容易に理解できる。例えば Fig 1 には $p_1 \to r_4$ となる。

この定義の別の見方として $a \to b$ はイベント $a$ がイベント $b$ に因果的な影響をもたらしている可能性があることを意味している。2 つのイベントがどちらも因果関係を持たない場合は並列である。例えば Fig 1 のイベント $p_3$ と $q_3$ は並行である。$q_3$ が $p_3$ より早い物理時間に発生しているように図を描いたとしても、プロセス $P$ は $p_4$ でメッセージを受け取るまでプロセス $Q$ が $q_3$ で何をしたかを知ることはできない (イベント $p_4$ の前に $P$ が知ることができるのはぜいせい $q_3$ で $Q$ が何をする予定か程度である)。

この定義は、たとえば [1] や [2] の第 1 章で述べられているような特殊相対性理論の不変時空の定式化に慣れている読者にとってはごく自然に見えるだろう。相対論ではイベントの順序は送信しえた (could) メッセージの観点から定義される。しかし我々はより現実的なアプローチとして実際に送信される (be sent) メッセージのみを考慮することにした。どのようなイベントが起きえたかを知ることなく、実際に起きたイベントだけを知ることによって、システムが正しく機能したかを判断することができるはずである。

¹何がイベントを構成するかの選択はプロセス内のイベント順序に影響する。例えばメッセージの受信はコンピュータの割り込みビットの設定や割り込みを処理するサブプログラムの実行を意味するかもしれない。割り込みは発生順に処理する必要がないため、この選択はプロセスのメッセージ受信イベントの順番に影響する。
²メッセージが順番通りに受信されない可能性があることに注意。複数のメッセージ送信を 1 つのイベントとすることもできるが、便宜上、1 つのメッセージ受信が他のメッセージ送信または受信と重ならないと仮定する。

論理クロック

ここでシステムにクロックを導入する。まず、クロックはイベントに数値を割り当てる方法であり、番号はイベントが発生した時刻という抽象的な観点から始める。より正確には各プロセス $P_i$ のクロック $C_i$ を、そのプロセスの任意のイベント $a$ に番号 $C_i\langle a\rangle$ を割り当てる関数と定義する。クロックのシステム全体は任意のイベント $b$ に番号 $C\langle b\rangle$ を割り当てる関数 $C$ によって表現される。ここで $b$ が $P_j$ のイベントであれば $C\langle b\rangle=C_j\langle b\rangle$ である。今のところ数値 $C_i\langle a\rangle$ と物理時間との関係については仮定していないため、クロック $C_i$ は物理クロックではなく論理クロックと考えることができる。現実の計時機構を持たないカウンターで実装してもよい。

ではこのようなクロックシステムが正確であるとはどういう意味か考えてみよう。物理的な時間を基準とすると物理的な時間を刻む時計を導入する必要があるため正確さの定義にはできない。そこで我々にはイベントの発生する順序に基づく定義が必要となる。もっとも強力な合理的条件はイベント $a$ が別のイベント $b$ の前に発生するとき、$a$ は $b$ よりも早い時刻に起きる必要があるということである。この条件をより正式に次のように述べる。

クロック条件. 任意のイベント $a, b$ に対して $a \to b$ であれば $C\langle a\rangle \lt C\langle b\rangle$ である。

条件が逆方向に成立することは期待できないことに注意。これは 2 つの並行イベントが意味的に同時に起きていると見なさなければならないためである。Fig 1 では $p_2$ と $p_3$ はいずれも $q_3$ と並行しているため、それらは $q_3$ と同時に起きていなければならないことを意味し、$p_2 \to p_3$ であるためクロック条件と矛盾する。

次の 2 つの条件が成立すればクロック条件が満たされることは "$\to$" の定義から容易に理解できる。

C1. $a$ と $b$ がプロセス $P_i$ のイベントであり $a$ が $b$ よりも前に起きていれば $\ci{i}{a} \lt \ci{i}{b}$ である。
C2. $a$ をプロセス $P_i$ によるメッセージ送信とし $b$ をプロセス $P_j$ によるそのメッセージの受信とすると $\ci{i}{a} \lt \ci{j}{b}$ である。

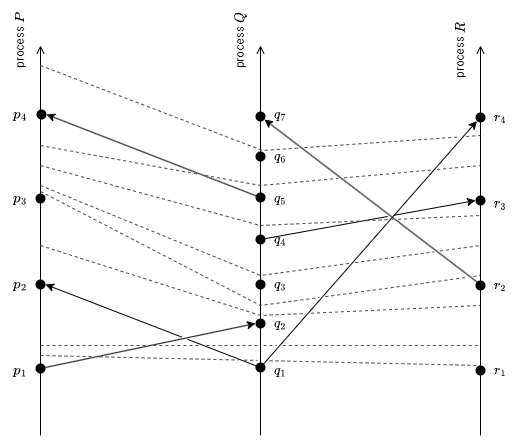
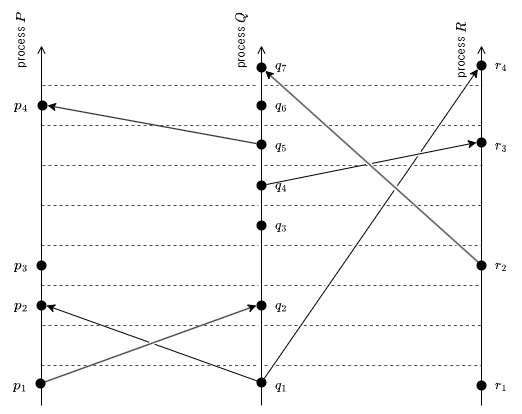
このクロックを時間-空間図で考えてみよう。あるプロセスのクロックはプロセスのイベントとイベントの間ですべての通じを "刻む" (tick) と想像する。例えば $a$ と $b$ がプロセス $P_i$ の連続するイベントで $\ci{i}{a} = 4$ と $\ci{i}{b} = 7$ であれば、この 2 つのイベントの間にクロックの刻み 5, 6, 7 が発生する。ここで異なるプロセスの同じ番号の刻みをすべて通る "刻み線" を描く。Fig 1 の時間-空間図から Fig 2 のような図を生成することができる。条件 C1 はプロセス線上の任意の 2 つのイベントの間には刻み線が存在しなければならないことを意味し、条件 C2 はすべてのメッセージ線が刻み線と交差する必要があることを意味する。$\to$ の絵の意味からこれら 2 つの条件がクロック条件を意味することは容易に理解できる。

我々はこの刻み線を時空間における直交座標系の時間座標線と考えることができる。これらの座標線をまっすぐにするために Fig 2 を書き直して Fig 3 を得ることができる。Fig 3 は Fig 2 と同じイベント系を表す有効な代替手段である。システムに物理時間の概念を導入しない限り (そのためには物理クロックを導入する必要がある)、これらの図のどちらがより適切な表現かを判断する方法はない。

読者には視覚的にプロセス間の 2 次元空間ネットワークを 3 次元空間図にすると分かりやすいかも知れない。プロセスとメッセージは引き続き線で表されるが刻み線は 2 次元の面となる。

ここでプロセスはアルゴリズムであり、イベントはその実行中の特定のアクションを表すと仮定する。ここではクロック条件を満たすプロセスにクロックを導入する方法を示す。プロセス $P_i$ のクロックはレジスタ $C_i$ で表されるため、$\ci{i}{a}$ は $C_i$ に含まれる値である。$C_i$ の値はイベント間で変化するため $C_i$ の変更自体はイベントを構成しない。

クロックのシステムがクロック条件を満たすことを保証するために条件 C1 と C2 を満たすことを保証する。条件 C1 は簡単で次の実装ルールを守るだけで良い:

IR1. 各プロセス $P_i$ は任意の 2 つの連続するイベント間で $C_i$ をインクリメントする。

条件 C2 を満たすには、各メッセージ $m$ にはそのメッセージが送信された時刻に等しいタイムスタンプ $T_m$ が含まれている必要がある。タイムスタンプ $T_m$ のメッセージを受信したプロセスは自身のクロックを $T_m$ より遅くなるように進めなければならない。より正確には次のようなルールがある。

IR2.
- (a) イベント $a$ がプロセス $P_i$ によるメッセージ $m$ の送信であれば、メッセージ $m$ にはタイムスタンプ $T_m = \ci{i}{a}$ が含まれている。
- (b) メッセージ $m$ を受信したプロセス $P_j$ は $C_j$ を現在の値以上かつ $T_m$ より大きい値に設定する。

IR2 (b) ではメッセージ $m$ の受信を表すイベントが $C_j$ の設定後に発生すると考える。(これは単に表記上の煩わしさであり現実の実装には関係がない。) IR2 は明らかに C2 を満たすことを保証している。したがって単純な実装ルール IR1 および IR2 はクロック条件が満たされていることを意味し、正しい論理クロックのシステムを保証している。

イベントの完全な順序付け

クロック条件を満たすクロックシステムを用いてシステムのすべてのイベント集合に完全な順序づけを行うことができる。これはイベントを発生順序順に並べるだけである。同着を解消するためにプロセスの任意の全順序 (arbitrary total ordering) $\prec$ を用いる。より正確には次のような関係 $\Rightarrow$ を定義する: $a$ をプロセス $P_i$ のイベント、$b$ をプロセス $P_j$ のイベントとすると (i) $\ci{i}{a} \lt \ci{j}{b}$ または (ii) $\ci{i}{a} = \ci{j}{b}$ かつ $P_i \prec P_j$ のいずれかの場合にのみ $a \Rightarrow b$ である。これが全順序を定義すること、およびクロック条件が $a \to b$ であれば $a \Rightarrow b$ を含意していることは容易に理解できる。言い換えれば関係 $\Rightarrow$ は "前に起きた" 部分順序を全順序に完成させる方法である³。

順序関係 $\Rightarrow$ はクロックのシステム $C_i$ に依存し一意ではない。クロック条件を満たす異なるクロックの選択があれば異なる関係 $\Rightarrow$ が得られる。$\to$ を拡張する任意の全順序関係 $\Rightarrow$ が与えられると、その関係をもたらすクロック条件を満たすクロックシステムが存在する。イベントのシステムによって一意に決定されるのは部分順序のみである。

イベントの全順序付けができることは分散システムを実装するうえで非常に有用である。実際、正しい論理クロックのシステムを実装する理由はこのような全順序付けを得るためである。この全順序イベントの利用法を次のような相互排他問題を解くことによって説明する。単一のリソースを共有する個定数のプロセス群で構成されるシステムについて考える。リソースは一度に 1 つのプロセスのみが利用できるため、衝突を避けるためにプロセス間で同期する必要がある: (I) リソースを許可されたプロセスは他のプロセスに許可される前にリソースを開放しなければならない。 (II) リソースに対する様々な要求はそれらが成された順に許可されなければならない。 (III) リソースを許可されたすべてのプロセスが最終的に (eventually) それを開放するならばすべての要求は最終的に許可される。

リソースは最初に一つのプロセスのみに許可されていると仮定する。

これらは至極当然の条件である。これは解が正しいとはどういう意味かを正確に特定している⁴。この条件がイベントの順序付けにどのように関与しているかを見てみよう。条件 II は同時に発行された 2 つの要求のうちどちらが最初に許可されるべきかについては何も述べていない。

これは自明ではない問題であることを認識することが重要である。要求を受け取った順に許可する中央スケジューリングプロセスを使っても追加の仮定がない限りうまく機能しない。これを確認するために $P_0$ をスケジューリングプロセスとし、$P_1$ は $P_0$ に要求を送り、次に $P_2$ にメッセージを送るとする。後者のメッセージを受信した $P_2$ は $P_0$ に要求を送る。$P_2$ の要求は $P_1$ の要求よりも先に $P_0$ に到達する可能性がある。このとき $P2$ の要求が先に許可されると条件 II に違反する。

この問題を解決するためにルール IR1 と IR2 を使用してクロックのシステムを実装し、それらを使って全イベントの全順序 $\Rightarrow$ を定義する。これによってすべての要求と解放操作の全順序が得られる。この順序を利用すれば解を求めることは用意である。各プロセスが他のプロセスの操作をすべて学習することを確認するだけである。

問題を単純化するためにいくつかの仮定を置く。これらは必須ではないが、実装の詳細に気を取られることを避けるために導入している。まず任意の 2 つのプロセス $P_i$ と $P_j$ について、$P_i$ から $P_j$ に送られるメッセージは送られたのと同じ順序で受信されると仮定する。さらにすべてのメッセージが最終的に受信されると想定する。(これらの想定はメッセージ番号とメッセージ確認プロトコルを導入することで回避できる。) またプロセスは他のすべてのプロセスに直接メッセージを送ることができると仮定する。

各プロセスは他のプロセスからは決して見えない独自の要求キュー (request queue) を保持している。最初要求キューには単一のメッセージ $T_0:P_0$ リソース要求が含まれていると仮定する。ここで $P_0$ は最初にリソースを許可されたプロセスであり、$T_0$ は任意のクロックの初期値より小さい値である。

次にこのアルゴリズムは以下の 5 つのルールによって定義される。便宜上、各ルールで定義されたアクションは単一のイベントを形成するものと想定する。

リソースを要求するために、プロセス $P_i$ は他のすべてのプロセスに $T_m:P_i$ リソース要求メッセージを送信し、そのメッセージを要求キューに入れる。ここで $T_m$ はメッセージのタイムスタンプである。
プロセス $P_j$ はメッセージ $T_m:P_i$ リソース要求メッセージを受信するとそれを要求キューに入れ $P_i$ に (タイムスタンプ付きの) 確認メッセージを送る。⁵
リソースを開放するために、プロセス $P_i$ はその要求キューから任意の $T_m:P_i$ リソース要求メッセージを取り除き、他のすべてのプロセスに (タイムスタンプ付きの) $P_i$ リソース開放メッセージを送信する。
プロセス $P_j$ が $P_i$ リソース開放メッセージを受信すると、その要求キューから任意の $T_m:P_i$ リソース要求メッセージを削除する。
プロセス $P_i$ は次の 2 つの条件が満たされたときにリソースを許可される: (i) 関係 $\Rightarrow$ によって要求キュー内の他のどの要求よりも前に順序付けられた $T_m:P_i$ リソース要求メッセージがキュー内に存在する。(メッセージの関係 $\Rightarrow$ を定義するために我々はメッセージを送信するイベントと識別する。) (ii) $P_i$ は他のすべてのプロセスから $T_m$ より後のタイムスタンプが付けられているメッセージを受信している。⁶

ルール 5 の (i) と (ii) は $P_i$ のローカルでテストされることに注意。

これらのルールによって定義されたアルゴリズムが条件 I, II, III を満たすことを検証するのは容易である。まず最初にルール 5 の条件 (ii) は、メッセージが順番に受信されるという仮定の下に $P_i$ が現在の要求に先行するすべての要求について学習したことを保証していることに注目する。ルール 3 と 4 は要求キューからメッセージを削除する唯一のルールであるため条件 I が成り立つことは容易に理解できる。条件 II は全順序 $\Rightarrow$ が部分順序 $\to$ を拡張するという事実から導かれる。ルール 2 は $P_i$ がリソースを要求した後にルール 5 の条件 (ii) が最終的に成立することを保証している。ルール 3 と 4 はリソースを許可された各プロセスが最終的にそれを開放するならばルール 5 の条件 (i) が最終的に成立し、条件 III を証明することを意味する。

これは分散アルゴリズムである。各プロセスは独立してこれらのルールに従い、中央同期プロセスや中央ストレージは存在しない。このアプローチはこのような分散マルチプロセスシステムに対して必要な同期を実装するために一般化できる。同期は、取り得るコマンドの集合 $C$、取り得る状態の集合 $S$、関数 $e: C \times S \to S$ で構成されるステートマシン (State Machine) の観点から指定される。関係 $e(C,S) = S'$ は、状態 $S$ のマシンでコマンド $C$ を実行するとマシンの状態が $S'$ に変わることを意味する。我々の例では集合 $C$ は $P_i$ リソース要求や $P_i$ リソース開放のすべてのコマンドで構成され、状態は待機中の要求コマンドで構成され、キューの先頭にある要求は現在許可されているものである。要求コマンドを実行すると要求キューの末尾に追加され、解放コマンドを実行するとキューからコマンドが削除される。⁷

各プロセスはすべてのプロセスが発行したコマンドを使用してステートマシンの実行を個別にシミュレートする。すべてのプロセスは (関係 $\Rightarrow$ を使用して)タイムスタンプに従ってコマンドを並べることから、それぞれのプロセスは同じコマンドのシーケンスを使用することになり同期が達成される。あるプロセスがタイムスタンプ $T$ のコマンドを実行できるのは、他のすべてのプロセスによって発行されたタイムスタンプ $T$ 以下のすべてのコマンドを学習したときである。正確なアルゴリズムは簡単なので省略する。

この方法によって、分散システムにおける任意の形式のマルチプロセス同期を実装することができる。しかし、このアルゴリズムはすべてのプロセスの積極的な参加を必要とする。あるプロセスは他のプロセスによって発行されたすべてのコマンドを認識していなければならない。このため、あるプロセスに障害が発生すると他のプロセスがステートマシンコマンドを実行できなくなりシステムが停止する。

故障の課題は難しい問題でありこの論文で詳しく説明することはできない。ただ、故障という概念全体が物理的な時間の文脈でしか意味を持たないことを確認する。物理的な事件がなければ、故障したプロセスと、イベント間で一時停止しているだけのプロセスを区別する方法はない。ユーザはシステムが "クラッシュ" したと判断できるのは応答を待つ時間が長すぎるために他ならない。個々のプロセスや通信回線の障害があっても動作する方法は [3] で説明されている。

³順序付け $\prec$ はプロセス間の優先順位を確立する。もし "より公平な" 方法が望まれるなら $\prec$ はクロック値の関数にすることができる。例えば $\ci{i}{a} = \ci{j}{b}$ かつ $j \lt i$ ならば、$j \lt \ci{i}{a} \bmod N \le i$ であれば $a \Rightarrow b$、そうでなければ $b \Rightarrow a$ である。ここで $N$ はプロセスの総数である。
⁴"最終的に" (eventually) という用語を正確にする必要があるが本題から余りにも大きく逸脱する必要がある。
⁵$P_j$ がすでに $T_m$ より後のタイムスタンプのメッセージを $P_i$ に送信している場合、この確認メッセージを送信する必要はない。
⁶$P_i \prec P_j$ であれば $P_i$ は $P_j$ からタイムスタンプが $\ge T_m$ のメッセージを受信していればよい。
⁷各プロセスが要求と解放の厳密に口語に行わなければ、解放コマンドの実行でキューから 0 個、1 個、またはそれ以上のリクエストが削除される可能性がある。

異常挙動

我々のリソーススケジューリングアルゴリズムは全順序 $\Rightarrow$ に従って要求を並べた。これにより次のような "異常挙動" (anomalous behavior) が起き得る。コンピュータが相互に接続された全国規模のシステムについて考える。ある人がコンピュータ A で要求 $A$ を発行し、別の都市にいる友人に電話して別のコンピュータ B で要求 $B$ を発行したとする。このとき、要求 $B$ のほうが低いタイムスタンプを受け取り、要求 $A$ より先に順序付けられることが十分にあり得る。これは優先順位情報がシステム外部のメッセージに基づいており、実際 $A$ が $B$ に先行していることをシステムが知るすべがないためである。

問題の根源をより詳しく考えてみよう。すべてのシステムイベントの集合を $\mathcal{S}$ とする。ここで $\mathcal{S}$ に含まれるイベントと、この例の電話のような他のすべての関連する外部イベントを含むイベント集合 $\underline{\mathcal{S}}$ を導入しよう。$\underline{\mathcal{S}}$ の "前に起きた" 関係を $\to^*$ とする。我々の例では $A \to^* B$ のはずが $A \not\to B$ だった。完全に $\underline{\mathcal{S}}$ 内のイベントに基づいており、これらのイベントを $\mathcal{S}$ の他のイベントと全く関連付けないアルゴリズムは、要求 $A$ が要求 $B$ より前に順序付けられることを保証できないことは明らかである。

このような異常挙動を回避するには 2 つの方法がある。第一の方法は順序 $\to^*$ に関する必要な情報を明示的にシステムに導入することである。この例では、要求 $A$ を発行した人はその要求のタイムスタンプ $T_A$ をシステムから受け取ることができる。したがって要求 $B$ を発行するとき彼の友人は $B$ に $T_A$ より遅いタイムスタンプを与えるように指定することができる。これはこの異常挙動を回避する責任をユーザに与えることになる。

第二のアプローチは次の条件を満たすクロックシステムを構築することである。

強いクロック条件. $\mathcal{S}$ 内の任意のイベント $a, b$ に対して: もし $a \to^* b$ なら $\c{a} \lt \c{b}$ である。

これは $\to^*$ が $\to$ より強い関係であるため通常のクロック条件より強力である。一般に我々の論理クロックではこの条件を満たさない。

ここで $\underline{\mathcal{S}}$ を "現実の" イベント集合とし、$\to^*$ を特殊相対論で定義されたイベントの部分順序とする。宇宙の謎の一つは互いに全く独立して動作する強いクロック条件を満足する物理時計のシステムを構築できることである。したがって我々は物理時計を使って異常挙動を排除することができる。そこでこのような物理時計に注目しよう。

物理クロック

時空間図に物理的な時間座標を導入し、$C_i(t)$ を物理時間におけるクロック $C_i$ の読み取り値を表すとする。⁸ 数学的な便宜上、このクロックは離散的な "刻み" ではなく連続して動作すると仮定する。(離散クロックはそれを読み取る時に最大 $\frac{1}{2}$ "刻み" の誤差を持つ連続クロックと考えることができる。) より正確には、$C_i(t)$ はクロックがリセットされる孤立したジャンプ不連続性を除いて、$t$ で微分可能な連続的な関数であると仮定する。このとき $dC_i(t)/dt$ は時間 $t$ におけるクロックの動作速度を表す。

クロック $C_i$ が真の物理クロックであるためにはほぼ正しい速度で動作する必要がある。つまり、すべての $t$ に対して $d C_i(t)/dt \approx 1$ を満たす必要がある。より正確には次の条件を満たすと仮定する:

PC1. すべての $i$ に対して $|dC_i(t)/dt-1| \lt \kappa$ となるような定数 $\kappa \ll 1$ が存在する。

一般的な水晶制御のクロックでは $\kappa \le 10^{-6}$ である。

個々のクロックがほぼ正しい速度で動作するだけでは十分ではない。すべての $i$, $j$, および $t$ に対して $C_i(t) \approx C_j(t)$ となるように同期しなければならない。より正確には次の条件が成り立つように十分に小さな定数 $\epsilon$ が必要である。

PC2. すべての $i$, $j$ に対して $|C_i(t) - C_j(t)| \lt \epsilon$ である。

Fig 2 の垂直距離を物理的な時間を表すと考えると、PC2 は 1 刻みの高さの変動が $\epsilon$ 未満であることを述べている。

2 つの異なるクロックが全く同じ速度で動くことはないことからそれらはますます離れてドリフトする傾向にある。したがって PC2 が常に成立するようなアルゴリズムを考案する必要がある。しかしまずは異常挙動を防ぐためには $\kappa$ と $\epsilon$ をどの程度小さくしなければならないかを検討しよう。関連する物理的なイベントのシステム $\underline{\mathcal{S}}$ が強いクロック条件を満たしていることを保証しなければならない。クロックが通常のクロック条件を満たすと仮定しているため、$a$ と $b$ が $\underline{\mathcal{S}}$ の $a \not\to b$ のイベントであるときにのみ強いクロック条件が成立することを求めれば良い。

イベント $a$ が物理時間 $t$ に発生し、$a \to b$ を満たす別のプロセスのイベント $b$ が物理時間 $t + \mu$ より後に発生するような数値 $\mu$ を導入する。つまり $\mu$ はプロセス間メッセージの最短伝送時間よりも小さくなる。プロセス間の最短距離を光速で割った値を $\mu$ とするのが常套手段である。しかし、$\underline{\mathcal{S}}$ 内のメッセージ伝送方法によっては $\mu$ がかなり大きくなる可能性がある。

異常挙動を避けるためには任意の $i$, $j$, および $t$ について $C_i(t + \mu) - C_j(t) \gt 0$ であることを確認する必要がある。これを PC1 および 2 と組み合わせると $\kappa$ と $\epsilon$ に必要な小ささと $\mu$ の値は次のように関連付けることができる。ここでクロックがリセットされるときは必ず進み決して戻らないと仮定する。(クロックを戻すと C1 に違反する可能性がある。) PC1 は $C_i(t + \mu) - C_i(t) \gt (1 - \kappa) \mu$ を意味する。PC2 を使用すると次の不等式が成立する場合に $C_i(t + \mu) - C_j(t) \gt 0$ と容易に推測できる: \[ \epsilon / (1 - \kappa) \le \mu \] この不等式と PC1 および PC2 は異常挙動が不可能であることを意味する。

ここで PC2 が成立することを保証するためのアルゴリズムを説明する。物理時刻 $t$ に送信され、時刻 $t'$ に受信されるメッセージを $m$ とする。ここで $\nu_m = t' - t$ をメッセージ $m$ の全遅延 (total delay) とする。この遅延はもちろん $m$ を受信するプロセスには分からない。しかし受信プロセスは $\mu_m \le \nu_m$ となるような最小遅延 (minimum delay) $\mu_m \gt 0$ を知っていると仮定する。ここで $\xi_m = \nu_m - \mu_m$ をメッセージの予測不可能な遅延 (unpredictable delay) と呼ぶ。

ここでルール IR1 と 2 を次のように物理クロックに特化する:

IR1'. 各 $i$ について、$P_i$ が物理時刻 $t$ でメッセージを受信しない場合、$C_i$ は $t$ で微分可能であり $dC_i(t)/dt \gt 0$ である。
IR2'.
- (a) $P_i$ が物理時刻 $t$ にメッセージ $m$ を送信する場合、$m$ はタイムスタンプ $T_m = C_i(t)$ を含む。
- (b) 時刻 $t'$ にメッセージ $m$ を受信したプロセス $P_j$ は、$C_j(t')$ を最大値 $(C_j(t' - 0), T_m + \mu_m)$ に等しく設定する。⁹

ルールは形式的には物理時間パラメータで指定されているが、プロセスは自分自身のクロックの読みと受信したメッセージのタイムスタンプを知るだけで良い。数学的な便宜上、各イベントは物理時間の正確な瞬間に発生し、同じプロセス内の異なるイベントは異なる時間に発生すると仮定している。これらのルールはルール IR1 と IR2 を特殊化したものであり、クロックのシステムはクロック条件を満たしている。現実のイベントが有限時間であるという事実はアルゴリズムの実装に支障を来さない。実装上の唯一の懸念は C1 が維持されるように離散的なクロック刻みが十分な頻度であることを確認することである。

ここでこのクロック同期アルゴリズムを用いて条件 PC2 を満たすことができることを示す。プロセスのシステムは有向グラフで記述され、プロセス $P_i$ からプロセス $P_j$ への弧は $P_i$ から $P_j$ へ直接メッセージが送られる通信路を表すとする。任意の $t$ において、物理時間 $t$ と $t + \tau$ の間に $P_i$ が $P_j$ に少なくとも 1 つのメッセージを送るとき、この弧の上を $\tau$ 秒ごとにメッセージが送られると言う。有向グラフの直径 (diameter) は、異なるプロセスの任意のペア $P_j$, $P_k$ に対して $P_j$ から $P_k$ への経路が最大で $d$ 個の弧を持つような最小の数 $d$ である。

PC2 の確立に加えて、次の定理はシステムの初回起動時にクロックが同期までの時間の長さを制限している。

定理. IR1' および IR2' のルールに常に従い直径 $d$ を持つ強結合プロセスグラフを想定する。任意のメッセージ $m$ に対して、ある定数 $\mu$ に対して $\mu_m \le \mu$ であり、すべての $t \ge t_0$ に対して (a) PC1 が成立し (b) $\tau$ 秒ごとに $\xi$ 未満の予測不可能な遅延のメッセージがすべての弧上で送信されるような定数 $\tau$ と $\xi$ が存在すると仮定する。このとき、PC2 はすべての $t \gtrsim t_0 + \tau d$ に対して $\epsilon \approx d(2 \kappa \tau + \xi)$ を満たす。ここで近似は $\mu + \xi \ll \tau$ を仮定している。

この定理の証明は意外と難しく付録で示す。物理クロックの同期問題については多くの研究が行われてきた。この問題の導入として [4] を参照されたい。文献に記載されている方法はメッセージ遅延 $\mu_m$ の推定やクロック周波数 $dC_i/dt$ を調整 (このような調整が可能なクロックの場合) するのに有用である。しかし、クロックが決して逆行しないという条件はこれまで研究されてきた状況とは異なるようであり、この定理は新しい結果であると考えられる。

⁸ここではニュートン時空を仮定する。時計の相対運動や重力の影響が無視できない場合、$C_i(t)$ を固有時間から任意に選んだ時間座標に変換して実際の時計の読みから推定する必要がある。
⁹$\displaystyle C_j(t' - 0) = \lim_{\delta \to 0} C_j(t' - |\delta|)$

考察

我々は "前に起きる" という概念が分散マルチプロセスシステムにおけるイベントの不変の部分順序を定義することを見てきた。この部分順序をいささか恣意的に全順序へ拡張するアルゴリズムについて説明し、この全順序を用いて簡単な同期問題を解決する方法を示した。今後の論文ではこのアプローチを拡張して同期問題を解決する方法を示す予定である。

このアルゴリズムで定義される全順序はやや恣意的である。システムのユーザが認識する順序と一致しない場合に異常挙動を引き起こす可能性がある。これは適切に同期された物理クロックを用いることで防ぐことができる。我々の定理はクロックがどれだけ厳密に同期できるかを示した。

分散システムではイベントの発生順序は部分順序に過ぎないことを認識することが重要である。この考え方はあらゆるマルチプロセスシステムを理解する上で有用だと考えている。それらを解決するためのメカニズムとは別に、マルチプロセッシングの基本的な問題を理解するのに役立つはずである。

付録

定理の証明

任意の $i$ と $t$ について、時刻 $t$ に $C_i$ と等しく設定され $C_i$ と同じ速度で動作するが決してリセットはされないクロックを $C_i^t$ と定義する。言い換えると、すべての $t' \ge t$ に対して \[ \begin{equation} C_i^t(t') = C_i(t) + \int_t^{t'} \left[ dC_i(t) / dt \right] dt \label{e1} \end{equation} \] ここですべての $t' \ge t$ に対して \[ \begin{equation} C_i(t') \ge C_i^t(t') \label{e2} \end{equation} \] であることに注意。

時刻 $t_1$ にプロセス $P_1$ がプロセス $P_2$ にメッセージを送信し、それが予測不可能な遅延 $\le \xi$ で時刻 $t_2$ に受信されたとする。ここで $t_0 \le t_1 \le t_2$ である。するとすべての $t \ge t_2$ に対して: \[ \begin{eqnarray*} C_2^{t_2}(t) & \ge & C_2^{t_2}(t_2) + (1 - \kappa)(t - t_2) & \mbox{[by ($\ref{e1}$) and PC1]} \\ & \ge & C_1(t_1) + \mu_m + (1 - \kappa)(t - t_2) & \mbox{[by IR2' (b)]} \\ & = & C_1(t_1) + (1 - \kappa)(t - t_1) - [(t_2 - t_1) - \mu_m] + \kappa(t_2 - t_1) \\ & \ge & C_1(t_1) + (1 - \kappa)(t - t_1) - \xi \end{eqnarray*} \] となる。したがって、これらの仮定を用いるとすべての $t \ge t_2$ に対して: \[ \begin{equation} C_2^{t_2}(t) \ge C_1(t_1) + (1 - \kappa)(t - t_1) - \xi \label{e3} \end{equation} \]

ここで $i=1,\ldots,n$ に対して $t_i \le t_i' \lt t_{i+1}$, $t_0 \le t_1$ であり、時刻 $t_i'$ にプロセス $P_i$ が $P_{i+1}$ にメッセージを送信し、それが時刻 $t_{i+1}$ に $\xi$ 未満の予測不可能な遅延を伴って受信されたとする。そして不等式 ($\ref{e3}$) を繰り返して起用すると $t \ge t_{n+1}$ について次の結果が得られる。\[ \begin{equation} C_{n+1}^{t_{n+1}}(t) \ge C_1(t_1') + (1 - \kappa)(t - t_1') - n \xi \label{e4} \end{equation} \] PC1, IR1' および IR2' より次のように推測される。\[ C_{n+1}(t) \ge C_1(t_1)+(1-\kappa)(t_1'-t_1) \] ($\ref{e4}$) と ($\ref{e2}$) を組み合わせるとすべての $t \ge t_{n+1}$ に対して次を得る。\[ \begin{equation} C_{n+1}(t) \ge C_1(t_1) + (1 - \kappa)(t - t_1) - n \xi \label{e5} \end{equation} \]

任意の 2 つのプロセス $P$ と $P'$ について、各 $P_i$ から $P_{i+1}$ への通信弧を持つ一連のプロセス $P=P_0,P_1,\ldots,P_{n+1}$, $n\le d$ の列を見つけることができる。仮定 (b) により、$t_i' - t_i \le \tau$ および $t_{i+1} - t_i' \le \nu$ である時間 $t_i$, $t_i'$ を見つけることができる。ここで $\nu = \mu + \xi$ である。したがって式 ($\ref{e5}$) の不等式は、$t \ge t_1 + d(\tau + \nu)$ の時は常に $n \le d$ が成立する。したがって任意の $i,j$ と $t1 \ge t_0$ かつ $t \ge t_1+d(\tau+\nu)$ であるような $t,t_1$ について次のようになる。\[ \begin{equation} C_i(t) \ge C_j(t_1) + (1 - \kappa)(t - t_1) - d \xi \label{e6} \end{equation} \]

ここで $m$ をタイムスタンプ $T_m$ を持つ任意のメッセージとし、時刻 $t$ に送信され時刻 $t'$ に受信されたものとする。$m$ は $C_m(t)=t_m$ かつ $C_m(t')=t_m+\mu_m$ となる一定即袖動作するクロック $C_m$ を持っていると仮定する。このとき $\mu_m \le t'-t$ は $dC_m/dt \le 1$ を意味する。ルール IR2' (b) は単に $C_j(t')$ を最大値 ($C_j(t'-0)$, $C_m(t')$) に設定するだけである。したがってクロックは他のクロックと等しく設定することによってのみリセットされる。

任意の時刻 $t_x \ge t_0 + \mu/(1-\kappa)$ について、時刻 $t_x$ で最大値を持つクロックを $C_x$ とする。すべてのクロックは $1+\kappa$ より小さい速度で動いているため、すべての $i$ とすべての $t \ge t_x$ に着いて次のようになる。\[ \begin{equation} C_i(t) \le C_x(t_x) + (1 + \kappa)(t - t_x) \label{e7} \end{equation} \] ここで次の 2 つのケースを考慮する: (i) $C_x$ がプロセス $P_q$ のクロック $C_q$ である。 (ii) $C_x$ がプロセス $P_q$ によって時刻 $t_1$ に送信されたメッセージのクロック $C_m$ である。(i) の場合 ($\ref{e7}$) は単純に次のようになる。\[ \begin{equation} C_i(t) \le C_q(t_x) + (1 + \kappa)(t - t_x) \tag{8i} \label{e8i} \end{equation} \] (ii) の場合、$C_m(t1) = C_q(t_1)$ かつ $dC_m/dt \le 1$ より次を得る。\[ C_x(t_x) \le C_q(t_1) + (t_x - t_1) \] したがって ($\ref{e7}$) は次を生成する。\[ \begin{equation} C_i(t) \le C_q(t_1) + (1 + \kappa)(t - t_1) \tag{8ii} \label{e8ii} \end{equation} \] $t_x \ge t_0 + \mu/(1 - \kappa)$ より \[ \begin{eqnarray*} C_q(t_x - \mu / (1 - \kappa)) & \le & C_q(t_x) - \mu & \mbox{[by PC1]} \\ & \le & C_m(t_x) - \mu & \mbox{[by choice of $m$]} \\ & \le & C_m(t_x) - (tx - t_1) \mu_m / \nu_m & \mbox{[$\mu_m \le \mu$, $t_x - t_1 \le \nu_m$]} \\ & = & T_m & \mbox{[by definition of $C_m$]} \\ & = & C_q(t_1) & \mbox{[by IC2'(a)]} \end{eqnarray*} \] したがって $C_q(t_x - \mu/(1 - \kappa)) \le C_q(t_1)$ であり、そのため $t_x - t_1 \le \mu/(1-\kappa)$ となり、したがって $t_1 \ge t_0$ となる。

(i) の場合に $t_1 = t_x$ とすると ($\ref{e8i}$) と ($\ref{e8ii}$) を組み合わせて、$t \ge t_x \ge t_0 + \mu/(1 - \kappa)$ となる任意の $t$, $t_x$ について、すべての $i$ に対して次のようなプロセス $P_q$ と $t_x-\mu/(1-\kappa)\le t_1\le t_x$ となる時刻 $t_1$ が存在すると推定できる。\[ \begin{equation} C_i(t) \le C_q(t_1) + (1 + \kappa)(t - t_1) \tag{9} \label{e9} \end{equation} \] $t \ge t_x + d(\tau + \nu)$ となる $t$ と $t_x$ を選ぶと ($\ref{e6}$) と ($\ref{e9}$) を組み合わせて、すべての $i$ について次のような $t_1$ とプロセス $P_q$ が存在する。\[ \begin{equation} C_q(t_1) + (1 - \kappa)(t - t_1) - d\xi \le C_i(t) \\ \le C_q(t_1) + (1 + \kappa)(t - t_1) \tag{10} \label{e10} \end{equation} \] $t = t_x + d(\tau + \nu)$ とすると次を得る。\[ d(\tau + \nu) \le t - t_1 \le d(\tau + \nu) + \mu / (1 - \kappa) \] ($\ref{e10}$) と組み合わせると次を得る。\[ \begin{equation} C_q(t_1) + (t - t_1) - \kappa d(\tau + \nu) - d\xi \le C_i(t) \\ \le C_q(t_1) + (t - t_1) + \kappa[d(\tau + \nu) + \mu/(1-\kappa)] \tag{11} \label{e11} \end{equation} \] $\kappa \ll 1$ と $\mu \le \nu \ll \tau$ という仮定を用いると ($\ref{e11}$) は以下の近似不等式に書き換えることができる。\[ \begin{equation} C_q(t_1) + (t - t_1) - d(\kappa\tau + \xi) \lesssim C_i(t) \\ \lesssim C_q(t_1) + (t - t_1) + d\kappa\tau \tag{12} \label{e12} \end{equation} \] これはすべての $i$ に対して成立するため \[|C_i(t) - C_j(t)| \lesssim d(2\kappa\tau + \xi)\] であり、これはすべての $t \gtrsim t_0 + d\tau$ に対して成立する。∎

証明での関係式 ($\ref{e11}$) により仮定 $\mu + \xi \ll \tau$ が無効な場合に $|C_i(t) - C_j(t)|$ の厳密な上限をもたらすことに注意。この証明の検討からクロックを高速に初期化し、何らかの理由で同期がとれなくなった場合に再同期するための簡単な方法が示唆された。各プロセスは他のすべてのプロセスに中継されるメッセージを送信する。この方法はどのプロセスからでも開始でき、各メッセージの予測不可能な遅延が $\xi$ 未満であると仮定すると同期を実行するに $2d(\mu + \xi)$ 秒しかかからない。

Acknowledgements

The use of timestamps to order operations, and the concept of anomalous behavior are due to Paul Johnson and Robert Thomas.

References

Schwartz, J.T. Relativity in Illustrations. New York U. Press, New York, 1962.
Taylor, E.F., and Wheeler, J.A. Space-Time Physics, W.H. Freeman, San Francisco, 1966.
Lamport, L. The implementation of reliable distributed multiprocess systems. To appear in Computer Networks.
Ellingson, C., and Kulpinski, R.J. Dissemination of system-time. IEEE Trans. Comm. Com-23, 5 (May 1973), 605-624.

翻訳抄

論理クロック (Lamport タイムスタンプ) に関する 1978 年の論文。

RF, L. Lamport. "Time, clocks, and the ordering of events in a distributed system." Commun. ACM 21 (1978): 558-565.