論文翻訳: Logical Physical Clocks and Consistent Snapshots in Globally Distributed Databases
Sandeep Kulkarni*, Murat Demirbas**, Deepak Madeppa**, Bharadwaj Avva**, and Marcelo Leone*
*Michigan State University
**University at Buffalo, SUNY
 Abstract
Abstract
分散システムにおける時間の扱いに関して、理論と実践の間には根本的な乖離が存在する。従来の分散システム理論は時間概念を意図的に排除し、並行性を論理的に扱うための抽象概念として "因果関係追跡" (causality tracking) を導入した。一方、実際のシステムでは厳密なクロック同期の実現が困難であることから、物理的な時刻情報 (NTP) を採用しつつも、ベストエフォート的な実装に留まっていた。この理論と実践の間のギャップを埋め、分散システムにおける時間管理の理論的基盤と実用的実装を整合させるため、本研究では論理クロックと物理クロックの双方の利点を統合したハイブリッド論理クロック (HLC) を提案する。HLC は論理クロックと同様に因果関係関係を捕捉可能であり、分散システムにおける一貫性のあるスナップショットの識別を容易にする。同時に、HLC は論理クロックを常に NTP クロックに近似した状態に保つため、物理クロックや NTP クロックの代替としても利用できる。さらに HLC は 64 ビット NTP タイムスタンプ形式に適合しており、NTP のよじれや不確実性に対しても耐性がある。本研究では、HLC が wait-free トランザクションの順序制御や、マルチバージョン型グローバル分散データベースにおけるスナップショット読み取り操作において、多くの利点をもたらすことを実証する。
Table of Contents
 1 導入
1 導入
 1.1 時間の簡潔な歴史
1.1 時間の簡潔な歴史
時間は幻想である。
- Albert Einstein
論理クロック (LC): LC [12] は 1978 年に Lamport によって分散システムにおけるイベントのタイムスタンプ付与と順序付けの手法として提案された。LC は物理的な時間 (例えば NTP クロック) とは独立した概念であり、ノードはクロックにアクセスできず、メッセージ遅延やノードの処理速度・処理能力に上限が存在しない。捕捉される因果関係は "happened-before" (hb) と呼ばれ、これは時間の経過ではなく情報の伝達に基づいて定義される1。LC は分散システム理論においては有用であるが、1) LC を使用するとイベントを物理的な時間軸と関連付けてクエリーを行うことが不可能である点、2) hb を捉えるために、LC は全ての通信が現在のシステム内で行われ、バックチャネル通信が存在しないことを前提としている点、といった現代の分散システム環境では実用的ではない点がいくつかある。これは現代の統合型で疎結合なシステム環境 (system of systems) においては時代遅れの前提条件である。
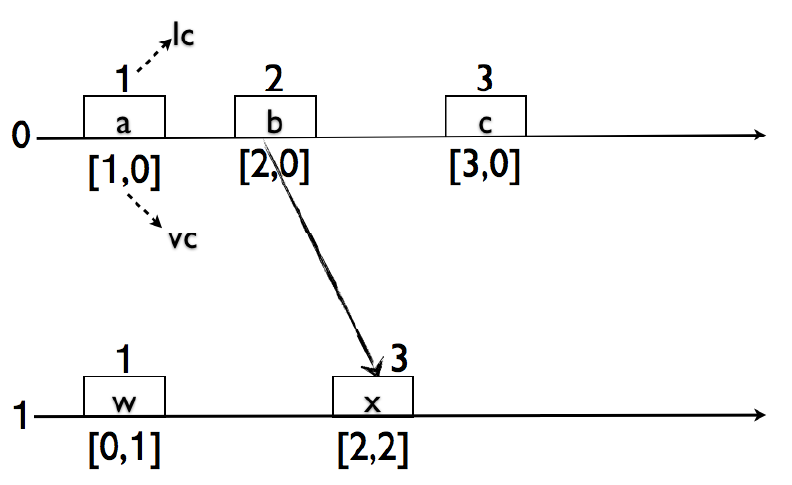
1988 年にはベクトルクロック (VC) [7, 19] が LC のベクトル化バージョンとして提案された。VC では各ノードでベクトルを保持し、そのノードが他のノードの論理クロックについて持っている知識を追跡する。LC は一貫性のあるスナップショットを 1 つの (関与するすべてのノードで同じ LC 値を持つもの) を見つけるのに対して、VC は可能なすべての一貫性のあるスナップショットを特定できる。これはアプリケーションのデバッグで有用である。Figure 1 に示すように、LC では (a, w) が一貫性カット (consistent cut) として検出されるが、VC は (b, w) や (c, w) も一貫性カットとして識別する。しかし残念ながら、VC の空間要件はシステム内のノード数に比例するため、実用的には許容できないレベルとなる。
物理時間 (PT): PT はネットワークタイムプロトコル (NTP) [20] によって同期されたノードの物理時計を利用する。分散システムにおいて完全なクロック同期を実現することは不可能であるため、PT には不確実性の範囲が付随する。PT は物理時刻を使用してタイムスタンプを付与することで LC の欠点を回避できるが、1) 不確実性の範囲が重複する場合、PT ではイベントの順序付けが不可能となる。NTP は通常、公開インターネット環境において数十ミリ秒単位の精度で時刻を維持でき、理想的な条件下のローカルエリアネットワーク内では 1 ミリ秒単位の精度を達成できる。しかし、非対称的な経路やネットワーク輻輳によって時折 100 ミリ秒以上の誤差が生じることがある。2) PTには、閏秒 [13, 14] や POSIX 時間への非単調更新 [8] といったいくつかのよじれ (kink) が存在し、これらによってタイムスタンプが逆行する現象が発生する可能性がある、という新たな欠点も生じる。
TrueTime (TT): TT は Google が分散型マルチバージョンデータベース Spanner [2] の開発のために最近提案した時刻同期方式である。TT は、各クラスタに配備された GPS 時計や原子時計によって実現される高精度なクロック同期機構に依存している。TT は LC/VC/PT の一部の欠点を回避できるが、新たな欠点も生じる: 1) TT の実装には専用ハードウェアと独自開発の高精度クロック同期プロトコルが必要であり、これは多くのシステム (例えばパブリッククラウドプロバイダーからリースしたノードを使用する場合など) にとっては実現が困難である。2) TT を因果関係を尊重するイベント順序付けに用いる場合、\(e \hb f\) ならば \(tt.e \lt tt.f\) という制約が必須となる。TT は純粋に物理クロックの同期のみに基づいているため、この制約を満たすために Spanner は必要に応じてイベント \(f\) の実行を遅延させる。このような遅延と並行処理能力の低下は、特にクロック同期精度の低い環境下では重大な制約要因となる。
ハイブリッド時間 (HT): HT とは、安定化因果決定論的マージ問題 (stabilizing causal deterministic merge problem) [10] を解決するために、VC と PT クロックの両方の特性を統合した時間概念として提案された手法である。HT では各ノードが自身の PT クロックに関する他ノードの知識を保持する VC を維持する。HT は PT クロックのクロック同期性という前提条件を利用して VC から不要なエントリを削除することで、因果関係追跡に伴うオーバーヘッドを削減する。実際のシステムにおいては、ノードの HT のサイズは、直近の \(\epsilon\) 時間枠内に通信を行ったノード数のみに依存する。ここで \(\epsilon\) は、クロック同期の不確実性を表すパラメータである。近年、Demirbas と Kulkarni [3] は HT を Spanner [2] の一貫性スナップショット問題の解決に適用する方法について検討を行っている。
 1.2 本研究の貢献
1.2 本研究の貢献
本論文では、分散システムにおける時刻同期とタイムスタンプ付与の理論 (LC) と実践 (PT) の間に存在するギャップを埋めることを目的とする。さらに、TT の保証を一般化・強化する新たな手法を提案する。
我々はハイブリット論理クロック (Hybrid Logical Clock; HLC) と呼ばれる論理クロック版の HT アルゴリズムを提案する。HLC は、物理クロック (PT および TT と同様の概念) と論理クロック (LC と同様の概念) の両方を改良したものである。HLC は常に自身の論理クロックを NTP クロックに近似させるように設計されており、これにより分散 Key-Value ストアやデータベースにおけるスナップショット読み取りなど、様々なアプリケーションにおいて物理クロックや NTP クロックの代替として使用することが可能となる。最も重要な点として、HLC は論理クロックの特性 (\(e \hb f \Rightarrow hlc.e \lt hlc.f\)) を保持するため、HLC はクロック同期の不確実性を待つ必要なく、事前の調整も必要とせず、事後的な方法で一貫性のあるグローバルスナップショットを取得し返却することができる。
HLC は NTP と後方互換性があり、64 ビットの NTP タイムスタンプ形式に適合する。さらに HLC は NTP プロトコルに対して重ね合わせ的に動作する (つまり、HLC は物理クロックを読み取るだけで更新は行わない) ため、HLC は NTP を使用するアプリケーションと干渉することなく並行して動作させることができる。加えて、HLC は特定のサーバ-クライアントアーキテクチャを必要としない汎用的な設計となっている。HLC は WAN 環境におけるピアツーピアノード構成でも動作し、各ノードが異なる NTP サーバを使用することを許容する2。セクション 3 では、HLC アルゴリズムを提示するとともに HLC の空間要件に関する厳密な上限値を証明し、この上限値が因果推論のための LC 特性を HLC が満たすのに十分であることを示す。
HLC は一般的な NTP の問題 (非単調な時刻更新を含む) を隠蔽することで耐性を提供し、さらに時刻同期が劣化した状態においても処理の進行と因果関係情報を捉えることができる。HLC は自己安定化機能を備えた耐障害性システムであり、セクション 4 で詳述するように、クロック変数の任意の破損に対しても耐性がある。
我々は HLC を実装し、様々な展開シナリオ下における HLC の運用実験結果を提供する。セクション 5 では、ストレステスト環境下においても HLC が適切に制御可能であり、クロック値のサイズが一定の範囲内に収まることを実証する。これらの実用的な境界は我々の分析で証明された理論的境界よりもはるかに小さい値である。我々の HLC 実装は https://github.com/AugmentedTimeProject から匿名で利用可能である。
HLC は分散データベース [2, 11, 15, 16, 22, 24] における一貫性のあるスナップショットの識別に直接的な応用がある。また、分散システムにおける因果メッセージロギング [1]、ビザンチン障害耐性プロトコル [9]、分散デバッグ [21]、分散ファイルシステム [18]、分散トランザクション [25] など、多くの分散システムプロトコルにおいても有用である。セクション 6 では、分散データベースにおけるスナップショット読み取りにおける HLC の利点を具体的に示す。
- 1イベント \(e\) がイベント \(f\) よりも時間的に先行する (\(e\) happened-before \(f\)) とは、\(e\) と \(f\) が同じノード上で発生し、\(e\) が \(f\) よりも時間的に先行している場合、または \(e\) が送信イベントであり、\(f\) がそれに対応する受信イベントである場合、または前二者に基づいて推移的に定義される。
- 2実際には、HLC はアドホックなクロック同期プロトコル [17] でも動作可能であり、NTP に限定されるものではない。
 2 予備知識
2 予備知識
分散システムは時間の経過とともにその構成ノード数が変動するノードの集合によって構成されるシステムである。各ノードは、送信動作、受信動作、およびローカル動作という 3 種類の動作を実行できる。タイムスタンプ付与アルゴリズムの目的はシステム内の各イベントに対してタイムスタンプを割り当てることにある。タイムスタンプ付与アルゴリズムは大文字で表記し、このアルゴリズムによって割り当てられたタイムスタンプは対応する小文字で表記する。例えば Lamport [12] の論理クロックアルゴリズムを LC と表記し、このアルゴリズムがイベント \(e\) に割り当てたタイムスタンプを \(lc.e\) と表記する。
happened-before \({\sf hb}\) はシステム内のイベント間の因果関係を捉える概念である。これは [12] で定義されているように、イベント \(e\) がイベント \(f\) よりも前に発生している (\(e\hb f\) と表記) とは、\(e\) と \(f\) が同じノード上で発生するイベントであり、\(e\) が \(f\) よりも先に発生している、あるいは \(e\) が送信イベントで \(f\) が対応する受信イベントである場合を指す推移的関係である。我々は \(\lnot(e\hb f) \land \lnot(f\ {\sf hb}\ e)\) の場合、イベント \(e\) と \(f\) が同時発生 (concurrent) している (\(e\,||\,f\) と表記) と言う。
既存の文献における研究成果に基づき、以下の命題が成り立つ: \[ e \hb f \Rightarrow lc.e \lt lc.f \\ lc.e = lc.f \Rightarrow e\,||\,f \\ e \hb f \Leftrightarrow vc.e \lt vc.f \] しかしながら、以下の主張は成り立たない: \[ e \hb f \Leftarrow lc.e \lt lc.f \\ lc.e = lc.f \Leftarrow e\,||\,f \\ e \hb f \Rightarrow pt.e \lt pt.f \]
 3 HLC: ハイブリッド論理クロック
3 HLC: ハイブリッド論理クロック
本セクションでは、我々の HLC アルゴリズムを紹介するためにまず単純な実装方法から始める。続いて HLC の正しさを証明し、その性能に関する厳密な上限値を示す。さらに、分散システムにおける HLC の有用な特徴についても詳細に解説する。
 3.1 問題定義
3.1 問題定義
HLC の目的は、LC が提供するものと同様の一方向因果関係検出 (one-wey causality detection) を実現しつつ、クロック値が常に物理クロック (NTP クロック) に近い値を維持することにある。HLC に関する正式な問題定義は以下の通りである。
分散システムにおいて、各イベント \(e\) に対してタイムスタンプ \(l.e\) を割り当てる。このとき、以下の条件を満たす必要がある:
\(e \hb f \Rightarrow l.e \lt l.f\)
\(l.e\) の空間要件は \(O(1)\) 個の整数で表現可能である。
\(l.e\) は有限の空間で表現される。
\(l.e\) は \(pt.e\) に近い値となる。すなわち \(|l.e-pt.e|\) は有界である。
第一の要件は HLC が提供する一方向因果関係情報を捉えるものである。第二の要件は、\(l.e\) の記憶領域要件が \(O(1)\) 個の整数で表現可能であることを意味する。複数の整数を単一の大きな整数にエンコードすることを防ぐため、\(l.e\) の更新処理は \(O(1)\) 回の操作で完了することを要求する。第三の要件は、\(l.e\) を表現するために必要な空間が有限であることを示しており、つまり無制限に増大しないことを意味する。実際には \(l.e\) のサイズは \(pt.e\) と同じであることが望ましく、NTP プロトコルではこれは 64 ビットに相当する。
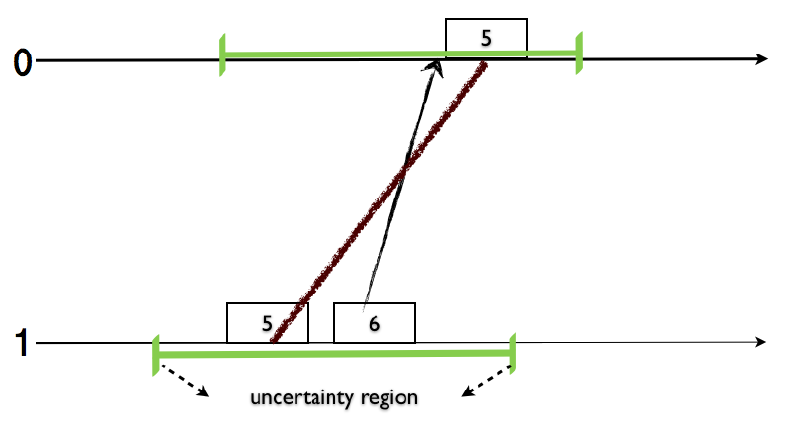
最後に、第四の要件は \(l.e\) が \(pt.e\) に近い値であるべきであることを規定している。これにより、我々は HLC を PT の代わりに使用できる。この利点を説明するため、設計者が (物理) 時刻 \(t\) でスナップショットを取得したい場合を考える。物理クロックは完全に同期していないため、Figure 2 に示すように異なるノードで時刻 \(t\) 時点での状態を読み取るだけでは一貫性のあるスナップショットを得ることはできない。一方、HLC を使用すれば、論理時刻 \(t\) 時点で全てのノードのスナップショットを取得することで、このような一貫性のあるスナップショットを得ることができる。このようなスナップショットが一貫性を持つことは保証されている。なぜなら、HLC の第一要件から \(l.e=l.f\Rightarrow e\,||\,f\) が成立するためである。セクション 6 では、協調を必要としない事後的な分散システム状態の一貫性のあるスナップショットをユーザが HLC で取得できるようにする仕組みについて、より詳細に解説する。
 3.2 ナイーブアルゴリズムの説明
3.2 ナイーブアルゴリズムの説明
\(l.e\) が \(pt.e\) に近い値となることを目標とする場合、ナイーブアルゴリズムではまず任意のイベント \(e\) において \(l.e \ge pt.e\) とする規則を採用する。我々は本アルゴリズムの設計を Figure 3 に示す。このアルゴリズムは LC アルゴリズムと同様の動作原理を持つ。初期状態では \(l\) の値は全ノードにおいて \(0\) に設定される。ノード \(j\) で送信イベント \(f\) が発生した場合、\(l.f\) には \(\max(l.e+1, pt.j)\) の値を代入する。ここで \(e\) はノード \(j\) における直前のイベントである。これにより、\(l.e \lt l.f\) と \(l.f \ge pt.f\) が保証される。同様に、ノード \(j\) で受信イベント \(f\) が発生した場合、我々は \(l.f\) に \(\max(l.e+1,pt.j)\) を設定する。ここで \(l.e\) はノード \(j\) における直前のイベントのタイムスタンプであり、\(l.m\) はメッセージ (すなわち送信イベント) のタイムスタンプである。これにより \(l.e \lt l.f\) および \(l.m \lt l.f\) が保証される。
Figure 3 に示すアルゴリズムが問題定義で示された最初の 2 つの要件を満たしていることは容易に確認できる。しかしながら、このナイーブなアルゴリズムは 4 つ目の要件を満たしておらず、これが空間制約下での表現における 3 つ目の要件の違反にもつながる。この 4 つ目の要件違反を示すため、Figure 4 に示す反例を参照されたい。この図は \(|l.e-pt.e|\) が無制限に増大していく様子を示している。ノード 1, 2, 3 間のメッセージングループは無限に繰り返すことができ、ループの各反復ごとに論理クロックと物理クロックのずれ (\(l-pt\) の差) は増大し続ける。
この無制限なクロックドリフト問題の根本原因は、ナイーブアルゴリズムが \(l\) を用いて、これまでに観測された \(pt\) 値の最大値と、新規イベント (ローカルイベント、送信イベント、受信イベント) による論理クロックの増分の両方の情報を保持しようとする点にある。この設計によりクロックは情報を失う。すなわち、新たに設定された \(l\) 値が \(pt\) 値に由来するものか (例えばノード 0 からノード 1 へのメッセージ送信の場合)、あるいは因果関係に由来するものか (その他のメッセージの場合) が不明確になる。このため、\({\sf hb}\) 関係を失うことなく \(l\) 値をリセットして \(l-pt\) の差を制限する適切な方法が存在せず、これは要件 1 の違反につながる可能性がある。
この反例は、ノードの物理クロックが当該ノード上の任意の 2 つのイベント間で少なくとも 1 回はインクリメントされるという要件を満たしている場合でも成立することに注意。Figure 4 はこの制約を \(pt\) と \(l\) の間に満たしているにもかかわらず、それでも \(|l-pt|\) の値は依然として無制限に増大し続ける。ただし、この反例が成立しない条件も存在し、単純なアルゴリズムで HLC 問題を十分に解決できる場合がある。具体的には、送信イベントと受信イベントに十分な時間が確保され、システム内のすべてのノードの物理クロックが少なくとも 1 回はインクリメントされる状況を仮定すれば Figure 4 の反例は成立せず、単純なアルゴリズムによって \(|l-pt|\) の値を有界に保つことができる。
システム内の全ノードにまたがって物理クロックの更新速度やイベント発生速度に関する仮定に依存して HLC の正しさと有界性を証明する代わりに、次セクションでは HLC を適切に実装する方法を示す。
| 1. | \( Initially \ lc.j := 0 \) | |
| 2. | \( {\bf Send \ or \ local \ event} \) | |
| 3. | \( \hspace{12pt}l.j := \max(l.j + 1, pt.j) \) | |
| 4. | \( \hspace{12pt}{\rm Timestamp \ with} \ l.c \) | |
| 5. | \( {\bf Receive \ event \ of \ message} \ m \) | |
| 6. | \( \hspace{12pt}l.j := \max(l.j + 1, l.m + 1, pt.j) \) | |
| 7. | \( \hspace{12pt}{\rm Timestamp \ with} \ l.j \) | |
 3.3 HLC アルゴリズム
3.3 HLC アルゴリズム
コンピュータサイエンスにおけるあらゆる問題は
さらなるレベルの間接参照によって解決可能である。
― David Wheeler ー
我々は反例から得られた知見を使用して正しい HLC アルゴリズムを開発した。このアルゴリズムでは、ナイーブアルゴリズムにおける \(l.j\) という表記を、\(l.j\) と \(c.j\) の 2 つの部分に拡張している。最初の部分 \(l.j\) は、これまでに学習した \(pt\) 情報の最大値を保持するための間接参照として機能し、\(c\) は \(l\) の値が等しい場合にのみ因果関係の更新を捉えるために使用される。
\({\sf hb}\) に違反することなく \(l\) をリセットする適切な場所が存在しなかったナイーブアルゴリズムとは対照的に、HLC アルゴリズムでは情報が最大 \(pt\) 値について到達またはそれを超えた時点で \(c\) をリセットすることが可能である。\(l\) はノード間で受信した最大 \(pt\) 値を示すものであり、イベントが発生するたびに連続的に増加するものではないため、一定の時間枠内では、以下のいずれかが必ず発生する: 1) ノードがより大きい \(l\) 値を含むメッセージを受信し、その \(l\) 値が更新されるとともに \(c\) もこれに対応してリセットされる、あるいは 2) 他のノードから情報を受信しない場合、ノードの \(l\) 値は変化せず、そのpt値が追いついてl値が更新され、同時に \(c\) もリセットされる。
HLC アルゴリズムの構造を Figure 5 に示す。初期状態では \(l\) と \(c\) の値はともに \(0\) に設定される。新たな送信イベント \(f\) が生成されると \(l.j\) は \(\max(l.e,pt.j)\) に設定される。ここで \(e\) は \(j\) ノードにおける直前のイベントを指す。ナイーブアルゴリズムと同様にこれにより \(l.j \ge pt.j\) が保証される。ただし "\(+1\)" の加算を削除したため \(l.e\) が \(l.f\) と等しくなる可能性がある。この問題に対処するため我々は \(c.j\) の値を利用する。\(c.j\) をインクリメントすることで辞書順比較3において \(\langle l.c, c.e\rangle \lt \langle l.f, c.f\rangle\) が成立することを保証する。\(l.e\) が \(l.f\) と異なる場合、\(c.j\) はリセットされ、これにより \(c\) の値が一定範囲内に収まることが保証される。新たな受信イベントが生成されると \(l.j\) は \(\max(l.e,l.m.pt.j)\) に設定される。ここで \(l.j\) が \(l.e\) と等しいか、\(l.m\) と等しいか、あるいはその両方であるかに応じて、\(c.j\) の値が設定される。
ナイーブアルゴリズムに対する反例について再考する。HLC アルゴリズムを適用した場合のこの例を Figure 6 に示す。ノード 1, 2, 3 の間でループを継続すると、ノード 1, 2, 3 の \(pt\) 値が \(l=10\) に追いつき、これを超えた後、\(c\) を \(0\) にリセットすることがわかる。これにより各ノードの \(c\) 変数が適切に制限される。
| 1. | \( Initially \ l.j := 0;\ c.j := 0 \) | |
| 2. | \( {\bf Send\ or\ local\ event} \) | |
| 3. | \( \hspace{12pt}l'.j := \max(l'.j, pt.j); \) | |
| 4. | \( \hspace{12pt}{\rm If}\ (l.j=l'.j)\ {\rm then}\ c.j := c.j + 1 \) | |
| 5. | \( \hspace{24pt}{\rm Else}\ c.j := 0; \) | |
| 6. | \( \hspace{12pt}{\rm Timestamp\ with}\ l.j, c.j \) | |
| 7. | \( \) | |
| 8. | \( {\bf Receive\ event\ of\ message}\ m \) | |
| 9. | \( \hspace{12pt}l'.j := l.j; \) | |
| 10. | \( \hspace{12pt}l.j := \max(l.j, l.m, pt.j); \) | |
| 11. | \( \hspace{12pt}{\rm If}\ (l.j = l'.j = l.m)\ {\rm then}\ c.j := \max(c.j, c.m) + 1 \) | |
| 12. | \( \hspace{24pt}{\rm Elseif}\ (l.j = l'.j)\ {\rm then}\ c.j := c.j + 1 \) | |
| 13. | \( \hspace{24pt}{\rm Elseif}\ (l.j = l.m)\ {\rm then}\ c.j := c.m + 1 \) | |
| 14. | \( \hspace{24pt}{\rm Else}\ c.j := 0 \) | |
| 15. | \( \hspace{12pt}{\rm Timestamp\ with}\ l.j, c.j \) | |

HLC アルゴリズムの正しさを証明するために、まずこのアルゴリズムが要件 1 を満たし、LC アルゴリズムとして使用できることを示す。これはアルゴリズム内で \(l\) 値と \(c\) 値がどのように更新されるかを見れば容易に理解できる。
定理 1. 任意の 2 つのイベント \(e\) と \(f\) に対して、\(e \hb f \Rightarrow (l.e,c.e) \lt (l.f,c.f)\) である。∎
次に HLC が要件 4 を満たすことを示す。この要件は HLC 値が PT 値に近いことを要求するものである。アルゴリズムにおける \(l\) の更新方法を考慮すると、定理 2 の証明は容易に理解できる。
定理 2. 任意のイベント \(f\) に対して、\(l.f \ge pt.f\) である。∎
定理 3. \(l.f\) は \(f\) が認識している最大クロック値を表す。言い換えると、\( l.f \gt pt.f \Rightarrow (\exists g: g \hb f \land pt.g = l.f) \) である。
Proof. 我々は新しいイベントが生成されるときに帰納法でこれを証明する。初期状態では、この命題は自明に満たされる。新しいイベント \(f\) が生成される場合を考える。
\(f\) が送信イベントで \(e\) が直前のイベントである場合、帰納法によって次が成り立つ。\[ l.e \gt pt.e \Rightarrow (\exists g: g \hb e \land pt.g = l.e) \] さらに、HLC アルゴリズムより、\(l.f \gt pt.f\) ならば \(l.f = l.e\) である。また \(e \hb f\) は真である。したがって次が成り立つ。\[ l.f \gt pt.f \Rightarrow (\exists g: g \hb f \land pt.g = l.f) \]
\(f\) が受信イベントで \(e\) が同じノード上の直前のイベント、\(m\) を受信したメッセージとする。
再び、\(l.f \gt pt.f\) が真ならば \(l.f\) は \(l.e\) または \(l.m\) に等しい。これらの各ケースの分析は前のケースと同様である。したがって次が成り立つ。\[ l.f \gt pt.f \Rightarrow (\exists g: g \hb f \land pt.g = l.f) \] ∎
定理 3 を使用して \(|l-pt|\) が有界であることを示すことができる。
系 1. 任意のイベント \(f\) に対して、\(|l.f - pt.f| \le \epsilon\) である。
Proof. クロック同期制約により \(e \hb f\) かつ \(pt.e \gt pt.f + \epsilon\) を満たす 2 つのイベント \(e\) と \(f\) が存在することはない。したがって、定理 3 からこの定理が導かれる。∎
最後に、要件 3 を証明するために HLC の \(c\) 値も有界であることを示す。これを実現するために定理 3 を拡張し、特定の時刻に生成されたイベントと \(c\) 値の関係を明らかにする。定理 4 で示すように \(c.f\) は時刻 \(l.f\) において生成されたイベントに関する情報を包含している。
定理 4. 任意のイベント \(f\) に対して、\[ \begin{align*} c.f = k \land k \gt 0 \Rightarrow & (\exists g_1, g_2, \ldots, g_k : \\ & (\forall j: i \le j \lt k: g_i \hb g_{i+1}) \\ & \land (\forall j : 1 \le j \le k : l.(g_i) = l.f) \\ & \land g_k \hb f) \end{align*} \]
Proof. 我々は帰納法によってこの命題を証明する。これは初期状態において自明に成立する。さらに \(c.f\) が \(0\) に設定される場合、この命題は自明に成立する。
送信イベントの生成において \(l.e\) が \(l.f\) と等しい場合に限り \(c.f\) が \(c.e+1\) に設定される。帰納法により、この定理の命題を満たす長さ \(c.e\) のシーケンスが存在する。さらに \(e \hb f\) かつ \(\lnot(e \hb e)\) が成り立つ。したがって、定理の命題を満たす長さ \(c.e+1\ (=c.f)\) のシーケンスが存在する。
\(c.f\) が \(c.e+1\) または \(c.m+1\) に設定される受信イベントに対しても同様の分析が適用される。∎
定理4から、以下の二つの系が導かれる。
系 2. 任意のイベント \(f\) に対して、\(c.f \le |\{g:g \hb f \land l.g = l.f)\}| が成立する。
系 3. 任意のイベント \(f\) に対して、\(c.f \le N * (\epsilon + 1)\) が成立する。
Proof. 系 2 より、任意のイベント \(f\) に対して \(c.f \le |\{g:g \hb f \land l.g=l.f)\}) が成り立つ。また定理 2 より \(l.g \ge pt.g\) である。さらに、クロック同期の前提により、\(g \hb f\) ならば \(pt.g \le pt.f+\epsilon\) となる。したがって、集合 \(\{g:g \hb f \land l.g = l.f)\}\) に含まれる可能性のあるイベントは、それを生成したノードの物理クロックが \([l.f,l.f+\epsilon]\) の範囲内にあったイベントのみである。ノードの物理クロックが任意の二つのイベント間で少なくとも 1 単位ずつ増加するという制約により、任意の単一ノード上にはそのようなイベントが最大で \(\epsilon+1\) 個しかない。以上より、系が成立することが証明される。∎
上記の境界はほぼ最適に近い値であるが、合理的な小さな仮定を追加することで \(c\) の境界を大幅に低減でき、その結果として割り当てる必要のある空間量を削減することが可能となる。
\(c\) の境界をさらに低減するための仮定: 我々は、メッセージ伝送の時間が十分に長く、全てのノードの物理クロックが少なくとも \(d\) だけ増加すると仮定する。ここで \(d\) は与えられたパラメータである。
ここで、ノード \(j\) で \(cf=k\)、\(k\gt 0\) となる状況を考える。前述の仮定に基づき、定理 4 によれば、定理 4 の条件を満たす \(k\) 個のイベント \(g_1, g_2, \ldots, g_k\) の列が存在する。言い換えると \(l.(g_1)=l.f\) である。\(g_1\) が生成されたノードを \(l\) とする。したがって、\(g_1\) が生成された時点で、\(pt.l\) は少なくとも \(l.f\) と等しかった。クロック同期に関する仮定により、\(f\) が生成された時点で、\(pt.l\) は少なくとも \(l.f+(k+1)\times d\) であった。クロック同期の制約を考慮すると、これは \(pt.f+\epsilon\) よりも小さい値でなければならない。これを簡略化すると、\(k\) は \(\epsilon/d+1+(pt.f-l.f)\) よりも小さい値となる。定理 2 から、以下の結論が得られる:
系 4. 前述の仮定の下で、\(c.f\) は最大でも \(\epsilon/d+1\) である。
\(d \ge 1\) の場合、Figure 4 に示した反例は成立せず、ナイーブアルゴリズムは有界性を持ち、かつ HLC 要件を満たすことになる。HLC アルゴリズムとナイーブアルゴリズムの違いは、HLC アルゴリズムは有界性を示すためにこのような仮定を必要としなかったが、有界性の範囲を縮小するためにこの仮定を利用したことである。
 3.4 HLCの特性
3.4 HLCの特性
HLC アルゴリズムは任意の分散アーキテクチャ向けに設計されており、クライアント・サーバーモデルをはじめとする他の環境にも容易に適用可能である。
我々は意図的に HLC を NTP への重ね合わせとして実装する方式を採用した。言い換えれば、HLC は物理クロックの値を読み取るのみで更新は行わない。したがって、あるノードがより新しいタイムスタンプを持つメッセージを受信した場合、物理クロック自体を変更する代わりに、\(l\) と \(c\) の値を用いてこの情報を記録・保持する。この設計は極めて重要であり、NTP のみを使用していた他のプログラムに影響を与えないようにするためのものである。これはまた、ノードの物理クロックが実際のウォールクロックから大幅にずれているにもかかわらず互いに同期されるという潜在的な問題を解決する。実際、わずかな非同期を許容してクロックを調整しようとすると、最終的にクロックが発散してしまうという結果が理論的に示されている [6]。最後に、HLC は同期のために NTP を利用するものの、その機能に完全に依存しているわけではない。特に、物理クロックがが任意のアドホックなクロック同期アルゴリズム [17] を採用している場合でも、HLC はそのようなサービスの上に重ね合わせて実装が可能であり、アドホックなネットワーク環境においても適用可能である。
- 3\((a,b) \lt (c,d) \Leftrightarrow ((a \lt c) \lor ((a=c) \land (b \lt d))\)
 4 HLCの障害耐性
4 HLCの障害耐性
 4.1 自己安定化
4.1 自己安定化
本セクションでは HLC に自己安定化 [4] を実装し、障害耐性を実現する手法について議論する。これにより、HLC が任意の状態に摂動/破損した場合でも最終的に正当な状態へと回復できる。
HLC の安定化は NTP クロックに対する HLC の重ね合わせ特性に基づいている。HLC は NTP クロックを変更しないため、ノードの物理クロックが NTP の補正や同期に干渉することはない。物理クロック/NTP クロックが安定化すると、定理 2 と補題 3 と 2 の観測結果に基づいて HLC を補正できる。これらの結果により、\(l-pt\) の最大許容値と \(c\) の最大値が明確に定義される。NTP による極端なクロック誤差や一時的なメモリ破損が発生した場合、これらの制約条件が破られる可能性がある。この場合、我々は物理クロックを基準とし、\(l\) と \(c\) の値をそれぞれ \(pt\) と \(0\) にリセットする。言い換えると、HLC の安定化は NTP クロックを介した \(pt\) の安定化プロセスの原理に従っている。
不良な HLC 値に起因する破損の拡散を抑制するため、我々は境界外のメッセージを拒否する規則を設けている。具体的には、\(l\) 値が \(pt\) から大きく乖離する原因となるメッセージの受信を単純に無視する。この防止措置は、メッセージ送信元が著しく高いクロック値を提供している場合に発動され、これはクロックの破損が発生している可能性を示唆している。\(c\) 値の破損を抑制するため、我々はその許容範囲を制限するように設計した。これにより、たとえ \(c\) 値が破損した場合でもその影響範囲は限定される。この方法で、最悪の場合でも \(c\) 値はロールオーバーするか、より現実的には \(l\) 値が \(pt\) から新たに取得された値またはメッセージ内で受信した別の \(l\) 値に再設定されることで、適切な値にリセットされることになる。
リセット補正処理と境界外メッセージ拒否処理のいずれも、ノードレベルでのローカルな補正動作であることに注意。HLC がこれらのいずれかの処理を実行した場合、問題のあるエントリを記録して検査用に保存するとともに、管理者に通知するための例外を発生させる。
 4.2 同期誤差のマスク処理
4.2 同期誤差のマスク処理
HLC を一般的な NTP 同期誤差に対して耐性を持たせるため、我々は \(l-pt\) ドリフトに十分な余裕を持たせている。これにより、NTP 同期のほとんど (99.9%) のよじれを円滑にマスクすることが可能となる。定理 2 および系 3 と 2 では、\(l-pt\) がクロック同期の不確実性 \(\epsilon\) (大まかに言えば NTP オフセット値の 2 倍) 内に収まることが示されているが、我々は \(l-pt\) 境界に非常に保守的な値 \(\Delta\) を設定している。この境界 \(\Delta\) は \(\epsilon\) の定数倍に設定でき、アプリケーションのセマンティクスによっては秒単位のオーダーにすることも可能である。この方法で、我々は一般的な NTP クロック同期誤差を HLC の通常動作の範囲内で許容しマスクすることができる。そして \(\Delta\) の境界が破られたとき、前セクションで述べたようにローカルリセット補正処理とメッセージ無視の抑止処理が自動的に発動する。
このアプローチにより HLC は同期遅延ノード (stragglers)、つまり \(pt\) がやや過去方向にドリフトしたクロックを持つノードに対しても耐性を持つ。NTP サーバーとの接続が切断されクロックが NTP 時間に対して遅れ始めたノードを仮定すると、このような同期遅延ノードであってもしばらくの間はシステムに追従し、最新かつ境界内で管理された HLC 時間を維持することができる。他のノードからメッセージを受信している限り、このノードは新しい/より大きい \(l\) 値を学習して採用する。このノードが新しい \(l\) 値を採用しない場合、\(c\) の値を \(1\) 増加させるが、これはシステム内の他のノードの \(c\) が過度に上昇する原因とはならない。たとえこのノードが高い \(c\) 値を持つメッセージを送信したとしても、他のノードは最新の時間情報を保持しているため、その \(c\) 値を無視して \(c=0\) を使用する。同様に、HLC は同期先行ノード (rushers) に対しても耐性を持つ。HLC のマスク処理許容範囲は Cassandra [8, 14] のような last-write-wins (LWW) データベースシステムにおいて特に有用である。我々はこの耐性特性について次のセクションで実証的に検証する。
 5 実験
5 実験
 5.1 AWS 環境におけるデプロイ結果
5.1 AWS 環境におけるデプロイ結果
実験には Amazon Web Services (AWS) の xlarge インスタンスを使用し、オペレーティングシステムとして Ubuntu 14.04 を採用した。各インスタンスは stratum 2 NTP サーバー 0.ubuntu.pool.ntp.org と同期設定されている。我々の基本設定では、すべてのインスタンスが TCP ソケットを介して相互に継続的にメッセージを送信し、別のスレッドで自分宛のメッセージを受信するようにプログラムした。送信されたメッセージの総数は 75,000 から 425,000 の範囲である。
同一 AWS リージョン内で基本設定 (全ノードが送信元かつ相互に送信を行う構成) を使用したところ次のの結果が得られた。値 "c" 各ノードの HLC の \(c\) 成分を示し、残りの列は頻度を示している。すなわち、各ノードの HLC が特定の \(c\) 値を示したイベントの割合を、全イベント数に対する比率で表している。各設定条件において 2 種類のNTP 同期レベルでデータを収集した。これはノードのクロックが NTP からどの程度ずれているかを示す平均オフセットで示されている。ノード上の NTP デーモンに同期処理のためのより多くの時間 (数時間) を与えると、NTP オフセット値はより小さくなることが分かった。我々は NTP オフセット情報の取得には "ntpdc -c loopinfo" と "ntpdc -c kerninfo" コマンドを使用した。
| c | offset=5ms | offset=1.5ms |
|---|---|---|
| 0 | 83.90 % | 83.66 % |
| 1 | 12.12 % | 12.03 % |
| 2 | 3.37 % | 4.09 % |
| 3 | 0.24 % | 0.21 % |
4 ノード構成の実験結果から、\(c\) 値が非常に低く、4 未満の値を示すことが明らかになった。これはセクション 3 で証明した最悪ケースの理論的境界よりもはるかに低い値である。また、改善された NTP 同期が \(c\) 値の分布をより低い値へとシフトさせる効果があることも確認された。この効果は特に 8 ノードおよび 16 ノードの実験でより顕著に観察された。NTP 同期の精度を落とした場合 (平均オフセット値 5ms)、最大の \(l-pt\) 差は 21.7ms に達した。\(l-pt\) 値の 90 パーセンタイル値は 7.8ms であり、その平均値は 0.2ms と算出された。一方、NTP 同期の精度を高めた場合 (平均オフセット値 1.5ms)、最大の \(l-pt\) 差は 20.3ms と観測された。\(l-pt\) 値の 90 パーセンタイル値は 8.1ms であり、その平均値は 0.2ms と算出された。
| c | offset=9ms | offset=3ms |
|---|---|---|
| 0 | 65.56 % | 91.18 % |
| 1 | 15.39 % | 8.82 % |
| 2 | 8.14 % | 0 % |
| 3 | 5.90 % | |
| 4 | 2.74 % | |
| 5 | 1.39 % | |
| 6 | 0.56 % | |
| 7 | 0.20 % | |
| 8 | 0.08 % | |
| 9 | 0.03 % |
8 ノードを使用した実験では NTP 同期の改善により \(c\) 値が低下したことが明らかになった。平均 NTP オフセットが 9ms の条件下では、最大 \(l-pt\) 差が 107.9ms に達した。\(l-pt\) 値の 90 パーセンタイル値は 41.4ms であり、その平均値は 4.2ms と算出された。平均 NTP オフセットが 3ms の条件では、最大 \(l-pt\) 差は 7.4ms であった。\(l-pt\) 値の 90 パーセンタイル値は 0.1ms であり、その平均値は 0ms と計算されている。
| c | offset=16ms | offset=6ms |
|---|---|---|
| 0 | 66.96 % | 75.43 % |
| 1 | 19.40 % | 18.51 % |
| 2 | 7.50 % | 3.83 % |
| 3 | 4.59 % | 1.84 % |
| 4 | 1.76 % | 0.32 % |
| 5 | 0.61 % | 0.06 % |
| 6 | 0.14 % | 0.01 % |
| 7 | 0.02 % |
16 ノードを使用した実験でも、すべてのノードがほぼ実線速度で相互通信を行っているにもかかわらず、極めて低い \(c\) 値が観測された。平均 NTP オフセットが 16ms の条件では、最大 \(l-pt\) 差が 90.5ms に達した。\(l-pt\) 値の 90 パーセンタイル値は 25.2ms、平均値は 2.3ms であった。平均 NTP オフセットが 6ms の条件では、最大 \(l-pt\) 差は 46.8ms であった。\(l-pt\) 値の 90 パーセンタイル値は 8.4ms、平均値は 0.3ms と算出された。
WAN デプロイ結果. 我々は WAN 環境でも HLC テスト実験を実施した。具体的には、AWS の異なるリージョン (アイルランド、米国東海岸、米国西海岸、東京) にそれぞれ配置した 4 台の m1.xlarge インスタンスを使用した。我々の結果によると、NTP オフセットが 3ms の場合、\(c=0\) となるケースが約 95% を占め、\(c=1\) となるケースが残りの 5% であった。これらの値は単一データセンター環境の対応する値よりも大幅に低い。最大 \(l-pt\) 差は極めて低く約 0.02ms に留まり、\(l-pt\) 値の 90 パーセンタイル値は 0ms であった。これらの値も単一データセンター環境の対応する値よりもさらに低い水準を示している。
WAN 環境で \(l\) 値と \(c\) 値が著しく低くなる理由は、WAN を介したメッセージ通信の遅延がクロック同期の不確実性 \(\epsilon\) よりもはるかに大きいためである。その結果、メッセージが受信された時点で、その \(l\) タイムスタンプは既に過去の時刻となっており、受信機側の \(l\) 値よりも小さい。メッセージ遅延の短い単一クラスタ環境が HLC テストにおいて最も要求の厳しいテストシナリオとなるため、我々は本発表で特にこの結果に焦点を当てて解説した。
 5.2 シミュレーションによるストレステストと障害耐性評価
5.2 シミュレーションによるストレステストと障害耐性評価
HLC の耐障害性をさらに詳細に分析するために、我々はイベント発生率が非常に高い場合やクロック同期が大幅に劣化した場合など、HTC に負荷がかかるシナリオで評価を行った。我々のシミュレーションでは、イベント発生率が 1 ミリ秒あたり 1 イベント、クロックドリフトが 10ms から 100ms の範囲内で変動するケースを検討した。定理 2 で示された \(l\) 値と \(pt\) 値の関係から、\(l\) 値と \(pt\) 値のドリフトはクロックドリフトの範囲内に制限される。したがって、我々は異なるイベントにおける \(c\) 値に焦点を当てて分析を実施した。
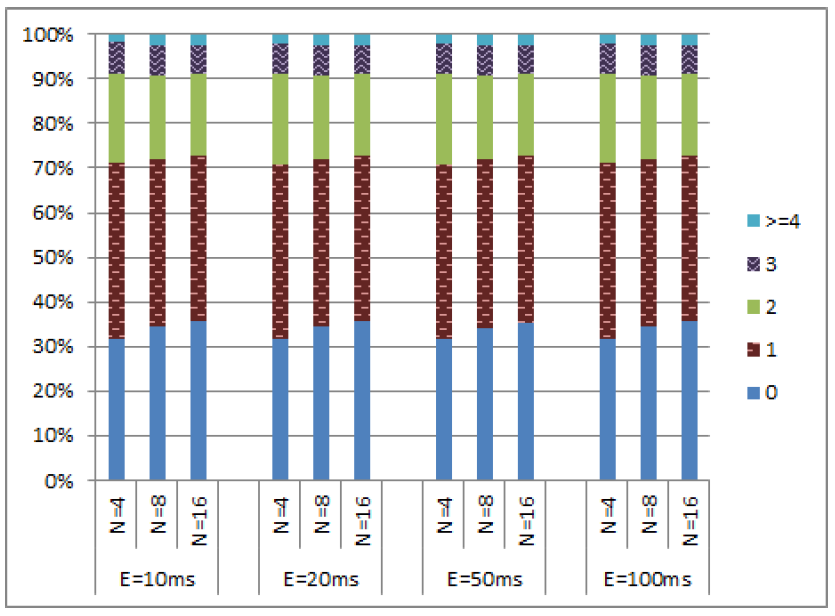
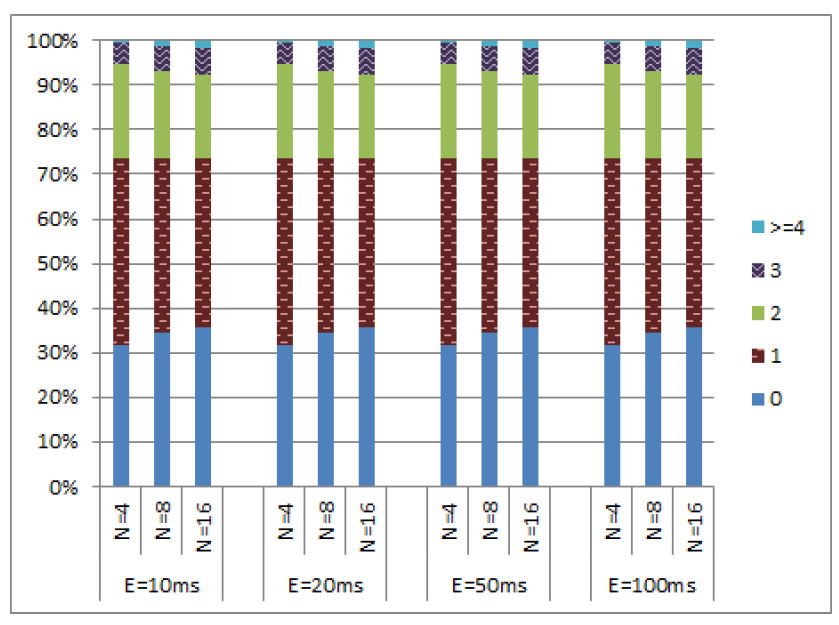
これらのシミュレーションでは、クロックドリフトが \(\epsilon\) を超えない限りノードの物理クロックを 1ms 進めることができる。ノードが物理クロックを進めることを許可されている場合、それを増加させるのは 50% の確率である。クロックを進めるときに一定の確率でメッセージ送信できる (このセクションのすべてのシミュレーションでは、この送信確率を 100% と仮定している)。我々はこのメッセージは最も早い実現可能なタイミングで送信し、実質的に送信時間を 0 とする。その結果は Figure 7 に示す通りである。これらの図が示すように、\(c\) 値の分布は \(\epsilon\) の値に対して比較的独立していた。さらに、99% 以上のイベントで \(c\) 値は 4 以下であり、\(c\) 値が 5 から 8 の範囲となるイベントは 1% 未満であった。
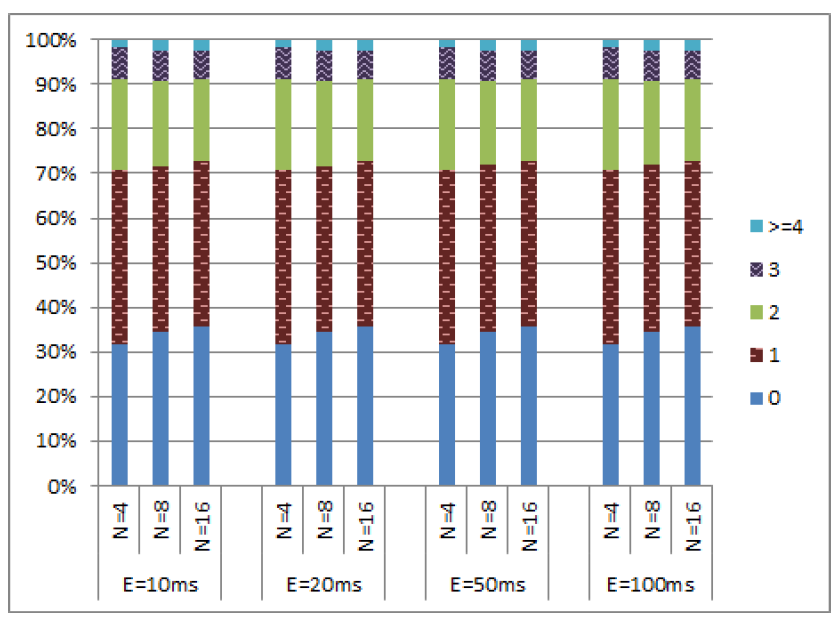
クロック同期が劣化した環境下における HLC の評価を行うため、システムに遅延同期ノードを追加した。このノードは常に他のノードよりも遅れて動作することで、クロックドリフトの制約を意図的に違反することが許可されている。我々は許容される境界のちょうど端に留まり、最大クロックとのクロックドリフト差が \(\epsilon\) である場合を想定する。また、遅延ノードが完全にクロックドリフトの制約を無視し、最大クロックに対して最大 \(5\epsilon\) の遅延が生じる場合についても検討した。その結果は Figure 8 および Figure 9 に示されている。遅延ノードが存在する場合でも 99% のイベントの \(c\) 値は 4 以下であった。ただし、これらのシミュレーションでは一部のイベントにおいて通常よりも高い \(c\) 値が観測された。特に、遅延ノードが許容境界の端部に位置している場合、遅延ノード上で最大 97 の \(c\) 値を示すイベントが観測された。遅延ノードのドリフトが \(5\epsilon\) までの範囲で許容された場合、遅延ノードのみで再び最大 514 の \(c\) 値が観測された。遅延ノードはシステム内の他のノードの \(c\) 値を上昇させなかったことが確認されている。
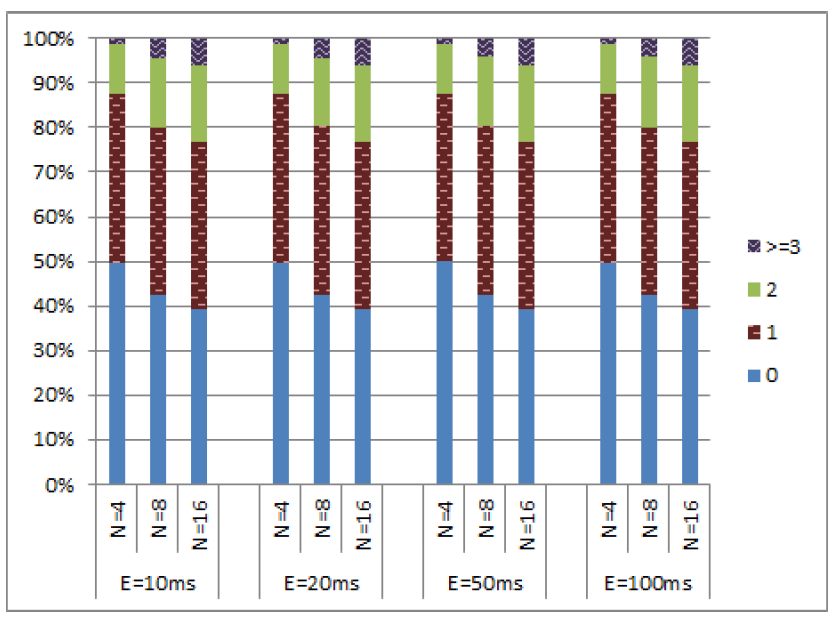
われわれはまた過度に先行するノードを導入した実験も実施した。Figure 10 および Figure 11 にその結果を示す。これらの実験で観測された最大の \(c\) 値は 8 であった。また \(c\) 値が 3 を超えるイベントの発生率は 1% 未満であった。
これらの実験結果から、遅延ノードは先行ノードよりもシステムの \(c\) 値により大きな影響を与えることが結論付けられる。ただし、その影響は自身のノードに限定されるものである。我々の実験では、各ノードは送信元を一様分布に従ってランダムに選択する。このため、先行ノードから送信されるメッセージは累積的な効果をもたらさない。一方で、すべてのノードから遅延ノードへ送信されるメッセージは遅延ノードの \(c\) 値を上昇させる要因となる。
 6 議論
6 議論
本セクションでは、分散データベースにおける一貫性のあるスナップショットを取得するための HLC の応用、\(l\) 値と \(c\) 値のコンパクトな表現手法、および関連研究について議論する
 6.1 スナップショット
6.1 スナップショット
スナップショット読み取り操作において、クライアントは特定の時点におけるデータのスナップショットを取得することに興味がある。HLC を用いることで、TrueTime と同様のスナップショット読み取りを実現可能である。さらに重要な点として、TT とは異なり、クロック値の不確実性に起因する遅延をトランザクションに発生させる必要がない。
我々のアプローチをより簡単に説明するため仮想ダミーイベントの概念を導入する。同一ノード上の 2 つのイベント \(e\) と \(f\) について、\(l.e \lt l.f\) が成立する場合、\(l\) 値が \([l.e+1,l.f]\) の範囲内にあり、\(c.f=0\) となるダミー (内部) イベントを定義する。(\(c.f=0\) の場合、シーケンスの最後のイベントは必ずしも必要ではない。) このようなダミーイベントを導入してもシステム内の他のイベントのタイムスタンプには影響を及ぼさないことに注意。ただし、この変更により任意の時刻 \(t\) に対して、すべてのノードに \(l\) 値が \(t\) に等しく \(c\) 値が \(0\) となるイベントが存在することが保証される。
仮想ダミーイベントの調整により時刻 \(t\) でのスナップショット読み取り要求に対して、我々はタイムスタンプ \(\langle l=t, c=0\rangle\) で値を取得できる4。我々の調整によってこのようなイベントが必ず存在することが保証される。さらに、要件 2 で言及した論理クロック \({\sf hb}\) の関係式により \(hlc.e=hlc.f \Rightarrow e\,||\,f\) が成り立つため、この時点において取得されたスナップショットは互いに一貫性を持ち、統一されたグローバルスナップショットを形成することが結論付けられる。さらに、定理 3 と系 2 に基づき、このスナップショットはグローバル時間がウィンドウ \([t-\epsilon,t]\) 内にある場合に対応する。
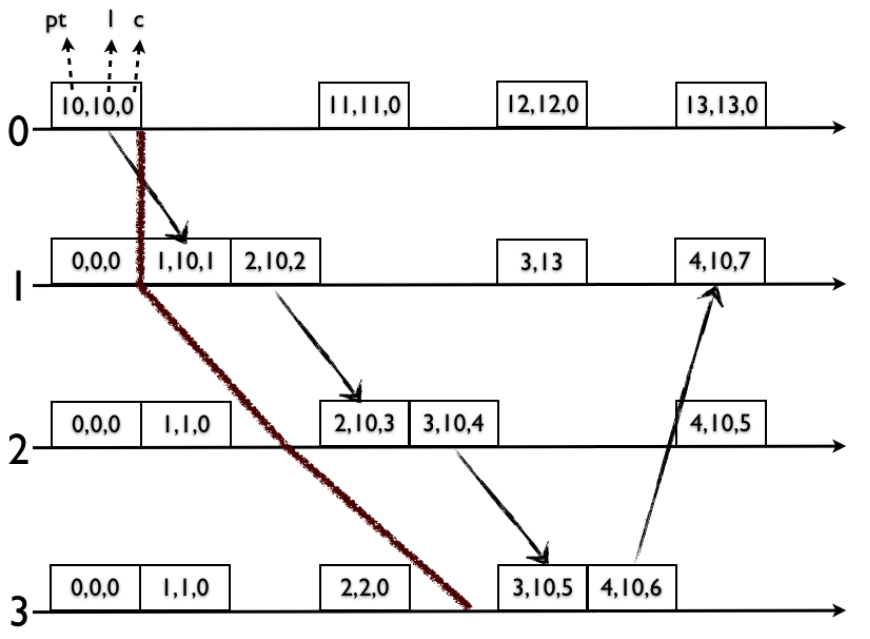
Figure 12 に、時刻 \(t=10\) でのスナップショット読み取り要求に対して一貫性のあるスナップショットを取得する具体例を示す。我々のアルゴリズムに従い、各ノードをタイムスタンプ \(\langle l=10,c=0\rangle\) の状態で読み取り、これは Figure 12 に示すスナップショットに対応する。
 6.2 \(l\) と \(c\) を用いたコンパクトなタイムスタンプ処理
6.2 \(l\) と \(c\) を用いたコンパクトなタイムスタンプ処理
NTP は 64 ビットのタイムスタンプを使用しており、これは 32 ビットの秒部分と 32 ビットの小数部分で構成される。(これにより \(2^{32}\) 秒 ― 136 年後 ― ごとにロールオーバーするタイムスケールと、理論上の分解能 \(2^{-32}\) 秒 ― 233 ピコ秒 ― が得られる。) HLC を単一の 64 ビットタイムスタンプで表現することは NTP クロックとの後方互換性を確保する上で非常に望ましい。NTP クロックとの互換性維持が重要な理由は、多くの分散データベースシステムや分散型キーバリューストアが NTP クロックを用いてレコードのタイムスタンプ付けと比較を行っているためである。
しかし HLC を単一の 64 ビットタイムスタンプとして表現するにはいくつかの課題がある。第一に、HLC アルゴリズムでは \(l\) と \(c\) を別々に維持し、物理クロックの経過時間による増加と、送信/受信/ローカルイベントによる因果関係の更新を区別する。第二に、\(pt\) を追跡することにより \(l\) のサイズはデフォルトで NTP タイムスタンプと同じ 64 ビットである。
我々は \(l\) と \(c\) を統合して単一の 64 ビットタイムスタンプに格納するために次のスキームを提案する。このスキームは Figure 5 に示す HLC アルゴリズムで、\(l\) が追跡する情報を \(pt\) の最上位 48 ビットに限定する。\(pt\) の値を 48 ビットに切り上げても、依然として \(pt\) をマイクロ秒の精度で追跡できる。NTP の同期精度を考慮するとこれは NTP 時刻を表現する上で十分な分解能である。\(pt\) の丸めは常に 48 ビット目まで切り上げる方式を採用する。Figure 5 の HLC アルゴリズムでは \(l\) の更新も同様に 48 ビット単位で行われ、イベント時に \(l\) の値が変化しない場合には、Figure 5 の HLC アルゴリズムに従って \(c\) をインクリメントすることでその変化を記録する。\(c\) には 16 ビットの余裕を持たせており、これにより最大 65536 までの値を表現可能となる。これは本論文のセクション 5 で示す実験結果からも明らかなように十分に広い範囲をカバーできる設計となっている。
このコンパクトな表現を使用してデータベースに保存するメッセージやデータ項目にタイムスタンプを付与する必要がある場合、我々は \(c\) を \(l\) に連結して HLC タイムスタンプを作成する。前述の分散型の一貫性スナップショット発見アルゴリズムはこのコンパクトな表現への変更によって影響を受けない。唯一必要な調整点はクエリー時間 \(t\) も 48 ビットに切り上げる必要がある点である。
 6.3 その他の関連研究
6.3 その他の関連研究
Dynamo [23] はレプリカへの更新の因果関係追跡のためのバージョンベクトルとして VC を採用している。Cassandra はレプリカへの更新操作に PT と LWW ルールを使用している。
Spanner [2] はグローバル規模で分散トランザクションを順序付け、分散データベース全体でのスナップショット読み取りを容易にするために TT を採用している。\(e\ {\sf hb}\ f \Rightarrow tt.e \lt tt.f\) を保証し、一貫したスナップショットを提供するために、Spanner はトランザクションコミット時に TT の不確実性区間を待つ必要があり、これが書き込み処理のスループットを制限する。しかし、これらの "コミット待機" により、Spanner はより強い性質の外部一貫性 (別名 strict serializability) を実現できる。つまり、トランザクション t1 が (絶対時間で) 別のトランザクション t2 の開始時刻よりも前にコミットした場合、t1 に割り当てられるコミットタイムスタンプは t2 のものよりも小さくなる。
HLC はクロックの不確実性を待つ必要がない。これは、HLC の更新ルールを使用して不確実性区間内の因果関係を記録できるためである。HLC は外部一貫性を提供するためにも採用でき、トランザクション終了後にクライアント通知待機を導入することで、書き込み処理のスループットを制限しないようにできる。
イベントの順序付けに関する代替アプローチはイベント間に明示的な関係を確立することである。この手法は Kronos システム [5] で例示されており、関心のある各イベントは Kronos サービスに登録され、アプリケーションが因果関係の観点から関心のあるイベントを明示的に識別する。これにより、システム内のイベント依存関係グラフを検索する追加のコストが生じるものの、アプリケーション固有の因果関係を捉えることができる。LC/VC/PT/HLC では対照的に、あるノードが連続する 2 つのイベントを実行する場合、2 番目のイベントは 1 番目のイベントに因果的に依存すると仮定する。したがって、イベントの順序付けは純粋にイベントに割り当てられたタイムスタンプのみに基づいて決定される。
- 4実際には \(\langle l=t,c=0\rangle\) だけでなく任意の \(\langle l=t,c=K\rangle\) に対してスナップショット読み取りを取得できる。
 7 結論
7 結論
本論文では、論理クロック (LC) の利点と物理時間 (PT) の利点を統合しつつ、それぞれの欠点を克服したハイブリッド論理クロック (HLC) を提案した。HLC は (一方向の) 因果関係情報が捕捉されることを保証するため LC の代替として使用できる。さらに HLC はノードに対して PT の可能なクロックドリフト範囲内の論理時刻を提供するため、PT を必要とするあらゆるアプリケーションで PT の代替として使用できる。HLC は厳密に単調増加性を有するため、NTP のよじれ (非単調な更新など) に耐性を持たせるためにアプリケーションで使用できる。
HLC は 64 ビットのメモリ空間で実装でき、NTP クロックと後方互換性もある。さらに HLC は NTP クロック値を読み取るだけで変更しないため、HLC を使用するアプリケーションが他の NTP 依存アプリケーションに影響を及ぼすことはない。
HLC は高い回復性を備えている。そのメモリ要件は理論解析によって厳密に規定されており、さらに我々の実験結果から厳密に制約されていることが明らかになっている。我々はこの特性を基盤として HLC に自己安定化障害耐性を設計する。
HLC は LC を精緻化したものであり、スナップショット読み取りのための一貫性スナップショットを取得するために使用できる。さらに、HLC と物理クロック間のドリフトは物理クロックのクロックドリフト量よりも小さいため、HLC で取得したスナップショットは特定の物理時刻におけるスナップショットとして十分に信頼できる選択肢となる。このため、HLC は特に他版分散データベースにおけるタイムスタンプ付与機構として特に有用である。例えば Spanner では TrueTime (TT) の代わりに使用でき、クロック同期不確実性ウィンドウ (clock synchronization uncertainty window) 内でイベントを遅延またはブロックする必要があるという TT の欠点の一つを克服できる。HLC は、アプリケーションイベントをアプリケーションが望む速度で生成することが可能となる。
 References
References
- K. Bhatia, K. Marzullo, and L. Alvisi. Scalable causal message logging for wide-area environments. Concurrency and Computation: Practice and Experience, 15(10):873–889, 2003.
- J. Corbett, J. Dean, et al. Spanner: Google's globally-distributed database. Proceedings of OSDI, 2012.
- M. Demirbas and S. Kulkarni. Beyond truetime: Using augmentedtime for improving google spanner. LADIS '13: 7th Workshop on Large-Scale Distributed Systems and Middleware, 2013.
- E. W. Dijkstra. Self-stabilizing systems in spite of distributed control. Communications of the ACM, 17(11), 1974.
- R. Escriva, A. Dubey, B. Wong, and E.G. Sirer. Kronos: The design and implementation of an event ordering service. EuroSys, 2014.
- R. Fan and N. Lynch. Gradient clock synchronization. In PODC, pages 320–327, 2004.
- J. Fidge. Timestamps in message-passing systems that preserve the partial ordering. Proceedings of the 11th Australian Computer Science Conference, 10(1):56–66, Feb 1988.
- K. Kingsbury. The trouble with timestamps. http://aphyr.com/posts/299-the-trouble-with-timestamps.
- R. Kotla, L. Alvisi, M. Dahlin, A. Clement, and E. Wong. Zyzzyva: Speculative byzantine fault tolerance. SIGOPS Oper. Syst. Rev., 41(6):45–58, October 2007.
- S. Kulkarni and Ravikant. Stabilizing causal deterministic merge. J. High Speed Networks, 14(2):155–183, 2005.
- Avinash Lakshman and Prashant Malik. Cassandra: Structured storage system on a p2p network. In Proceedings of the 28th ACM Symposium on Principles of Distributed Computing, PODC '09, pages 5–5, 2009.
- L. Lamport. Time, clocks, and the ordering of events in a distributed system. Communications of the ACM, 21(7):558–565, July 1978.
- The future of leap seconds. http://www.ucolick.org/~sla/leapsecs/onlinebib.html.
- Another round of leapocalypse. http://www.itworld.com/security/288302/another-round-leapocalypse.
- C. Li, D. Porto, A. Clement, J. Gehrke, N. Preguica, and R. Rodrigues. Making geo-replicated systems fast as possible, consistent when necessary. OSDI, 2012.
- W. Lloyd, M. Freedman, M. Kaminsky, and D. Andersen. Don't settle for eventual: Scalable causal consistency for wide-area storage with cops. In SOSP, pages 401–416, 2011.
- M. Maroti, B. Kusy, G. Simon, and A. Ledeczi. The flooding time synchronization protocol. SenSys, 2004.
- A. Mashtizadeh, A. Bittau, Y. Huang, and D. Mazieres. Replication, history, and grafting in the ori file system. In SOSP, pages 151–166, 2013.
- F. Mattern. Virtual time and global states of distributed systems. Parallel and Distributed Algorithms, pages 215–226, 1989.
- D. Mills. A brief history of ntp time: Memoirs of an internet timekeeper. ACM SIGCOMM Computer Communication Review, 33(2):9–21, 2003.
- B. Sigelman, L. Barroso, M. Burrows, P. Stephenson, M. Plakal, D. Beaver, S. Jaspan, and C. Shanbhag. Dapper, a large-scale distributed systems tracing infrastructure. Technical report, Google, Inc., 2010.
- Y. Sovran, R. Power, M. Aguilera, and J. Li. Transactional storage for geo-replicated systems. In SOSP, pages 385–400, 2011.
- W. Vogels. Eventually consistent. Communications of the ACM, 52(1):40–44, 2009.
- Z. Wu, M. Butkiewicz, D. Perkins, E. Katz-Bassett, and H. Madhyastha. Spanstore: Cost-effective geo-replicated storage spanning multiple cloud services. In SOSP, pages 292–308, 2013.
- Y. Zhang, R. Power, S. Zhou, Y. Sovran, M. Aguilera, and J. Li. Transaction chains: Achieving serializability with low latency in geo-distributed storage systems. In SOSP, pages 276–291, 2013.
翻訳抄
分散システムにおける論理クロックと物理時刻の長所を統合したハイブリッド論理クロック (HLC) を提案し、因果関係追跡と物理時刻への近似を両立させながら、64 ビット NTP 形式での実装と一貫スナップショット取得を可能にした 2014 年の論文。
- KULKARNI, Sandeep S., DEMIRBAS, Murat, MADEPPA, Deepak, AVVA, Bharadwaj and LEONE, Marcelo. Logical Physical Clocks and Consistent Snapshots in Globally Distributed Databases. In: AGUILERA, Marcos K., QUERZONI, Leonardo and SHAPIRO, Marc (eds.). Principles of Distributed Systems: 18th International Conference, OPODIS 2014, Cortina d'Ampezzo, Italy, December 16-19, 2014. Proceedings. Cham: Springer International Publishing, 2014, pp. 17-32. Lecture Notes in Computer Science, vol. 8878. ISBN 978-3-319-14472-6. Available from: https://doi.org/10.1007/978-3-319-14472-6_2