$ \def\vector#1{\boldsymbol{#1}} $

Version Vector

2021年8月28日 #VV #VersionVector #CausalConsistency

概要

Version Vector (VV) は並行して発生するイベントの因果関係 (causality, happened-before relation) を追跡するための機構。因果一貫性 (causal consistency) と呼ばれる一貫性モデルにおいて、競合する更新の因果関係を追跡しながら表現するために使用されている。

一般に結果整合性を持つ分散システムは可用性とスケーラビリティの面で優れている反面、システムを構成するレプリカノード間に一時的な不整合を許容している。このノード間の状態の差異はシステムのアンチエントロピー (anti-entropy) 機構によって検出と修復が行われる。ノード間の状態の不一致はそのデータの読み込み要求があったとき (Read Repair) や、またはバックグラウンドで Merkle Tree や Version Vector などを使用して検出する[3]。

VV は結果整合性をもつ Key-Value ストアにおいて異なるノード間で同時に発生する異なる更新操作を追跡し競合を検出するために使用されている。ただし、検出した競合をどう解決するかについて VV は考慮していない。競合の解決は対象とするイベントの性質とアプリケーション要件に依存する。CRDT [4] は並行性によって一時的に複数のバージョンが発生したとしても競合フリーでマージ可能なデータ型について論議している。

分散 Key-Value ストアはその単純な API とデータモデルにもかかわらず内部で因果一貫性を扱う機構は複雑である。VV 以降に提案されている新しい機構は、競合の検出と修復以外にも以下の課題の解決に取り組んでいる。

因果関係を捉えることが可能な論理クロックのメタデータはタイムスタンプのような単純なデータと比べてかなり大きくなる。空間効率を上げるためにさらなる最適化が必要である。
因果関係の追跡をノード ID に関連付けて行う場合、あるノードがシステムから離脱してそのまま復帰しないときに、そのノードに関連する因果情報をシステム全体で永遠に維持し続けなければならないという課題がある。これはノード離脱 (node churn) と呼ばれ、初期の DynamoDB や Riak では領域に上限があり LRU でエントリの削除を行っていた。ただしその解決方法は安全ではなく誤った競合を検出する可能性がある。
分散削除は因果関係の追跡と分断耐性の両方を維持しながらキーに関連する情報を削除することが困難という課題である。一部のノードがキーの削除に成功したとしてもその後の同期で復活したり、既に削除されたキーと同じキーで新たに設定された値を古い値が上書きするといった問題が起きる可能性がある。キーのメタデータを削除することなく墓石 (tombstone; 削除マーカーとして使う特殊な値) を維持し続けなければならない可能性がある。

これらの課題に加えて、単純な Version Vector の時間・空間的な効率の悪さや後述する兄弟爆発といった問題を解決するために、Dotted Version Vector [2] や Bitmap Version Vector [1] のような派生バージョンが多数提案されている。

概要
因果一貫性モデル
壁掛け時計
Lamport タイムスタンプ
ハイブリッド論理クロック
Causal Histories
Vector Clock
Version Vector
参考文献

因果一貫性モデル

あるイベント $e_a$ が別のイベント $e_b$ の前に起きている (happened-before) と決定できるとき $e_b$ は $e_a$ に起因するという。因果一貫性はこのようなイベントごとの因果関係を追跡することでそれらの順序を部分的に定義する¹。因果一貫性において因果関係が決定できないイベントは「並行」または「同時」であるとみなされる。

Fig 1 は $A$, $B$, $C$ の 3 つのノードで構成される分散システムにおいて、それぞれのノードで因果一貫性に基づいて発生しているイベントの例を示している。例えば $a_2$ は $\{c_1,a_1,b_2\}$ のイベントに起因し、$c_2$ や $b_4$ とは並行するイベントである。

Fig 1. 3 ノードで構成される分散システムでの因果関係に基づく非同期イベントの例。

因果一貫性を説明する上でしばしば 1 つの離散イベントや更新操作の発生時点をドット (dot) と呼ぶ (Fig 1 における各ノードの直線上のイベント発生点 dot はそれぞれドットである: ドットはアナログ時計盤上の時間を表す点のこと; on the dot で点の上に針が重なっている状態 = 時間きっかり、という意味)。ドットは何らかの識別子 $i$ とその識別子ドメインでアトミックに単調増加する整数カウンター $c$ のペア $(i,c)$ で表現され、基本的に分散システム全体での各イベントに対するグローバルに一意な識別子である。ただし、論文によっては特定のイベント発生点を指して "ドット" と呼んでいることもあり文脈による使い分けに少し注意を払う必要がある。

識別子にノード ID を使用する場合、例えば $a_2$ はドット $(A,2)$ として表現できる。それ以外にも (スケーラビリティが問題にならなければ) クライアント ID を使用することもできる。

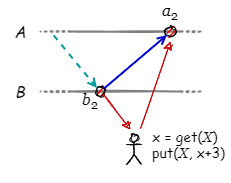
典型的な因果関係は read-modify-write パターン (get-put 操作) である。Fig 2 の例では最初にノード $B$ の $b_2$ を末尾とするコンテキストから値 $x$ を get し、次にその値を +3 加算してノード $A$ 上の新しいイベント $a_2$ として put している。この一連の操作によって $a_2$ が $b_2$ に起因することは明らかである。

イベントの因果関係は異なるノードで関連付けられることもあるし、単一のノード内で並行して複数の因果関係が発生することもある。しかし、システム全体としてのイベント順序を考えるとき Fig 1 でのノードの概念はそれほど重要でないこともある。システムのイベントの因果関係は Fig 3 のように平坦なグラフ構造で表すこともできる。

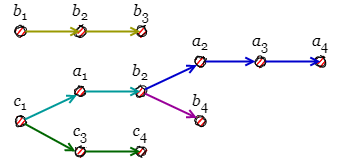
Fig 3 において因果関係が複数に分岐するとき、並行する異なるコンテキストが発生したこと、つまり競合が発生したことを意味している (概念上は git のブランチ機能を想像しても良い)。ここで 2 つの問題がある。

ノード間で発生している競合をどのように検出するか。これは単一のノードでどのように因果関係を記録し、それをノード間で比較できるようにするかを意味する。
ノード間で発生している競合をどのように修復するか。

このページではの並行するイベントを検出するためのデータ構造とその比較方法に焦点を当てる。

修復に関しての最も簡単な解決方法は、より後に発生したイベントがそれより前の全てのイベントを上書きする Last Write Wins (LWW) または Longest Version History Wins (LVH) と呼ばれるポリシーである。これはすべてのノードで何らかの論理クロックやバージョン付け機構に基づいてイベントを順序付けていることを前提としている。

一般に LWW は各ノードの最後のイベントのみを記録しておけば良いため空間効率は良い。しかし、書き込み操作が成功したとしても後に取り消される lost update や dead step と呼ばれる状況が発生する可能性を常に考慮しなければならならない。

CRDT (conflict-free replicated data type) ではどのようなデータ構造であれば並行して発生した競合を自動的に解決できるかについて定義している。

¹半順序または部分順序 (partial ordering)。すべてのイベントが完全に順序付けられるものは全順序 (total ordering)であり線形可能性 (linearizability) を持つため強い一貫性を達成している。

壁掛け時計

壁掛け時計 (wall-clock; ウォールクロック、物理時計) は参加者全員が見ることのできる共通の実時計を指す言葉である。具体的にはすべてのノードで完全に同期されている理想上のローカル時刻であったり、または時刻認証サーバのような役割を指している (このような理想上のクロックにしたがって全体が進行する方法をロックステップ (lockstep) とも呼ぶ)。Fig 4 は Fig 1 の例を壁掛け時計に基づくように書き直したものである。修復に LWW を適用するのであれば、ノード $A$, $B$, $C$ は最終的にそれぞれ $a_4$, $b_4$, $c_4$ のみを保存していればよく、システム全体は同期が進行するに連れてもっとも最後に発生したイベント $c_4$ の状態に収束するだろう。

Cassandra は壁掛け時計のタイムスタンプを使用して設計を簡素化している。しかし、広域分散しているすべてのノードの時刻を正確に同期させることは現実的には困難である (NTP の Slew モードでも秒間 0.5[ms] 程度の規模で誤差調整が差し込まれる; ノード間の 0.5[ms] の差はイベント順序が逆転するには十分な時間である)。また中央的な時刻認証サーバや順序サービスを設置すればそれが SPoF やボトルネックとなりスケーラビリティが低下する。タイムスタンプの重複も起きることから、現実のタイムスタンプのみに依存する方法はあまり現実的ではなく、後述のハイブリッド論理クロックを検討するほうが良い。

Lamport タイムスタンプ

分散システムであっても単一のノード内に限定すればセマフォや CAS を用いてアトミックなカウンターを実装することは難しくはない。Lamport タイムスタンプ [7] は各ノードが持つカウンター値をそれぞれ単調増加させることでイベント順序を決定する簡単な論理クロックアルゴリズムである。

アルゴリズム. 各ノードの論理クロックは初期値 0 から開始する。過去に因果関係を持たないイベントが発生するとローカルの論理クロックを 1 つ増加させるだけだが、イベントが過去の別のイベントに起因している場合は、ローカルの論理クロックと起因元イベントの論理クロックを比較し、より大きい論理クロック値に 1 つ加算してローカルの論理クロックを更新する。

Fig 5 は Fig 1 の例を Lamport タイムスタンプを使って書き直したものである。例えば $a_2$ は論理クロック値が 2 のノード $A$ 上で発生しているが、論理クロック値 3 の $e_{b_2}$ に起因していることから、$a_2$ の発生によってノード $A$ の論理クロックは 4 に更新される。

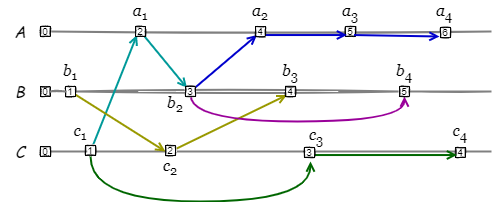
Lamport タイムスタンプは現実のタイムスタンプではないため時刻同期の問題は発生しないが、論理クロックの単調増加が保証できるのは単一のノード内に限定されているため、システム全体では半順序でありイベントの論理クロック値が重複(並行)する。[7] ではこれを全順序化する手段として、ノード ID とカウンターを組み合わせた値 (つまりドット) を論理クロックとし、カウンター値が同一の場合はノード ID の大小を考慮する方法が紹介されている。

Lamport タイムスタンプはこのような少しの修正で分散システムのイベント順序を全順序で結論付けることができるが、本質的に競合の発生が多く、また因果関係を追跡しないことから正確な競合解決方法を取ることが難しい。イベントが特定のノードに偏るとそのノードの論理クロックが急激に進み、相対的にそれ以外のノードのイベントが「過去のもの」になりやすい。これは LWW のようなアルゴリズムを採用しているとき問題となるだろう。

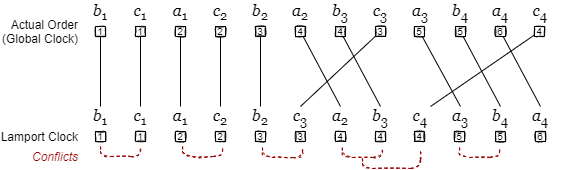
Fig 6. Fig 5 を Lamport タイムスタンプで順序付けした差異。

Fig 6 は Fig 5 を実際のイベント順序とみなし、同クロックを $A \lt B \lt C$ として Lamport タイムスタンプで順序付けした差異である。この規模であっても $c_3$ と $c_4$ の 2 箇所でイベント逆転が起きており、それらは隣り合うイベントが入れ替わる程度ではない。

ハイブリッド論理クロック

ハイブリッド論理クロック[5] (HLC; hybrid logical clock) は壁掛け時計と Lamport タイムスタンプを組み合わせた手法である。論理クロック $(t,c)$ はタイムスタンプ $t$ と整数カウンター $c$ で構成され、ある程度同期の取れた分散システムでタイムスタンプの重複やノードの時刻遅延の問題を解消している。Lamport タイムスタンプと比べてノード間で並行するイベントの論理クロックが重複 (競合) する頻度が低い利点がある。

論理クロック $(t,c)$ を持つイベント $e$ が存在し、$e$ に起因する別のイベント $e'$ の発生時刻を $t'$ とするとき、$e'$ の論理クロックは式 ($\ref{hlc}$) のように決定する。\[ \begin{equation} \left\{ \begin{array}{ll} (t', 0) & \ \ \mbox{if $t' \gt t$} \\ (t, c+1) & \ \ \mbox{if $t' \le t$} \end{array} \right. \label{hlc} \end{equation} \] つまり、新しく発生した $e'$ が $e$ より後であることがタイムスタンプから自明であればタイムスタンプを使用し、そうでなければカウンター値をインクリメントすることによって順序を保持するようにフォールバックしている。

HLC 自体はイベントの因果関係を完全に追跡できるものではないが、ある程度正確な現実のタイムライン上のイベント順序のみを追跡できれば良い場合に考慮することができる。

Causal Histories

Causal Histories はイベントの因果関係を追跡できる (おそらく) もっとも単純な方法。ローカルで新しいイベントが発生すると、現在のローカルの最新論理クロック集合と、イベントの起因する論理クロック集合の和集合に新しいカウンターを追加したものをイベントの論理クロックとする。

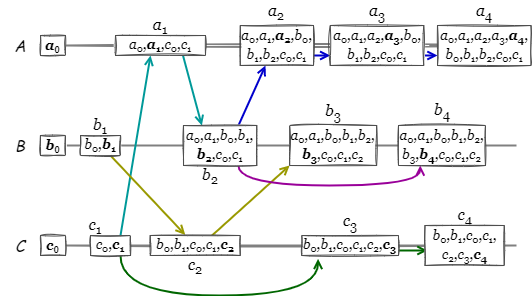
イベント $e_i$ の論理クロックを集合 $H_i$ とするとき、$H_1 \subseteq H_2$ であれば $e_2$ は $e_1$ に起因している。より効率的な判断では $H_1$ に含まれる最新のイベント (Fig 7 で太字で表記している値) が $H_2$ に含まれているかで判断することができる。例えば $H_{c_2}$ は $c_2$ を最新に持つが、$H_{a_3}$ には $c_2$ が含まれていないため $a_3$ は $c_2$ に起因していないと判断できる。

Causal History では同一のノード内で並行する因果関係を記述できないことに注意。言い換えると、同一ノード上のイベントはかならず因果関係を持つことを強制される。例えば $c_2$ は $b_1$ に起因しているが、$c_1$ とも因果関係を持つことになっている。

Causal Histories は因果関係を持つ全てのイベントを保持することから空間効率が悪い。Vector Clock はイベントの連続を圧縮している。

Vector Clock

Vector Clock は Causal Histories で連続する数値の集合として表現されていた論理クロックを圧縮し空間効率を向上した方法。別の見方では Lamport タイムスタンプで各ノードが管理していたただ 1 つの整数カウンターをノード個数分の整数カウンターに拡張した見ることもできる。Causal Histories と同様にイベント間の因果関係を表現することができるが、同一ノード内で並行する因果関係を記述できない点も同じである。

設定. システムを構成するノード数を $n$ としたとき、それぞれのノードは長さ $n$ の整数カウンターで構成されるベクトル $(t_1,\ldots,t_n)=\vector{t}$ で表される論理クロックを持つ。各整数カウンターの初期値は 0 である。
割当. あるノード $i$ 上でイベントが発生したとき、まずノード $i$ は自身の論理クロック $\vector{t}$ 上のカウンター $t_i$ をインクリメントする。次に、発生したイベントの起因元のイベントの論理クロックのカウンターそれぞれでに対して比較し、より大きい値を採用する。
```
def allocate(node, current_clock, causal_clock):
  new_clock = []
  for t1, t2 in zip(current_clock, causal_clock):
    new_clock.append(max(t1, t2))
  new_clock[node] += 1     # このノードのカウンター値はこのノード以外にインクリメントされない前提
  return new_clock
```

比較. 2 つのイベント $e_a$ と $e_b$ がそれぞれ論理クロック $\vector{t}_a$, $\vector{t}_b$ を持っているとする。$\vector{t}_a$ の少なくとも一つの要素が対応する $\vector{t}_b$ の要素より小さく、それ以外のすべての要素が小さいか等しい場合、$e_a$ は $e_b$ より前のイベントである。

from enum import Enum
class Causal(Enum):
  BEFORE = 1; AFTER = 2; SAME = 3; CONCURRENT = 4

def compare(e1, e2):
  state = Causal.SAME
  for t1, t2 in zip(e1, e2):
    if t1 < t2:
      if state == Causal.AFTER:
        return Causal.CONCURRENT
      state = Causal.BEFORE
    elif t1 > t2:
      if state == Causal.BEFORE:
        return Causal.CONCURRENT
      state = Causal.AFTER
  return state

print(compare([0, 0], [0, 0]))   # Causal.SAME
print(compare([0, 0], [0, 1]))   # Causal.BEFORE
print(compare([0, 1], [0, 0]))   # Caulsa.AFTER
print(compare([0, 1], [1, 0]))   # Causal.CONCURRENT

Fig 8 は Fig 1 を Vector Clock で書き直したものである。ノード上の Vector Clock の各整数カウンターは単調増加し、特にノード自身のカウンターは +1 ずつ増加している。また上記のアルゴリズムで因果関係を依存グラフ化すると Fig 3 と同等になることが分かる。

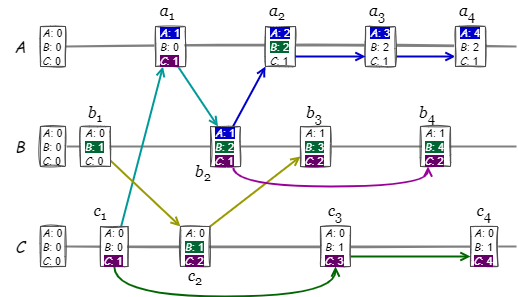
Fig 8 のイベント $b_2$ の論理クロックは Causal Histories 観点で $\{a_1,$ $b_1,$ ${\bf b}_2,$ $c_1\}$ と表記できる。Vector Clock の観点ではノード ID とのマップ $\{A \mapsto 1,$ $B \mapsto 2,$ $C \mapsto 1\}$, {A:1, B:2, C:1} または簡略に $[1,2,1]$ と表記する。

Causal Histories と同様に、Vector Clock でも論理クロック内の最後のイベントを比較することで効率的に因果関係を判断することができる。このため最後のイベントを $[1,2,1]b_2$ のように枠外に出したり [1,2,1] のように強調表示すると利便性が高い。このように枠外に表記されるような最後のイベントをドットと呼ぶ。

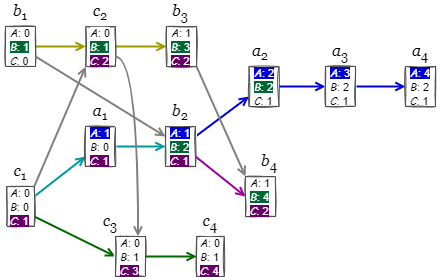
Vector Clock の各イベントの因果関係からグラフを構築すると Fig 9 のように表すことができる。これは Fig 3 の構造に同一ノード内の因果関係を強制したものである。

vector clock graph — Fig 9. Vector Clock を使ったイベントの因果関係のグラフ表現。

現実的な実装ではノードの参加や離脱によってシステムを構成するノード数 $n$ が固定できなかったり、参加しているがイベントには関与しないノードが存在することから、ベクトルではなくマップ (key-value) で保持することになる。しかし、あるノードが離脱したままシステムに復帰しない場合、そのノードのために各ノードが割り当てているカウンターの領域は残り続けることになる。

Version Vector

Version Vector [6] はパーティション分断が発生したネットワークでデータのレプリカが独立して更新された場合にその競合を検出することを意図して提案された。その機構は Vector Clock とほとんど同じのためしばしば混乱が見られるが、論理クロック機構そのものではなく、論理クロックに何が関連付けられているかという用途上の目的で使い分けられている。

Version Vectors are not Vector Clocks によれば、Vector Clock が全てのイベントの半順序シーケンスに関連付けられるのに対して、Version Vector はあるノードの状態遷移の最終状態のみに関連付けられる (つまり Version Vector は最終状態を引き起こしたイベントシーケンスは考慮しない)。したがって Version Vector は Vector Clock の要約表現、畳み込み結果とも言える。Key-Value ストアのようにキーに対する値の最終状態のみを追跡する用途では一般に Version Vector を使用する。

Version Vector はドット $(i,c)$ の集合として表される。識別子にノード ID を使用すれば Fig 8 と同様となるが、識別子をクライアント ID にすることも不可能ではない (DynamoDB ではクライアント ID も使用する[2]; ただし空間計算量はクライアント数に線形に増えるためスケールが難しくなる)。

Version Vector が対象とする Key-Value ストアの基本的な操作は get(key) と put(key,value,context) である。get(key) は (value,context) ペアを返す。get で得られる context は「どの因果に基づいて得た値か (具体的には起因する Version Vector)」を示しており、それを使用して行った put() 操作によって競合を検出することができる。

Fig 10 の例は、3 つのノードで複製される値をクライアントから並行して更新したときの、各ノードの Version Vector の変化を表している。ここで $\alpha|\beta$ は並行 (競合) する $\alpha$ と $\beta$ の並行値 (concurrent values) を示している (競合の解決方法が明確であれば競合を解決した後の値を示している)。説明のために更新のタイミングで a1 などのマーカーを置き、これをコンテキストとしている。

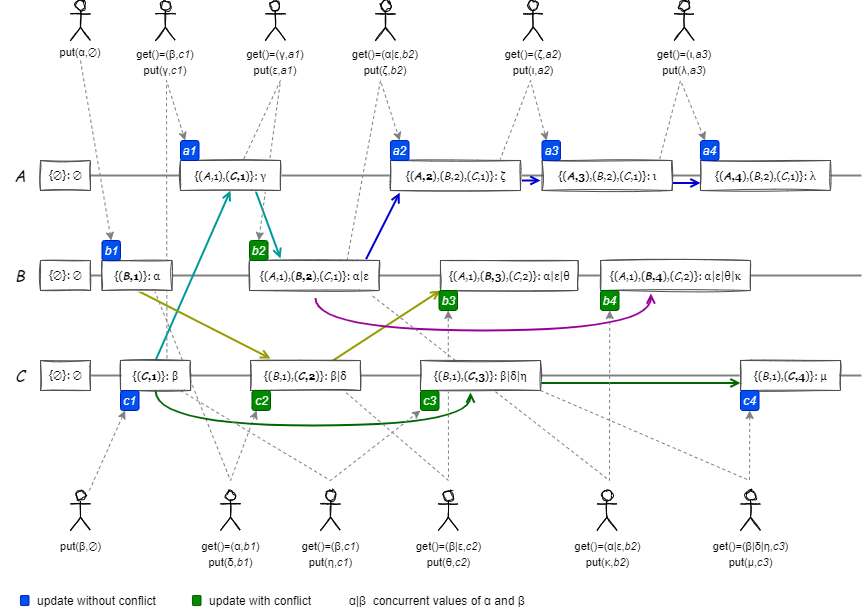
version vectors — Fig 10. Version Vector による、あるキーに対する最終状態の追跡。

すべてのノードは空の Version Vector と空の値で開始する。クライアントは特定のコンテキストに基づいて値を更新する (指定するコンテキストがない場合は $\emptyset$ を指定する)。ノードのコンテキストが更新操作のコンテキストより前であれば、その操作は競合していないため値は単純に置き換えられる (例:a2)。ノードのコンテキストが更新操作のコンテキストより後であったり (例:c3)、並行している場合 (例:b3) は並行値となる。

例えば b2 の更新操作は起因する a1 と b1 の論理クロックが競合しているため並行値 $\alpha|\epsilon$ となるが、a1 と b2 に起因する a2 は競合していないため単純に $\zeta$ (ゼータ) で上書きすることができる。

DynamoDB は Version Vector を使用して並行する書き込みを検出しタグ付けしている。

兄弟爆発の問題

競合を自動的にマージできないケースでは、競合を検出したときに並行値 $\alpha|\beta|\gamma$ を列 $[\alpha,\beta,\gamma]$ のような形で保持する必要がある。ここで並行値に含まれる $\alpha$, $\beta$, $\gamma$ をそれぞれ兄弟 (siblings) と呼ぶ。

Fig 11 のコンテキスト x1, x2, x3 に焦点を当てたとき、x3 の更新による値 $\gamma$ はコンテキスト x1 に起因していることから、正しくは競合ではなく x1 の状態だった $\alpha$ を上書きすべきである。しかし x2 の Version Vector ではそれを判断するための情報が欠落している。この意味で (ノード ID を識別子とする) Version Vector は同一のノード上で並行する因果関係を正確に表現する能力が欠落しており、更新 c3 で誤った競合の検出を引き起こしている。

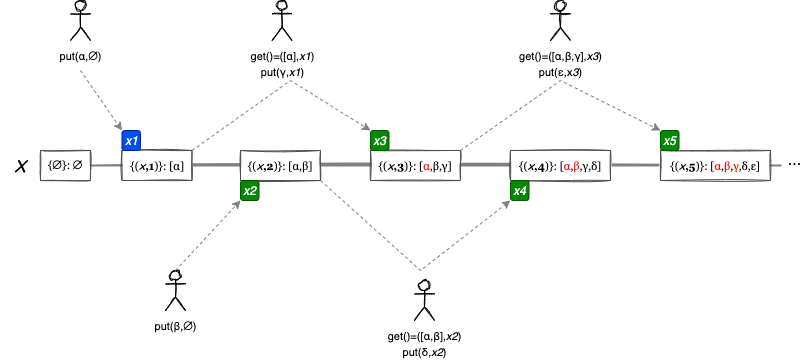
Version Vector Problem (Sibling Explosion) — Fig 11. 同一のノードで並行する更新を行った場合、ノード ID を識別子とする Version Vector では同一のコンテキストの置き換えが起きない。

Fig 11 のように競合する更新が繰り返されたとき (インターリーブ書き込み)、この競合の誤検出によって兄弟の数が更新回数対して線形に増加する可能性がある。兄弟が増えることでメッセージサイズが大きくなり、サーバやクライアントの負荷が増え、処理に時間がかかることでより競合が発生しやすくなり、さらに兄弟が増えるというフィードバックループに陥ることで兄弟爆発 (sibling explosion) と呼ばれる状態が発生する。これは特に多数のクライアントが同時に更新を行う高負荷環境を想定したときにスケーラビリティの問題となる。

Dotted Version Vector

Dotted Version Vector [2] (DVV) はこのようなインターリーブ書き込みによる兄弟爆発を回避するために、兄弟をそのコンテキストと関連付けて保存する。新しい更新を行うときには因果関係のある Version Vector を更新しその値を置き換える。

先述の競合の誤検出は Fig 10 でも c1-c3 や b2-b4 で起きている。Fig 12 は c1-c3 部分を DVV で置き換えたものである (見やすさのため若干変更している)。例えば y2 ではドット $\{X:1,Y:0\}=[1,0]$ に値 $\delta$ を関連付けて保存している。また y3 ではコンテキスト $[0,1]$ に対する更新操作であることが明らかであるため $\beta$ を $\eta$ に置き換えている。

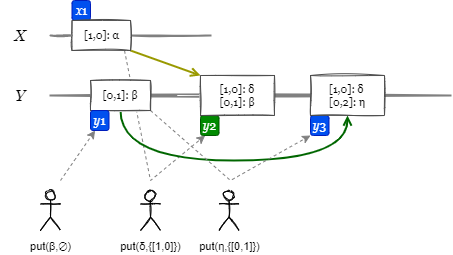
DVV は兄弟ごとにドットを保持することで不正確な並行値の発生を排除し、因果関係を持つ値を正しく置き換えることができる。Riak は DVV 使用して大量の並行書き込みをより効率的に処理できるようにしている。

DVV により同一ノードで並行する更新で競合の誤検出が発生する問題は解決するが、それでも並行している操作と同じ数の兄弟が発生する可能性が残っている。(クライアントがコンテキストを正しく認識すると仮定すると) 並行する操作は最悪でクライアント数となる。したがってクライアント数が想定できない環境での DVV はまだ問題が残っている。

Bitmap Version Vector

DVV は Key-Value ストアに対して特定のキーに関連付けられているコンテキストでのみ一意となる論理クロックである (object-wide)。このため、例えば put(Y, get(X) + 1) といったような、異なるキー間の更新の因果関係を追跡することができない。システムで一意となる論理クロックを構築するためにはノード単位の論理クロック (node-wide) と組み合わせる必要がある。

Bitmap Version Vector[1] (BVV) はシステムで一意な論理クロックを生成するために、ノード論理クロックとキー論理クロックのペアである Dotted Causal Container (DCC) という論理クロックを使用する。

BVV は論理クロックを使用する Key-Value ストアの中でもキーの分散削除が可能である。削除されたキーのコンテキストを永久に保存したり、または削除されたキーが再び現れたり、削除後に作成された新しいキーを喪失することがない。

ノード論理クロック (node logical clock) はそのノードが管理するキー全体の書き込み操作に関連付けられる集合である。ノード ID を識別子とするドット集合として表される。ローカルノードのドットは連続となるが、自分以外のノードのドットはキーごとに同期されるため非連続となるかもしれない。ただし、ノード間で同期が進むに連れてドットの前方のギャップが解消され連続となることから簡潔なデータ表現を用いることができる。

例えばノード論理クロック $\{(a,1)$, $(a,2)$, $(a,3)$, $(a,5)$, $(a,6)$, $(b,1)$, $(b,2)\}$ は前方の連続するドットをまとめることで式 ($\ref{bvv1}$) のように表すことができ、またはノード ID のマップとすることで ($\ref{bvv2}$) のように表すことができる。\[ \begin{eqnarray} \{(a,1),(a,2),(a,3),(a,5),(a,6),(b,1),(b,2)\} & \equiv & ([(a,3),(b,2)], \{(a,5),(a,6)\}) \label{bvv1} \\ & \equiv & \{a \mapsto (3, \{5,6\}), b \mapsto (2,\{\})\} \label{bvv2} \\ & \equiv & \{a \mapsto (3, 22), b \mapsto (2, 0) \} \label{bvv3} \end{eqnarray} \] 式 ($\ref{bvv1}$) のペア表記の第一要素 (最大連続ドット) は Version Vector、第二要素 (非連続ドット) はドット集合である。ドットをできるだけ連続にすることでノード論理クロックはコンパクトになるのは明らかだろう。ローカルノードに対するノード論理クロックは必ず連続となるため非連続ドットは常に空集合である。

さらに、Fig 13 で表すように、非連続ドット部分のドットの有無を 0/1 のビットマップに展開し単一の整数とすることで、式 ($\ref{bvv3}$) のような簡潔な表現を行うことができる。

式 ($\ref{bvv3}$) 表記の値は (base, bitmap) ペアである。このように表記されたノード論理クロックをビットマップ化された (bitmapped) Version Vector と呼ぶ。

キー論理クロック (key logical clock) は DVV のような機構である。

Bitmap Version Vector のノードは局所的に調整されたデータしか交換しないため、障害が発生したときにデータの一貫性を保つことができない。オブジェクトの因果関係を完全に削除することを保証しておらず、古くなったノード ID がノード論理クロックを汚染するためノード離脱がうまくサポートできていない。

参考文献

Ricardo Gonçalves, Paulo Sérgio Almeida, Carlos Baquero, and Victor Fonte. 2015. "Concise Server-Wide Causality Management for Eventually Consistent Data Stores." In Distributed Application and Interoperable Systems, 66-79. Berlin: Springer.
Almeida P.S., Baquero C., Gonçalves R., Preguiça N., Fonte V. 2014. "Scalable and Accurate Causality Tracking for Eventually Consistent Stores. In Distributed Applications and Interoperable Systems. DAIS 2014. Lecture Notes in Computer Science, vol 8460. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-43352-2_6
Alex Petrov. 2019. "Database Internals: A Deep Dive into How Distributed Data Systems Work", O'REILLY 978-1492040347
Shapiro M., Preguiça N., Baquero C., Zawirski M. (2011) Conflict-Free Replicated Data Types. In: Défago X., Petit F., Villain V. (eds) Stabilization, Safety, and Security of Distributed Systems. SSS 2011. Lecture Notes in Computer Science, vol 6976. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-24550-3_29
Kulkarni S.S., Demirbas M., Madappa D., Avva B., Leone M. (2014) Logical Physical Clocks and Consistent Snapshots in Globally Distributed Databases. In: Aguilera M.K., Querzoni L., Shapiro M. (eds) Principles of Distributed Systems. OPODIS 2014. Lecture Notes in Computer Science, vol 8878. Springer, Cham. https://doi.org/10.1007/978-3-319-14472-6_2
D.S. Parker, G.J. Popek, G. Rudisin, A. Stoughton, B.J. Walker, E. Walton, J.M. Chow, D. Edwards, S. Kiser, C. Kline. Detection of Mutual Inconsistency in Distributed Systems. In Journal of Parallel and Distributed Computing Volume 6, Issue 3, June 1989, Pages 498-514
RF, L. Lamport. "Time, clocks, and the ordering of events in a distributed system." Commun. ACM 21 (1978): 558-565.

Version Vector

概要

Table of Contents

因果一貫性モデル

壁掛け時計

Lamport タイムスタンプ

ハイブリッド論理クロック

Causal Histories

Vector Clock

Version Vector

兄弟爆発の問題

Dotted Version Vector

Bitmap Version Vector

参考文献