論文翻訳: Scalable and Accurate Causality Tracking for Eventually Consistent Stores
Paulo Sérgio Almeida1, Carlos Baquero1,
Ricardo Gonçalves1, Nuno Preguiça2, and Victor Fonte1
1 HASLab, INESC Tec & Universidade do Minho
{psa,cbm,tome,vff}@di.uminho.pt
2 CITI/DI, FCT, Universidade Nova de Lisboa
nuno.preguica@fct.unl.pt
 概要
概要
クラウドコンピューティング環境でのデータストレージシステムは、障害やネットワーク分断があっても良好なパフォーマンスと可用性を提供するために楽観的レプリケーションに依存していることが多い。このような環境では同時並行に実行された更新を正確かつ効率的に識別できることが重要である。楽観的レプリケーションにおける因果関係のトラッキングを行う現在のアプローチは同時更新の問題を抱えている。これらのアプローチは (1) 書き込み数やユニーククライアント数に応じて線形に増加する情報を維持するための複製が必要となるためスケールせず、(2) クライアント ID に基づくバージョンベクトルからエントリを削除したりサーバ ID に基づくバージョンベクトルを使うことで、因果関係に関する情報を喪失し誤ったコンフリクトを引き起こす。我々は従来の Key-Value ストア API をサポートしながら因果関係を正確かつスケーラブルに把握し、誤ったコンフリクトを回避するような新しい論理クロック機構と論理クロックフレームワークを提案する。この機構はデータレプリカごとに簡潔な情報を保持し、レプリカサーバ数に対してのみ線形であり、データレプリカをレプリカサーバとバージョン数に対して線形に比較・マージすることができる。
Table of Contents
- 概要
- 1 導入
- 2 システムモデルとデータストア API
- 3 現行のアプローチ
- 4 Dotted Version Vectors
- 5 Dotted Version Vector Sets
- 6 分散 Key-Value ストアでの dvv と dvvs の使用
- 7 複雑性と評価
- 8 関連研究
- 9 結びの辞
- References
- 翻訳抄
 1 導入
1 導入
Amazon の Dynamo システム [5] は Cassandra [10] や Riak [9] のような新世代のデータベースに重要な影響を与えた。これらのシステムは分断耐性、書き込み可用性、結果整合性に重点を置いている。これらのシステムの根底にある理論的根拠は、整合性、可用性、分断耐性という 3 つの同時目標に直面したときに、同じシステムで達成できるのはそのうちの 2 つだけであるという観察に由来している [3, 6]。分断を排除できない地理レプリケーションの運用環境では高可用性を実現するために必然的に整合性の要件が緩和される。
これらのシステムではデータストアが常に書込み可能な設計になっており、同一のデータ項目に対するレプリカが一時的に乖離しても後で修復することができる。Cassandra で採用されているシンプルな修復方法は、どの同時更新が優先されるべきかを知るために wall-clock タイムスタンプを使用する。この last writer wins (lww) ポリシーは更新の喪失につながる可能性がある。これを回避するためには、因果関係のある同時更新を表現し、それらが調整されるまで維持することのできるアプローチが必要である。
同時データ更新の正確な追跡は十分に確立された因果関係追跡機構 [11, 14, 20, 19, 2] を注意深く使用することで達成できる。特にデータストレージシステムではバージョンベクトル (vv) [14] によってシステムが任意の組み合わせで複製バージョンを比較し、それらが同等であるか、同時であるか、一方が他方を置き換えたかを検出することができる。しかしセクション 3 で説明するように、vv がサーバ ID で使われた場合には同時実行の値を正確に表現する能力に欠け、クライアント ID で使われた場合にはスケーラブルではない。
我々は新しいシンプルな因果関係追跡ソリューションである Dotted Version Vector ([16] で簡単に紹介されている) を導入し、これらの制約を克服してスケーラブル (サーバ ID を使用) かつ完全に正確 (同じサーバの同時書き込みを表現) な因果関係追跡を可能にする。これは、新しい書き込みイベントのをその因果関係のある過去から明示的に分離することで行っている。これにより 2 つのクロック間の因果関係を (バージョンベクトルのサイズに応じた線形でなく) 定数時間で確認できるという利点もある。
この論文では Dotted Version Vectors (dvv) を完全に説明するだけではなく 2 つの新しいコントリビューションを行っている。まず 2 つの DVV 制約を改善し、同時進行する DVV のセットを単一のデータ構造に効率的にまとめる新しいコンテナ (DVV セットまたは dvvs) を提案した上で (1) dvvs の表現は線形ではなく並行値の数に依存しない (2) 2 つのレプリカサーバの単一のキーに対する比較と同期は並行値の数に関して 2 次ではなく線形である。
我々の最後のコントリビューションは、結果整合性のあるシステムにおいて因果関係を正しく追跡するために論理クロックが実装すべき一連の機能を明確に定義した一般的なフレームワークである。我々はこのフレームワークを用いて dvv と dvvs の両方を実装した。
この論文の残りの部分は次のように構成されている。セクション 2 では論文の以降のためのシステムモデルを提示している。セクション 3 では因果関係追跡に対する現行のメカニズムを調査し比較する。セクション 4 では我々のメカニズム dvv を紹介し、セクション 5 ではそのコンパクトなバージョンである dvvs を紹介する。さらにセクション 6 では論理クロックの一般的なフレームワークを提案し dvv と dvvs の両方でその実装を行う。セクション 7 では現行のメカニズムと提案したメカニズムの漸近的な複雑さと dvvs の評価を行う。セクション 8 では追加の技術について簡単に説明する。最後にセクション 9 で結論を述べる。
 2 システムモデルとデータストア API
2 システムモデルとデータストア API
我々は \({\sf get}({\it key})\) と \({\sf put}({\it key},{\it value},{\it context})\) という 2 つの操作を提供する標準的な Dynamo-like な key-value ストアを考える。\({\sf get}\) はペア \(({\it value}({\it s}),{\it context})\)、つまり因果関係のある並行値の値またはセット、そして値に含まれる因果関係の知識をエンコードする不透明な \({\sf context}\) を返す。\({\sf put}\) は与えられた \({\sf context}\) に関連付けられたすべての値に優先する単一の値を提出する。この \({\sf context}\) は新規の値を書き込む場合には空、値を更新する場合は、以前の \({\sf get}\) によってクライアントに返された不透明なデータ構造である。この \({\sf context}\) は因果関係の情報をエンコードしており、API で使用することで \({\sf get}\) とそれに続く \({\sf put}\) の間に happens-before [20] 関係を生成することができる。
我々はノードが非同期のメッセージパッシングで通信する、共有メモリを持たない分散システムを想定している。このシステムは (例えば数百のオーダーの) サーバノードに対して同時並行で \({\sf get}\) や \({\sf put}\) 要求を行う多数の (例えば数千の) クライアントによって構成されている。各キーは、そのキーのレプリカノードと呼ばれる、サーバノードの小さなサブセット (例えば 3 ノード) に複製されている。クライアント、サーバ、レプリカの規模のオーダーが異なることが、スケーラブルな因果関係追跡機構の設計に重要な役割を果たす。
ここで我々は次のような仮定を置いている: グローバルな分散協調メカニズムがなくノードがアトミックなブロックを得るために内部的な同時実行制御を行うことができること; セッションのようなクライアント-サーバ間のアフィニティがなくクライアントはレプリカサーバノードから読み取って別のレプリカサーバノードに書き込むことを自由に行えること; ビザンチン故障はない; サーバノードは安定したストレージを持っている; ノードは警告なしに故障しても後に安定したストレージ内の最後の状態で回復することができる。
我々は異なるキー間の因果関係を追跡することを目的としていないため、残りの部分では暗黙の了解として単一のキーに対する操作に焦点を当てる。つまりこれから説明するサーバのデータ構造はすべてキーごとのものになっている。キーのグループ化を検討する場合、[13] のような手法を適用することでさらに節約できる可能性があるが、それについては今後の課題とする。
 3 現行のアプローチ
3 現行のアプローチ
異なるメカニズム間の比較を簡単にするために、クライアントである Mary と Peter、それに 1 つのレプリカノード間の簡単な実装例を紹介する。この例では Fig 1 に示すように、Peter はまず空のコンテキストを持つ新しいオブジェクトのバージョン \({\rm v_1}\) を書き込み、その結果あるサーバの状態は \(A\) となる。Peter はサーバの状態 \(A\) を読み込み、現在のバージョン \({\rm v_1}\) とコンテキスト \({\sf ctx}_A\) を返す。一方、Mary は空のコンテキストで新しいバージョン \({\rm v_2}\) を書き込み、その結果サーバは状態 \(B\) となる。Mary は状態 \(A\) を読まずに \({\rm v_2}\) を書き込んだため、因果関係が追跡されているなら、状態 \(B\) には \({\rm v_1}\) と \({\rm v_2}\) の両方が並行バージョンとして含まれているはずである。最後に、Peter は以前のコンテキスト \({\sf ctx}_A\) を使用して \({\rm v_1}\) を \({\rm v_3}\) に更新して状態 \(C\) となる。因果関係が正しく表現されていれば \({\rm v_1}\) は \({\rm v_3}\) に取って代わられ、\({\rm v_2}\) は \({\rm v_3}\) と並行しているため、状態 \(C\) には \({\rm v_2}\) と \({\rm v_3}\) しか存在しないはずである。ここで、様々な因果関係追跡アプローチがこの例にどのように対処するかを説明して Table 1 にまとめた。
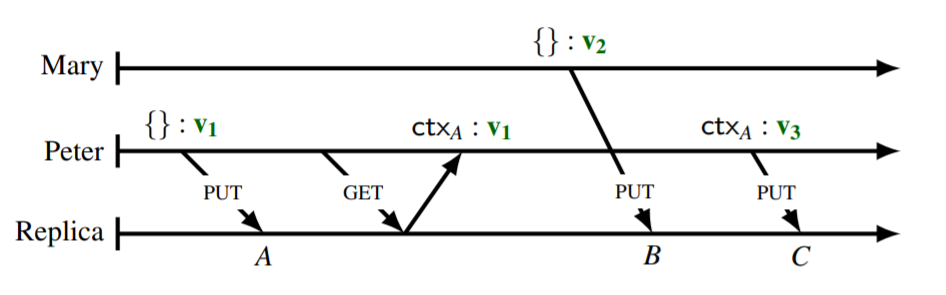
Last Writer Wins (lww). Cassandra のように lww ポリシーを適用するシステムでは、同時更新は保存状態としては表現されておらず最後の更新のみが優先される。lww ポリシーの下では、この例では \({\rm v_2}\) が失われることになるだろう。いくつかの特定のアプリケーションセマンティクスは lww ポリシーと互換性があるが、この単純化されたアプローチは他の多くのアプリケーションセマンティクスには適切ではない。一般的に、すべての更新で競合の解決を考慮するのであれば、同時進行する更新を正しく追跡することが不可欠である。
Causal Histories (ch). Causal Histories [20] は一意の書き込み識別子の集合によって単純に記述される。これらの識別子は一意の識別子と単調なカウンターで生成できる。この例ではサーバ識別子 \(r\) を使用しているがクライアント識別子を使用することもできる。ここで重要なのは、因果関係を正しく表現するためには識別子はグローバルに一意でなければならないということである。\({\it id}_n\) を \({\it id}\) で表されるエンティティの \(n^{\it th}\) 番目のイベントの表記とする。因果関係の部分的な順序は集合の包含関係としてこれらの集合を比較することによって正確に追跡することができる。2 つの \({\sf ch}\) はどちらも他方を含まない、つまり \(A \, \| \, B\) (これは \(A \not\subseteq B \land B \not\subseteq A\) と同値) なら同時である。この例からも分かるように \({\sf ch}\) は因果関係を正確に追跡することができるが、書き込み数に応じて線形増加するという大きな欠点がある。
Version Vectors (vv). バージョンベクトルは \({\sf ch}\) が各 \({\it id}\) のイベントシーケンスにギャップがないことを条件に \({\sf ch}\) を効率的に表現するものである。vv は識別子からカウンターへのマッピングであり、ペア \(({\it id},{\it counter})\) のセットとして書くことができる。各ペアはその \({\it id}\) に対するイベントのセット: \(\{{\it id}_n \mid 0 \gt n \ge {\it counter}\}\) を表している。部分順序の観点から、\(\forall (i,c_a) \in A \cdot \exists(i,c_b) \in B \cdot c_a \le c_b\) の場合のみ \(A \le B\) である。ここでも \(A \, \| \, B\) (\(A \not\le B \land B \not\le A\) と同値) である。vv にクライアント識別子とサーバ識別子のどちらを使うかは次に述べるように大きな影響を及ぼす。
クライアントごとの ID を使った Version Vectors (VVclient). このアプローチはクライアントの一意な識別子として vv を使用する。更新は \({\sf put}\) で発行されたクライアント ID を用いてサーバに登録される。この方法では、同時に実行されるクライアントの書き込みが vvclient の異なる ID で表現されるため、システムの並行性と因果関係を正確に符号化するのに十分な情報が得られる。しかし、vvclient はそのキーに書き込みを行ったすべてのクライアント ID を保存することになるためスケーラビリティが犠牲となる。Dynamo のようなシステムでは vvclient のエントリを特定のしきい値で刈り込み (pruning) することで補おうとしているが、一般的には誤った並行性が発生しさらなる調停が必要となる。また刈り込みの度合いが高いほどシステムにおける誤った並行性の度合いも高くなる。
サーバごとの ID を使った Version Vectors (VVserver). vvserver で因果関係を追跡する場合、つまりサーバ識別子で vv を使用する場合、異なるサーバノードで処理される同時更新を正しく検出することができる。しかし、同時更新が同じサーバ内で処理されているときに並行値 - 兄弟 (siblings) - を別々に表現する方法がない。(lww のように) 兄弟を上書きして情報が失われることを回避するための一般的な解決策は、すべての兄弟を同じ vvserver の下にグループ化し、個々の因果関係情報を喪失することである。これは誤った並行性になりやすい。なぜなら、書き込みの \({\sf context}\) が因果関係的にサーバ vvserver を支配している場合、すべての兄弟は古くなったとみなされ新しい値で置き換えられるか、あるいは、因果関係上の過去の兄弟であっても新しい値は現在の兄弟に追加されなければならいためである。
この例では、実際には Table 2 においての vvserver 以外の因果的に正しいメカニズムのように \({\rm v_3}\) が \({\rm v_1}\) を置き換えなければならないが、3 つの値 \(\{\)\({\rm v_1}\)\(,\)\({\rm v_2}\)\(,\)\({\rm v_3}\)\(\}\) すべてで実行を終了している (lww を除く)。
vvserver では、クライアントの読み込み-書き込みサイクルが同じサーバ上で同時に行われる他の書き込みと干渉すると誤った並行性が発生する可能性がある。これは、多数のクライアントが同時に書き込みを行う高負荷時に特に問題となる可能性がある。遅延が大きいときに他の同時書き込みと干渉せずに読み込み-書き込みサイクルを完了できない場合、兄弟のセットは増え続けるだろう。これによりメッセージのサイズが大きくなり、サーバの負荷は重くなり、ポジティブフィードバックのループに陥り、兄弟爆発 (sibling explosion) と呼ばれる状況が発生する。
| lww | ch | vvclient | vvserver | dvv | dvvs | |
|---|---|---|---|---|---|---|
| \(A\) | 17h00: \({\rm v_1}\) | \(\{r_1\}\): \({\rm v_1}\) | \(\{(p,1)\}\): \({\rm v_1}\) | \(\{(r,1)\}\): \({\rm v_1}\) | \(((r,1),\{\})\): \({\rm v_1}\) | \(\{(r,1,[\)\({\rm v_1}\)\(])\}\) |
| \({\sf ctx}_A\) | \(\{\}\) | \(\{r_1\}\) | \(\{(p,1)\}\) | \(\{(r,1)\}\) | \(\{(r,1)\}\) | \(\{(r,1)\}\) |
| \(B\) | 17h03: \({\rm v_2}\) | \(\{r_1\}\): \({\rm v_1}\) \(\{r_2\}\): \({\rm v_2}\) |
\(\{(p,1)\}\): \({\rm v_1}\) \(\{(m,1)\}\): \({\rm v_2}\) |
\(\{(r,2)\}\): \(\{\)\({\rm v_1}\),\({\rm v_2}\)\(\}\) | \(((r,1),\{\})\): \({\rm v_1}\) \(((r,2),\{\})\): \({\rm v_2}\) |
\(\{(r,2,[\)\({\rm v_2}\),\({\rm v_1}\)\(])\}\) |
| \(C\) | 17h07: \({\rm v_3}\) | \(\{r_2\}\): \({\rm v_2}\) \(\{r_1,r_3\}\): \({\rm v_3}\) |
\(\{(m,1)\}\): \({\rm v_2}\) \(\{(p,2)\}\): \({\rm v_3}\) |
\(\{(r,3)\}\): \(\{\)\({\rm v_1}\),\({\rm v_2}\),\({\rm v_3}\)\(\}\) | \(((r,2),\{\})\): \({\rm v_2}\) \(((r,3),\{(r,1)\})\): \({\rm v_3}\) |
\(\{(r,3,[\)\({\rm v_3}\),\({\rm v_2}\)\(])\}\) |
 4 Dotted Version Vectors
4 Dotted Version Vectors
我々はレプリカノードごとに 1 つの \({\it Id}\) を使用するだけで結果整合性を持つストレージを実現する、従来のバージョンベクトル (vv) の代替として使用できる正確なメカニズムを提供する。Dotted Version Vectors (dvv) の基本的な考え方は、vv を利用して個々の因果関係のあるイベント ─ dot ─ を他の連続したイベントから分離して表現できるようにすることである。ドットは過去の因果関係から切り離されており、書き込みをグローバルかつ一意に識別する。これにより同じサーバ上での同時書き込みを異なるドットで表現することができる。
Fig 1 の例では、状態 \(B\) において \({\rm v_1}\) と \({\rm v_2}\) が同じように空のコンテキストで書き込まれたにも関わらず、両方とも固有のドットで表現されていることが分かる。Peter による最後の書き込みでは、\({\rm v_1}\) のドット (および dvv) よりもコンテキストが優先されるため \({\rm v_1}\) が正しく上書きされ、コンテキストよりも新しいドットを持つ \({\rm v_2}\) が維持される。これに対して vvserver はすべての兄弟を一つの vv にまとめているため、ドットを分離することで得られるこの区別を失ってしまい、\({\rm v_1}\) が \({\rm v_3}\) によって古くなっていることを知ることができない。
 4.1 定義
4.1 定義
dvv はペア \((d,v)\) で構成され、\(v\) は従来の vv、ドット \(d\) はペア \((i,n)\) であり、\(i\) はノード識別子、\(n\) は整数である。ドットは書き込みとそれに関連するバージョンを一意に表し、vv は因果関係のある過去 (つまりそのコンテキスト) を表している。dvv で表される因果関係イベント (またはドット) は、論理的なクロックを因果関係履歴に変換する関数 \({\sf toch}\) によって生成することができる (\({\sf ch}\) はドットの集合とみなすことができる): \[ \begin{eqnarray*} {\sf toch}(((i,n),v)) & = & \{i_n\} \cup {\sf toch}(v), \\ {\sf toch}(v) & = & \bigcup_{(i,n) \in v} \{i_m \mid 1 \ge m \ge n \}, \end{eqnarray*} \] ここで \(i_n\) はノード \(i\) が生成する \(n^{\it th}\) 番目のドットを示し、\({\sf toch}(v)\) は同じ関数だが従来の vv に対するものである。この定義により vv で表現できない \({\sf ch} \{ a_1,b_1,b_2,c_1,c_2,c_4\}\) は \({\sf dvv}((c,4),\{(a,1),(b,2),(c,2)\})\) で表現できるようになる。
 4.2 部分順序
4.2 部分順序
dvv の部分順序は ch の包含の観点で定義することができる。すなはち: \[ X \le Y \Leftrightarrow {\sf toch}(X) \subseteq {\sf toch}(Y) \] 各ドットがグローバルにユニークなイベントとして生成される場合 (便宜上、任意の非写像的な ID に対する \((i,n)\in v\) かつ \(v[i]=0\) に対して \(v[i]=n\) という表記を使用して) dvv の値の部分順序は \[ ((i,n),u) \lt ((j,m),v) \Leftrightarrow n \le v[i] \land u \le v \] となり、ここで従来の vv のポイントワイズ比較 \(u \le v \Leftrightarrow \forall_{(i,n)\in u \cdot} n \le v[i]\) が使用される。
ドットを因果関係のある過去と分離しておくことの重要な帰結は、\(X\) のドットが \(Y\) の因果的過去に含まれていれば、\(Y\) は \(X\) に起因して生成されていることを意味し、したがって \(Y\) も \(X\) の因果的過去が含まれていることになる。つまり vv 成分の比較は必要なく、順序は (実質的に定数時間でマップデータ構造にアクセスできると仮定して) 単純に次のように \(O(1)\) で計算することができる。\[ ((i,n),u) \lt ((j,m),v) \Leftrightarrow n \lt v[i] \]
 5 Dotted Version Vector Sets
5 Dotted Version Vector Sets
前のセクションで紹介した Dotted Version Vectors (dvv) はサーバに基づく ID を使用して因果関係を正確に表現することができる。なお、dvv は各並行バージョン: \(\{({\it dvv}_1,v_1),({\it dvv}_2,v_2),\ldots\}\) に対して保持される。さらに操作はほとんどの場合単一のインスタンスではなく dvv の集合を扱うことになる。
ここではレプリカノードの特定のキーに対する \(({\it dvv},{\it version})\) の集合を、その集合全体の因果関係を記述する単一のコンテナデータ型である Dotted Version Vector Set (dvvs) インスタンスで表現することを提案する。dvvs は記述されている dvv 集合に対する共通の知識を因数分解し、厳密に関連する情報のみを情報のみを単一のデータ構造に保持する。これにより、非常に簡潔な表現が得られるだけでなく、操作の時間複雑性も軽減される。並行値はデータ構造の中でインデックス化されて順序付けられ、トラバーサルが効率的に行われる。
 5.1 クロックの集合から集合のクロックへ
5.1 クロックの集合から集合のクロックへ
バージョンの集合に対する論理クロックを得るために、各ノードにおいて dvv の集合全体がコンパクトな vv で表現できるという事実を探る。形式的には、この不変性は dvv の任意の集合 \(S\) について、各ノード ID \(i\) に対して、\(S\) 内の \(i\) に対するすべてのドットがあるドットまで連続した範囲を形成することを意味する。この不変量があると仮定できるのはセクション 6.3 で詳述するフレームワークのプロトコルルールに従う場合のみであることに注意。
この不変性を仮定すると、バージョンの集合を 2 段階で変換することにより \(({\it dvv},{\it version})\) の集合の論理クロックを得ることができる。最初のステップでは dvv 内のドットと vv の点ごとの最大値によって集合全体の単一の vv ─ トップベクトル ─ を計算する; さらに、集合内の各 dvv に対して vv 成分を破棄する。例として次の集合: \[ \{(((r,4),\{(r,3),(s,5)\}),v_1),(((r,5),\{(r,2),(s,3)\}),v_2),(((s,7),\{(r,2),(s,6)\}),v_3)\} \] はトップベクトル \(\{(r,5),(s,7)\}\) を生成し \(({\it dot},{\it version})\) の集合: \[ \{((r,4),v_1),((r,5),v_2),((s,7),v_3)\} \] に変換される。
最初の変換により各バージョンの特定の因果関係となる過去という知識が失われた。しかしこの知識は我々の目的には必要ない。洞察は、バージョンの別の集合 \(S\) と比較したときに、ある集合から (dot,version) ペア \((d,v)\) を破棄するかどうかを知るためには、\(S\) のどのバージョンが \(d\) を支配しているかを正確に知る必要はなく、あるバージョンが支配していることを知るだけで良いということである。バージョン \(v\) が \(S\) に存在しないがそのドット \(d\) が \(S\) 全体 (トップペクトルで表されるようになった) の因果関係情報に含まれているのであれば、\(v\) は古くなっており削除できることが分かる。
第二ステップでは、各サーバ ID のすべてのドットが、対応するトップベクトルのエントリまでの連続したシーケンスを形成しているという知識を使用する。従って、トップベクトルの各エントリにバージョン (兄弟) のリストを関連付けることができ、各ドットはリスト内の対応するバージョンの位置によって暗黙的に導かれる。この例では、全体の酒豪は次のように単純に記述される: \[ \{(r,5,[v_2,v_1]),(s,7,[v_3])\} \] ここで各リストの先頭は、対応するノードでより最近に生成されたバージョンに対応する。最初のバージョンは、そのエントリのトップベクトルの最大値に対応するドットを持ち、2 番目のバージョンは最大値から 1 を引いた値を持ち、以下同様である。
 5.2 定義
5.2 定義
dvvs はトリプル \((i,n,l)\) の集合であり、それぞれサーバ ID、整数、および並行バージョンのリストを含んでいる。dvvs はバージョンの集合とそのドットを記述し、そのリスト内での位置によって暗黙的に与えられる。またペア \((i,n)\) から得られる vv によって与えられる、集合的な因果関係の履歴に関する知識のみを記述する。
 6 分散 Key-Value ストアでの dvv と dvvs の使用
6 分散 Key-Value ストアでの dvv と dvvs の使用
このセクションでは各キーへの書き込みの因果関係を正確かつ効率的に追跡するために、最新の分散型 Key-Value ストアで論理クロック (特に dvv と dvvs) を使用する方法を示す。我々の解決策はデータベーsが \({\sf get}\) や \({\sf put}\) のリクエストを処理する際に使用する一般的なワークフローで構成されている。これに向けて論理クロックを介した操作のカーネルを定義し、その上にワークフローを定義する。次に、これらの操作を我々が提案する論理クロック (最初は dvv、次に dvvs) を介してインスタンス化する。
Fig 2 に示すように、我々はいくつかのステップを実行する \({\sf get}\) 操作と \({\sf put}\) 操作の両方をサポートする。まずカーネル操作を定義しよう。
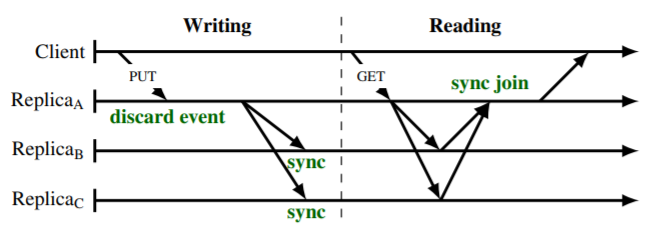
\({\sf sync}\) 関数. \({\sf sync}\) 関数はそれぞれが兄弟のセットを意味する 2 つのクロックセットを取り、破棄されたクロックを削除したあとに残った兄弟のクロックセットを返す。この関数は実際の表現に関わらず、クロックの部分的な順序に関してのみ一般的な定義を持つことができる: 式 (\(\ref{1}\))。
\({\sf join}\) 関数. \({\sf join}\) 関数はクロックセットを取り、受け取ったセット内のすべての兄弟の集合的な因果関係の過去を記述する単一のクロックを返す。実際の \({\sf join}\) の実装は窃盗に対応する ch 内のすべてのイベント (ドット) の和集合を実行することに対応する、すなはち式 (\(\ref{2}\)) を満たす任意の関数である。
\({\sf discard}\) 関数. \({\sf discard}\) 関数はクロックの集合 \(S\) (兄弟を表す) とクロック \(C\) (コンテキストを表す) を取り、コンテキスト \(C\) に含まれるために破棄されたすべての兄弟を \(S\) から破棄する。\({\sf discard}\) は \({\sf sync}\) と同様にクロックの部分的な順序の観点からのみ単純な一般的定義を持っている: 式 (\(\ref{3}\))。
\({\sf event}\) 関数. \({\sf event}\) 関数はクロックの集合 \(S\) (兄弟を表す) とクロック \(C\) (コンテキストを表す)、レプリカノードの識別子 \(r\) を取り、\(r\) で生成された新しいユニークなイベント (ドット) によって与えられ因果関係のある過去に \(C\) を持つ新しいバージョンを表すための新しいクロックを返す。実装は式 (\(\ref{4}\)) に従わなければならない。
\[ \begin{eqnarray} {\sf sync}(S_1,S_2) & = & \{ x \in S_1 \mid \not\exists y \in S_2, x \lt y \} \cup \{ x \in S_2 \mid \not\exists y \in S_1, x \lt y \} \label{1} \\ {\sf toch}({\sf join}(s)) & = & \bigcup \{{\sf toch}(x) \mid x \in S \} \label{2} \\ {\sf discard}(S,C) & = & \{ x \in S \mid x \not\le C \} \label{3} \\ {\sf toch}({\sf event}(C,S,r)) & = & {\sf toch}(C) \cup \{{\sf next}(C,S,r)\} \label{4} \end{eqnarray} \] ここで \({\sf next}\) は \(r\) で生成された次の新しいユニークイベント (ドット) を表し、\(C\), \(S\) および \(r\) が与えられれば決定論的に定義することができる。
 6.1 get 処理
6.1 get 処理
関数 sync と join を使って get 操作を定義する: サーバは get リクエストを受け取ると、レプリカノードの部分集合にそのキーのバージョンとクロックの集合を問い合わせ、sync をペアごとに適用して "マージ" することができる。ただしサーバは正常な応答に必要ないと判断した場合はこのフェーズを省略することができる。必要な情報が揃うと、因果関係の情報から取り除かれた値と、クロックに join を適用した結果のコンテキストがクライアントに返さえる。sync はレプリカノード間のアンチエントロピー同期などのタイミングでも使用できる。
 6.2 put 処理
6.2 put 処理
put リクエストを受け取ると、サーバはサーバ自身がそのリクエストで指定されたキーのレプリカノードでなければレプリカノードに転送する。書き込まれるキーのレプリカではないノードは、例えば vvclient を使用して put リクエストを調整することができる。これはクライアント ID を使用してクロックを更新しその結果をレプリカノードに伝達できるためである。しかし vvserver, dvv, dvvs などのサーバ ID を使用するクロックは、調整ノードが自身の ID を使用してクロックに一意のイベントを生成する必要がある。リクエストをレプリカノードに転送しなければ、レプリカノード以外のノードの ID がクロックに追加され、レプリカノード (例えば 3) だけではなくサーバの総数 (例えば 100) に比例することになる。
与えられたキーに対するクロックの集合 \(S_r\) を含むレプリカノード \(r\) が put リクエストを受け取ると、まず discard 機能を使って \(S_r\) から古くなったバージョンの削除を開始し \(S'_r\) を生成する。また、イベント付きの新しいバージョンのための新しいクロック \(u\) を生成する。最後に、\(u\) は古くなっていないバージョンの集合 \(S'_r\) に追加され \(S''_r\) が生成される。
サーバは \(S''_r\) をローカルに保存し、他のレプリカノードに伝播させ、クライアントに成功を通知することができる。この 3 つのステップの順序はシステムの耐久性とレプリケーションパラメータに依存する。\(S''_r\) を受け取ったそれぞれのレプリカは sync 関数を用いて自分のローカルバージョンに \(S''_r\) を適用する。
各キーに対してコーディネータのステップ (バージョンの破棄、新しいバージョンの作成、および古くなっていないバージョンの集合への追加) は所定の put を提供するときにアトミックに実行されなければならない。これはローカルな同時性制御によって簡単に取得でき、異なるキーに対するローカルな操作間の完全な同時実行を妨げるものではない。同じキーに対する操作の場合、レプリカは連続する put のステップをパイプライン化することでスループットを最大化することができる (安定したストレージへのバージョンの書き込みなど、いくつかのステップは既にシリアライズされている必要があることに注意)。
 6.3 ローカルの簡潔さの維持
6.3 ローカルの簡潔さの維持
前述したように dvv と dvvs の両方にはその簡潔さを維持するためにサーバ維持しなければならない重要な不変条件がある。
不変条件 1 (ローカルクロックの簡潔さ). サーバのすべてのキーはローカルのバージョンとクロックの集合が関連付けられており、それらは集合的に、因果関係イベントの連続した集合によって論理的に表現することができる。
この普遍条件を実施するために我々は 2 つの設計上の選択を行った: (ルール 1) サーバはローカルおよび/またはリモートで取得したバージョンの部分集合で get に応答することはできず、集合全体のみを送信する必要がある。(ルール 2) コーディネータはローカルのすべての同時実行バージョン (兄弟) を送信することなく、新しいバージョンをリモートノードに複製することはできない。
1 つめのルールがなければ、クライアントは因果関係履歴に任意のギャップを含むコンテキストを持つ新しい値を読み書きすることでキーを更新することができる。dvv は 1 つのギャップ (連続した過去とドットの間) しかサポートしておらず、dvvs はサポートしないため、dvv も dvvs もこれをサポートするのには十分な表現力はない。
2 つめのルールがなければ、書き込みによって兄弟が作成される可能性があり、このクロックではそれを別々に表現することができないため dvvs は明らかに機能しない。dvv でも動作する可能性はあるが、最終的に一部のサーバがキーのローカルでの簡潔な表現を持っていないことになり (例えばネットワークが前の兄弟を失った)、そのサーバは他のサーバに接続せずに get に応答できなくなる (ルール 1 参照)。これはレイテンシーが低下し、パーティション分断の場合に可用性も低下する可能性がある。
 6.4 Dotted Version Vectors
6.4 Dotted Version Vectors
dvv の関数 sync と discard は、セクション 4.2 で定義された dvv の部分順序を使用することでその一般的な定義に従って簡単に実装することができる。
ここで 2 つの関数を使用する: 関数 ids は vv, dvv または dvv の集合からペアの識別子の集合を返す。maxdot 関数は dvv または dvv の集合とサーバ ID を受け取り、そのサーバ化のイベントの最大シーケンス番号を返す。\[ \begin{eqnarray*} {\sf ids}((i,\_)) & = & \{i\}, \\ {\sf ids}(((i,\_),v)) & = & \{i\} \cup {\sf ids}(v) \\ {\sf ids}(S) & = & \bigcup_{s \in S} {\sf ids}(s) \\ {\sf maxdot}(r,((i,n),v)) & = & \max(\{n \mid i = r\} \cup \{ v[r]\}) \\ {\sf maxdot}(r,S) & = & \max(\{0\} \cup \{{\sf maxdot}(r,s) \mid s \in S\}) \end{eqnarray*} \]
 6.5 Dotted Version Vector Sets
6.5 Dotted Version Vector Sets
dvv ではインターフェースを少し変更する必要がある: 関数はクロックの集合ではなく単一の dvvs を受け取るようになり、event は新しく生成されたバージョンを dvvs を直接挿入するようになった。
ここではわかりやすく完結にするために、\(R\) をレプリカノードの ID の完全な集合と仮定し、dvvs 内に ID \(i\) が存在しない場合は暗黙のうちに \((i,0,[])\) という要素に昇格させる。個々では次の関数を使用する: \({\sf first}(n,l)\) はリスト \(l\) の最初の \(n\) 個の要素 (要素数が \(n\) 未満の場合はリスト全体、\(n\) が正でない場合は空リスト) を返す。\(l\) の要素数を返す \(|l|\)、リスト \(l\) の先頭に \(x\) を追加する \([x\mid l]\)。そして関数 merge である: \[ {\sf merge}(n,l,n',l') = \left\{ \begin{array}{ll} {\sf first}(n-n'+|l'|, l), & \ \ \mbox{if $n \ge n'$} \\ {\sf first}(n'-n+|l|,l'), & \ \ \mbox{otherwise} \end{array} \right. \]
関数 discord は dvvs \(S\) と vv \(C\) を取り、\(S\) の中で \(C\) によって古くなった値を破棄する。同様に sync は 2 つの dvv を受け取り古くなった値を削除する。関数 join は単純に先頭のベクトルを返しリストを破棄する。関数 event は新しいイベントを生成するだけではなくパラメータとして明示的に渡された新しい値を dvvs に挿入するように調整された。これは \(r\) によって実行された新しいイベントで表現された新しい値 \(v\) を含む新しい dvvs を返し、したがって \(r\) のリストの先頭に追加される。コンテキストは因果関係の情報をトップのベクトルに伝達するためのみに使用され、バージョンごとに保持することはない。\[ \begin{eqnarray*} {\sf sync}(S,S') & = & \{(r,\max(n,n'), {\sf merge}(n,l,n',l')) \mid r \in R, (r,n,l) \in S, (r,n',l') \in S'\}, \\ {\sf join}(C) & = & \{(r,n) \mid (r,n,l) \in C\} \\ {\sf discard}(S,C) & = & \{(r,n,{\sf first}(-C(r),l)) \mid (r,n,l) \in S\} \\ {\sf event}(C,S,r,v) & = & \{(i,n+1,[v\mid l]) \mid (i,n,l) \in S \mid i=r \} \cup \\ & & \{(i,\max(n,C(i),l) \mid (i,n,l) \in S \mid i \ne r \} \end{eqnarray*} \]
 7 複雑性と評価
7 複雑性と評価
Table 2 は 1 つのキーに対する因果関係追跡メカニズムの空間と時間の複雑性を示している。\(U\) は更新 (書き込み) の数、\(C\) は書き込みクライアントの数、\(R\) はレプリカサーバの数、\(V\) は並行バージョン (兄弟) の数、\(S_w\) と \(S_r\) は \({\sf put}\) と \({\sf get}\) に関わるレプリカノードの数とする。\(U\) と \(C\) は一般に \(R\) と \(V\) より数桁大きいことに注意。ここで提示した複雑性の尺度はマップやセットへのアクセスまたは更新にかかる時間が事実上一定であることを前提としている。また、エントリ数に線形な pairwise traversal を可能にする順序付きマップ/セットを想定している。
| lww | ch | vvclient | vvserver | dvv | dvvs | ||
|---|---|---|---|---|---|---|---|
| Space | \(\tilde{O}(1)\) | \(\tilde{O}(U)\) | \(\tilde{O}(c \times V)\) | \(\tilde{O}(R + V)\) | \(\tilde{O}(R \times V)\) | \(\tilde{O}(R + V)\) | |
| Time | event | - | \(\tilde{O}(1)\) | \(\tilde{O}(1)\) | \(\tilde{O}(1)\) | \(\tilde{O}(V)\) | \(\tilde{O}(R)\) |
| join | - | \(\tilde{O}(U \times V)\) | \(\tilde{O}(C \times V)\) | \(\tilde{O}(1)\) | \(\tilde{O}(R \times V)\) | \(\tilde{O}(R)\) | |
| discard | - | \(\tilde{O}(U \times V)\) | \(\tilde{O}(C \times V)\) | \(\tilde{O}(R)\) | \(\tilde{O}(V)\) | \(\tilde{O}(R + V)\) | |
| sync | - | \(\tilde{O}(U \times V^2)\) | \(\tilde{O}(C \times V^2)\) | \(\tilde{O}(R + V)\) | \(\tilde{O}(V^2)\) | \(\tilde{O}(R + V)\) | |
| PUT | \(\tilde{O}(1)\) | \(\tilde{O}(S_w \times U \times V^2)\) | \(\tilde{O}(S_w \times C \times V^2)\) | \(\tilde{O}(S_w \times (R + V))\) | \(\tilde{O}(S_w \times V^2)\) | \(\tilde{O}(S_w \times (R + V))\) | |
| GET | \(\tilde{O}(1)\) | \(\tilde{O}(S_r \times U \times V^2)\) | \(\tilde{O}(S_r \times C \times V^2)\) | \(\tilde{O}(S_r \times (R + V))\) | \(\tilde{O}(R \times V + S_r \times V^2)\) | \(\tilde{O}(S_r \times (R + V))\) | |
| Causally Correct | ✘ | ✔ | ✔ | ✘ | ✔ | ✔ | |
lww は因果関係を追跡せず兄弟を無視するため時間的にも空間的にも定数である。空間的には ch と vvclient はそれぞれ書き込みとクライアント数に対して線形に増加するためうまくスケールしない。dvv は一般的にキーごとの同時実行性がほとんどないことを考えると適切にスケールするが、それでも兄弟ごとに dvv を必要とする。考慮されたクロックの中では dvvs と vvserver の空間的複雑性が最も優れているが後者は正確ではない。
我々のフレームワーク (セクション 6) に従うと、時間的複雑性は1:
- \({\sf put}\) は \(\tilde{O}({\it discard} + {\it event} + S_w \times {\it sync})\)、\({\sf get}\) は \(\tilde{O}({\it join} + S_r \times {\it sync})\) である。
- \({\it event}\) は ch, vvclient, vvserver に対して効率的で \(\tilde{O}(1)\) であり、dvv では各値のクロックをチェックする必要があるため \(V\) に線形であり、dvvs ではローカルクロックへのコンテキストのマージも行うため \(\tilde{O}(R)\) である。
- \({\it join}\) はクロックが既に一つしかないため vvserver に対して定数である。ch, vvclient, dvv ではそれらすべてのクロックをマージした量である。dvvs では \({\it join}\) は単にクロックからトップペクトルを抽出するだけである。
- \({\it discard}\) は dvv では V にのみ線形である。これは 2 つのクロックの部分的な順序を一定時間でチェックできるからである。ch と vvclient ではコンテキストを各バージョンのクロックと比較しなければならない。vvserver と dvvs は常にコンテキストを 1 つのクロックと比較し、さらに dvvs はバージョンのリストをトラバースする必要がある。
- \({\it sync}\) は \({\it discard}\) に似ているが、バージョンの集合を単一のコンテキストと比較するのではなく、バージョンの 2 つの集合を比較する。さらに、ch, vvclient, dvv の複雑さは \({\it discard}\) と似ているが、線形ではなく \(V\) の二次関数となっている。vvserver と dvvs が一つのクロックしか持たないため \({\it sync}\) の複雑性は \(V\) に対して線形となる。
 7.1 評価
7.1 評価
我々は dvv と dvvs を Erlang で実装し、NoSQL である Riak データストアと統合した2。dvvs の因果関係追跡の精度とその兄弟爆発問題を克服する能力を評価するため、2 つの等価な 5 ノード Riak クラスタを構築し、1 つは dvvs を使用しもう一つは vvserver を使用した。
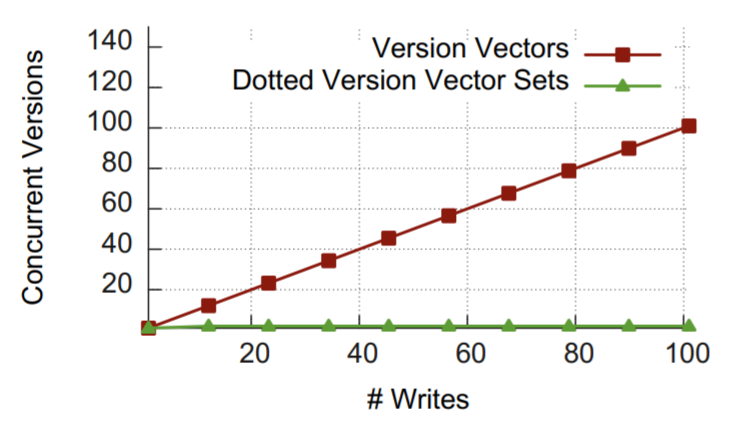
そして我々は次のような等価なスクリプト3を実行した: Peter (\(P\)) と Mary (\(M\)) が同じキーに対して 50 回ずつ、読み書きサイクルが重なるように書き込みと読み込みを行う (\(P\) は書き込んでから読み込み、次に \(M\) は書き込んでから読み込みを交互に繰り返す)。Fig 3 は新しい書き込みのたびに兄弟の数が増えてゆく様子を示している。vvserver のクラスタは間違った並行性が爆発的に増加し、100 回の書き込み後に 100 のバージョンが並行発生している。クライアントが最新のコンテキストで書き込みを行うたびにサーバ内のクロックが既に変更されていたため、兄弟が生成され追加されている。しかし、dvvs では各書き込みが他のクライアントの最新の書き込みと衝突するものの、因果関係のある古い兄弟 (そのクライアントが最後に読み込んだときに存在していたすべての兄弟) を検出して削除する。このように dvvs を導入したクラスタでは同じ 100 回の書き込みのあとに各クライアントからの最後の書き込みという 2 つの兄弟しか存在しなかった。
最後の、dvvs は Riak の最新リリースでデフォルトの論理クロック機構として採用されるなど、業界では早くから採用されている。想定通り、dvvs は Riak の実運用で問題となっていた複数のクライアントが同じキーに書き込みを行ったときの兄弟爆発問題を克服した。
- 1表記を単純化するためにビッグ \(O\) の変種の \(\tilde{O}\) を使用している。これは整数カウンターとユニーク ID のサイズを対数的に無視する。
- 2https://github.com/ricardobcl/Dotted-Version-Vectors
- 3https://gist.github.com/ricardobcl/4992839
 8 関連研究
8 関連研究
分散システムにおける因果関係の役割は Lamport [11] で導入され、その後のメカニズムや理論 [11, 14, 20, 19, 2, 4] の基礎を確立した。セクション 3 では結果整合性のあるストアで一般的に使用されるソリューションの問題について論議した。このセクションではその他の関連研修について説明する。
エンティティ数の変動 (Variability in the Number of Entities). 基本的なベクトルベースのメカニズムはノードやレプリカの数が変動しても対応できるように一般化できる。一般的な戦略は識別子をカウンターにマップし識別子の集合の動的な変化に対応することである。追加は一意の識別子の生成に依存する。削除は他の複数のサーバとの通信が必要な場合もあれば [7]、単一のサーバとの通信が必要な場合もある [15, 1]。dvv と dvvs はクライアントへの識別子の割当を避けているが、これらの手法はサーバのセットの変更をサポートすることができる。
競合に関する例外 (Exceptions on Conflicts). 一部のシステムでは異なるクライアントからの同時 PUT 操作を検出して更新を拒否したり (CVS や subversion などのバージョン管理システム)、更新を保持するが競合が解消されるまでそれ以上のアクセスを拒否しないもの (Coda [8] のオリジナルバージョンなど) がある。このような場合、サーバごとに 1 つのエントリを持つバージョンベクトル (vv) を使用すれば十分である。ただしこれらのソリューションは最新の地理複製データベースの重要な "特徴" である書き込み可用性を犠牲にする。
表現の圧縮 (Compacting the Representation). 一般に、並行性を登録できる独立したエンティティの集合よりもコンパクトなフォーマットを使用すると因果関係の表現が失われる [4]。Plausible クロック [21] では複数のレプリカからのイベントカウントの同じベクトルエントリに凝縮しているため誤った並行性が発生する。不要なエントリを削除するためにいくつかのアプローチが提案されており、安全ではあるが実行時のコンセンサスが必要なもの (Roam [18] など) や、高速ではあるが安全でないもの (Dynamo [5] など) などは因果関係のエラーに繋がる可能性がある。
拡張と表現力の追加 (Extensions and Added Expressiveness). Depot [12] では、各更新に関連する vv は同じノードの前回の更新以降に更新されたエントリのみを含む。しかし各ノードは依然としてすべてのクライアントとサーバのエントリを vv を維持する必要がある。同様のシナリオでは、同じアプローチを我々のソリューションの補完として使用することができる。他のシステムでは多数のオブジェクトを管理しているという事実を使用して各オブジェクトの情報を少なく維持している。WinFS [13] はファイルシステム内のすべてのオブジェクトに対して基本の vv を維持し、各オブジェクトに対しては簡潔な vv ベースのち外のみを維持する。Cimbiosys [17] はピア・ツー・ピアシステムで同じ手法を使用している。これらのシステムではサーバごとに 1 つのエントリしか保持しないためセクション 3 で vvserver について述べたように、異なるクライアントから同じサーバに送信された同時更新にタグ付けするために 2 つの vv を生成することはできない。WinFS には同期の乱れを処理するメカニズムがあり、vv に登録されたイベントに例外を登録することにより非連続な因果関係の履歴を符号化することができる。例えば \(\{a_1,a_2,b_1,c_1,c_2,c_4,c_7\}\) は \(\{(a,2),(b,1),(c,7)\}\) と例外 \(\{c_3,c_5,c_6\}\) で表現できる。しかしシステムワークフローで dvv を使用する場合は vv の外にある更新イベントが最大で 1 つ必要であるため、バージョンごとに 1 つのドットで十分である。dvvs はさらに進んで、すべての因果関係情報を vv に凝縮できる一方で、複数の暗黙のドットを残すことができる。これにより、任意の数の同時クライアントを許容するのに十分な表現力が保証され、一般的な非逐次 ch を符号化する際のサイズの複雑さを回避することができる。Wang ら [22] は (dvv のように) 比較時間が \(O(1)\) の vv の変種を提案しているが、vv のエントリは順序を維持しなければならないことが他の操作の時間が定数となることを妨げている。さらに vvserver に関連する問題も発生するが我々は dvvs で解決した。
 9 結びの辞
9 結びの辞
我々は更新イベント感の因果関係を追跡するための新しいソリューションである Dotted Version Vectors について詳細に説明した。基本的な考え方は因果関係の履歴上にさらに独立したイベントを追加することである。これはレプリカの数に対して線形サイズを維持しながら同時進行する並行バージョン (兄弟) 間で確立されたすべての因果関係を補足するのに十分な表現力を持っている。
次に我々はよりコンパクトノア表現である Dotted Version Vector Sets を提案した。これは 1 つのデータ構造で兄弟の集合の因果関係情報を正確に表現することができる。これによりレプリカと兄弟の数に線形で、空間的にも時間的にも複雑にすることなく因果関係を正確に追跡することが可能な現状のすべてのメカニズムより優れている。
最後に、分散データストは絵のリクエストに関する一般的なワークフローを紹介した。このワークフローでは因果関係を追跡するメカニズムに必要な基本操作を抽象化し要素化している。そして、これらのカーネル操作を用いて我々の両方のメカニズムを実装した。
Acknowledgements. This research was partially supported by FCT/MCT projects PEst-OE/EEI/UI0527/2014 and PTDC/EEI-SCR/1837/2012; by the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no 609551, SyncFree project; by the ERDF - European Regional Development Fund through the COMPETE Programme (operational programme for competitiveness) and by National Funds through the FCT – Fundação para a Ciência e a Tecnologia (Portuguese Foundation for Science and Technology) within project FCOMP-01-0124-FEDER-037281.
 References
References
- Almeida, P.S., Baquero, C., Fonte, V.: Interval tree clocks. In: Baker, T.P., Bui, A., Tixeuil, S. (eds.) OPODIS 2008. LNCS, vol. 5401, pp. 259–274. Springer, Heidelberg (2008)
- Birman, K.P., Joseph, T.A.: Reliable communication in the presence of failures. ACM Trans. Comput. Syst. 5(1), 47–76 (1987)
- Brewer, E.A.: Towards robust distributed systems (abstract). In: Proceedings of the Nineteenth Annual ACM Symposium on Principles of Distributed Computing, PODC 2000, p. 7. ACM, New York (2000)
- Charron-Bost, B.: Concerning the size of logical clocks in distributed systems. Information Processing Letters 39, 11–16 (1991)
- DeCandia, G., Hastorun, D., Jampani, M., Kakulapati, G., Lakshman, A., Pilchin, A., Sivasubramanian, S., Vosshall, P., Vogels, W.: Dynamo: amazon’s highly available key-value store. In: Proceedings of Twenty-First ACM SIGOPS SOSP, pp. 205–220. ACM (2007)
- Gilbert, S., Lynch, N.: Brewer’s conjecture and the feasibility of consistent available partition-tolerant web services. ACM SIGACT News, 2002 (2002)
- Golding, R.A.: A weak-consistency architecture for distributed information services. Computing Systems 5(4), 379–405 (1992)
- Kistler, J.J., Satyanarayanan, M.: Disconnected operation in the Coda file system. In: Thirteenth ACM Symposium on Operating Systems Principles, vol. 25, pp. 213–225. Asilomar Conference Center, Pacific Grove (1991)
- Klophaus, R.: Riak core: building distributed applications without shared state. In: ACM SIGPLAN Commercial Users of Functional Programming, CUFP 2010, p. 14:1. ACM, New York (2010), http://doi.acm.org/10.1145/1900160.1900176
- Lakshman, A., Malik, P.: Cassandra: a decentralized structured storage system. SIGOPS Oper. Syst. Rev. 44, 35–40 (2010)
- Lamport, L.: Time, clocks and the ordering of events in a distributed system. Communications of the ACM 21(7), 558–565 (1978)
- Mahajan, P., Setty, S., Lee, S., Clement, A., Alvisi, L., Dahlin, M., Walfish, M.: Depot: Cloud storage with minimal trust. In: OSDI 2010 (October 2010)
- Malkhi, D., Terry, D.: Concise version vectors in winFS. In: Fraigniaud, P. (ed.) DISC 2005. LNCS, vol. 3724, pp. 339–353. Springer, Heidelberg (2005)
- Parker, D.S., Popek, G., Rudisin, G., Stoughton, A., Walker, B., Walton, E., Chow, J., Edwards, D., Kiser, S., Kline, C.: Detection of mutual inconsistency in distributed systems. Transactions on Software Engineering 9(3), 240–246 (1983)
- Petersen, K., Spreitzer, M.J., Terry, D.B., Theimer, M.M., Demers, A.J.: Flexible update propagation for weakly consistent replication. In: Sixteen ACM Symposium on Operating Systems Principles, Saint Malo, France (October 1997)
- Preguiça, N., Baquero, C., Almeida, P.S., Fonte, V., Gonçalves, R.: Brief announcement: Efficient causality tracking in distributed storage systems with dotted version vectors. In: Proceedings of the 2012 ACM Symposium on PODC, pp. 335–336. ACM (2012)
- Ramasubramanian, V., Rodeheffer, T.L., Terry, D.B., Walraed-Sullivan, M., Wobber, T., Marshall, C.C., Vahdat, A.: Cimbiosys: a platform for content-based partial replication. In: Proceedings of the 6th USENIX Symposium on NSDI, Berkeley, CA, USA, pp. 261–276 (2009)
- Ratner, D., Reiher, P.L., Popek, G.J.: Roam: A scalable replication system for mobility. MONET 9(5), 537–544 (2004)
- Raynal, M., Singhal, M.: Logical time: Capturing causality in distributed systems. IEEE Computer 30, 49–56 (1996)
- Schwarz, R., Mattern, F.: Detecting causal relationships in distributed computations: In search of the holy grail. Distributed Computing 3(7), 149–174 (1994)
- Torres-Rojas, F.J., Ahamad, M.: Plausible clocks: constant size logical clocks for distributed systems. Distributed Computing 12(4), 179–196 (1999)
- Wang, W., Amza, C.: On optimal concurrency control for optimistic replication. In: Proc. ICDCS, pp. 317–326 (2009)
翻訳抄
結果整合性を持つ Key-Value ストア間で更新の競合を検出し追跡するための機構である Version Vector を、空間的および時間的に効率化した Dotted Version Vectors (DVV) および Dotted Version Vector Sets (DVVS) に関する 2014 年の論文。DVVS は Riak が採用してる。
- Almeida P.S., Baquero C., Gonçalves R., Preguiça N., Fonte V. (2014) "Scalable and Accurate Causality Tracking for Eventually Consistent Stores. In: Magoutis K., Pietzuch P. (eds) Distributed Applications and Interoperable Systems. DAIS 2014. Lecture Notes in Computer Science, vol 8460. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-43352-2_6

