論文翻訳: A Tree Clock Data Structure for Causal Orderings in Concurrent Executions

概要

動的手法は並行プログラムを解析するためのスケーラブルで効率的な方法である。これらの技術では、プログラムのすべての動作を分析する代わりに単一のプログラム実行に焦点を当ててエラーを検出する。多くの場合、これらの手法における重要なステップは実行中のイベント間の因果的順序付けを定義することであり、この順序はスレッドの論理時刻を格納する単純なデータ構造であるベクトルクロック (vector clock) を用いて計算される。ベクトルクロックの 2 つの基本操作、つまり結合とコピーには \(\Theta(k)\) の時間が必要である。ここで \(k\) はスレッドの数である。したがって \(k\) が大きい場合には計算上のボトルネックとなる。

この研究ではプログラム実行における因果的順序付けを計算するためにベクトルクロックに変わる新しいデータ構造であるツリークロック (tree clock) を導入する。ツリークロックの結合とコピーは変更を受けるエントリの数にほぼ比例した時間がかかるため、この 2 つの操作はアプリケーションごとの先天的な (a-priori) \(\Theta(k)\) コストが発生しない。古典的な happens-before (HB) 半順序の計算に使用すると、他のデータ構造が漸近的な実行時間の短縮にならないという意味でツリークロックが最適であることを示す。さらに schedulable-happens-before (SHB) や Mazurkiewicz (MAZ) 半順序など他の半順序を計算できるため汎用性の高いデータ構造であることを示す。我々の実験によるとベクトルクロックをツリークロックに置き換えるだけで計算速度がベンチマークあたり平均 2.02 倍 (MAZ) から 2.66 倍 (SHB)、2.97 倍 (HB) にまで高速になることが示されている。これらの結果はツリークロックが並行性解析に広く応用できる標準的なデータ構造となる可能性があることを示している。

Table of Contents

1. 概要
   1. CCS CONCEPTS
   2. キーワード
2. 1 導入
3. 2 準備
   1. 2.1 並行モデルとトレース
   2. 2.2 半順序、ベクトル時間、ベクトルクロック
   3. 2.3 Happens-Before 半順序
4. 3 ツリークロックデータ構造
   1. 3.1 直感
   2. 3.2 ツリークロック
5. 4 happens-before に対するツリークロック
6. 5 他の反順序におけるツリークロック
   1. 5.1 Schedulable-Happens-Before
   2. 5.2 Mazurkiewicz 半順序
7. 6 実験
8. 7 関連研究
9. 8 結論
10. ACKNOWLEDGEMENTS
11. REFERENCES
12. A  証明
13. B  HB ツリークロックの例
14. C  ベンチマーク
15. 翻訳抄

CCS CONCEPTS

• Software and its engineering → Software verification and validation;
• Theory of computation → Theory and algorithms for application domains; Program analysis.

キーワード

concurrency, happens-before, vector clock, dynamic analyses

1 導入

並行プログラムの解析はスレッド間通信の非決定性により形式手法における主要な課題の一つである。予期しない通信パターンによって意図された不変性が破られる可能性があるため、通信インターリーブの大きな空間はプログラマにとって大きな課題となる。またこれらのパターンは微妙であるためバグを発見するために指数関数的に大きな空間を探索する必要があり検証が困難な作業となる [41]。その結果、並行処理のバグを効率的に理解し検出するために多大な努力が払われている [10, 19, 34, 58, 63, 68]。

動的解析と半順序付け。並行プログラム検証のスケーラビリティ問題に対する一般的なアプローチの一つは動的解析 (dynamic analysis) [23, 36, 39, 45] である。このような技法はプログラム全体ではなくプログラムの実行を解析することで欠陥をかっけんすると言う控えめな目標を掲げている。この手法ではバグがないことを証明することはできないが、静的解析よりも遙かにスケーラブルであり、通常はエラーを確実に報告することができる。このような利点により動的解析は並行プログラムのエラー検出に非常に効果的で広く利用されている。

並行実行を解析する事実上すべての手法の最初のステップは実行イベント間の因果的な順序付けを確立することである。因果関係の概念はアプリケーションによって異なるが、その推移的な性質からこれらのイベント間の半順序 (partial order) として自然に表現できるようになる。著名な例として Mazurkiewicz 半順序 (MAZ) があり、これはしばしば並行トレース (concurrent trace) [7, 40] (別名 ShashaSnir トレース [57]) を表現する標準的な方法として機能する。もう一つの一般的な半順序は Lamport の happens-before (HB) [32] であり、当初は分散システム [55] の文脈で提案された。マルチスレッドプログラムのテストにおいて、半順序は動的競合検出技術において重要な役割を果たしており、基礎となる解析の健全性、完全性、実行時間のトレードオフを探るために徹底的に利用されてきた。HB [18, 23, 29, 45, 56], schedulably-happens-before (SHB) [35], causally-precedes (CP) [59], weak-causally-precedes (WPC) [30], doesn't-commute (DC) [49], そして strong/weak-dependently-precedes (SDP/WDP) [27], M2 [44] と SyncP [37] などがその代表例である。競合検出以外にも、アトミック性違反 [8, 25, 38], デッドロック [53, 61] その他の平行性脆弱性 [66] など、平行性のバグを検出し再現するためによく半順序が使用される。

動的解析におけるベクトルクロック。実行イベント間の半順序を決定する計算タスクはベクトルクロックと呼ばれる単純なデータ構造を用いて実現されることが多い。非公式には、ベクトルクロック \(\mathbb{C}\) は実行中のプロセス/スレッドによってインデックス付けされた整数配列であり、システム全体に関するプロセスの知識を簡潔に符号化している。スレッド \(t_1\) に関連付けられたベクトルクロック \(\mathbb{C}_{t_1}\) の場合、\(\mathbb{C}_{t_1}(t_2)=i\) であればスレッド \(t_2\) の最初の \(i\) 個のイベントの後に \(t_1\) の最新のイベントが半順序で並んでいることを意味する。したがってベクトルクロックは 2 つのイベントのベクトルタイムスタンプのポイント単位の順序づけにより関心のある半順序に関するイベント間の順序をキャプチャすることでシームレースに半順序をキャプチャする。このような理由からベクトルクロックは HB の半順序を効率的に計算するのに役立っており [21, 22, 39]、HB 以外にも半順序に基づく解析を効率的に実装するために広く普及している [23, 30, 31, 35, 38, 49, 53, 61]。

ベクトルクロックの基本的な操作は \(\mathbb{C}_{t_1} \leftarrow \mathbb{C}_{t_1} \sqcup \mathbb{C}_{t_2}\) の点単位 (point-wise) の結合である。この結合はスレッド \(t_2\) から \(t_1\) への因果的な順序付けが行われるたびに発生する。操作上、結合はスレッド \(t\) ごとに \(\mathbb{C}_{t_1}(t) \leftarrow \max(\mathbb{C}_{t_1}(t), \mathbb{C}_{t_2}(t))\) を更新することによって実行され、因果的な順序付けの推移性をキャプチャする (\(t_1\) が \(t_2\) について学習すると同時に、\(t_2\) が知っている他のスレッド \(t\) についても学習する)。\(t_1\) が \(t\) の後のイベントを認識している場合、この操作は空であることに注意。\(k\) スレッドではベクトルクロックの結合に \(\Theta(k)\) 時間がかかり、\(k\) が中程度のシステムでもすぐにボトルネックになる可能性がある。このことから次のような疑問が生まれる。空の更新を積極的に回避することで結合処理を高速化することは可能だろうか? このようなタスクの課題は結合処理自体の効率に由来する。結合処理はベクトルサイズに対して線形時間しか必要としないため、どのような改善も劣線形時間 (sub-linear time)、すなはちつまりベクトルクロックの特定のエントリにさえ触れないように処理しなければならない。この考え方の具体的な例を説明し、この研究における重要な洞察を示す。

動機となる例. Figure 1 の例を考える。これは 6 個のスレッドを備えた並行システムから部分的なトレースと各イベントのベクトルタイムスタンプを示している。イベント \(e_2\) がイベント \(e_3\) より前に順序付けされると、\(t_2\) のベクトルクロック \(\mathbb{C}_{t_2}\) は \(\mathbb{C}_{t_1}\) のベクトルクロックと結合される。つまり \(\mathbb{C}_{t_1}\) の \(t_j\) 番目のエントリが \(\mathbb{C}_{t_1}(t_j)\) と \(\mathbb{C}_{t_2}(t_j)\) の大きい方に更新される¹。ここでスレッド \(t_2\) がスレッド \(t_3\) を介してスレッド \(t_3\), \(t_4\), \(t_5\), \(t_6\) の現在時刻を学習したとする。イベント \(e_1\) のベクトルタイムスタンプの \(t_3\) 番目の成分はイベント \(e_2\) の対応する成分より大きいため、\(t_1\) はイベント \(e_3\) で実行された結合を通じてスレッド \(t_4\), \(t_5\), \(t_6\) に関する新しい情報を学習することができない。したがって単純な点単位の更新はインデックス \(j=\{3,4,5,6\}\) に対して冗長となる。残念ながら、ベクトルクロックの平坦な構造はそのような推論に適さず、これらの冗長な操作を避けることができない。

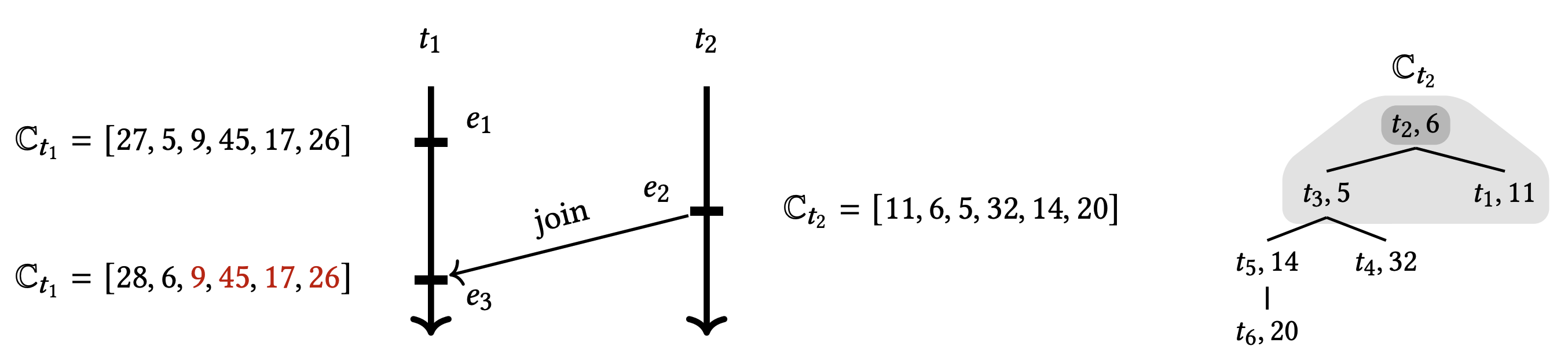
この問題を軽減するために我々はツリークロックと呼ばれるベクトル時間を保持するための新しい階層ツリー状データ構造を導入する。ツリーのノードはベクトルクロックのエントリと同様にローカルクロックをエンコードする。さらに、ツリー構造は中間スレッドを介してどのクロックが学習されたかを推移的に補足する。Figure 1 (右) は \(\mathbb{C}_{t_2}\) のベクトル時間をエンコードした (単純化) ツリークロックである。スレッド \(t_3\) をルートとするサブツリーは、\(t_2\) が \(t_3\) を介して \(t_4\), \(t_5\), \(t_6\) の現在時刻を推移的に (transitively) 学習したことを表している。結合操作 \(\mathbb{C}_{t_1} \leftarrow \mathbb{C}_{t_1} \sqcup \mathbb{C}_{t_2}\) を実行するために \(\mathbb{C}_{t_2}\) のルートから開始し、次のようにツリーを横断する。現在のノード \(u\) が与えられると、\(u\) は \(t_1\) に知られていないスレッドの時刻を表す場合に限り (if and only if) \(u\) の子ノードに進む。したがってこの例では、結合操作はツリー全体にはアクセスせずツリーの明るい灰色の領域のみにアクセスして結合を計算するため、結合操作の劣線形実行時間をもたらす。

直接単調性 (direct monotonicity) と呼ばれる上記の原理はツリークロックが利用する 2 つの重要な考え方の 1 つである。もう一つは間接単調性 (indirect monotonicity) である。ツリークロックのデータ構造を開発する上で重要な技術的課題は、(i) 直接単調性と間接単調性を利用して効率的な更新を実行すること、(ii) 直接単調性と間接単調性が将来の操作でも維持されるように更新を実行すること、にある。セクション 3.1 ではこれら 2 つの原則の背後にある直感を詳しく説明する。

貢献. 我々の貢献は次の通り。

1. 我々は並行実行における論理時刻を保持するための新しいデータ構造であるツリークロックを導入する。従来のベクトルクロックのフラットな構造とは対照的に、ツリークロックの動的な階層構造はプロセス間のアドホックな通信パターンを自然に捉えている。これにより劣線形時間で実行される結合やコピーの操作が可能になる。データ構造としてツリークロックはさまざまな順序関係の計算に使用できるため高い汎用性を備えている。

2. どのような入力トレースに対してもツリークロックを他のデータ構造に置き換えても総計算時間を (漸近的に) 改善できないという意味で、我々はツリークロックが HB を計算するための最適なデータ構造であることを証明する。一方、ベクトルクロックにはこの特性がない。

3. MAZ および SHB の半順序に対するツリークロックベースのアルゴリズムを示すことで、ツリークロックの汎用性を説明する。

4. MAZ、SHB、HB の半順序を計算するためにツリークロックデータ構造の大規模な実験評価を行い、標準的なベクトルクロックデータ構造と性能を比較した。我々の結果は、ベクトルクロックをツリークロックに置き換えるだけで計算速度が平均で最大 2.97 倍高速になることが分かった。この実験結果を考慮すると半順序ベースのアルゴリズムでベクトルクロックをツリークロックに置き換えることで多くのアプリケーションで大幅な改善が期待できると考えている。

1. ¹ ベクトルクロック [29] を使用した動的解析の多くのプレゼンテーションと同様に、スレッドのクロックのローカルエントリは、それが実行する各イベントの後に 1 ずつ増加すると仮定する。Figure 1 では \(e_1\) が実行された後、\(\mathbb{C}_{t_1}\) の \(t_1\) 番目のエントリが 27 から 28 に増加する。

2 準備

このセクションでは関連する表記法を開発し、並行実行、半順序、ベクトルクロックに関する標準的な概念を示す。

2.1 並行モデルとトレース

イベントとトレース. 我々は並行実行プログラムのトレースは異なるスレッドによって実行される一連のイベントとして表されると考える。各イベントはタプル \(e=\langle i, t, {\rm op}\rangle\) である。ここで \(i\) は \(e\) の一意内弁と識別子、\(t\) は \(e\) を実行するスレッドの識別子、\({\rm op}\) は \(e\) によって実行される操作であり、以下のタイプのいずれかである²。

1. \({\rm op} = {\sf r}(x)\), \(e\) がグローバル変数 \(x\) を読み込むことを表す。
2. \({\rm op} = {\sf w}(x)\), \(e\) がグローバル変数 \(x\) に書き込むことを表す。
3. \({\rm op} = {\sf acq}(\ell)\), \(e\) がロック \(\ell\) を獲得することを表す。
4. \({\rm op} = {\sf rel}(\ell)\), \(e\) がロック \(\ell\) を解放することを表す。

スレッド識別子を \({\sf tid}(e)\)、\(e\) の操作を \({\rm op}(e)\) と表記する。読み取り/書き込みイベント \(e\) に対し、\(e\) がアクセスする (一意の) 変数を \({\rm Variable}(e)\) で表す。多くの場合、識別子 \(i\) を無視し \(e\) を \(\langle t, {\rm op}\rangle\) と表す。さらに我々は \(e\) のスレッドに興味がないことがしばしばあり、その場合は単純に \(e\) をその操作で表す (例えばイベント \({\sf r}(x)\))。\(e\) の変数が重要でないときはそれも省略されます (例えば読み取りイベントを \({\sf r}\) と参照することがある)。

(具体的な) トレースはイベント列 \(\sigma=e_1,\ldots,e_n\) である。トレース \(\sigma\) は、\(\sigma\) に現れるイベントの集合に対する全順序 (total order) \(\le_{\sf tr}^\sigma\) (トレース順序 (trace order) と読む) を定義する。つまり \(e=e'\) か、\(\sigma\) 内で \(e\) が \(e'\) より前に出現するか、どちらかの場合に限り \(e \le_{\sf tr}^\sigma e'\) となる。\(e \ne e'\) であれば \(e \lt_{\sf tr}^\sigma\) と言う。\(\sigma\) はロックのセマンティクスを尊重する必要がある。つまり \({\sf acq}_1(\ell) \lt_{\sf tr}^\sigma {\sf acq}_2(\ell)\) となるようなロック \(\ell\) と、そのロック \(\ell\) 上の 2 つの獲得イベント \({\sf acq}_1(\ell)\), \({\sf acq}_2(\ell)\) に対して、\(\sigma\) に \({\sf tid}({\sf acq}_1(\ell))={\sf tid}({\sf rel}_1(\ell))\) かつ \({\sf acq}_q(\ell) \lt_{\sf tr}^\sigma {\sf rel}_1(\ell) \lt_{\sf tr}^\sigma {\sf acq}_2(\ell)\) となるロック解放イベント \({\sf rel}_1(\ell)\) が存在する。最後に、\(\sigma\) に現れるスレッド識別子の集合を \({\rm Thrds}_\sigma\) で表す。

スレッド順序. トレース \(\sigma\) が与えられたとき、スレッド順序 (thread order) \(\le_{\sf TO}^\sigma\) は \({\sf tdi}(e_1)={\sf tid}(e_2)\) かつ \(e_1 \le_{\sf tr}^\sigma e_2\) である場合に限り \(e_1 \leq_{\sf TO}^\sigma e_2\) を満たす最小の半順序である。\(\sigma\) 内のイベント \(e\) に対して、\(e\) のローカル時刻 \({\rm lTime}^\sigma(e)\) は、トレース \(\sigma\) 内の \(e\) より前に現れ、\({\sf tid}(e)\) によっても実行されるイベントの数、すはなち \({\rm lTime}^\sigma(e)=|\{e'|e' \le_{\sf TO}^\sigma e\}|\) である。このペア \(({\sf tid}(e),{\sf lTime}^\sigma(e))\) はトレース \(\sigma\) 内のイベント \(e\) を一意に識別する。

競合するイベント. もし (i) \({\rm Variable}(e_1)={\rm Variable}(e_2)\) であり、(ii) \({\sf tid}(e_1)\ne{\sf tid}(e_2)\) であり、(iii) \(e_1\), \(e_2\) の少なくとも一つが書き込みイベントである場合、\(\sigma\) 内の 2 つのイベント \(e_1\) と \(e_2\) は競合していると言い \(e_1 \asymp e_2\) と表記する。並行解析の標準的なアプローチは、事前に定義された因果関係の概念にしたがって因果的に独立であり同時に実行可能な競合イベントを検出することである。

2.2 半順序、ベクトル時間、ベクトルクロック

集合 \(S\) 上の半順序は、\(S\) の要素に関する反射的 (reflexive)、推移的 (transitive)、反対称的 (anti-symmetric) な二項関係である。半順序は並行実行を分析するための標準的な数学的対象である。このような手法の背後にある主な考え方は、分析対象のトレース \(\sigma\) のイベントのセットに半順序 \(\le_{\sf P}^\sigma\) を定義することである。直感的に \(\le_{\sf P}^\sigma\) は因果関係 (causality) を捉えている ── \(\sigma\) の 2 つのイベントが \(\le_{\sf P}^\sigma\) によって順序付けられているのであれば、それらの相対的な順序は維持されなければならない。さらに重要なことは、2 つのイベント \(e_1\) と \(e_2\) が \(\le_{\sf P}^\sigma\) によって順序付けされていない場合 (\(e_1 ||_{\sf P}^\sigma e_2\) と表記)、それらは同時であると見なすことができる。この原則はすべての半順序に基づく並行解析の骨格を形成する。

このような半順序を構築するための素朴なアプローチは、\(\sigma\) のイベントに対する非巡回有向グラフとして明示的に表現し、それから必要に応じてグラフ検索を実行して 2 つのイベントが順序付けされているかどうかを判断することである。一方、ベクトルクロックは半順序をより効率的に表現できるため、ほとんどの半順序ベースのアルゴリズムにおいて重要なデータ構造となっている。ベクトルクロックを使用することでイッステムの監視にも適したストリーミングアルゴリズムを設計することができる。これらのアルゴリズムはベクトルタイムスタンプ (vector timestamp) [21, 22, 39] をイベントに関連付けることでタイムスタンプ間の点単位の順序付けが基礎となる半順序を反映する。ここでこれらの概念を形式化しよう。

ベクトルタイムスタンプ. トレース中のスレッドの集合 \({\rm Thrds}\) を固定しよう。ベクトルタイムスタンプ (または単にベクトルタイム) はマップ \(V:{\rm Thrds} \to \mathbb{N}\) である。これは次の操作をサポートする。\[ \begin{array}{lclr} V_1 \sqsubseteq V_2 & {\rm iff} & \forall t: V_1(t) \le V_2(t) & \mbox{(Comparison)} \\ V_1 \sqcup V2 & = & \lambda t: \max(V_1(t), V_2(t)) & \mbox{(Join)} \\ V[t' \to +i] & = & \lambda t: \left\{ \begin{array}{ll} V(t)+i, & \mbox{if $t=t'$} \\ V(t), & \mbox{otherwise} \end{array} \right. & \mbox{(Increment)} \end{array} \] \(V_1 \sqsubseteq V_2\) かつ \(V_2 \sqsubseteq V_1\) であることを \(V_1=V_2\) と書く。ベクトルタイムスタンプがどのように半順序の効率的な暗黙的表現を提供するかを見てみよう。

半順序のタイムスタンプ. \(\le_{\sf TO}^\sigma \subseteq \le_{\sf P}^\sigma\) となるような \(\sigma\) のイベント集合に対して定義された半順序 \(\le_{\sf P}^\sigma\) について考える。この場合、イベント \(e\) の P-タイムスタンプを次のベクトルタイムスタンプとして定義する: \[ C_e^{\le_{\sf P}^\sigma} = \lambda u: \max\left\{ {\rm lTime}^\sigma(f) \,|\, f \le_{\sf P}^\sigma e, {\sf tid}(f)=u \right\} \] つまり \(C_e^{\le_{\sf P}^\sigma}\) は半順序 \(\le_{\sf P}^\sigma\) の中で \(e\) より前に順序付けられているような、それぞれのスレッドで最後に出現したイベントのタイムスタンプを含んでいる。\(C_e^{\le_{\sf P}^\sigma}({\sf tid}(e))={\rm lTime}^\sigma(e)\) であることに注意。次の観察は、上で定義したタイムスタンプが順序 \(\le_{\sf P}^\sigma\) を正確に捉えていることを示している。

補題 1. \(\le_{\sf P}^\sigma\) を \(\le_{\sf TO}^\sigma \subseteq \le_{\sf P}^\sigma\) となるようなトレース \(\sigma\) のイベント集合上で定義された半順序とする。このとき \(\sigma\) の任意の 2 つのイベント \(e_1\), \(e_2\) に対して \(C_{e_1}^{\le_{\sf P}^\sigma} \sqsubseteq C_{e_2}^{\le_{\sf P}^\sigma} \Leftrightarrow e_1 \le_{\sf P}^\sigma e_2\) が得られる。

つまり補題 1 は 2 つのイベントが \(\le_{\sf P}^\sigma\) にしたがって順序付けされているかどうかを確認するには、それらのベクトルタイムスタンプを比較するだけで十分であることを意味している。

ベクトルクロックデータ構造. トレースのイベント上の印が順序を確立する場合、イベントのタイムスタンプはトレース内の他のイベントのタイムスタンプを用いて算出される。各イベントのタイムスタンプを明示的に保存する代わりに、アルゴリズムが実行されているいくつかのイベントのタイムスタンプのみを保存すれば十分な場合が多い。通常、べうとる時間を保存するにはベクトルクロックと呼ばれるデータ構造が使用される。ベクトルクロックはスレッド識別子によってインデックス付けされた単純な整数配列として実装され、ベクトルタイムスタンプに対するすべての操作をサポートする。このデータ構造の便利難点はインプレース操作 (in-place operation) を実行できることである。特に、対応するベクトル時刻演算の結果を元のインスタンスに格納する \({\sf Join}(\cdot)\)、\({\sf Copy}(\cdot)\)、\({\sf Increment}(\cdot,\cdot)\) などのメソッドがある。例えばベクトルクロック \(\mathbb{C}\) とベクトル時刻 \(V\) の場合、関数の呼び出し \(\mathbb{C}.{\sf Join}(V)\) は値 \(\mathbb{C} \sqcup V\) を \(\mathbb{C}\) に格納する。これらの核操作はすべてのスレッド識別子 (配列表現のインデックス) に対して反復される。したがってベクトルクロックデータ構造の連結操作の実行時間は \(\Theta(k)\) となる。ここで \(k\) はスレッドの数である。同様にコピー操作と比較操作にも \(\Theta(k)\) 時間がかかる。

2.3 Happens-Before 半順序

Lamport の Happens-Before (HB) [32] は並行実行の解析に最も頻繁に使用される半順序の 1 つであり、動的な競合検出などの領域で広く使用されている。ここでは HB を用いてベクトルクロックの欠点を説明しツリークロックのデータ構造の基礎を形成する。後のセクションでは Schedulably-Happens-Before と Mazurkiewicz 半順序などの他の半順序にもツリークロックができようできることを示す。

Happens-Before. トレース \(\sigma\) が与えられたとき、\(\sigma\) の happens-before (HB) 半順序 \(\le_{\sf HB}^\sigma\) は、以下の条件を満たす \(\sigma\) のイベントに対する最小の半順序である。

1. \(\le_{\sf TO}^\sigma \subseteq \le_{\sf HB}^\sigma\)

2. \({\sf rel}(\ell) \le_{\sf tr}^\sigma {\sf acq}(\ell)\) である同じロック \(\ell\) 上のすべての解放イベント \({\sf rel}(\ell)\) と取得イベント \({\sf acq}(\ell)\) について、\({\sf rel}(\ell) \le_{\sf HB}^\sigma {\sf acq}(\ell)\) が成立する。

トレース \(\sigma\) の 2 つのイベント \(e_1\) と \(e_2\) について、我々は \(e_1 ||_{\sf HB}^\sigma e_2\) を使用して \(e_1 \le_{\sf HB}^\sigma e_2\) でも \(e_2 \le_{\sf HB}^\sigma e_1\) でもないことを示す。我々は \(e_1 \ne e_2\) かつ \(e_1 \le_{\sf HB}^\sigma e_2\) のとき \(e_1 \lt_{\sf HB}^\sigma e_2\) と言う。あるトレース \(\sigma\) で (i) \(e_1 \asymp e_2\) かつ (ii) \(e_1 ||_{\sf HB}^\sigma e_2\) の場合、\(\sigma\) の 2 つのイベント \(e_1\) と \(e_2\) は happens-before (データ) 競合にあると言う。

happens-before アルゴリズム. 補題 1 に照らして、HB に基づく競合検出はベクトルタイムスタンプの観点から \(\le_{\sf HB}^\sigma\) 半順序を構築し、これを用いて競合を検出する。\(\le_{\sf HB}^\sigma\) を構築するためのコアアルゴリズムを Algorithm 1 に示す。このアルゴリズムはすべてのスレッド \(t \in {\rm Thrds}\) に対してベクトルクロック \(\mathbb{C}_t\) を維持し、すべてのロック \(\ell\) に対して同様のベクトルクロック \(\mathbb{C}_\ell\) を維持する。イベント \(e=\langle t,{\sf op}\rangle\) を処理するときに更新 \(\mathbb{C}_t.{\sf Increment}(t,1)\) を実行するが、これは暗黙的なものでありAlgorithm 1 には示されていない。さらに \({\rm op} = {\sf acq}(\ell)\) または \({\rm op} = {\sf rel}(\ell)\) の場合、アルゴリズムは対応する手続きを実行する。\(e\) の HB-タイムスタンプは \(e\) が処理された直後に \(\mathbb{C}_{\sf tid}(e)\) に格納された値になる。

ベクトルクロックを使用した実行時間. トレース \(\sigma\) に \(n\) 個のイベントと \(k\) 個のスレッドがある場合、Algorithm 1 とベクトルクロックを使用して HB 半順序を計算するには \(O(n\cdot k)\) がかかる。すべてのベクトルクロックの結合およびコピー操作がすべての \(k\) スレッドに渡って反復されるため 2 次境界 (quadratic bound) が発生する。

1. ² 表示を容易にするために fork および join イベントは無視する。このようなイベントの処理は簡単である。

3 ツリークロックデータ構造

このセクションでは並行分散システムにおける論理時間を表現するための新しいデータ構造であるツリークロックを紹介する。まずツリークロックの背後にある直感を説明し、次にデータ構造の詳細を説明する。

3.1 直感

ベクトルクロックと同様に、ツリークロックは他のスレッドのイベントに関するスレッドの知識を記録するベクトルタイムスタンプを表す。したがって各スレッド \(t\) について、ツリークロックは \(t\) の最後の既知のローカル時刻を記録する。ただしフラットなベクトルクロックとは異なりツリークロックはこの情報を階層的に維持する。ノードはスレッドのローカル時刻を保存し、ツリー構造はこの情報が中間スレッドを通じてどのように推移的に取得されたかを記録する。次の例では \({\sf acq}(\ell)\), \({\sf rel}(\ell)\) というシーケンスを表すために \({\sf sync}(\ell)\) という操作を使用する。

1. 直接単調性 (direct monotonicity). Algorithm 1 のようなベクトルクロックベースのアルゴリズムは、直感的にすべてのスレッドに関するスレッド \(t\) の知識を取得するベクトルクロック \(\mathbb{C}_t\) を維持することは前に述べた。しかしこの情報がどのように取得されたかは保持していない。例で示すように、この情報がどのように取得されたかに関する知識は結合操作で活用できる。Figure 2a に示すトレース \(\sigma\) の HB 半順序の計算を考える。イベント \(e_7\) では \(e_6 \le_{\sf HB}^\sigma\) (Figure 2a の破線) であるため、スレッド \(t_4\) はスレッド \(t_3\) を通じてトレース中のイベントに関する情報を推移的に学習する。これはスレッド \(t_3\) のクロック \(\mathbb{C}_{t_3}\) と結合することで達成される。ベクトルクロックを使用したこのような欠乏には、長さ 4 の 2 つのベクトルの点単位の最大値を取得する必要があるため、4 つのステップを要する。

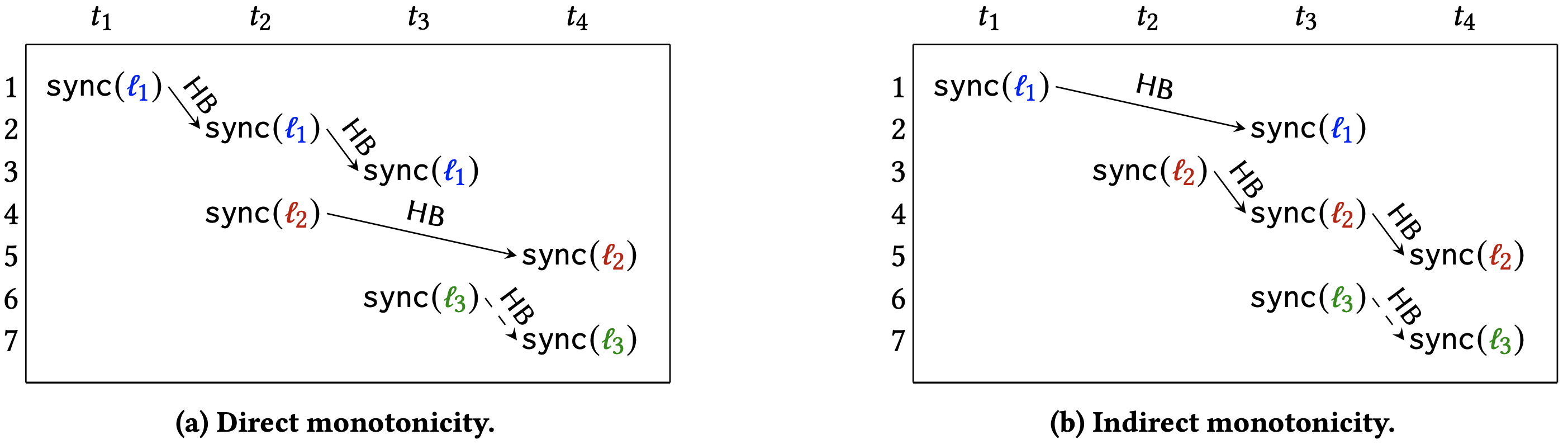
これらのタイムスタンプに加えて、これらのタイムスタンプが各クロックでどのように更新されたかを維持するとする。これにより次のような観察が可能となる。

1. スレッド \(t_3\) はスレッド \(t_2\) のイベント \(e_2\) を通じて \(t_1\) のイベント \(e_1\) を推移的に認識している。

2. スレッド \(t_4\) (\(e_7\) での結合前) はスレッド \(t_2\) のイベント \(e_1\) から \(e_4\) を認識している。

結合前、\(t_4\) は \(t_3\) と比較して \(t_2\) のより新しいビューを持っているため、スレッド \(t_3\) がスレッド \(t_2\) を介して世界について知っているすべての情報を認識している。したがって結合を実行するときに 2 つのクロック内のスレッド \(t_1\) に対応するコンポーネントを調べる必要がない。ツリークロックはこのような追加情報を維持することによりベクトルタイムスタンプのいくつかの成分を検査することを回避し、劣線形更新を行うことができる。

間接単調性 (indirect monotonicity). ここで "スレッドのビューがどのように更新されたか" に関する情報に加えて "スレッドのビューがいつ更新されたか" も維持すると、結合操作のコストがさらに削減できることを示す。Figure 2b のトレース \(\sigma\) について考える。スレッド \(t_4\) の各イベントでは 2 つの結合操作を実行することによってスレッド \(t_3\) を通じて推移的にイベント \(e_1\), \(e_2\), \(e_3\) について学習する。イベント \(e_7\) で、スレッド \(t_4\) はスレッド \(t_3\) (つまり \(e_6\) の新しいイベントを発見する。ただしスレッド \(t_1\) および \(t_2\) 荷関する知識を更新する必要はない。スレッド \(t_1\) および \(t_2\) に関するスレッドの \(t_3\) の情報は、スレッド \(t_4\) が認識しているイベント \(e_4\) の時点までに取得されている。したがって知識が何時取得されたかに関する情報も保持されている場合、この形式の "間接単調性" を利用してベクトルタイムスタンプのすべてのコンポーネントの検査を回避できる。

ベクトルクロックのフラットな構造は情報共有の推移性を欠いているため、単調性に基づく論証が失われ、結果として空虚な演算が発生する。一方、ツリークロックはその階層構造において推移性を維持する。これにより直接・間接の単調性についての推論が可能となり冗長な操作が回避される。

3.2 ツリークロック

次にツリークロックのデータ構造を詳しく説明する。

1. \(T = (\mathcal{V},\mathcal{E})\) は \(({\sf tid},{\rm clk},{\rm aclk}) \in {\rm Thrds} \times \mathbb{N}^2\) 形式のノードのルートツリー (rooted tree) である。すべてのノード \(u\) は \({\rm aclk}\) の降順で順序付きリスト \({\rm Chld}(u)\) にその子を格納する。また \(u\) の親へのポインタ \({\rm Prnt}(u)\) を \(T\) に保存する。

2. \({\rm ThrMap}: {\rm Thrds} \to \mathcal{V}\) は \({\rm ThrMap}(t) = ({\sf tid},{\rm clk},{\rm aclk})\) の場合に \(t={\sf tid}\) という特性を持つスレッドマップ (thread map) である。

\(T\) のルートを \(T.{\rm root}\) で表し、ツリークロック \(TC\) に対して \(TC\) のルートツリーを \(TC.{\rm T}\)、スレッドマップを \(TC.{\rm ThrMap}\) でそれぞれ参照する。\(T\) のノード \(u=({\sf tid},{\rm clk},{\rm aclk})\) に対して、\(u.{\sf tid}={\sf tid}\)、\(u.{\rm clk}={\rm clk}\)、\(u.{\rm aclk}={\rm aclk}\) とし、\({\sf tid}(e)={\sf tid}\) かつ \({\rm lTime}(e)={\rm clk}\) であるような一意のイベント \(e\) を \(u\) が指している (point to) と言う。直感的には \(u={\rm Prnt}(u)\) であれば \(u\) は次の情報を表している。

1. \(TC\) はスレッド \(u.{\sf tid}\) のローカル時刻 \(u.{\rm clk}\) を持っている。

2. \(u.{\rm aclk}\) は \(v.{\sf tid}\) のアタッチメント時間 (attachment time) であり、\(v\) が \(u.{\sf tid}\) の \(u.{\rm clk}\) について学習したときの \(v\) のローカル時刻である (これは \(u\) が \(v\) にアタッチされたときの時刻になるだろう)。

当然、\(u=T.{\rm root}\) であれば \(u.{\rm aclk}=\perp\) である。Figure 3 参照。

ツリークロック操作. ベクトルクロックと同様にツリークロックは初期化、更新、比較の機能を提供する。注目すべき主な操作が 2 つある。一つ目は \({\sf Join}\)で、\(TC_1.{\sf Join}(TC_2)\) はツリークロック \(TC_2\) を \(TC_1\) に結合する。ベクトルクロックとは対照的にこの操作はセクション 3.1 で概説した直接および間接の単調性を使用して \(TC_1\) と \(TC_2\) (可能な場合) のサイズで劣線形時間で結合を実行する。二つ目は \({\sf MonotoneCopy}\) で、\(TC_1 \sqsubseteq TC_2\) が分かっているときに \(TC_1.{\sf MonotoneCopy}(TC_2)\) は \(TC_1\) に \(TC_2\) をコピーする。これが成り立つ場合、コピー操作は結合と同じセマンティクスを持ち、したがって結合を劣線形時間で実行する原理が \({\sf MonotoneCopy}\) にも適用されるという考えである。

アルゴリズム 2 はこの機能の擬似コードの説明を示している。左の列の関数はツリークロックに対して実行可能な操作を示し、右の列はより複雑な関数 \({\sf Join}\) と \({\sf MonotoneCopy}\) のヘルパールーチンを示す。以下では各機能を直感的に説明する。

1. \({\sf Init}(t)\). この関数はノード \(u=(t,0,\perp)\) を作成することでスレッド \(t\) に属するツリークロック \(TC_t\) を初期化する。ノード \(u\) は常に \(TC_t\) のルートとなる。この初期化関数はスレッドのクロックを表すツリークロックにのみ使用される。リリースイベントのベクトル時間を保持するための補助ツリークロックはこの初期化を実行しない。

2. \({\sf Get}(t)\). この関数は単に \(TC\) 二格納されているスレッド \(t\) の時間を返すが、\(t\) が \(TC\) に存在しない場合は 0 を返す。

3. \({\sf Increment}(i)\). この関数は \(TC\) のルートノードの時刻をインクリメントする。これは \({\sf Init}\) を使用して初期化されたツリークロックでのみ使用される。つまりツリークロックは常にツリーのルートに格納されるスレッドに属する。

4. \({\sf LessThan}(TC')\). この関数は \(TC\) のベクトル時間を \(TC'\) のベクトル時間と比較する。つまり \(TC \sqsubseteq TC'\) の場合は True を返す。

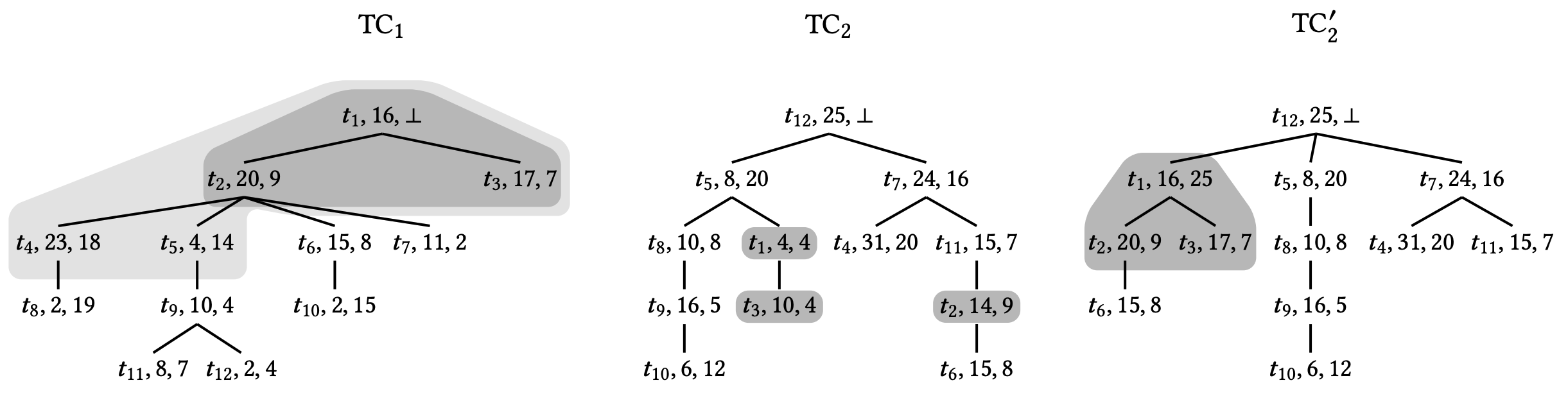
5. \({\sf Join}(TC')\). この関数は \(TC'\) との結合操作、つまり \(TC \leftarrow TC \sqcup TC'\) の更新を実装する。大まかに言うとこの関数は次の手順を実行する。

   1. ルーチン \({\sf getUpdatedNodesJoin}\) は \(TC'\) の事前順序トラバーサル (pre-order traversal) を実行し、\(TC\) と比較して \(TC'\) で進行した \(TC'\) のノードをスタック \(\mathcal{S}\) に収集する。トラバーサルは直接または間接の単調性により早期に停止する可能性があるため、このルーチンは通常劣線形時間を要する。

   2. ルーチン \({\sf detachNodes}\) は \({\sf tid}\) が \(\mathcal{S}\) に現れるノードをツリー内で再配置するために \(TC\) から切り離す。

   3. ルーチン \({\sf attachNodes}\) は前のステップで切り離された \(TC\) ノードを更新し、ツリー内で再配置する。このステップは \({\sf getUpdatedNodesJoin}\) によって計算された進行中のノードを含む \(TC'\) のサブツリーと同一の \(TC\) のノードのサブツリーを効率的に生成する。

   4. 最後に、\({\sf Join}\) の最後の 4 行は前のステップで構築されたサブツリーを \(TC\) のルート \(z\) の下、\({\rm Chld}(z)\) リストの先頭に追加する。

   Figure 4 に図を示す。

6. \({\sf MonotoneCopy}(TC')\). この関数は \(TC \sqsubseteq TC'\) を仮定したコピー操作 \(TC \leftarrow TC'\) を実装する。この関数は \({\sf Join}\) と非常に似ている。主な違いは、今回はそれぞれの時刻が等しい場合でも \(TC\) のルートは常に \(TC'\) で進行したと見なされることである。これは \(TC\) のルートを現在のノードから \({\sf tid}\) が \(TC'\) のルートに等しい者に変更するために必要である。Figure 5 に図を示す。

   \({\sf Join}\) と \({\sf MonotoneCopy}\) でツリークロックの階層構造を利用する重要な部分は \({\sf getUpdatedNodesJoin}\) と \({\sf getUpdatedNodesCopy}\) である。それぞれの場合において、\(u'\) が \(TC\) の時刻に対して進んでいる場合のみ、親 \(u\) からその子 \(v'\) に進み (Figure 2a 参照)、直接単調性を捉える。さらに \(TC\) が \(u'\) 上の \(v'\) のアタッチメント時間をまだ確認していない場合にのみ、\(u'\) の子 \(v'\) から次の子 \(v''\) (\({\sf Chld}(u')\) の出現順) に進み、間接単調性を捉える。

備考 1 (定数時間エポックアクセス). 関数 \(TC.{\sf Get}(t)\) はベクトルクロックと同様に \(TC\) に格納されているスレッド \(t\) の時間を \(O(1)\) で返す。これによりベクトルクロックからすべてのエポック関連の最適化 [23, 50] をツリークロックに適用できるようになる。

4 happens-before に対するツリークロック

HB 半順序の計算にツリークロックがどのように使用されるかを見てみよう。まず次の観察から始める。

補題 2 (コピーの単調性). Algorithm 1 がロック解除イベント \(\langle t, {\sf rel}(\ell)\rangle\) を処理する直前に \(\mathbb{C}_\ell \sqsubseteq \mathbb{C}_t\) が得られる。

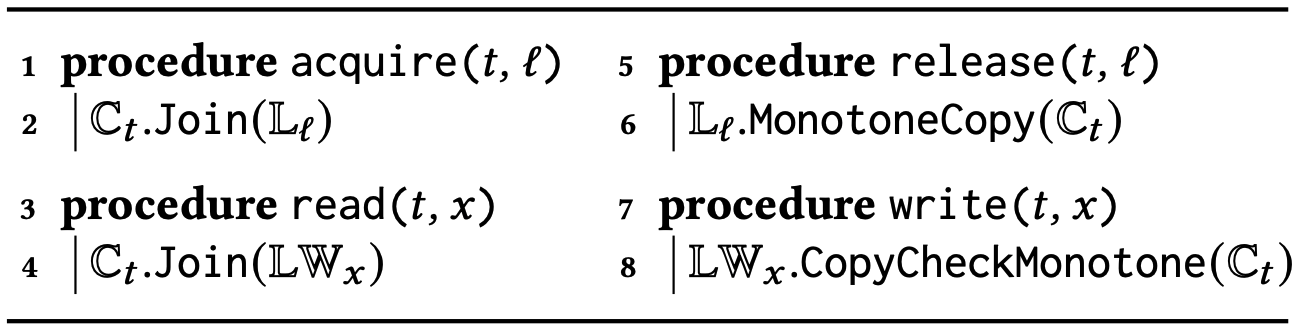
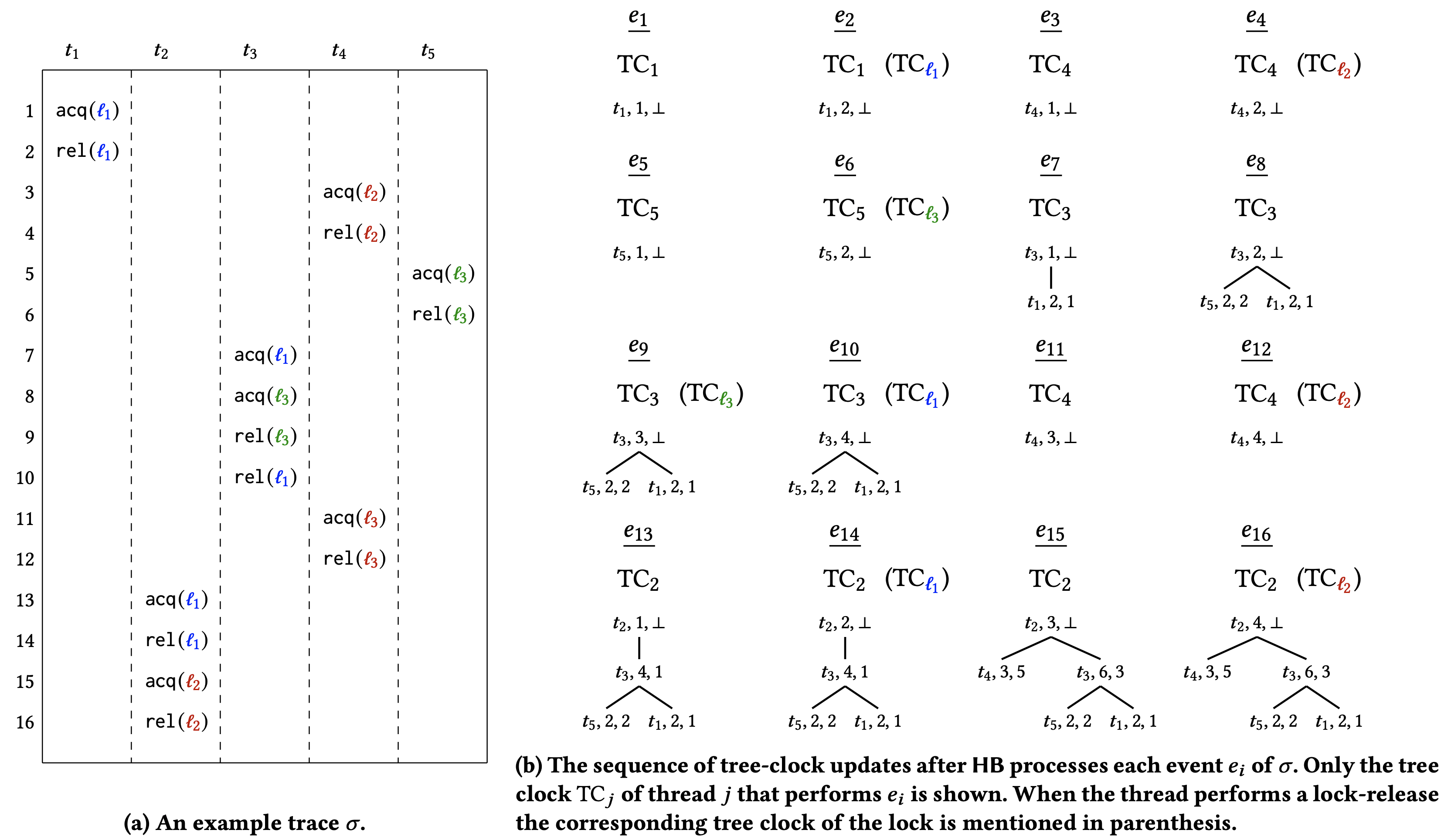
HB に対するツリークロック. アルゴリズム 3 はベクトル時間を実装するためのツリークロックデータ構造を使用して HB を計算するアルゴリズムを示している。ロック取得イベントを処理するとき、ベクトルクロック結合操作はツリークロック結合に置き換えられている。さらに補題 2 を考慮すると、ロック解除イベントを処理するときベクトルクロックのコピー操作はツリークロックの単調コピーに置き換えられている。トレース \(\sigma\) でのアルゴリズム 3 の実行例については、実行中にツリークロックがどのように成長するかを示す Appendix B を参照。

正しさ (correctness). ここでアルゴリズム 3 が実際に HB 半順序を計算することを示す。ツリークロックの 2 つの単調性不変式から開始する。

補題 3. 任意のツリークロック \(\mathbb{C}\) と \(\mathbb{C}\) のノード \(u\) について考える。任意のツリークロック \(\mathbb{C}'\) に対して次の主張が成り立つ。

1. 直接単調性: \(u.{\rm clk} \le \mathbb{C}'.{\sf Get}(u.{\sf tid})\) ならば、\(u\) のすべての子孫 \(w\) に対して \(w.{\rm clk} \le \mathbb{C}'.{\sf Get}(u.{\sf tid})\) が成り立つ。

2. 間接単調性: \(v.{\rm aclk} \le \mathbb{C}'.{\sf Get}(u.{\sf tid})\) かつ \(v\) が \(u\) の子であるならば、\(u\) のすべての子孫 \(w\) について \(w.{\rm clk} \le \mathbb{C}'.{\sf Get}(w.{\sf tid})\) が成り立つ。

次の補題は上記の不変式から導き出され、ツリークロックを使用するアルゴリズム 3 がすべてのイベントの正しいタイムスタンプ、つまり HB のツリークロックの正確さを計算することを確立する。

補題 4. アルゴリズム 3 がイベント \(e\) を処理するとき、ツリークロック \(\mathbb{C}_{{\sf tid}(e)}\) に格納されるベクトルクロックは \(\mathbb{C}_e^{\le_{\sf HB}^\sigma}\) である。

データ構造の最適化 (data structure optimality). ベクトルクロックと同様に、ツリークロックを使用した HB の計算には最悪でも \(\Theta(n\cdot k)\) 時間がかかり、動的な競合予想 [31] などの一般的なアプリケーションではこの二次境界が厳しい可能性が高いことが知られている。ただし、ツリークロックは結合およびコピー操作に劣線形時間がかかるのに対して、ベクトルクロックでは常にベクトルサイズに線形 (つまり \(\Theta(k)\)) 時間がかかることが分かっている。ここで、ツリークロックよりも効率的なデータ構造はあるのか? より一般的には、ベクトル時刻を表す HB アルゴリズムの最も効率的なデータ構造は何だろうか? という当然の疑問が生じる。この問いに答えるためにベクトル時間作業 (vector-time work) を定義する。これはベクトル時間を格納するために使用される実際のデータ構造に関係なく、HB が実行する必要のあるデータ構造操作の数に下限を与える。そしてツリークロックがこの下限に一致し、HB の最適化が達成されることを示す。

ベクトル時間作業 (vector-time work). 一般的な HB アルゴリズム (Algorithm 1) を考慮し、\(\mathcal{D}=\{\mathbb{C}_1,\mathbb{C}_2,\ldots,\mathbb{C}_m\}\) を使用するベクトル時間データ構造の集合とする。トレース \(\sigma\) でのアルゴリズム実行について考える。ある \(1 \le i \le |\sigma|\) が与えられたとき、アルゴリズムが \(\sigma\) の \(i\) 番目のイベントを処理した後、\(\mathbb{C}_j\) で表されるベクトル時間を \(\mathbb{C}_j^i\) と記述する。\(\sigma\) 上のベクトル時間作業 (または略して vt-work) を \[ {\rm VTWork}(\sigma) = \sum_{1 \le i \le |\sigma|} \sum_j \left| t \in {\rm Thrds}: C_j^{i-1}(t) \ne C_j^i(t) \right| \] と定義する。つまり処理されたイベントごとに、イベントを処理した結果変更されたベクトル時間エントリの数を追加し、\({\rm VTWork}(\sigma)\) はアルゴリズム全体の過程におけるエントリ更新の合計数をカウントする。vt-work は各 \(\mathbb{C}_j\) を表現するために使用されるデータ構造に依存せず、\[ n \le {\rm VTWork}(\sigma) \le n \cdot k \] の不等式を満たすことに注意。

ベクトル時間の最適化 (vector-time optimality). 入力トレース \(\sigma\) が与えられたとき、ベクトル時間を格納するデータ構造 \(DS\) を使用して \(\sigma\) を処理する HB アルゴリズム (Algorithm 1) にかかる時間を \(\mathcal{T}_{DS}(\sigma)\) とする。直感的には \({\rm VTWork}(\sigma)\) は \(DS\) の状態が変化した回数を捉えている。ベクトル時間を明示的に表すデータ構造の場合、\({\rm VTWork}(\sigma)\) は \(\mathcal{T}_{DS}(\sigma)\) の自然な下限を示す。したがって \(\mathcal{T}_{DS} = O({\rm VTWork}(\sigma))\) の場合、データ構造 \(DS\) は vt-最適であると言う。ベクトルクロックが vt-最適でないことを理解するのは難しくない。つまり \(DS=VC\) をベクトルクロックのデータ構造とすると、\({\rm VTWork}(\sigma)=O(n)\) であるが \(\mathcal{T}_{DS}(\sigma) = \Omega(n \cdot k)\) である単純なトレース \(\sigma\) を構築でき、したがって実行時間は \(\sigma\) 上で実行する必要のある vt-work よりも \(k\) 倍となる。これに対して次の定理はツリークロックが vt-最適であることを示している。

定理 1 (ツリークロック最適化). 任意の入力トレース \(\sigma\) に対して \(\mathcal{T}_{TC}(\sigma) = O({\rm VTWork}(\sigma))\) が成り立つ。

定理 1 の背後にある重要な観察は、HB がツリークロックを使用する場合、すべての結合と単調コピー操作でアクセスされるツリークロックのエントリ総数 (つまり Figure 4 と Figure 5 の明るい灰色領域のサイズの合計) が \(\le 3 \cdot {\rm VTWork}(\sigma)\) であるということである。

備考 2. 定理 1 は、ツリークロックがすべての入力に対して vt-最適であるという意味でツリークロックの強い最適性を立証している。これは一部の入力に対してのみ保証される通常の最適性の概念とは対照的である。

5 他の反順序におけるツリークロック

5.1 Schedulable-Happens-Before

SHB は HB を強化したもので、競合検出のコンテキストで最近 [35] で導入された。トレース \(\sigma\) と読み取りイベント \(r\) が与えられたとき、\({\rm lw}_\sigma(r)\) を \({\rm Variable}(w) = {\rm Variable}(r)\) で \(r\) より前の \(\sigma\) の最後の書き込みイベントとする。SHB は次を満たす最小の反順序である。

1. \(\le_{\sf HB}^\sigma \subseteq \le_{\sf SHB}^\sigma\)

2. すべての読み取りイベント \(r\) に対して \({\rm lw}_\sigma(r) \le_{\sf SHB}^\sigma r\) が成り立つ。

SHB のアルゴリズム. HB と同様に SHB の半順序はベクトル時間 [35] を使用して入力トレース \(\sigma\) の単一パスによって計算される。SHB アルゴリズムは HB と同様に同期イベント (つまり \({\sf acq}(\ell)\) と \({\sf rel}(\ell)\)) を処理する。さらに各変数 \(x\) に対して、アルゴリズムは \(x\) 上の最新の書き込みイベントのベクトル時間を格納するデータ構造 \({\rm LW}_x\) を維持する。書き込みイベント \({\sf w}(x)\) が発生するとベクトル時間 \(\mathbb{C}_{{\sf tid}(w)}\) が \({\rm LW}_x\) にコピーされる。一方、読み取りイベント \({\sf r}(x)\) が発生するとアルゴリズムは \({\rm LW}_x\) を \(\mathbb{C}_{{\sf tid}(r)}\) に結合する。

ツリークロックを使った SHB. ツリークロックは SHB アルゴリズムでベクトル時間を格納するためのデータ構造として直接使用できる。擬似コードはアルゴリズム 4 を参照。重要な新要素は \(\mathbb{C}_t\) のベクトル時間を \({\rm LW}_x\) にコピーする 8 行目の \({\sf CopyCheckMonotone}\) 関数である。\({\sf MonotoneCopy}\) とは対照的にこのコピーは単調である保証はない。つまり \({\rm LW}_x \not\sqsubseteq \mathbb{C}_t\) となる可能性がある。ただしツリークロックを使えばこのテストに必要な時間は定数である。内部的には、\({\sf CopyCheckMonotone}\) は \({\rm LW}_x \sqsubseteq \mathbb{C}_t\) の場合に \({\sf MonotoneCopy}\) を実行し (劣線形時間で実行)、そうでない場合はツリークロック全体に対してディープコピーを実行する (線形時間で実行)。実際にはほとんどの場合 \({\sf CopyCheckMonotone}\) の結果は \({\sf MonotoneCopy}\) となり非常に効率的であることが予想される。重要な洞察は、\({\sf MonotoneCopy}\) が使用されない場合に \({\rm LW} \not\sqsubseteq \mathbb{C}_t\) となり、競合 \(({\rm lw}_\sigma(r), r)\) が発生することである。したがってディープコピーが実行される回数は、\(\sigma\) における読み取りから最後の書き込みまでの間の書き込み-読み取り競合の数によって制限される。

5.2 Mazurkiewicz 半順序

Mazurkiewicz(マズルケビッチ)半順序 (MAZ) [40] は、どのイベントを並べ替えることができるかを定義する独立関係を使用して、並行実行を代数的に表現する標準的な方法である。この代数処理により、逐次プログラムの検証から並行プログラムの言語包含問題を自然に解くことができる [7]。そのため、動的分析 [25, 38, 42]、一貫性の保証 [57]、ステートレスモデル検査 [26] などに深く応用されており、並列性の文脈で最も研究されている半順序である。共有メモリ並行処理では、標準の独立関係により 2 つのイベントが競合する場合は依存、そうでない場合は独立とみなす [28]。特に MAZ は次の条件を満たす半順序である。

1. \(\le_{\sf HB}^\sigma \subseteq \le_{\sf MAZ}^\sigma\)

2. \(e_1 \le_{\sf tr}^\sigma e_2\) かつ \(e_1 \asymp e_2\) であるような 2 つのイベント \(e_1\) と \(e_2\) ごとに \(e_1 \le_{\sf MAZ}^\sigma e_2\) が成り立つ。

ツリークロックによる MAZ. MAZ の計算アルゴリズムは SHB と同様である。主な違いは、MAZ には読み出しから書き込みまでの順序 (read-to-write ordering) が含まれるため、スレッド \(t\) の最後のイベント \({\sf r}(x)\) のベクトル時間 \(\mathbb{R}_{t,x}\) を保存する必要があることである。さらに集合 \({\rm LRDs}_x\) を使用して最新の \({\sf w}(x)\) イベントの後に \({\sf r}(x)\) イベントを実行したスレッドを保存する。これにより読み取りイベントとその後の書き込みイベントの間の順序付けは、中間的な書き込みから書き込みへの順序付けを介して推移的に続くため、最初の読み出しから書き込みまでの順序付けにのみ計算時間を費やすことができる。全体的にこのアプローチは HB や SHB と同様に MAZ の効率的な時間計算量 \(O(n\cdot k)\) をもたらす。擬似コードはアルゴリズム 5 を参照。

6 実験

このセクションではツリークロックデータ構造の実装と実験的評価について報告する。これらの実験の主な目的はプログラムの並行実行で論理時間を追跡するためのベクトルクロックに対するツリークロックの実用的な利点を評価することである。

実装. 我々は Java で実装しアルゴリズム 2 に忠実に従っている。ツリークロックのデータ構造は長さ \(k\) (スレッド数) の 2 つの配列で表現される。最初の配列はツリーの形状をエンコードし、二つ目の配列は標準的なベクトルクロックののように整数のタイムスタンプをエンコードする。効率化のため、再帰的なルーチンは反復処理とした。

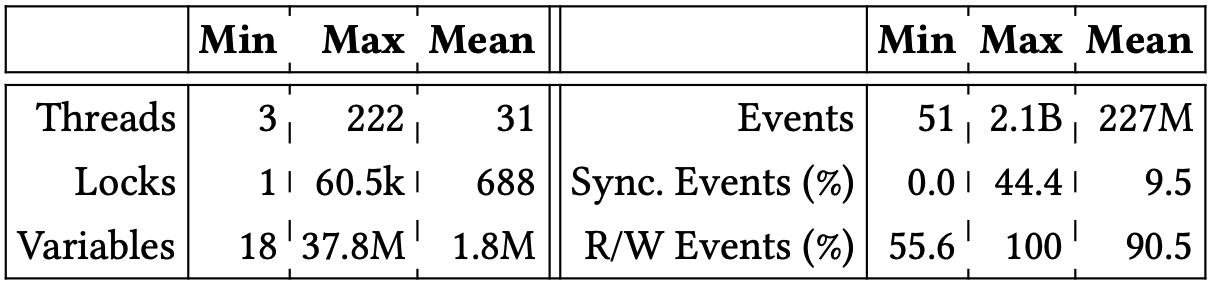
ベンチマーク. 我々のベンチマークセットはベンチマークスイートおよび最近の文献に見られる標準的なベンチマークで構成されている。特に IMB Contest suite [19]、Java Grande suite [60]、DaCapo [9]、SIR [16] の Java ベンチマークを使用した。さらに DataRaceOnAccelerator [54]、DataRaceBench [33]、OmpSCR [17]、および NAS parallel benchmark [6] からの実行時間とスレッド数が調整可能な OpenMP ベンチマークプログラムと、CORAL [1, 2]、ECP proxy application [3]、Mantevo project [4] のベンチマークスイートを含む大規模 OpenMP アプリケーションを使用した。各ベンチマークは RV-Predict [51] (Java プログラム用) および ThreadSanitizer [56] (OpenMP プログラム用) ツールを使用して単一の並行トレースをログに記録するために計測および実行された。全体としてこのプロセスにより評価に使用した 153 個のベンチマークトレースの大規模なセットが得られた。生成されたベンチマークトレースに関する集約情報を Table 1 に示す。個々のトレースに関する情報は Appendix C の Table 3 に記載されている。

セットアップ. 各トレースはツリークロックと標準ベクトルクロックの両方を使用して MAZ, SHB, HB の各半順序を計算するために処理された。これにより本論文の目的である、それぞれの半順序を計算する際にツリークロックによってもたらされる高速化を直接観測することができる。

これらの半順序の計算は通常、分析の最初の要素であるため、一般に全体的な解析で得られる高速化の影響を次のように評価した。競合するイベント \(e_1\), \(e_2\) の各ペアについて、これらのイベントが対応する半順序に関して同時であるか (\(e_1 ||_{\sf HB}^\sigma e_2\) かどうか) を計算した。このテストは、そのようなペアがデータ競合を構成する動的競合検出 (HB と SHB の場合) や、モデルチェッカーがこのようなイベントペアを識別し並行プログラムのすべての Mazurkiewicz トレースを網羅的に列挙する途中でそのペアを逆にしようとするステートレスモデルチェック (MAZ の場合) で実行される。公平な比較のために、HB の場合はツリークロックとベクトルクロックの両方で解析を高速化するため一般的なエポック最適化 [23] を使用した (備考 1 参照)。一貫性を保つためにすべての測定は 3 回繰り返し平均時間を報告した。

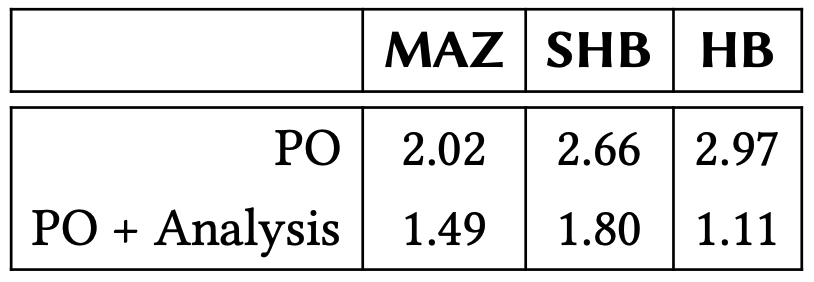
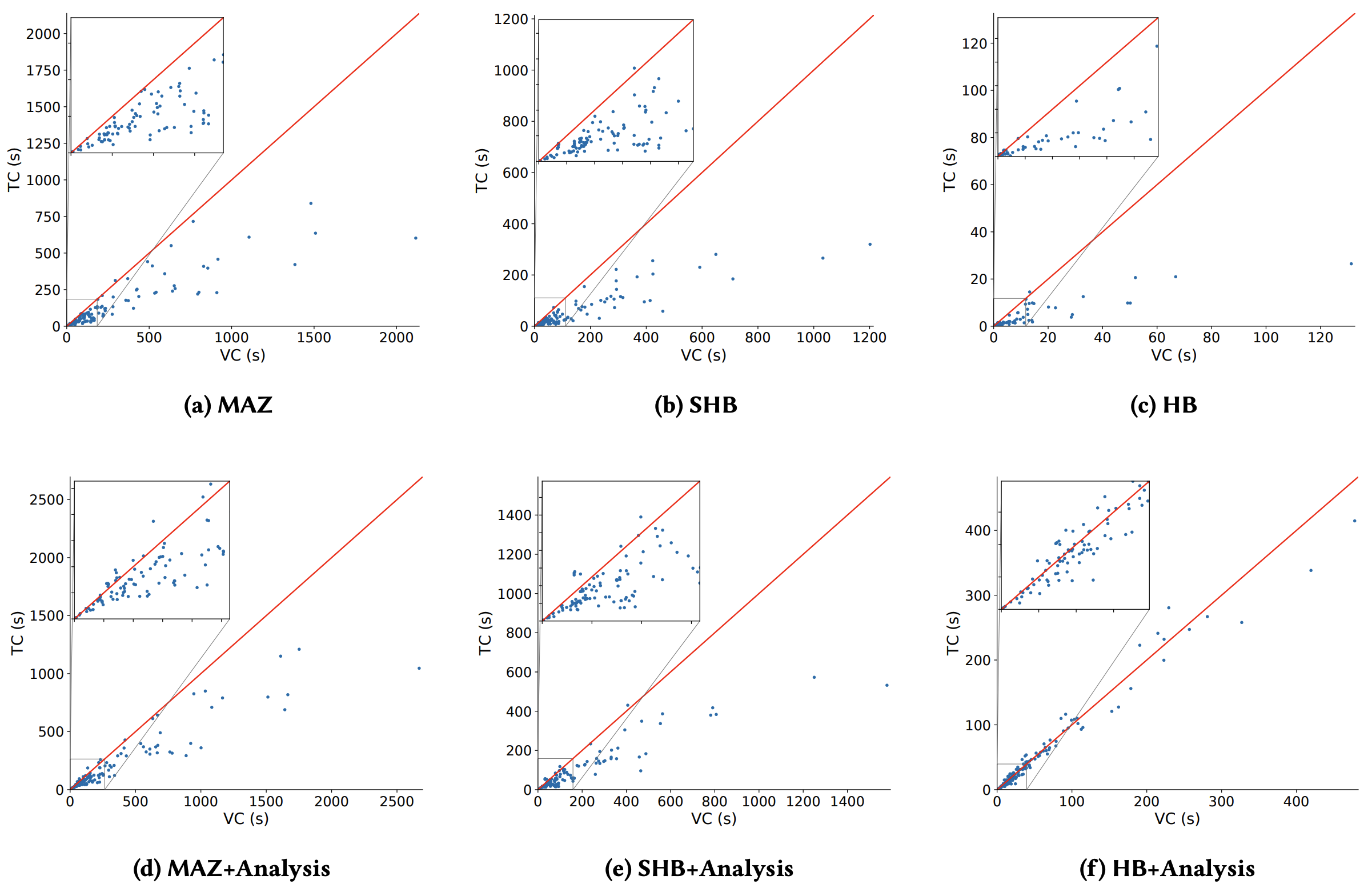
実行時間. Table 2 はそれぞれの半順序について分析コンポーネントを使用した場合と使用しない場合のすべてのベンチマークの平均速度向上を示している。ツリークロックは 3 つの半順序すべての計算で実行時間を短縮するのに非常に効果的であることが分かるが、最も重要な影響を与えたのは SHB であり平均速度向上は 2.53 倍であった。MAZ と SHB の場合、この高速化は全体の解析時間の大幅な高速化にもつながる。一方、ツリークロックを使用した HB はベクトルクロックを使用した場合よりも 2 倍高速だが、この高速化が全体の解析時間に与える影響は小さくなる。この観察の背後にある理由は単純である。SHB と MAZ はあらゆる種類のイベントを使用して定義されているため計算量が遙かに多くなる。一方 HB は同期イベント (\({\sf acq}\) と \({\sf rel}\)) のみで定義されベンチマークトレースでは平均してイベントの \(\simeq\)9.5% のみが同期イベントである。我々の分析ではすべてのイベントを考慮するため HB 計算コンポーネントが閉める時間は全体の分析時間のごく一部である。ただし、より同期が多いプログラム、またはより軽量な分析 (すべての変数ではなく特定の変数でのデータ競合をチェックする場合など) では、ツリークロックの高速化が分析全体でより大きくなることに注意。トレース中の同期イベントの割合が増加するにつれて速度が向上する傾向が観察される。さらにスレッド数が多い場合に高速化が顕著になることが観察される。

Figure 6 はすべてのベンチマークにおけるツリークロック時間とベクトルクロック時間の詳細を示している。ツリークロックのほとんどがすべての半順序でベクトルクロックを上回っており、場合によっては大幅にパフォーマンスが優れていることが分かる。興味深いことにより負荷の高いベンチマーク (つまりより時間がかかるベンチマーク) において高速化がより大きくなる傾向がある。ごく希にツリークロックが遅くなる場合もあるがそれはほんの小さな要因によるものである。それらはツリークロックの劣線形更新がわずかな改善の可能性しか得られないトレースであり、(ベクトルとは対照的な) より複雑なツリー構造を維持するオーバーヘッドを正当化するものではない。とはいえ全体的なツリークロックは MAZ, HB, SHB のそれぞれに一貫して十分な高速化をもたらしている。最後の、これらの高速化はすべてそれぞれの半順序を計算するアルゴリズムやデータ構造との相互作用を最適化することなく、基礎となるデータ構造を置き換えるだけで直接得られることを指摘しておく。

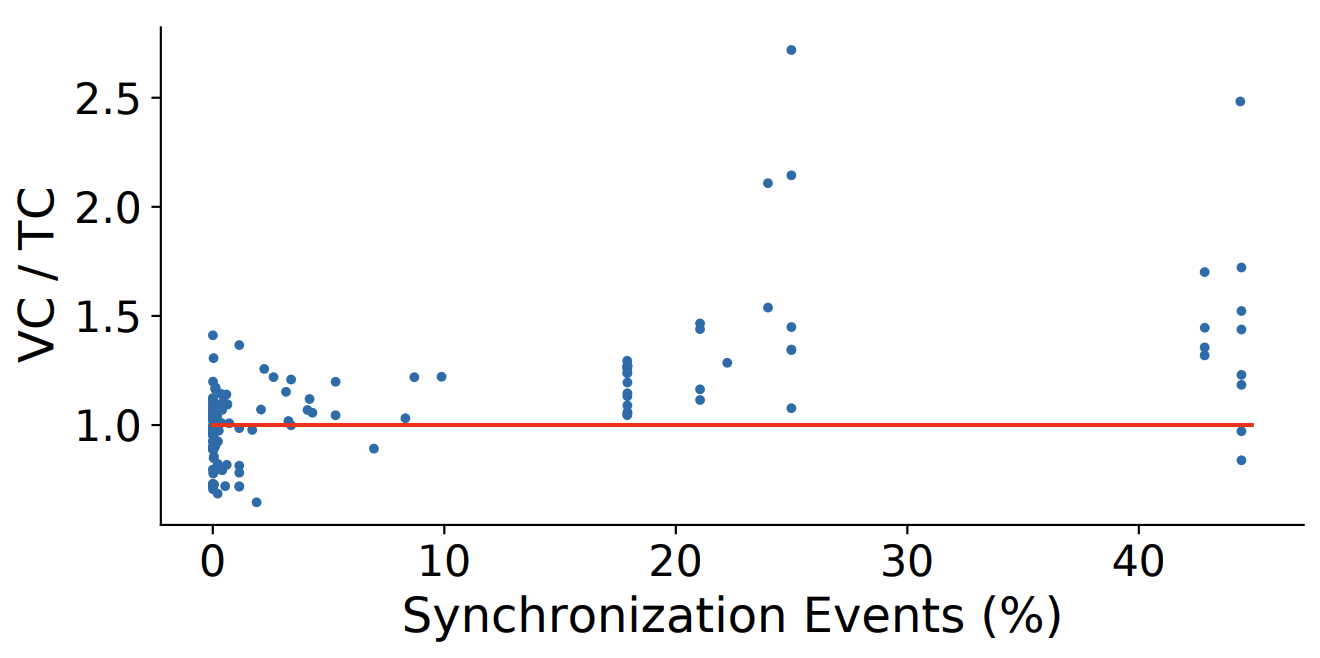
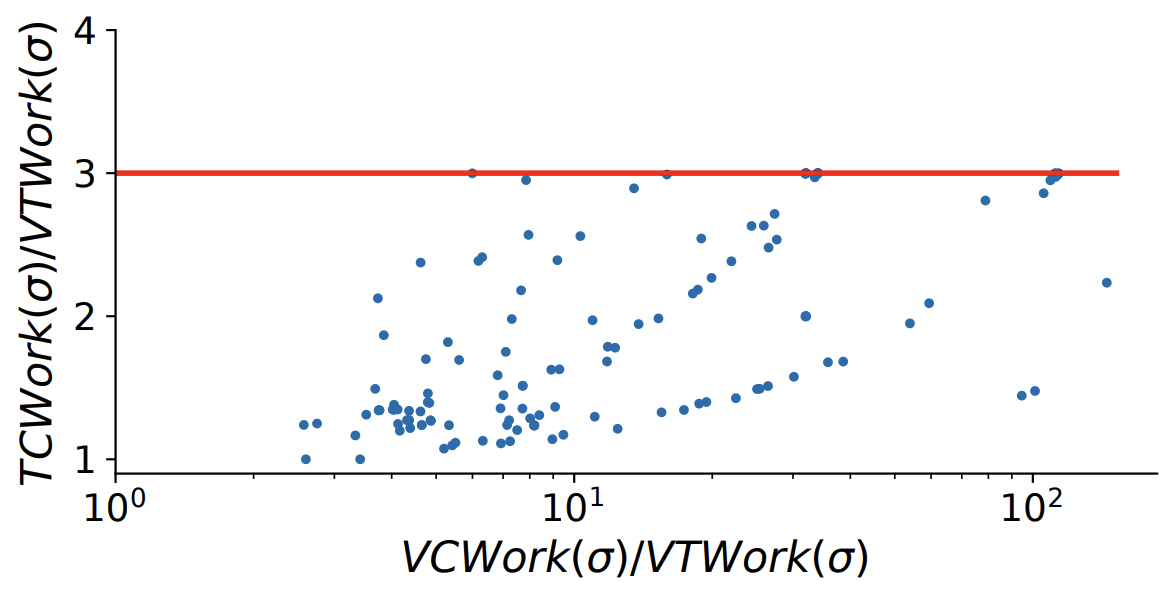
ベクトル時間作業との比較. 我々は各データ構造を使用して更新されたエントリの総数も調査した。メトリクス \({\rm VTWork}(\sigma)\) (セクション 4) は HB 半順序を計算するときにベクトル時間の任意の実装が実行しなければならない更新の最小量を測定することは以前に述べた。同様にデータ構造ツリークロックとベクトルクロックをそれぞれ使用する場合、各イベントの処理時に更新されるエントリの数に対応するメトリクス \({\rm TCWork}(\sigma)\) と \({\rm VCWork}(\sigma)\) を定義できる。これらのメトリクスはベンチマークスイートで HB 半順序を計算するために Figure 8 で可視化されている。この図から \({\rm VCWork}(\sigma)/{\rm VTWork}(\sigma)\) 比がかなり大きいことを示している。対照的に \({\rm VCWork}(\sigma)/{\rm VTWork}(\sigma)\) 比は通常かなり小さくなる。ベクトルクロックとツリークロックの間の実行時間の違いは \({\rm TCWork}(\cdot)\) と \({\rm VCWork}(\cdot)\) 間の不一致を反映している。次に、ツリークロックの最適性 (定理 1)、つまり \({\rm TCWork}(\sigma) \le 3 \cdot {\rm VTWork}(\sigma)\) の背後にある直感を以前に述べた。Figure 8 は \({\rm TCWork}(\sigma)/{\rm VTWork}(\sigma)\) 比が 100 近くまで増加している一方で、\({\rm TCWork}(\sigma)/{\rm VTWork}(\sigma)\) 比が 3 の上限に収まっていることから、この理論的境界を裏付けている。さらに一歩進んで Figure 9 はデータセット内の各半順序の \({\rm VCWork}(\sigma)/{\rm TCWork}(\sigma)\) 比を示している。結果は、ベクトルクロックがツリークロックに比べて不要な作業を多く行っていることを示しており、ツリークロックの高速化の原因を実験的に示している。Figure 9 は高速化の可能性が高い (55 倍に達する) ことを示しているが、1 回のツリークロック演算は 1 回のベクトルクロック演算よりも計算量が多いため、我々の実験 (Figure 6) での実際の高速化はより小さいものになる。

スケーラビリティ. ツリークロックのスケーラビリティについてより深く理解するために、通信パターンを一定に保ちながらスレッド数とロック数のパラメータを制御してカスタムベンチマークで一連の制御実験を行った。各トレースは 1,000 万のイベントで構成され、スレッド数は 10〜360 の間で変化する。各トレースは、ランダムに選択されたスレッドがランダムに選択されたロック \(l\) に対し、\(acq(l)\) のあとに \(rel(l)\) という 2 つの連続した操作を実行する方法で生成されている。我々は 4 つの方法を検討した: (a) すべてのスレッドが単一の共通ロックを介して通信する場合 (single lock)、(b) (a) と似ているが、ロックが 50 個あり、スレッドの 20% が残りのスレッドと比較して 5 倍の確率で操作を実行する場合 (50 locks, skewed)、(c) \(k-1\) クライアントスレッドがスレッドごとに専用のロックを介して単一のサーバスレッドと通信する場合 (star topology)、(d) (a) と似ているが、スレッドのペアごとに専用のロックを介して通信する場合 (pairwise communication)。得られた結果を Figure 10 に示す。シナリオ (a) の設定ではツリークロックがベクトルクロックよりも一定の割合で高速化する様子を示している。シナリオ (b) でロック数を増やすと、スレッド通信の独立性が高まりツリークロックの利点はわずかに減少している可能性がある。スレッドのサブセットは他のスレッドよりアクティブであるため、タイムスタンプはスレッドを通じて頻繁に交換され、この設定でもツリークロックが高速となる。シナリオ (c) はツリークロックが繁栄するケースを表している。ベクトルクロックにかかる時間はスレッドの数とともに増加するがツリークロックの場合は一定のままである。これは、すべてのスレッドが他のスレッドの状況を認識しているにもかかわらず、スター型トポロジーにより平均してすべてのツリークロックのエントリにしか影響しないことを意味しているためである。直感的にはスター型通信トポロジーはツリーの形状に (ほぼ) スター型の自然な影響を与えてこの効果をもたらす。最後に、シナリオ (d) はすべてのスレッドのペアが互いに通信可能で、通信はスレッドのペアごとに固有のロックを介して行われるため、ツリークロックの最悪ケースを表している。このパターンではツリーロックの利点が向こうになり、複雑さが増すと全体的な速度が低下する。ただしこの最悪のシナリオでもツリークロックとベクトルクロックの差は比較的小さいままである。

7 関連研究

他の半順序とツリークロック. 冒頭で述べたように HB と SHB 意外にも多くの半順序がベクトルクロックを用いて動的解析を行う。このような場合、ツリークロックは部分的または完全にベクトルクロックを置き換えることができ、場合によってはここで示したデータ構造への小さな拡張が必要になることもある。特に WPC [30], DC [46], SDP [27] の半順序に対するツリークロックの興味深い応用が期待される。

動的解析の高速化. ベクトルクロックに基づく動的競合解析は遅いことが知られており [52]、多くの先行研究がこれを軽減することを目的としてきた。最も顕著なパフォーマンスのボトルネックはベクトルタイムスタンプのサイズがスレッド数に線形に依存することである。理論的な限界 [12] にもかかわらず、先行研究はトレースの特別な構造 [5, 13, 15, 20, 62] を利用して簡潔なベクトル時間の表現を可能にしてる。Goldilocks [18] アルゴリズムはベクトルタイムスタンプの代わりにロックセットを使用して HB 順序付けを推論するが深刻な側道低下が発生する [23]。FastTrack [23] の最適化では簡潔なアクセス履歴を維持するためにエポックが使用されており、我々の研究はこの最適化を補完している。ツリークロックは他のクロック (スレッドクロックとロッククロック) の最適化を提供する。クロック表現におけるその他の最適化は動的スレッドの生成に対応している [46, 47, 64]。速度低下のもう一つの要因は、プログラムの計測と高価なメタデータの同期である。ハードウェア支援 [14, 69]、ハイブリッド競合検出 [43, 67]、静的解析 [24, 48]、高度な所有権プロトコル [11, 50, 65] など、いくつかのアプローチがこの速度低下を最小限に抑えることを試みてきた。

8 結論

並列実行で論理時間を保持するための新しいデータ構造であるツリークロックを導入した。標準的なベクトルクロックとは対照的にツリークロックは通信パターンを動的にその構造に取り込み、結合やコピー操作を劣線形時間で実行することができるため、これらの操作の従来のオーバーヘッドを可能な限り回避できる。さらにベクトルクロックとは対照的にツリークロックは HB 半順序の計算に最適なベクトル時間であり、絶対的に必要なものに比べ最大でも定数倍の作業しか行わないことを示した。最後に、我々の実験ではツリークロックが MAZ, SHB, HB の半順序を計算する実行時間を大幅に短縮し、ベクトルクロックに代わる有望な代替手段になることを示している。将来の興味深い研究には ThreadSanitizer [56] などのインライン分析にツリークロックを組み込むことも考えられる。このオンライン設定で解析の原子性を維持するための追加の同期の使用はベクトルクロックとツリークロックの両方で同一であり同じ粒度となる。しかしツリークロックによって実行される高速な結合は、特に SHB や MAZ のような同期がすべてのイベント (つまり同期、またアクセスイベントも) に対して発生する半順序の場合にベクトルクロックと比較して輻輳が軽減される可能性がある。この評価は今後の研究に委ねる。最後に、ツリークロックはベクトルクロックのドロップイン置換であるため、メタデータの同期による速度低下を最小限に抑える既存の技術 (セクション 7) のほとんどはツリークロックに直接適用可能である。

ACKNOWLEDGEMENTS

We thank anonymous reviewers for their constructive feedback on an earlier draft of this manuscript. Umang Mathur was partially supported by the Simons Institute for the Theory of Computing. Mahesh Viswanathan is partially supported by grants NSF SHF 1901069 and NSF CCF 2007428.

REFERENCES

1. CORAL-2 Benchmarks. https://asc.llnl.gov/coral-2-benchmarks. Accessed: 2021-08-01.
2. CORAL Benchmarks. https://asc.llnl.gov/coral-benchmarks. Accessed: 2021-08-01.
3. ECP Proxy Applications. https://proxyapps.exascaleproject.org. Accessed: 2021-08-01.
4. Mantevo Project. https://mantevo.org. Accessed: 2021-08-01.
5. Kunal Agrawal, Joseph Devietti, Jeremy T. Fineman, I-Ting Angelina Lee, Robert Utterback, and Changming Xu. Race Detection and Reachability in Nearly SeriesParallel DAGs. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’18, page 156–171, USA, 2018. Society for Industrial and Applied Mathematics. doi:10.1137/1.9781611975031.11.
6. D. H. Bailey, E. Barszcz, J. T. Barton, D. S. Browning, R. L. Carter, L. Dagum, R. A. Fatoohi, P. O. Frederickson, T. A. Lasinski, R. S. Schreiber, H. D. Simon, V. Venkatakrishnan, and S. K. Weeratunga. The NAS Parallel Benchmarks—Summary and Preliminary Results. In Proceedings of the 1991 ACM/IEEE Conference on Supercomputing, Supercomputing ’91, page 158–165, New York, NY, USA, 1991. Association for Computing Machinery. doi:10.1145/125826.125925.
7. A. Bertoni, G. Mauri, and N. Sabadini. Membership problems for regular and context-free trace languages. Information and Computation, 82(2):135–150, 1989. doi:10.1016/0890-5401(89)90051-5.
8. Swarnendu Biswas, Jipeng Huang, Aritra Sengupta, and Michael D. Bond. DoubleChecker: Efficient Sound and Precise Atomicity Checking. In Proceedings of the 35th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI ’14, pages 28–39, New York, NY, USA, 2014. ACM. doi:10.1145/2594291.2594323.
9. Stephen M. Blackburn, Robin Garner, Chris Hoffmann, Asjad M. Khang, Kathryn S. McKinley, Rotem Bentzur, Amer Diwan, Daniel Feinberg, Daniel Frampton, Samuel Z. Guyer, Martin Hirzel, Antony Hosking, Maria Jump, Han Lee, J. Eliot B. Moss, Aashish Phansalkar, Darko Stefanović, Thomas VanDrunen, Daniel von Dincklage, and Ben Wiedermann. The DaCapo Benchmarks: Java Benchmarking Development and Analysis. In OOPSLA, 2006. doi:10.1145/1167515.1167488.
10. Hans-J. Boehm. How to Miscompile Programs with “Benign” Data Races. In Proceedings of the 3rd USENIX Conference on Hot Topic in Parallelism, HotPar ’11, page 3, USA, 2011. USENIX Association. URL: http://dl.acm.org/citation.cfm?id=2001252.2001255.
11. Michael D. Bond, Milind Kulkarni, Man Cao, Minjia Zhang, Meisam Fathi Salmi, Swarnendu Biswas, Aritra Sengupta, and Jipeng Huang. OCTET: Capturing and Controlling Cross-Thread Dependences Efficiently. In Proceedings of the 2013 ACM SIGPLAN International Conference on Object Oriented Programming Systems Languages & Applications, OOPSLA ’13, page 693–712, New York, NY, USA, 2013. Association for Computing Machinery. doi:10.1145/2509136.2509519.
12. Bernadette Charron-Bost. Concerning the size of logical clocks in distributed systems. Information Processing Letters, 39(1):11 – 16, 1991. doi:10.1016/0020-0190(91)90055-M.
13. Guang-Ien Cheng, Mingdong Feng, Charles E. Leiserson, Keith H. Randall, and Andrew F. Stark. Detecting Data Races in Cilk Programs That Use Locks. In Proceedings of the Tenth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA ’98, pages 298–309, New York, NY, USA, 1998. ACM. doi:10.1145/277651.277696.
14. Joseph Devietti, Benjamin P. Wood, Karin Strauss, Luis Ceze, Dan Grossman, and Shaz Qadeer. RADISH: Always-on Sound and Complete Race Detection in Software and Hardware. In Proceedings of the 39th Annual International Symposium on Computer Architecture, ISCA ’12, page 201–212, USA, 2012. IEEE Computer Society. doi:10.1109/ISCA.2012.6237018.
15. Dimitar Dimitrov, Martin Vechev, and Vivek Sarkar. Race Detection in Two Dimensions. In Proceedings of the 27th ACM Symposium on Parallelism in Algorithms and Architectures, SPAA ’15, page 101–110, New York, NY, USA, 2015. Association for Computing Machinery. doi:10.1145/2755573.2755601.
16. Hyunsook Do, Sebastian G. Elbaum, and Gregg Rothermel. Supporting Controlled Experimentation with Testing Techniques: An Infrastructure and its Potential Impact. Empirical Software Engineering: An International Journal, 10(4):405–435, 2005. doi:10.1007/s10664-005-3861-2.
17. A.J. Dorta, C. Rodriguez, and F. de Sande. The OpenMP source code repository. In 13th Euromicro Conference on Parallel, Distributed and Network-Based Processing, pages 244–250, 2005. doi:10.1109/EMPDP.2005.41.
18. Tayfun Elmas, Shaz Qadeer, and Serdar Tasiran. Goldilocks: A Race and Transaction-Aware Java Runtime. In Proceedings of the 28th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI ’07, pages 245–255, New York, NY, USA, 2007. ACM. doi:10.1145/1250734.1250762.
19. Eitan Farchi, Yarden Nir, and Shmuel Ur. Concurrent Bug Patterns and How to Test Them. In Proceedings of the 17th International Symposium on Parallel and Distributed Processing, IPDPS ’03, pages 286.2–, Washington, DC, USA, 2003. IEEE Computer Society. URL: http://dl.acm.org/citation.cfm?id=838237.838485.
20. Mingdong Feng and Charles E. Leiserson. Efficient Detection of Determinacy Races in Cilk Programs. In Proceedings of the Ninth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA ’97, page 1–11, New York, NY, USA, 1997. Association for Computing Machinery. doi:10.1145/258492.258493.
21. Colin Fidge. Logical Time in Distributed Computing Systems. Computer, 24(8):28–33, August 1991. doi:10.1109/2.84874.
22. Colin J. Fidge. Timestamps in message-passing systems that preserve the partial ordering. In Proc. 11th Australian Comput. Science Conf., pages 56–66, 1988.
23. Cormac Flanagan and Stephen N. Freund. FastTrack: Efficient and Precise Dynamic Race Detection. In Proceedings of the 30th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI ’09, pages 121–133, New York, NY, USA, 2009. ACM. doi:10.1145/1542476.1542490.
24. Cormac Flanagan and Stephen N. Freund. RedCard: Redundant Check Elimination for Dynamic Race Detectors. In Giuseppe Castagna, editor, ECOOP 2013 – ObjectOriented Programming, pages 255–280, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg. doi:10.1007/978-3-642-39038-8_11.
25. Cormac Flanagan, Stephen N. Freund, and Jaeheon Yi. Velodrome: A Sound and Complete Dynamic Atomicity Checker for Multithreaded Programs. In Proceedings of the 29th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI ’08, pages 293–303, New York, NY, USA, 2008. ACM. doi:10.1145/1375581.1375618.
26. Cormac Flanagan and Patrice Godefroid. Dynamic partial-order reduction for model checking software. In Proceedings of the 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL ’05, page 110–121, New York, NY, USA, 2005. Association for Computing Machinery. doi:10.1145/1040305.1040315.
27. Kaan Genç, Jake Roemer, Yufan Xu, and Michael D. Bond. Dependence-aware, unbounded sound predictive race detection. Proc. ACM Program. Lang., 3(OOPSLA), October 2019. doi:10.1145/3360605.
28. Patrice Godefroid, J. van Leeuwen, J. Hartmanis, G. Goos, and Pierre Wolper. Partial-Order Methods for the Verification of Concurrent Systems: An Approach to the State-Explosion Problem. Springer-Verlag, Berlin, Heidelberg, 1996.
29. Ayal Itzkovitz, Assaf Schuster, and Oren Zeev-Ben-Mordehai. Toward Integration of Data Race Detection in DSM Systems. J. Parallel Distrib. Comput., 59(2):180–203, November 1999. doi:10.1006/jpdc.1999.1574.
30. Dileep Kini, Umang Mathur, and Mahesh Viswanathan. Dynamic Race Prediction in Linear Time. In Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2017, pages 157–170, New York, NY, USA, 2017. ACM. doi:10.1145/3062341.3062374.
31. Rucha Kulkarni, Umang Mathur, and Andreas Pavlogiannis. Dynamic Data-Race Detection Through the Fine-Grained Lens. In Serge Haddad and Daniele Varacca, editors, 32nd International Conference on Concurrency Theory (CONCUR 2021), volume 203 of Leibniz International Proceedings in Informatics (LIPIcs), pages 16:1–16:23, Dagstuhl, Germany, 2021. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.CONCUR.2021.16.
32. Leslie Lamport. Time, Clocks, and the Ordering of Events in a Distributed System. Commun. ACM, 21(7):558–565, July 1978. doi:10.1145/359545.359563.
33. Chunhua Liao, Pei-Hung Lin, Joshua Asplund, Markus Schordan, and Ian Karlin. DataRaceBench: A Benchmark Suite for Systematic Evaluation of Data Race Detection Tools. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC ’17, New York, NY, USA, 2017. Association for Computing Machinery. doi:10.1145/3126908.3126958.
34. Shan Lu, Soyeon Park, Eunsoo Seo, and Yuanyuan Zhou. Learning from Mistakes: A Comprehensive Study on Real World Concurrency Bug Characteristics. In Proceedings of the 13th International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS XIII, pages 329–339, New York, NY, USA, 2008. ACM. doi:10.1145/1346281.1346323.
35. Umang Mathur, Dileep Kini, and Mahesh Viswanathan. What Happens-after the First Race? Enhancing the Predictive Power of Happens-before Based Dynamic Race Detection. Proc. ACM Program. Lang., 2(OOPSLA):145:1–145:29, October 2018. doi:10.1145/3276515.
36. Umang Mathur, Andreas Pavlogiannis, and Mahesh Viswanathan. The Complexity of Dynamic Data Race Prediction. In Proceedings of the 35th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS ’20, page 713–727, New York, NY, USA, 2020. Association for Computing Machinery. doi:10.1145/3373718.3394783.
37. Umang Mathur, Andreas Pavlogiannis, and Mahesh Viswanathan. Optimal prediction of synchronization-preserving races. Proc. ACM Program. Lang., 5(POPL), January 2021. doi:10.1145/3434317.
38. Umang Mathur and Mahesh Viswanathan. Atomicity Checking in Linear Time Using Vector Clocks. In Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS ’20, page 183–199, New York, NY, USA, 2020. Association for Computing Machinery. doi:10.1145/3373376.3378475.
39. Friedemann Mattern. Virtual time and global states of distributed systems. In M. Cosnard et. al., editor, Parallel and Distributed Algorithms: proceedings of the International Workshop on Parallel & Distributed Algorithms, pages 215–226. Elsevier Science Publishers B. V., 1989.
40. Antoni Mazurkiewicz. Trace Theory. In Advances in Petri Nets 1986, Part II on Petri Nets: Applications and Relationships to Other Models of Concurrency, pages 279–324. Springer-Verlag New York, Inc., 1987. doi:10.1007/3-540-17906-2_30.
41. Madanlal Musuvathi, Shaz Qadeer, Thomas Ball, Gerard Basler, Piramanayagam Arumuga Nainar, and Iulian Neamtiu. Finding and Reproducing Heisenbugs in Concurrent Programs. In Proceedings of the 8th USENIX Conference on Operating Systems Design and Implementation, OSDI ’08, pages 267–280, Berkeley, CA, USA, 2008. USENIX Association. URL: http://dl.acm.org/citation.cfm?id=1855741.1855760.
42. Robert H.B. Netzer and Barton P. Miller. On the Complexity of Event Ordering for Shared-Memory Parallel Program Executions. In In Proceedings of the 1990 International Conference on Parallel Processing, pages 93–97, 1990.
43. Robert O’Callahan and Jong-Deok Choi. Hybrid Dynamic Data Race Detection. SIGPLAN Not., 38(10):167–178, June 2003. doi:10.1145/966049.781528.
44. Andreas Pavlogiannis. Fast, Sound, and Effectively Complete Dynamic Race Prediction. Proc. ACM Program. Lang., 4(POPL), December 2019. doi:10.1145/3371085.
45. Eli Pozniansky and Assaf Schuster. Efficient On-the-fly Data Race Detection in Multithreaded C++ Programs. SIGPLAN Not., 38(10):179–190, June 2003. doi:10.1145/966049.781529.
46. Raghavan Raman, Jisheng Zhao, Vivek Sarkar, Martin Vechev, and Eran Yahav. Efficient data race detection for async-finish parallelism. Formal Methods in System Design, 41(3):321–347, Dec 2012. doi:10.1007/s10703-012-0143-7.
47. Veselin Raychev, Martin Vechev, and Manu Sridharan. Effective Race Detection for Event-Driven Programs. In Proceedings of the 2013 ACM SIGPLAN International Conference on Object Oriented Programming Systems Languages & Applications, OOPSLA ’13, page 151–166, New York, NY, USA, 2013. Association for Computing Machinery. doi:10.1145/2509136.2509538.
48. Dustin Rhodes, Cormac Flanagan, and Stephen N. Freund. BigFoot: Static Check Placement for Dynamic Race Detection. In Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2017, page 141–156, New York, NY, USA, 2017. Association for Computing Machinery. doi:10.1145/3062341.3062350.
49. Jake Roemer, Kaan Genç, and Michael D. Bond. High-coverage, Unbounded Sound Predictive Race Detection. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2018, pages 374–389, New York, NY, USA, 2018. ACM. doi:10.1145/3192366.3192385.
50. Jake Roemer, Kaan Genç, and Michael D. Bond. SmartTrack: Efficient Predictive Race Detection. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2020, page 747–762, New York, NY, USA, 2020. Association for Computing Machinery. doi:10.1145/3385412.3385993.
51. Grigore Rosu. RV-Predict, Runtime Verification. https://runtimeverification.com/predict/, 2021. Accessed: 2021-08-01.
52. Caitlin Sadowski and Jaeheon Yi. How Developers Use Data Race Detection Tools. In Proceedings of the 5th Workshop on Evaluation and Usability of Programming Languages and Tools, PLATEAU ’14, page 43–51, New York, NY, USA, 2014. Association for Computing Machinery. doi:10.1145/2688204.2688205.
53. Malavika Samak and Murali Krishna Ramanathan. Trace Driven Dynamic Deadlock Detection and Reproduction. In Proceedings of the 19th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP ’14, page 29–42, New York, NY, USA, 2014. Association for Computing Machinery. doi:10.1145/2555243.2555262.
54. Adrian Schmitz, Joachim Protze, Lechen Yu, Simon Schwitanski, and Matthias S. Müller. DataRaceOnAccelerator – A Micro-benchmark Suite for Evaluating Correctness Tools Targeting Accelerators. In Ulrich Schwardmann, Christian Boehme, Dora B. Heras, Valeria Cardellini, Emmanuel Jeannot, Antonio Salis, Claudio Schifanella, Ravi Reddy Manumachu, Dieter Schwamborn, Laura Ricci, Oh Sangyoon, Thomas Gruber, Laura Antonelli, and Stephen L. Scott, editors, Euro-Par 2019: Parallel Processing Workshops, pages 245–257, Cham, 2020. Springer International Publishing. doi:10.1007/978-3-030-48340-1_19.
55. Reinhard Schwarz and Friedemann Mattern. Detecting causal relationships in distributed computations: In search of the holy grail. Distributed computing, 7(3):149–174, 1994. doi:10.1007/BF02277859.
56. Konstantin Serebryany and Timur Iskhodzhanov. ThreadSanitizer: Data Race Detection in Practice. In Proceedings of the Workshop on Binary Instrumentation and Applications, WBIA ’09, page 62–71, New York, NY, USA, 2009. Association for Computing Machinery. doi:10.1145/1791194.1791203.
57. Dennis Shasha and Marc Snir. Efficient and Correct Execution of Parallel Programs That Share Memory. ACM Trans. Program. Lang. Syst., 10(2):282–312, April 1988. doi:10.1145/42190.42277.
58. Yao Shi, Soyeon Park, Zuoning Yin, Shan Lu, Yuanyuan Zhou, Wenguang Chen, and Weimin Zheng. Do I Use the Wrong Definition?: DeFuse: Definition-use Invariants for Detecting Concurrency and Sequential Bugs. In Proceedings of the ACM International Conference on Object Oriented Programming Systems Languages and Applications, OOPSLA ’10, pages 160–174, New York, NY, USA, 2010. ACM. doi:10.1145/1869459.1869474.
59. Yannis Smaragdakis, Jacob Evans, Caitlin Sadowski, Jaeheon Yi, and Cormac Flanagan. Sound Predictive Race Detection in Polynomial Time. In Proceedings of the 39th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL ’12, pages 387–400, New York, NY, USA, 2012. ACM. doi:10.1145/2103656.2103702.
60. L. A. Smith, J. M. Bull, and J. Obdrzálek. A Parallel Java Grande Benchmark Suite. In Proceedings of the 2001 ACM/IEEE Conference on Supercomputing, SC ’01, pages 8–8, New York, NY, USA, 2001. ACM. doi:10.1145/582034.582042.
61. Martin Sulzmann and Kai Stadtmüller. Two-phase dynamic analysis of messagepassing go programs based on vector clocks. In Proceedings of the 20th International Symposium on Principles and Practice of Declarative Programming, PPDP ’18, New York, NY, USA, 2018. Association for Computing Machinery. doi:10.1145/3236950.3236959.
62. Rishi Surendran and Vivek Sarkar. Dynamic Determinacy Race Detection for Task Parallelism with Futures. In International Conference on Runtime Verification, pages 368–385. Springer, 2016. doi:10.1007/978-3-319-46982-9_23.
63. Tengfei Tu, Xiaoyu Liu, Linhai Song, and Yiying Zhang. Understanding RealWorld Concurrency Bugs in Go. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS ’19, page 865–878, New York, NY, USA, 2019. Association for Computing Machinery. doi:10.1145/3297858.3304069.
64. Xinli Wang, J. Mayo, W. Gao, and J. Slusser. An Efficient Implementation of Vector Clocks in Dynamic Systems. In PDPTA, 2006.
65. Benjamin P. Wood, Man Cao, Michael D. Bond, and Dan Grossman. Instrumentation bias for dynamic data race detection. Proc. ACM Program. Lang., 1(OOPSLA), October 2017. doi:10.1145/3133893.
66. Kunpeng Yu, Chenxu Wang, Yan Cai, Xiapu Luo, and Zijiang Yang. Detecting Concurrency Vulnerabilities Based on Partial Orders of Memory and Thread Events. In Proceedings of the 29th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, ESEC/FSE 2021, page 280–291, New York, NY, USA, 2021. Association for Computing Machinery. doi:10.1145/3468264.3468572.
67. Yuan Yu, Tom Rodeheffer, and Wei Chen. RaceTrack: Efficient Detection of Data Race Conditions via Adaptive Tracking. SIGOPS Oper. Syst. Rev., 39(5):221–234, October 2005. doi:10.1145/1095809.1095832.
68. M. Zhivich and R. K. Cunningham. The Real Cost of Software Errors. IEEE Security and Privacy, 7(2):87–90, March 2009. doi:10.1109/MSP.2009.56.
69. P. Zhou, R. Teodorescu, and Y. Zhou. HARD: Hardware-Assisted Lockset-based Race Detection. In 2007 IEEE 13th International Symposium on High Performance Computer Architecture, pages 121–132, 2007. doi:10.1109/HPCA.2007.346191.

A  証明

(省略)。

B  HB ツリークロックの例

Figure 11 はトレース \(\sigma\) でのアルゴリズム 3 の実行例を示しており、実行中にクロックがどのように成長するかを示している。この図はスレッドのツリークロック \(\mathbb{C}_t\) を示している。ロック \(\mathbb{C}_\ell\) のツリークロックはロック開放イベントを処理した後のロック \(\mathbb{C}_\ell\) の単なるコピーである (図内の括弧に示されている)。Figure 12 は \(\sigma\) の最後のイベントに対する \({\sf Join}\) 操作と \({\sf MonotoneCopy}\) 操作の詳細である。

C  ベンチマーク

翻訳抄

因果一貫性において、Version Vector の因果履歴をベクトルからツリー構造にすることで処理の計算量をレプリカ数に対する線形から劣線形に改善するという 2022 年の論文。

1. Umang Mathur, Andreas Pavlogiannis, Hünkar Can Tunç, and Mahesh Viswanathan. 2022. A Tree Clock Data Structure for Causal Orderings in Concurrent Executions. In 27th ACM International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’22), February 28-March 4, 2022, Lausanne, Switzerland. ACM, New York, NY, USA, 18 pages. https://doi.org/10.1145/3503222.3507734