論文翻訳: Conflict-free Replicated Data Types
Marc Shapiro, INRIA & LIP6, Paris, France
Nuno Preguiça, CITI, Universidade Nova de Lisboa, Portugal
Carlos Baquero, Universidade do Minho, Portugal
Marek Zawirski, INRIA & UPMC, Paris, France
 Abstract
Abstract
結果整合性 (EC; eventual consistency) の下でデータ複製を行うと、どのレプリカもリモート同期を行うことなく更新を受け入れることができる。これにより (クラウドなどの) 大規模な分散システムの性能とスケーラビリティが保証される。しかしながら、これまでの EC アプローチはその場しのぎでエラーを発生させやすいものだった。我々の研究は形式的な強い結果整合性 (SEC; strong eventual consistency) モデルの下で収束するための十分条件を研究した。これらの条件を満たすデータ型を Conflict-free Replicated Data Type (CRDT) と呼ぶ。どのような CRDT レプリカでも、数多くの故障が発生したとしても自己安定的に収束することが保証されている。この論文では、一般的な 2 つのアプローチ (状態ベースと操作ベース) と、それらに関連する十分条件を形式化している。この論文ではクリーンなセマンティクスを持ち、追加と削除の両方の操作をサポートする集合など、多くの有用な CRDT を研究し、より複雑なデータ型についても深く考察している。CRDT 型は大規模な分散アプリケーションを開発するために構成することができ、興味深い理論的特性を持っている。
キーワード: eventual consistency / 結果整合性, replicated shared objects/ 複製共有オブジェクト, large-scale distributed systems / 大規模分散システム.
Table of Contents
 1 導入
1 導入
レプリケーションと一貫性は WWW、ピアツーピア、クラウドコンピューティングプラットフォームなどの大規模な分散システムに不可欠な機能である。標準的な「強い一貫性」アプローチでは、更新をグローバルな順序で直列する[10]。これはパフォーマンスとスケーラビリティのボトルネックとなる。さらに、強い一貫性は可用性は分断耐性と相反している[8]。
遅延耐性のあるネットワークやオフラインでの操作、クラウドコンピューティング、P2P システムのように、ネットワークの遅延が大きい場合やパーティショニングが問題となる場合、結果整合性によって可用性とパフォーマンスが向上する[17,20]。更新は一部のレプリカで同期を取らずに行われ、その後、他のレプリカに送信される。すべての更新は最終的にすべてのレプリカで非同期に、場合によっては異なる順序で実行される。同時に行われた更新は競合する可能性があり、競合の調停にはコンセンサスとロールバックが必要になる場合がある。1
このような弱い一貫性はある分類のアプリケーションでは受け入れられるだろう。しかし競合の解決は困難である。文献は正しい楽観的システムを設計するための指針をほとんど提供していないし、その場しのぎのアプローチは脆弱でエラーが発生しやすい。例えば Amazon ショッピングカートの同時実行性の異常[3]などが見られる。
我々は結果整合性に関するシンプルで理論的に健全なアプローチを提案する。このシステムモデルである Strong Eventual Consistency (SEC) は競合の解消とロールバックの複雑さを回避する。競合フリーはどれだけ失敗しても safety と liveness を確保する。SEC は競合がないことを保証する簡単な数学的性質、すなはち半格子における単調性や可換性を利用する。簡単な例のカウンターはインクリメントとデクリメントの演算が一致するため、(オーバーフローがないと仮定すると) 収束する。我々の競合フリー複製データ型 (CRDT) では、更新は同期を必要とせず、CRDT のレプリカは正しい共通状態に収束することが証明されている。CRDT はネットワークの遅延、障害、切断が起きても応答性、可用性、拡張性を維持する。
重要な CRDT が存在することが知られている。例えば我々は以前に Treedoc、協調的なテキスト編集を行うためのシーケンス CRDT [14]を発表した。この論文の目的は CRDT の原理と実践に関する知識を深めることである。この論文のコントリビューションは以下の通り:
- CAP 問題に対する解決策である Strong Eventual Consistency (SEC)
- Strong Eventual Consistency (SEC) と CRDT の正式な定義
- SEC の 2 つの十分条件
- SEC が逐次整合性と比較できないことを示す
- 整数ベクトルやカウンターをなどの基本的な CRDT の説明
- 集合やグラフを含むより高度な CRDT
CRDT 設計の包括的なポートフォリオについては別冊の技術レポート[18]を参照。
- 1競合とは、個別には正しいかもしれないが組み合わせるとある不変量 (invariant) に違反する同時更新の組み合わせのこと。
 2 システムモデル
2 システムモデル
非同期のネットワークで相互に接続されたプロセスのシステムについて考える。このネットワークは分断と回復する可能性がある。非ビザンチンプロセスの有限集合 \(\Pi=\{p_0,\ldots,p_{n-1}\}\) を想定する。\(\Pi\) のプロセスは静かにクラッシュする可能性がある。クラッシュしたプロセスは永遠にクラッシュしたままの場合もあれば、記憶域をそのままに回復する場合もある。クラッシュしていないプロセスは正常 (correct) という。
 2.1 状態ベースのオブジェクト
2.1 状態ベースのオブジェクト
このセクションでは複製されたオブジェクトを、いわゆる状態ベース (state-based) のスタイルで指定する。直感的には Figure 1 のようになる。更新を実行すると単一のレプリカの状態が更新される。それぞれのレプリカは時々、自分のローカルな状態を他のレプリカに送信し、他のレプリカは受信した状態を自分の状態にマージする。このようにしてすべての更新は最終的にすべてのレプリカに直接または間接的に到達する。
一般性を損なわないように、ここでは各プロセスに 1 つのレプリカを持つ 1 つのオブジェクトについて考える。オブジェクトはタプル \((S, s^0, q, u, m)\) である。プロセス \(p_i\) のレプリカはペイロードと呼ばれる状態 \(s_i \in S\) を持ち、初期状態は \(s^0\) である。オブジェクトのクライアントはクエリーメソッド \(q\) でオブジェクトの状態を読み取り、更新メソッド \(u\) で変更することができる。メソッド \(m\) はリモートのレプリカから状態をマージする役割を果たす。メソッドは (\(q\), \(u\), \(m\) のいずれでも) 1 つのレプリカで実行される。
すべての更新をそれぞれのレプリカに障害耐性のある方法で最終的に配信するシステムはゴシッピングやアンチエントロピーなどの文献でよく知られている [5, 13]。ここでは簡単のために、すべてのアーク (グラフ理論での有向接続している頂点のペア) が fair-lossy チャネルである全接続された通信グラフを仮定する。\(p_i\) のレプリカは (正常なら) 現在の状態を無限の頻度で \(p_j\) に送信し、レプリカ \(p_j\) は (正常なら) メソッド \(m\) を実行して受信した状態をローカルの状態にマージする。
前提条件が満たされているメソッドは有効化されていると言う。有効化されているメソッドは呼び出されるとすぐに実行されると仮定する。あるレプリカでのメソッド実行は 1 から順に番号が振られる。レプリカ \(i\) での \(k\) 番目のメソッド実行は \(f_i^k(a)\) と表記し、\(f\) は \(q\), \(u\), \(m\) のいずれか、\(a\) は引数を表している。\(K_i(f)\) はレプリカ \(i\) での \(f\) の実行順序、つまり \(i=j\) なら \(K_i(f_j^k(a)) = k\)、そうでなければ未定義であることに注意 (多少表記を乱すが、曖昧さがない場合は上付き、下付き、引数を削除することがある)。
レプリカの状態はそれぞれのメソッドが実行されるされるたびに順次番号付けされてゆく。したがってレプリカ \(i\) の初期状態は \(s_i^0 = s_j^0\) である。\(k\) 番目のメソッド実行の前は \(s_i^{k-1}\)、その後は \(s_i^k\) という状態になる。ここで遷移を \(s_i^{k-1} \bullet f_i^k(a) = s_i^k\) と表記する。
\(s\) と \(s'\) に対するすべてのクエリーが同じ結果を返す場合、状態は等価 \(s \equiv s'\) であると定義する。クエリーは副作用を持たない。つまり \((s \bullet q) \equiv s\) である。
定義 2.1 ((状態ベースの) 因果履歴). オブジェクトの因果履歴 \(C=[c_1,\ldots,c_n]\) (ここで \(c_i\) は一連の \(c_i^0,\ldots,c_i^k,\ldots\) に広がる) を次のように定義する。初期状態ではすべての \(i\) に対して \(c_i^0 = \emptyset\) である。もし \(i\) の \(k\) 番目のメソッド実行が: (i) クエリー \(q\) ならば、因果履歴は変化しない。すなはち \(c_i^k = c_i^{k-1}\); (ii) (\(u_i^k(a)\) で表記される) 更新ならば、因果履歴に追加される。すなはち \(c_i^k = c_i^{k-1} \cup \{u_i^k(a)\}\); (iii) マージ \(m_i^k(s_{i'}^{k'})\) ならば、ローカルとリモートの履歴は統合される: \(c_i^k = c_i^{k-1} \cup c_{i'}^{k'}\)
あるレプリカの因果履歴にある更新が含まれている時、その更新はそのレプリカで配信されたと言う。\(u'\) を実行するときには \(u\) が配信される場合にのみ更新 \(u\) は \(u'\) の前に起きて (happened-before) いる: \(u \to u' \overset{\rm def}{=} u \in c_j^{k-1}\). ここで \(u'\) はレプリカ \(p_j\) で実行され \(K_j(u')=k\) となる。更新は、どちらも前に起きていなければ並行である: \(u || u' \overset{\rm def}{=} u \not\to u' \land u' \not\to u\)。因果履歴は形式的な推論手段であり、通常は具体的な実装では必要ないことに注意。
状態ベースのオブジェクトでは、通信の仮定を考慮するとすべての更新が最終的にすべてのレプリカに配信されると結論づけることができる。しかしこれだけではレプリカの収束を補償するには不十分である。具体的にはマージメソッド \(m\) は no-op の場合、あるレプリカで実行された更新は他のレプリカに影響を与えず決して収束することはない。
 2.2 強い結果整合性
2.2 強い結果整合性
非公式には、結果整合性とはクライアントが更新を停止しても最終的にすべてのレプリカが同じ最終値に到達することを意味している。我々はこの直感を以下のように捉えている:
定義 2.2 (結果整合性 (EC)). 最終的な配信: ある正常なレプリカに配信された更新は最終的にすべての正常なレプリカに配信される: \(\forall i, j : f \in c_i \Rightarrow \lozenge f \in c_j\). 収束: 同じ更新を配信した正常なレプリカは最終的に同等の状態に到達する: \(\forall i,j: \square c_i = c_j \Rightarrow \lozenge \square s_i \equiv s_j\). 終了: すべてのメソッドの実行は終了する。
EC システムの中にはある更新を即時実行したあとに他の更新と衝突していることに気づき、その衝突を解決するためにロールバックするものがある [19]。これはリソースの無駄であり、一般的にはすべてのレプリカが同じ方法で競合を解決するようなコンセンサスが必要である。これを回避するためにより強い条件が必要である。
定義 2.3 (強い結果整合性 (SED)). あるオブジェクトが最終的に一貫している場合、そのオブジェクトは強い結果整合性であり、強い収束: 同じ更新を配信した正常なレプリカは等価の状態である: \(\forall i,j: c_i = c_j \Rightarrow s_i \equiv s_j\).
 2.3 状態ベースの Convergent Replicated Data Type (CvRDT)
2.3 状態ベースの Convergent Replicated Data Type (CvRDT)
ここで状態ベースのオブジェクトにおける強い収束のための十分条件を提案する。結び半束 (join semilattice) (以下、単に半束) とは、すべてのペアに対して最小上界 (least upper bound) (LUB) \(\sqcup\) を備えた部分順序 \(\le\) である: \(m = x \sqcup y\) は、\(\forall m',x \le m' \land y \le m' \Rightarrow x \le m \land y \le m \land m \le m'\) の場合にのみ \(\le\) の下で \(\{x,y\}\) の Least Upper Bound である。このことから \(\sqcup\) は次のようになる: 可換: \(x \sqcup y = y \sqcup x\); 冪等: \(x \sqcup x = x\); 結合: \(x \sqcup y) \sqcup z = x \sqcup (y \sqcup z)\)。
定義 2.4 (単調半束オブジェクト (monotonic semilattice object)). \((S,\le, s^0, q, u, m)\) で記される、部分順序 \(le\) を備えた状態ベースのオブジェクトで次の性質を持つものを単調半束と呼ぶ: (i) ペイロード値の集合 \(S\) が \(\le\) で順序付けられた半束を形成する。(ii) 状態 \(s\) とリモート状態 \(s'\) をマージすると 2 つの状態の LUB が計算される、つまり \(s \bullet m(s') = s \sqcup s'\). (iii) 状態は更新によって単調に非減少する、つまり \(s \le s \bullet u\).
定理 2.1 (Convergent Replicated Data Type (CvRDT)). 最終的な配信と終了を仮定すると、単調半束特性を満たす任意のステートベースのオブジェクトは SEC である。
証明. 先述で完全接続された通信グラフのレプリカが無限に繰り返して状態を送信・結合すると仮定したように最終的な配信の条件は満たされている。一般性を損なわないようにすべての操作が有効であると仮定する (そうでなければその操作の呼出は no-op となる); さらにある単一のレプリカで操作が実行されると仮定している。これらの条件下で操作は無限ループや再帰がなければ終了する。これは真であるとみなされる。
次に強い収束について証明することに焦点を当てる。まず定義 2.4 では自発的な状態更新やロールバックができないことに注意: レプリカがある状態 \(s\) にあるとき、更新 \(u\) またはマージ \(m\) を実行することに寄ってのみ状態を変更することができる。
レプリカ \(i\) と \(j\) について考える。証明の過程は \(c_i = c_j\) である。更新は一意であるためこれらのレプリカは以下の条件でしか同じ更新を配信することができない:
- これらのレプリカは初期状態であり、したがって \(s_i \equiv s_j\)。
- 実行中に \(c_i^p \subset c_j^q\) となる時点 \(p\), \(q\) があった。\(p_i\) では \(k \gt p\) の場合に状態 \(s: s = s_j^q\) を含むマージがあり、すべての \(f_j^k\) 操作は非変更であるか、\(s \subseteq s_j^q\) とマージされる。したがって \(\sqcup\) が LUB であることから \(s_i \equiv s_j\) (\(\equiv s_j^q)\) である。
- 実行中に \(c_j^q \subset c_i^p\) となる時点 \(p\), \(q\) があった。これは前のケースの対称で証明される。
- 実行中に \(c_i^p \not\subset c_j^q\) かつ \(c_j^q \not\subset c_i^p\) となる時点 \(p\), \(q\) があった。\(p_i\) では \(k \gt p\) の場合に状態 \(s: s_j^q \subseteq s \subseteq s_j^q \cup s_i^p\) を含むマージがあり、すべての \(f_i^k\) 操作は非変更であるか \(s \subseteq s_j^q \cup s_i^p\) とのマージである。逆に \(p_j\) では \(k \gt q\) の場合に状態 \(s: s_i^p \subseteq s \subseteq s_j^q \cup s_i^p\) を含むマージがあり、すべての \(f_j^k\) 操作は非変更であるか \(s \subseteq s_j^q \cup s_i^p\) とのマージである。これらの条件では \(c_i = c_j = c_i^p \cup c_j^q\) であり、\(\sqcup\) の LUB 特性のため \(s_i \equiv s_j\) (\(\equiv s_i^p \sqcup s_j^q \equiv s_j^q \sqcup s_i^p\)) である。
レプリカは無限に繰り返して状態を送信したりマージすることからこれらの条件は無限に発生する。最後に、\(\sqcup\) 推移性 (transitivity) によって同じ更新を配信するすべてのレプリカは等価の状態を描くこととなる。
CvRDT は最新の更新情報の LUB に向かって収束する。ここで \(x \le y \land y \le x \Rightarrow x \equiv y\) である必要がある。
 2.4 操作ベースの Commutative Replicated Data Type (CmRDT)
2.4 操作ベースの Commutative Replicated Data Type (CmRDT)
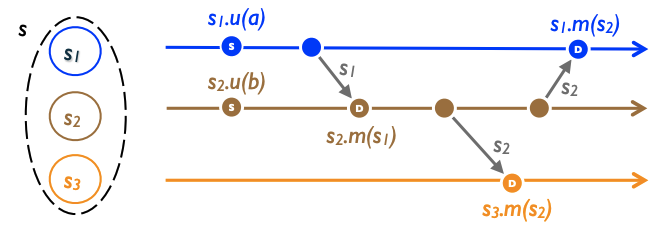
状態ベースのスタイルに代わって、複製されたオブジェクトを操作ベース (または op-based) のスタイルで指定することができる。操作ベースのオブジェクトはタプル \((S,s^0,q,t,u,P)\) であり \(S\), \(s^0\), \(q\) (それぞれ状態ドメイン、初期状態、クエリーメソッド) は前述と同じ意味を持つ。操作ベースのオブジェクトはマージメソッドを持たず、代わりに更新はペア \((t,u)\) に分割される。ここで \(t\) は副作用のない (side-effect-free) prepare-update メソッドであり、\(u\) は effect-update メソッドである (これらの引数は Figure 2 の \(t(a)\) と \(u(a')\) のように異なる場合がある)。prepare-update は操作が呼び出された単一のレプリカ (操作の送信元 (source)) で実行される。送信元では prepare-update メソッド \(t\) の直後に effect-update メソッド \(u\) が実行される、つまり \(f_i^{k-1} = t \Rightarrow f_i^k = u\) (そうでなければ連続する更新の間に因果関係がないことになる)。

effect-update メソッドはすべてのレプリカ (下流側 (downstream) という) で実行される。送信元のレプリカは次に説明する配信関係 \(P\) で指定される通信プロトコルを用いて effect-update を下流のレプリカに配信する。
状態と因果関係に関して \(f\) が \(q\), \(t\), \(u\) のいずれかを参照することを覗いて前述と同じ表記を使用する。クエリーと prepare-update メソッドはともに副作用がない、つまり \(s \bullet q \equiv s \bullet t \equiv s\) である。
定義 2.5 ((操作ベースの) 因果履歴). オブジェクトの因果履歴 \(C = \{c_1,\ldots,c_n\}\) を次のように定義する。初期状態ではすべての \(i\) に対して \(c_i^0 = \emptyset\) であり、\(i\) での \(k\) 番目のメソッド実行が: (i) クエリー \(q\) または prepare-update \(t\) では因果履歴は変化しない、すなはち \(c_i^k = c_i^{k-1}\); (ii) effect-update \(u_i^k(a)\) では \(c_i^k = c_i^{k-1} \cup \{u_i^k(a)\}\) である。
レプリカの因果履歴に更新が含まれているとき、その更新はレプリカに配信されているという。更新 \((t',u')\) が実行されたときに更新 \((t,u)\) が配信されている場合に限り \((t,u)\) は \((t',u')\) より前に起きている (happend-before): \((t,u) \to (t',u') \Leftrightarrow u \in c_j^{k-1}\). ここで \(t'\) は \(p_j\) で実行され、\(k=K_j(t')\) である。並行する更新の定義は上記の通りである。
我々は信頼性の高い因果的順序付けがされたブロードキャスト通信プロトコルを想定している。つまり、すべてのメッセージをすべての受信者に正確に一度 (exactly once)、happened-before と一致する順序で配信するプロトコルである。このようなプロトコルは分散システムの標準的な機能であり、コンセンサスを必要とせず、(前述で仮定したように) ネットワーク分断が最終的に回復する限りすべての正常なプロセスに配信される。これにより、happened-before で関連付けられた 2 つの更新はすべてのレプリカで同じ順序で実行されることになる: \((t,u) \to (t',u') \Rightarrow \forall i, K_i(u) \lt K_i(u')\). ただし、並行する更新は任意の順序で配信される。
定義 2.6 (可換性 (commutativity)). \(u\) と \(u'\) の両方が有効になっている到達可能なレプリカの状態 \(s\) に対して、\(u\) (resp. \(u'\)) は状態 \(s \bullet u'\) (resp. \(s \bullet u\)) で有効なままであり、\(s \bullet u \bullet u' \equiv s \bullet u' \bullet u\) であれば、更新 \((t,u)\) と \((t',u')\) は収束 (commute) する。
操作ベースのオブジェクトが収束するための十分条件がそのすべての並行計算が収束することが明らかである。この条件を満たすオブジェクトを Commutative Replicated Data Type (CmRDT) と呼ぶ。
\(P\) は配信の前提条件、つまり前提条件が満たされている場合のみ effect-update メソッド \(u\) は有効化される。これを時間的 (temporally) に解釈する、つまりレプリカ \(i\) での \(u\) の配信は \(P(s_i,u)\) が真となるまでは遅れる可能性がある。そのため liveness に対しては配信が最終的に可能になることを証明する義務が加わる。そこで因果的に順序付けられたブロードキャストが \(P\) を保証するのに十分である前提条件にスコープを限定する。
定理 2.2 (Commutative Replicated Data Type (CmRDT)). 更新の因果的な配信とメソッドの終了を仮定すると、並行するすべての更新で可換性の特性を満たし、その配信の前提条件が因果的な配信によって満たされる任意の操作ベースのオブジェクトは SEC である。
証明. 配信仕様 \(P\) を満たす信頼性の高い因果的なブロードキャストによってすべての正常なレプリカに更新が配信されると仮定する。一度配信された操作を配信されなかったことにすることはできない。また、すべての CmRDT メソッドはよくできており (well formed) 終了すると想定する。そこで強い収束 (strong convergence) を証明することに焦点を当てる。
任意の 2 つの正常なレプリカ \(p_i\) と \(p_j\) について考える。仮定の下では (新しい操作が発生しなければ) 最終的に 2 つのレプリカは同じ操作を配信することになり \(c_i=c_j\) となる。\(c_i\) の任意の 2 つの更新 \(f(a)\), \(f'(a')\) について: (i) \(f(a) \to f'(a')\) であれば、因果的な配信の仮定により \(\forall p_i\) 適用順序は因果関係 \(K_i(f(a)) \lt K_i(f'(a'))\) と一致する; (ii) \(f(a)\,||\,f'(a')\) のように因果的に関係がない場合、それらは収束しなければならず、任意の相対順序で配信することができる。任意のレプリカ \(p_i\) では適用順序 \(K_i(f(a)) \lt K_i(f'(a'))\) と \(K_i(f(a)) \gt K_i(f'(a'))\) の両方が同じ効果をもたらす。すべての場合において 2 つのレプリカは同等の抽象状態 \(s_i \equiv s_j\) に到達する。
推移律により \(\forall i,j: c_i = c_j \Rightarrow s_i \equiv s_j\) である。
 3 いくつかの結果
3 いくつかの結果
 3.1 障害耐性と CAP 定理
3.1 障害耐性と CAP 定理
CAP 定理とは強い一貫性 (C)、可用性 (A)、ネットワーク分断耐性 (P) を同時に保証することが不可能であるというものである [8]。大規模な環境ではネットワーク障害の発生が避けられないため、実際のシステムでは一貫性と可用性のいずれかを犠牲にしなければならない。実際には可用性が優先されることが多い [3] が、これは一貫性の保証をすべて放棄することを意味するのだろうか?
No: SEC が解決策を提供する。SEC のレプリカはネットワークの状態によらず常に read と write が可能である。SEC オブジェクトのレプリカの通信可能な任意のサブセットは、たとえネットワークの残りの部分から分断されていても、最終的に収束する。SEC は強い一貫性よりは弱いが、それにもかかわらず強い結果収束を明確に保証する。
SEC は、SEC オブジェクトが \(n-1\) までの同時故障を許容するという究極な形の障害耐性を提供する。驚くべきことに SEC はコンセンサスを得る必要がない。
 3.2 CvRDTs と CmRDTs は等価
3.2 CvRDTs と CmRDTs は等価
 3.2.1 状態ベースのオブジェクトの操作ベースのエミュレーション
3.2.1 状態ベースのオブジェクトの操作ベースのエミュレーション
定理 3.1 (CmRDT エミュレーション). 任意の SEC 状態ベースオブジェクトは、対応するインターフェースの SEC 操作ベースオブジェクトによってエミュレートできる。
証明. タプル \((S,\le,s^0,q,u,m)\) で表される CvRDT が与えられた場合、ここで指定する CmRDT オブジェクト \((S,s^0,q,t,u',P)\) によってそれをエミュレートできる。
CvRDT の状態とクエリーは同じ定義を使った CmRDT をエミュレートすることで直接保存し処理することができる。prepare-update \(t(a)\) は、更新 \(u(a)\) と同じインターフェース (同じ定義域の引数を取り同じ値域の値を返す) を持つ。これは現在のレプリカ状態 \(s\) のコピーに対して更新 \(u(a)\) を適用した結果を記録する: \(s' = s \bullet u(a)\); \(u(a)\) の返値はクライアントに渡される。記録された状態 \(s'\) は実際の effect-update \(u'(s')\) の引数として使用され、CmRDT の基本プロトコルによってすべてのレプリカに配信される。前提条件 \(P\) は無制限でいつでも配信が可能である。effect-update \(u'(s')\) は元の CvRDT メソッドを使用して受信した状態をマージする: \(s \bullet u'(s') \overset{\rm def}{=} s \bullet m(s')\).
マージは常に収束するため更新 \(u'(s')\) は収束し、通信が信頼できるのでエミュレートされた CvRDT のすべての更新を伝播する、強い結果整合性を持つ CmRDT を得る。
 3.2.2 操作ベースオブジェクトの状態ベースエミュレーション
3.2.2 操作ベースオブジェクトの状態ベースエミュレーション
操作ベースオブジェクトの状態ベースのエミュレーションは、本質的には、エピデミックな信頼できる因果的ブロードキャストの仕組みを公式化するものである。
定理 3.2 (CvRDT エミュレーション). 任意の SEC 操作ベースのオブジェクトは、対応するインターフェースの SEC 状態ベースのオブジェクトでエミュレートすることができる。
証明. (省略)
エミュレートしているオブジェクトはドメイン \(S \times U \times U\) 上の単調半束を形成する。操作の呼び出しや配信はそれを関連するメッセージ集合に追加し、したがって部分順序で状態を進行する。マージメソッド \(m\) は \(M\) 集合の和集合を取り (場合のよっては) \(D\) を更新するように定義されているため LUB 操作である。この構造はセクション 4.2 で取り上げる Wuu と Bernstein のログに似ている。
 3.3 SEC は逐次一貫性とは比較できない
3.3 SEC は逐次一貫性とは比較できない
状態ベースのレプリカはクエリー、更新およびマージメソッドを逐次実行する。CRDT は逐次的な動作に加えて、強い収束性を満たす必要のある並行的な動作を指定する。これから示すように、これによって逐次一貫性を持つシステムでは不可能な実行が可能となる。
操作 \({\it add}(e)\) と \({\it remove}(e)\) を持つ集合 CRDT \(S\) について考える。\({\it add}(e)\) の直後に状態は \(e \in S\) を満たす; \({\it remove}(e)\) の後に状態は \(e \not\in S\) を満たす。例えば \({\it remove}(e) \to {\it add}(e)\) 後の状態が \(e \in S\) を満たすように逐次実行では最後の更新が勝つ。また \({\it add}(e)\,||\,{\it remove}(e')\) 後の状態が \(e \in S \land e' \not\in S\) を満たすように、異なる要素の並行する追加と削除は独立している。
同一要素の並行する更新については代替セマンティクスの選択がある。同じ要素の追加と削除を並行に行う場合、追加が勝つか、削除が勝つか、または最も大きい IP アドレスを持つレプリカの更新が勝つか、区別される状態 \(\bot\) にリセットされるか、といった具合である。これらの代替案はいずれも強い収束条件を満たしており、アプリケーションによってはどれも妥当である。
ここで add-wins という選択肢を考えてみよう: \({\it add}(e)\,||\,{\it remove}(e)\) 後に状態は \(e \in S\) を満たす。レプリカ \(p_0\) は \({\it add}(e)\); \({\it remove}(e')\) を逐次実行する。並行してレプリカ \(p_1\) が \({\it add}(e')\); \({\it remove}(e)\) を実行する。そして、レプリカ \(p_3\) は \(p_0\) と \(p_1\) の状態をマージする。並行の仕様により \(p_3\) の最終状態は \(e \in S \land e' \in S\) を満たす。このような状態は \({\it remove}(e)\) か \({\it remove}(e')\) のいずれかが最後となるような逐次的に一貫した実行では決して起きない。このようにしてすべての更新は最終的に SEC オブジェクトには逐次一貫性がないものが存在する。
次にその逆について考える。故障がない場合、逐次一貫性のあるオブジェクトは SEC である。確かに、逐次一貫性はすべてのレプリカが同じ状態で終了しなければならない単一の操作順序によって定義される。しかし、一般的なケースでは逐次一貫性はコンセンサスを必要とし、これは \(n-1\) 個の故障が存在する場合には解決できない。したがって SEC は逐次一貫性とは比較できない。
 4 CRDT の例
4 CRDT の例
ここでは既存の文献で知られているいくつかの基本的な CRDT を復習する。これらは後で高レベルのオブジェクトを構築するために組み合わせる。ここでは利便性のために状態ベースまたは操作ベースの仕様を使用する。一般的には状態ベースの方がコンパクトで形式的な推論がしやすく、操作ベースの方が実装しやすいと観測している。
 4.1 整数ベクトルとカウンター
4.1 整数ベクトルとカウンター
整数ベクトルの状態指向の仕様について考える: \((\mathbb{N}^n\), \([0,\ldots,0]\), \(\le^n\), \([0,\ldots,0]\), \({\it value}\), \({\it inc}\), \(\max^n)\). ベクトル \(v,v' \in \mathbb{N}^n\) は \(v \le^n v' \Leftrightarrow \forall j \in [0..n-1]\), \(v[i] \le v'[i]\) で (部分) 順序付けされる。クエリー呼び出し \({\it value}()\) はローカルのペイロードをのコピーを返す。更新 \({\it inc}(i)\) はインデックス \(i\) のペイロードエントリをインクリメントする。すなはち \(s \bullet {\it inc}(i) = [s'[0],\ldots,s'[n-1]]\) であり、\(i=j\) なら \(s'[j]=s[j]+1\) でありさもなくば \(s'[j] = s[j]\) である。2 つのベクトルをマージするとインデックスごとの最大値を取る、つまり \(s \bullet \max^n(s') = [\max(s[0], s'[0]), \ldots, \max(s[n-1], s'[n-1])]\) である。これが CRDT であることの証明は省略する。
各プロセス \(p_i\) が自身のインデックス \({\it inc}(i)\) をインクリメントするように制約されている場合、これは良く知られたベクトルクロック [11] である。
インクリメントのみの整数カウンターも非常によく似ている; 唯一の違いは状態 \(v\) のベクトルのクエリー呼び出し \({\it value}()\) が \(|v| \overset{\rm def}{=} \sum_j v[j]\) を返すことである。インクリメントとデクリメントの両方が可能な整数カウンターを構築するには、基本的に 2 つのインクリメントのみのカウンター \(I\) と \(D\) を関連付ける。インクリメントすると \(I\) がインクリメントされ、デクリメントすると \(D\) がインクリメントされ、\({\it value}()\) は \(|I| - |D|\) を返す。順序付けメソッド \(\le\) は \((I,D) \le (I',D') \overset{\rm def}{=} I \le^n I' \, \land \, D \le^n D'\) と定義される。
 4.2 U-集合, 写像, ログ
4.2 U-集合, 写像, ログ
もう一つの単純な CRDT 構造は追加専用の集合オブジェクト \((S,\subseteq,\emptyset,{\it value},{\it add}(e),\cup)\) である。ペイロードは任意の集合である; 集合は包含によって順序付けられている。クエリー \({\it value}()\) はローカルのペイロードのコピーを返す。更新 \({\it add}(e)\) は集合に要素 \(e\) を追加する、つまり \(s \bullet {\it add}(e) = s \cup \{e\}\) である。\(\subseteq\) で順序付けられた集合が \(\cup\) を LUB 演算子とする半束を形成することはよく知られている。\({\it add}\) の定義により単調であることは明らかである。したがって追加専用の集合は CRDT である。
Wuu と Bernstein はこれらの基本的な構成要素を組み合わせてさらに CRDT を構築している [22]。彼らは 2 つの追加専用の集合 \(A\) と \(R\) を関連付けることで \({\it add}\) と \({\it remove}\) 操作の両方を持つ集合を提案している; 要素を追加すると \(A\) に追加され、削除すると \(R\) に追加される; クエリー \({\it value}()\) は集合の差 \(A \backslash R\) を返す。(\(R\) はしばしば墓石集合 (tombstone set) と呼ばれる。クライアントは現在 \(A\) にある要素のみを削除することができる)。彼らはすべての要素が一意であり、一度だけ追加されると仮定していることに注意; その構成を U-集合 [18] (U-set) と呼んでいる。Wuu と Bernstein は U-集合からディクショナリデータ型を明白な方法で導き出す。
ログは複製されたオブジェクトであり、そのペイロードは (event, timestamp) ペアの集合 (初期状態は空集合) が含まれる。ここでは各プロセスが通常の方法でベクトルクロックを維持していると仮定している [11]。イベント \(e\) がプロセス \(i\) で発生するとそのプロセスは更新 \({\it add}(e)\) を呼び出す。更新メソッドはベクトルクロックを更新し (例えば状態 \(v\) に) 集合にペア \((e,v)\) を追加する。タイムスタンプは各エントリが一意であることを保証する。マージメソッドはローカル集合とリモート集合の和集合を取る。
無制限の成長を回避するために、Wuu と Bernstein は不要なエントリを破棄する分散ガベージコレクションアルゴリズムを提案している。\(n-1\) 個の故障を許容するためにすべてのプロセスに配信されたエントリのみを破棄することができる。ベクトルクロックのエントリ \(v_i[j]=k\) の場合プロセス \(i\) がプロセス \(p_j\) の \(k\) 個の最初のイベントをすべて配信したことを意味する。各レプリカはペイロードにすべてのリモートのベクトルクロックのコピーを保持している。各リモートサイトに対するマージの手続きは最大のバージョンベクトルを保持する。そして、レプリカはログエントリのタイムスタンプがすべてのリモートベクトルクロックよりも小さくなった時点でそのログエントリを破棄することができる。このアルゴリズムはコンセンサスを必要としないが、度のプロセスも故障していない場合にのみ live になる。しかしガベージコレクションの liveness はメインアルゴリズムの正しさに影響しないため、これは許容できるかもしれない。
このアルゴリズムは他のデータ型にも適合可能である。例えば U-集合内の削除された要素の \(A\) および \(R\) のエントリを破棄する場合などである。
 5 有向グラフ CRDT
5 有向グラフ CRDT
次に、より複雑なデータ型の有向グラフ (directed graph) CRDT をどのように設計するかについて考える。グラフは重要な汎用データ構造である。例えば最短経路問題や Web の PageRank など、重要なアプリケーションやアルゴリズムがグラフ上に構築されている。
 5.1 思考実験
5.1 思考実験
グラフ設計の動機付けとして Web 検索エンジンを設計するという "思考実験" について考える。この検索エンジンは Web の構造を表す有向グラフを使用する。このグラフは特に PageRank の計算に使用される。このようなアプリケーションは大量のデータを処理し多くの更新を行う。効率とスケーラビリティのため処理は非同期で行う必要があり、即応性のために処理は加算的 (incremental) に行う必要がある。即応性のために各ページがクロールされるのと同程度の速さで加算的に処理されるべきである。処理にはトランザクションのような同期は必要なく CRDT が理想である。
まず最初にクロールするための初期 URL を含む集合 CRDT で開始する。いくつかのクローラープロセスが並行して実行され、それぞれが集合からいくつかの URL を取り出してダウンロードする (同じページが 2 回ダウンロードされることもあるが正しさには影響しない)。
クローラーは新しいページを見つけるとそれに対応する \({\it addVertex}\) を実行する。すべてのページに対してそれに含まれているリンクを解析し、そのページの前のバージョンが残っていればそれと比較し、対応する \({\it addArc}\) と \({\it removeArk}\) を実行する。最後に、リンクされたページの URL をクロール対象の集合に追加する。\({\it addArc}\) はアークの最後尾にあるページがまだ見つかっていない (存在していないかもしれない) 場合でも動作する必要があるが、そのようなアークは機能しないことに注意。対応するアークの検索は失敗するはずである。同様にノードが削除された場合、そのノードに付随するすべてのアークが消滅する。このようにして我々の CRDT の動作は機能しない URL を含むことが許されている Web ページの動作と一致する。リンクされたページが生成されるとナビゲーションや PageRank の計算などでリンクが関連してゆく。
Web アプリケーションではグラフが巨大になるため、レプリカ間で状態を送信してマージするのには非常にコストがかかる。そのため操作ベースのアプローチを採用している。
 5.2 アーク削除のための設計案
5.2 アーク削除のための設計案
有向グラフとは \(A \subseteq V \times V\) となるような、それぞれ頂点とアークと呼ばれるペア \((V,A)\) の集合である。更新の際にはアークの先と後の頂点が共に存在するという不変条件を維持する必要がある。したがって \(A\) にアークを追加するにはその 2 つの頂点が \(V\) に存在するという前提条件があり、逆に頂点を削除するにはその頂点をサポートするアークが存在しない場合に限られる。これらは prepare-update の前提条件となっている。さらに、システムは並行する \({\it addArc}(v',v'')\,||\,{\it removeVertex}(v')\) が不変条件に違反しないことを保証しなければならない。いくつかの選択肢を考えることができる: (i) \({\it removeVertex}(v')\) を優先する: \(v'\) へ入出するすべての辺 (edge) は副次的に削除される。これは削除された頂点を含むすべてのアークを隠すことで簡単に実装することができる。(ii) \({\it addArc}(v',v'')\) を優先する: \(v'\) と \(v''\) のいずれかが削除されている場合にそれを復元する。これには明示的に削除されたノードを再作成する必要がある。(iii) \({\it removeVertex}(v')\) を並行するすべての \({\it addArc}\) 操作が実行されるまで遅延される。これには同期が必要であり、非同期と障害耐性の目標に反している。完全な選択は存在しない。以下では我々のアプリケーションのシナリオに適切な選択肢 (i) を選択する。
 5.3 グラフ仕様
5.3 グラフ仕様
Figure 3 は有向グラフ CRDT の仕様を示したものである。次のセクションではこのオブジェクトが実際に CmRDT であることを証明する。
| 1. | \( {\sf payload} \ {\rm set} \ V, A \) | // ペアの集合 {(element \(e\), unique-tag \(w\)), ...} |
| 2. | \( \hspace{12pt}{\sf initial} \ \emptyset,\emptyset \) | // \(V\): 頂点集合; \(A\): アーク集合 |
| 3. | \( {\sf query} \ {\it lookup}({\sf vertex} \ v): {\sf boolean} \ b \) | |
| 4. | \( \hspace{12pt}{\sf let} \ b = (\exists w: (v, w) \in V) \) | |
| 5. | \( {\sf query} \ {\it lookup}({\sf arc}(v',v'')): {\rm boolean} \ b \) | |
| 6. | \( \hspace{12pt}{\sf let} \ b = ({\it lookup}(v')\,\land\,{\it lookup}(v'')\,\land\,(\exists w: ((v',v''),w) \in A) \) | |
| 7. | \( {\sf update} \ {\it addVertex}({\rm vertex} \ v) \) | |
| 8. | \( \hspace{12pt}{\sf prepare} \ (v) : w \) | |
| 9. | \( \hspace{24pt}{\sf let} \ w = {\it unique}() \) | // \({\it unique}()\) は一意の値を返す |
| 10. | \( \hspace{12pt}{\sf effect} \ (v, w) \) | |
| 11. | \( \hspace{24pt}V := V \cup \{(v,w)\} \) | // \(v+{\sf unique \ tag}\) |
| 12. | \( {\sf update} \ {\it removeVertex}({\rm vertex} \ u) \) | |
| 13. | \( \hspace{12pt}{\sf prepare} \ (v): R \) | |
| 14. | \( \hspace{24pt}{\sf pre} \ {\it lookup}(v) \) | // 事前条件 |
| 15. | \( \hspace{24pt}{\sf pre} \ \not\exists v': {\it lookup}((v,v')) \) | // \(v\) は既存のアークの先側ではない |
| 16. | \( \hspace{24pt}{\sf let} \ R=\{(v,w) \mid \exists w : (v,w) \in V\} \) | // \(V\) 内の \(v\) を含むすべての一意のペアを収集 |
| 17. | \( \hspace{12pt}{\sf effect} \ (R) \) | |
| 18. | \( \hspace{24pt}V := V \, \backslash \, R \) | |
| 19. | \( {\sf update} \ {\it addArc}({\rm vertex} \ v', {\rm vertex} \ v'') \) | |
| 20. | \( \hspace{12pt}{\sf prepare} \ (v', v''): w \) | |
| 21. | \( \hspace{24pt}{\sf pre} \ {\it lookup}(v') \) | // 先側のノードが存在しなければならない |
| 22. | \( \hspace{24pt}{\sf let} \ w = {\it unique}() \) | // \({\it unique}()\) は一意の値を返す |
| 23. | \( \hspace{12pt}{\sf effect} \ (v',v'',w) \) | |
| 24. | \( \hspace{24pt}A := A \cup \{((v', v''), w)\} \) | // \((v',v'')+{\sf unique \ tag}\) |
| 25. | \( {\sf update} \ {\it removeArc}({\rm vertex} \ v', {\rm vertex} \ v'') \) | |
| 26. | \( \hspace{12pt}{\sf prepare}(v', v''): R \) | |
| 27. | \( \hspace{24pt}{\sf pre} \ {\it lookup}((v', v'')) \) | // \({\it arc}(v', v'')\) が存在 |
| 28. | \( \hspace{24pt}{\sf let} \ R = \{((v', v''), w) \mid \exists w: ((v', v''), w) \in A\} \) | |
| 29. | \( \hspace{12pt}{\sf effect}(R) \) | // \(A\) 内の \({\it arc}(v',v'')\) を含むすべての一意のペアを収集 |
| 30. | \( \hspace{24pt}A := A\,\backslash\,R \) | |
この CRDT は頂点集合とアーク集合の 2 つを内部に保持している。頂点 \(v\) を追加するには、prepare-update メソッドが一意の識別子 \(w\) を作成し、effect-update メソッドがペア \((v,w)\) を頂点集合に追加する。この方法では各頂点が一意な内部識別子を持つことになる。同じ頂点が 2 回追加された場合、その 2 つの追加は 2 つの一意な識別子によって区別される。検索では重複を隠すことができる。
頂点 \(v\) を削除するために、prepare-update は \(v\) を含むペアの集合 \(R\)、すなはち送信元レプリカで既知のすべてのコピーを計算し、effect-update メソッドはすべてのレプリカの頂点集合からこの同じ集合 \(R\) を削除する。操作は因果的順序で配信されるため、effect-update メソッドが一部のレプリカで実行されると \(R\) の各ペアごとに対応する \({\it addVertex}\) 操作が既に実行されている。そのためセクション 4.2 の状態ベースの解決策とは異なり集合は墓石を保持する必要がない。
同じ頂点が並行して削除され追加された場合、新しい一意の識別子が削除の prepare-update によって計算された集合に含まれていないため \({\it addVertex}\) が勝利する。頂点が観測された場合にのみ削除することができるため、このアプローチは逐次実行と一致する。アークについても同様のアプローチが用いられる。
頂点を削除するために送信元レプリカはその頂点が観測されているかどうか、またその頂点が既存の任意のアークの先側ではないかをチェックする。逆にアークを追加するにはその先側のノードが存在しなければならないが、後側の存在についてはチェックしない。検索メソッドはそのようなアークの存在をマスクするだろう。しかし、のちに後側が追加されるとアークは可視化される。同様に並行する更新はアークの先側である頂点が削除されることがある。しかし検索メソッドはそのようなアークをマスクする。
 5.4 有向グラフが CRDT である証明
5.4 有向グラフが CRDT である証明
このセクションでは Figure 3 の仕様が CRDT であることを証明する。effect-update は常に有効であり、またコードを検査するとすべてのメソッドの実行が終了することが分かるので、終了は次のようになる。
補題 5.1. \({\it addVertex}(v')\) と \({\it addVertex}(v'')\) は収束する。
証明. \({\it addVertex}(v')\) は一意の識別子 \(u'\) を生成する; \({\it addVertex}(v'')\) は一意の識別子 \(u''\) を生成する。任意の初期状態 \(S=(V,A)\) に対して両操作をどのような順序で実行しても最終状態は同じ \[ \begin{eqnarray*} S \bullet {\it addVertex}(v') \bullet {\it addVertex}(v'') & = & (V \cup \{(v',u')\} \cup \{(v'',u'')\},A) \equiv \\ S \bullet {\it addVertex}(v'') \bullet {\it addVertex}(v') & = & (V \cup \{(v'',u'')\} \cup \{(v',u')\},A) \end{eqnarray*} \] となる。
補題 5.2. \({\it removeVertex}(v')\) と \({\it removeVertex}(v'')\) は収束する。
証明. \({\it removeVertex}(v')\) は除去されるペアの集合 \(R'\) を算出する; \({\it removeVertex}(v'')\) は集合 \(R''\) を算出する。任意の初期状態 \(S=(V,A)\) に対して両操作をどのような順序で実行しても最終状態は同じ \[ \begin{eqnarray*} S \bullet {\it removeVertex}(v') \bullet {\it removeVertex}(v'') & = & (V\,\backslash\,R'\,\backslash\,R'',A) \equiv \\ S \bullet {\it removeVertex}(v'') \bullet {\it removeVertex}(v') & = & (V\,\backslash\,R''\,\backslash\,R',A) \end{eqnarray*} \] となる。
補題 5.3. 並行する \({\it addVertex}(v')\) と \({\it removeVertex}(v'')\) は収束する。
証明. \({\it addVertex}(v')\) は一意な識別子 \(u'\) を生成する; \({\it removeVertex}(v'')\) は集合 \(R''\) を生成する。\(u''\) が新鮮な一意の識別子であるため \((v',u') \not\in R''\) である。したがって任意の初期状態 \(S=(V,A)\) に対して両操作をどのような順序で実行しても最終的な状態は同じ \[ \begin{eqnarray*} S \bullet {\it addVertex}(v') \bullet {\it removeVertex}(v'') & = & (V \cup \{(v',u')\}\,\backslash R'',A) \equiv \\ S \bullet {\it removeVertex}(v'') \bullet {\it addVertex}(v') & = & (V\,\backslash\,R''\cup \{(v',u')\},A) \end{eqnarray*} \] となる。
アークの証明も同様であるため省略する。最終的には頂点とアークの操作が共通であることを証明する必要がある。しかし頂点に対する操作とアークに対する操作は分離した内部集合を修正するため、どのような順序でも両方の操作を実行すればただちに同じ状態となる。
定理 5.1. Figure 3 の仕様は CmRDT である。
証明. effect-update メソッドは常に有効であり並行する操作の任意のペアは上記の補題により収束する。
 6 先行研究との比較
6 先行研究との比較
結果整合性は可用性の高い大規模な非同期システムにおける活発な研究テーマとなっている [17, 20]。多くの先行研究 [3 など] とは対照的に、我々は可換性と半束の理論に基づいた形式的なアプローチを採用している。
状態ベースのアプローチは、唯一の更新操作が代入であるレジスタのようなオブジェクトのために考案された。これは NFS, AFS, Coda のようなファイルシステムや Dynamo [3], Riak のような Key-Value ストアで広く使われている。操作ベースのアプローチは、データベースなど状態を転送するコストが高すぎる場合や、Bayou [13] や IceCube [15] などの協調システムなど、操作セマンティクスが重要な場合に使用される。
CRDT のコンセプトが明らかになったのはごく最近のことだが関連する設計は以前から発表されている。Johnson と Thomas は LWW-Register [9] を考案した。彼らは並行する更新の調整に last-writer-wins (LWW) ルールを用いる、作成、更新、削除が可能なレジスタのデータベースを提案している。LWW は並行する更新を喪失するという代償を払って操作の全体的な順序を保証する。
並行する編集には Ellis と Gibbs [7] による Operational Transformation (OT) の関連コンセプトが用いられている。即応性を確保するためにローカル操作は直ちに実行される。操作は収束するように設計されていないが、しかし、更新を受信したレプリカは以前に実行された並行する更新と同様の結果を得るためにその更新を変換する。分散アーキテクチャのための OT アルゴリズムが提案されているが、Oster らはそのほとんどが正しくないことを示している [12]。我々は最初から可換性を考慮して設計したほうがよりクリーンでシンプルであると信じている。
CvRDT の基礎は Baquero と Moura [1] によって導入された。我々は彼らの研究を CmRDT で拡張しいくつかの新しい結果を得た。CRDT の概念は並行する編集のための逐次 CRDT である Treedoc に関する研究で Shapiro と Preguiça によって考案された [14]。Logoot は CRDT Counter [21] に基づくアンドゥ機能をサポートする別の逐次 CRDT である。
Roh ら [16] は関連する概念である Replicated Abstract Data Type を独自に開発した。彼らは LWW を更新の部分順序に一般化し、それを利用していくつかの LWW スタイルのクラスを定義している。
Burckhardt と Leijen は、共有された抽象データ型に対する Concurrent Revision プログラミングモデルを提案しており、分岐したリビジョンが再び結合するまで分離して実行される。結合は 3-way マージ関数 [2] に基づく。彼らはアーベル群上に構築された ADT に対して単純な逐次マージ関数が存在することを示している。我々もまた同様の、ただしより疎結合な複製モデルにおいて CRDT と逐次一貫性の関係を実証している。
Ducourthial らは自己安定化問題を解決するためにある特性を持つ代数的構造を研究している [6]。彼らは "サイレント" タスクのためにいわゆる r-operator を提案している [4]。強い収束は、ある限られた数の攪乱更新のサイレントタスクと見ることができる。しかしこの 2 つのアプローチには違いがある。自己安定化システムが任意のメモリ破壊に耐性を持たなければならないのに対して、共有された可変型オブジェクトは更新操作を実行することによってのみ永続的に状態を変化させなければならない。さらに CvRDT の状態が単調半束を構成するのに対して r-operator は全順序を要求する。
 7 結論
7 結論
我々は、いくつかの簡単な数学的特性によって結果整合性が保証される複製データ型の概念である CRDT を紹介した。状態ベースのスタイルでは、オブジェクトの連続した状態は単調半束を形成し、マージは最小の上限を算出する。操作ベースのスタイルでは並行する操作は収束しなければならない。通信サブシステムが (操作ベースのオブジェクトでは因果的順序で) 最終的な配信を保証すると仮定すると、CRDT は同期を必要とせず共通の正しい方向に向かって収束することが保証される。
集合のような簡単な CRDT の例をいくつか紹介し、大規模な Web 検索エンジンで使用できる有向グラフ CRDT の構築方法を詳しく説明した。我々のデータ型は並行する更新があってもクリーンで決定論的セマンティクスを持っている。
遅延許容ネットワーク、センサーネットワーク、ピアツーピアネットワーク、協調コンピューティングなど、多くの大規模分散システムにおいて結果整合性は重要な技術である。しかし、これまでのところ結果整合性に関する研究のほとんどはアドホックなものだった。我々の CRDT の中には以前から文献や慣習的に知られていたものも含まれているが体系的な研究を行ったものはこの研究が初めてである。我々は結果整合性がしっかりとした理論的・実用的な基盤を得るためにこの研究が必要であると考えている。
今後の研究は理論面と実践面の両方である。理論面では CRDT で実現可能な計算のクラス、CRDT の複雑さのクラス、CRDT でサポート可能な不変条件のクラス、CRDT と自己安定化や集約などの概念との関係などを理解することである。実用面ではここで規定されたデータ型をライブラリとして実装し、実際のアプリケーションで使用してその聖堂を分析的、実験的に評価することを計画している。もう一つの方向性は、状態のコミットやグローバルリセットの実行のような非クリティカルで頻度の低い同期操作をサポートすることである。またより強力なグローバルな不変条件についても確率的またはヒューリスティックな手法を用いて検討している。
 References
References
- Carlos Baquero and Francisco Moura. Specification of convergent abstract data types for autonomous mobile computing. Technical report, Departamento de Informática, Universidade do Minho, October 1997.
- Sebastian Burckhardt and Daan Leijen. Semantics of concurrent revisions. Programming Languages and Systems, pages 116–135, 2011.
- Giuseppe DeCandia, Deniz Hastorun, Madan Jampani, Gunavardhan Kakulapati, Avinash Lakshman, Alex Pilchin, Swaminathan Sivasubramanian, Peter Vosshall, and Werner Vogels. Dynamo: Amazon’s highly available key-value store. In Symp. on Op. Sys. Principles (SOSP), volume 41 of Operating Systems Review, pages 205–220, Stevenson, Washington, USA, October 2007. Assoc. for Computing Machinery.
- S. Delaët, Bertrand Ducourthial, and S. Tixeuil. Self-stabilization with R-operators revisited. Self-Stabilizing Systems, pages 68–80, 2005.
- Alan J. Demers, Daniel H. Greene, Carl Hauser, Wes Irish, and John Larson. Epidemic algorithms for replicated database maintenance. In Symp. on Principles of Dist. Comp. (PODC), pages 1–12, Vancouver, BC, Canada, August 1987. Also appears Op. Sys. Review 22(1): 8-32 (1988).
- Bertrand Ducourthial. R-semi-groups: a generic approach for designing stabilizing silent tasks. In Int. Conf. on Stabilization, Safety, and Security of Distributed Systems (SSS), pages 281–295, Berlin, Heidelberg, 2007. Springer-Verlag.
- C. A. Ellis and S. J. Gibbs. Concurrency control in groupware systems. In Int. Conf. on the Mgt. of Data (SIGMOD), pages 399–407, Portland, OR, USA, 1989. Assoc. for Computing Machinery.
- Seth Gilbert and Nancy Lynch. Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services. SIGACT News, 33(2):51–59, 2002.
- Paul R. Johnson and Robert H. Thomas. The maintenance of duplicate databases. Internet Request for Comments RFC 677, Information Sciences Institute, January 1976.
- Leslie Lamport. Time, clocks, and the ordering of events in a distributed system. Communications of the ACM, 21(7):558–565, July 1978.
- Friedmann Mattern. Virtual time and global states of distributed systems. In Int. W. on Parallel and Distributed Algorithms, pages 215–226. Elsevier Science Publishers B.V. (North-Holland), 1989.
- Gérald Oster, Pascal Urso, Pascal Molli, and Abdessamad Imine. Proving correctness of transformation functions in collaborative editing systems. Rapport de recherche RR-5795, LORIA – INRIA Lorraine, December 2005.
- K. Petersen, M. J. Spreitzer, D. B. Terry, M. M. Theimer, and A. J. Demers. Flexible update propagation for weakly consistent replication. In Symp. on Op. Sys. Principles (SOSP), pages 288–301, Saint Malo, October 1997. ACM SIGOPS.
- Nuno Preguiça, Joan Manuel Marquès, Marc Shapiro, and Mihai Leţia. A commutative replicated data type for cooperative editing. In Int. Conf. on Distributed Comp. Sys. (ICDCS), pages 395–403, Montréal, Canada, June 2009.
- Nuno Preguiça, Marc Shapiro, and Caroline Matheson. Semantics-based reconciliation for collaborative and mobile environments. In Int. Conf. on Coop. Info. Sys. (CoopIS), volume 2888 of Lecture Notes in Comp. Sc., pages 38–55, Catania, Sicily, Italy, November 2003. Springer-Verlag GmbH.
- Hyun-Gul Roh, Myeongjae Jeon, Jin-Soo Kim, and Joonwon Lee. Replicated abstract data types: Building blocks for collaborative applications. Journal of Parallel and Dist. Comp., (To appear) 2011.
- Yasushi Saito and Marc Shapiro. Optimistic replication. ACM Computing Surveys, 37(1):42–81, March 2005.
- Marc Shapiro, Nuno Preguiça, Carlos Baquero, and Marek Zawirski. A comprehensive study of Convergent and Commutative Replicated Data Types. Rapport de recherche 7506, Institut Nat. de la Recherche en Informatique et Automatique (INRIA), Rocquencourt, France, January 2011.
- Douglas B. Terry, Marvin M. Theimer, Karin Petersen, Alan J. Demers, Mike J. Spreitzer, and Carl H. Hauser. Managing update conflicts in Bayou, a weakly connected replicated storage system. In 15th Symp. on Op. Sys. Principles (SOSP), pages 172–182, Copper Mountain, CO, USA, December 1995. ACM SIGOPS, ACM Press.
- Werner Vogels. Eventually consistent. ACM Queue, 6(6):14–19, October 2008.
- Stephane Weiss, Pascal Urso, and Pascal Molli. Logoot-undo: Distributed collaborative editing system on P2P networks. IEEE Trans. on Parallel and Dist. Sys. (TPDS), 21:1162–1174, 2010.
- Gene T. J. Wuu and Arthur J. Bernstein. Efficient solutions to the replicated log and dictionary problems. In Symp. on Principles of Dist. Comp. (PODC), pages 233–242, Vancouver, BC, Canada, August 1984.
翻訳抄
因果一貫性を使用する Version Vector のような並行する更新を追跡できるシステムで自動的に競合を解決できるデータ型についての 2011 年の論文。
- Marc Shapiro, Nuno Preguiça, Carlos Baquero, Marek Zawirski. Conflict-free Replicated Data Types. [Research Report] RR-7687, 2011, pp.18. ffinria-00609399v1f
