アルゴリズム

ゴシッププロトコル

Takami Torao #Gossip
  • このエントリーをはてなブックマークに追加

概要

ゴシッププロトコル (gossip protocol, gossipping) または感染プロトコル (epidemic protocol) はネットワーク上で情報をマルチキャストする方法の一つ。現実社会でうわさ話や感染症が伝播する過程と似たモデルのプロトコルである。ランダムグラフに基づく非構造化 P2P ネットワークや、強い調整者の存在しない分散ハッシュテーブルといった分散システムにおいて、緩やかな方法で最新の情報を共有する (anti-entropy) 目的でよく使用されている。

次のアプリケーションはグラフ構造のネットワーク上でのゴシッププロトコルによる情報伝達を表している。これは新しく受信したメッセージを、そのメッセージの送信元以外のすべての隣接するノードに送信し、すでに受信しているメッセージを受信した場合は無視するという最も単純なプロトコルである。

ラウンド -
総メッセージ -
無視メッセージ -

Table of Contents

  1. 概要
  2. アルゴリズム
    1. Rumor Spreading
    2. Epidemic Broadcast Tree
  3. アプリケーションへの適用例
    1. データ共有とクエリー
    2. ノード数の見積もり
      1. 平均化法
      2. HyperLogLog
    3. リーダー選出
    4. メンバーシップサンプリング
  4. 参考リンク

アルゴリズム

大規模ネットワークの P2P 環境では、ある時点でネットワークに参加しているすべてのノードを把握することは困難である。このような環境では、あるノードが知っているネットワーク上の一部のノード (隣接ノード) のみと情報を交換することでゴシッププロトコルを行う。

参加しているすべてのノードが分かっているような小規模なネットワークでは、すべてのノードに直接送信すれば良いため、非効率なゴシッププロトコルを選択する理由はなくこの記事では対象としない。P2P の教本ではそのような構成でノードをランダムに選択して情報交換を繰り返すというモデルのゴシッププロトコルを説明しているものもある。

ゴシッププロトコルの実装では次の 2 つの挙動を併用することが多い。

  • PUSH: 自分が最新の情報を得るとすぐに他のノードへ伝達する。PULL に比べて序盤の伝播速度は速いが、終盤では非効率で遅く、さらに全てのノードに情報が伝搬されたことを保証した上で伝搬の連鎖を停止することができない。つまり、どのような条件で伝搬を停止したとしても、確率的に選択されず取り残されている unreach なノード (susceptible node) が発生していないことを保証する手段がない。

  • PULL: 定期的に他のノードと接続して情報交換を行う。伝搬速度は遅いがいずれネットワーク全体に情報が伝搬することを確率的に保証することができる。特に、自分以外のほとんどのノードが最新状態であれば最新情報を得られる可能性が高いことから PUSH の unreach ノード問題を補うことができる。全てのノードが最新状態であれば PULL は無駄な通信となる。

あるノードが別のノードと一回情報を交換する期間をラウンド (round) としたとき、新しい情報がノード総数 \(N\) のネットワーク全体に伝播するために必要なラウンド数は \(N\) に対して対数オーダー \(O(\log N)\) である。したがって、ゴシックプロトコルは \(N\) の大きな大規模ネットワークにおいても効率的に情報を伝搬することができるが、その反面、無駄な通信が多く最終的にネットワーク負荷の高さが問題となることが多い。

Rumor Spreading

ゴシッププロトコルの一種にうわさ拡散 (rumor spreading, rumor mongering) または単にゴシッピング (gossipping) と呼ばれる PUSH 挙動の方法がある。これはノード \(P\) が自分の情報を更新して別のノード \(Q\) への伝播を試みたとき、\(Q\) が既にその情報を持っていた場合、ある一定の確率 (またはその状況に遭遇した回数) でそれ以上の伝播を中止する方針である。

通信相手が目的の情報を持っていたときに拡散を停止する確率を \(p=1/k\) としたとき、ネットワーク上で unreach のまま取り残されるノードの比率 \(s\) は式 (\(\ref{s}\)) で表すことができる (wolfram|alpha のグラフ)。

\[ \begin{equation} s = e^{-(k+1)(1-s)} \label{s} \end{equation} \]
s

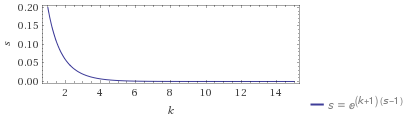
式 (\(\ref{s}\)) より \(k=1\) では全体の 20% 以上が unreach なノードになりうるが、\(k=4\) では unreach なノードをネットワーク全体の 0.7% 未満まで低下させることができる。

このうわさ拡散はネットワーク上の少数のノードしか情報が更新されていない状況では速やかな情報拡散を行い、多数のノードが情報を保持するに伴って拡散を鈍化させネットワークの負荷を低く調整する特徴がある。前述の通りすべてのノードに情報が行き渡る前に停止する可能性はあるが、定期的な PULL による拡散を併用することで取り残された unreach ノード問題を解消することができる。

Epidemic Broadcast Tree

Epidemic Broadcast Tree (EBT) は、古典的なゴシッププロトコルの冗長性問題を解決するために設計された、ハイブリッド型ブロードキャストプロトコルである。通常の Epidemic Protocol では各ノードがランダムに選択サイタ複数のピアにメッセージを送信するため \(O(N^2)\) のメッセージ複雑度が発生する。EBT は高い信頼性と低レイテンシを維持しながらこれを \(O(N)\) に削減する。EBT は構造化・非構造化の両方の P2P ネットワークに適用可能だが、実用的には中規模程度のハイブリッド P2P ネットワークを想定している (完全にオープンな環境では追加でメンバーシップ管理機構が必要となる)。

EBT の核心はメッセージ伝播過程で動的にスパニングツリーを構築することである。各ノードは受信したメッセージごとに次の 2 つの状態を管理する:

  1. Eager Push 接続: ツリー内の辺。メッセージ本体を即座に転送。

  2. Lazy Push 接続: ツリー外の辺。メッセージ ID のみを通知。

ノードが新規のメッセージを受信すると、最初の送信元を親ノードとしてツリーに組み込み、2 回目以降の同一データ受信は無視されるため、各リンクでメッセージは最大 1 回のみ転送される。Lasy Push で通知を受信したにもかかわらずメッセージを受信せずタイムアウトした場合、メッセージ伝播経路に障害があったと想定して Lasy Push 元のノードにメッセージを pull で要求する。

EBT は Secure Scuttlebutt (SSB) や IPFS Pubsub、Hyperswarm などの分散システムで採用されている。特にログ型データ構造を持つアプリケーションとの相性が良く、append-only なメッセージストリームの効率的同期に適している。

アプリケーションへの適用例

ゴシッププロトコルは可用性を重視する分散データベースや P2P ネットワークにおいて一般的な設計手法である。一般的に以下の 2 点を目的として利用される。

  1. ネットワーク上で情報を共有する。
  2. ネットワーク全体の集約処理を行う。

ただしこれらは悪意的な行動をするビザンチンノードが存在しないことを前提としている。

データ共有とクエリー

データ共有は最もよく見かける利用例であり、分散システムのクラスタや P2P ネットワーク全体でコンフィギュレーションを同期するようなケースで利用されている。また P2P ファイル共有においてネットワーク全体にクエリーを伝播させて該当するデータを持つノードが応答するような flooding もゴシッピングの一種である。

ノード数の見積もり

平均化法

ネットワークに参加している各ノード \(P_i\) が任意の初期値 \(x_i\) を持っており、ランダムに選択したノード \(P_j\) と通信してその平均値 \(\frac{x_i+x_j}{2}\) を双方の新しい値とすること繰り返すと、いずれすべてのノードが同じ値 \(\frac{\sum_i x_i}{N}\) を持つ状態に収束する。

ここで、あるノード \(P_0\) のみが初期値 \(x_0=1\) を持ち、それ以外のすべてのノードが初期値 \(x_i=0\) を持った状態でこの過程を行うと、最終的に値は全ノード数の逆数 \(\frac{1}{N}\) に収束する。つまり、これによりネットワークに参加しているすべてのノード数 \(N\) の推定値を得ることができる。

この推定値 \(N\) は利用統計やネットワーク機能の最適化のためのパラメータとして使用することができる。

HyperLogLog

後述する Brahms プロトコルのようにすべてのノードがアクティブだと知っているノード ID をブロードキャストすることで、HyperLogLog でそのカーディナリティ (異なりの数) の概算を得ることができる。ただしオフラインになったノードを減算することはできないため定期的にリセットが必要であるため「ネットワークで24時間に観測されたノード数」のように使用できる。

リーダー選出

ノード数の見積もりと同様の方法でリーダー選出を行うことができる。例えば各ノードは \((0,1]\) 区間でランダムに選んだ数値を \(m_i\) として保持する。ノード \(P_i\) と \(P_j\) が情報交換するときに新しい値を \(\max(m_i, m_j)\) とし、\(m_i \lt m_j\) であれば \(P_i\) はリーダー選挙に負けたことを意味する。

この方法ではどのノードがリーダーとして選出されたかを確定するのは難しいが、自分がリーダーではないことが確定した時点で行うべき動作がある場合や、リーダーではないと確定するまでリーダーとして振る舞って良い場合 (例えば最終的に他のノードにリーダーが確定すればその処理結果が無効化される場合など) のような楽観的動作が許容できる設計で利用することができる。

信頼できないノードが混在する場合は、認証されたネットワーク環境 (すべてのノードが他のすべてのノードの公開鍵を持っている、あるいは信頼済みの CA から発行された証明書付きの公開鍵のみを信用する) で VRF などの検証可能な乱数生成アルゴリズムを使うことができる。

メンバーシップサンプリング

Brahms サンプリングはノードの参加と離脱が自由な動的に変換するネットワークからランダムに最大 \(n\) 個のノードを選ぶ確率的データ構造を使ったゴシップに基づくプロトコルである。これは動的ネットワークで実行統計のサンプリングや隣接ノードをどのように決めるかを解決する。

参考リンク

  1. Andrew S. Tanenbaum, Maarten van Steen 他 (2009) 分散システム第二版, ピアソン