分散アルゴリズム

論文翻訳: Efficient and Scalable Multiprocessor Fair Scheduling Using Distributed Weighted Round-Robin

Takami Torao 2009年の論文
  • このエントリーをはてなブックマークに追加
Tong Li
Dan Baumberger
Scott Hahn
Intel Corporation
2111 NE 25th Ave., Hillsboro, OR, USA
{tong.n.li,dan.baumberger,scott.hahn}@intel.com

概要

公平性 (fairness) はオペレーティングシステムのスケジューラに必須の要件である。残念ながら、既存の公平なスケジューリングアルゴリズムはマルチプロセッサに対して不正確であったり非効率的である。この問題はハードウェア産業が大規模なマルチコアプロセッサの生産を続ける中でますます深刻になってきている。この論文では、この問題を解決する新しいスケジューリングアルゴリズムである分散重み付きラウンドロビン (DWRR; Distributed Weighted Round-Robin) を紹介する。分散スレッドキューと小さな追加のオーバーヘッドを持つことで DWRR は高い効率性とスケーラビリティを実現する。従来の優先順位付けのものに比べて、DWRR はユーザがスレッドへの重みを指定することができ、一定の誤差範囲の下で正確な比例 CPU シェアリングを実現することができる。DWRR は、レイテンシーやスループットと言った他のシステム属性を対象とした既存のスケジューラポリシーと協調して動作する。その結果、さまざまな製品 OS に対する実用的なソリューションを提供する。DWRR の汎用性を実証するために我々は Linux カーネル 2.6.22.15 と 2.6.24 に DWRR を実装した。これらは大きく異なる 2 つのスケジューラ設計を表している。我々の評価は DWRR は多様なワークロードに対して正確に比例する公平性と高いパフォーマンスを実現していることを示している。

カテゴリとサブジェクト記述子 D.4.1 [Operating Systems]: Process Management - Scheduling
一般用語 Algorithms, Design, Experimentation, Performance, Theory
キーワード Fair scheduling, distributed weighted round-robin, multiprocessor, lag

Table of Contents

  1. 概要
  2. 1. 導入
  3. 2. 背景と公平なスケジューリング
    1. 2.1 GPS モデル
    2. 2.2 先行研究
      1. 2.2.1 仮想時間に基づくアルゴリズム
      2. 2.2.2 ラウンドロビンアルゴリズム
      3. 2.2.3 他のアルゴリズム
  4. 3. 分散重み付きラウンドロビン
    1. 3.1 概要
    2. 3.2 アルゴリズム
      1. 3.2.1 ラウンドスライシング
      2. 3.2.2 Round Balancing
      3. 3.2.3 Dynamic Events and Infeasible Weights
      4. 3.2.4 Performance Considerations
    3. 3.3 Example
  5. 4. Implementation
  6. 5. Experimental Results
    1. 5.1 Fairness
    2. 5.2 Performance
      1. 5.2.1 Migration Overhead
      2. 5.2.2 Overall Performance
  7. 6. Analytical Results
    1. 6.1 Invariants
    2. 6.2 Fairness
  8. 7. Conclusion
  9. Acknowledgements
  10. References
  11. 翻訳抄

1. 導入

比例公平スケジューリング (proportional fair scheduling) はオペレーティングシステム、ネットワーキングそしてリアルタイムシステムなどで長年研究されている。従来のアプローチはそれぞれのタスクに重みを割り当て、スケジューラーは各タスクがその重みに比例したサービス時間を受けることを保証するというもの [26] である。完全な公平性を実現するには実現不可能 (infeasible) な程度の無限小のスケジューリング・クオンタ (scheduling quanta) が必要となるため、すべての実用的なスケジューラは小さな誤差範囲を得ることを目標に近似を行っている。

比例フェアネス (proportional fairness) はよく定義されているが Mac OS*, Solaris*, Windows* や Linux* バージョン 2.6.23 以前などほとんどの汎用 OS では採用されていない。これらの OS では飢餓状態 (starvation) を抑止し "妥当な" 公平性を模索する不明瞭な公平性の概念が採用されてる。これらの設計では、スケジューラは優先度の高いスレッドの順にスレッドをディスパッチする。それぞれのスレッドに対してスケジューラは、疎のスレッドが一度のディスパッチでどれだけ長く実行できるかを決めるタイムスライス (または quantum) を割り当てる。高い優先度を持つスレッドは大きなタイムスライスを受け取る ─ それがどの程度の大きさになるかは、スレッドの優先度に比例する関数ではなく経験的に決定されることが多い。公平性を高めるため、スケジューラは優先度も動的に調整する。例えば、スレッドの優先度を時間とともに減衰させ、スレッドがしばらく実行されていない場合は増大させるなどである [12, 18]。タイムスライスと同様に、減衰率といったこれらの調整パラメータもしばしば経験的に決定され、非常にヒューリスティックである。

公平性の正確な定義と実施の欠如は 3 つの問題を引き起こす可能性がある。第一に、高い CPU 負荷の元では飢餓状態と I/O 性能の低下を引き起こす可能性がある。ある例として我々は Windows XP* と Linux* カーネル 2.6.22.15 を搭載したデュアルコアシステム上で 32 個の CPU 負荷の高いスレッドを実行した。どちらの場合もウィンドウシステムはすぐに飢餓状態となり無反応となった。第二に、正確な公平性の欠如はリアルタイムアプリケーションに対するサポート不足を引き起こす可能性がある。比例公平スケジューリングはマルチプロセッサ上で周期的なリアルタイムタスクを適切にスケジューリングする唯一の既知の方法である [1, 29]。第三に、正確なリソースプロビジョニングを必要とするデータセンタなどのサーバ環境のサポートが不十分となる。従来のデータセンタではクライアントにサービスを提供するために個別のシステムを使用していたが、マルチコアプロセッサの登場によりより多くのサービスを 1 台のサーバに集約して床面積と電力を節約することが可能となった。このような環境では 1 つのマルチプロセッサシステムが重要度やサービス品質 (QoS; quality-of-service) 要件が異なる複数のクライアントアプリケーションに対してサービスを提供する。その OS は各アプリケーションのサービス時間を正確に制御できる必要がある。

多くの比例公平スケジューリングアルゴリズムが存在するが、大規模マルチプロセッサに対する実用的なソリューションをていきょうするものはない。ほとんどのアルゴリズムはグローバル実行キューを使用しているため、非効率的でスケーラブルではない。これらのグローバル構造体へのアクセスはデータ競合を防ぐためにロックを必要とし、これは CPU の数が多い場合に過剰な直列化とロック競合を引き起こす可能性がある。さらに、グローバルキューへの書き込みは他の CPU によって共有されているキャッシュラインを無効化し、バストラフィックを増加させ、パフォーマンスを低下させる可能性がある。CPU ごとの実行キューに基づくアルゴリズムはこれらの問題を解決するが、既存の全てのアルゴリズムは公平性が弱いか、レイテンシに敏感なアプリケーションに対して遅いかのどちらかである。マルチコアアーキテクチャの普及に伴い OS は公平スケジューリングのための効率的でスケーラブルな設計に追い付いてゆかなければならない。

この論文では以下の特徴を持つ新しいスケジューリングアルゴリズムである分散重み付きラウンドロビン (DWRR; distributed weighted round-robin) を導入する:

  • 正確な公平性. DWRR は、一般化プロセッサ共有 (GPS; generalized processor sharing) モデル [26] を用いてシステム内のスレッドや CPU の数に依存せず、一定の誤差範囲で正確な比例フェアネスを実現する。
  • 効率的でスケーラブルな運用. DWRR は CPU ごとに実行キューを使用し、スレッドが動的に到着、出発、重み変更する場合でも、既存の OS スケジューラに低いオーバーヘッドを追加するだけである。
  • 柔軟なユーザ制御. DWRR は各スレッドの優先度に基づいてデフォルトの重みを割り当て、ユーザが QoS を制御するためにスレッドの重みを指定するための追加サポートを提供する。
  • 高性能. DWRR はレイテンシやスループットのような他のシステム属性を対象とした既存のスケジューラポリシーと強調して動作するため、正確な公平性と同様に高いパフォーマンスを実現することができる。

本稿の残りの部分は以下のように構成されている。セクション 2 では背景と関連する研究について述べる。セクション 3 では DWRR アルゴリズムについて述べる。Linux 実装についてセクション 4 で、実験結果についてセクション 5 で論議し、DWRR は低いオーバーヘッドで正確な公平性を実現していることを示す。セクション 6 では、DWRR の公平性特性の形式的な解析を行い、完全なフェアネスを持つ理想化された GPS システムと比較して一定の誤差範囲を実現していることを証明する。セクション 7 で結論付ける。

2. 背景と公平なスケジューリング

Generalized Processor Sharing (GPS) は完全な公平性を実現する理想的なスケジューリングアルゴリズムである。すべての実用的なスケジューラは GPS を近似しており、公平性を計測するためのリファレンスとして使用している。

2.1 GPS モデル

\(P\) 個の CPU と \(N\) 個のスレッドを持つシステムを考える。それぞれのスレッド \(i, 1 \le i \le N\) は重み \(w_i\) を持つ。スケジューラは (1) 作業量保存 (work-conserving) を行うする、つまり実行可能なスレッドが存在するなら CPU をアイドル状態にすることはない。(2) スレッドの重みに正確に比例する CPU 時間を割り当てる。このようなスケジューラは Generalized Processor Sharing (GPS) と呼ばれる[26]。\(S_i(t_1,t_2)\) をスレッド \(i\) が間隔 \([t_1,t_2]\) で受け取る CPU 時間とする。GPS スケジューラは次のように定義される [26]。

定義 1 . GPS スケジューラとは、\([t_1,t_2]\) 間で継続的に実行可能な任意のスレッド \(i\) に対して \[ \frac{S_i(t_1,t_2)}{S_j(t_1,t_2)} \ge \frac{w_i}{w_j}, \ j=1,2,\ldots,N \] を維持し、\(w_i\) と \(w_j\) の両方がその間隔で固定されるスケジューラである。

この定義から GPS の 2 つの特性が導かれる:

特性 1 . スレッド \(i\) と \(j\) の両方が \([t_1,t_2]\) において固定された重みを持ち継続的に実行可能であれば、GPS は \[ \frac{S_i(t_1,t_2)}{S_j(t_1,t_2)} = \frac{w_i}{w_j} \] を満たす。
特性 2 . もし実行可能なスレッドの集合 \(\Phi\) とその重みが区間 \([t_1,t_2]\) を通して変化しないならば、GPS は任意のスレッド \(i \in \Phi\) に対して \[ S_i(t_1,t_2) = \frac{w_i}{\sum_{j\in \Phi} w_j} (t_2 - t_1) P \] を満たす。

ほとんどの先行研究では GPS モデルを単一プロセッサのスケジューリングに適用している。マルチプロセッサの場合では、いくつかの重みの割り当てが実行不能となることがあるため GPU スケジューラは存在しない可能性がある [9]。例えば \(w_1=1\) と \(w_2=10\) を持つ 2 つのスレッド 2 CPU システムを考えると、スレッドは一度に 1 つの CPU でしか実行できないため、システムが作業量保存を行わない限り、スレッド 2 がスレッド 1 の 10 倍の CPU 時間を受け取ることは不可能である。Chandra ら [9] は以下のような定義を導入している:

定義 2 . 任意の区間 \([t_1,t_2]\) において、スレッド \(i\) の重み \(w_i\) は \[ \frac{w_i}{\sum_{j \in \Phi} \gt \frac{1}{P} \] であれば実行不可能である。ここで \(\Phi\) は \([t_1,t_2]\) で変化しない実行可能なスレッドの集合であり、\(P\) は CPU 数である。

実現不可能な重みはシステムの能力を超えるリソース要求を表している。Chandra ら [9] は、\(P\) 個の CPU システムにおいて \(P-1\) 以下のスレッドが実現不可能な重みをもつ可能性があることを示した。彼らは実現不可能な重みを、それに最も近い実現可能な重みに変換することを提案した。この変換によりどのようなマルチプロセッサシステムでも GPS スケジューラをうまく定義することができる。

GPS スケジューラは理想とされているが、定義 1 が成立するため、すべての実行可能なスレッドが同時に実行され無限小のクアンタでスケジューリングされなければならず、これは実現不可能である。したがって、すべての実用的な公平スケジューラは GPS を近似的にエミュレートしており、公平性と時間複雑性の 2 つの側面で評価される。遅延 (lag) は公平性に対して一般的に使用される指標である [1]。スレッド \(i\) と \(j\) はともに実行可能で \([t_1,t_2]\) 区間で固定の重みを持つと仮定する。あるアルゴリズム \(A\) の下で \(i\) と \(j\) が \([t_1,t_2]\) で受け取る CPU 時間を \(S_{i,A}(t_1,t_2)\) と \(S_{j,A}(t_1,t_2)\) と表記する。

定義 3 . 任意の区間 \([t_1,t_2]\) に対して、時刻 \(t \in [t_1,t_2]\) でのスレッド \(i\) の遅延は \[ {\it lag}_i(t) = S_{i,{\it GPS}}(t_1,t) - S_{i,A}(t_1,t) \] である。

時刻 \(t\) での正の遅延は、GPS での場合よりスレッドがサービスを受けていないことを意味しており、負の遅延はその逆を意味している。全ての公平なスケジューリングアルゴリズムは正と負の遅延に上限を付けるように機能する ─ より小さな上限はより公平なアルゴリズムである。一方、スレッド数を \(N\) としたときに遅延上限が \(O(N)\) 関数となる場合、システム内のスレッド数が増加するにつれてアルゴリズムは GPS から逸脱してしまうことから、公平性は貧弱でスケーラブルではなくなる。

2.2 先行研究

公平スケジューリングのルーツは、オペレーティングシステム、ネットワーク、およびリアルタイムシステムにある。ある分野のために設計されたアルゴリズムは他の分野にも適用できることが多いため、3 つの分野すべての先行研究を調査し 3 つのカテゴリに分類した。

2.2.1 仮想時間に基づくアルゴリズム

これらのアルゴリズムはタスクやネットワークパケットごとに仮想時間を定義する。慎重に設計することで一定の遅延上限で最も強い公平性を達成することができる。欠点は、タスクやパケットの順序付けに依存して \(O(\log N)\) また場合によっては \(O(N \log N)\) の時間を必要とすることである。また、強力な公平性は多くの場合、中央集権化された実行キューに依存していてこれらのアルゴリズムの効率性とスケーラビリティを制限している。次に我々はこのカテゴリの代表的なアルゴリズムについて述べる。

ネットワークでは Demers ら [10] が単一リンク公平スケジューリングのためのパケット送出時間に基づく重み付き公平キュー (WFQ) を提案している。Parekh and Gallager [26] は WFQ が定数で正の遅延上限を達成するが負の遅延上限は \(O(N)\) であることを示した。ここで \(N\) はフローの数である。WF2Q [3] は WFQ を改良し正の遅延と負の遅延の両方で定数の上限を達成することを示した。Blanquer and Özden [4] は WFQ と WF2Q をマルチリンクスケジューリングへと拡張した。それ以外のアルゴリズム [13, 15, 16] はパケット仮想到着時間を使用しており、WFQ と同様の上限を持っている。

リアルタイムシステムでは前のアルゴリズム [1, 2] は定数の遅延上限が得られていた。多くの研究では汎用 OS にリアルタイムサポートを追加することが検討されている。Earliest Eligible Virtual Deadline First (EEVDF) [31] は正負の遅延上限が定数であるのに対して、Biased Virtual Finishing TIme (BVFT) [24] は WFQ と同様の上限を得ることができた。汎用 OS では Surplus Fair Scheduling (SFS) [9], Borrowed-Virtual-Time (BVT) [11], Start-time Fair Queuing (SFQ) [14], および Linux 2.6.23 で導入された Completely Fair Scheduler (CFS) などが WFQ と類似して設計されており、正の遅延は定数だが負の遅延は \(O(N)\) を獲得している。

多くのシステム [19, 22, 30] は公平なスケジューリングを実現するために Earliest Deadline First (EDF) や Rate Monotonic (RM) アルゴリズム [21] を使用している。Eclipse OS [5] は Move-To-Rear List Scheduling (MTR-LS) を導入している。明示的に仮想時間を使用しているわけではないが、これらのアルゴリズムはすべて原理的に WFQ と類似しているため、同様の遅延上限と \(O(\log N)\) の時間複雑性を持つ。

2.2.2 ラウンドロビンアルゴリズム

これらのアルゴリズムは重み付きラウンドロビン (WRR) [23] を拡張したものであり、ラウンドロビン順にフローを処理し、各フローに対してその重みに比例した数のパケットを送信する。ラウンドロビンアルゴリズムは \(O(1)\) の時間複雑性を持つため非常に効率的である。しかし、一般的には \(O(N)\) の遅延上限を持つ弱い公平性を持っている。それにもかかわらず、タスクやフローの重みが実際に合理的な想定に基づいてある定数で結合している場合、それらは一定の正または負の遅延上限で実現することができる。したがって、ラウンドロビンアルゴリズムは OS が使用するには効率的でスケーラブルな公平スケジューリングを実現するための完全な候補となる。

残念ながら、Group Ratio Round-Robin (SRR) [17], Virtual-Time Round-Robin (VTRR) [25], Deficit Round-Robin (DRR) [28] のようなほとんどの既存のラウンドロビンアルゴリズムは、中央集権キューや重み行列を使用していることからマルチプロセッサではスケーラブルではない。我々の知る限りでは Grouped Distributed Queues (GDQ) [7] は DWRR を除く唯一の汎用 OS スケジューリングアルゴリズムであり、正負の定数の遅延上限を実現し、分散スレッドキューを使用している。しかし GDQ は既存のスケジューラを大幅に変更する必要があり現実的な解決策とはならない。また動的な優先度や負荷分散など、レイテンシやスループットを最適化する既存の OS スケジューラのポリシーとは互換性がないため、GDQ はパフォーマンス低下を引き起こす可能性がある。これに対して DQRR はそれらのポリシーと協調して動作し、基盤となるスケジューラの高い性能を維持する。

2.2.3 他のアルゴリズム

抽選スケジューリング (lottery scheduling) [33] は遅延上限期待値 \(O(\sqrt{N})\) と最悪上限 \(O(N)\) を持つランダム化アルゴリズムである。Stride スケジューリング [32] はこれを決定論的な \(O(\log N)\) の遅延上限に改善したものだが、それでも公平性は弱い。どちらのアルゴリズムも時間的複雑さ \(O(\log N)\) を持つ。Petrou ら [27] はより早い応答時間を得るために抽選スケジューリングを拡張したが、一般的にはその時間複雑性は改善されなかった。最近 Chandra and Shenoy [8] はスレッド集合の公平なスケジューリングをサポートするために階層型マルチプロセッサスケジューリング (H-SMP) を提案しており DWRR を補間することができる。H-SMP はスレッドグループに CPU の整数を割り当てる空間スケジューラと、以前の公平スケジューラを使用して残りの CPU 帯域幅をプロビジョニングする補助スケジューラで構成される。

3. 分散重み付きラウンドロビン

このセクションでは DWRR の概要とアルゴリズムの詳細の論議、そして動作の例を示す。

3.1 概要

DWRR は FreeBSD* 5.2, Linux* 2.6, Solaris* 10, そして Windows Server* 2003 など CPU ごとの実行キューを使用する既存のスケジューラ上で動作する。DWRR はその名が示すように WRR の分散バージョンである。WRR の問題点はラウンドロビンの順序を維持するためにグローバルキューを必要とし ─ 各ラウンドでスケジューラはキューをスキャンしキューの順序でスレッドをスケジュールする。DWRR では、公平性を実現するために、スレッドを各ラウンドで同じ順序で実行する必要がないことを観測した ─ これらはラウンドあたりの総実行時間がそれらの重みに比例する限り任意の順序で何度でも実行することができる。

DWRR は各 CPU に対して初期値が 0 のラウンド番号を保持する。各スレッドに対してそのラウンドスライスを \(w \cdot B\) と定義する。ここで \(w\) はスレッドの重み、\(B\) はシステム全体の定数、ラウンドスライス単位である。DWRR におけるラウンドとは、システム内のすべてのスレッドがそのラウンドスライスのうちに空くなことも 1 を完了する最短時間のことである。スレッドのラウンドスライスはそれぞれのラウンドでそのスレッドが受け取ることを許可される総 CPU 時間を決定する。例えば、スレッドが重み 2 を持ち \(B\) 値が 30ms であるなら、各ラウンドで最大 60ms を実行に充てることができる。\(B\) 値は実装の選択である。セクション 6 で我々が示すように、小さな \(B\) は強い公平性をもたらす代わりにパフォーマンスは低く、またその逆もある。

スレッドがラウンドスライスを使い切ったとき、個のスレッドはラウンドを終了したことになる。したがって DWRR はこのスレッドが再び実行されるのを防ぐために CPU の実行キューからこのスレッドを削除する。この CPU 上のすべてのスレッドが現在の DWRR ラウンドを終了すると、DWRR は他の CPU を検索して終了していないスレッドを移動させる。見つからない場合、CPU はそのラウンド番号をインクリメントし、すべてのローカルスレッドがフルラウンドスライスで次のラウンドに進むことを許可する。

Figure 1: DWRR per-CPU スレッドキュー。曲線はスレッドを表している。round-active と round-expired は同じデータ構造を使用する。

3.2 アルゴリズム

このセクションでは DWRR の詳細を述べる。DWRR は各 CPU 上でラウンドスライシングを行って局所公平性を実現し、CPU 間ではラウンドバランシングを行うことで大域公平性を実現する。

3.2.1 ラウンドスライシング

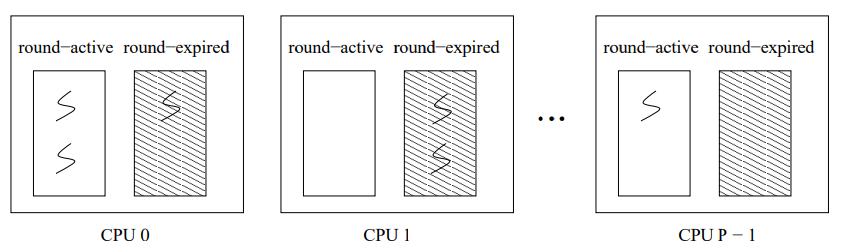
我々が round-active と呼ぶ各 CPU 上の既存の実行キューに加えて、DWRR ではもう一つのキュー round-expired を追加する。スケジューラの命名法では一般に "キュー" と呼ばれているが、

3.2.2 Round Balancing

3.2.3 Dynamic Events and Infeasible Weights

3.2.4 Performance Considerations

3.3 Example

4. Implementation

5. Experimental Results

5.1 Fairness

5.2 Performance

5.2.1 Migration Overhead

5.2.2 Overall Performance

6. Analytical Results

6.1 Invariants

6.2 Fairness

7. Conclusion

Acknowledgements

References

  1. S. K. Baruah, N. K. Cohen, C. G. Plaxton, and D. A. Varvel. Proportionate progress: A notion of fairness in resource allocation. Algorithmica, 15(6):600–625, June 1996.
  2. S. K. Baruah, J. E. Gehrke, C. G. Plaxton, I. Stoica, H. AbdelWahab, and K. Jeffay. Fair on-line scheduling of a dynamic set of tasks on a single resource. Information Processing Letters, 64(1):43–51, Oct. 1997.
  3. J. C. R. Bennett and H. Zhang. WF2Q: Worst-case fair weighted fair queueing. In Proceedings of IEEE INFOCOM ’96, pages 120–128, Mar. 1996.
  4. J. M. Blanquer and B. Özden. Fair queuing for aggregated multiple links. In Proceedings of ACM SIGCOMM ’01, pages 189–197, Aug. 2001.
  5. J. Bruno, E. Gabber, B. Özden, and A. Silberschatz. The Eclipse operating system: Providing quality of service via reservation domains. In Proceedings of the 1998 USENIX Annual Technical Conference, pages 235–246, June 1998.
  6. B. Caprita, W. C. Chan, J. Nieh, C. Stein, and H. Zheng. Group ratio round-robin: O(1) proportional share scheduling for uniprocessor and multiprocessor systems. In Proceedings of the 2005 USENIX Annual Technical Conference, pages 337–352, Apr. 2005.
  7. B. Caprita, J. Nieh, and C. Stein. Grouped distributed queues: Distributed queue, proportional share multiprocessor scheduling. In Proceedings of the 25th ACM Symposium on Principles of Distributed Computing, pages 72–81, July 2006.
  8. A. Chandra and P. Shenoy. Hierarchical scheduling for symmetric multiprocessors. IEEE Transactions on Parallel and Distributed Systems, 19(3):418–431, Mar. 2008.
  9. A. Chandra, M. Adler, P. Goyal, and P. Shenoy. Surplus fair scheduling: A proportional-share CPU scheduling algorithm for symmetric multiprocessors. In Proceedings of the 4th Symposium on Operating Systems Design and Implementation, pages 45–58, Oct. 2000.
  10. A. Demers, S. Keshav, and S. Shenker. Analysis and simulation of a fair queueing algorithm. In Proceedings of ACM SIGCOMM ’89, pages 1–12, Sept. 1989.
  11. K. J. Duda and D. R. Cheriton. Borrowed-virtual-time (BVT) scheduling: Supporting latency-sensitive threads in a general-purpose scheduler. In Proceedings of the 17th ACM Symposium on Operating System Principles, pages 261–276, Dec. 1999.
  12. D. H. J. Epema. Decay-usage scheduling in multiprocessors. ACM Transactions on Computer Systems, 16(4):367–415, Nov. 1998.
  13. S. J. Golestani. A self-clocked fair queueing scheme for broadband applications. In Proceedings of IEEE INFOCOM ’94, pages 636–646, June 1994.
  14. P. Goyal, X. Guo, and H. M. Vin. A hierarchical CPU scheduler for multimedia operating systems. In Proceedings of the Second Symposium on Operating Systems Design and Implementation, pages 107–121, Oct. 1996.
  15. P. Goyal, H. M. Vin, and H. Cheng. Start-time fair queueing: A scheduling algorithm for integrated services packet switching networks. IEEE/ACM Transactions on Networking, 5(5):690–704, Oct. 1997.
  16. A. G. Greenberg and N. Madras. How fair is fair queuing. Journal of the ACM, 39(3):568–598, July 1992.
  17. C. Guo. SRR: An O(1) time complexity packet scheduler for flows in multi-service packet networks. IEEE/ACM Transactions on Networking, 12(6):1144–1155, Dec. 2004.
  18. J. L. Hellerstein. Achieving service rate objectives with decay usage scheduling. IEEE Transactions on Software Engineering, 19(8):813–825, Aug. 1993.
  19. I. Leslie, D. McAuley, R. Black, T. Roscoe, P. Barham, D. Evers, R. Fairbairns, and E. Hyden. The design and implementation of an operating system to support distributed multimedia applications. IEEE Journal on Selected Areas in Communications, 14(7):1280–1297, Sept. 1996.
  20. T. Li, D. Baumberger, D. A. Koufaty, and S. Hahn. Efficient operating system scheduling for performance-asymmetric multi-core architectures. In Proceedings of the 2007 ACM/IEEE Conference on Supercomputing, Nov. 2007.
  21. C. L. Liu and J. W. Layland. Scheduling algorithms for multiprogramming in a hard-real-time environment. Journal of the ACM, 20(1):46–61, Jan. 1973.
  22. C. W. Mercer, S. Savage, and H. Tokuda. Processor capacity reserves: Operating system support for multimedia applications. In Proceedings of the First IEEE International Conference on Multimedia Computing and Systems, pages 90–99, May 1994.
  23. J. B. Nagle. On packet switches with infinite storage. IEEE Transactions on Communications, 35(4):435–438, Apr. 1987.
  24. J. Nieh and M. S. Lam. A SMART scheduler for multimedia applications. ACM Transactions on Computer Systems, 21(2):117–163, May 2003.
  25. J. Nieh, C. Vaill, and H. Zhong. Virtual-time round-robin: An O(1) proportional share scheduler. In Proceedings of the 2001 USENIX Annual Technical Conference, pages 245–259, June 2001.
  26. A. K. Parekh and R. G. Gallager. A generalized processor sharing approach to flow control in integrated services networks: The single-node case. IEEE/ACM Transactions on Networking, 1(3):344–357, June 1993.
  27. D. Petrou, J. W. Milford, and G. A. Gibson. Implementing lottery scheduling: Matching the specializations in traditional schedulers. In Proceedings of the 1999 USENIX Annual Technical Conference, pages 1–14, June 1999.
  28. M. Shreedhar and G. Varghese. Efficient fair queueing using deficit round robin. IEEE/ACM Transactions on Networking, 4(3):375–385, June 1996.
  29. A. Srinivasan. Efficient and Flexible Fair Scheduling of Realtime Tasks on Multiprocessors. PhD thesis, University of North Carolina at Chapel Hill, 2003.
  30. D. C. Steere, A. Goel, J. Gruenberg, D. McNamee, C. Pu, and J. Walpole. A feedback-driven proportion allocator for real-rate scheduling. In Proceedings of the Third Symposium on Operating Systems Design and Implementation, pages 145–158, Feb. 1999.
  31. I. Stoica, H. Abdel-Wahab, K. Jeffay, S. K. Baruah, J. E. Gehrke, and C. G. Plaxton. A proportional share resource allocation algorithm for real-time, time-shared systems. In Proceedings of the 17th IEEE Real-Time Systems Symposium, pages 288–299, Dec. 1996.
  32. C. A. Waldspurger. Lottery and Stride Scheduling: Flexible Proportional-Share Resource Management. PhD thesis, Massachusetts Institute of Technology, Sept. 1995.
  33. C. A. Waldspurger and W. E. Weihl. Lottery scheduling: Flexible proportional-share resource management. In Proceedings of the First Symposium on Operating Systems Design and Implementation, pages 1–12, Nov. 1994.
  • Intel, Intel Pentium, and Intel Xeon are trademarks or registered trademarks of Intel Corporation or its subsidiaries in the United States and other countries.
  • *Other names and brands may be claimed as the property of others.

翻訳抄

優先度を重みづけされたプロセッサにラウンドロビンでジョブを割り当てるアルゴリズムに関する 2009 年の論文。

  1. Tong Li, Dan Baumberger, Scott Hahn. Efficient and scalable multiprocessor fair scheduling using distributed weighted round-robin. ACM Sigplan Notices, 2009, 44.4:65-74.