論文翻訳: The Byzantine Generals Problem

LESLIE LAMPORT, ROBERT SHOSTAK, and MARSHALL PEASE
SRI International

Abstract

信頼性の高いコンピュータシステムは誤動作したコンポーネントがシステムの別の部分に矛盾した情報を与えてしまうことに対処しなければならない。このような状況は抽象的に、ビザンツ軍の将軍たちが敵対する都市に軍隊を展開しているように表現ができる。将軍たちは使者 (messenger) によってのみコミュニケーションを取りながら共通の戦闘計画に合意しなければならない。しかし、そのうちの一人または数人が裏切り者で、他のものを混乱させようとするかも知れない。この問題は忠実な将軍たちが合意に達することを保証するアルゴリズムを見つけることである。口頭のメッセージのみを用いた場合、この問題は 3 分の 2 より多い将軍が忠実である場合にのみ解決可能であることが示される。つまり、1 人の裏切り者が 2 人の忠実な将軍を混乱させることができる。偽造不可能な方法で記述されたメッセージを用いれば、この問題は将軍の人数や裏切り者の可能性にかかわらず解決可能である。そしてこの解決方法の信頼性の高いコンピュータシステムへの応用を論議する。

カテゴリとサブジェクト記述子: C.2.4. [Computer-Communication Networks]: Distributed Systems - network operating systems; D4.4. [Operating Systems]: Communication management - network communication; D.4.5 [Operating Systems]: Reliability - fault tolerance
一般用語: Algorithms, Reliability
その他のキーワードとフレーズ: Interactive consistency

Table of Contents

1. Abstract
2. 1. 導入
3. 2. 不可能性の結果
4. 3. 口頭メッセージを用いた解
5. 4. 署名付きメッセージを用いた解
6. 5. 通信経路の欠落
7. 6. 高信頼性システム
8. 7. 結論
9. References
10. 翻訳抄

1. 導入

信頼性の高いコンピュータシステムは一つまたは複数のコンポーネントの故障に対処できなければならない。故障したコンポーネントはしばしば見落とされがちな挙動 ─ つまりシステムの別の部分に矛盾した情報を送信する可能性がある。このような故障に対処する問題は、抽象的にはビザンチン将軍問題 (Byzantine Generals Problem) として表現される。この論文の大部分は抽象化されたこの問題について論議し、最後に我々の解決策が信頼性の高いコンピュータシステムの実現にどのように利用できるかを示す。

ビザンツ軍のいくつかの師団が敵の都市の外に陣取り、それぞれの師団はそれぞれの将軍によって指揮されていると想定する。将軍は使者によってのみ互いに連絡を取ることができる。敵の様子を偵察した後、彼らは共通の作戦を決めなければならない。しかし一部の将軍は裏切り者で、忠実な将軍たちが合意に達することを妨げようとする可能性がある。将軍たちは次のことを保証するアルゴリズムを持たなければならない。

• A. 忠実な将軍たちは同じ作戦行動を決定する

忠実な将軍たちはアルゴリズムの通りの行動をするが裏切り者は何をしても良い。アルゴリズムは裏切り者が何をしようとも条件 A を保証しなければならない。

忠実な将軍たちは合意に達するだけでなく合理的な作戦に合意する必要がある。したがって我々はまた次のことも確認したい。

• B. 少数の裏切り者たちは忠実な将軍たちに不正な作戦を採用させることができない

条件 B は不正な作戦が何であるかを正確に述べる必要があるため定式化が困難であり、我々はそれを試みることをしない。代わりに各将軍がどのように判断に至るかを考える。それぞれの将軍は敵を観測しその観測結果を他の将軍に伝える。\(i\) 番目の将軍が伝達した情報を \(v(i)\) とする。各将軍は何らかの方法で \(v(1)\), \(\ldots\), \(v(n)\) の値を組み合わせて一つの作戦にする。ここで \(n\) は将軍の数である。条件 A はすべての将軍が同じ方法で情報で情報を組み合わせることで達成され、条件 B はロバストな方法を使うことで達成される。例えば攻撃か退却かだけを決めるのであれば、\(v(i)\) はどちらの選択肢がベストかについての将軍 \(i\) の意見とし、最終的な決定は彼らの間の多数決に基づくことができる。忠実な将軍たちが 2 つの可能性の間でほぼ等しく分かれている場合にのみ少数の裏切り者が決定に影響を与え、その場合はどちらの決定も不正と言うことはできない。

このアプローチは条件 A と B を満たす唯一の方法ではないかも知れないが、我々が知っている唯一の方法である。この方法はそれぞれの将軍が値 \(v(i)\) を互いに伝達する方法を仮定している。明らかな方法は \(i\) 番目の将軍が使者を使って \(v(i)\) を他の将軍に送ることである。しかし、条件 A を満たすには忠実な将軍たちが同じ値 \(v(1)\), \(\ldots\), \(v(n)\) を得る必要があり、裏切り者の将軍は別々の将軍に異なる値を送る可能性があることからうまく機能しない。条件 A が成立するためには次の条件が必要である。

• 1. すべての忠実な将軍たちは同じ情報 \(v(1)\), \(\ldots\), \(v(n)\) を取得しなければならない

条件 1 は、裏切り者の \(i\) 番目の将軍が別々の将軍に異なる値を送信する可能性があるため、ある将軍が \(i\) 番目の将軍から直接得た \(v(i)\) の値を必ずしも使用できないことを暗に意味している。これは注意深くしなければ、条件 1 を満たす場合に、たとえ \(i\) 番目の将軍が忠実であったとしてもある将軍が \(i\) 番目の将軍によって送信されたものとは異なる \(v(i)\) の値を使用する可能性が出てくる。条件 B を満たすためにはこのようなことは許されてはならない。例えば忠実な将軍たちが全員 "攻撃" という値を送ってきた場合、少数の裏切り者が忠実な将軍たちに "退却", \(\ldots\), "退却" という値に基づいて決断させることは許されない。したがって各 \(i\) について次のような要件を設ける:

• 2. もし \(i\) 番目の将軍が忠実であれば、彼が送った値はすべての忠実な将軍によって \(v(i)\) の値として使用されなければならない

条件 1 は、すべての \(i\) について (\(i\) 番目の将軍が忠実かどうかにかかわらず) 次のような条件に書き換えることができる。

• 1'. 任意の 2 人の忠実な将軍は同じ値 \(v(i)\) を使用する

条件 1' と条件 2 は \(i\) 番目の将軍によって送信された単一の値に関する条件である。したがって、一人の将軍がどのように他の将軍に自分の値を送るかという問題に限定して考えることができる。これを司令官 (commander) である将軍が副官 (lieutenant> に命令を送るという言葉で表現すると次のような問題が得られる。

ビザンチン将軍問題. 司令官である将軍は \(n-1\) 人の副官に次のような命令を送らなければならない。

• IC1. すべての忠実な副官は同じ命令に従う。
• IC2. 司令官である将軍が忠実であれば、すべての忠実な副官らは彼の送る命令に従う。

条件 IC1 と IC2 は対話的整合性条件と呼ぶ。司令官が忠実であれば IC2 から IC1 が導かれることに注意。ただし司令官が忠実である必要はない。

当初の問題を解くには、ビザンチン将軍問題の解法を用いて \(i\) 番目の将軍が "私の値として \(v(i)\) を使え" という命令を送り、他の将軍は副官として行動することになる。

2. 不可能性の結果

ビザンチン将軍問題は一見して単純な問題である。この困難さは、将軍たちが口頭でしかメッセージを送れない場合に 3 分の 2 より多い将軍が忠実でなければ解決策が成立しないという驚くべき事実によって示されている。特に将軍が 3 人しかいない場合、裏切り者が 1 人でもいると解決策は存在しない。口伝のメッセージ内容は完全に送信者の制御下にあり、裏切り者の送信者はどんなメッセージでも送信することができる。このようなメッセージはコンピュータが互いに送信する通常のメッセージタイプに相当する。セクション 4 ではこのようなことがない、署名され記述されたメッセージについて考える。

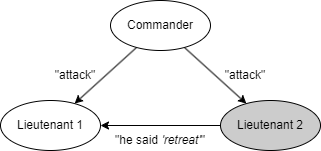
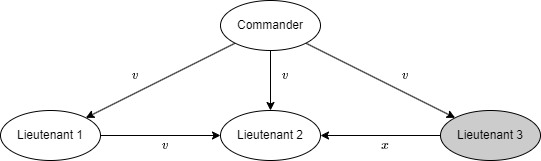
ここで、口伝のメッセージでは 3 将軍解 (three-general solution) で 1 人の裏切り者も対処できないことを示す。簡単のために "攻撃" (attack) か "退却" (retreat) しか判断できない場合を考える。まず Fig. 1 に描かれているシナリオについて考える。このシナリオでは Commander は忠実で "攻撃" 命令を送信するが、Lieutenant 2 は裏切り者で Lieutenant 1 に "退却" 命令を受けたと報告する。IC2 を満たすためには Lieutenant 1 は攻撃の命令に従わなければならない。

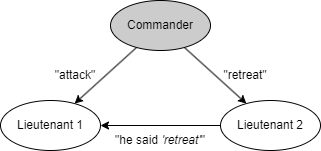
ここで Fig. 2 に示すような別のシナリオを考えてみよう。司令官が裏切り者で Lieutenant 1 に "攻撃" 命令を、Lieutenant 2 に "退却" 命令を送る。Lieutenant 1 は誰が裏切り者かを知らないので、司令官が実際に Lieutenant 2 にどのようなメッセージを送ったかを知ることはできない。したがって、この 2 つの図のシナリオは Lieutenant 1 には全く同じに見える。もし裏切り者が一貫して嘘をつき続けるのであれば、Lieutenant 1 にはこの 2 つの状況を区別するすべはないのでどちらも "攻撃" 命令に従わなければならない。したがって Lieutenant 1 は司令官から "攻撃" 命令を受けたのなら必ずそれに従わなければならない。

しかし同様の議論から Lieutenant 2 が司令官から "退却" 命令を受けたなら Lieutenant 1 が "攻撃" 命令を受けていたとしてもそれに従わなければならないことが分かる。したがって Fig. 2 のシナリオでは Lieutenant 2 は "退却" 命令に、Lieutenant 1 は "攻撃" 命令に従わなければならず条件 IC1 に違反する。したがって、裏切り者が 1 人いる場合に有効な 3 将軍解は存在しない。

一見、説得力があるように見えるかもしれないが、読者にはこのような非厳密的な推論には十分な疑いを持つことを強く勧める。この結果は確かに正しいが、我々は無効な結果に対して同様にもっともらしい "証明" を見たことがある。コンピュータサイエンスや数学の分野でこの種のアルゴリズムの研究ほど非正規な推論が誤りに繋がる可能性が高い分野もないと我々は考えている。1 人の裏切り者を処理できる 3 将軍の解決法の不可能性についての厳密な証明は [3] を参照。

この結果を用いて、\(m\) 人の裏切り者に対して \(3m+1\) より少ない将軍での解決法は存在しないことを示すことができる¹。この証明は矛盾を用いたものである。\(3m\) 以下のグループに対してこのような解決法を仮定し、それを使って 1 人の裏切り者で機能するビザンチン将軍問題の 3 将軍の解を構築するが、これは不可能であることが分かっている。2 つのアルゴリズムの混同を避けるため、想定解 (assumed solution) の将軍をアルバニア将軍 (Albanian generals)、構成解 (constructed solution) の将軍をビザンチン将軍と呼ぶことにする。したがって、\(3m\) 以下のアルバニア将軍が \(m\) 人の裏切り者に対処できるアルゴリズムから出発して、3 人のビザンチン将軍が 1 人の裏切り者に対処できる解決法を構築する。

各ビザンチン将軍がアルバニア将軍のおよそ 1/3 を模擬することで 3 将軍の解が得られる。つまり各ビザンチン将軍は最大 \(m\) のアルバニア将軍を模擬している。ビザンチン司令官はアルバニア司令官 + 最大で \(m-1\) 人のアルバニア副官を模擬しており、ビザンチン副官 2 人はそれぞれ最大で \(m\) 人のアルバニア副官を模擬している。ビザンチン将軍の 1 人が裏切り者でも最大 \(m\) 人のアルバニア人を模擬できるため、最大 \(m\) 人のアルバニア将軍が裏切り者である。したがって想定解はアルバニア将軍について IC1 と IC2 が成立することを保証する。IC1 により忠実なビザンチン副官に模擬されているすべてのアルバニア副官は彼が従うべき同じ命令に従うことになる。アルバニア将軍の解決法の条件 IC1 と IC2 がビザンチン将軍に相当する条件を含意することは容易に確認できるので、必要な不可能解を構成したことになる。

ビザンチン将軍問題を解くことが難しいのは厳密な合意に達することが必要だからだと思うかも知れない。しかしそうではなく、近似的な合意を得ることも厳密な合意を得ること同程度に難しいことを示す。ここでは正確な戦闘計画に合意する代わりにおおよその攻撃時刻だけ合意しなければならないとする。より正確には司令官が攻撃時刻を命令すると仮定し、次の 2 つの条件が成立することを要求する:

• IC1'. 忠実な副官は互いに 10 分以内に攻撃する。
• IC2'. 司令官が忠実であれば、すべての忠実な副官は司令官の命令で与えられた時間から 10 分以内に攻撃する。

(攻撃の前日に命令が出されて処理され、命令を受けた時刻は関係なく、命令された攻撃時刻のみが重要であると想定する。)

ビザンチン将軍問題同様、この問題は 1/3 より多い将軍が忠実でない限り解決不可能である。このことを証明するためにまず、1 人の裏切り者がいても対処できる 3 将軍解があれば、1 人の裏切り者がいても対処できるビザンチン将軍問題の 3 将軍解を構成できることを示す。司令官が "攻撃" または "退却" の命令を送りたいとする。彼は想定されるアルゴリズムを使って、攻撃時刻 1:00 を送信して攻撃を命令し、攻撃時刻 2:00 を送信して退却を命じる。各副官は次の手順で命令を出す。

1. 副官は司令官から攻撃時刻を受け取った後に次のいずれかを行う:
   1. 1:10 以前であれば攻撃する。
   2. 1:50 移行であれば退却する。
   3. それ以外であれば手順 2 に進む。
2. 別の副官にステップ 1 でどのような判断を下したか問う。
   1. 別の副官が判断に至ったのであれば、彼と同じ判断を下す。
   2. そうでなければ退却する。

IC2' より、司令官が忠実であれば忠実な副官はステップ 1 で正しい命令を得るため IC2 が満たされる。司令官が忠実であれば IC2 から IC1 が成り立つため、司令官が裏切り者であるという仮定の下で IC1 を証明すれば良い。裏切り者は最大でも 1 人であるため、これは両方の副官が忠実であることを意味する。IC1' より、もし片方の副官がステップ 1 で攻撃を判断すればもう一方はステップ 1 で退却はできない。したがって 1 の段階で 2 人が同じ判断をするか、少なくともどちらかが 2 の段階まで判断を先延ばしにすることになる。この場合、両者が同じ判断に至ることは容易に分かるため IC1 が満たされる。したがって裏切り者 1 人に対処するビザンチン将軍問題の 3 将軍解を構成したことになるが、これは不可能である。したがって、ある裏切り者の存在で IC1' と IC2' を維持する 3 将軍アルゴリズムはあり得ない。

1 人の将軍が他の \(m\) 人の将軍を模擬するという方法を用いて、\(3m+1\) 人より少ない将軍を持つ解は \(m\) 人の裏切り者に対処できないことを証明できるようになった。この証明は元のビザンチン将軍問題の証明と同様であり読者に任せる。

• ¹より正確には、2 人の将軍では問題が自明なので、3 人以上の将軍の場合にそのような解決法は存在しない。

3. 口頭メッセージを用いた解

上記で裏切り者が \(m\) 人居る場合に口伝を用いたビザンチン将軍問題の解を求めるには少なくとも \(3m+1\) 人の将軍が必要であることを示した。ここでは \(3m+1\) 人以上の将軍がいる場合の解決法を示す。しかし、まずは "口頭メッセージ" (oral message) の意味を正確に説明する。各将軍は他の将軍にメッセージを送るアルゴリズムを実行することになっており、忠実な将軍は彼のアルゴリズムを正しく実行すると仮定する。口頭メッセージの定義は将軍のメッセージシステムに関して我々が行う次の仮定に具現化されている:

• A1. 送信されたすべてのメッセージは正しく配信される。
• A2. メッセージの受信者は誰がメッセージを送信したかを知っている。
• A3. メッセージの欠落を検出することができる。

A1 により裏切り者は他の 2 人の将軍の送るメッセージを妨害することができず、A2 により偽のメッセージを持ち込んで彼らを混乱させることができない。したがって仮定 A1 と A2 により裏切り者は他の 2 人の将軍の間の通信を妨害することができない。仮定 A3 は単にメッセージを送らないことで決定を妨げようとする裏切り者を阻止する。これらの仮定の実際の実装についてはセクション 6 で述べる。

このセクションおよび次セクションのアルゴリズムでは各将軍が他のすべての将軍に直接メッセージを送ることができることを要求している。セクション 5 ではこのような要求のないアルゴリズムについて述べる。

裏切り者の司令官はどのような命令も送らないようにすることができる。副官は何らかの命令に従わなければならないため、そのような場合に従うべき規定の命令が必要である。我々は RETREAT (退却) を規定の命令とする。

我々はすべての非負整数 \(m\) に対して司令官が \(n-1\) 人の副官に命令を送る口伝 (Oral Message) アルゴリズム \({\rm OM}(m)\) を帰納的に定義する。我々は \({\rm OM}(m)\) が \(3m+1\) 以上の将軍に対して最大 \(m\) の裏切り者が存在する場合にビザンチン将軍問題を解決することを示す。このアルゴリズムは副官が "命令に従う" というより "値を得る" という言葉で表現する方がより便利であることが分かる。

このアルゴリズムでの関数 \({\rm majority}\) は \(v_i\) の値の過半数が \(v\) と等しければ \({\rm majority}(v_1,\ldots,v_{n-1})\) が \(v\) に等しくなるという性質を仮定する。(実際には \(n\) ごとに 1 つこのような関数列を想定している。) \({\rm majority}(v_1,\ldots,v_{n-1})\) の値には 2 つの自然な選択肢がある:

1. \(v_i\) の中で過半数値があればその値。なければ RETREAT;
2. \(v_i\) が順序集合に由来すると想定した場合の中央値。

次のアルゴリズムは前述した \({\rm majority}\) の性質のみを必要とする。

アルゴリズム \({\rm OM}(0)\).

1. 司令官は各副官に彼の値を送信する。
2. 各副官は司令官から受信した値を使用する。値を受け取らなかった場合は RETREAT とする。

アルゴリズム \({\rm OM}(m), m \gt 0\).

1. 司令官は各副官に彼の値を送信する。
2. 各 \(i\) について、副官 \(i\) が司令官から受信する値を \(v_i\) とし、または値を受け取らない場合は RETREAT とする。副官 \(i\) はアルゴリズム \({\rm OM}(m-1)\) の司令官として値 \(v_i\) を他の \(n-2\) の副官のそれぞれに送信する。
3. 各 \(i\) と \(j \ne i\) について、\(v_j\) を副官 \(i\) がステップ 2 で副官 \(j\) から受信した値 (アルゴリズム \({\rm OM}(m-1)\) を使用) とし、または値を受け取らない場合は RETREAT とする。副官 \(i\) は値 \({\rm majority}(v_1,\ldots,v_{n-1})\) を使用する。

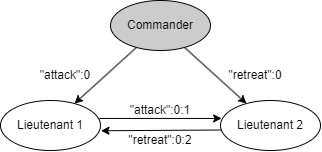
このアルゴリズムがどのように機能するかを理解するために \(m=1\), \(n=4\) のケースを考える。Fig. 3 は Lieutenant 3 が裏切り者で Commander が値 \(v\) を送信したときに Lieutenant 2 が受信するメッセージを示している。\({\rm OM}(1)\) の最初のステップでは司令官が 3 人の副官全員に \(v\) を送信する。次のステップで Lieutenant 1 は自明なアルゴリズム \({\rm OM}(0)\) を使って Lieutenant 2 に値 \(v\) を送信し、また同じステップで裏切り者の Lieutenant 3 は Lieutenant 2 に別の値 \(x\) を送信する。ステップ 3 では Lieutenant 2 は \(v_1=v_2=v\) と \(v_3=x\) となり、正しい値 \(v={\rm majority}(v,v,x)\) を得ることができる。

次に司令官が裏切り者の場合でどうなるかを見える。Fig. 4 は裏切り者の司令官が任意の 3 つの値 \(x\), \(y\), \(z\) を 3 人の副官に送った場合に副官たちが受信する値を表している。各副官は \(v_1=x\), \(v_2=y\), \(v_3=z\) を得るため、3 つの値 \(x\), \(y\), \(z\) が等しいかどうかにかかわらず、ステップ 3 で全員が同じ値 \({\rm majority}(x,y,z)\) を得ることになる。

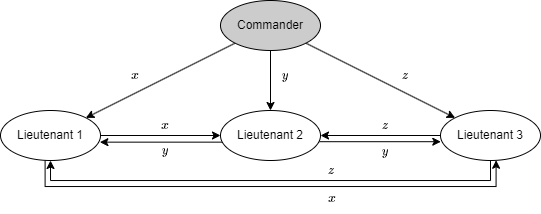
再帰的アルゴリズム \({\rm OM}(m)\) はアルゴリズム \({\rm OM}(m-1)\) の \(n-1\) 回の実行を呼び出し、\({\rm OM}(m-2)\) の \(n-2\) 回の実行を呼び出し、と続く。これは \(m \gt 1\) の場合に副官が他の副官に数多くのメッセージを送ることを意味する。これらの異なるメッセージを区別する何らかの仕組みが必要である。それぞれの副官 \(i\) がステップ 2 で送信する値 \(v_i\) に数値 \(i\) の接頭辞を付ければすべての曖昧さが取り除かれることが分かるだろう。再帰が "展開" するにつれてアルゴリズム \({\rm OM}(m-k)\) は \((n-1)\cdots(n-k)\) 回呼び出されて \(k\) 人の副官の番号列を接頭辞とする値を送信することになる。

任意の \(m\) に対するアルゴリズム \({\rm OM}(m)\) の正しさを証明するためにまず次の補題を証明する。

補題 1. 任意の \(m\) と \(k\) に対して、\(2k+m\) 人より多い将軍と最大 \(k\) 人の裏切り者が存在する場合、アルゴリズム \({\rm OM}(m)\) は IC2 を満足する。

証明. 証明は \(m\) に対する帰納法で行う。IC2 は司令官が忠実である場合に起こるべきことを定めているに過ぎない。A1 を用いると司令官が忠実であれば自明なアルゴリズム \({\rm OM}(0)\) が機能することは容易に分かるため、\(m=0\) に対してこの補題は真である。以下 \(m-1\), \(m \gt 0\) に対して真であると仮定し、\(m\) に対して証明する。

ステップ 1 では忠実な司令官は \(n-1\) 人すべての副官たちに値 \(v\) を送信する。ステップ 2 でそれぞれの忠実な副官が \(n-1\) 人の将軍と共に \({\rm OM}(m-1)\) を適用する。仮説 \(n \gt 2k+m\) より \(n-1 \gt 2k+(m-1)\) であり、帰納法を適用して、それぞれの忠実な副官は各副官 \(j\) ごとに \(v_j=v\) を得ると結論づけることができる。したがって、それぞれの忠実な副官は \(n-1\) 個の値 \(i\) の過半数で \(v_i=v\) を持つため、ステップ 3 で \({\rm majority}(v_1,\ldots,v_{n-1})=v\) を得て IC2 を証明する。∎

次の定理はアルゴリズム \({\rm OM}(m)\) がビザンチン将軍問題を解決することを主張するものである。

定理 1. 任意の \(m\) に対して、\(3m\) 人より多い将軍と最大 \(m\) 人の裏切り者が存在する場合、アルゴリズム \({\rm OM}(m)\) は IC1 と IC2 を満足する。

証明. 証明は \(m\) に対する帰納法で行う。裏切り者がいない場合に \({\rm OM}(0)\) が IC1 と IC2 を満たすことは容易に分かる。そこで \({\rm OM}(m-1)\) について定理が成り立つと仮定し、\({\rm OM}(m)\), \(m \gt 0\) について証明する。

まず司令官が忠実である場合を考える。補題 1 の \(k\) を \(m\) とすると \({\rm OM}(m)\) は IC2 を満たすことが分かる。司令官が忠実であれば IC2 より IC1 が成り立つため、司令官が裏切り者である場合のみ IC1 を検証する必要がある。

裏切り者は最大でも \(m\) 人であり、司令官はそのうちの 1 人であるため、副官のうち多くても \(m-1\) 人が裏切り者である。将軍は \(3m\) 人より多いため副官は \(3m-1\) 人より多く、\(3m-1 \gt 3(m-1)\) である。したがって、帰納仮説を適用して \({\rm OM}(m-1)\) が IC1 と IC2 を満たすと結論づけることができる。したがって各 \(j\) について 2 人の忠実な副官はステップ 3 で \(v_j\) で同じ値を取得する。(これは 2 人の副官のうち 1 人が副官 \(j\) であれば IC2 より、そうでなければ IC1 より導かれる。) したがって、任意の 2 人の忠実な副官は同じ値のベクトル \(v_1,\ldots,v_{n-1}\) を得るため、ステップ 3 で同じ値 \({\rm majority}(v_1,\ldots,v_{n-1})\) を得て IC1 が証明される。∎

4. 署名付きメッセージを用いた解

Fig. 1 と Fig. 2 のシナリオで見たように裏切り者の偽証能力がビザンチン将軍問題を困難にしている。この能力を制限することができれば問題はより簡単に解決することができる。その一つの方法は、裏切り者が偽造不可能な署名付きメッセージを送れるようにすることである。より正確には A1-A3 に以下の仮定を追加する。

• A4. (a) 忠実な将軍の署名は偽造できず、署名されたメッセージ内容のいかなる変更も検出することができる。(b) 誰でも将軍の署名の真偽を検証できる。

裏切り者の将軍の署名については何も仮定していないことに注意。特に、裏切り者の署名が他の裏切り者によって偽造されることを許容し、それによって裏切り者間の共謀を許容する。

署名付きのメッセージを導入したことで 1 人の裏切り者に対処するために 4 人の将軍が必要という以前の議論は成り立たなくなった。実際、3 将軍解が存在する。ここで、任意の数の将軍に対して \(m\) 人の裏切り者に対処するアルゴリズムを示す。(将軍の数が \(m+2\) より少なければこの問題は無意味 (vacuous) である。)

このアルゴリズムは、司令官が署名付きの命令を各副官に送信する。それぞれの副官はその命令に自分の署名を加えて他の副官たちに送信し、副官たちは署名を加えて他の副官たちに送信し、と続く。つまり、ある副官は 1 つの署名付きメッセージを受信し、そのコピーをいくつか作成し、それらのコピーに署名して送信しなければならない。これらのコピーをどのように取得するかは問題ではない; 単一のメッセージはコピーされるかもしれないし、それぞれのメッセージが必要に応じて署名され配布される同一のメッセージのスタックで構成されているかもしれない。

我々のアルゴリズムは 1 つの命令を得るために、一連の命令に適用される関数 \({\rm choice}\) を仮定している。この関数に対する唯一の要件は

1. 集合 \(V\) が単一の要素 \(v\) からなる場合、\({\rm choice}(V)=v\) とする。
2. \({\rm choice}(\emptyset)={\rm RETREAT}\)。ここで \(\emptyset\) は空集合である。

要素に順序があると仮定して \({\rm choice}(V)\) を \(V\) の中央要素とする定義もあり得ることに注意。

次のアルゴリズムでは将軍 \(i\) によって署名された値 \(x\) を \(x:i\) と表記する。したがって \(v:j:i\) は値 \(v\) が \(j\) によって署名され、その \(v:j\) がさらに \(i\) によって署名されていることを表している。将軍 \(0\) を司令官とする。このアルゴリズムでは、各副官 \(i\) はこれまでに自身が受信した適切に署名された命令の集合を含む集合 \(V_i\) を保持する。(司令官が忠実であればこの集合は単一の要素より多くを含むことはないはずである。) 彼が受信した命令の集合である \(V_i\) と、彼が受信したメッセージの集合を混同しないように。同じ命令であっても多くの異なるメッセージがあるかもしれない。

アルゴリズム \({\rm SM}(m)\).

初期値 \(V_i=\emptyset\)

1. 司令官は自身の値に署名してすべての副官に送信する。
2. それぞれの \(i\) に対して:
   1. 副官 \(i\) が司令官から \(v:0\) 形式のメッセージを受信し、まだ何の命令も受けていない場合
      1. 副官は \(V_i\) を \(\{v\}\) に設定する;
      2. 副官は \(v:0:i\) を他のすべての副官に送信する。
   2. 副官 \(i\) が \(v:0:j_1:\cdots:j_k\) 形式のメッセージを受信し、\(v\) が \(V_i\) の集合に含まれていない場合
      1. 副官は \(v\) を \(V_i\) に追加;
      2. \(k \lt m\) であれば副官はメッセージ \(v:0:j_1:\cdots:j_k:i\) を \(j_1,\ldots,j_k\) を除くすべての副官に送信する。
3. 各 \(i\) について: 副官 \(i\) がそれ以上メッセージを受け取らなくなると、彼は \({\it choice}(V_i)\) の命令に従う。

ステップ 2 で副官 \(i\) はすでに集合 \(V_i\) に存在する命令 \(v\) を含むメッセージを無視することに注意。

ここではステップ 3 で副官がそれ以上のメッセージを受け取らないことをどのように判断するかは明記していない。\(k\) に関する帰納法により、\(k \le m\) の副官 \(j_1,\ldots,j_k\) の各列に対して、ステップ 2 で 1 人の副官が \(v:0:j_1:\cdots:j_k\) 形式のメッセージを最大 1 つ受信できることが容易に示される。

副官 \(j_k\) がそのようなメッセージを送信するか、さもなくばそのようなメッセージを送信しないことを報告するメッセージを送信するという要求があれば、すべてのメッセージを受信したときを決定することは容易である。(仮定 A3 より、副官は裏切り者の副官 \(j_k\) がこれら 2 つのメッセージのどちらも送信していないことを判断できる。) あるいはタイムアウトを用いてこれ以上のメッセージが届かなくなるタイミングを判断することも可能である。タイムアウトの使用についてはセクション 6 で説明する。

ステップ 2 では、副官 \(i\) は値の後に署名が続くという適切な形式を持たないメッセージをすべて無視することに注意。メッセージのコピーを避けるために同一のメッセージパケットを使用する場合、これは、適切な署名が同一の数に満たないパケットを破棄することを意味する。(メッセージが \(k\) 人の副官に署名されていれば \((n-k-2)(n-k-3)\cdots(n-m-2)\) 個のコピーが存在するはずである。)

Fig. 5 は司令官が裏切り者である 3 将軍ケースでアルゴリズム \({\rm SM}(1)\) を示している。司令官は片方の副官に "attack" 命令を、他方の副官に "retreat" 命令を送信する。双方の副官はステップ 2 で 2 つの命令を受け取るため、ステップ 2 の後は \(V_1=V_2=\{\)"attack", "retreat"\(\}\) であり、そして双方の副官は \({\rm choice}(\{\)"attack", "retreat"\(\})\) に従う。この洞察から、司令官の署名が 2 つの異なる命令に記載されており、A4 ではそのような署名を作成できるのが司令官だけであることを示していることから、Fig. 2 と異なり副官は司令官が裏切り者であることを知る。

アルゴリズム \({\rm SM}(m)\) では副官は命令の受領を確認するために自分の名前に署名する。彼が命令に署名を加えた \(m\) 番目の副官であれば、その署名は受信者によって他の誰にも中継されないので余計なものである。(より正確には仮定 A2 より不要である。) 特に副官は \({\rm SM}(1)\) において自分のメッセージに署名する必要はない。

ここでこのアルゴリズムの正しさを証明する。

定理 2. 任意の \(m\) に対して、裏切り者が最大 \(m\) 人であれば \({\rm SM}(m)\) はビザンチン将軍問題を解く。

証明. まず IC2 を証明する。もし司令官が忠実であればステップ 1 で署名した命令 \(v:0\) をすべての副官に送信する。したがってすべての忠実な副官はステップ 2.A で命令 \(v\) を受信するだろう。さらに、裏切り者の副官は \(v':0\) 形式の異なるメッセージを偽造できないため、忠実な副官はステップ 2.B で追加の命令を受け取ることはない。したがって、それぞれの忠実な副官 \(i\) に対してステップ 2 で得られた集合 \(V_i\) は \({\rm choice}\) 関数の特性 1 によりステップ 3 で従うことになる単一の命令 \(v\) で構成される。これで IC2 が証明される。

司令官が忠実であれば IC1 は IC2 から導かれるため IC1 を証明するには司令官が裏切り者である場合のみを考えれば良い。忠実な 2 人の副官 \(i\) と \(j\) はステップ 2 で受信した命令の集合 \(V_i\) と \(V_j\) が同じであればステップ 3 で同じ命令に従う。したがって IC1 を証明するには、ステップ 2 で \(i\) が命令 \(v\) を \(V_i\) に入れるなら、\(j\) もステップ 2 で同じ命令 \(v\) を \(V_j\) に入れなければならないことを証明すれば十分である。そのためには \(j\) がその命令を含む適切に署名されたメッセージを受信することを示さなければならない。\(i\) がステップ 2.A で命令 \(v\) を受信すれば、ステップ 2.A.ii でそれを \(j\) に送信するため (A1 により) \(j\) はそれを受信する。ステップ 2.B で \(i\) が命令を \(V_i\) に追加した場合、\(v:0:j_1:\cdots:j_k\) 形式の最初のメッセージを受信する必要がある。もし \(j\) が \(j_r\) の 1 人であれば、A4 により彼はすでに命令 \(v\) を受信しているはずである。そうでなければ 2 つのケースを考える:

1. \(k \lt m\). この場合、\(i\) はメッセージ \(v:0:j_1:\cdots:j_k:i\) を \(j\) に送信するので、\(j\) は命令 \(v\) を受信しなければならない。
2. \(k = m\). 司令官が裏切り者であるため最大 \(m-1\) 人の副官が裏切り者である。したがって副官 \(j_1,\ldots,j_m\) の少なくとも 1 人は忠実である。この忠実な副官は最初に値 \(v\) を受信したときに \(j\) に送信していなければならないので、したがって \(j\) はその値を受け取らなければならない。

これで証明は完了である。∎

5. 通信経路の欠落

ここまでで将軍は他のすべての将軍に直接メッセージを送信できると仮定してきた。ここでこの仮定を外す。その代わりに誰が誰にメッセージを送れるかについて何らかの制限を与える物理的な障壁を仮定する。将軍は単純²有限無向グラフ \(G\) のノードを形成すると考える。ここで 2 つのノード間の弧はそれらの 2 つの将軍がメッセージを直接送信できることを示す。ここで \(G\) が完全接続であると仮定したアルゴリズム \({\rm OM}(m)\) と \({\rm SM}(m)\) をより一般的なグラフに拡張する。

口頭メッセージアルゴリズム \({\rm OM}(m)\) を拡張するために次の定義が必要である。ここで 2 人の将軍が弧によって連結しているなら隣接 (neighbor) と呼ぶ。

定義 1.

(a) ノードの集合 \(\{i_1,\ldots,i_p\}\) は以下の場合にノード \(i\) の隣接の正規集合 (regular set of neighbors) であるという。

1. すべての \(i_j\) が \(i\) に隣接しており
2. \(i\) と異なる任意の将軍 \(k\) に対して各 \(i_j\) から \(i\) を経由しない \(k\) への経路 \(\gamma_{j,k}\) が存在し、それらの経路 \(\gamma_{j,k}\) はどれも \(k\) 以外に共通するノードを持っていない。

(b) すべてのノードが \(p\) 個の異なるノードからなる隣接の正規集合を持つグラフ \(G\) は \(p\)-正則という。

Fig. 6 は単純 3-正則グラフの例を示す。Fig. 7 は中央のノードが 3 つのノードを含む隣接の正規集合を持たないため 3-正則ではないグラフの例である。

我々は \({\rm OM}(m)\) を拡張し、将軍のグラフ \(G\) が \(3m\)-正則であれば、\(m\) 人の裏切り者が存在してもビザンチン将軍問題を解くアルゴリズムにする。(\(3m\)-正則グラフは少なくとも \(3m+1\) ノードを含む必要があることに注意。) すべての正の整数 \(m\) と \(p\) に対して将軍のグラフ \(G\) が \(p\)-正則のとき、アルゴリズム \({\rm OM}(m,p)\) を次のように定義する。(\(G\) が \(p\)-正則でないとき \({\rm OM}(m,p)\) は定義されない。) 定義は \(m\) に対する帰納法を用いている。

アルゴリズム \({\rm OM}(m,p)\).

0. 司令官に隣接する \(p\) 人の副官で構成される正規集合 \(N\) を選ぶ。
1. 司令官は \(N\) の副官それぞれに自身の値を送信する。
2. \(N\) の各 \(i\) について、副官 \(i\) が司令官から受信する値を \(v_i\) とし、値を受け取らない場合は RETREAT とする。副官 \(i\) は \(v_i\) を他のすべての副官 \(k\) に次のように送信する:
   1. \(m=1\) の場合、定義 1 の a.ii の部分で存在が保証されている経路 \(\gamma_{i,k}\) に沿って値を送ることで。
   2. \(m \gt 1\) の場合、\(G\) から元の司令官を削除して得られる将軍のグラフに対してアルゴリズム \({\rm OM}(m-1,p-1)\) の司令官として行動する。
3. \(N\) の \(i \ne k\) となる各 \(k\) と各 \(i\) に対して、ステップ 2 で副官 \(k\) が副官 \(i\) から受信した値を \(v_i\) とし、値を受信しなかった場合は RETREAT とする。副官 \(k\) は値 \({\rm majority}(v_{i_1},\ldots,v_{i_p})\) を使用する。ここで \(N=\{i_1,\ldots,i_p\}\) である。

\(p\)-正則グラフから 1 つのノードを削除すると \((p-1)\)-正則グラフが残ることに注意。したがってアルゴリズム \({\rm OM}(m-1,p-1)\) をステップ 2.B に適用することができる。

ここで裏切り者が最大 \(m\) 人のときに \({\rm OM}(m,3m)\) がビザンチン将軍問題を解決することを証明する。証明はアルゴリズム \({\rm OM}(m)\) の証明と同様であるため概略を述べるにとどめる。これは次のような補題 1 の拡張から始まる。

補題 2. 任意の \(m \gt 0\) と任意の \(p \ge 2k+m\) に対して、裏切り者が最大でも \(k\) 人であればアルゴリズム \({\rm OM}(m,p)\) は IC2 を満足する。

証明. \(m = 1\) の場合、副官は \({\rm majority}(v_1,\ldots,v_p)\) という値を得る。ここで各 \(v_i\) は司令官が彼に値を送るために使用した経路から切り離された経路で彼に送られた値である。裏切り者は最大でも \(k\) 人であり、\(p \ge 2k+1\) であるから、それらの経路の半分以上は忠実な副官だけで構成されている。したがって司令官が忠実であれば値 \(v_i\) の過半数は彼が送信した値と等しくなり IC2 が満たされることを意味する。

ここで \(m-1\), \(m \gt 1\) の補題を仮定する。司令官が忠実であれば \(N\) の \(p\) 人の副官はそれぞれ正しい値を得ることができる。\(p \gt 2k\) より、そのうちの過半数は忠実であり、帰納仮説により、そのうちのそれぞれが正しい値を忠実な副官に送る。したがってそれぞれの忠実な副官は過半数の正しい値を取得し、これによりステップ 3 の正しい値を取得する。∎

アルゴリズム \({\rm OM}(m,3m)\) の正しさは次の結果の直接的な結果である。

定理 3. 任意の \(m \gt 0\) と任意の \(p \ge 3m\) に対して、裏切り者が最大でも \(m\) 人であればアルゴリズム \({\rm OM}(m,p)\) はビザンチン将軍問題を解決する。

証明. 定理 2 により、\(k = m\) とすると \({\rm OM}(m,p)\) は IC2 を満たすことが分かる。司令官が忠実であれば IC1 は IC2 から導かれるため、司令官が裏切り者であるという仮定の下で IC1 を証明すればよい。そのためにステップ 3 ですべての忠実な副官が同じ値の集合 \(v\) を得ることを証明する。\(m = 1\) の場合、\(N\) に属する副官を含むすべての者が忠実であり、経路 \(\gamma_{i,k}\) が司令官を通らないためこれに従う。\(m \gt 1\) の場合、\(p \ge 3m\) は \(p-1 \ge 3(m-1)\) を意味するため簡単な帰納法を適用することができる。∎

このアルゴリズム \({\rm OM}(m)\) の拡張はグラフ \(G\) が \(3m\)-正則であることを必要とし、これはかなり強い接続性仮説³ (connectivity hypothesis) である。実際、将軍が \(3m+1\) 人 (必要最小数) いるとき、\(3m\)-正則は完全接続性を意味し、アルゴリズム \({\rm OM}(m,3m)\) はアルゴリズム \({\rm OM}(m)\) に削減する。これに対してアルゴリズム \({\rm SM}(m)\) は最も弱い接続性仮説を許容するように拡張するのは簡単である。まずビザンチン将軍問題が解けるようになるまでにどれだけの接続性が必要になるかを考えよう。 IC2 は忠実な副官が司令官に従うことを要求している。司令官が副官と通信できなければこれは明らかに不可能である。特に司令官から副官へのすべてのメッセージが裏切り者を中継するなら副官が司令官の命令を受信することを保証する方法はない。同様に 2 人の副官が裏切り者を中継することによってのみ通信可能なら IC1 は保証されない。

ビザンチン将軍問題が解ける最も弱い接続性の仮説は忠実な将軍によって形成される部分グラフが接続されていることである。我々はこの仮説の下で将軍の数を \(n\) として裏切り者の数に関係なくアルゴリズム \({\rm SM}(n-2)\) が解となることを示す。もちろん、将軍がメッセージを送れる場所にしか送らないようにアルゴリズムを修正しなければならない。より正確にはステップ 1 で司令官は署名した命令を隣接する副官のみに送信する。ステップ 2.B で副官 i は \(j_r\) の中にいない隣接しているすべての副官にのみメッセージを送信する。

我々はより一般的な結果を次に証明する。ここでグラフの直径 (diameter) は任意の 2 つのノードが最大 \(d\) 個の弧を含む経路によって接続されるような最小の \(d\) の数である。

定理 4. 任意の \(m\) と \(d\) に対して、裏切り者が最大でも \(m\) 人しか存在せず、忠実な将軍の部分グラフが直径 \(d\) であるとき、アルゴリズム \({\rm SM}(m+d-1)\) は (上記の修正を加えて) ビザンチン将軍問題を解決する。

証明. この証明は定理 2 の証明と非常に似ているためここでは概略を述べるにとどめる。IC2 を証明するために、仮説により忠実な司令官から副官 \(i\) まで \(d-1\) 以下の忠実な副官を経由する経路があることを観測する。これらの副官は命令が \(i\) に届くまで正しく中継する。前述と同様に裏切り者が異なる命令を偽造することはできないと仮定する。

IC1 を証明するために、司令官が裏切り者であると仮定して忠実な副官 \(i\) が受信した命令は忠実な副官 \(j\) も受信することを示さなければならない。\(i\) が \(j\) によって署名されていない命令 \(v:0:j_1:\cdots:j_k\) を受信したとする。\(k \lt m\) であれば \(i\) はその命令をまだ受信していないすべての隣接ノードに送り、追加の \(d-1\) ステップ以内に \(j\) にリレーされるだろう。\(k \ge m\) ならば最初の \(m\) 人の署名者のうち 1 人は忠実でなければならず、その隣接ノード全員に送っていなければならず、忠実な将軍たちによって中継され、\(d-1\) ステップ以内に \(j\) に到達するだろう。∎

系 (corollary). 忠実な将軍のグラフが接続されている場合、(上記で変更した) \({\rm SM}(n-2)\) は \(n\) 人の将軍たちのビザンチン将軍問題を解く。

証明. 忠実な将軍たちのグラフの直径を \(d\) とする。連結グラフの直径はノードの数より小さいため、忠実な将軍は \(d\) 人以上で、裏切り者は \(n-3\) 人以下でなければならない。この結果は \(m=n-d-1\) とすることで定理から導かれる。∎

定理 4 は忠実な将軍たちの部分グラフが連結していることを仮定している。その証明は簡単に拡張でき、そうでない場合であっても、裏切り者が最大でも \(m\) 人であればアルゴリズム \({\rm SM}(m+d-1)\) は次の 2 つの特性を持つことが示される:

1. 忠実な将軍のみを経由する最大 \(d\) の長さの経路で結ばれた 2 つの忠実な将軍は同じ命令に従うだろう。
2. 司令官が忠実であれば、忠実な将軍のみを経由する最大 \(m+d\) の長さの経路で彼に結ばれている忠実な副官は彼の命令に従うだろう。

• ²単純グラフ (simple graph) とは、任意の 2 つのノードを結ぶ弧がたかだか 1 つで、すべての弧が異なる 2 つのノードを結ぶものである。
• ³Dolev の最近のアルゴリズム [2] はより少ない接続性を必要とする。

6. 高信頼性システム

高信頼性のコンピュータシステムを実装するために、根本的に信頼性の高い回路部品を使うこと以外に我々が知っている唯一の方法は、複数の異なる "プロセッサ" を使って同じ結果を計算し、それらの出力に対して多数決を行って単一の値を取得することである。(投票はシステム内部で行ってもよいし、出力のユーザによって外部で実行してもよい。) このことは個別のチップ故障から保護するために冗長回路を用いて高信頼性コンピュータを実装する場合でも、核攻撃による個々のサイトの破壊から保護するために冗長コンピューティングサイトを用いた弾道ミサイル防衛システムを実現する場合でも同じである。違いはただ複製された "プロセッサ" のサイズだけである。

高信頼性を達成するための多数決は故障していないプロセッサすべてが同じ出力を生成するという前提で行われる。これはすべてのプロセッサが同じ入力を使用する限り正しい。しかし、単一の入力データは単一の物理コンポーネント (例えば信頼性の高い部品のある回路やミサイル防衛システムのあるレーダーサイト) から得られるものであり、故障しているコンポーネントは他のプロセッサに異なる値を与える可能性がある。さらに、故障していない入力ユニットであっても値を変更中に別のプロセッサが読みだせば異なる値を得ることもある。たとえば 2 つのプロセッサが進行中のクロックを読み取る場合、一方が古い値を取得し、もう一方が新しい値を取得する可能性がある。これを防ぐにはクロックの進行に合わせて読み出しを同期させるしかない。

多数決が高信頼システムをもたらすためには次の 2 つの条件を満たす必要がある:

1. 故障していないプロセッサはすべて同じ入力値を使用しなければならない (したがってそれらは同じ出力を生成する)。
2. 入力ユニットが故障していない場合、故障していないすべてのプロセスはそれが提供する値を入力として使用する (したがってそれらは正しい出力を生成する)。

これらはちょうど我々の対話型整合性条件 IC1 と IC2 であり、"司令官" は入力を生成するユニット、"副官" はプロセッサ、"忠実" は非故障を意味する。

この問題を "ハードウェア" で解決しようとするのは魅力的なことである。例えばすべてのプロセッサが同じ入力値を得られるように、すべてのプロセッサに同じ配線から入力値を読み取らせることが考えられる。しかし入力ユニットに故障があると、あるプロセッサは "0" と解釈し別のプロセッサは "1" と解釈するような境界ぎりぎりの信号を送る可能性がある。故障しているかもしれない入力装置から異なるプロセッサが同じ値を得ることを保証するには、プロセッサ間で通信してビザンチン将軍問題を解決するしか方法はない。

もちろん故障した入力装置は意味のない入力値を提供するかもしれない。ビザンチン将軍の解決法でできることは、すべてのプロセッサが同じ入力値を使うことを保証することだけである。もしその入力が重要なものであれば冗長な値を提供するいくつかの別の入力装置が必要である。例えばミサイル防衛システムには冗長化された処理サイトだけでなく冗長化されたレーダーが必要である。ただし、入力が冗長化されていても信頼性は達成できないため、故障していないプロセッサが冗長データを使って同じ出力を生成することを保証する必要がある。

入力装置に故障はなく、値を変更中に読み取られことで異なる値を得た場合あっても、やはり故障していないプロセッサが妥当な入力値を取得する必要がある。関数 \({\rm majority}\) と \({\rm choice}\) を中央値関数とすると、我々のアルゴリズムは故障していないプロセッサが得る値は入力装置の提供する値の範囲内にあるという特性を持っていることを示すことができる。したがって、入力ユニットが妥当な範囲の値を生成する限り正常なプロセッサは妥当な値を得ることができる。

これまでにいくつかの解決策を示したが、それらは計算機システムの観点ではなくビザンチン将軍の観点で述べられてきた。ここではどのようにこれらの解を高信頼計算機システムに適用できるかを検討する。もちろん "将軍" アルゴリズムをプロセッサで実装することに問題はない。問題は、仮定 A1-A3 (アルゴリズム \({\rm SM}(m)\) の仮定 A1-A4) を満たすメッセージパッシングシステムを実装することにある。ここでこれらの仮定を順に検討する。

A1. 仮定 A1 は故障していないプロセッサが送信したメッセージはすべて正しく配信されることを示している。実際のシステムでは通信回路に障害が発生する可能性がある。口頭メッセージアルゴリズム \({\rm OM}(m)\) および \({\rm OM}(m,p)\) では、2 つのプロセッサをつなぐ通信回線の障害はプロセッサの 1 つが故障した場合と区別がつかない。したがって、プロセッサまたは通信回線の故障であるかどうかにかかわらず、これらのアルゴリズムが \(m\) 個までの故障が存在する場合にのみ機能することを保証できる。(もちろん、同じプロセッサに接続されている複数の通信回線の故障は単一のプロセッサ障害に相当する。) 通信回線の障害が発生しても署名付きメッセージの偽造はできないと仮定すれば (後述するように非常に合理的な仮定)、署名付きメッセージアルゴリズム \({\rm SM}(m)\) は通信回線の故障に影響を受けない。より正確には、定理 4 は通信回線の故障があっても有効である。通信回線の障害は単に通信回線を取り除いたのと同じ効果、つまりプロセッサグラフの接続性を低下させる。

A2. 仮定 A2 はプロセッサが受信したあらゆるメッセージの送信元を特定できることを示している。実際に必要なのは故障したプロセッサが故障していないプロセッサに成りすますことができないようにすることである。これは、具体的にはプロセス間通信がメッセージ交換ネットワーク (message switching network) ではなく固定回線 (fixed lines) を介して行われることを意味している。(もし交換ネットワークを使うなら故障したネットワークノードを考慮しなければならずビザンチン将軍問題が再び発生する。) 別のプロセッサへのなりすましはそのメッセージを偽造することを意味するため、A4 を仮定してすべてのメッセージに署名すれば仮定 A2 は必要ないことに注意。

A3. 仮定 A3 はメッセージの欠落を検出できることを要求している。メッセージの欠落は一定時間内にそれが到着しないこと、つまりタイムアウト規則を使用することによってのみ検出することができる。A3 を満たすためにタイムアウトを使用するには次の 2 つの仮定が必要である:

1. メッセージの生成と送信に必要な時間の最大値が決まっている。
2. 送信者と受信者はある一定の最大誤差の範囲内で同期されたクロックを持つ。

受信者はメッセージが到着するまでにどれくらい待つ必要があるかを知っている必要があるため最初の仮定が必要なのは明らかである。(生成時刻とは、メッセージを生成するために必要なすべての入力を受け取った後にプロセッサがメッセージを送信するまでにかかる時間である。) 2 番目の仮定が必要なことはあまり自明ではない。しかしビザンチン将軍問題を解くにはこの仮定または同等の仮定が必要であることを示すことができる。より正確には、次の場合にのみ将軍が行動を起こすようなアルゴリズムを許すとする。

1. ある固定された初期時刻 (すべての将軍で同じ)。
2. メッセージの受信時。
3. ランダムに選ばれた時間が経過したとき。(つまり将軍はタイマーをランダムな値に設定し、タイマーが切れたときに行動することができる。)

(これにより同期クロックの構築を許可しない、我々が想定するもっとも一般的なクラスのアルゴリズムが得られる。) メッセージの伝達遅延に上限があったとしても、メッセージを任意に迅速に送信できるなら、そのようなアルゴリズムではビザンチン将軍問題を解くことができないことが示される。さらに、裏切り者に許される唯一の不正な行動がメッセージ伝達の失敗であるように制限を設けたとしても解は得られない。この結果の証明はこの論文の範囲外である。伝達遅延に上限と下限を設定することによってプロセッサはメッセージの往復でクロックを実装できることに注意。

上記の 2 つの仮定により未送信メッセージの検出は容易である。\(\mu\) をメッセージの生成と送信の最大遅延とし、故障していないプロセッサのクロックが互いに最大 \(\tau\) だけ異なっていると仮定する。このとき、故障していないプロセッサが自分のクロックの時間 \(T\) までに生成を開始する必要のあるメッセージは、受信者のクロックの時間 \(T+\mu+\tau\) までにその宛先に到着する。したがって、もし受信者がその時間までにメッセージを受け取らなかった場合、それは送信されていないと見なすことができる。(もしそれ以降に到着したのであれば送信者が故障しているに違いないため、このアルゴリズムの正しさはメッセージが送信されたかどうかには依存しない。) 入力プロセッサが自身の値を送信する時刻を固定することにより、プロセッサが各メッセージを自分のクロックのいつまで待つ必要があるかを計算することができる。例えばアルゴリズム \({\rm SM}(m)\) では、プロセッサは \(k\) 個の署名を持つ任意のメッセージに対して \(T_0 + k(\mu + \tau)\) まで待つ必要がある。ここで \(T_0\) は司令官がアルゴリズムの実行を開始する (彼のクロックでの) 時刻である。

2 つのクロックは正確に同じ速度で動いているわけではないため、最初にどれだけ正確に同期させたとしても定期的に再同期しなければいずれは任意の時間のずれが発生する。そのため、一部のプロセッサに故障が発生した場合でも、プロセッサのクロックを一定の範囲内ですべて同期させるという問題がある。これはビザンチン将軍問題自体と同じくらい難しい問題である。クロック同期問題には、我々のビザンチン将軍問題と密接に関連する解決策が存在する。これらについては今後の論文で紹介する予定である。

A4. 仮定 A4 では、プロセッサが故障していないプロセッサの署名を偽造できないような方法で自身のメッセージに署名できることを要求している。署名とはプロセス \(i\) がデータ項目 \(M\) から生成する冗長情報 (redundant information) \(S_i(M)\) である。\(i\) が署名したメッセージはペア \((M,S_i(M))\) で構成される。A4 の a と b の部分を満たすには、関数 \(S_i\) は次の 2 つの特性を持つ必要がある:

1. プロセッサ \(i\) が故障していなければ、どの故障プロセッサも \(S_i(M)\) を生成することはできない。
2. \(M\) と \(X\) が与えられたとき、\(X\) が \(S_i(M)\) と等しいことはどのプロセスでも判断できる。

\(S_i(M)\) は単なるデータ項目であり、故障プロセッサはどのようなデータ項目も生成できるため、特性 a は決して保証されない。しかし違反の可能性を限りなく小さくすることでシステムの信頼性を限りなく高めることができる。それがどのように行われるかは予想される故障の種類によって異なる。注目すべき 2 つのケースがある:

1. ランダムな不正動作 (random malfunction). \(S_i\) を適当に "ランダム化" する関数とすることで、プロセッサのランダムな不正動作が正しい署名を生成する確率を、ランダムな選択手続きを通じて正しい署名を生成する確率、つまり取り得る署名の数の逆数と本質的に等しくすることができる。これを行うための一つの方法として次のようなものがある。メッセージは \(P\) より小さい正の整数で符号化されていると仮定し、\(P\) は 2 の累乗とする。\(S_i(M)\) は \(M * K_i \bmod P\) と等しく、\(K_i\) は \(P\) より小さいランダムに選ばれた奇数とする。\(K_i^{-1}\) を \(P\) より小さく \(K_i * K_i^{-1} \equiv 1 \bmod P\) となるような唯一の値とすると、プロセスは \(M \equiv X * K_i^{-1} \bmod P\) をテストすることによって \(X = S_i(M)\) を確認することができる。他のプロセッサがメモリに \(K_i\) を持っていない場合、そのプロセッサが単一の (非ゼロの) メッセージ \(M\) に対して正しい署名 \(M * K_i\) を生成できる確率は \(1/P\) でなければならない: これはランダム選択によってそうなる確率である。(もしプロセッサが簡単な方法で \(K_i\) を入手できるなら、故障プロセッサ \(j\) が \(S_j(M)\) を算出する時に \(K_i\) を \(K_j\) に置き換えて \(i\) の署名を偽造する可能性が高くなることに注意。)

2. 悪意的な知性 (malicious intelligence). 故障プロセッサが悪意のある知性によって誘導されている場合、例えばシステムを混乱させようとしている人間に操作されている完全に正常なプロセッサである場合、署名関数 \(S_i\) の構築は暗号上の問題となる。この問題の解決方法については [1] と [4] を参照。

プロセスがすでにその署名を認識している場合、署名 \(S_i(M)\) を生成することは簡単であることに注意。したがって同じメッセージに 2 回署名する必要がないことが重要である。つまり \({\rm SM}(m)\) を繰り返し使用して一連の値を配布する場合、一意性を保証するために値にシーケンス番号を付加する必要がある。

7. 結論

我々は様々な仮説の元でビザンチン将軍問題に対するいくつかの解を提示し、それらが信頼性の高いコンピュータシステムの実装にどのように利用できるかを示した。これらの解法は必要な時間とメッセージ数の両方で高コストである。アルゴリズム \({\rm OM}(m)\) と \({\rm SM}(m)\) は共に \(m+1\) までの長さのメッセージ経路を必要とする。言い換えれば、それぞれの副官は司令官から発信され他の \(m\) 人の副官を経由して中継されたメッセージを待たなければならないかも知れない。Fischer と Lynch は、これが \(m\) 人の裏切り者に対処できるすべての解法に当てはまることを示したので、その点で我々の解法は最適である。完全に連結していないグラフに対する我々のアルゴリズムでは最大 \(m+d\) の長さのメッセージ経路が必要である。ここで \(d\) は忠実な将軍の部分グラフの直径である。我々はこれも最適であると考える。

\({\rm OM}(m)\) と \({\rm SM}(m)\) のアルゴリズムは最大で \((n-1)(n-2)\cdots(n-m-1)\) 個のメッセージを送信する。メッセージを組み合わせることで必要なメッセージの数は確実に減らすことができる。また転送される情報量も削減できるかも知れないがこれについては詳細に研究されていない。しかし引き続き多数のメッセージが必要になることが予想される。

恣意的な不正動作に対して信頼性を達成することは困難な問題であり、その解決策は本質的にコストがかかると思われる。コストを削減する唯一の方法は起き得る故障の種類を想定することである。例えば、コンピュータは応答しなくなる場合はあっても不正な応答をすることはないと想定できることがよくある。ただし、極めて高い信頼性が要求される場合はそのような想定を置くことができず、ビザンチン将軍の解決法の全コストが必要となる。

References

1. DIFFIE, W., AND HELLMAN, M.E. New directions in cryptography. IEEE Trans. Inf. Theory IT-22 (Nov. 1976), 644-654.
2. DOLEV, D. The Byzantine generals strike again. J. Algorithms 3, 1 (Jan. 1982).
3. PEASE, M., SHOSTAK, R., AND LAMPORT, L. Reaching agreement in the presence of faults. J. ACM 27, 2 (Apr. 1980), 228-234.
4. RIVEST, R.L., SHAMIR, A., AND ADLEMAN, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 2 (Feb. 1978), 120-126.

翻訳抄

ビザンチン将軍問題に関する 1982 年の論文。すべてのプロセスが完全グラフで接続している構成において、署名なしのアルゴリズムでビザンチン将軍問題を解くには \(n \ge 3m+1\) が必要。署名ありのアルゴリズムでは \(n \ge m+2\) が必要。完全グラフではない場合、署名なしアルゴリズムは \(3m\)-正則グラフであればビザンチン将軍問題を解くことができる。署名ありでは、正常なプロセスで構成される部分グラフが接続グラフであれば解くことができる。

1. LAMPORT, Leslie; SHOSTAK, Robert; PEASE, Marshall. The Byzantine Generals Problem. In: ACM Transactions on Programming Languages and Systems, Vol.4, No.3. 1982.