ビザンチン障害耐性
 概要
概要
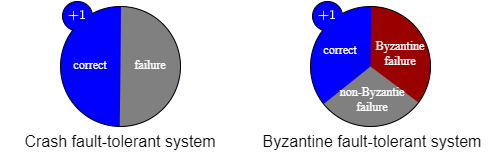
BFT (Byzantine fault-tolerance) またはビザンチン障害耐性はビザンチン障害プロセスが含まれていても安全な合意を達成することのできる性質である (あるいはその性質を持つ合意アルゴリズムを BFT とも呼ぶ)。またそのような性質を持つ合意をビザンチン合意 (Byzantine agreement) と呼ぶ。BFT の代表的な合意アルゴリズムには pBFT, BFT-SMaRt, Tendermint-BFT, HotStuff-BFT などがある。
BFT に対して Crash-Recovery 障害までを対象としている障害耐性を CFT (crash fault-tolerance) と呼ぶことがある。Raft や Zab などのプロトコルはデータセンターのような信頼できる環境で実行することを想定している分散システムは CFT である。
BFT の性質を持つ分散合意アルゴリズムは最終的にある一つの状態を共有しなければならない。より正確に表現すると:
\(n\) 個のプロセス \(P_0, P_1, \ldots, P_{n-1}\) がそれぞれ状態 \(s_i \in \{0,1\}\) を持つとする。1) 故障していないプロセス \(P_0\) が初期状態 \(s_0 = s \in \{0,1\}\) をとるとき、2) アルゴリズムの終了時に全ての故障していないプロセスが \(s_i = s\) の状態をとる。
Table of Contents
 ビザンチン将軍問題
ビザンチン将軍問題
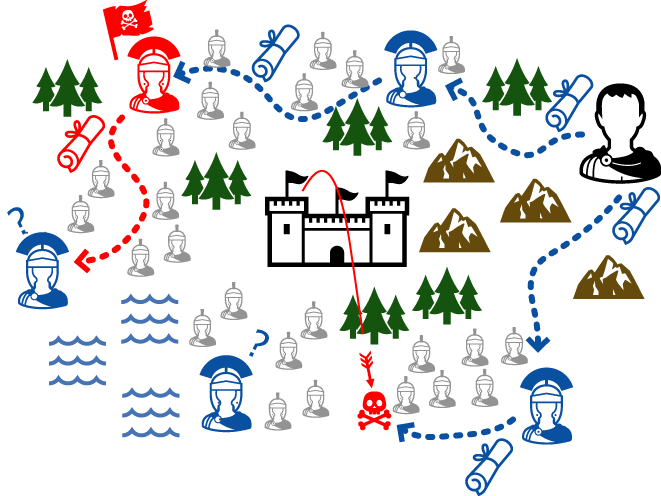
ビザンチン将軍問題 (Byzantine Generals Problem) またはビザンチン合意問題は、分散システムにおけるサブシステム間の合意の困難さを表す例として挙げられる想定問題である。
城壁に囲まれた都市を複数の部隊で攻撃することを想定する。作戦を遂行するためには将軍と城壁を取り囲んでいる各部隊の指揮官たちがその時々の作戦に合意しなければならない。しかし、以下の状況を考慮することによって問題が複雑化する。
- 部隊は互いに遠く離れている。司令官たちがコミュニケーションをとるには伝令員を走らせる必要があり、意思疎通にタイムラグがある。
- 一部の指揮官は攻撃や撤退を望んで命令を改ざんしたり握りつぶすかもしれない。
- 一部の指揮官はうっかり次の部隊に伝え忘れたり別の伝令書を届けてしまうかもしれない。
- 寝返りや作戦妨害をもくろむ指揮官や伝令員が紛れ込んでいて命令書をすり替えるかもしれない。
- 伝令員が敵の弓矢に倒れたり、伝令を放棄して逃げ出してしまうかもしれない。
- 後に出発した伝令員が先に出発した伝令員を追い越すかもしれない。
ビザンチン合意問題では、このような状況でも正しい指揮官が正しい合意を行えるかを議論する。
裏切り者の指揮官は不正のためであればどのような行動も取りうるとする。分散合意アルゴリズムがビザンチン問題耐性を持つかは以下の条件を保証できるかに依存する。
- 正しい指揮官は全員が同じ命令に従う。
- 少数の裏切り指揮官は正しい指揮官に不正な命令を遂行させることができない。
アルゴリズムは裏切り者の行動に関係なく条件 1. を保証する必要がある。また、正しい司令官は単に作戦命令の内容を検証するだけではなくではなく、合意のための過程も検証すべきである。
分散システムにおいては、全てのノードがある一連のルールの元で動作するよう設計し、各ノードはトランザクションを自分のデータベースに追加する前に多数のノードでトランザクション検証が正しく行われたことを検証しなければならない。現実的な実装方法として分散システムのネットワークは伝令員を走らせるより遙かに低コストでメッセージを伝達することができるため富豪的なアプローチを取ることは可能である。
 BFT 仮定
BFT 仮定
ビザンチン故障の存在しない信頼できる非同期ネットワークでの合意は一般に過半数以上のプロセスの承認によって達成される。システムが許容可能な故障プロセス数を \(f\) としたとき、合意にはそれを上回る \(f+1\) 個以上の非故障プロセスが必要であり、結果的にシステムには \(n \ge 2f+1\) 個のプロセスが必要となる。例えば分散ストレージではクラスタの過半数である \(f+1\) 個のノードに保存が完了した時点でそのデータは確定したことになりシステムから喪失したり後で覆されることはなくなる。
非同期 BFT の考えはこの延長にあり、ネットワークに \(f\) 個のビザンチン故障プロセスが存在し、かつ、正常なプロセスの \(f\) 個が非ビザンチン故障をしたとしても、\(f+1\) 個のプロセスが正常に機能していればビザンチン合意することはない (正しい値で合意するか、棄却で合意する) という前提に基づく。したがって \(f\) 個のビザンチン故障を許容するネットワークの全プロセス数 \(n\) は \(f+\)\(f+\)\(f+1\) となり式 (\(\ref{n3f1}\)) のように表される。\[ \begin{eqnarray} n \ge 3f + 1 \label{n3f1} \end{eqnarray} \] この BFT を達成するための前提「\(n = 3f + 1\) のネットワークにおいてビザンチン故障プロセスが \(f\) を超えて存在しない」ことを BFT 仮定と呼ぶ。
BFT に関する表記方法には全プロセス数 \(n\) に基づいて \(\frac{2}{3}n+1\) というような表現もある。これは全体の \(2/3\) を示していることが明確で分かりやすいが端数の扱いが正確ではなく、実際には floor や ceil を考慮する必要がある。このため、この記事では故障数 \(f\) に基づく表記をしている。
同期ネットワークや、すべてのプロセスが認証済みの環境では \(2f+1\) で BFT を達成することができる。
 定足数
定足数
BFT 仮定での定足数 (quorum) とは、合意のために必要な正常なプロセス数、あるいは正常なプロセスの応答数である。したがって、\(f\) 個のビザンチン故障と \(f\) 個の非ビザンチン故障を許容する定足数 \(Q_1\) は式 (\(\ref{quorum1}\)) の通りである。\[ \begin{equation} Q_1 = f+1 \label{quorum1} \end{equation} \] ここで、合意のために集める応答には正常な応答と区別できないビザンチン応答が最大 \(f\) 個紛れ込んでいる可能性があることに注意。しかし \(f+Q_1\) 個の応答が集まれば、ビザンチン応答を除外したとしても残りの正常なプロセスの応答数が \(Q_1\) に到達していることは明らかであるため合意に到達したと見なすことができる。したがって、定足数を確保するために必要な応答数は式 (\(\ref{quorum2}\)) のように表される。\[ \begin{equation} Q_2 = 2f+1 \label{quorum2} \end{equation} \]
文献や実装によってはビザンチン応答を含む式 (\(\ref{quorum2}\)) を定足数と呼んでいることもあり、\(Q_1\) と \(Q_2\) はしばしば混乱を招いている。
 例1: 原則的な定足数
例1: 原則的な定足数
Fig 2 は \(f=2\) 構成を表している。7 個のプロセスに \(x=🍇\) を保存するように要求を出すが、そのうち 2 個は実際には値を保存していないにもかかわらず OK 応答を返している可能性がある。したがって、少なくとも定足数 \(Q_1=3\) 個の正常なプロセスで値が保存されていることを保証するには \(Q_2=2f+1=5\) の応答を待つ必要がある。
\(Q_2\) 個の応答を確認した直後に \(f=2\) 個の正常なプロセスが非ビザンチン故障したとしても、それがどのような組み合わせであっても少なくとも 1 プロセスは最新状態を持って機能していることから、システムはいくつかの手段で一貫性を保証する動作を行うことができる。
\(f+1\) 個の応答を確認しただけでは、実際には 1 個の正常なプロセスしか値を保存できていない可能性があり、次の瞬間にそのプロセスが非ビザンチン故障を起こすとシステムから最新の状態が喪失することになる。したがって成功応答が \(f+1\) 個では障害耐性のある合意に達したとは言えない。
 例2: 照会系での定足数の緩和
例2: 照会系での定足数の緩和
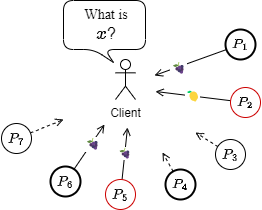
同じリクエストに対してすべての正常なプロセスは同じ応答をするという分散合意の特性を利用して、正常なプロセスの状態を変更しないような照会系 (冪等/idempotent) の処理で定足数を緩和することができる。すなはち、同じ応答 \(x\) が \(Q_1=f+1\) 個集まればそのうち少なくとも 1 個は正常なプロセスの応答であるため、正常なプロセスの応答は \(x\) であると判断できる。
Fig 3 はその例を示している。クライアントは \(x\) の値を問い合わせ、🍇という応答が \(f+1=3\) 個そろった時点で (たとえそれにビザンチン応答が含まれていたとしても) 正常なプロセスの応答は \(x=🍇\) であることを保証することができる。
もちろん「ビザンチンプロセスの応答は合意の判断には使わない」という原理原則に従うのであれば \(Q_2\) 個の応答を待っても良い。
 例3: BFT 仮定下で安全な部分集合
例3: BFT 仮定下で安全な部分集合
BFT 仮定下の \(n=3f+1\) 個のプロセス集合 \(S\) から部分集合 \(S'\) を作成することを考える。このとき、\(S'\) に含まれなかったプロセスは、\(S\) において非ビザンチン故障を起こし応答できなくなったプロセスと等価と考えることができる。非ビザンチン故障は \(f\) 個まで許容できることから、\(S'\) のプロセス数が \(n' \ge 2f+1\) であれば \(S'\) での合意が安全であることを保証できるし、\(Q_2\) 個の応答を確保できれば合意に到達することも可能である (許容可能な非ビザンチン故障数 \(f\) を消費してしまっているので可用性は低下していることに注意)。
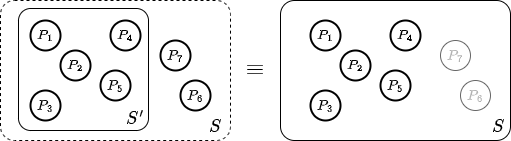
BFT プロトコルは一般に通信複雑性が高く、pBFT のように \(O(n^3)\) でメッセージ交換を行うプロトコルでは合意に参加するプロセスは少ないほうが良い。部分集合化による可用性の低下は、最初 \(n'_1=2f+1\) の部分集合から開始し、合意に失敗するたびに \(n'_2=n'_1+1\), \(n'_3=n'_2+1\), ... のように部分集合を大きくしてゆくアイディアで緩和することができるだろう。
例 1 の考えは「集まった応答数が \(Q_2\) に到達すれば合意が可能」だったが、これは「\(n\) 個の中から \(Q_2\) 個のプロセスを任意に選択したとしても、そのすべての応答が得られれば合意が可能」という示唆である。
 BFT 仮定が破られた時の挙動
BFT 仮定が破られた時の挙動
Fig 5 は、ビザンチン故障と非ビザンチン故障が混在する状況において、正しい合意が可能か (Acceptable)、棄却で合意するか (Rejected)、またはビザンチン勢力による合意の乗っ取りが可能か (Collapse) を、定足数の確保に必要な応答数 \(Q_1\) と \(Q_2\) のケースそれぞれで示している。
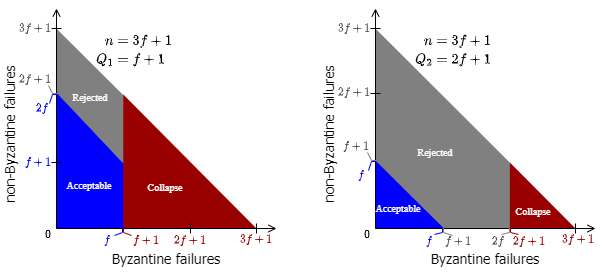
一般的な \(Q_2=2f+1\) の設定では、BFT 仮定が崩れてビザンチン故障プロセスが \(f\) 個を超えたとしてもただちに合意の乗っ取りが可能になるわけではなく、\(2f\) 個までなら合意が失敗 (棄却で合意) するだけである。つまり、BFT 仮定の下ではビザンチン故障プロセスが \(f\) を超えると Liveness が欠落し、\(2f\) を超えると Safety が欠落する。
 制約
制約
BFT 仮定で \(f\) を定めるには合意に参加するプロセス数 \(n\) が確定していなければならない。つまり Pure P2P ネットワークのように、ある時点での参加ノードが不確定なネットワークでは BFT を適用することができない。
また合意時点の全プロセス数 \(n\) が確定したとしても、本当に悪意的なプロセスは検出されないように紛れ込もうとするし、方針の相違や利益相反で特定の時点から離反し始めることもある。このため強制力がなく相利共生の合意が取れていない自由参加型のネットワークでは \(f\) を定めることが現実的に不可能である (相手側から見ればこちらが悪意的な振る舞いかもしれないし、それは単に解釈や方針の違いかもしれない)。
この記事では以下のように状況を整理する。
 ビザンチン故障の最大数を完全に制御できる状況
ビザンチン故障の最大数を完全に制御できる状況
システム設計で \(f\) を定められる状況では BFT は安全性を保障できる。つまり safety はシステム的に担保され、非ビザンチン故障が \(f\) プロセス以下という条件付きで liveness も担保される。古典的な BFT はおおむねこの前提で論議されている。
- \(f+1\) 個のノードをプライベートネットワークに設置し、残りの \(2f\) 個のノードを DMZ に設定することで、DMZ 側のすべてのノードが侵入され乗っ取られたとしても全体の合意を乗っ取られることはない。REST API などを用いて外部ネットワークからのアクセスを可能にするために一部のノードを DMZ に設置したい場合など。
- \(2f+1\) 個のノードを自社で用意し、残りの \(f\) 個のノードは他社やオープンなネットワークから公募すれば、外部のノードすべてが結託しても自社の合意を乗っ取られることがない。合意結果を遅延ゼロで即時配信する目的で外部のノードを合意に参加させたい場合など。
- 分散合意に関わるソフトウェアをアップデート、構成変更、または別のソフトウェアに置き換えようとしている。新バージョンのソフトウェアがどのような挙動をとっても、\(f\) 個の非ビザンチン故障を許容しながら間違った合意に達せずサービスを継続することを保証するために、\(2f+1\) 個のノードを現バージョンのままとし、\(f\) 個のノードを新バージョンで置き換えて様子を見る。
- 外部監査や実行統計を計測する目的で、ソフトウェアや構成の異なるノードを合意に常設することを考えたとき、そのノード数が \(f\) 個までであれば、それらがどのような動作をしたとしても全体の合意に影響することはない。
このような状況であればビザンチン故障プロセスが \(f\) を超えない (safety, liveness を維持) または \(2f\) 個を超えない (liveness は喪失しても safety は維持) というシステム制約も可能である。
 ビザンチン故障の最大数を完全には制御できない状況
ビザンチン故障の最大数を完全には制御できない状況
システム設計で \(f\) を定められない状況では、\(f\) は「合意が達成可能な上限数」という前提にとどまり、それを超えると合意に失敗したりビザンチン合意がなされる可能性がある。つまり safety も liveness も条件付きでしか保証されない (加えてその条件は社会的協調やゲーム理論といった不確かな判断に基づく可能性がある)。これは safety を保証できない不完全な分散合意となることから別にビザンチン合意のリスクを許容または排除できる制度やシステム設計が必要である。P2P ネットワークやブロックチェーンの文脈で BFT が適用されるケースはこの状況を想定していることがある。
- 協定を結んでいるいくつかの組織で合意を行う。一組織あたりで提供するノード数が \(f\) を超えないようにすることで、一つの組織が不正な判断をしても全体の合意には影響がないようにする。
- P2P ネットワークから無作為に選ばれたノードで合意を行う。このネットワークを構成するノードの 2/3 以上は自社が管理していることから、選択に含まれるビザンチン故障ノード数の期待値は \(f\) 程度である。
ビザンチン故障プロセスが \(f\) を超える可能性がある状況では、当然ながらビザンチン故障プロセスが \(2f+1\) 個以上になれば safety を維持することができない。
 合意に参加するプロセス数が確定できない状況
合意に参加するプロセス数が確定できない状況
合意に参加するノード数 \(n\) もビザンチン故障プロセス数 \(f\) も定めることができないため、BFT 仮定に基づく合意を適用できない。
- Pure P2P ネットワークのように、ある時点での参加ノード数が不確定な状況では BFT 仮定に基づく合意は不可能である。
- 自律走行型の自動車が周囲の自動車と合意して (赤信号や濃霧、落下物の検知などで) 全体の流れを停止したり発車しようとしたとき、"周囲" に含まれる範囲が車によって異なるため合意に参加する自動車を確定することはできない。
このような状況では、何か確定性のある定量値に基づいてネットワークから委員会や動的クォーラムといった集合を選出する必要がある。
 例
例
いくつかの例を考えてみよう。正常なプロセスが 🍎 を提案しビザンチン故障プロセスが 🍇 を提案すると仮定する (二価; bivalent)。このとき、全体のコンセンサスは 🍎 で合意するか、または合意に到達できず却下するか (却下に合意するか) のどちらかの状態となる必要がある。
- \(n=7\), \(f=2\) 構成においてビザンチン障害が 2 プロセスあり、正常な 5 プロセスのうち 2 プロセスが応答できなかった。このとき提案は (🍎×3, 🍇×2) となり \(f+1=3\) 個集まった 🍎 で合意する。
- \(n=7\), \(f=2\) 構成においてビザンチン障害が 2 プロセスあり、正常な 5 プロセスのうち 3 プロセスが応答できなかった。このとき提案は (🍎×2, 🍇×2) となり、どちらも \(f+1=3\) 個を満たさないため却下で合意する。
- \(n=7\), \(f=2\) 構成において実際のビザンチン障害が 3 プロセスあり、正常な 4 プロセスのうち 2 プロセスが応答できなかった。このとき提案は (🍎×2, 🍇×3) となり \(f+1=3\) 個集まった 🍇 で合意する。
- \(n=7\), \(f=2\) 構成において実際のビザンチン障害が 3 プロセスあり、正常な 4 プロセス全てが正しく応答した。このとき、提案は最終的に (🍎×4, 🍇×3) となるが、通常はパフォーマンスを考慮して先に \(f+1\) を満たした方で合意する。つまり提案の到達タイミングによってプロセスごとに合意値が異なる可能性がある。
2. のケースでは、正常だが応答できないプロセス数が \(f\) を超えたとしても、式 (\(\ref{n3f1}\)) が満たされる限り、正常なプロセスは却下で合意する (🍇 で合意することはない)。また 3. および 4. のケースでは \(f\) を超えるビザンチン故障プロセスが含まれているため 🍇 で合意することが可能となる。
このように、ビザンチン耐性合意は BFT 仮定が崩れている状況では深刻な状態不整合を引き起こす可能性を潜在的に抱えている。いくつのビザンチンプロセスが入り込むかわからないネットワークでは、電子署名のような暗号技術を使用して合意内容が不正であることを第三者が検出できること (Safety の確保)、また大きなノード集合から合意ごとにランダムにメンバーを入れ替えるといった方法でビザンチン勢力が乗っ取りを継続的に維持できないこと (Liveness の確保) の追加の対策を必要とする。
 証明
証明
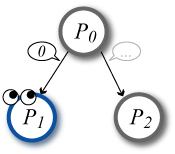
以下では説明を簡単にするために \(P_0\) を提案役とし \(P_1\) の視点で記述している。
定理1 : 故障プロセス数を \(f\) とすると、\(n=3\), \(f=1\) の場合にビザンチン合意問題を解くアルゴリズムは存在しない。
提案者 \(P_0\) と他の \(P_1, P_2\) という 3 つのプロセスにおいて、\(P_1\) は \(P_0, P_1\) のどちらか、あるいは両方に故障が発生しているか分からないと仮定する。
上記は \(P_2\) が沈黙するケースでも同じである。電子署名を使用して \(P_i \xrightarrow{x} P_j\) を改ざんできないようにすることは可能だが、故障プロセスによる沈黙のケースを防ぐことはできない。
\(n=3\) 構成において \(f=1\) の故障プロセスの存在により \(P_1\) は \(P_0\) と \(P_1\) のどちらにも従うことができず、例えば固定値のような値を採用することもできないことは明かだろう。
さらに、\(f=2\) のケースではビザンチンプロセスによる合意の乗っ取りが可能となる。
以上の説明を使用して \(n \gt 3\) のケースで同様の定理を導くことができる。
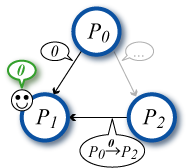
定理2 : \(n \le 3f\) の場合にビザンチン合意問題を解くアルゴリズムは存在しない。
\(n \le 3f\) を満たす任意の \((n, f)\) に対して \(n\) 個のプロセス \(P_0, P_1, \ldots, P_{n-1}\) を以下の 3 つの集合 \(\vector{P}'_0, \vector{P}'_1, \vector{P}'_2\) に分ける。\[ \left\{ \begin{array}{ccl} \vector{P}'_0 & = & \{P_0, P_3, \ldots\} \\ \vector{P}'_1 & = & \{P_1, P_4, \ldots\} \\ \vector{P}'_2 & = & \{P_2, P_5, \ldots\} \end{array} \right. \]
それぞれのプロセス集合は、自分以外のプロセス集合が合意した値に対して内包する \(|\vector{P}'_i| \le f\) 個のプロセスが合意した結果を以てそれぞれのプロセス集合がある値に合意するためには、いずれか一つの
それぞれのプロセス集合を \(n=3\), \(f=1\) として定理 1 とする。この仮定の下では \(n=3\), \(f=1\) の各プロセス \(P'_0, P'_1, P'_2\) は合意可能なアルゴリズム \(\mathcal{A}_{3,1}\) が存在する。それぞれのプロセスが \(\vector{V}_0, \vector{V}_1, \vector{V}_2\) のプロセス集合を生成して、それらの間でアルゴリズム \(\mathcal{A}_{}\) を実行する。
ここで \(|\vector{P}'_i| \le f\) である。合意可能なアルゴリズム \(\mathcal{A}_{n,f}\) が存在すると仮定する。 pBFT: Practical Byzantine Fault Tolerance
pBFT: Practical Byzantine Fault Tolerance
 シミュレーション
シミュレーション
BFT の代表的なプロトコルである pBFT のシミュレーション。Proposer プロセスの提案で全ての正常なプロセスが合意できるかを表している。\(n\) を全てのプロセス数、\(f\) を故障しているプロセス数とする。
| # | pre-prepare | prepare | commit |
|---|
参考リンク
- Leslie Lamport, Robert Shostak, Marshall Pease (1982) The Byzantine Generals Problem