論文翻訳: Impossibility of Distributed Consensus with One Faulty Process

Abstract

コンセンサスの問題にはプロセスの非同期システムが含まれており、そのいくつかは信頼性が欠落していることがある。課題は、信頼できるプロセスが 2 値の下で合意することである。本論文では、この課題に対するどのようなプロトコルであっても、たった 1 つでも不完全なプロセスが含まれるのなら終了に達しない可能性を持つことを示している。対照的に、同期のケースでは "Byzantine Generals" 問題として解決が知られている。

Table of Contents

1. Abstract
2. 1 Introduction
3. 2 Consensus Protocols
4. 3 Main Result
5. 4 Initially Dead Processes
6. 5 Conclusion
7. 参考文献

1 Introduction

リモートプロセス間で合意に達するという課題は分散コンピューティングにおける最も基本的な問題の一つであり、分散データ処理、分散ファイル管理、および障害耐性のある分散アプリケーションに対する数多くのアルゴリズムの中核である。

この問題のよく知られた形式は分散データベースシステムで発生する ”transaction commit problem" である [6,13,15-17,21-241] ([151] で引用されている G.LeLann の私信も参照)。問題は、特定のトランザクションの処理に関与しているすべてのデータマネージャプロセスが、トランザクションの結果をデータベースに反映させるか、それらを破棄するかについて合意することである。例えば何らかの理由で一部のデータベースマネージャが必要なトランザクション処理を実行できなかった場合、破棄のアクションが必要となることがある。どのような決定が下されても、データベースの一貫性を保つためにすべてのデータベースマネージャは同じ決定をしなければならない。

参加しているプロセスとネットワークが完全に信頼できるものであれば "commit" 問題に必要なタイプの合意に達することは簡潔明瞭である。しかし、実際のシステムではプロセスのクラッシュ、ネットワーク分断、メッセージの紛失・改変・重複など様々な障害が発生する可能性がある。不完全なプロセスが完全に発狂してしまう可能性や、さらには悪意を持った計画に従ってメッセージを送信する可能性もあるビザンチン型 [5,7,11,14,18,191] の障害を考慮することもできる。したがって、そのような障害が発生した場合でも可能な限り信頼性の高い合意プロトコルが望まれている。もちろん、どのようなプロトコルでも頻繁すぎるまたは重大すぎる障害に屈する可能性があるため、希望の最良解は"期待する" 障害の規定数に耐えられるプロトコルである。

我々は本稿において、完全な非同期コンセンサスプロトコルは単一のプロセス死も許容できないという驚くべき結果を示す。我々はビザンチン障害を考慮せず、またメッセージシステムが信頼できると仮定する -- 正しく正確に 1 度だけ (exactly once) メッセージを配信する。これらの仮定を置いたにもかかわらず、折の悪いタイミングで一つのプロセスが停止すると、どのような分散コミットプロトコルでも合意に達することができなくなる可能性がある。したがって、この重要な問題には、コンピューティング環境におけるさらなる仮定や許容される障害の種類に大きな制限がないかぎり堅牢な解決策はない!

我々の証明において重要なことは処理が完全に非同期であることである; つまり、プロセス間の相対速度やメッセージ配信の遅延時間については想定を置いていない。また、プロセスは同期クロックにアクセスできないと想定しているため、例えばタイムアウトに基づくアルゴリズムは使用することはできない。(特に [6] の解決策は適用できない。) 最終的に、我々はプロセスの死を検出する能力を仮定していないため、あるプロセスが別のプロセスを死んだ (完全に停止した) のか、それとも非常にゆっくり動いているのかを知ることは不可能である。

我々の不可能性の結果は非常に弱い形のコンセンサス問題でさえも当てはまる。すべてのプロセスが初期値 {0, 1} で開始すると仮定する。非障害プロセスは適切な決定状態に入ることによって {0, 1} 値を決定する。決定を下すすべての非障害プロセスは同じ値を選択しなければならない。不可能性証明の目的のために、我々はあるプロセスが eventually に決定を下すことだけを必要とする。(もちろん、興味のあるどのようなアルゴリズムもすべての非障害プロセスが決定を下す必要があるだろう。) 例えば 0 が常に選択されるという些細な解決策は、0 と 1 の両方を取りうる決定値であると規定する事によって除外されるが、おそらく初期構成は異なる。

我々のシステムモデルは不可能性証明を限りなく適用可能にするためかなり強力である。プロセスはメッセージの意味によって通信するオートマタ (おそらく無限に多くの状態を持つ) としてモデル化される。一つのアトミックなステップにおいて、プロセスはメッセージの受信を試み、メッセージが配信されたかどうか (そして配信された場合はどのメッセージか) に基づいてローカルの計算処理を実行し、他のプロセスに対して任意だが有限のメッセージセットを送信することができる。特に "atomic broadcast" 機能が想定されているため、もし任意の非故障プロセスがメッセージを受信したならば、すべての非故障プロセスが受信しているという前提の上で、プロセスは他のすべてのプロセスに対して 1 ステップで同じメッセージを送信することができる。宛先のプロセスが無制限に受信を試行する限りすべてのメッセージは最終的 (eventually) に配信されるが、メッセージは任意の長さで遅延し順序どおりに配信されない可能性がある。

現在使用されている非同期コミットプロトコルはすべて "window of vulnerability" (脆弱性の窓) -- つまり単一プロセスの遅延やアクセス不能によってアルゴリズム全体が無期限待機を引き起こす可能性があるようなアルゴリズム実行中の時間枠が存在するように見受けられる。我々の不可能性結果は、すべてのコミットプロトコルがそのような "window" を持ち、民間伝承的に広く信じられている確証を裏付けるものである。

2 Consensus Protocols

コンセンサスプロトコル \(P\) は \(N\) 個のプロセスの非同期システムである (\(N \ge 2\))。各プロセス \(p\) は \(\{b,0,1\}\) の値をとる 1 ビットの入力レジスタ \(x_p\) と出力レジスタ \(y_p\)、そして容量制限のない内部記憶領域を持つ。入力/出力レジスタ内の値はプログラムカウンタや内部記憶装置とともに内部状態を構成する。初期状態は入力レジスタを除く全ての固定開始値を規定する; 特に出力レジスタは値 \(b\) で開始する。出力レジスタが \(0\) または \(1\) の値をとる状態は決定状態として認識される。\(p\) は遷移関数に従って決定論的に作用する。プロセスが一度決定状態に至ると遷移関数は出力レジスタの値を変更することができない; つまり出力レジスタは "write-once" である。システム \(P\) 全体はそれぞれのプロセスに関連する遷移関数と入力レジスタの初期値によって特定される。

プロセスは互いにメッセージを送信して通信する。メッセージは \((p,m)\) のペアで、\(p\) は宛先プロセスの名前、\(m\) は固定領域 \(M\) からの "message value" である。メッセージシステムは、メッセージバッファと呼ばれる、送信されたがまだ配信されていないメッセージのマルチセットを管理している。これは2つの抽象操作をサポートする:

したがって、メッセージシステムは \({\rm receive}(p)\) が無制限に実行されたときにメッセージバッファ内のすべてのメッセージ \((p,m)\) が最終的に配信されるという条件のみを前提として非決定論的に動作する。特に、メッセージシステムはたとえメッセージ \((p,m)\) がバッファ内に存在していたとしても、\({\rm receive}(p)\) の応答に有限の回数 \(\emptyset\) を返すことが許されている。

システム構成はメッセージバッファの内容と共に各プロセスの内部状態で構成されている。初期構成は各プロセスが初期状態で開始しメッセージバッファがからの構成である。

ステップはある構成を別の構成にし、単一のプロセス \(p\) によるプリミティブなステップからなる。\(C\) を構成とする。ステップは 2 段階で起きる。まず \(m \in M \cup \{\emptyset\}\) 値を得るために \({\rm receive}(p)\) が \(C\) のメッセージバッファで実行される。次に \(C\) における \(p\) の内部状態と \(m\) に応じて、\(p\) は新しい内部状態に突入し、他のプロセスに有限のメッセージセットを送信する。プロセスは決定論的であるためステップは \(e = (p,m)\) ペアによって完全に決定される。これを事象 (event) と呼ぶ。(この "event" は \(p\) による \(m\) の受理として考えられるべきである。) \(e(C)\) は結果として得られる構成を表し \(e\) は \(C\) に適用できると表現する。事象 \((p,\emptyset)\) は常に \(C\) に適用できるため、プロセスは常に別のステップとなる事ができる点に注意。

\(C\) からのスケジュールは、\(C\) から開始し順番に適用できる事象の有限または無限シーケンス \(\sigma\) である。関連付けられた一連のステップは実行 (run) と呼ばれる。もし \(\sigma\) が有限であれば \(\sigma(C)\) は結果の構成を表すとする。これを \(C\) から到達可能であるという。ある初期設定から到達可能な構成はアクセス可能と言う。以下では、言及されたすべての構成はアクセス可能であると仮定する。

以下の補題はスケジュールの "commutativity" (可換性) 特性を表している。

補題 1 . ある構成 \(C\) から、スケジュール \(\sigma_1\), \(\sigma_2\) がそれぞれ構成 \(C_1\), \(C_2\) に至ると仮定する。\(\sigma_1\) および \(\sigma_2\) のそれぞれのステップをとるプロセスのセットが互いに素である場合、\(\sigma_2\) を \(C_1\) に適用することができ、\(\sigma_1\) を \(C_2\) に適用することができ、両方とも同じ構成 \(C_3\) をもたらすことができる ( Figure 1 参照)

証明. \(\sigma_1\) と \(\sigma_2\) は相互作用しないため結果はシステム定義から直ちに得られる。□

あるプロセス \(p\) が \(y_p = \nu\) の決定状態にある場合、構成 \(C\) は決定値 (decision value) \(\nu\) を持つ。コンセンサスプロトコルは 2 つの条件を満たす場合に部分的に正しい (partially correct)。

1. アクセス可能な構成が複数の決定値を持たない。
2. 各 \(\nu \in \{0,1\}\) に対してあるアクセス可能な構成は決定値 \(\nu\) を持つ。

プロセス \(p\) は無限に多くのステップを取るという条件で実行において非故障 (nonfaulty) であり、そうでなければ故障 (faulty) である。多くとも 1 のプロセスが故障していて、非故障プロセスに送信されたすべてのメッセージが最終的に受信されるという条件で実行は許容できる (admissible)。

ある実行がその実行で決定状態に達するという条件で、実行は決定的 (deciding) 実行である。コンセンサスプロトコル \(P\) は、それが部分的に正しい場合 1 故障にもかかわらず完全に正しい (totally correct in spite of one fault) ものであり、すべての許可された実行は決定的実行である。我々の主な定理はコンセンサス問題に対する部分的に正しいプロトコルそれぞれが決定的な実行ではないある許容できる実行を持っていることを示している。

3 Main Result

定理 1 . たった一つの故障だったとしても完全に正しいコンセンサスプロトコルは存在しない。
THEOREM 1. No consensus protocol is totally correct in spite of one fault.

証明. 逆に \(P\) を一つの故障を持つにもかかわらず完全に正しい合意プロトコルであると仮定する。我々は最終的に矛盾につながる一連の補題を証明する。

基本的な考えはプロトコルが永遠に決定的ではない状況を示すことである。これには 2 つのステップがある。まず決定がまだ事前に決定されていないある初期構成が存在していることを論議する。次に、システムを特定の決定にコミットするようなステップを取ることを回避する容認可能な実行を構成する。

\(C\) を構成とし \(V\) を \(C\) から到達可能な構成の決定値集合とする。\(C\) は \(|V| = 2\) のときに2価 (bivalent) である。\(C\) は \(|V|=1\) のときに1価 (univalent) であり、対応する決定値に従って 0価 (0-valent) または1価 (1-valent) とする。\(P\) の全体的な正しさ、および常に許容可能な実行が存在するという事実によって、\(V \neq \emptyset\) である。□

補題 2 . \(P\) は 2 価の初期構成を持つ。

証明. そうではないと仮定する。この場合、\(P\) は仮定された部分的正当性により 0 価と 1 価の両方の初期構成を持たなければならない。単一のプロセス \(p\) の初期値 \(x\) だけが異なる場合、2つの初期構成を隣接している (adjacent) と呼ぶ。任意の2つの初期構成はそれぞれ次に隣接している初期構成のチェーンによって連結されている。したがって 1 価の初期構成 \(C_1\) に隣接した 0 価の初期構成 \(C_0\) が存在しなければならない。初期値が異なるプロセスを \(p\) とする。

ここで、プロセス \(p\) がステップを取らない \(C_0\) に対してある許可された決定的実行を考慮し、\(\sigma\) を関連付けられたスケジュールとする。そして \(\sigma\) は \(C\) にも適用することができ、2 つの実行における対応する構成はプロセス \(p\) の内部状態を除いて同一である。両方の実行が最終的に同じ決定地に到達することは容易に分かる。値が 1 の場合、\(C_0\) は 2 価; そうでなければ \(C_1\) は 2 価である。いずれの場合も 2 価の初期構成が存在しないと仮定したことと矛盾する。□

補題 3 . \(C\) を \(P\) の 2 価構成とし、\(e = (p,m)\) を \(C\) に適用できる事象とする。\(e\) を適用せずに \(C\) から到達することのできる構成の集合を \(\mathcal{C}\) とし、\(\mathcal{D} = e(\mathcal{C}) = \{e(E) | E \in \mathcal{C}\) and \(e\) is ablicable to \(E\}\) とする。このとき \(\mathcal{D}\) は 2 価の構成を含む。

証明. \(e\) は \(C\) に適用可能であることから、\(\mathcal{C}\) の定義とメッセージを任意に遅延させられることができるという事実から、\(e\) は各 \(E \in \mathcal{C}\) に適用可能である。

ここで \(\mathcal{D}\) が 2 価の構成を含まず、したがってすべての構成 \(D \in \mathcal{D}\) が 1 価であると仮定する。我々は矛盾を導く。

\(E_i\) を \(C, i=0, 1\) から到達可能な \(i\) 価構成とする。(\(E\) は \(C\) が 2 価であるため存在する。) もし \(E_i \in \mathcal{C}\) であれば \(F_i=e(E_i) \in \mathcal{D}\) であり、そうでなければ \(E_i\) に到達する際に \(e\) が適用されたため \(E_i\) が到達可能な \(F_i \in \mathcal{C}\) が存在する。いずれの場合も \(F_i\) は 2 価ではない (\(F_i \in \mathcal{D}\) で \(\mathcal{D}\) 2 価の構成を含まないため) ため \(F_i\) は \(i\) 価であり、\(E_i\) と \(F_i\) の一方は他方から到達可能である。\(F_i \in \mathcal{D}\), \(i=0,1\) より \(\mathcal{D}\) は 0 価と 1 価の構成両方を含む。

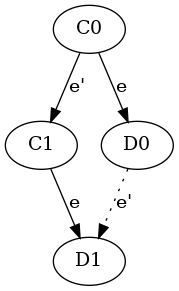
単一のステップで一方が他方から発生した場合、2つの構成は近傍 (neighbors) と呼ぶ。簡単な機能法により \(D_i=e(C_i)\) が \(i\) 価, \(i=0,1\) であるような近傍 \(C_0, C_1 \in \mathcal{C}\) が存在する。一般性を失うことなく \(C_1=e'(C_0)\), \(e'=(p',m')\) である。

ケース1. \(p' \neq p\) の場合、補題 1 により \(D_1 = e'(D_0)\) である。0 価構成のどのような後続も 0 家であるため不可能である。(Figure 2 参照)

ケース2. \(p' = p\) の場合、\(p\) がステップを取らない \(C_0\) からあらゆる有限の決定実行を考慮することができる。

対応するスケジュールを \(\sigma\) とし \(A = \sigma(C_0)\) とする。補題 1 から \(\sigma\) は \(D_i\) に適用可能であり、これは \(i\) 価の構成 \(E_i = \sigma(D_i)\), \(i=0,1\) を導く。補題 1 より \(e(A) = E_0\), \(e(e'(A))=E_1\) である。(Figure 3 参照) したがって \(A\) は 2 価である。しかし、\(A\) の実行が (前提によって) 決定しているためこれは不可能であり、\(A\) は 1 価でなければならない。

いずれの場合も矛盾に達するため \(\mathcal{D}\) には 2 価の構成が含まれている。□

どのような実行構成も2価の初期構成から1価の構成へと進むため、2価から1価へ進むある単一のステップが存在しなければならない。このようなステップは最終的に決定値を決定する。ここで我々は、そのようなステップを回避してシステムを実行することが常に可能であり、許可できる非決定実行につながることを示す。

実行は初期構成から始まり段階的に構築される。我々は実行が次の方法で許容されることを保証する。プロセスのキューは最初は任意の順序で維持され、構成内のメッセージバッファはメッセージが送信された時間に従い最も早いメッセージが先頭に来るように順序付けられる。各ステージは1つ以上のステップで構成される。プロセスキューの最初のプロセスが、ステージの開始時にそのメッセージキューが空でなかった場合にその最も早いメッセージを受信する、というステップを取ることでステージは終了する。その後このプロセスはプロセスキューの最後に移動される。このようなステージの無限のシーケンスでは、すべてのプロセスは無限に多いステップを取り、それに送られたすべてのメッセージを受信する。したがって実行は許容可能である。もちろん我々の問題は到達される決定を避けるような方法でこれを行うことである。

\(C_0\) を 2 価の初期構成としその存在は補題 2 によって保証された。実行は \(C_0\) から始まり、すべてのステージが 2 価の構成から開始することを確認する。ここで構成 \(C\) が 2 価で、プロセス \(p\) がプライオリティキューの先頭にあるとする。もしあるなら \(C\) のメッセージバッファ内の \(p\) への最初のメッセージを \(m\) とし、なければ \(\emptyset\) とする。\(e=(p,m)\) とする。補題 3 により \(e\) が最後に適用される事象であるスケジュールによって \(C\) から到達可能な 2 価の構成 \(C'\) が存在する。ステップの対応するシーケンスはステージを定義する。

各ステージは 2 価の構成で終了するため、無限スケジュールの構成における各ステージは成功する。結果の実行は許容され、どのような決定にも到達しない。したがって \(P\) は完全に正しくない。□

4 Initially Dead Processes

この章では過半数の非故障プロセスがプロトコルの実行中に停止しない状況において、\(N\) 個のプロセスに対するコンセンサス問題を解決するプロトコルを紹介する。しかしながら、どのプロセスが最初に死んでいて、どのプロセスが死んでいないかを事前に知ることはできない。

プロトコルは 2 段階で機能する。第 1 段階の間、プロセスは各プロセスに対応するノードを持つ有向グラフ \(G\) を構築する。各プロセスは自分のプロセス番号を含むメッセージをブロードキャストしてから、他の \(L-1\) プロセスからのメッセージを待機する。ここで \(L = \lceil (N+1)/2 \rceil\) である。\(i\) から \(j\) へメッセージを受信した場合、\(G\) は \(i \to j\) の辺を持つ。

第 2 段階では、各プロセスがこの段階の完了時に、それぞれのプロセス \(k\) が、そのような全ての \(j\) の初期値と共に \(G^+\) 内の \(k\) に入社する全ての辺 \((j,k)\) を知っているという意味で \(G^+\) (\(G\) の推移閉包) を構築する。

この段階を実行するために、各プロセスは他の全てのプロセスに対してそのプロセス番号と初期値を、第1段階で得た \(L-1\) プロセスの名前と共にブロードキャストする。そしてそれらが知っている \(G\) 内の各祖先から第2段階のメッセージを受信するまで待機する。初期状態では、第一段階の間に直接得た \(L-1\) プロセスについてのみ知っているが、第二段階で受け取ったメッセージから追加の祖先について学習する。

この時点で、各プロセスは自分自身の祖先と \(G\) の端を全て知っている。この情報を使用して、それぞれの祖先に入射する \(G^+\) のすべての辺を計算する。そして、どの祖先が \(G^+\) の初期 (initial) クリーク、つまり入力辺のないクリークに属しているかを判断する。これを行うために、ノード \(k\) 自身が \(k\) の祖先である全てのノード \(j\) の祖先であるならばノード \(k\) が初期クリーク内にある、という事実を利用する。\(G^+\) の各ノードは少なくとも \(L-1\) の先行ノードがあるため、初期クリークは一つだけ存在しうる; それは少なくとも \(L\) の濃度 (cardinality) を持ち、第二段階を完了する全てのプロセスは、其れを構成する一連のプロセスを正確に認識している。

最後に、各プロセスは任意の合意されたルールを用いて初期クリークにおけるプロセスの初期値に基づいて決定を行う。全てのプロセスは初期クリークの全てのメンバーの初期値を認識しているため、それらは全て同じ決定に到達する。

このプロトコルの正しさは次の定理を証明する。

定理2 . その実行中にどのプロセスも死ぬことがなく、厳密に過半数のプロセスが初期状態で生きているという条件が与えられたとき、全ての非故障プロセスが常に決定に達するという部分的に正しい合意プロトコルが存在する。
THEOREM 2. There is a partially correct consensus protocol in which all nonfaulty processes always reach a decision, provided no processes die during its execution and a strict majority of the processes are alive initially.

5 Conclusion

フォールトトレラント協調コンピューティングの自然で重要な問題は、完全に非同期の計算モデルでは解決できないことを示した。これらの結果は、そのような問題が実際に "解決" できないことを示すものではない; むしろこれらは、現実的なプロセッサと通信タイミングの過程をよりよく反映した分散コンピューティングのより洗練されたモデルと、そのような問題のためのそれほど厳しくない要件の必要を指摘している。(例えば終了は確率1のみで必要とされるかも知れない。) これらの結果の最初の発表 [12] に続いて、進展はこれら [1-4, 9, 10, 20, 25] の両方のラインに沿って成された。

参考文献

1. MICHAEL J. FISCHER, NANCY A. LYNCH, MICHAEL S. PATERSON (1985) Impossibility of Distributed Consensus with One Faulty Process
2. A Brief Tour of FLP Impossibility