論文翻訳: Multiversion Concurrency Control - Theory and Algorithms
PHILIP A. BERNSTEIN and NATHAN GOODMAN
Harvard University
 Abstract
Abstract
並行性制御とは、共有データベース上で並行実行されているプログラムが発行する複数の操作を同期する処理である。並行性制御の目的は、逐次処理 (非インターリーブ) と同じ効果を持つ実行を保証することである。マルチバージョンデータベースシステムでは、データ項目への各書き込み操作ごとに、そのデータ項目の新しいコピー (またはバージョン) を生成する。本論文では、マルチバージョンデータベースシステムにおける並行性制御アルゴリズムの正当性を分析するための理論体系を提案する。我々はこの理論を用いて、いくつかの新しいアルゴリズムと従来から公開されているアルゴリズムを詳細に分析する。
Table of Contents
- Abstract
- 1. 導入
- 2. 基本直列化可能性理論
- 3. マルチバージョン直列可能性理論
- 4. マルチバージョン・タイムスタンプ方式
- 5. マルチバージョン・ロック機構
- 6. マルチバージョン混合方式
- 7. 結論
- REFERENCES
- 翻訳抄
 1. 導入
1. 導入
データベースシステム (database system, DBS) は、データベース内のデータ項目に対する読み取り操作と書き込み操作を実行するプロセスである。トランザクション (transaction) は、DBS に対して読み取りと書き込みを発行するプログラムを指す。複数のトランザクションが並行実行されると、DBS によりそれらの読み取りと書き込みがインターリーブで実行されることによって望ましくない結果を生じる可能性がある。並行性制御 (concurrency control) はこのような望ましくない結果を回避するための処理機構である。具体的には、並行性制御の目的は、直列的 (非インターリーブ) 実行と同じ結果が得られる実行を保証することである。このような実行形態を直列化可能 (serializable) と呼ぶ。
DBS は、読み取りと書き込みが実行される順序を制御することで直列化可能な実行を達成する。DBS に操作が投入されると、DBS はその操作を即座に実行するか、あるいは後で処理するために遅延させるか、または操作自体を拒否することができる。操作が拒否された場合、その操作を発行したトランザクションはアボート (abort) される。これはすなわち、該当トランザクションによるすべての書き込みが取り消され、それらの書き込みによって生成された値を読み取った他のトランザクションもアボートされることを意味する。
操作を拒否される主な理由は、その操作が "遅すぎた" ことである。たとえば、通常の読み取り操作は、本来読み取るべきだった値がすでに上書きされている場合に拒否される。このような拒否は各データ項目の古いコピーを保持することで回避できる。そうすれば、遅れた読み取り操作には、たとえ "上書き" されたとしても、そのデータ項目の古い値を提供することができる。
マルチバージョン (multiversion) DBS では、データ項目 \(x\) への各書き込みは \(x\) の新しいコピー (またはバージョン (version)) を生成する。\(x\) への各読み取りに対して、DBSは \(x\) の複数のバージョンのうち 1 つを選択して読み取る。書き込みは互いに上書きすることはなく、また読み取りは任意のバージョンを読み取り可能であるため、DBS は読み取りと書き込みの順序をより柔軟に制御できる。マルチバージョン特性を活用するいくつかの興味深い並行性制御アルゴリズムが提案されている [1, 2, 6, 7, 17, 19, 20, 21]。この問題に関する理論的研究には [15] と [21] が挙げられる。
この論文は、マルチバージョン DBS のための並行性制御アルゴリズムの正当性を解析するための理論体系を提案する。我々はいくつかの新しいマルチバージョンアルゴリズムを提示し、この理論を用いて新しいアルゴリズムと以前に公開されたいくつかのアルゴリズムを解析する。
セクション 2 では、非マルチバージョンデータベースにおける並行性制御理論を概説する。セクション 3 では、この理論をマルチバージョンデータベースに拡張する。セクション 4 からセクション 6 では、この理論を用いてマルチバージョン並行性制御アルゴリズムを解析する。
 2. 基本直列化可能性理論
2. 基本直列化可能性理論
データベースの並行性制御アルゴリズムを分析するための標準的な理論は直列化可能性理論 (serializability theory) が知られている [4, 5, 8, 14, 16, 21]。直列化可能性理論は特定の実行が正当であるための厳密な条件を定義し、並行性制御アルゴリズムが許容する実行順序を分析するための手法である。このため並行性制御アルゴリズムはそのすべての実行結果が正しい場合に正しいと判定される。
このセクションではマルチバージョンを用いない場合の直列化可能性理論について概説する。
 2.1 システムモデル
2.1 システムモデル
我々は DBS が分散されていると仮定し、Lamport による分散実行モデル [13] を採用する。このモデルでは、システムはメッセージの送受信によって相互に通信するプロセスの集合で構成される。このモデルは実行順序を happens-before 関係の観点で記述する。happens-before 関係におけるイベント (event) とは、プロセスによる操作の実行、メッセージの送信、またはメッセージの受信のいずれかである:
単一プロセス内の happens-before 関係はそのプロセス内のイベント間の任意の半順序関係として定義される。システム全体での happens-before 関係 (\(\lt\) と表記) とは、(1) \(e\) と \(f\) がプロセス \(P\) 内のイベントであり、\(P\) において \(e\) が \(f\) より前に起きている場合に \(e\lt f\) であり、(2) \(e\) が "プロセス \(P\) がメッセージ \(M\) を送信する" イベントで \(f\) が "プロセス \(Q\) がメッセージ \(M\) を受信する" イベントである場合に \(e\lt f\) である、という条件を満たすシステム内の全イベントに対する最小の半順序関係である。条件 (1) は \(\lt\) が各プロセス内のイベント発生順序と一致していなければならないことを述べている。条件 (2) はメッセージが送信される前に受信されることがないことを規定している。そして \(\lt\) がこれらの条件を満たす最小の半順序であるため、条件 (2) は異なるプロセス間でイベントの順序を決定する唯一の方法である。
この論文ではより抽象的なレベルで議論を進める。以降、(セクション 6 で簡潔に触れるのを除いて) プロセスとメッセージについて明示的に言及することを避ける。具体的には、各トランザクションを 1 つのプロセスと見なし、各データ項目は別々のプロセスによって管理されていると仮定してもよい。(我々の結果はこれらの仮定に依存しない。) これらの仮定の下では各データベース操作は 2 回のメッセージ交換を伴う。トランザクション \(T_i\) がデータ \(x\) を読み取るには、\(T_i\) は \(x\) を管理するプロセスにメッセージを送信しなければならない。また \(x\) の値を返すには、\(x\) を管理するプロセスから \(T_i\) にメッセージを送信しなければならない。書き込みも同様のメッセージパターンが必要であり、この場合の返信メッセージは単に書き込みが完了したことを確認するだけである。また、これらの仮定の下では、1 つのデータ項目に関連するいかなる決定やイベントの順序付けも局所的な処理であり、複数のデータ項目に関連する決定や順序付けは分散処理となる。我々が用いる抽象化により、メッセージ交換やそれに関連する問題を隠蔽することができ、より高い抽象レベルで並行性制御に関する議論を行うことが可能となる。
 2.2 ログ
2.2 ログ
直列化可能性理論は実行をログ (log) によってモデル化する。ログは、各トランザクションに代わって実行された読み取りおよび書き込み操作を識別し、それらの操作が実行された順序を示す。ログは Lamport の happens-before 関係の抽象化である。
トランザクションログ (transaction log) は単一のトランザクションの許容可能な実行を表す。形式的には、トランザクションログは半順序集合 (poset; partially ordered set) \(T_i=(\Sigma_i,\lt_i)\) として定義される。ここで \(\Sigma_i\) はトランザクション \(i\) (のある実行) によって発行された読み取りと書き込みの集合であり、\(\lt_i\) はそれらの操作が実行されるべき順序を示す。ここでトランザクションログを図式的に表現する。\[ T_1 = \begin{array}{c} r_1[x] \searrow \\ r_1[z] \nearrow \end{array} w_1[x] \] これは、\(T_1\) が \(x\) と \(z\) を並列に読み取り、その後 \(x\) に書き込むというトランザクションを表している。(おそらく書き込まれる値は読み取られた値に依存しているだろう。)
我々は、トランザクション \(T_i\) によって発行されたデータ項目 \(x\) に対する読み取り (書き込み) 操作を \(r_i[x]\) (\(w_i[x]\)) と表す。この表記法を明確にするために、どのトランザクションもデータ項目を複数回読み取ったり書き込んだりしないと仮定する。なお、この論文の結果はこの仮定に依存しない。
\(T=\{T_0,\ldots,T_n\}\) をトランザクションログの集合とする。\(T\) 上の DBS ログ (または単純にログ) は \(T_0,\ldots,T_n\) の実行を表す。形式的には、\(T\) 上のログは半順序集合 \(L=(\Sigma,\lt)\) であり、以下の条件を満たす:
\(\Sigma = \bigcup_{i=0}^n \Sigma_i\) である。
\(\lt \supseteq \bigcup_{i=0}^n \lt_i\) である。
すべての \(r_j[x]\) は少なくとも一つの先行する \(w_i[x]\) が存在する (\(i=j\) も可能)。ここで \(w_i[x]\) が \(r_j[x]\) に先行するとは、\(w_i[x] \lt r_i[x]\) と同義である。
競合する操作のすべての組み合わせは \(\lt\) 関係にある (2 つの操作が競合する (conflict) とは、それらが同じデータ項目に対して操作を行い、少なくとも一方が書き込み操作である場合を指す)。
条件 (1) は、DBS が \(T_0,\ldots,T_n\) によって投入されたすべての操作を実行し、それ以外の操作は一切実行しないことを示している。条件 (2) は、DBS が各トランザクションの規定したすべての操作順序を尊重することを述べている。条件 (3) は、あるトランザクションがその初期値を書き込むまで、いかなるトランザクションもそのデータ項目を読み取ることができないことを述べている。条件 (4) は、DBS が競合する操作を逐次的に実行することを述べている。例えば、\(T_i\) が \(x\) を読み、\(T_j\) が \(x\) を書き込む場合、\(r_i[x]\) happens before \(w_j[x]\) かその逆であり、それらの操作が同時に発生することはない。
以下のトランザクションログを考える: \[ T_0 = \begin{array}{c} w_0[x] \\ w_0[y] \\ w_0[z] \end{array}, \quad T_1 = \begin{array}{c} r_1[x] \searrow \\ r_1[z] \nearrow \end{array} w_1[x] \] \(\{T_0,T_1\}\) 上の可能なログのいくつかを以下に示す: \[ \begin{eqnarray} \begin{array}{clclc} w_0[x] & \to & r_1[x] & \searrow \\ w_0[y] & & \downarrow & & w_1[x] \\ w_0[z] & \to & r_1[z] & \nearrow \\ \end{array} \label{eq1} \\ \nonumber \\ \begin{array}{clclc} w_0[x] & \to & r_1[x] & \searrow \\ w_0[y] & & \uparrow & & w_1[x] \\ w_0[z] & \to & r_1[z] & \nearrow \\ \end{array} \label{eq2} \\ \nonumber \\ \begin{array}{clclc} w_0[x] & \to & r_1[x] & \searrow \\ w_0[y] & & & & w_1[x] \\ w_0[z] & \to & r_1[z] & \nearrow \\ \end{array} \label{eq3} \\ \end{eqnarray} \] 推移律によって暗示される順序は通常描かれないことに注意。例えば \(w_0[x] \lt w_1[x]\) という順序関係は \(w_0[x] \lt r_1[x] \lt w_1[x]\) から導かれるため図中には記載されていない。
DBS は、\(T_1\) が並列実行を許可している場合でも \({\rm read}(x)\) と \({\rm read}(z)\) を逐次的に処理することが許されることに注意 ((\(\ref{eq1}\)) と (\(\ref{eq2}\)) 参照)。ただし DBS は \(T_1\) によって規定されているいかなる操作順序も逆転したり削除することはできない。
与えられたトランザクションログ
に対し、以下は \(\{T_0,T_1,T_2,T_3,T_4\}\) に関するログである:
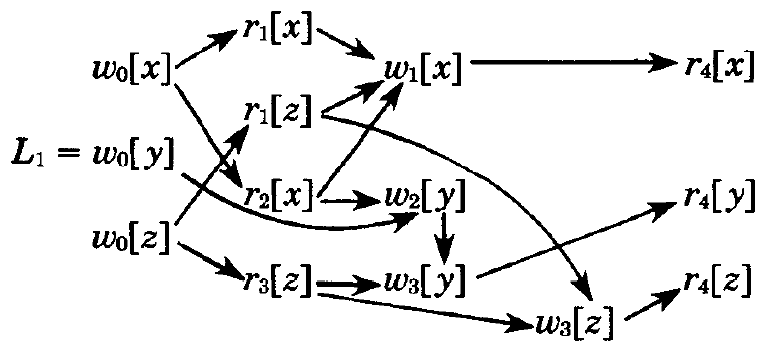
以下は同一のトランザクションに関する別のログである: \[ L_2 = w_0[x]\,w_0[y]\,w_0[z]\,r_2[x]\,w_2[y]\,r_1[x]\,r_1[z]\,w_1[x]\,r_3[z]\,w_3[y]\,w_3[z]\,r_4[x]\,r_4[y]\,r_4[z] \] 我々がログを列として記述する場合、例えば \(L_2\) のような表記では、そのログが全順序であることを意味する。つまり、各操作は次に続く操作とそれ以降のすべての操作に先行する。したがって \(L_2\) では \(w_0[x] \lt w_0[y] \lt w_0[z] \lt r_2[x] \ldots\) という関係が成立する。
 2.3 ログの等価性
2.3 ログの等価性
直観的には、2 つのログは各トランザクションが両方のログで同じ計算を実行する場合に等価である。我々はログの等価性をトランザクション間の情報フローの観点から形式化する。
\(L\) を \(\{T_0,\ldots,T_n\}\) 上のログとする。\(L\) において、(1) \(w_i[x]\) と \(r_j[x]\) が \(L\) 内の操作であり、(2) \(w_i[x] \lt r_j[x]\) であり、(3) これらの操作の間に他の \(w_k[x]\) が存在しない場合、トランザクション \(T_j\) は \(T_i\) から \(x\) を読み取る (\(T_j\) reads-\(x\)-from \(T_i\))。\(\{T_0,\ldots,T_n\}\) で示される 2 つのログは、reads-from 関係が同一である場合に等価 (equivalent) とみなされ \(\equiv\) で表記される。すなわち、すべての \(i,j\) および \(x\) について、片方のログにおいて \(T_j\) reads-\(x\)-from \(T_i\) の場合にのみもう一方のログでもその条件が成立する。この定義により、各トランザクションが両方のログでデータベースから同じ値を読み取ることを保証する。
前のセクションで述べたログ \(L_1\) と \(L_2\) を考える。これらのログは同じ read-from を持つ: \[ \begin{array}{l} T_1 \text{ reads-$x$-from } T_0, T_1 \text{ reads-$z$-from } T_0; \\ T_2 \text{ reads-$x$-from } T_0; \\ T_3 \text{ reads-$z$-from } T_0; \\ T_4 \text{ reads-$x$-from } T_1, T_4 \text{ reads-$y$-from } T_3, T_4 \text{ reads-$z$-from } T_3; \end{array} \] したがって \(L_1 \equiv L_2\) が成立する。
このログ等価性の定義は、ログによって生成される最終的なデータベース状態を無視している。たとえば、ログ \[ L = w_0[x]\,w_1[x] \quad \text{and} \quad L' = w_1[x]\,w_0[x] \] は、たとえ両ログで異なるトランザクションが \(x\) の最終値を生成していても等価と見なされる。各ログにおいて \(x\) の最終値を書き込むトランザクションを同一にすることを要求することで、この等価性の概念をより厳密に定義することがしばしば望ましい。これは、(1) 他のすべてのトランザクションの後に続いてデータベース全体を読み取る "最終トランザクション" を追加する (たとえばログ \(L_1\) と \(L_2\) における \(T_4\)) こと、(2) 等価性を "ログが同じ reads-from と同じ最終トランザクションを持つ" こと、と再定義することでモデル化できる。
 2.4 直列化可能ログ
2.4 直列化可能ログ
直列ログ (serial log) は \(\Sigma\) 上の全順序ログであり、すべてのトランザクションペア \(T_i\) と \(T_j\) についてについて、\(T_i\) のすべての操作が \(T_j\) のすべての操作に先行するか、その逆である (たとえばセクション 2の \(L_2\))。直列ログは、並行性が全く存在しない実行を表す。各トランザクションは、次のトランザクションが開始する前に最初から最後まで実行される。したがって、並行性制御の観点から、すべての直列ログは明らかに正しい実行を表している。
他のどのようなログが正しい実行を表すか? 並行性制御の観点から見ると、正しい実行とは、並行性が認識できない実行を指す。つまり、ある実行が正しいとは、それが並行性が存在しない場合の実行と等価であることを意味する。直列ログは後者の実行を表すため、正しいログ (correct log) とは直列ログと等価な任意のログのことを指す。このようなログは直列化可能 (SR; serializable) と呼ばれる。
セクション 2.2 のログ \(L_2\) は SR である。これはセクション 2.3 で定義した直列ログ \(L_2\) と等価であるためである。したがって \(L_1\) は正しいログと結論づけられる。
 2.5 直列化可能性定理
2.5 直列化可能性定理
\(L\) を \(\{T_0,\ldots,T_n\}\) 上のログとする。\(L\) の直列化グラフ (serialization graph) \(SG(L)\) は、ノードが \(T_0,\ldots,T_n\) で構成され、辺がすべて \(T_i \to T_j\) (\(i \ne j\)) の有向グラフである。ここで \(T_i\) における何らかの操作が \(T_j\) における何らかの操作よりも前に発生し、かつ競合する関係にある。例えばログ \(L_1\) の直列化グラフは
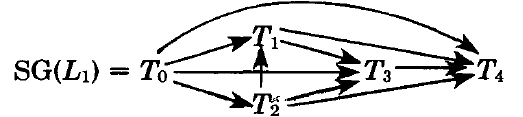
\(w_0[x] \lt r_1[x]\) のため辺 \(T_0 \to T_1\) が存在し、\(r_1[z] \lt w_3[z]\) のため辺 \(T_1 \to T_3\) が存在し、以下同様である。
直列化可能性定理 [4, 8, 14, 16, 21]. \(SG(L)\) が非循環であれば、\(L\) は SR である。
 3. マルチバージョン直列可能性理論
3. マルチバージョン直列可能性理論
マルチバージョン DBS では各書き込みが新しいバージョンを生成する。我々は \(x\) のバージョンを \(x_i,x_j,\ldots\) と表記する。ここで添字はそのバージョンを書き込んだトランザクションのインデックスである。バージョンに対する操作は \(r_i[x_j]\) や \(w_i[x_i]\) と表記する。
 3.1 マルチバージョンログ
3.1 マルチバージョンログ
\(T=\{T_0,\ldots,T_n\}\) をトランザクションログの集合とする (セクション 2.2 で定義した通り、各操作はデータ項目を参照するものとする)。\(T\) を実行するために、マルチバージョン DBS は \(T\) の "データ項目操作" を "バージョン操作" に変換する必要がある。我々はこの変換を、各 \(w_i[x]\) を \(w_i[x_i]\) に、各 \(r_i[x]\) をある \(j\) について \(r_i[x_j]\) にマップする関数 \(h\) によって形式化する。
\(T\) 上のマルチバージョン DBS ログ (または単に MV ログ) は半順序集合 \(L = (\Sigma,\lt)\) であり、以下の条件を満たす:
ある変換関数 \(h\) に対して \(\Sigma = h(\bigcup_{i=1}^n \Sigma_i)\) である。
各 \(T_i\) とすべての操作 \(\mathrm{op}_i\) と \(\mathrm{op}'_i\) に対して、\(\mathrm{op}_i \lt \mathrm{op}'_i\) であれば \(h(\mathrm{op}_i) \lt h(\mathrm{op}'_i)\) である。
\(h(r_j[x]) = r_j[x_i]\) であれば \(w_i[x_i] \lt r_j[x_i]\) である。
条件 (1) は、各トランザクションによって投入された操作が適切なマルチバージョン操作に変換されることを述べている。条件 (2) は、MV ログがトランザクションによって規定されたすべての順序を保持することを述べている。条件 (3) は、トランザクションがそのバージョンが生成されるまでそのバージョンを読み取ることができないことを述べている。
以下はセクション 2 の \(\{T_0,T_1,T_2,T_3,T_4\}\) に対する MV ログである。
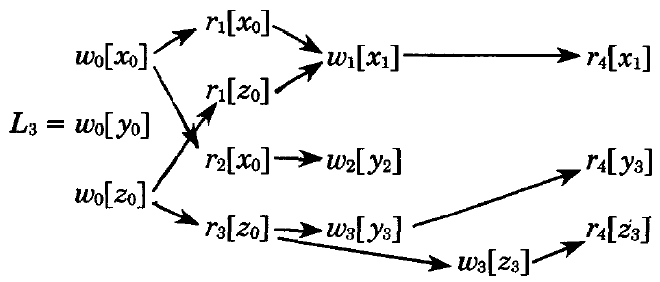
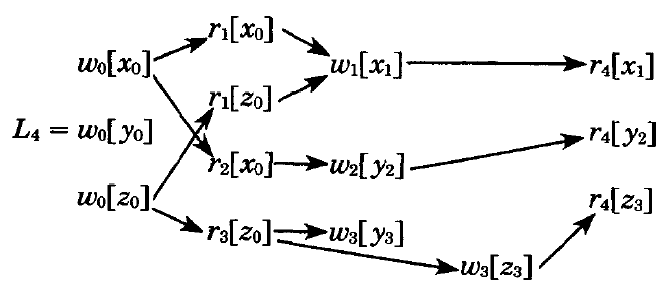
集合 \(T\) 上のすべての MV ログは \(h(w_i[x])=w_i[x_i]\) であるため書き込み操作は同じであるが、読み取り操作は同じである必要はない。例えば \(L_4\) では \(r_4[y_3]\) ではなく \(r_4[y_2]\) を持つ点が異なる。
 3.2 MV ログの等価性
3.2 MV ログの等価性
基本的な直列化可能性理論のほとんどの定義と結果は MV ログにも適用可能である。我々はそれらの定義と結果において "データ項目" の概念を単に "バージョン" に置き換えるだけでよい。しかし MV ログの構造はこの扱いを簡単にする。このセクションではセクション 2.3 とセクション 2.4 内容を MV ログ向けに再定式化する。
\(L\) を \(\{T_0,\ldots,T_1\}\) 上の MV ログとする。\(L\) において、トランザクション \(T_j\) が \(T_i\) によって生成された \(x\) のバージョンを読み取る場合、それは \(L\) において \(T_j\) reads-\(x\)-from \(T_i\) であることを意味する。定義により \(T_i\) によって生成される \(x\) のバージョンは \(x_i\) である。したがって \(T_j\) が \(x_i\) を読み取る場合に \(T_j\) reads-\(x\)-from \(T_i\) である。つまり \(h\) が "データ項目の読み取り" を "バージョンの読み取り" に変換する方法によって決定されることを意味しており、すなわち \(L\) における reads-from 関係は変換関数 \(h\) によって決定される。
\(\{T_0,\ldots,T_n\}\) 上の 2 つの MV ログが同じ reads-from 関係を持つとき、それらは等価であり \(\equiv\) と表記する。MV ログにおける reads-from 関係はその読み取り操作によって決定される。つまり \(T_j\) read-\(x\)-from \(T_i\) とは \(r_j[x_i]\) がログの操作である場合に限られる。したがって 2 つのログはそれらが同じ読み取り操作を持つ場合に限り等価である。さらに、同じトランザクション上のすべての MV ログは同じ書き込みを持つため、等価性は自明な条件に帰着する。
事実 1. トランザクション集合 \(T\) 上の 2 つの MV ログは、同じ操作を持つ場合に限り等価である。
二つの "バージョン操作" が同じバージョンを操作し、片方が書き込みである場合、それらは競合 (conflict) する。MV ログで起き得る競合パターンは 1 種類のみである。すなわち、\(\mathrm{op}_i \lt \mathrm{op}'_j\) でそれらの操作が競合しているならば、\(\mathrm{op}_i\) は \(w_i[x_i]\) であり、かつ \(\mathrm{op}_j\) は \(r_j[x_i]\) である。各書き込みが新しいバージョンを生成するため \(w_i[x_i] \lt w_j[x_i]\) 形式の競合は起きえない。また \(T_j\) は \(x_i\) が生成されるまで \(x_i\) を読み取れないため \(r_j[x_i] \lt w_i[x_i]\) 形式の競合も起きえない。したがって、MV ログにおけるすべての競合は read-from 関係に対応するものである。
MV ログの直列化グラフ (serialization graph) は通常のログと同様に定義される。MV ログにおいて競合は高度に構造化されているため、直列化グラフの構造は非常に単純である。ここで \(L\) を \(\{T_0,\ldots,T_n\}\) 上の MV ログとする。\(SG(L)\) は、ノード \(T_0,\ldots,T_n\) と、ある \(x\) について \(T_j\) reads-\(x\)-from \(T_i\) であるような辺 \(T_i \to T_j\) (\(i\ne j\)) で構成される。すなわち、ある \(x\) について \(r_j[x_i]\) が \(L\) の操作である場合に限り、\(T_i \to T_j\) が存在する。これにより次が得られる。
事実 2. \(L\) と \(L'\) は \(T\) 上の MV ログとする。
\(L\) と \(L'\) が同じ操作を持つならば、\(SG(L)=SG(L')\) である。
\(L\) と \(L'\) が等価であるならば、\(SG(L)=SG(L')\) である。
前のセクションで述べたログ \(L_3\) と \(L_4\) に対する直列化グラフを以下に示す:

(セクション 2.4 の \(SG(Li)\) と比較せよ)
 3.3 1-コピー直列性
3.3 1-コピー直列性
データベースが複数のバージョンを持つ場合でもユーザーは各データ項目のコピーが 1 つだけ存在するかのように自身のトランザクションが動作することを期待するが、直列ログは常にこのように動作するわけではない。以下に簡単な例を示す。\[ w_0[x_0]\,w_0[y_0]\,r_1[x_0]\,w_1[y_1]\,r_2[y_0]\,w_2[x_2] \] \(T_1\) が \(T_0\) と \(T_2\) の間に配置され \(y\) に新しい値を設定した後であっても、\(T_2\) reads-\(y\)-from \(T_0\) となる。この動作は、\(y\) のコピーが 1 つだけの場合には再現できない。1-コピーデータベースでは、\(T_0\) が \(T_1\) の前に実行され、\(T_1\) が \(T_2\) の前に実行される場合、\(T_2\) は必ず \(T_1\) によって生成された \(y\) の値を読み取らなければならない。
したがって、我々は許可可能な直列ログの集合を制限しなければならない。
直列 MV ログ \(L\) が 1-コピー直列 (one-copy serial) (または 1-直列) であるとは、すべての \(i,j\) および \(x\) について \(T_j\) reads-\(x\)-from \(T_i\) の場合、\(i=j\) であるか、または \(T_i\) が \(x\) の任意のバージョンに書き込む \(T_j\) に先行する最後のトランザクションであることを意味する。(\(L\) は全順序であるため、この定義における "最後" という語は明確に定義されている。) 上記のログは 1-直列ではない。なぜなら \(T_2\) reads-\(y\)-from \(T_0\) だが \(w_0[y_0] \lt w_1[y_1] \lt r_2[y_0]\) であるためである。以下の \(L_5\) は 1-直列である。\[ L_5 = w_0[x_0]\,w_0[y_0]\,w_0[z_0]\,r_2[x_0]\,w_2[y_2]\,r_1[z_0]\,r_1[z_0]\,w_1[x_1]\,r_3[z_0]\,w_3[y_3]\,w_3[z_3]\,r_4[x_1]\,r_4[y_3]\,r_4[z_3] \]
ログが 1-直列のログと等価である場合、そのログは 1-コピー直列化可能 (one-copy serializable) (または 1-SR) である。たとえばセクション 3.1 の \(L_3\) は、事実 1 によって検証できるように、\(L_5\) と等価である。したがって \(L_3\) は 1-SR である。\(L_4\) はどの 1-直列ログとも等価でない (\(L_4\) と同じ操作を持つすべての可能な直列ログをチェックすることで検証できる)。したがって \(L_4\) は 1-SR ではない。
直列ログが 1-直列でなくても 1-SR である可能性がある。たとえば、\[ w_0[x_0]\,r_1[x_0]\,w_1[y_1]\,r_2[x_0]\,w_2[y_2] \] は \(T_2\) が \(T_1\) の代わりに \(T_0\) から \(x\) を読み取るため 1-直列ではない。しかしこれは以下と等価であるため 1-SR である: \[ w_0[x_0]r_2[x_0]r_1[x_0]w_1[y_1]w_2[y_2] \]
1-コピー直列化可能性はマルチバージョン並行性制御のための我々の正当性の基準である。以下の定理はこの基準を正当化し、MV ログが 1-SR である場合に限り、その MV ログが直列非 MV ログ (serial non-MV log) と同様に動作することを証明するものである。
まず、我々はログ等価性の概念を拡張し、MV ログと非 MV ログの両方を扱えるようにする。\(L\) と \(L'\) を \(T\) 上の (MV または非 MV) ログとする。\(L\) と \(L'\) が同じ read-from 関係を持つ場合に等価 (equivalent)、\(\equiv\) である。
1-SR 等価性定理. \(L\) を \(T\) 上の MV ログとすると、\(L\) が 1-SR である場合に限り、\(L\) は \(T\) 上の直列で非 MV ログである。
Proof.
(IF方向). \(L_s\) を \(L\) と等価な 1-直列ログとする。\(L_s\) の各 \(w_i[x_i]\) を \(w_i[x]\) に、\(r_j[x_i]\) を \(r_j[x]\) に変換することで、直列な非 MV ログ \(L'_s\) を形成する。\(L_s\) における任意の reads-from 関係、すなわち \(T_j\) reads-\(x\)-from \(T_i\) という関係を考える。\(L_s\) は 1-直列であるため \(w_i[x_i]\) と \(r_j[x_i]\) の間に \(w_k[x_k]\) は存在しない。したがって、\(L'_s\) においても \(w_i[x]\) と \(r_j[x]\) の間に \(w_k[x]\) は存在しない。つまり \(L'_s\) において \(T_j\) reads-\(x\)-from \(T_i\) である。これにより \(L'_s \equiv L_s\) が確立される。\(L_s \equiv L\) であることから推移律により \(L \equiv L'_s\) が導かれる (\(\equiv\) は等価関係であるため)。
(ONLY IF 方向). \(L'_s\) を \(L\) と等価で直列な非 MV ログと仮定する。\(L'_s\) を直列 MV ログ \(L_s\) に変換する。各 \(w_i[x]\) を \(w_i[x_i]\) に写像し、各 \(r_j[x]\) を、\(L'_s\) において \(T_j\) reads-\(x\)-from \(T_i\) となるような \(r_j[x_i]\) に写像する。この変換は reads-from 関係を保持するため、\(L_s \equiv L'_s\) である。推移律により \(L \equiv L_s\) である。
あとは \(L_s\) が 1-直列であることを証明すれば十分である。\(L'_s\) における任意の reads-from 関係、すなわち \(T_j\) reads-\(x\)-from \(T_i\) という関係を考える。\(L'_s\) は非 MV ログであるため \(w_i[x]\) と \(r_j[x]\) の間に \(w_k[x]\) は存在しない。したがって \(L_s\) では \(w_i[x_i]\) と \(r_j[x_i]\) の間に \(w_k[x_k]\) は存在しない。したがって \(L_s\) は 1-直列である。∎
 3.4 1-直列化可能性定理
3.4 1-直列化可能性定理
我々は MV ログが 1-SR であるかどうかを判定するために修正版の直列化グラフを使用する。ログ \(L\) とデータ項目 \(x\) が与えられたとき、\(x\) のバージョン順序 (version order) とは、\(L\) に書き込まれた \(x\) のすべてのバージョン上の任意の (非反射的 (nonreflexive)) 全順序である。\(L\) のバージョン順序 \(\ll\) はすべてのデータ項目に対するバージョン順序の和集合である。セクション 3.1 の \(L_3\) (またはセクション 3.3 の \(L_5\)) に対する可能なバージョン順序は次のとおりである: \[ \ll = \left\{ \begin{array}{l} x_0 \ll x_1 \\ y_0 \ll y_2 \ll y_3 \\ z_0 \ll z_3 \end{array} \right. \]
\(L\) とバージョン順序 \(\ll\) が与えられたとき、マルチバージョン直列化グラフ (multiversion serialization graph) \(MVSG(L,\ll)\) は \(SG(L)\) に次の辺を追加したものである:
\(k \ne i\) であるような \(L\) 内の各ノード \(r_k[x_j]\) と \(w_i[x_i]\) について、\(x_i \ll x_j\) であれば \(T_i \to T_j\) を追加し、そうでなければ \(T_k \to T_i\) を追加する。
例えば

(セクション 2.5 の \(SG(L_1)\) と比較せよ。)
次の定理はマルチバージョン並行性制御アルゴリズムを分析するための我々の主要なツールである。
1-直列化可能性定理. MVログ \(L\) は、\(MVSG(L,\ll)\) が非循環であるようなバージョン順序 \(\ll\) が存在する場合に限り、1-SR である。
Proof.
(IF 方向). \(L_s\) を \(MVSG(L,\ll)\) のトポロジカルソートによって誘導される直列 MV ログとする。つまり \(L_s\) は \(MVSG(L,\ll)\) をトポロジカルソートして形成され、各ノード \(T_i\) がソート順に列挙されるたびに \(L\) における \(T_i\) の操作が \(L\) と一致する任意の順序で \(L_s\) に 1 つずつ追加される。\(L_s\) は \(L\) と同じ操作を持つため、事実 1 により \(L \equiv L_s\) である。
残りは \(L_s\) が 1-直列であることを証明すれば十分である。任意の reads-from 状況、つまり \(T_k\) reads-\(x\)-from \(T_j\) という状況を考える。\(w_i[x_i]\) を \(x\) のバージョン上での任意の書き込みとする。\(x_i \ll x_j\) ならば \(MVSG\) 定義の規則 (1) によりグラフは \(T_i \to T_j\) を含む。この辺は \(T_j\) が \(L_s\) において \(T_i\) の前に配置される。\(x_j \ll x_i\) であれば、規則 (1) により \(MVSG(L,\ll)\) は \(T_k \to T_i\) を含む。どちらの場合でも \(T_i\) は \(L_s\) において \(T_j\) と \(T_k\) の間に挟まれることは防止される。\(T_i\) は \(x\) への任意の書き込みであったため、これは \(L_s\) において \(x\) のバージョンを書き込むいかなるトランザクションも \(T_j\) と \(T_k\) の間に存在しないことを証明する。したがって \(L_s\) は 1-直列である。
(ONLY IF 方向). \(L\) と \(\ll\) が与えられたとき、MVSG 定義の命題 (1) で規定されるグラフを \(MV(L,\ll)\) とする。命題 (1) は \(L\) における操作と \(\ll\) のみに依存し、\(L\) における操作の順序には依存しない。したがって \(L_1\) と \(L_2\) が同じ操作を持つマルチバージョンログである場合、\(MV(L_1,\ll) = MV(L_2,\ll)\) はすべてのバージョン順序 \(\ll\) について成立する。
\(L_s\) を \(L\) と等価な 1-直列ログとする。\(SG(L_s)\) のすべての辺は "左から右" へ配置される。つまり \(T_i \to T_j\) であれば \(T_i\) は \(L_s\) において \(T_j\) の前に位置する。\(L_s\) 内で \(T_i\) が \(T_j\) より前である場合に限り \(x_i \ll x_j\) であるというように \(\ll\) を定義する。\(MV(L_s,\ll)\) のすべての辺も左から右へ配置される。したがって \(MVSG(L_s,\ll)\) \(=\) \(MV(L_s,\ll)\) \(\cup\) \(SG(L_s)\) 内のすべての辺も左から右へ配置される。これは \(MVSG(L_s,\ll)\) が非循環であることを意味する。
事実 1 により \(L\) と \(L_s\) は同じ操作を持つ。したがって \(MV(L,\ll)=MV(L_s,\ll)\) が成り立つ。事実 2 により \(SG(L)=SG(L_s)\) である。したがって \(MVSG(L,\ll)=MVSG(L_s,\ll)\) である。\(MVSG(L_s,\ll)\) が非循環であることから \(MVSG(L,\ll)\) もそうであることが導かれる。∎
セクション 4 から 6 では 1-直列化可能性定理を使用してマルチバージョン並行性制御アルゴリズムを分析する。このセクションの最後に複雑性に関する結果を示す。
 3.5 1-直列化可能性は NP-完全である
3.5 1-直列化可能性は NP-完全である
1-SR 複雑性定理. MV ログが 1-SR であるかどうかを判定することは NP 完全問題である。
Proof.
(NP クラスへの帰属性). \(L\) を \(T\) 上の MV ログとする。\(T\) 上の 1-直列ログ \(L_s\) を推測し、\(L_s \equiv L\) が成立することを検証する。事実 1 により、ログの操作集合を比較することで \(L_s \equiv L\) を検証できる。
(NP-困難性). この問題はログ SR 問題 ([9, 14, 16] の問題 SR 33) からの還元である。\(L'\) を \(T\) 上の非 MV ログとする。\(L'\) を同等の MV ログ \(L\) に変換するには、\(L'\) で \(T_j\) reads-\(x\)-from \(T_i\) となるように、各 \(w_i[x]\) を \(w_i[x_i]\) に変換し、各 \(r_j[x]\) を \(r_j[x_i]\) に変換すれば良い。1-SR 等価性定理により、\(L\) が 1-SR である必要十分条件は \(L \equiv L'_s\) となるような非 MV 直列ログ \(L'_s\) が存在する場合である。ただし、推移律により \(L'_s\) は \(L'\) が SR である場合に限り存在する。したがって \(L'\) は \(L\) が 1-SR である場合に限り SR である。∎
Papadimitriou と Kanellakis は関連する問題が NP 完全であることを証明している [15]: 従来のログ \(L\) が与えられたとき、\(w_i[x] \lt r_j[x]\) を満たす何らかの \(x_i\) に対して、各 \(w_i[x]\) を \(w_i[x_i]\) に、各 \(r_j[x]\) を \(r_j[x_i]\) に変換することで、\(L\) を 1-SR な MV ログに変換は可能か? この問題は、操作をスケジュールした後に読み取り用のバージョンを選択することに対応している。一方、我々の問題は、操作をスケジュールすると同時にバージョンを選択することに対応している。
 4. マルチバージョン・タイムスタンプ方式
4. マルチバージョン・タイムスタンプ方式
我々が知る最も初期のマルチバージョン並行性制御アルゴリズムは Reed で提案されたマルチバージョンタイムスタンプアルゴリズム [17] である。
各トランザクション \(T_i\) には実行開始時に一意のタイムスタンプ (timestamp) \(TS(i)\) が割り当てられる。直観的には、タイムスタンプはトランザクションが開始した "時刻" を示す。形式的には、タイムスタンプは単に数値であり、各トランザクションが異なるタイムスタンプを割り当てられるという性質を持つ。各読み取りと書き込みは、それを発行したトランザクションのタイムスタンプが付与され、各バージョンはそれを書き込んだトランザクションのタイムスタンプが保持される。
操作は先着順で処理される。しかし、データ項目操作からバージョン操作への変換により、操作がタイムスタンプ順に処理されたかのように見える。
アルゴリズムは次のように動作する。
\(r_i[x]\) は \(r_i[x_k]\) に変換される。ここで \(x_k\) は \(\le TS(i)\) で最大のタイムスタンプを持つ \(x\) のバージョンである。
\(w_i[x]\) には 2 つのケースがある。DBS が \(TS(k) \lt TS(i) \lt TS(j)\) となるような \(r_j[x_k]\) をすでに処理している場合、\(w_i[x]\) は拒否される (rejected)。そうでなければ \(w_i[x]\) は \(w_i[x_i]\) に変換される。直観的には、\(w_i[x]\) は \(r_j[x_k]\) を無効化することになる場合に拒否される。
我々は、このアルゴリズムの正当性を証明するために直列化可能性理論を適用する。そのためには、アルゴリズムを直列化可能性理論の観点から述べなければならない。我々は上記のアルゴリズムの記述から、アルゴリズムが生成するすべてのログが満たす性質を推論する。これらの特性が我々のアルゴリズムの形式的定義を形成する。我々は直列化可能性理論を使用して、これらのログ性質が 1-直列化可能性を導くことを証明する。
次の性質が我々の MV タイムスタンプアルゴリズム (MV timestamping algorithm) の形式的定義を形成する。\(L\) を \(\{T_0,\ldots,T_n\}\) 上の MV ログとする。
| TS1. | すべての \(T_i\) は一意性条件を満たす数値タイムスタンプ \(TS(i)\) を持つ。つまり \(i=j\) の場合に限り \(TS(i) = TS(j)\) が成り立つ。 |
| TS2. | すべての \(r_k[x_j]\) と \(w_i[x_i]\) は \(\lt\)-関係である。すなわち \(r_k[x_j] \lt w_i[x_i]\) またはその逆である。 |
| TS3.1. | すべての \(r_k[x_j]\) について \(TS(j) \le TS(k)\) である。 |
| TS3.2. | \(i \ne j\) であるすべての \(r_k[x_j]\) と \(w_i[x_i]\) について、\(w_i[x_i] \lt r_k[x_j]\) であれば \(TS(i) \lt TS(j)\) または \(TS(k) \leq TS(i)\) のいずれかである。 |
| TS4. | \(i \ne j\) であるすべての \(r_k[x_j]\) と \(w_i[x_i]\) について、\(r_k[x_j] \lt w_i[x_i]\) であれば \(TS(i) \lt TS(j)\) または \(TS(k) \leq TS(i)\) のいずれかである。 |
性質 TS1 はトランザクションが一意のタイムスタンプを持つことを述べているだけである。TS2 はアルゴリズムの動作記述に暗黙的に含まれており、この性質がなければ "DBS が \(r_j[x_k]\) をすでに処理している場合…" という条件は明確に定義されない。TS3 は、\(r_k[x_j]\) が処理される時点で \(x_j\) が \(TS(k)\) 以下でもっとも大きいタイムスタンプを持つ \(x\) のバージョンであることを述べている。TS4 は、DBS が \(r_k[x_j]\) を処理した後に \(TS(j) \leq TS(i) \lt TS(k)\) となるような \(w_i[x_i]\) を処理しないことを述べている。
性質 TS3.2 と TS4 は簡約できる。TS2 により \(r_k[x_j]\) と \(w_i[x_i]\) は \(\lt\)-関係にある。したがって TS3.2 と TS4 は次と等価である。
| TS5. | \(i \ne j\) であるすべての \(r_k[x_j]\) と \(w_i[x_i]\) について、\(TS(i) \lt TS(j)\) または \(TS(k) \leq TS(i)\) のいずれかである。 |
我々はこれらの性質を満たす任意のログが 1-SR であることを証明する。言い換えれば、MV タイムスタンプは正しい並行性制御アルゴリズムである。
マルチバージョン・タイムスタンプ定理. MV タイムスタンプアルゴリズムによって生成されるすべてのログは 1-SR である。
Proof. \(L\) をアルゴリズムによって生成されるログとする。バージョン順序を \(x_i \ll x_j\) ならば \(TS(i) \lt TS(j)\) と定義する。我々は \(MVSG(L,\ll)\) におけるすべての辺がタイムスタンプ順序であることを証明する。つまり \(T_i \to T_j\) が辺ならば \(TS(i) \lt TS(j)\) である。
\(T_i \to T_j\) を \(SG(L)\) の辺とする。この辺は reads-from 状況に対応する。すなわち、ある \(x\) について \(T_j\) reads-\(x\)-from \(T_i\) である。TS3.1 より \(TS(i) \le TS(j)\) である。TS1 より \(TS(i) \ne TS(j)\) である。したがって \(TS(i) \lt TS(j)\) となり目的が達成される。
MVSG 定義の規則 (1) によって導入される任意の辺を考える。\(w_i[x_i]\)、\(w_j[x_j]\)、および \(r_k[x_j]\) を規則 (1) で規定された操作とすると以下の 2 つのケースが考えられる。
(1) \(x_i \ll x_j\)
このとき辺は \(T_i \to T_j\) である。我々の \(\ll\) の定義から \(TS(i) \lt TS(j)\) が導かれる。
(2) \(x_j \ll x_i\)
このとき辺は \(T_k \to T_i\) である。TS5 より \(TS(i) \lt TS(j)\) または \(TS(k) \le TS(i)\) のいずれかである。\(\ll\) の定義では \(TS(j) \lt TS(i)\) を要求するため最初の選択肢は不可能である。TS1 により \(TS(k) \neq TS(i)\) である。したがって \(TS(k) \lt TS(i)\) となり目的が達成される。
これにより \(MVSG(L,\ll)\) におけるすべての辺がタイムスタンプ順序であることが証明される。タイムスタンプは数値であり、したがって全順序であるため、\(MVSG(L,\ll)\) が非循環であることが導かれる。したがって、1-直列化可能性定理により、\(L\) は 1-SR である。∎
 5. マルチバージョン・ロック機構
5. マルチバージョン・ロック機構
Bayer ら [1, 2] と Stearns および Rosenkrantz [20] はロック機構と同様の手法を用いて同期するマルチバージョンアルゴリズムを提示している。このセクションでは彼らのアルゴリズムの一般化について考察する。前のセクションと同様にまずアルゴリズムの非形式的な記述から始め、次にアルゴリズムによって導かれるログの性質を定式化する。最後に、これらのログの性質が 1-直列化可能性を含意することを証明する。
各トランザクションと各バージョンは認証済み (certified) または未認証 (uncertified) の 2 つの状態のいずれかに存在する。トランザクションが開始された時点では未認証であり、バージョンが書き込まれた時点でも未認証である。アルゴリズムの後続処理によってトランザクションとそれが書き込んだすべてのバージョンが認証済みとなる。"認証済み" の概念は [20] の "クローズ済み" (closed) に対応する。
\(c_i[x_i]\) を "\(x_i\) が認証される" というイベントとする。アルゴリズムは、すべての \(c_i[x_i]\) と \(r_k[x_j]\) が \(\lt\)-関係であることを要求する。またすべての \(c_i[x_i]\) と \(c_j[x_j]\) は \(\lt\)-関係でなければならない。したがってバージョン順序は \(c_i[x_i] \lt c_j[x_j]\) の場合に限り \(x_i \ll x_j\) と定義される。
アルゴリズムは次のように動作する。
まず \(r_i[x]\) は \(r_i[x_k]\) に変換される。ここで \(x_k\) は \(x\) の (\(\ll\) に関して) 最後の認証済みバージョン、または任意の未認証バージョンのいずれかである。アルゴリズムはこれらのバージョンのどちらを読み取るかを決定するためにどのような規則を使用してよい。
次に \(w_i[x]\) は \(w_i[x_i]\) に変換される。前述のとおりこの時点では \(x_i\) は未認証である。
最後に、トランザクションの実行が完了すると、DBS はそのトランザクションとそれが書き込んだすべてのバージョンを認証しようと試みる。\(T_i\) が書き込んだすべてのデータ項目 \(x\) について、DBS は \(x\) に対して \(T_i\) 用の認証ロック (certify-lock) を設定しようとする。この操作が成功するのは、他のトランザクションがすでに \(x\) に対して認証ロックを持っていない場合に限られる。ロックが設定できない場合、\(T_i\) はロックが設定できるまで待機する。\(T_i\) がすべての認証ロックを取得した時点で、さらに 2 つの条件が満たされなければならない:
| C1. | \(T_i\) が読み取った \(k \ne i\) であるような各 \(x_k\) について、\(x_k\) は認証済みである。 |
| C2. | \(T_i\) が書き込んだ各 \(x_i\) と、すでに認証されている \(x\) の各バージョン \(x_k\) について、\(x_k\) を読み取ったすべてのトランザクションは認証済みである。 |
C1 の達成は時間の問題に過ぎない。C1 が満たされると、それを偽にするような将来のいかなるイベントは発生しない。C2 を達成するために我々は \(x\) に認証トークン (certify-token) を設定し、将来の読み取りが \(x\) の認証済みバージョンを読み取らないようにする。代わりにそれらは \(x_i\) または他の未認証バージョンの \(x\) を読むことができる。
これらの条件が成立すると \(T_i\) は認証済みであると宣言される。この事実は \(T_i\) が書き込んだすべてのバージョンにブロードキャストされる。バージョン \(x_i\) がこの情報を受け取るとそれも認証される。すなわちイベント \(c_i[x_i]\) が発生する。\(x_i\) が認証されると、\(x_i\) 上の認証ロックと認証トークンが解放される。
ほとんどのロックアルゴリズムと同様に、このアルゴリズムはデッドロックが発生する可能性がある。このデッドロックは、認証ロックの待機と、条件 C1 と C2 の待機という 2 つの独立した原因から生じる可能性がある。デッドロックを検出するために、アルゴリズムは有向ブロッキンググラフ (blocking graph) を使用できる。このグラフのノードはトランザクションを表し、\(T_i\) と \(T_j\) の進行をブロックしているすべての \(T_i \to T_j\) を辺とする。このグラフに循環が生じている場合に限りデッドロックが存在する [11a, 12]。また [3, 18] のようなデッドロック防止スキームも使用できる。システムは 2 種類のデッドロックを別々に追跡すべきである。認証ロックに起因するデッドロックを解決するために、システムは 1 つ以上のトランザクションにデッドロックを解消するために十分な数の認証ロックを解放させる必要がある。これらのトランザクションは後でこれらのロックの再取得を試みることができる。C1 と C2 に起因するデッドロックを解消するためには、システムは 1 つ以上のトランザクションをアボート (abort) しなければならない。(アルゴリズムがトランザクションに未認証バージョンを読むことを許可する場合、カスケードアボートが可能である。)
このアルゴリズムは次のログ性質を誘導する。これらの性質は MV ロックアルゴリズム (MV locking algorithm) の形式的定義を形成する。\(L\) を \(\{T_0,\ldots,T_n\}\) 上の MV ログとする。この \(L\) にアルゴリズムにおける重要なイベントを表す記号を拡張する。具体的には、各 \(T_i\) に対して \(c_i\) を "\(T_i\) が認証済みと宣言される" というイベントを表すものとし、\(T_i\) によって書き込まれた各バージョン \(x_i\) に対して \(cl_i[x_i]\) を "DBS が \(T_i\) のために \(x\) に認証ロックを設定する" というイベントを表すものとし、各 \(x_i\) に対して \(c_i[x_i]\) を "\(x_i\) が認証される" というイベントを表すものとする。
| L1.1. | すべての \(T_i\) について、\(c_i\) は \(T_i\) のすべての読み取りと書き込みに続く。 |
| L1.2. | \(T_i\) に書き込まれたすべてのバージョン \(x_i\) について、\(cl_i[x_i] \lt c_i \lt c_i[x_i]\) である。 |
性質 L1 はトランザクションが実行後に認証されること、すべての認証ロックはトランザクションが認証される前に取得されなければならないこと、およびトランザクションはそのバージョンが認証される前に認証されなければならないことを述べている。
| L2.1. | すべての \(cl_i[x_i]\) と \(cl_j[x_j]\) は \(\lt\)-関係である。 |
| L2.2. | すべての \(x_i\) と \(x_j\) について、\(cl_i[x_i]\) ならば \(c_i[x_i] \lt cl_j[x_j]\) である。 |
L2 は認証ロックが競合 (conflict) すること、すなわち 2 つのトランザクションが同じデータ項目に対して認証ロックを同時に保持できないことを述べている。
| L3.1. | すべての \(r_k[x_j]\) と \(c_i[x_i]\) は \(\lt\)-関係である。 |
| L3.2. | \(i \ne j\) であるようなすべての \(r_k[x_j]\) と \(w_i[x_i]\) について、\(c_i[x_i] \lt r_k[x_j]\) かつ \(c_j[x_j] \lt r_k[x_j]\) ならば、\(c_i[x_i] \lt c_j[x_j]\) である。 |
L3 は読み取りを変換する規則を表現している。\(r_k[x_j]\) が発生する時点で \(x_j\) が既に認証されている場合、\(x_j\) はその時点での最後の認証済みバージョンである。
| L4.1. | \(k \ne j\) であるすべての \(r_k[x_j]\) について、\(c_j[x_j] \lt c_k\) である。 |
| L4.2. | \(i \ne j\) であるすべての \(r_k[x_j]\) と \(w_i[x_i]\) について、\(r_k[x_j] \lt c_i[x_i]\) かつ \(c_j[x_j] \le c_i\) ならば、\(c_k \lt c_i\) である。 |
これらの最後の性質は、それぞれ認証条件 C1 と C2 に対応する。
次の補題は L1-L4 から有用な性質を抽出する。
補題 1. \(T_i\) と \(T_j\) を \(x\) を書き込むトランザクションとする。このとき、
\(cl_i[x_i] \lt c_i \lt c_i[x_i] \lt cl_j[x_j] \lt c_j \lt c_j[x_j]\) または
\(cl_j[x_j] \lt c_j \lt c_j[x_j] \lt cl_i[x_i] \lt c_i \lt c_i[x_i]\) のいずれかである。
Proof. L2.1 の条件は \(cl_i[x_i]\) と \(cl_j[x_j]\) が \(\lt\)-関係であることを要求する。仮に \(cl_i[x] \lt cl_j[x_j]\) と置く。L1.2 により \(cl_i[x_i] \lt c_i \lt c_i[x_i]\) であり、L2.2 により \(cl_j[x_j] \lt c_j \lt c_j[x_j]\) である。L1.2 を再度適用すると \(cl_j[x_j] \lt c_j \lt c_j[x_j]\) である。これにより補題 1 で許容される最初の可能性が証明される。もし \(cl_j[x_j] \lt cl_i[x_i]\) であれば、同じ議論により第二の可能性が導かれる。∎
補題 2. 性質L1-L4は次を含意する:
L5. \(k \ne j\) であるすべての \(r_k[x_j]\) について、\(c_j \lt c_k\) である。 L6. \(i \ne j\) であるすべての \(r_k[x_j]\) と \(w_i[x_i]\) について、\(c_i \lt c_j\) または \(c_k \lt c_i\) のいずれかである。
Proof. (L5). L1 により \(c_j \lt c_j[x_j]\) である。L4.1 により \(c_j[x_j] \lt c_k\) である。L5 は推移律により従う。(L6). 論理的操作を使用すると L3.2 は次のように表現できる:
| L3.2'. | \( \begin{split} (c_i[x_i] \lt r_k[x_j]) & \Rightarrow (c_i[x_i] \lt r_k[x_j]) \land \lnot (c_j[x_j] \lt r_k[x_j]) \\ & \lor (c_i[x_i] \lt c_j[x_j]) \end{split} \) |
L3.1 により、右辺の第 1 行は次のように簡約される: \[ (c_i[x_i] \lt r_k[x_j]) \land (r_k[x_j] \lt c_j[x_j]) \] 推移律によりこれは \((c_i[x_i] \lt c_j[x_j])\) を含意し、したがって右辺全体が \(c_i[x_i] \lt c_j[x_j]\) を含意する。補題 1 によりこれは \(c_i \lt c_j\) を含意する。したがって L3.2' は次を含意する:
| L3.2". | \((c_i[x_i] \lt r_k[x_j]) \Rightarrow c_i \lt c_j\) |
同様に、L4.2 は次のように表現できる:
| L4.2'. | \((r_k[x_j] \lt c_i[x_i]) \Rightarrow \lnot (c_j[x_j] \lt c_i) \lor (c_k \lt c_i)\) |
補題 1 により \(c_j[x_j]\) と \(c_i\) は \(\lt\)-関係である。したがって右辺の第 1 項は \((c_i \lt c_j[x_j])\) に簡約される。補題 1 を再度適用するとこれは \(c_i \lt c_j\) と等価である。したがって L4.2' は次と等価である:
| L4.2". | \((r_k[x_j] \lt c_i[x_i]) \Rightarrow c_i \lt c_j \lor c_k \lt c_i\) |
L3.1 は \(r_k[x_j]\) と \(c_i[x_i]\) が \(\lt\)-関係であることを要求する。これにより L3.2" と L4.2" の左辺を削除し、それらを次のように結合できる: \[ \text{for every } r_k[x_j] \text{ and } c_i[x_i], \quad c_i \lt c_j \land c_k \lt c_i \] \(c_i[x_i]\) が存在するのは \(w_i[x_i]\) が存在する場合に限るため L6 を導く。∎
ここで我々はこれらの性質を満たす任意のログが 1-SR であること、つまり MV ロックは正しい並行性制御アルゴリズムであることを証明する。
マルチバージョン・ロック定理. MV ロックアルゴリズムによって生成されるすべてのログは 1-SR である。
Proof. アルゴリズムによって生成されるログを \(L\) とする。\(x_i \ll x_j\) ならば \(c_i \lt c_j\) とバージョン順序を定義する。我々は、\(T_i \to T_j\) が辺であれば \(c_i \lt c_j\) であるとという、\(MVSG(L,\ll)\) におけるすべての辺が認証順序 (certification order) であることを証明する。
\(T_i \to T_j\) を \(SG(L)\) の辺とする。この辺は reads-from 状況に対応する。つまり、ある \(x\) について \(T_j\) reads-\(x\)-from \(T_i\) である。L5 により \(c_i \lt c_j\) である。
MVSG 定義の規則 (1) によって導入される任意の辺について考える。\(w_i[x_i]\), \(w_j[x_j]\), \(r_k[x_j]\) を規則 (1) で規定される操作とする。ここで 2 つのケースがある。
\(x_i \ll x_j\): このとき辺は \(T_i \to T_j\) である。\(c_i \lt c_j\) は我々の \(ll\) 定義から導かれる。
\(x_j \ll x_i\): このとき辺は \(T_k \to T_i\) である。
L6 により \(c_i \lt c_j\) または \(c_k \lt c_i\) のいずれかである。\(\ll\) の定義は \(c_j \lt c_i\) を要求するため最初の選択肢は不可能である。したがって、\(c_k \lt c_i\) の目的を達する。
これにより \(MVSG(L,\ll)\) におけるすべての辺が認証順序であることが証明される。認証順序は半順序 (\(L\) そのもの) に埋め込まれているため、\(MVSG(L,\ll)\) が非循環であることが導かれる。したがって、1-直列化可能性定理により \(L\) は 1-SR である。∎
Stearns と Rosenkrantz のアルゴリズム [20] は我々の研究と 2 つの点で異なる。彼らのアルゴリズムは、任意の時点でデータ項目の未認証バージョンを最大 1 つしか存在させない。これは書き込み操作時に書き込みロックの設定を要求することで実現される。その結果、彼らのアルゴリズムではいかなるデータ項目についても 1 つの認証済みバージョンと最大 1 つの未認証バージョン、つまり最大 2 つバージョンしか必要としない。これはデータベース復旧とうまく適合する [10]。Stearns と Rosenkrantz は、データ項目の認証済みバージョンをその "前値" (before-value)、未認証バージョンをその "後値" (after-value) とそれぞれ定義している。もう 1 つの違いはデッドロック処理に関するものである。彼らのアルゴリズムは、タイムスタンプに基づく興味深い新しいデッドロック回避スキームを使用している。
Bayer らのアルゴリズム [1, 2] も各データ項目に対して最大 2 つのバージョンを使用する。[20] と同様に、データ項目のバージョンはその前値と後値によって識別される。Stearns と Rosenkrantz とは異なり、Bayer らはブロッキンググラフを使用してデータ項目の読み取りをバージョンの読み取りに変換する。彼らは常に正しいバージョンを選択できることを証明している。つまり、読み取りはログを非 1-SR にすることがなく、デッドロックを引き起こすこともない。これは、読み取り専用トランザクション (照会処理; query) が最小限の同期遅延で実行可能であり、デッドロックの危険もなく実行できる優れた性質である。
 6. マルチバージョン混合方式
6. マルチバージョン混合方式
Prime Computer 社は興味深いマルチバージョンアルゴリズムを開発した [7]。Prime 社のアルゴリズムはセクション 5 の終わりで示したアルゴリズムと同様に、並行性制御とデータベース復旧を統合したものである。ただし、それらのアルゴリズムとは異なり、Prime 社のアルゴリズムはデータ項目の複数の認証済みバージョンを活用できる。Computer Corporation of America はこの Prime 社のアルゴリズムを採用し Adplex DBS [6 に実装している。このセクションでは Prime 社のアルゴリズムの一般化について考察する。
我々が研究するアルゴリズムは混合方式 (mixed method) と呼ばれるものである。混合方式とは、ロック方式とタイムスタンプ方式を組み合わせた並行性制御アルゴリズムである [3]。混合方式は一貫したタイムスタンプ生成 (consistent timestamp generation) という新しい問題を導入する。タイムスタンプ方式では競合するトランザクションをタイムスタンプを使用して順序付ける。直観的には、\(T_i\) と \(T_j\) が競合する場合、\(TS(i) \lt TS(j)\) である場合に限り \(T_i\) は \(T_j\) の前に同期される。ロック方式はその場で (on-the-fly) トランザクションを順序付ける。直観的には、\(T_i\) と \(T_j\) が競合する場合、\(c_i \lt c_j\) である場合に限り \(T_i\) は \(T_j\) の前に同期される。ロック方式とタイムスタンプ方式を統合するには、これらの同期順序を一貫させる必要がある。
我々のアルゴリズムでは、読み取り専用トランザクション (照会処理) の処理に MV タイムスタンプ方式を使用し、一般的なトランザクション (更新処理) を処理するために MV ロック方式を使用する。照会処理と更新処理には次の 2 つの性質を満たすタイムスタンプが割り当てられる:
\(T_i\) と \(T_j\) を更新処理とする。\(c_i \lt c_j\) ならば \(TS(i) \lt TS(j)\) である。
\(T_q\) を照会処理、\(T_i\) を更新処理とする。\(r_q[x_k] \lt w_i[x_i]\) ならば \(TS(q) \lt TS(i)\) である。
一貫性のあるタイムスタンプ生成器 (consistent timestamp generator) は、これらの性質を満たす任意のタイムスタンプ割り当てる方式を指す。
我々のアルゴリズムは Lamport クロック (Lamport clock) を用いて一貫性のあるタイムスタンプを生成する。分散システムの議論はセクション 2 で述べた。Lamport クロックは 2 つの条件に従って各イベントに番号 (タイム (time) と呼ばれる) を割り当てる。
| LC1. | イベント \(e\) と \(f\) が同じプロセスで発生したものであり、\(e\) が \(f\) の前に起きた場合、\(\mathrm{time}(e) \lt \mathrm{time}(f)\) が成立する。 |
| LC2. | イベント \(e\) が "プロセス \(P\) がメッセージ \(M\) を送信"、\(f\) が "プロセス \(Q\) がメッセージ \(M\) を受信" である場合、\(\mathrm{time}(e) \lt \mathrm{time}(f)\) が成立する。 |
LC1 は各プロセスがローカルなクロックまたはカウンターを使用することで容易に達成できる。LC2 は、各メッセージの送信時にローカルクロック時刻を付与することで実装できる。プロセス \(Q\) が \(Q\) のローカル時刻より大きい時刻 \(t\) を持つメッセージを受信した場合、\(Q\) は自身のクロックを \(t\) まで進める。
| LC. | 分散システム内のイベント \(e\) と \(f\) について、\(e \lt f\) ならば \(\mathrm{time}(e) \lt \mathrm{time}(f)\) が成立する [13]。 |
LC はまさに我々が一貫したタイムスタンプを生成するために必要な条件である。更新処理 \(T_i\) が認証されると、その認証を行うプロセスは \(TS(i)=\mathrm{time}(c_i)\) を割り当てる。LC により \(c_i \lt c_j\) ならば \(\mathrm{time}(c_i) \lt \mathrm{time}(c_j)\) である。したがって \(TS(i) \lt TS(j)\) の目的を達する。システムはクエリー \(T_q\) が実行を開始すると \(TS(q)\) を現在の Lamport クロック以下に設定する。これにより、すべての読み取り操作 \(r_q[x_k]\) について \(TS(q) \lt \mathrm{time}(r_q[x_k])\) である。\(r_q[x_k] w_i[x_i]\) となるような任意の書き込み操作 \(w_i[x_i]\) を考える。ロック性質 L1 (セクション 5 参照) により \(w_i[x_i] \lt c_i\) であり、したがって推移律により \(r_q[x_k] \lt c_i\) である。LC により \(\mathrm{time}(r_q[x_k]) \lt \mathrm{time}(c_i)\) が導かれる。したがって \(TS(q) \lt TS(i)\) の目的を達する。
我々はアルゴリズムを詳細に記述する。
システムは Lamport クロックを維持する。
更新処理はセクション 5 の MV ロックアルゴリズムを使用する。
更新処理 \(T_i\) が認証されるとシステムは \(TS(i) = \mathrm{time}(c_i)\) を割り当てる。このタイムスタンプは \(T_i\) が書き込んだすべてのバージョンに送信される。したがって、承認済みバージョンにはタイムスタンプが付与されるが、認証されていないバージョンには付与されない。
照会処理 \(T_q\) の実行が開始されると、システムは \(TS(q)\) を現在の時刻以下に設定する。
\(T_q\) による任意の読み取り操作 \(r_q[x]\) を考える。セクション 4 と同様に我々はこれを \(r_q[x_k]\) に変換したい。ここで \(x_k\) は \(TS(q)\) より小さい最大のタイムスタンプを持つ \(x\) のバージョンである。しかし認証されていないバージョンにはタイムスタンプが付与されていないため注意が必要である。任意の認証されていない \(x\) バージョンが取り得るタイムスタンプの下限を \(t\) とする。具体的には \(t = \min\{\mathrm{time}(cl_i[x_i])\,|\,\text{$x_i$ is uncertified}\}\) とする。\(cl_i[x_i] \lt c_i\) であるため \(\mathrm{time}(cl_i)\) は \(\mathrm(c_i) = TS(i)\) の下限である。したがって \(t\) は任意の未承認 \(x_i\) のタイムスタンプの下限である。
再度 \(r_q[x]\) について考える。\(x\) に認証されていないバージョンが存在しないか、あるいは \(TS(q) \lt t\) ならば、\(r_q[x]\) は \(TS(q)\) 未満の最大のタイムスタンプを持つ \(x\) のバージョン \(x_k\) を読み取る。そうでなければ \(r_q[x]\) はその条件が満たされるまで待機する。(これは最終的に発生する。)
アルゴリズムによって導出されるログの特性は MV タイムスタンプとロックによって生じる性質の単純な組み合わせである。その正当性の証明はセクション 4 とセクション 5 で示されたものと同様の方法で行える。
マルチバージョン混合方式定理 (multiversion mixed method theorem). MV 混合方式によって生成されるすべてのログは 1-SR である。
Prime 社のアルゴリズムは我々のものと 2 つの点で異なる。最も重要な違いは、Prime 社のアルゴリズムでは明示的なタイムスタンプを使用しないことである。すべての認証イベントは \(\lt\)-関係である。すなわち \(c_1,\ldots,c_n\) は全順序である。このアルゴリズムは認証されたすべてのトランザクションのリスト \(CL\) を保持しており、\(T_i\) が認証されるとその識別子 \(i\) が \(CL\) に追加される。照会処理 \(T_q\) が実行を開始すると、それは \(CL\) のコピーを作成し \(CL(q)\) と表記する。\(T_q\) が読み取り操作 \(r_q[x]\) を発行すると、\(k \in CL(q)\) となるような \(x\) の (\(\ll\) 関係おいて) 最新のバージョン \(x_k\) を読み取る。我々はこの動作を混合方式の特殊ケースとして分析できる。各更新処理 \(T_i\) が認証の全順序におけるその位置に等しいタイムスタンプを割り当てられると想定する。すなわち \(TS(i) = t\) となるのは \(T_i\) が \(t\) 番目に承認されるトランザクションである場合に限る。また \(T_q\) には \(0 \lt \epsilon \lt 1\) としたタイムスタンプ \(TS(q) = |CL(q)| + \epsilon\) が割り当てられていると仮定する。これはタイムスタンプを一貫して割り当てる方法である。我々のアルゴリズムの下で \(T_q\) を実行すると Prime 社のアルゴリズムと同じバージョンを読み取ることになる。我々のアルゴリズムは 1-SR を満たすことから、Prime 社のアルゴリズムも同様に 1-SR を満たすことが導かれる。
もう 1 つの重要な違いは、Prime 社が更新処理に対して制限付きのマルチバージョンロック方式、すなわち 2フェーズロック [8] を採用している点である。書き込み操作が行われる際には書き込みロックが設定されるため、いかなるデータ項目も複数の未認証バージョンを持つことはない。さらに \(T_i\) が \(x\) を書き込み完了した時点で、他の更新処理 \(T_j\) は \(T_i\) が認証されるまで \(x\) を読み取ることができなくなり、その逆も同様である。このため各更新処理は実行を完了した時点で直ちに認証可能となる。
この設計の結果として照会処理と更新処理が完全に分離される。照会処理は更新処理を遅延させたりアボートさせることはなく、逆に更新処理が照会処理を遅延させたりアボートさせることもない。
Prime 社のアルゴリズムは認証イベントを全順序付けする必要があるため、集中型 DBS において最も自然に実装される。
次の変種は分散 DBS により適した実装方法である。
システムは Lamport クロックを維持する。
更新処理は 2 フェーズロック機構を使用する。このため各更新処理が実行を完了した時点ですぐに認証可能となる。システムは一般的なアルゴリズムと同様に \(TS(i) = \mathrm{time}(c_i)\) を割り当てる。
照会処理はタイムスタンプを用いて処理酢される。これも一般アルゴリズムとまったく同じである。
このアルゴリズムは照会処理と更新処理を Prime のアルゴリズムとほぼ同等のレベルで完全に分離する。照会処理は更新処理を遅延させたりアボートさせることはなく、逆に更新処理が照会処理をアボートさせることもない。ただし、1 つの条件下では更新処理が照会処理を遅延させる可能性がある。照会処理 \(T_q\) が \(x\) を読み取った時点で更新処理 \(T_i\) が \(x\) に対する認証ロックを保持しており、かつ \(TS(q)\) がその認証ロックの時刻よりも後である場合、\(T_q\) は \(T_i\) が \(x\) を認証するまで待機しなければならない。
 7. 結論
7. 結論
この論文はマルチバージョン・データベースにおける並行性制御問題を考察した。マルチバージョン・データベースは、並行性制御に新たな側面をもたらす。トランザクションはデータ項目に対する操作 (たとえば \(\mathrm{read}(x)\) や \(\mathrm{write}(x)\)) を発行するが、システムはこれらをバージョンを指定した操作に変換 (translate) しなければならない。単一バージョンデータベースでは並行性制御の正しさ読み取り操作と書き込み操作の処理順序に依存する。一方、マルチバージョンデータベースでの正しさは順序だけではなく変換 (translation) にも依存する。
我々はマルチバージョン・データベースの変換処理の側面を説明するために並行性制御理論を拡張した。その中核となる概念が 1-コピー直列化可能性 (one-copy serializability) である。すなわち、マルチバージョンデータベースにおけるトランザクションの実行が、単一バージョンデータベースにおける同じトランザクションの逐次的実行と等価である場合、その実行は 1-コピー直列化可能 (1-SR) である。マルチバージョン並行性制御アルゴリズムが正しいとは、そのすべての実行が 1-SR であることを指す。我々は実行が 1-SR であるための効果的で必要十分条件を導出し、これらの条件はバージョン順序 (version order) の概念が用いられる。さらに我々は、これらの条件を検証するためのグラフ構造であるマルチバージョン直列化グラフ (multiversion serialization graph, MVSG) を提案した。バージョン順序が定まれば、その実行の MVSG が非循環である場合に限り実行は 1-SR である。MVSG は単一バージョン並行性制御理論で広く用いられている直列化グラフに類似した概念である。
我々はこの理論を 3 種類のマルチバージョン並行性制御アルゴリズムに適用した。1 つのアルゴリズムはタイムスタンプを使用し、1 つはロックを使用し、1 つはロックとタイムスタンプを組み合わせている。タイムスタンプ方式のアルゴリズムは Reed [17] の研究に基づく。ロック方式は Bayer ら [1, 2] と Stearns と Rosenkrantz [20] の研究に着想を得て一般化したものである。組み合わせアルゴリズムは Prime Computer 社が開発したアルゴリズム [7] を一般化したものであり、Computer Corporation of America によって使用されている [6]。
 REFERENCES
REFERENCES
- BAYER, R., ELHARDT, E., HELLER, H., AND REISER, A. Distributed concurrency control in database systems. In Proc. 6th Int. Conf Very Large Data Bases (Montreal, Oct. 1-3, 1980), ACM, New York, 1980, pp. 275-284.
- BAYER, H., HELLER, H., AND REISER A. Parallelism and recovery in database systems. ACM Trans. Database Syst. 5, 2 (June 1980), 139-156.
- BERNSTEIN, P. A., AND GOODMAN, N. Concurrency control in distributed database systems. ACM Comput. Surv. 13, 2 (June 1981) 185-221.
- BERNSTEIN, P. A., SHIPMAN, D. W., AND WONG, W. S. Formal aspects of serializability in database concurrency control. IEEE Trans. Softw. Eng. SE-5, 3 (May 1979), 203-215.
- CASANOVA, M. A. The Concurrency Control Problem of Database Systems. Lecture Notes in Computer Science, vol. 116, Springer-Verlag, New York, 1981. (Originally published as Tech. Rep. TR-17-79, Center for Research in Computing Technology, Harvard University, 1979.)
- CHAN, A., FOX, S., LIN, W. T. K., NORI, A., AND RIES, D. R. The implementation of an integrated concurrency control and recovery scheme. In Proc. 1982 ACM SIGMOD Conf Management of Data (Orlando, Fla., June 2-4, 1982), M. Schkolnick, Ed., ACM, New York, 1982, pp. 184-191.
- DUBOURDIEU, D. J. Implementation of distributed transactions. In Proc. 1982 Berkeley Workshop on Distributed Data Management and Computer Networks, pp. 81-94.
- ESWARAN, K. P., GRAY, J. N., LORIE, R. A., AND TRAIGER, I. L. The notions of consistency and predicate locks in a database system. Commun. ACM 19, 11 (Nov. 1976), 624-633.
- GAREY, M. R., AND JOHNSON, D. S. Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman and Company, San Francisco, 1979.
- GRAY, J. N. Notes on database operating systems. In Operating Systems: An Advanced Course, Lecture Notes in Computer Science, vol. 66, Springer-Verlag, New York, 1978, pp. 393-481.
- HOLT, R. C. Some deadlock properties of computer systems. ACM Comput. Surv. 4, 3 (Sept. 1972), 179-196.
- KING, P. F., AND COLLMEYER, A. J. Database sharing-an efficient mechanism for supporting concurrent processes. In Proc. 1974 NCC, AFIPS Press, Montvale, N.J., 1974.
- LAMPORT, L. Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21, 7 (July 1978), 558-565.
- PAPADIMITRIOU, C. H. The serializability of concurrent database updates. J. ACM 26, 4 (Oct. 1979), 631-653.
- PAPADIMITRIOU, C. H., AND KANELLAKIS, P. C. On concurrency control by multiple versions. In Proc. ACM Symp. Principles of Database Systems (Los Angeles, March 29-31, 1982), ACM, New York, 1982, pp. 76-82.
- PAPADIMITRIOU, C. H., BERNSTEIN, P. A., AND ROTHNIE, J. B., JR. Some computational problems related to database concurrency control. In Proc. Conf. Theoretical Computer Science, (Waterloo, Ontario, Aug. 1977).
- REED, D. Naming and synchronization in a decentralized computer system. Tech. Rep. MIT/LCS/TR-205, Dept. Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Sept. 1978.
- ROSENKRANTZ, D. J., STEARNS, R. E., AND LEWIS, P. M., II System level concurrency control for distributed database systems. ACM Trans. Database Syst. 3, 2 (June 1978), 178-198.
- SILBERSCHATZ, A. A multi-version concurrency control scheme with no rollbacks. In Proc. ACM SIGACT-SIGOPS Symp. Principles of Distributed Computing (Ottawa, Canada, Aug. 18-20, 1982), ACM, New York, 1982, pp. 216-223.
- STEARNS, R. E., AND ROSENKRANTZ, D. J. Distributed database concurrency controls using before-values. In Proc. 1981 ACM SIGMOD Conf Management of Data, ACM, New York, 1981, pp. 74-83.
- STEARNS, R. E., LEWIS, P. M., II, AND ROSENKRANTZ, D. J. Concurrency controls for database systems. In Proc. 17th Symp. Foundations of Computer Science, IEEE, New York, 1976, pp. 19-32.
翻訳抄
MVCC として知られる、マルチバージョンデータベースシステムにおける並行性制御アルゴリズムの正当性を分析するための包括的な理論的フレームワークを確立し、1-コピー直列化可能性の概念とマルチバージョン直列化グラフによる判定手法を提示した 1983 年の論文。
- BERNSTEIN, Philip A. and GOODMAN, Nathan. Multiversion Concurrency Control - Theory and Algorithms. ACM Transactions on Database Systems. 1983, vol. 8, no. 4, pp. 465-483. ISSN 0362-5915. DOI: 10.1145/319996.319998.
