アルゴリズム

Federated Byzantine Agreement

Takami Torao #FBA
  • このエントリーをはてなブックマークに追加

概要

Federated Byzantine Agreement (FBA; 連合ビザンチン合意) は合意に参加する参加者それぞれの信頼に基づくクォーラム (quorum) と呼ばれる部分ネットワークを形成する P2P 向けのコンセンサス機構である。従来のビザンチン合意 (BA; Byzantine Agreement) 機構と比べてノードの参加が自由である (permissionless) という点が大きな特徴となっている。

その柔軟性の副作用として全体の効率や障害耐性がネットワーク構造に大きく依存することから、完全なランダムグラフ型 P2P ではなく、ある程度の範囲まで管理されたネットワーク構成とよく考慮された設計を必要とする。実際には SCP (Stellar Consensus Protocol) のようなより上位のレイヤーの基本的な設計方針として導入されている。

Table of Contents

  1. 概要
  2. アルゴリズム
    1. スロット
    2. クォーラムとスライス
    3. 階層化システムの例
  3. 従来のビザンチン合意との違い
  4. References

FBA の基本的な発想はネットワークをクォーラムスライス (quorum slice) と呼ばれる適切な規模のコンセンサス単位に分割することである。スライスは相互にリンクしており、複数のスライスに属しているノードがスライス間のゲートウェイの役割を持つことでコンセンサスをネットワークに波及させるクォーラムを形成する構造になっている。

ネットワークのスライス化は従来の BFT などで生じていた高いトラフィックを最小限のネットワークに閉じ込める効果を持つことから、ネットワークリソースの消費量を大きく削減することができる。このためスライス化によって大規模ネットワークで FBA を展開することを可能にするが、一方で合意の速度が遅くなるというトレードオフが発生する。

FBA に参加するノードは FBA ネットワーク上のすべてのノードを事前に認識する必要はなく、代わりに、自分がどのノードを信頼するかを選択してクォーラムスライスを作成する。自身のスライスから波及した少なくとも一つのクォーラム内のすべてのノードでステートメントが受理されれば、そのステートメントは合意されたとみなしている。

FBA は最初 Ripple によって実装され、その後 Stellar [1] によって形式化されたと言われている。その他にも Flare で導入されている。

アルゴリズム

スロット

FBA ではそれぞれの更新処理にスロット (slot) と呼ばれる識別子を割り当てて識別する。具体的には、更新処理とはメッセージやログ、またはトランザクションといったデータであり、スロットはそれらの更新処理を線形化 (linearize) したり因果一貫性を追跡するためのインデックスや ID に相当する。

ノード \(v\) がスロット \(i\) の更新処理 \(x_i\) を実行しようとするとき、(1) \(i\) が依存する他のすべてのスロットの更新処理が既に適用されており、(2) \(v\) が判断を依存しているすべてのノードが \(x_i\) の適用を安全に行えることに合意できれば、更新処理 \(x_i\) を実行することができる。更新処理 \(x_i\) の合意が形成された時点で \(x_i\) の内容を変更したり取り消すことはできない。この不可逆的な状態を \(x_i\) が外部化された (externalized) と言う。

クォーラムとスライス

FBA はノードの参加と離脱が自由であることから固定的なコンセンサスグループを想定することができない。その代わり、各ノードは FBA ネットワーク上で自分が信頼できる (自分と合意形成が可能と考える) 別のノードを指定する。この信頼先の単位をクォーラムスライス (quorum slice) または単にスライスと言う。

ノード \(v\) は特定のスロットに関する何らかのステートメントを主張するために自身が信頼するノード集合とメッセージを交換する。その後 \(v\) は、\(v\) のいずれかのスライスに属するすべてのノードがこのステートメントを受理するとそのステートメントは合意された (正常なノードがこのステートメントに反論することはない) とみなす。故障しているノードを選択していても合意を進行できるようにするためにノードは複数のスライスを持つことができる。

Fig 1 の例はノード \(v\) が選択した依存先のスライスを示している。\(v\) は 2 つのスライスを構成しており、それぞれ \(\{v\), \(v_a\), \(v_b\}\) と \(\{v\), \(v_a\), \(v_c\), \(v_d\}\) である (スライスには暗黙的に \(v\) 自身が含まれる)。この例での \(v_a\) のように複数のスライスで共通のノードを持つこともできる。

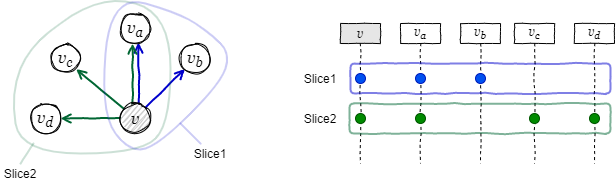
Quorum Slice
Fig 1. あるノード \(v\) を主体に見た信頼とスライスの例。

この例では \(v\) があるステートメントの合意を得る場合、ステートメントを \(\{v_a,\ldots,v_d\}\) の全てに送信し、Slice 1 または Slice 2 のどちらかに含まれるすべてのノードが受理すればステートメントは合意されたと見なすことができる。ここで送信先のノードはさらに自身が依存するノードとステートメントの関する合意を形成することに注意。

ここでノード \(v\) を構成するスライスの集合を \(Q(v)\) と表記する。Fig 1 の例では \(Q(v)=\{\{v,\) \(v_a,\) \(v_b\},\) \(\{v,\) \(v_a,\) \(v_c,\) \(v_d\}\}\) である。各ノードがこのようなスライスを持つことで FBA ネットワーク全体で依存関係の有方向グラフが形成される。

Fig 2 は \(v_1\) から \(v_7\) までのノードの依存関係を示したネットワークの例である (各ノードはただ 1 つのスライスを持つと仮定する)。\(v_1\) が何らかのステートメントを主張するとき、\(v_1\) 自身の受理に加えて \(v_2\) と \(v_3\) の受理が必要だが、\(v_2\) や \(v_3\) が受理するにはさらに別のノードとの合意が必要である。この依存関係を追跡すると最終的に \(v_1\) のステートメントはすべてのノードで受理されることが必要となる。一方で \(v_5\) が主張するステートメントは \(v_6\), \(v_7\) でのみ受理されれば良い。

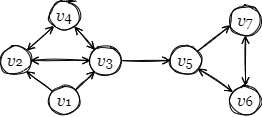
Quorum
Fig 2. ノードの依存関係を示した有方向グラフの例。

ここで Fig 2 において \(\{v_1,\) \(\ldots,\) \(v_7\}\) ように依存関係が接続グラフを形成している単位をクォーラム (quorum) と呼ぶ。FBA およびクォーラムは [1] において以下のように定義されている:

  • Federated Byzantine Agreement System (FBAS) はノード集合 \(V\) と、各ノードに対して 1 つ以上のクォーラムスライスを特定するクォーラム関数 \(Q: V \to 2^{2^V} \backslash \{\emptyset\}\) からなるペア \(\langle V,Q \rangle\) である (\(2^x\) は \(x\) の冪集合)。ここでノードは自身のすべてのクォーラムスライスに暗に属している。つまり \(\forall v \in V\), \(\forall q \in Q(v)\), \(v \in q\) である。
    • compounding
  • FBAS \(\langle V,Q\rangle\) のノード集合 \(U \subseteq V\) は、\(U \ne \emptyset\) かつ \(U\) に含まれる各ノードのスライスが \(U\) に含まれている場合、つまり \(\forall v \in U\), \(\exists q \in Q(v)\) で \(q \subseteq U\) であればクォーラムである。

クォーラムは交差 (quorum intersection) によって結合しより大きなクォーラムを形成することができる。ネットワークのある部分が交差していない場合、つまり (すべてのノードは正常だがスライスの構成により) 非連結グラフとなっている場合はそれぞれのクォーラムが独立して合意を形成するため競合や矛盾が発生する。

FBA ネットワークに存在する故障ノードの集合を \(B\) とする。ノード \(v\) の各スライスが \(B\) のノードを少なくとも 1 つ含んでいる場合、\(v\) の liveness 特性は破られる。このような \(v\) の合意の進行を阻害する故障ノードの集合を \(v\)-blocking と呼ぶ。

クォーラムによる構成は柔軟性が高く、十分に考慮して設計すれば障害耐性の高いネットワークを構築することができる。一方で、クォーラム交差が脆弱化しやすく、無配慮に構築するとノード故障や悪意的ノードが交差を専有して合意が達成できなくなったり (liveness の欠落) 矛盾したステートメントに合意する (safety の欠落) 可能性がある。

階層化システムの例

FBA のクォーラムとスライスによる構造は Fig 3 は階層構造で構成した FBA システムの例である。上位層は 4 つのノードで構成されており (ビザンチン障害かどうかに関わらず) \(f=1\) 個までのノード故障を想定している。つまり上位層のあるノードがステートメントを主張するとき、自身を含む 3 つのノードが受理すれば上位層での合意が形成されたとみなすことができる。したがって 4 つのノードはそれぞれ Fig 3 の右側のように 3 つのスライスを持ち、その中の少なくとも 1 つのスライスが納得すればステートメントは受理されたとみなすことができる。

下位層に属するノードは (下位層のノードに依存するのではなく) 上位層のノードを選るためには、依存先の異なる 2 つのスライスを持てば十分である。

Tiered FBA System
Fig 3. 階層化構成した FBA システムの例。

同様に直上の層と接続して層を重ねてゆくことで多階層の構造を構築することができる。

従来のビザンチン合意との違い

前述の通り、従来の BFT (Byzantine Fault-Tolerant) 機構と FBA との最も大きな違いは合意を形成するノード集合の構成が動的に変化するという点である。

BFT は \(f\) 個のビザンチン故障を許容するために \(3f+1\) ノードで構成する。これは決定論的なビザンチン障害耐性をもたらす代わりに参加ノードを固定しなければならない (ノードの参加/離脱のメンバーシップ変更も合意が必要である)。一方で、参加ノードが動的に変化することを前提とした FBA では固定の定足数に依存せず、ノード \(v\) のステートメントは \(v\) が選択したクォーラムの一つに含まれるすべてのノードがステートメントを受理したことを示す投票を集めることで合意されたとみなす。

また Fig 3 の上位層は \(3f+1=4\) 構成の BFT と同じであること考えると、従来のビザンチン合意アルゴリズムに基づく固定的なコンセンサスグループの構成は FBA における特殊なクォーラム構成に一般化することができる。

References

  1. MAZIERES, David. The stellar consensus protocol: A federated model for internet-level consensus. Stellar Development Foundation, 2015, 32.
  2. Aspasia Zoi. Study of consensus protocols and improvement of the Federated Byzantine Agreement (FBA) algorithm, UPCommons, 2019