論文翻訳: Synchronous Byzantine Agreement with Expected \(O(1)\) Rounds, Expected \(O(n^2)\) Communication, and Optimal Resilience
ラウンド期待値 \(O(1)\)、通信期待値 \(O(n^2)\)、そして最適な回復力を備えた同期ビザンチン合意

Abstract

我々は \(n=2f+1\) 個の当事者間で最適な数の \(f\) 個の故障を許容する、同期的かつ認証された設定におけるビザンチン合意のための新しいプロトコルを提示する。我々のプロトコルは、ラウンド複雑性の期待値 \(O(1)\) と通信複雑性の期待値 \(O(n^2)\) を達成している。予想される正確なラウンド複雑性は、静的な敵対者に対して 10 ラウンド、強い急襲の (strongly rushing) 適応的敵対者に対して 16 ラウンドである。なお比較として同じ設定における過去のプロトコルでは 29 ラウンドを必要とする。

Table of Contents

1. Abstract
2. 1 導入
   1. 1.1 技術概要
3. 2 モデル
4. 3 同期ビザンチン Synod プロトコル
   1. 3.1 コアプロトコル
   2. 3.2 安全性、終了、有効性
   3. 3.3 適応的敵対者に対抗するランダムリーダー選出
   4. 3.4 ラウンド複雑性と通信複雑性
5. 4 ビザンチンブロードキャストと合意
6. 5 クロック同期
7. Acknowledgements
8. References
9. 翻訳抄

1 導入

ビザンチン合意 (Byzantine agreement) [24] は分散コンピューティングや暗号技術における基礎的な問題である。この問題は障害耐性を持つ分散システム [5, 9, 22, 33]、安全なマルチパーティ計算 [7, 17]、そして最近では暗号通貨 [4, 21, 28, 29] の構築に使用されている。ビザンチン合意では、それぞれが初期入力値を保持する \(n\) 個の当事者のグループが共通の値にコミットすることを望んでいるが、最大 \(f\) 個の当事者がビザンチン故障を持ち、プロトコルから任意に逸脱する可能性がある。ビザンチンブロードキャスト (Byzantine broadcast) と呼ばれる密接に関連した問題では各当事者が入力値を保持する代わりに値をブロードキャストしようとする唯一の送信者 (sender) が存在する。些末な解決策を排除するためにどちらの問題にも追加の妥当性要件が追加されている。

ビザンチン合意とビザンチンブロードキャストは様々な仮定、特にタイミング仮定 (同期、非同期、または部分同期) とセットアップ仮定 (暗号、公開鍵基盤 (PKI)) の下で研究されてきた。これらの仮定が障害耐性の限界に大きな影響を与えることが現在では広く理解されている。特にビザンチン合意とビザンチンブロードキャストは両方とも部分同期または非同期で \(f \lt n/3\) が必要である。しかしデジタル署名と PKI を用いた同期の下ではビザンチン合意は \(f \lt n/2\)、ビザンチンブロードキャストは \(f \lt n-1\) で解くことができる。

この論文では同期かつ認証済み (つまり電子署名と PKI を想定) の設定におけるビザンチン合意を考察する。我々が考慮する効率性指標は (1) ラウンド複雑性、すなはちプロトコルが終了するまでの通信ラウンド数、および (2) 通信複雑性、すはなちプロトコルの間に当事者間で交換される情報量である。便宜上、当事者間で交換される署名の数を用いて通信複雑性を測定する。各署名が \(\lambda\) ビットであると仮定すると、通信複雑性に \(\lambda\) を乗じることで漸近的な通信複雑性がビット単位で得られる。

同期および非同期設定では Dolev と Strong が \(f \lt n-1\) の決定論的ビザンチンブロードキャストプロトコルを与えた [12]。彼らのプロトコルは \(f+1\) のラウンド複雑性と \(O(n^2)\) の通信複雑性を達成している。\(f+1\) ラウンド複雑性は決定論的プロトコルの下限と一致する [12, 15]。ラウンド複雑性をさらに改善させるためにランダム化プロトコルが導入されている [6, 14, 16, 31]。我々の知る限り、最も効率の良いプロトコルは Kats と Koo によって提案されたものであり、これは \(f \lt n/2\) のビザンチン合意を期待値 29 ラウンドで解決する⁶。

この研究では通信複雑性の期待値を \(O(n^2)\) に、ラウンド複雑性の期待値を 16 に改善する。我々のプロトコルではしきい値署名 [8, 32] を使用して通信料を削減し、ランダムなリーダー選出サブルーチンを使用してラウンド数を削減する。ランダムリーダー選出サブルーチンは共通コインプロトコル (common-coin protocol) を使用して構築でき、文献 [8, 27] では単一ラウンドと \(O(n^2)\) 通信のものが存在する。Cachin ら [8] のプロトコルは静的敵対者に対して安全であり、Loss と Moran [27] のプロトコルは適応型敵対者に対して安全である。これらを用いて次の結果を得る。

定理 1. 同期認証ビザンチン合意 (synchronous authenticated Byzantine agreement) は

• 単一ラウドの共通コインプロトコルを想定した静的な敵対者に対して期待値 10 ラウンドと期待値 \(O(n^2)\) 通信
• 適応的に安全な単一ラウンドの共通コインプロトコルを想定した強い急襲の適応型敵対者に対して期待値 16 ラウンドと期待値 \(O(n^2)\) 通信

を \(f \lt n/2\) で解くことができる。

我々のプロトコルは非常に強力な、我々が強い急襲の適応的敵対者 (strongly rushing adaptive adversary) と呼ぶ敵対者の存在下でも機能することは注目に値する。この敵対者はどの \(f\) 個の当事者をいつ故障させるかを適応的に決定できる。また "強い急襲" とは、ラウンド \(r\) である当事者 \(h\) から他の当事者に送られたメッセージを敵対者が観測した後に当事者 \(h\) を故障させると決めたとき、\(h\) の round-\(r\) メッセージが他の誠実な当事者たちに届く前にネットワークから削除できることを意味している。対照的に標準的な急襲の敵対者は誠実な参加者の round-\(r\) メッセージを観測した後に自分の round-\(r\) メッセージを決定できるが、ラウンド \(r\) で \(h\) を故障させたのであれば \(h\) の round-\(r\) メッセージを他の当事者たちから "取り戻す" または変更することはできない。Dolev-Strong と Kats-Koo プロトコルはこのような強い急襲の適応的敵対者に対しても機能する。

\(O(1)\) 期待値ラウンドは明らかに漸近的に最適である。自然な疑問は二次通信量の期待値がさらに改善されるかどうかである。Dolev と Reischuk [11] の研究をもとにした後続の研究 [1] では強い急襲の適応的敵対者に対して \(\Omega(f^2)\) のメッセージ期待値が必要である。King-Saia [20] と我々の後続研究 [1] は準二次通信を用いてビザンチン合意を解決する。当然のことながら、これらのプロトコルは標準的な急襲の適応的敵対者には有効だが強い急襲の適応的敵対者には有効ではない。

• 論文の予備稿は 2017 年に ePrint に掲載された [2]。このバージョンはそのビザンチン合意部分が改善され組み込まれたものである。
• ⁶Kats と Koo [19] は彼らの論文で通信複雑性を分析していない。我々の理解では、付録で展開されたプロトコルは、同様にしきい値署名と二次共通コインプロトコルを組み込むことによって \(O(n^2)\) 通信複雑性を達成できる。

1.1 技術概要

このプロトコルはビザンチンブロードキャスト/合意で要求される合意 (この論文の残りでは安全性 (safety) と呼ぶ) と終了 (termination) を保証するが有効性 (validity) の弱い概念を提供する。具体的には以下を実現する:

• Termination: すべての誠実な当事者は最終的にコミットする。
• Agreement/safety: すべての誠実な当事者は同じ値をコミットし、
• Validity: すべての誠実な当事者が同じ値 \(v\) に対する証明書で開始し、ビザンチンの当事者が矛盾する値に対する証明書で開始しない場合、すべての誠実な当事者は \(v\) にコミットする。

セクション 4 ではビザンチン合意またはビザンチンブロードキャストを解決するためにこれらの証明書を取得する方法について解説する。

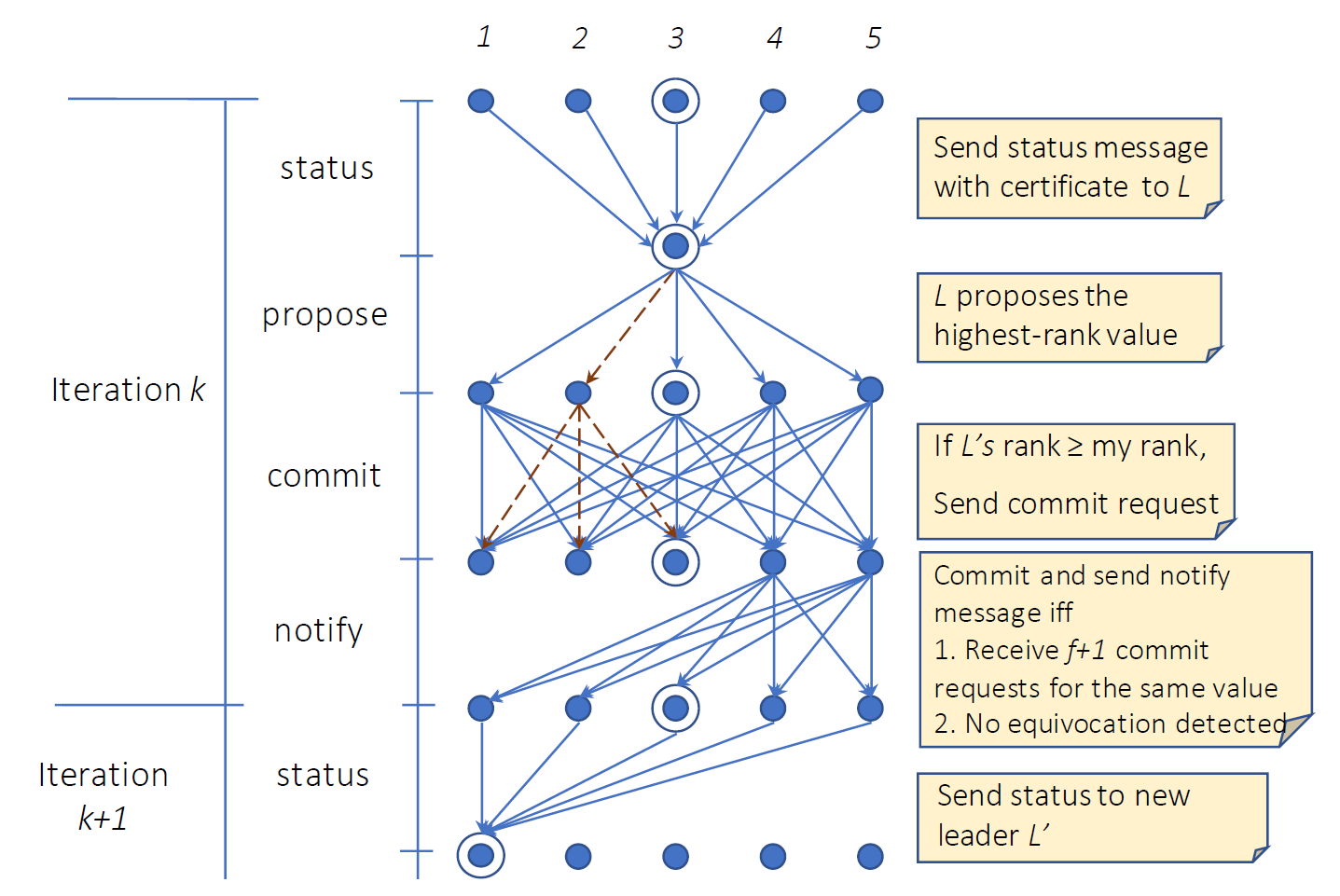
コアプロトコルは繰り返し実行される。各反復では一意のリーダーが選出される。新しいリーダーは前のリーダーが残した状態をピックアップしてその繰り返しで値を提案する。その後、当事者はリーダーの値 \(v\) に投票する。より詳細には、各反復は 4 ラウンドで構成されている。最初の 3 ラウンドは Paxos や PBFT と概念的に似ている: (1) リーダーがシステムの状態を学習し、(2) リーダーが値を提案し、(3) 当事者が値に投票する。当事者が同じ値に対して \(f+1\) 票を獲得しリーダーの曖昧さを検知できなければその値でコミットする。ここで我々は別のラウンドを追加する: (4) ある当事者がコミットすると、そのコミットについて他の当事者に通知する。通知を受け入れたほかの当事者はコミットされた値を受け入れ (accept)、将来のリーダーにその値を保証する。

理想的には、リーダーが誠実であればその反復の最後に \(v\) に対する \(f+1\) 票を受け取った時点で \(v\) をコミットする。ビザンチンのリーダーは鄭亜案しないことで簡単にその反復を無駄にすることができる。しかし次のようなより巧妙な攻撃を実行することもできる: (1) 矛盾する提案を別々の誠実者に送る、または (2) 提案を一部の誠実な当事者に送信するが、すべての当事者には送信しない。このようなビザンチン的な振る舞いが安全性を損なわないようにしなければならない。

等価性チェックの必要性. 最初の攻撃に対する安全性を確保するために、当事者は all-to-all ラウンドの通信に参加してリーダーの提案を相互に転送し等価性のチェックを行う。もしある当事者がリーダーの矛盾を検出した場合、つまりリーダーから 2 つの競合する署名済み提案を観測した場合、たとえ \(f+1\) 票を獲得していてもコミットしない。

notify ラウンドの必要性. 二番目の攻撃を使用すると、ビザンチンのリーダーはすべてではないが一部の誠実な当事者に値 \(v\) をコミットさせることができる。他の誠実な当事者が \(v\) がコミットされたことを知らない場合、後続の反復で \(v' \ne v\) をコミットする可能性がある。したがって誠実な当事者 \(h\) が値 \(v\) をコミットするときはいつでも、\(h\) は他のすべての誠実な当事者にそのコミットを通知する必要がある。\(h\) は受け取った \(h+1\) 票をブロードキャストすることでこれを行うことができる。別の当事者 \(h'\) がそのような通知を受け取ると、値 \(v\) を "受け入れ" る。ある当事者が \(v\) を受け入れ、のちの反復で提案 \(v' \ne v\) を受け取った場合、\(v'\) への投票が安全であるという証拠が示されない限り \(v'\) に投票することはない。詳細セクション 3 を参照。

安全性、終了、および有効性. 安全性は、誠実な当事者がコミットするときは (1) 他の当事者は同じ反復で異なる値をコミットできない (等価性チェックのため)、(2) 他の値はその後の反復で十分な票を集められない (誠実者の notify のため) ことで確保される。有効性は同様の論議から導かれる: すべての誠実な当事者が同じ認定済み (つまり受け入れられている) 値 \(v\) でプロトコルを開始し、ビザンチン当事者が異なる認定済み値を持っていない場合、\(v\) だけが十分な票を集めることができる。終了は誠実な当事者 \(h\) が \(f+1\) 個の notify メッセージを受信すると達成される。このとき \(h\) はこれらの \(f+1\) 通知を他のすべての当事者に送信し終了する。\(h\) が送信した \(f+1\) 個の通知により、次のラウンドでほかのすべてのパーティが終了することが保証される。誠実なリーダーが現れた場合、すべての当事者はその繰り返しで終了する。

ラウンド複雑性と通信複雑性. \(2f+1\) 当事者のうち \(f+1\) 誠実者が存在するため反復ごとにランダムなリーダーを選出することでプロトコルは期待値として 2 回の反復で終了する。敵対的モデルに応じて各反復は 4 ラウンドから 7 ラウンドになる。それぞれのラウンドは \(O(n^2)\) のメッセージ (all-to-all) を使用し、各メッセージの単位は単一の署名又は単一の \((f+1)\)-out-of-\(n\) しきい値署名である。そのためプロトコルは期待値 \(O(1)\) ラウンドで実行され、期待値 \(O(n^2)\) 通信を使用する。

Paxos, PBFT, XPaxos, そして我々のプロトコル. 抽象的には子のコアプロトコルは Paxos [23] の synod アルゴリズムに似ているが、同期およびビザンチン設定に適合している。synod アルゴリズムの主な考え方は、一人の誠実な当事者でクォーラムの交差 [23] を保証することである。Paxos の核となる考え方は、値をコミットする前にサイズ \(f+1\) のクォーラムを形成することである。\(n=2f+1\) では 2 つのクォーラムは常に 1 つの Paxos の誠実な当事者で交差する。この交差にいる誠実な当事者は将来のリーダーにコミットされている値を尊重するよう強いるだろう。\(f\) 個のビザンチン故障を許容するため、PBFT [9] は \(n=3f+1\) のうちサイズ \(2f+1\) のクォーラムを使用する。2 つのクォーラムが \(f+1\) の当事者で交差し、そのうち 1 個は誠実者であることが保証されている。PBFT と同様に、我々も \(f+1\) 個の当事者でクォーラムが交差することを保証する必要がある。ただしこれには合計で \(n=2f+1\) 個の当事者を持つ新しい技術が必要である。一方ではサイズ \(f+1\) の交差はサイズ \(1.5f+1\) のクォーラムを必要とするようである。(Thunderella [30] と呼ばれる後続の研究はこのクォーラムサイズを使用して楽観的なケースを改善している。) 一方、\(f+1\) (誠実な当事者の数) より大きなクォーラムサイズは必然的にビザンチン当事者が含まれて、その結果 liveness を失うようである。コアプロとｋルセ説明したように我々の同期 notify ラウンドはサイズ \(2f+1\) のポストコミットクォーラム (post-commit quorum) を形成し、それはサイズ \(f+1\) の任意のプレコミットクォーラム (pre-commit quorum) と \(f+1\) 当事者で交差する。これにより交差に誠実な当事者が 1 人はいるという要件を満たす。さらに、ポストコミットクォーラムの当事者はメッセージを受け取るだけなので liveness には影響を与えない。

また我々のプロトコルは XPaxos [26] と類似している部分もある。XPaxos では、ビューの変更には (リーダーを変更するだけではなく) \(f+1\) 個のアクティブなレプリカのセットを変更することが含まれている。古いビューのすべてのアクティブなレプリカが新しいビューのすべてのアクティブなレプリカに通知する限り、新しいビューにはビュー間で状態を保持できる誠実なレプリカが 1 つ存在することになる。ただし XPaxos はすべての \(f+1\) 個のアクティブなレプリカがすべて誠実である場合にのみ処理が進む。これに対して我々のプロトコルは、リーダーが誠実であることのみで進行が可能である。

ビザンチンブロードキャストとビザンチン合意の実現. コアプロトコルはすでに安全性と終了を保証しているため、その弱い有効性をビザンチンブロードキャスト/合意が必要とするレベルまで高める技術が必要なだけである。我々のプロトコルは、プロトコルを呼び出す前に 1 ラウンドの all-to-all 通信を使用してこれを達成する。これによりビザンチン合意を達成するために \(n\) 個の並列ビザンチンブロードキャストを合成するという標準的な変換を回避することができる。その結果、我々のビザンチン合意プロトコルはコアプロトコルと同じ漸近ラウンド/通信複雑性を持つことになる。

2 モデル

我々は同期を想定している。ラウンドの開始時に誠実な当事者 \(i\) が他の誠実な当事者 \(j\) にメッセージを送信すると、そのメッセージはラウンドの終わりまでに到着することが保証されている。ここではロックステップ実行 (lock-step execution)、すなはち当事者が各ラウンドに同時に参加し同時に退出することを前提としたプロトコルについて説明する。セクション ?? の後半では限定されたメッセージ遅延からロックステップ実行を起動するためのクロック同期プロトコルを提示する。

我々はデジタル署名と信頼できるセットアップ (trusted setup) を仮定する。信頼できるセットアップフェーズでは信頼できるディーラーが各当事者の電子署名やほかの暗号プリミティブのための公開鍵/秘密鍵ペアを生成し、各当事者の公開鍵を証明する。我々は当事者 \(i\) によって署名されたメッセージ \(x\) を \(\langle x \rangle_i\) と表記する。すなはち \(\langle x \rangle_i =\) \((x,\sigma)\) で \(\sigma\) は当事者 \(i\) が秘密署名鍵を使用して生成したメッセージ \(x\) の署名である。効率化のためにメッセージのハッシュダイジェストに署名するのが通例である。メッセージはレイヤー内の複数の当事者 (または同じ当事者) によって署名できる。すはなち \(\langle\langle x \rangle_i \rangle_j =\) \(\langle x,\sigma_i\rangle_j =\) \((x,\sigma_i,\sigma_j)\)、ここで \(\sigma_i\) は \(x\) の署名、\(\sigma_j\) は \(x \ || \ \sigma_i\) のである (\(||\) は連結を表す)。文脈が明確な場合は署名者を省略して \(\langle x \rangle\) または \(\langle \langle x \rangle \rangle\) と表記する。

ランダムリーダー選出サブルーチンが必要である。前述のようにこのサブルーチンは共通コインプロトコル [8, 27] や検証可能なランダム関数 [28] を用いてインスタンス化することが可能である。また上位レベルのプロトコルに任せることもできる。例えば暗号通貨では proof-of-work に基づいてリーダーを選出するだろう。

強い急襲の適応的敵対者を想定する。信頼済みセットアップフェーズのあと、敵対者はプロトコル実行中にどの \(f\) 個の当事者を破損させるか、そしていつそれぞれの当事者を破損させるかを適応的に決定することができる。しかし敵対者は移動可能 (mobile) でないことに注意。ビザンチン当事者の破損を解除して破損割当量を回復することはできない。また敵対者は強い急襲を行う。各ラウンドにおいて敵対者は任意の当事者 \(i\) から他の当事者 \(j\) へのメッセージを観測している。もし敵対者がこの時点で \(i\) を破損することを決定すると、\(i\) がメッセージを送信した他の誠実な当事者 (存在すれば) のうちどれに送るかと、\(i\) が送信したどのメッセージを送るかをそのラウンド内で制御する。

3 同期ビザンチン Synod プロトコル

3.1 コアプロトコル

コアプロトコルは \(n=2f+1\) 個の当事者を持つ同期ビザンチン synod プロトコルである。コア synod プロトコルの目的はすべての誠実な当事者が最終的に同じ値 (合意) でコミットする (終了) ことを保証することである。また次のような有効性の概念を実現する: もし (1) すべての誠実な当事者が同じ値で開始し、この値の証明書を持っており、(2) 敵対者が矛盾した値の証明書で開始していない場合、すべての誠実な当事者がこの値にコミットする。セクション 4 ではビザンチンブロードキャストとビザンチン合意を実現するために単一のプレラウンドを用いてこれらの証明書を取得する方法を示す。説明を簡単にするためにセクション 3 ではコアプロトコルを提示しながら一時的に静的敵対者を仮定する。静的敵対者は信頼済みセットアップフェーズの後、プロトコルが始まる前にどの当事者を破損させるかを決定する必要がある。

ここでプロトコルの詳細を説明する。リーダーが反復 \(k\) で値 \(v\) を提案するとき、その提案はランク \(k\) であると言い、それらをタプル \((v,k)\) と書く。最初の反復は \(k=1\) である。各当事者 \(i\) は受理した提案を記録するために反復全体で状態 \({\sf accepted}_i=(v_i,k_i,\mathcal{C}_i)\) を内部的に維持する。最初に各当事者 \(i\) は \({\sf accepted}_i := (\perp,0,\perp)\) で初期化する。後に当事者 \(i\) が \((v,k)\) を受理する場合、\({\sf accepted}_i := (v,k,\mathcal{C})\) を設定する。ここで \(\mathcal{C}\) は反復 \(k\) で \(v\) が合法的に受け入れられたことを証明する (certifies)。\(\mathcal{C}\) は提案 \((v,k)\) に対する \(f+1\) 個の \({\sf commit}\) リクエストからなる (詳細はプロトコル参照)。我々はまた \(\mathcal{C}\) は \((v,k)\) を証明する (certifies)、あるいは \((v,k)\) に対する証明書であると言う。提案は、それが行われた反復番号によってランク付けされる。すはなち \((v,k)\) は \(k\gt k'\), \(k\lt k'\), \(k=k'\) のときそれぞれ \((v',k')\) より上位、下位、または同等とランク付けされる。証明書はそれが証明する提案によってランク付けされる。当事者がメッセージを "ブロードキャスト" するというのは、自分自身を含むすべての当事者にメッセージを送信することを意味する。

ラウンド 0 (\({\sf elect}\))

すべての当事者は [8] のしきい値コイントススキームに参加する。彼らのスキームは 1 ラウンドのコストがかかり、すべての当事者にランダム列を出力する。このランダム列の \(n\) 余剰は現在の反復 \(k\) に対するランダムなリーダー \(L_k\) を定義する。以下簡略化のために \(L_k\) を \(L\) と書く。

ラウンド 1 (\({\sf status}\))

各当事者 \(i\) は \(L\) に \(\langle k, {\sf status}, v_i, k_i, \mathcal{C}_i \rangle\) メッセージを送信し、現在受理している値を報告する。

このラウンドの終わりに、もし当事者 \(i\) が \(L\) に最高の証明書を報告した場合 (\(i\) は \(L\) 自身かもしれない)、\(L\) は \({\sf accepted}_L =\) \((v_L,k_L,\mathcal{C}_L) :=\) \((v_i,k_i,\mathcal{C}_i)\) を設定する。どの当事者も証明書を報告しなければ \(L\) は \(v_L\) を自由に選択し \(k_L:=0\) と \(\mathcal{C}_L:=\perp\) を設定する。

ラウンド 2 (\({\sf propose}\))

\(L\) は署名付き提案 \(\langle\langle k, {\sf propose}, v_L \rangle_L, k_L, \mathcal{C}_L \rangle_L\) をブロードキャストする。

このラウンドの終わりに、当事者 \(i\) は上記のリーダー提案で受け取った証明書が \(i\) がリーダーに報告したものより低くない場合、つまり \(k_L \ge k_i\) の場合に \(v_{L\to i} := v_L\) を設定する。そうでない場合 (リーダーが故障している)、\(v_{L\to i} := \perp\) を設定する。

ラウンド 3 (\({\sf commit}\))

\(v_{L \to i} \ne \perp\) の場合、当事者 \(i\) は提案 \(\langle k, {\sf propose}, v_{L \to i} \rangle_L\) を他のすべての当事者に転送し、\(\langle k, {\sf commit}, v_{L \to i} \rangle_i\) リクエストをブロードキャストする。

ラウンドの終わりに、当事者 \(i\) が \(v' \ne v_{L \to i}\) となるような正規に署名された提案 \(\langle k, {\sf propose}, v' \rangle_L\) を転送されたなら、この反復ではコミットしない (リーダーは曖昧である)。一方、当事者 \(i\) が \(v=v_{L \to i}\) となる \(f+1\) 個の \(\langle k,{\sf commit},v \rangle_j\) リクエストを受け取った場合、\(v\) でコミットしてその内部状態 \(\mathcal{C}_i\) をこれらの \(f+1\) 個の \({\sf commit}\) リクエストを連結したものに設定する。つまり、当事者 \(i\) は一致する \(f+1\) 個の \({\sf commit}\) 要求を受信し、かつ、リーダーの曖昧さを検出しない場合にのみコミットする。

ラウンド 4 (\({\sf notify}\)

当事者 \(i\) が前のラウンドで値 \(v\) でコミットしている場合、通知 \(\langle\langle {\sf notify},v \rangle_i,\mathcal{C}_i \rangle_i\) を他のすべての当事者に送信する。

ラウンドの終わりに、当事者 \(i\) が \(\langle\langle {\sf notify},v \rangle_j, \mathcal{C}\rangle_j\) メッセージを受信すると、\({\sf accepted}_i =\) \((v_i,k_i,\mathcal{C}_i) :=\) \((v,k,\mathcal{C})\) を設定することで \(v\) を受理する。もし当事者 \(i\) が値の異なる複数の有効な \({\sf notify}\) メッセージを受信したとき (これがどのように起きるかはセクション 3.2 の最後で説明する)、任意の一つを受理することができる。最後に、当事者 \(i\) は反復カウンター \(k\) をインクリメントして次の反復に入る。

早期かつ非同期的な終了. プロトコル中の任意の時点で、ある当事者が \(f+1\) の個別の当事者から (証明書を除く) 通知ヘッダー (notification headers) \(\langle {\sf notify}, v \rangle\) を収集した場合、この \(f+1\) 個の通知ヘッダを他のすべての当事者に送信して終了する。これにより最初の誠実な当事者が終了するとき他のすべての誠実な当事者は \(n+1\) 個の通知ヘッダを受信し次のラウンドで終了することができる。

3.2 安全性、終了、有効性

このセクションではセクション 3.1 のコアプロトコルが安全性、終了、および弱い有効性の概念を提供することを証明する。

安全性. まず理解を助けるためにいくつかの直感的な説明をする。安全性のために考慮すべきシナリオは、誠実な当事者 \(h\) が反復 \(k^*\) で値 \(v^*\) をコミットする場合である。まずビザンチン当事者が反復 \(k^*\) において \(v^*\) 以外の値に対する証明書を持ちえないことを示す。したがって、他のすべての誠実な当事者は誠実な当事者 \(h\) から \({\sf notify}\) を受信すると反復 \(k^*\) の終了時に \(v^*\) を受理する。したがって、\(v^*\) 以外の値は反復 \(k^* + 1\) で十分な票を得られず、したがって反復 \(k^* + 2\) で十分な票を得られず、といった具合になる。そして安全性は帰納的に成立する。

ここで我々は証明書に関する次の補題を証明することで上記の直感を形式化する: 誠実な当事者が一度コミットすると、その反復および将来の反復におけるすべての証明書はそのコミットされた値のみを証明することができる。

補題 1. 当事者 \(h\) がコミットする最初の誠実な当事者であり、反復 \(k^*\) で \(v^*\) に対してコミットするとする。もし \((v,k^*)\) に対する証明書 \(\mathcal{C}\) が存在するなら、\(v=v^*\) である。

証明. \(\mathcal{C}\) は \(v\) に対する \(f+1\) 個の \({\sf commit}\) リクエストで構成されなければならない。これらのうち少なくとも一つは誠実な当事者 (\(h_1\) と呼ぶ) に由来するものである。しがたって、\(h_1\) はリーダーから \(v\) に対する提案を受信しており、その提案を他のすべての当事者に転送していなければならない。もし \(v \ne v^*\) であれば、\(h\) はリーダーの曖昧性を検出し、この反復で \(v^*\) にコミットすることはないだろう。したがって \(v=v^*\) を得る。

補題 2. 反復 \(k\) の開始時に (1) すべての誠実な当事者 \(i\) が \((v,k_i)\) に対する証明書を持ち、(2) すべての矛盾する証明書がより低いランク、つまり \(v \ne v'\) であるような \((v',k')\) に対するすべての証明書がすべての誠実な \(i\) に対してかならず \(k' \lt k\) であるとすると、上記 2 つの条件は反復 \(k\) の最後に保持される。

証明. ある当事者 (誠実かビザンチン) が \(v' \ne v\) に対して以前に持っていたものよりより高い証明書を取得したとする。このとき、それはある誠実な当事者 (\(h\) と呼ぶ) から反復 \(k\) で \(\langle k,{\sf commit},v'\rangle_h\) を受信していなければならない。\(h\) はな服 \(k\) の開始時に \((v,k_h)\) に対する証明書を持っていることに注意。\(h\) が \(v'\) に対する \({\sf commit}\) リクエストを送信するためには、リーダー \(L_k\) は \(k' \ge k_h\) となるような \((v',k')\) の証明書を示さなければならず、これは条件 (2) と矛盾する。

簡単な機能用により、上記の 2 つの条件は反復の開始時に真であれば永遠に真であることを示している。

定理 2 (安全性). ある 2 つの誠実な当事者がそれぞれ \(v\) と \(v'\) でコミットしたとき、\(v = v'\) である。

証明. 当事者 \(h\) が最初にコミットする誠実な当事者で、反復 \(k^*\) で \(v^*\) に対してコミットするとする。反復 \(k^*\) の \({\sf notify}\) ラウンドの後、すべての誠実な当事者は \((v^*,k^*)\) に対する証明書を受け取り \(v^*\) を受理する。さらに補題 1 より反復 \(k\) での \(v \ne v^*\) に対する \((v,k^*)\) の証明書は存在し得ない。よって反復 \(k\) の終了時点で補題 2 の 2 つの条件が成立する。つまりこの時点から \(v^*\) 以外の証明書は生成し得ない。誠実な当事者が \(v\) にコミットするためには \(k \ge k^*\) となる \((v,k)\) に対する証明書が存在しなければならない。したがって \(v = v^*\) となる。同様に \(v' = v^*\) であり \(v = v'\) となる。

終了. 次に、誠実なリーダーはすべての誠実な当事者がその反復の終わりまでに終了することを保証することを示す。

定理 3 (終了). 反復 \(k\) のリーダー \(L_k\) が誠実であれば、すべての誠実な当事者は反復 \(k\) の 1 ラウンド後 (またはそれ以前) に終了する。

証明. 誠実なリーダー \(L_k\) はすべての当事者に提案を送信する。これは \({\sf status}\) ラウンドで収集した最も高い証明書によって報告された値を提案するだろう。この証明書は誠実な当事者が保持するどの証明書よりも低くなることはない。さらに、デジタル署名の偽造不可能性によりビザンチン当事者が \(L\) を不正に避難することもできない。したがって、すべての誠実な当事者は \(v\) に対する \({\sf commit}\) リクエストを送信し、\(v\) に対する \(f+1\) 個の \({\sf commit}\) リクエストを受信し、\(v\) に対する通知ヘッダを送信し、\(v\) に対する \(f+1\) 個の通知ヘッダを受信し (これが反復 \(k\) の終了)、そして次のラウンドで終了するだろう。(\(f+1\) 個の通知ヘッダを受信し早期に終了することも可能である。)

有効性. 次にコアプロトコルが達成する有効性について述べる。定理ではコアプロトコルに入力される \((v,0)\) の初期証明書が存在すると仮定している。これらの初期署名所はコアプロトコルを呼び出す上位レベルのプロトコルによって提供される (セクション 4 参照)。

定理 4 (有効性). (1) すべての誠実な当事者が \(v\) を証明する初期証明書 \(\mathcal{C}\) で開始し、(2) どのビザンチン当事者も \(v' \ne v\) を証明する \(\mathcal{C}'\) を持っていないのであれば、すべての誠実な当事者は \(v\) でコミットする。

証明. 証明は補題 2 と定理 3 から明快である。入力規約は各 \(k_i=0\) で補題 2 の 2 つの条件を満たす。補題 2 により、以降のすべての反復において \(v\) のみが証明を持つことができ、したがって \(v\) のみがコミットされることができる。定理 3 により、誠実なリーダーが出現するとすべての誠実な当事者は \(v\) にコミットするだろう。

最後に、証明で明示的に扱う必要のない興味深いシナリオを挙げる。誠実な当事者がコミットする前に、ビザンチン当事者は同じ反復内で複数の値の証明書を取得することができる。特にビザンチンリーダーは \(f\) 個のビザンチン当事者すべてに 2 つの値 \(v\) と \(v'\) を提案する。(2 つ以上の値を持つ例も同様である。) そしてビザンチン当事者たちはそれらの間で両方の値の \(f\) 個の \({\sf commit}\) リクエストを交換する。さらにビザンチンリーダーは \(v\) と \(v'\) を異なる誠実な当事者たちに提案する。ここで、誠実な当事者からそれぞれの値に対する \({\sf commit}\) 要求がもう 1 つあれば、ビザンチン当事者は \(v\) と \(v'\) の両方に対する証明賞を得ることができ、誠実な当事者に異なる証明書 (\({\sf notify}\) メッセージ) を示すことで異なる値を受理させることができる。しかしこの反復では誠実な当事者はコミットしないため、安全性の違反には繋がらない: リーダーは誠実な当事者に曖昧さを示したため、すべての誠実な当事者は転送された提案から曖昧さを検出しコミットを拒否する。このシナリオは我々のプロトコルに同期性の仮定と電子署名の使用の両方が必要であることを示すものである。どちらか一方が欠けると曖昧さを確実に検出することができず、どのようなプロトコルも \(f \lt n/3\) の制約を受けることになる。完全性を期すために上記のシナリオも終了特性の違反にも繋がらないことに注意。反復の終わりには誠実な当事者はどちらの値も受け入れることができる。しかし次の反復では 2 つの値は同じランクであるため、他の値を受理したにもかかわらずいずれかの値に投票できる。

3.3 適応的敵対者に対抗するランダムリーダー選出

これまでに発表されたプロトコルは適応的な敵対者に対して期待される一定ラウンドを達成することができない。敵対者は反復の \({\sf elect}\) ラウンド後にリーダーが誰であるかを知る。そして直ちに \(L\) を破損させいかなる提案も送れないようにすることができる。このようにして敵対者はプロトコルを \(f\) 回反復するよう強制する。

適用的安全性に向けた最初の修正は、\({\sf elect}\) ラウンドを \({\sf propose}\) ラウンドの後、\({\sf commit}\) ラウンドの前に移動することです。これは \(L\) が破損するまでにすべての誠実な当事者がすでにその提案を受け取っていることを期待するものである。これは \(L_k\) が明らかになる前に、すなはち状態を集め提案を作成するための \({\sf status}\) と \({\sf propose}\) のラウンドにおいて、すべての当事者が潜在的なリーダーとして行動すべきであることを意味する。\({\sf commit}\) ラウンド以降は \(L\) の提案のみが関連する。

しかしこの考え方だけでは十分ではない。\({\sf elect}\) ラウンドの最後に \(L\) を特定した敵対者は \(L\) を破損させ \(L\) の秘密鍵を使って曖昧な提案に署名し、それをすべての誠実な当事者に転送する。誠実な当事者は \(L\) からの曖昧さを検出しこの反復ではコミットしない。我々は再びこのプロトコルを \(f\) 回反復実行することを余儀なくされる。

そのために、各当事者はリーダーが明らかになる前に、自分の提案を "準備" するステップを追加する必要がある。その後、"準備された" 提案のみが曖昧さチェックで考慮される。準備ステップは、ある当事者 \(h\) が準備中は誠実であったがその後に破損した場合、敵対者が \(h\) に変わって "準備された" 曖昧な提案を作成できないことを保証する必要がある。我々は次のように 2 つのラウンドで準備ステップを実現する。

• ラウンド P1 (\({\sf prepare}_1\)) 各当事者 \(i\) は自分の提案 \(\langle v_i,k\rangle_i\) をブロードキャストする。

• ラウンド P2 (\({\sf prepare}_2\)) 前のラウンドで当事者 \(j\) が当事者 \(i\) から提案 \(\langle v_i,k\rangle_i\) を受け取った場合、当事者 \(j\) は提案に署名し、当事者 \(i\) に \(\langle v_i,k\rangle_j\) を送り返す。

提案 \((v_i,k)\) が個別の当事者から \(f+1\) 個の署名を含んでいる場合、その提案は準備されていると言う。それぞれの誠実な当事者は自分の提案を準備することができる。もし当事者 \(i\) が 2 回の \({\sf prepare}\) ラウンドで誠実で、その後にのみ破損した場合、当事者 \(i\) に変わって矛盾する提案を準備するには少なくとも 1 つの誠実な当事者の署名を偽造する必要があるが、計算的に限られた敵対者にはそれができない。

強い急襲の適応的敵対者に対するコアプロトコルは現在 \({\sf status}\), \({\sf prepare}_1\), \({\sf prepare}_2\), \({\sf propose}\), \({\sf elect}\), \({\sf commit}\), \({\sf notify}\) の 7 ラウンドである。安全性と有効性の証明は静的のケースから変更されていない。終了の証明とラウンド複雑性の分析は、(1) 各リーダー \(L_k\) が明らかにされる時点まで誠実である可能性が \(\gt 1/2\) であること、(2) 反復 \(k\) の \({\sf propose}\) ラウンドの終了までに \(L_k\) がまだ誠実であれば、すべての誠実な当事者はその提案が有効とみなして反復 \(k\) の 1 ラウンド後に終了することを観測した時点でも成立する。

検証可能なランダム関数に基づくリーダー選出 [28] は我々の \({\sf prepare}\) ラウンドと合わせることで (通常の) 急襲の適応型敵対者に対して期待値で 2 回の反復を達成することができる。しかし強い急襲の適応型敵対者に対しては、敵対者がリーダーを受け取った後にそのランクを公表するのを阻止することができるため \(f\) 回の反復を実行するだろう。

3.4 ラウンド複雑性と通信複雑性

最初の誠実なリーダーによって収量が保証される。ランダムなリーダー選出サブルーチンは、各リーダーが誠実である確率を \((f+1)/(2f+1) \gt 1/2\) を保証するため、コアプロトコルは期待値 2 回の反復と \(f+1\) の \({\sf notify}\) を転送する 1 つの追加ラウンドで終了する。したがって、1 回の反復に \(r\) ラウンドを要する場合、我々のコアプロトコルが終了するのには \(2r+1\) ラウンドで終了することが期待される。敵対者が適応的で強い急襲であれば各反復は \(r=7\) ラウンドを必要とする。敵対者が適応的で通常の急襲であれば \({\sf elect}\) ラウンドは \({\sf propose}\) と並行してこなうことができ、各反復は \(r=6\) ラウンドとなる。敵対者が静的 (急襲であってもなくても) の場合、2 つの \({\sf prepare}\) ラウンドは必要なく、\({\sf elect}\) ラウンドは \({\sf status}\) または \({\sf propose}\) ラウンドのどちらかと並行して行うことができ、1 回の反復に \(r=4\) ラウンドを要する。

次に我々は通信複雑性を分析する。各ラウンドは \(O(n^2)\) の通信を消費することを示す。したがってコアプロトコルは (敵対者が適応的か静的か、急襲かどうかにかかわらず) 期待値 \(O(n^2)\) 通信を必要とする。まず、証明書は \(f+1\) 個の署名で構成されるが、しきい値署名を使用してそのサイズを単一の署名に縮小できることに留意されたい [8, 18, 25, 32]。

1. \({\sf status}\) ラウンドでは、各当事者は現在受け入れている証明書を他のすべての当事者に報告する (リーダーは明かされていないのですべての当事者がリーダーになる可能性がある)。
2. \({\sf prepare}_1\) では、各当事者はサイズ \(O(1)\) の署名された提案を他のすべての当事者に送信する。
3. \({\sf prepare}_2\) では、各当事者はサイズ \(O(1)\) の二重の署名付き提案を他のすべての当事者に送り返す。
4. \({\sf proposal}\) ラウンドでは、各当事者は証明書を含む提案を他のすべての当事者に送信する。(HotStuff プロトコル [3] の提案に従い、提案には \({\sf status}\) メッセージを含む必要はない。)
5. \({\sf elect}\) ラウンドでは、Loss と Moran [27] による共通コインプロトコルで \(O(n^2)\) 通信を要する。
6. \({\sf commit}\) ラウンドでは、各当事者は \(O(1)\) サイズの \({\sf commit}\) メッセージを他のすべての当事者に送信する。
7. \({\sf notify}\) ラウンドでは、各当事者は証明書を含む \({\sf notify}\) メッセージを他のすべての当事者に送信する。
8. 最後に、終了前に各当事者は \(f+1\) 個の通知ヘッダ \(\langle {\sf notify},v\rangle\) を他のすべての当事者に送信する。これは単一のしきい値署名に減らすことができる。

4 ビザンチンブロードキャストと合意

このセクションではコアプロトコルを用いて \(f \lt n/2\) の場合の同期認証ビザンチンブロードキャストと合意を解く方法を説明する。両問題とも誠実な当事者が初期署名所を取得してコアプロトコルを呼び出す "プレラウンド" を設計する。

ビザンチンブロードキャスト. ビザンチンブロードキャストでは所定の送信者がある値を \(n\) 個の当事者に送信しようとする。ソリューションは 3 つの要件を満たす必要がある:

• (終了) すべての誠実な当事者たちは最終的にコミットする
• (合意) すべての誠実な当事者たちは同じ値にコミットする
• (有効性) もし送信者が誠実であればすべての誠実な当事者たちは送信者がブロードキャストした値でコミットする

所定の送信者を \(L_s\) とする。プレラウンドでは \(L_s\) は署名付きの値 \(\langle v_s \rangle_{L_s}\) を各当事者にブロードキャストする。送信者によるこのような署名付き値は \((v_s,0)\) を証明する初期証明書である。その後、コアプロトコルを起動する。安全性と終了は定理 2 と 3 によって満たされる。もし所定の送信者が誠実であれば、各誠実な当事者は \((v_s,0)\) に対する証明書を持ち、矛盾する初期証明書は存在せず、定理 4 の条件を満たす。したがって有効性は満たされる。

ビザンチン合意. ビザンチン合意では各当事者は初期入力値を保持する。ソリューションはビザンチンブロードキャストと同じ終了要件と合意要件を満たす必要がある。いくつかの有効性の概念が存在する。我々は強い全会一致 (strong unanimity) [13] として知られている一般的なものを採用する:

• (有効性). すべての誠実な当事者が同じ入力値 \(v\) を保持する場合、それらはすべて \(v\) にコミットする。

プレラウンドではすべての当事者 \(i\) がその値 \(\langle v_i \rangle_i\) をブロードキャストする。同じ値 \(v\) に対する個別の当事者からの \(f+1\) 個の署名は \((v,0)\) に対する初期証明書を形成する。次にコアプロトコルを起動する。定理 2 と 3 により安全性と終了が満たされている。すべての誠実な当事者が同じ入力値を持つ場合、それらは \(v\) の初期証明書を持ち、競合するｓｙ機証明書は存在しえず、定理 4 の条件を満たす。したがって有効性は満たされる。

プロトコルの効率はコアプロトコルの分析から明らかである。両プロトコルともコアプロトコルより 1 ラウンド多く、コアプロトコルと同じ \(O(n^2)\) の通信複雑性が必要である。

5 クロック同期

重要な問題は、このセクションの主題である同期性の仮定がどの程度現実的であるかということである。同期性の仮定は本質的にすべての誠実なレプリカのメッセージが時間内に到着することを示している。これには 2 つのプロパティが必要である: (i) メッセージの遅延が有限であること、(ii) ロックされたステップの実行、つまり誠実なレプリカが各ラウンドをほぼ同時に開始すること。第二の特性は重要である。レプリカ \(i\) がレプリカ \(j\) よりかなり早くラウンドに入った場合、\(j\) のメッセージの到着を待たずに \(i\) が早くラウンドを終えてしまう可能性がある。例えば我々のプロトコルの場合、これによって \(i\) がリーダーの曖昧さを検出できなくなり安全違反となる可能性がある。

XFT の論文は特定のアプリケーションでメッセージ遅延が有限であることを仮定する正当性が示された [26]。しかしロックされたステップ実行を強制するメカニズムが必要である。この目的のために、我々は次のクロック同期プロトコルを使用する。これはビザンチン合意の外側で興味深いかもしれない。これは Dolev ら [10] によるクロック同期プロトコルの変種である。重要な変更は、しきい値署名の使用を簡易にするために当事者が (順次ではなく) 並列に独立して署名することである。

プロトコルは既知の時間間隔で実行される。各間隔を "日" (day) と呼ぶ。

Round 0 (\({\sf sync}\))

当事者 \(i\) のクロックが \(X\) 日の始まりになったら、自身を含むすべての当事者に \(\langle {\sf sync},X \rangle_i\) メッセージを送信する。

Round 1 (\({\sf new\mbox{-}day}\))

当事者 \(j\) が個別の当事者から \(f+1\) 個の \(\langle {\sf sync},X\rangle\) メッセージを (\(f+1\) 個の \({\sf sync}\) メッセージまたは単一の \({\sf new\mbox{-}day}\) メッセージとして) 初めて受け取ると、当事者 \(j\) は:

• 自身のクロックを \(X\) 日の始まりに設定する
• 他のすべての当事者に、個別の当事者からの \(f+1\) 個の \(\langle {\sf sync},X\rangle\) メッセージの連結である \({\sf new\mbox{-}day}\) メッセージを送信する

上記のプロトコルはメッセージ遅延境界 \(\Delta\) とクロックドリフト境界から lock-step 同期をブートストラップする。各 \({\sf sync}\) メッセージは当事者のローカルクロックによってトリガーされ、他の当事者がいつ \(X\) 日を開始するかには依存しない。\(f+1\) 同期メッセージはより効率的にしきい値署名に置き換えることができる。このプロトコルは、各日の最初に誠実な当事者のクロック差異を最大でもメッセージ遅延境界 \(\Delta\) までリフレッシュする。最初に新しい日を迎える誠実な当事者は \({\sf new\mbox{-}day}\) メッセージをブロードキャストし、他のすべての誠実な当事者に \(\Delta\) 時間以内に新しい日を始めさせるだろう。\({\sf new\mbox{-}day}\) メッセージを得ることは、少なくとも 1 つの誠実な当事者が有効な \({\sf sync}\) メッセージを送信したことを意味し、前日から実際に約 1 日が経過したことを保証する。そして各ラウンドの持続時間を \(2\Delta+\phi\) に設定することができる。ここで \(\phi\) は "日" における 2 つの誠実な当事者間の最大クロックドリフトである。

Acknowledgements

We thank Dahlia Malkhi and Benjamin Chan for many useful discussions.

References

1. Ittai Abraham, T-H. Hubert Chan, Danny Dolev, Kartik Nayak, Rafael Pass, Ling Ren, and Elaine Shi. Communication complexity of byzantine agreement, revisited. arXiv preprint, 1805.03391, 2018.
2. Ittai Abraham, Srinivas Devadas, Danny Dolev, Kartik Nayak, and Ling Ren. Synchronous byzantine agreement with expected \(O(1)\) rounds, expected \(O(n^2)\) communication, and optimal resilience. Cryptology ePrint Archive, Report 2018/1028, 2018. https://eprint.iacr.org/2018/1028.
3. Ittai Abraham, Guy Gueta, and Dahlia Malkhi. Hot-stuff the linear, optimal-resilience, one-message bft devil. arXiv preprint arXiv:1803.05069, 2018.
4. Ittai Abraham, Dahlia Malkhi, Kartik Nayak, Ling Ren, and Alexander Spiegelman. Solida: A blockchain protocol based on reconfigurable byzantine consensus. OPODIS, 2017.
5. Atul Adya, William J. Bolosky, Miguel Castro, Gerald Cermak, Ronnie Chaiken, John R. Douceur, Jon Howell, Jacob R. Lorch, Marvin Theimer, and Roger P. Wattenhofer. FARSITE: Federated, available, and reliable storage for an incompletely trusted environment. ACM SIGOPS Operating Systems Review, 36(SI):1-14, 2002.
6. Michael Ben-Or. Another advantage of free choice (extended abstract): Completely asynchronous agreement protocols. In Proceedings of the second annual ACM symposium on Principles of distributed computing, pages 27-30. ACM, 1983.
7. Michael Ben-Or, Shafi Goldwasser, and Avi Wigderson. Completeness theorems for non-cryptographic faulttolerant distributed computation. In Proceedings of the 20th annual ACM symposium on Theory of computing, pages 1-10. ACM, 1988.
8. Christian Cachin, Klaus Kursawe, and Victor Shoup. Random oracles in Constantinople: Practical asynchronous byzantine agreement using cryptography. Journal of Cryptology, 18(3):219-246, 2005.
9. Miguel Castro and Barbara Liskov. Practical byzantine fault tolerance. In OSDI, volume 99, pages 173-186, 1999.
10. Danny Dolev, Joseph Halpern, Barbara Simons, and Ray Strong. Dynamic fault-tolerant clock synchronization. Journal of the ACM, 42(1):143-185, 1995.
11. Danny Dolev and Rudiger Reischuk. Bounds on information exchange for byzantine agreement. Journal of the ACM (JACM), 32(1):191-204, 1985.
12. Danny Dolev and H. Raymond Strong. Authenticated algorithms for byzantine agreement. SIAM Journal on Computing, 12(4):656-666, 1983.
13. Cynthia Dwork, Nancy Lynch, and Larry Stockmeyer. Consensus in the presence of partial synchrony. Journal of the ACM, 35(2):288-323, 1988.
14. Pesech Feldman and Silvio Micali. An optimal probabilistic protocol for synchronous byzantine agreement. SIAM Journal on Computing, 26(4):873-933, 1997.
15. Michael J. Fischer and Nancy A. Lynch. A lower bound for the time to assure interactive consistency. Information processing letters, 14(4):183-186, 1982.
16. Matthias Fitzi and Juan A Garay. Effcient player-optimal protocols for strong and differential consensus. In Proceedings of the twenty-second annual symposium on Principles of distributed computing, pages 211-220. ACM, 2003.
17. Shafi Goldwasser, Silvio Micali, and Avi Wigderson. How to play any mental game, or a completeness theorem for protocols with an honest majority. In Proc. of the 19th Annual ACM STOC, volume 87, pages 218-229, 1987.
18. Guy Golan Gueta, Ittai Abraham, Shelly Grossman, Dahlia Malkhi, Benny Pinkas, Michael K Reiter, Dragos- Adrian Seredinschi, Orr Tamir, and Alin Tomescu. SBFT: a scalable decentralized trust infrastructure for blockchains. arXiv preprint 1804.01626, 2018.
19. Jonathan Katz and Chiu-Yuen Koo. On expected constant-round protocols for Byzantine agreement. In Annual International Cryptology Conference, volume 4117, pages 445-462. Springer, 2006.
20. Valerie King and Jared Saia. Breaking the \(O(n^2)\) bit barrier: scalable byzantine agreement with an adaptive adversary. Journal of the ACM, 58(4):18, 2011.
21. Eleftherios Kokoris Kogias, Philipp Jovanovic, Nicolas Gailly, Ismail Khoffi, Linus Gasser, and Bryan Ford. Enhancing Bitcoin security and performance with strong consistency via collective signing. In 25th USENIX Security Symposium, pages 279-296. USENIX Association, 2016.
22. John Kubiatowicz, David Bindel, Yan Chen, Steven Czerwinski, Patrick Eaton, Dennis Geels, Ramakrishan Gummadi, Sean Rhea, Hakim Weatherspoon, Westley Weimer, and Ben Zhao. Oceanstore: An architecture for global-scale persistent storage. ACM Sigplan Notices, 35(11):190-201, 2000.
23. Leslie Lamport. The part-time parliament. ACM Transactions on Computer Systems, 16(2):133-169, 1998.
24. Leslie Lamport, Robert Shostak, and Marshall Pease. The Byzantine generals problem. ACM Transactions on Programming Languages and Systems, 4(3):382-401, 1982.
25. Benoît Libert, Marc Joye, and Moti Yung. Born and raised distributively: Fully distributed non-interactive adaptively-secure threshold signatures with short shares. Theoretical Computer Science, 645:1-24, 2016.
26. Shengyun Liu, Christian Cachin, Vivien Quéma, and Marko Vukolic. XFT: practical fault tolerance beyond crashes. In 12th USENIX Symposium on Operating Systems Design and Implementation, pages 485-500. USENIX Association, 2016.
27. Julian Loss and Tal Moran. Combining asynchronous and synchronous Byzantine agreement: The best of both worlds. Cryptology ePrint Archive 2018/235, 2018.
28. Silvio Micali. Algorand: The effcient and democratic ledger. arXiv:1607.01341, 2016.
29. Rafael Pass and Elaine Shi. Feasibilities and infeasibilities for achieving responsiveness in permissionless consensus. In International Symposium on Distributed Computing. Springer, 2017.
30. Rafael Pass and Elaine Shi. Thunderella: Blockchains with optimistic instant confirmation. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 3-33. Springer, 2018.
31. Michael O. Rabin. Randomized Byzantine generals. In Proceedings of the 24th Annual Symposium on Foundations of Computer Science, pages 403-409. IEEE, 1983.
32. Victor Shoup. Practical threshold signatures. In International Conference on the Theory and Applications of Cryptographic Techniques, pages 207-220. Springer, 2000.
33. Lidong Zhou, Fred Schneider, and Robbert van Renesse. COCA: A secure distributed online certification authority. ACM Transactions on Computer Systems, 20(4):329-368, 2002.

翻訳抄

2019 年の論文。

1. Abraham, I., Devadas, S., Dolev, D., Nayak, K., Ren, L. (2019). Synchronous Byzantine Agreement with Expected \(O(1)\) Rounds, Expected \(O(n^2)\) Communication, and Optimal Resilience. In Financial Cryptography and Data Security. FC 2019. Lecture Notes in Computer Science(), vol 11598. Springer, Cham. https://doi.org/10.1007/978-3-030-32101-7_20