分散アルゴリズム
\( \newcommand{\argmax}{\mathop{\rm arg~min}\limits} \newcommand{\argmin}{\mathop{\rm arg~min}\limits} \)

論文翻訳: HotStuff: BFT Consensus in the Lens of Blockchain

Takami Torao 2019年の論文 #HotStuff #LibraBFT
  • このエントリーをはてなブックマークに追加
Maofan Yin 1,2 , Dahlia Malkhi 2 , Michael K. Reiter 2,3 , Guy Golan Gueta 2 , and Ittai Abraham 2
1 Cornell University, 2 VMware Research, 3 UNC-Chapel Hill

Abstract

部分同期モデルのリーダー型ビザンチン障害耐性レプリケーションプロトコルである HotStuff を紹介する。HotStuff のネットワーク通信が同期化されると、正しいリーダーがレプリカ数に対して線形増加する通信複雑性で、実際のネットワーク遅延 (最大遅延ではない) の速度でプロトコルを合意に導く ─ 応答性 (responsiveness) と呼ばれる特性 ─ ことができる。我々の知る限り HotStuff はこれらの特性を併せ持つ最初の部分同期 BFT レプリケーションプロトコルである。HotStuff は古典的な BFT の基礎とブロックチェーンとの架け橋となる新しいフレームワークを中心に構築されている。他の既知のプロトコル (DLS, PBFT, Tendermint, Caspter) や我々のプロトコルを共通のフレームワークで表現することができる。

100 以上の複製を持つネットワーク上で展開した我々の HotStuff は BFT-SMaRt のスループットと待ち時間に匹敵する成果を達成し、(BFT-SMaRt の cubic に対して) リーダーのフェールオーバー時の通信フットプリントが線形である。

Table of Contents

  1. Abstract
  2. 1 Introduction
  3. 2 Related Work
  4. 3 Model
  5. 4 Basic HotStuff
    1. 4.1 Phases
    2. 4.2 Data Structure
    3. 4.3 Protocol Specification
    4. 4.4 Safety, Liveness, and Complexity
  6. 5 Chained HotStuff
  7. 6 Implementation
  8. 7 One-Chain and Two-Chain BFT Protocols
    1. 7.1 DLS
    2. 7.2 PBFT
    3. 7.3 Tendermint and Casper
  9. 8 Evaluation
    1. 8.1 Setup
    2. 8.2 Base Performance
    3. 8.3 Scalability
    4. 8.4 View Change
  10. 9 Conclusion
  11. Acknowledgements
  12. References
  13. A - Proof of Safety for Chained HotStuff
  14. B - Proof of Safety for Implementation Pseudocode
    1. B.1 Remarks
  15. 翻訳抄

1 Introduction

ビザンチン障害耐性 (BFT) とはコンピューティングシステムの運用に不可欠な動作を実行しながら、そのコンポーネントの任意障害 (つまりビザンチン障害) に耐える能力のことである。ステートマシンレプリケーション (SMR) [35, 47] の文脈では、システム全体として \(n\) 個の決定性レプリカに状態がミラーされる複製サービスを提供する。BFT SMR プロトコルは、非故障レプリカがクライアントから開始されたサービスコマンドの実行順序に合意することを保証するために使用されている。これにより \(n-f\) 個の非故障レプリカが同じようにコマンドを実行し、各コマンドに対して同じ応答を生成することが保証される。一般と同様に、我々はここで部分同期通信モデル [25] に着目している。これによって、メッセージ転送に関する既知の限界 \(\Delta\) が、ある未知の global stabilization time (GST) 後に成り立つ。このモデルでは非故障レプリカが同じ順序で同じコマンドに合意するために \(n \ge 3f+1\) 個必要であり (例 [12])、進行は GST 後にのみ決定性を持って保証される[27]。

BFT SMR プロトコルが最初に考案されたとき、典型的なターゲットシステムのサイズはローカルエリアネットワーク上に展開された \(n=4\) または \(n=7\) だった。しかし、ブロックチェーンへの適用によってもたらされたビザンチン障害耐性への新たな関心はより大きな \(n\) に拡張できるソリューションを必要としている。例えばビットコインのようなものがサポートしている permissionless ブロックチェーンとは対照的に、いわゆる permissioned ブロックチェーンはコマンドを順序づけた台帳を集合的に管理する固定個数のレプリカを含んでおり、言い換えれば SMR をサポートしている。それらの permissioned の性質にもかかわらず、数百または数千のレプリカが想定される (例 [42, 30])。さらに、ワイドエリアネットワークへの展開には通信遅延の大きな変動に対応するために \(\Delta\) を設定する必要がある。

The scaling challenge. 部分同期モデルにおける最初の実用的 BFT レプリケーションソリューションである PBFT [20] の導入以来、多数の BFT ソリューションがそのコアである 2-phase パラダイムの周辺に構築された。これは安定したリーダーがたった 2 回のメッセージ交換でコンセンサスの決定を進めることができる点で実用的ある。第一段階は \((n-f)\) 票から成る定足数の証明書 \((QC)\) の形成により提案の一意性が保証される。第二段階では、次のリーダーがレプリカを安全な提案に確信して投票できるようにしている。

新しいリーダーが情報を収集してレプリカに提案するための view-change と呼ばれるアルゴリズムがレプリケーションの中心である。残念なことに 2-phase パラダイムに基づく view-change は単純なものとはほど遠く[38]、バグを発生させやすく[4]、中程度のシステムサイズであっても深刻な通信ペナルティが発生する。新しいリーダーは \((n-f)\) レプリカから情報をリレーする必要があり、各レプリカは自分が分かっている最も高い \(QC\) を報告する。新しい提案だけを伝達する認証子 (authenticator) (デジタル署名やメッセージ認証コード) だけをカウントしても BFT 内で \(O(n^3)\) 認証子の通信フットプリントを持ち、複数の認証子をしきい値デジタル署名 (例: [18, 30] を介して結合したバリアントは \(O(n^2)\) 認証子を送信する。単一のコンセンサス決定に達する前に \(O(n)\) 個の view-change が発生した場合に送信される認証子の総数は PBFT において \(O(n^4)\) であり、しきい値署名があっても \(O(n^3)\) である。このスケーリング問題への挑戦は PBFT だけではなく、それ以降に開発された他の多くのプロトコル、例えば Prime[9], Zyzzyva[34], Upright[22], BFT-SMaRt[13], 700BFT[11] および SBFT[30] を悩ませてきた。

HotStuff は 3-phase コアを中心に展開しており、新しいリーダーは自分が知っている最高の \(QC\) を選ぶだけで良い。また、レプリカがそのフェーズで投票した後に、リーダーによる証明を全く必要とせずに「考えを変える (change their mind)」ことを可能にするための第 2 のフェーズが導入されている。これにより前述の複雑さが軽減されると同時にリーダー交代プロトコルが大幅に簡略される。最後に、全てのフェーズを (ほとんど) 正規化すると HotStuff をパイプライン化し、頻繁にリーダーをローテーションさせることが非常に簡単となる。

我々の知る限り Tendermint[15, 16] や Casper[17] のようなブロックチェーン分野における BFT プロトコルのみがこのような単純なリーダー体制に従っている。しかしこれらのシステムは同期コアの周りに構築されており、提案は、広域 peer-to-peer ゴシップネットワーク上でのメッセージ伝播に要する最悪時間に対応しなければならない事前に決定された間隔で行われる。そうすることでそれらは最も実用的な BFT SMR ソリューション (前述を含む) の特徴、すなはち楽観的応答[42] (optimistic responsiveness) を放棄している。形式張らずに言うと、応答性 (responsiveness) は一度指定された非故障リーダーが、実際のメッセージ遅延のみに依存した状況で、メッセージ送信遅延の既知の上限[10] と関係なく、時間的にプロトコルをコンセンサスに導くことができる事を必要とする。我々のモデルにとってより適切なことは楽観的応答であり、GST に達した後の有益の (うまく行けば共通の) 状況でのみ応答を必要とする。楽観的であってもなくても、Tendermint/Casper のようなデザインでは応答性が排除されている。最も \(QC\) の高い誠実なレプリカが存在するかも知れないが、リーダーはそれを知り得ないことが難点である。これによって無限の進展を妨げるようなシナリオを作ることができる (詳細な liveness シナリオについてはセクション 4.4 参照)。実際、重要なプロトコルステップで必要な遅延を組み込むことができないと、いくつかの既存の配備で報告されているように、liveness を完全に失う結果をもたらす可能性がある。例えば [3, 2, 19] 参照。

Our contributions. HotStuff と呼ぶ、我々の知る限り以下の 2 つの特徴を達成する最初の BFT SMR プロトコルを提示する:

  1. 線形ビュー変更: GST の後に正しいリーダーが選択されるとコンセンサスを決定するために \(O(n)\) 認証子のみが送信される。これはリーダー交代のケースが含まれる。その後、GST 後にコンセンサスに達するための通信コストはカスケードリーダー障害の最悪ケースで \(O(n^2)\) 認証子である。
  2. 楽観的応答性: GST 後、適切なリーダーが指定されると、最初の \(n-f\) 応答だけを待って、進行を進めさせる提案を作成できることを保証する必要がある。これはリーダーが交代する場合も含んでいる。

もう一つの HotStuff の特徴は、プロトコルをコンセンサスに導く新しいリーダーのコストが現在のリーダーのコストよりも大きくないことである。このように HotStuff はリーダーの頻繁な引き継ぎをサポートしており、これはチェーンの品質を保証するブロックチェーンのコンテキストで有用であると主張されている[28]。

HotStuff は各ビューに別のフェーズを追加することでこの特性を実現している。これはリーダーの交換プロトコルを大幅に簡素化する代わりにレイテンシーにわずかな代償を払う。この交代では実際のネットワーク遅延のみが発生するが、これは通常、実際の \(\Delta\) よりも遙かに小さいものである。このため追加のレイテンシーは、線形 view-change を達成するための応答性を放棄する前プロトコルで発生するレイテンシーよりも遙かに小さいと予想される。さらに、セクション 5 で紹介する効率的なパイプラインによりスループットは影響を受けない。理論的な寄与に加えて HotStuff は、一般的な BFT レプリケーションの理解と実際のプロトコルの実現化に関する洞察も提供する (セクション 6 参照):

  • ノードのグラフを介した BFT レプリケーションフレームワーク。Safety は投票およびコミットグラフのルールによって指定される。Liveness は新しいノードでグラフを拡張する Pacemaker によって個別に指定される。
  • このフレームワークの中でいくつかの既知のプロトコル (DLS, PBFT, Tendermint および Casper) から一つの新しい (我々の HotStuff) へのキャスト。

HotStuff にはそのメカニズムの経済性のために驚くほど単純であるという追加の利点がある: レプリカがそれぞれをどのように扱うかを決定する 2 つのメッセージタイプとシンプルなルールしか存在しない。Safety はノードグラフ上の投票とコミットルールによって指定される。Liveness を達成するために必要とされる機構は Pacemaker 内にカプセル化され、safety で必要とされる機構から明確に分離されている。同時に、それはいくつかの既知のプロトコル (DLS, PBFT, Tendermint および Casper) をマイナーバリエーションとして表すことができるという点で表現に富んでいる。部分的にこの柔軟性はノードのグラフに対する操作に由来し、従来の BFT 基盤と現代的なブロックチェーンとの橋渡しをする。

我々は HotStuff のプロトタイプ実装と予備評価について説明する。HotStuff は 100 を超えるレプリカを使用してネットワーク上に展開され、コードの複雑さが HotStuff を遙かに超える BFT-SMaRt などの成熟したシステムに匹敵し、場合によってはそれを超えるスループットとレイテンシーを実現する。さらに、HotSport の通信フットプリントは頻繁なリーダー交代に直面しても一定のままであるが、BFT-SMaRt はレプリカ数と共に二次関数的に増加することを示す。

Table 1: Performance of selected protocols after GST.
Protocol Correct leader Authenticator complexity
Leader failure (view-change)		 \(f\) leader failures Responsiveness
DLS [25] \(O(n^4)\) \(O(n^4)\) \(O(n^4)\)
PBFT [20] \(O(n^2)\) \(O(n^3)\) \(O(fn^3)\) ✔
SBFT [30] \(O(n)\) \(O(n^2)\) \(O(fn^2)\) ✔
Temdermint [15] / Casper [17] \(O(n^2)\) \(O(n^2)\) \(O(fn^2)\)
Temdermint* / Casper* \(O(n)\) \(O(n)\) \(O(fn)\)
HotStuff \(O(n)\) \(O(n)\) \(O(fn)\) ✔
※しきい値署名を使用して署名を組み合わせることができるが、この最適は元の研究には記載されていない。

ビザンチン故障に直面してコンセンサスに達することは Lamport ら[37]によって Byzantine Generals Problem として策定され、「ビザンチン故障」という用語も生み出した。最初の同期ソリューションは Pease ら[43] によって提供され、後に Dolev and Strong [24] によって改善された。この改良されたプロトコルには \(O(n^3)\) の通信複雑度があり、これは Dolev と Reischuk [23] によって最適であることが示された。ランダム性を使用するリーダーベースの同期プロトコルは Katz and Koo [32] によって提供され、\((n-1)/2\) の復元力を備えた予期された constant-round ソリューションを示している。

一方、非同期の構成では Fischer ら[27]が単一の障害に直面した非同期構成で問題が決定論的に解決できない事を示した。さらに、あらゆる非同期ソリューションに対して \((n-1)/3\) の復元力が Ben-Or [12] によって証明された。この不可能性を回避するために 2 つのアプローチが考案された。1 つは Ben-Or [12] によって最初に示されたランダム性によるもので、プロセスがコンセンサスに収束するまでプロセスごとに独立したランダムコインフリップを使用する。後の研究では暗号化手法を使用して予測不可能なコインを共有し、複雑度を一定の予想されるラウンドまで抑えて \(O(n^3)\) 通信を行った[18]。

2 番目のアプローチは Dwork, Lynch and Stockmeyer (DLS) [25] が最初に示した部分同期による。このプロトコルは非同期期間中の safety を維持し、システムが同期状態になった後、DLS は termination を保証する。一度同期が維持されると DLS は \(O(n^4)\) の総通信と決定ごとの \(O(n)\) ラウンドを発生させる。

ステートマシンレプリケーションはクライアントリクエストを順序付け正しいレプリカがその順序で実行するコアのコンセンサスによる。SMR におけるコンセンサスの繰り返しの必要性により、Lamport は安定したリーダーが線形通信と 1 往復で意思決定を行う効率的なパイプラインを運用するプロトコルである Paxos [36] を考案した。同様の補強により Castro and Liskov [20, 21] は PBFT という名の効率的なリーダーベースのビザンチン SMR プロトコルを開発した。PBFT の安定したリーダーは \(O(n^2)\) 通信と決定あたり 2 round-trip を必要とし、リーダー交代プロトコルは \(O(n^3)\) 通信を発生する。PBFT は BFT-SMaRt [13] を含むいくつかのシステムに展開されている。Kotla らは Zyzzyva [34] というプロトコルで PBFT に楽観的な線形経路を導入した。これは Upright [22] や Byzcoin [33] などのいくつかのシステムで使用された。楽観的経路は線形の複雑度を持つが、リーダー交代プロトコルは \(O(n^3)\) のままである。Abraham ら [4] は後に Zyzzyva の safety 違反を指摘し修正を提示した [5, 30]。一方でプロトコル自体の複雑さを軽減するために Song らは Bisco [49] を提案した。これは \(5f+1\) レプリカを必要とする楽観的な経路で低レイテンシーのシンプルな 1 ステッププロトコルである。SBFT [30] は \(O(n^2)\) 通信ビュー変更プロトコルを導入する。このプロトコルは楽観的な線形の 1 round-trip 決定を伴う安定したリーダープロトコルをサポートする。これは 2 つの方法の組み合わせで通信の複雑度を軽減している: Reiter [46] によるコレクターベースの通信パラダイムと、Cachin ら [18] によるプロトコル投票のしきい値暗号化による署名の組み合わせ。

ランダム化を採用するリーダーベースのビザンチン SMR プロトコルが Ramasamy ら [44] によって提示され、HoneyBadgerBFT という名前のリーダーレス変種が Miller ら [39] によって開発された。それらのコアでは、それらのランダム化ビザンチンソリューションはランダムか非同期ビザンチンコンセンサスを採用しており、その最も知られている通信複雑度は \(O(n^3)\) であり (上記参照)、バッチ処理によってコストを償却している。しかし直近ではこの HotStuff 論文のアイディアに基づいて、PODC'19[8] への並行提出では通信複雑度がさらに \(O(n^2)\) へ改善されている。

ビットコインのコアは Nakamoto コンセンサス [40] として知られているプロトコルである。これは確率論的な safety 保証のみをもち、finality を持たない同期プロトコルである ([28, 41, 6] の分析を参照)。これは参加者が不明な permissionless モデルで動作し Proof-of-Work を介して復元力が保持される。前述のように、最近のブロックチェーンソリューションは様々な方法で Proof-of-Work ソリューションと従来の BFT ソリューションをハイブリッド化している [26, 33, 7, 17, 29, 31, 42]。これらのハイブリッドソリューションおよびその他のソリューションでリーダーを交代させる必要性は HotStuff の背後にある動機を提供する。

3 Model

我々は \(i \in [n]\) でインデックス付けされた \(n=3f+1\) レプリカの固定セットで構成されるシステムを考慮する。ここで \([n] = \{1,\ldots,n\}\) である。\(f=|F|\) レプリカまでの集合 \(F \subset [n]\) はビザンチン故障であり、それ以外は正しいレプリカである。我々はしばしばビザンチンレプリカが敵対的に調整されていると見なし、敵対者はこれらのレプリカが保持する全ての内部状態を学習する (それらの暗号鍵を含む、下記参照)。

ネットワークは point-to-point であり、認証されて信頼性がある: 正しいレプリカが別の正しいレプリカからメッセージを受信するのは後者が前者にメッセージを送信した場合のみである。我々が「ブロードキャスト」に言及するとき、ブロードキャスターが関与しておりそれが正常なら、自分自体を含む全てのレプリカに同じ point-to-point メッセージを送信する。我々は Dwork ら [25] の部分同期モデルを採用している。既知の限界 \(\Delta\) と未知の Global Stabilization Time (GST) が存在し、その GST の後、正しいレプリカ間の全ての転送は時間 \(\Delta\) 内に到着する。我々のプロトコルは常に safety を保証し、GST 後の上限尽き期間内の進行を保証する (GST の前に進行を保証することは不可能である [27]。実際には GST 後の十分に長い間システムが安定している (つまりメッセージが \(\Delta\) 時間以内に到着する) のであれば、我々のプロトコルは進行を保証するが、そうすることで永遠に論議が簡素化されると想定している。

Cryptographic primitives. HotStuff はしきい値署名[48, 18, 14] を使用している。\((k,n)\)-しきい値署名スキームでは、全てのレプリカが保持する単一の公開鍵が存在し、\(n\) 個のレプリカはそれぞれ個別の秘密鍵を保持している。\(i\) 番目のレプリカはメッセージ \(m\) に部分署名 (partial signature) \(\rho_i \leftarrow {\it tsign}_i(m)\) を提供するためにその秘密鍵を使用することができる。部分署名 \(\{\rho_i\}_{i\in I}\) は \(m\) 上での電子署名 \(\sigma \leftarrow {\it tcombine}(m,\{\rho_i\}_{i\in I})\) を作り出すために使用することができる。ここで \(|I|=k\) と各 \(\rho_i \leftarrow {\it tsign}_i(m)\) である。それ以外のレプリカは公開鍵と \({\it tverify}\) 関数を使用して署名を検証することができる。もしそれぞれの \(i \in I\), \(|I|=k\) に対して \(\rho_i \leftarrow {\it tsign}_i(m)\) であり、\(\sigma \leftarrow {\it tcombine}(m,\{\rho_i\}_{i\in I})\) であれば、\({\it tverify}(m,\sigma)\) は true を返す必要がある。ただし、オラクル \(\{{\it tsign}_i(\cdot)\}_{i\in [n] \backslash F}\) へのオラクルアクセスを与えられた場合であっても、\(k-f\) より明らかに少ない試行回数でこれらのオラクルの \({\it tsign}_i(m)\) を求める敵対者が (例えば \({\it tverify}(m,\sigma)\) が true となるような) メッセージ \(m\) に対する署名 \(\sigma\) を生成する確率は無視することができる。この論文で我々は \(k=2f+1\) のしきい値を使用する。ここでも、我々は通常プロトコル説明には暗黙的な \({\it tverify}\) の呼び出しを残している。

また、我々は任意の長さの入力を固定長の出力にマッピングする暗号学的ハッシュ関数 \(h\) (メッセージダイジェスト関数とも呼ばれる) も必要とする。このハッシュ関数は衝突耐性[46]を持たなければならない。簡単に言うと、敵対的に生成された入力 \(m\) と \(m'\) が \(h(m)=h(m')\) となる確率が無視できる必要がある。そのため \(h(m)\) はプロトコルで一意な入力 \(m\) に対する識別子として機能する。

Complexity measure. 我々が注目する複雑さはの尺度は認証子複雑性である。特にこれは \(i\in[n]\) における全てのレプリカに対して、GST 後にコンセンサス決定に到達するためにプロトコルのレプリカ \(i\) が受信する認証子の数の合計である。(繰り返すが最悪ケース[27]では GST の前に全くコンセンサス決定には達しない。) ここで認証子は部分署名または署名である。認証子複雑性はいくつかの理由で通信複雑度に有用な尺度である。第一に、ビット複雑度のようだがメッセージ複雑度のようではなく、通信トポロジーに関する不必要な詳細を隠蔽する。例えば、1 つの認証子を伝送する \(n\) 個のメッセージのカウントは \(n\) 個の認証子を伝送する 1 つのメッセージと同じである。第二に、認証子複雑度は、それぞれのコンセンサス決定 (またはそのコンセンサス決定に向けて提案された各ビュー) が単調に増加するカウンターによって識別される、繰り返しコンセンサスに到達する我々のようなプロトコルのコストをとらえるにビット複雑度よりも適している。つまりこのようなカウンターは無限に増加するため、そのようなカウンターを送信するプロトコルのビット複雑度は制限することができない。第三に、現実的には電子署名の生成や検証、部分署名の生成や結合のための暗号操作は、典型的にそれらを使用するプロトコルにおいて最も計算集約的な操作であることから、認証子の複雑さは同様にプロトコルの計算負荷についての洞察も提供する。

4 Basic HotStuff

HotStuff は State Machine Replication (SMR) の問題を解決する。SMR の中核はクライアントによって増え続けるコマンド要求のログを決定するためのプロトコルである。ステートマシンのレプリカは一貫した順序でコマンドを適用する。クライアントは全てのレプリカにコマンド要求を送信し、それらの \((f+1)\) 個からの応答を待機する。ほとんどの場合、クライアントを議論から省略し、クライアント要求の番号付けと重複排除に関する問題は標準的な文献に従う。

基本的な HotStuff ソリューションは Algorithm 2 に示されている。プロトコルは単調増加するビュー番号で番号付けされた一連のビューで機能する。各 \({\it viewNumber}\) は全てのレプリカに知られている一意の専任リーダーが存在する。各レプリカにはローカルデータ構造として保留コマンドのツリー (tree) が格納される。各ツリーノード (node) には、提案されたコマンド (またはそれらのバッチ)、プロトコルに関連づけられたメタデータ、および親リンクが含まれている。特定のノードに引かれている枝 (branch) は、親リンクのアクセスからツリールートまでの経路である。プロトコルの期間中に、単調に生長する枝がコミットされる。コミットが行われるには、枝を提案する特定のビューのリーダーが、PREPARE, PRE-COMMIT, COMMIT の 3-phase で \((n-f)\) レプリカの定足数から票を集める必要がある。

プロトコルの重要な要素はリーダー提案に対して定足数証明書 (quorum certificate) (略して "QC") と呼ばれる \((n-f)\) 票の集まりである。この QC は特定のノードとビュー番号に関連づけられている。\({\it tcombine}\) 機能は単一の認証子として \((n-f)\) 個の署名済み票の表現を作成するためにしきい値署名方式を使用する。

以下にフェーズごとのプロトコルロジックの動作説明と、それに続く Algorithm 2 の正確な仕様を示し、safety, liveness および複雑性の論議でセクションを締めくくる。

4.1 Phases

PREPARE フェーズ. 新しいリーダーに対するプロトコルは \((n-f)\) レプリカから NEW-VIEW メッセージを集めることで開始する。以下に説明するように NEW-VIEW メッセージは \({\it viewNumber}\) (最初のビューを含む) へ遷移するときにレプリカから送信され、レプリカが受信した最も高い \({\it prepareQC}\) (無い場合は \(\perp\)) を運搬する。

リーダーは \({\it prepareQC}\) が形成された最も高い先行ビューを持つ枝を選択するためにこれらのメッセージを処理する。リーダーは NEW-VIEW メッセージの中から \({\it highQC}\) で示される最も高いビューを持つ \({\it prepareQC}\) を選択する。\({\it highQC}\) は \((n-f)\) レプリカの中で最も高いため、より高いビューのどれもコミット決定を達成しない。従って \({\it highQC}.{\it node}\) によって引かれる枝は安全である。

安全な枝を選択するための NEW-VIEW 収集は現職のリーダーによって省略されることがある。このとき現職リーダーは単純に自分の持つ中で最も高い \({\it prepareQC}\) を \({\it highQC}\) として選択する。我々はこの最適化をセクション 6 に延期し、このセクションでは単一な統合リーダープロトコルについてのみを説明する。PBFT のようなプロトコルとは異なり、リーダープロトコルにこのステップを含めることは容易であり、状況にかかわらず、プロトコルの他の全てのフェーズと同様に線形オーバーヘッドが発生することに注意。

リーダーは \({\rm createLeaf}\) 機能を使用して \({\it highQC}.{\it node}\) の末尾を新しい提案で拡張する。このメソッドは新しいの葉ノードを子として生成し、子ノードに親のダイジェスト値を埋め込む。そしてリーダーはその新しいノードを PREPARE メッセージで他の全てのレプリカに送信する。子の提案には安全性を正当化するための \({\it highQC}\) が含まれている。

リーダーから現在のビューの PREPARE メッセージを受信すると、レプリカ \(r\) は \({\rm safeNode}\) 判定を使用してそれを受け入れるかを決定する。受け入れられた場合、レプリカは提案に対する \({\it tsign}_r\) によって生成された) 部分署名を備えた PREPARE 票をリーダーに送信する。

\({\bf safeNode}\) 判定. この \({\rm safeNode}\) 判定はプロトコルの中心的な要素である。これは QC 正当性 \(m.{\it justify}\) を含む提案メッセージ \(m\) を調べ、\(m.{\it node}\) が安全に受け入れられるかを判断する。提案を受け入れる safety ルールは \(m.{\it node}\) の枝が現在ロックされているノード \({\it lockedQC}.{\it node}\) から拡張されているかである。一方で、\(m.{\it justify}\) が現在の \({\it lockedQC}\) より高いビューを持つ場合にレプリカが \(m\) を受け入れることが liveness ルールである。2 つのルールのうちいずれかが成り立つのであれば判定は true である。

PRE-COMMIT フェーズ. リーダーが現在の提案 \({\it curProposal}\) に対する \((n-f)\) 個の PREPARE 票を受信すると、それらを \({\it prepareQC}\) に結合する。リーダーは PRE-COMMIT メッセージで \({\it prepareQC}\) をブロードキャストする。レプリカは提案の署名済みダイジェストを持つ PRE-COMMIT 票でリーダーに応答する。

COMMIT フェーズ. COMMIT フェーズは PRE-COMMIT フェーズに似ている。リーダーが \((n-f)\) PRE-COMMIT 票を受信すると、それらを \({\it precommitQC}\) に結合し、COMMIT メッセージでブロードキャストする; レプリカは COMMIT 票でそれに応答する。重要なことに、\({\it lockedQC}\) を \({\it precommitQC}\) に設定することによって、その時点でレプリカは \({\it precommitQC}\) でロックされる (Algorithm 2 の 25 行目)。これはコンセンサス決定となる場合に備えて提案の safety を守るために重要である。

DECIDE フェーズ. リーダーは \((n-f)\) COMMIT 票を受け取るとそれらを \({\it commitQC}\) に結合する。リーダーは \({\it commitQC}\) を組み立てると DECIDE メッセージによって他の全てのレプリカに送信される。レプリカは DECIDE メッセージを受信すると \({\it commitQC}\) 具現化された提案をコミットされた決定と見なし、コミットされた枝でコマンドを実行する。レプリカは \({\it viewNumber}\) をインクリメントし次のビューを開始する。

\({\bf nextView}\) 割り込み. 全てのフェーズで、レプリカは補助的な \({\rm nextView}({\it viewNumber})\) 機能によって決定されるタイムアウト期間までビュー \({\it viewNumber}\) のメッセージを待機する。\({\rm nextView}({\it viewNumber})\) が待機を中断すると、レプリカは \({\it viewNumber}\) をインクリメントし次のビューを開始する。

4.2 Data Structure

Message. プロトコルのメッセージ \(m\) には Algorithm 1 で示されている \({\rm msg}()\) 機能を使って入力される固定セットのフィールドがある。\(m\) は送信者の現在のビュー番号である \({\it curView}\) に自動的にスタンプされる。それぞれのメッセージはタイプ \(m.{\it type}\) \(\in \{\) NEW-VIEW, PREPARE, PRE-COMMIT, COMMIT, DECIDE\(\}\) を持つ。\(m.{\it node}\) は提案されたノード (提案された枝の葉ノード) を含んでいる。省略可能なフィールド \(m.{\it justify}\) がある。リーダーは様々なフェーズの QC を伝搬するために常にこのフィールドを使用する。レプリカは最も大きい \({\it prepareQC}\) を伝搬するために NEW-VIEW でこれを使用する。レプリカの役割で送信される各メッセージには、タプル \(\langle m.{\it type},m.{\it viewNumber},m.{\it node}\rangle\) を介した送信者による部分署名 \(m.{\it partialSig}\) が含まれている。これは \({\rm voteMsg}()\) 機能で追加される。

Quorum certificates. タプル \(\langle {\it type},{\it viewNumber},{\it node}\rangle\) 上の Quorum Certificate (QC) は、\((n-f)\) レプリカによって署名された同じタプルの署名のコレクションを結合するデータ型である。QC \(qc\) が与えられると、\({\it qc}.{\it type}\), \({\it qc}.{\it viewNumber}\), \({\it qc}.{\it node}\) を使用して元のタプルと一致するフィールドを参照する。

Tree and branches. それぞれのコマンドはさらに、親ノードのハッシュダイジェストである親リンクを含むノードでラップされる。我々は擬似コードから実装の詳細を省略する。このプロトコル期間、レプリカはノードに引かれた枝が既にそのローカルツリーに存在する場合にのみメッセージを配信する。現実的には、遅延している受信者は他のレプリカから不足しているノードを取得することで追いつくことができる。簡潔化のためこれらの詳細も擬似コードからは省略されている。ある枝が他方の拡張でない場合、2 つの枝は競合する。2 つのノードはそれらによって引かれた枝が競合している場合に競合する。

Bookkeeping variables. レプリカはプロトコルの状態を記録するために追加のローカル変数を使用する: (i) \({\it viewNumber}\) は初期値を 1 とし、決定の完了か \({\rm nextView}\) 割り込みのどちらかによってインクリメントされる; (ii) ロックされた定足数証明書 \({\it lockedQC}\) は初期値を \(\perp\) とし、レプリカが投票した COMMIT に対する最も高い QC を保存する; (iii) \({\it prepareQC}\) は初期値を \(\perp\) とし、レプリカが PRE-COMMIT に投票した最も高い QC を保存する。さらに、コマンドのコミットログを増加的に実行するために、レプリカは枝が実行された最上位のノードを維持する。簡潔のために以下では省略する。

4.3 Protocol Specification

Algorithm 2 で指定されたプロトコルはビューごとに反復するルートして説明している。それぞれのビューでは、レプリカは自身の役割に基づいて引き続きフェーズを実行する。これは "as" ブロックの連続で記述されている。レプリカは複数の役割を持つことができる。例えばリーダーは (通常の) レプリカでもある。ロールをまたぐ as ブロックの実行は並行して進めることができる。as ブロックそれぞれの実行はアトミックである。\({\rm nextView}\) 割り込みはどのような as ブロックでもすべての操作を中止し "Finally" ブロックへジャンプする。

Algorithm 1 Utilities (for replica \(r\)).
Algorithm 2 Basic HotStuff protocol (for replica \(r\)).

4.4 Safety, Liveness, and Complexity

Safety. 我々は最初に \({\it tverify}(\langle {\it qc}.{\it type},{\it qc}.{\it viewNumber},{\it qc}.{\it node}\rangle,{\it qc}.{\it sig})\) が true であるときに定足数証明書 \(qc\) が有効 (valid) であると定義する。

補題 1. \({\it qc}_1.{\it type}={\it qc}_2.{\it type}\) であり、かつ \({\it qc}_1.{\it node}\) が \({\it qc}_2.{\it node}\) と矛盾する、いかなる有効な \({\it qc}_1\), \({\it qc}_2\) も \({\it qc}_1.{\it viewNumber} \ne {\it qc}_2.{\it viewNumber}\) となる。

Proof. 矛盾を示すために \({\it qc}_1.{\it viewNumber} = {\it qc}_2.{\it viewNumber} = v\) とする。有効な QC はそれに対する \(n-f=2f+1\) 票 (つまり部分署名) でのみ形成できるため、\(v\) と同じフェーズで 2 度投票した正しいレプリカが存在しなければならない。疑似コードでは各ビューのそれぞれのフェーズで 1 度だけ投票することができるため不可能である。
∎

定理 2. もし \(w\) と \(b\) が競合するノードである場合、正しいレプリカによって両方ともコミットすることはできない。

Proof. この重要な定理を矛盾によって証明する。\({\it qc}_1\) が有効な \({\it commitQC}\) (つまり \({\it qc}_1.{\it type}=\) COMMIT) を示す \({\it qc}_1.{\it node} = w\)、\({\it qc}_2\) が有効な \({\it commitQC}\) を示す \({\it qc}_2.{\it node} = b\) とする。\(v_1 = {\it qc}_1.{\it viewNumber}\), \(v_2 = {\it qc}_2.{\it viewNumber}\) とする。補題 1 より \(v_1 \ne v_2\) である。一般性を失わず (W.l.o.g.) \(v_1 \lt v_2\) と仮定する。

\(v_1\) より大きく、有効な \({\it prepareQC}\), \({\it qc}_s\) (つまり \({\it qc}_s.{\it type}=\) PREPARE) の存在する中で最も小さいビューを \(v_s\) で示す。ここで \({\it qc}_s.{\it viewNumber} = v_s\) であり \({\it qc}_s.{\it node}\) は \(w\) と競合する。正式にはあらゆる \({\it prepareQC}\) に対して以下の判定を定義する: \[ E({\it prepareQC}) := (v_1 \lt {\it prepareQC}.{\it viewNumber} \le v_2) \land ({\it prepareQC}.{\it node} \ \mbox{conflicts with} \ w) \] ここで最初のスイッチングポイント \({\it qc}_s\) を設定できる: \[ {\it qc}_s := \argmin_{\it prepareQC} \left\{ {\it prepareQC}.{\it viewNumber} \ | \ {\it prepareQC} \ \mbox{is valid} \ \land E({\it prepareQC}) \right\} \] 前提としてこのような \({\it qc}_s\) が存在する必要がある点に注意; 例えば \({\it qc}_s\) はビュー \(v_2\) で作成された \({\it prepareQC}\) となりうる。

部分的な結果 \({\it tsign}_r(\langle {\it qc}_1.{\it type}, {\it qc}_1.{\it viewNumber}, {\it qc}_1.{\it node}\rangle)\) を送信した正しいレプリカのうち、\(r\) を最初に \({\it tsign}_r(\langle {\it qc}_s.{\it type}, {\it qc}_s.{\it viewNumber}, {\it qc}_s.{\it node}\rangle)\) を提出したものとする; さもなくば \({\it qc}_1.{\it sig}\) か \({\it qc}_2.{\it sig}\) のいずれかが作成できなかったこととなるためそのような \(r\) は必ず存在する。ビュー \(v_1\) の間、レプリカ \(r\) は Algorithm 2 の 25 行目でロック \({\it lockedQC}\) を \(w\) の \({\it precommitQC}\) に更新する。\(v_s\) が最小であるため、\({\it qc}_s\) が形成される前にレプリカ \(r\) が \(w\) によってひかれた枝上に持っているロックは変更されない。そうでなければ、17行目が25行目より前にあるため、\(r\) はより小さいビューを持つ他の \({\it prepareQC}\) を確認している必要があり、最小性に反している。ここで、ビューの PREPARE フェーズでの \({\rm safeNode}\) の呼び出しとレプリカ \(r\) による \({\rm safeNode}\) の呼び出しを考えてみる。仮定より、\(m.{\it node}\) は \({\it lockedQC}.{\it node}\) と競合し、Algorithm 1 の 26 行目の論理和は false となる。さらに、\(m.{\it justify.viewNumber} \gt v_1\) は \(v_s\) の最小性に違反するため、Algorithm 1 の 27 行目の離散値も false である。従って、\({\rm safeNode}\) は false を返さねばならず、\(r\) はビュー内の競合する枝に対して PREPARE 投票を行うことができない。これは矛盾である。
∎

Liveness. 前のセクションには未定義の 2 つの関数、\({\rm reader}\) と \({\rm nextView}\) が存在している。それらの定義はプロトコルの safety に影響しないが liveness には影響する。それらの候補を定義する前に、GST 後にすべての正しいレプリカが \(T_f\) 中にビュー \(v\) に残り、ビュー \(v\) のリーダーが正しいなら決定に到達するような有限の時間 \(T_f\) があることを我々は最初に示した。以下では \({\it qc}_1\) と \({\it qc}_2\) が有効で \({\it qc}_1.{\it node} = {\it qc}_2.{\it node}\), \({\it qc}_1.{\it viewNumber} = {\it qc}_2.{\it viewNumber}\) であれば \({\it qc}_1\) と \({\it qc}_2\) は一致すると表現する。

補題3. \({\it lockedQC} = {\it precommitQC}\) のように正しいレプリカがロックされている場合、少なくとも \(f+1\) 個の正しいレプリカが \({\it lockedQC}\) に一致する \({\it prepareQC}\) に投票した。

Proof. レプリカ \(r\) が \({\it precommitQC}\) でロックされているとする。次に PREPARE フェーズ (Algorithm 2 の 10 行目) で一致する \({\it prepareQC}\) に対して \((n-f)\) 票が投じられた。そのうちで、少なくとも \(f+1\) は正しいレプリカからのものであった。
∎

定理 4. GST の後、\(T_f\) の間にすべての正しいレプリカがビュー \(v\) に残り、ビュー \(v\) のリーダーが正しいなら、決定に達するような有限の時間 \(T_f\) が存在する。

Proof. 新しいビューから開始し、リーダーは \((n-f)\) 個の NEW-VIEW メッセージを収集し、PREPARE メッセージをブロードキャストする前にその \({\it highQC}\) を算出する。すべてのレプリカ (リーダー自身を含む) の中で保持しているロックが最も高いものが \({\it lockedQC} = {\it precommitQC}^*\) であるとする。補題 3 より、\({\it prepareQC}^*\) に一致する \({\it precommitQC}^*\) に投票した少なくとも \(f+1\) 個の正しいレプリカが存在することが分かっており、すでにそれらの NEW-VIEW メッセージでリーダーに送信している。従って、リーダーはこれらの NEW-VIEW メッセージの少なくとも 1 つで \({\it prepareQC}^*\) を知っており、PREPARE メッセージで \({\it highQC}\) として使用しなければならない。この仮定により、すべての正しいレプリカはビュー内で同期化され、リーダーは非故障である。従って、すべての正しいレプリカは PREPARE フェーズで投票を行う。これは、\({\rm safeNode}\) で Algorithm 1 の 27 行目の条件が満たされるためである (メッセージ内の \({\it node}\) がレプリカの古い \({\it lockedQC}.{\it node}\) と競合し、26 行目はそうならない場合でも)。次に、リーダーがこのビューの有効な \({\it prepareQC}\) を組み立てた後、すべてのレプリカが次のすべてのフェーズで投票し、新しい決定につながる。GST の後、これらのフェーズが完了するまでの期間 \(T_f\) は有限の長さである。

このプロトコルは明示的な "\(\Delta\) 待ち" ステップがないため楽観的応答性 (optimistically responsive) を持ち、\({\rm safeNode}\) の理論的離散は 3-phase パラダイムの助けを借りて古いロックを上書きするために使われる。
∎

ここで \({\rm leader}\) および \({\rm nextView}\) の単純な構造を示す。これは GST の後、最終的にリーダーが正しいビューに到達し、すべての正しいレプリカが \(T_f\) 時間の間にビューに存在することを保証するために十分である。リーダーはビュー番号からレプリカへの決定的なマッピングを返し、最終的にはすべてのレプリカをローテーションするだけで十分である。\({\rm nextView}\) に可能な解決はタイムアウト間隔を維持する exponential back-off メカニズムを使用することである。各ビューに入るとタイマーが設定される。何も解決せずにタイマーが切れると、レプリカは間隔を 2 倍にして \({\rm nextView}\) を呼び出してビューを進める。間隔は毎回 2 倍となるので、最終的にはすべての正しいレプリカの待機間隔は、少なくとも共通の \(T_f\) のオーバーラップが存在することになり、その間、リーダーは決定を下すことができる。

Livelessness with two-phases. ここで "2-phase" HotStuff における無限に非決定的なシナリオを簡単に説明する。これは Casper や Tendermint に同期遅延を導入する必要性と (楽観的) 応答性を放棄する必要性の説明でもある。

2-phase の HotStuff 変種では PRE-COMMIT フェーズを省略して直接 COMMIT に進行する。\({\it prepareQC}\) で投票するとレプリカはロックされる。ビュー \(v\) でリーダーが \(b\) を提案したとする。これによって PREPARE フェーズが完了し、いくつかのレプリカの \(r_v\) が \({\it prepareQC}\) (\({\it qc}\) など) に \({\it qc}.{\it node}=b\) のように投票する。従って \(r_v\) は \({\it qc}\) でロックされる。非同期ネットワークのスケジューリングにより、残りのレプリカは \({\it qc}\) を受信せずにビュー \(v+1\) に移行する。

ここでは次のような single-view トランスクリプトを無限に繰り返す。システムで最も高い \({\it prepareQC}\) (つまり \({\it qc}\)) を保持する \(r_v\) のみでビュー \(v+1\) を開始する。新しいリーダー \(l\) は \(r_v\) を除く \(2f+1\) 個のレプリカから新しいビューのメッセージを収集する。これらの中で最も高い \({\it prepareQC}\) である \({\it qc}'\) はビュー \(v-1\) を持ち、\(b' = {\it qc}'.{\it node}\) は \(b\) と競合する。次に \(l\) は \(b'\) を拡張する \(b''\) を提案する。\(b'\) に対して \(2f\) の正しいレプリカが投票で応答するが、\(r_v\) は \({\it qc}\) でロックされ、\(b''\) は \(b\) と競合し、\({\it qc}'\) は \({\it qc}\) よりも小さいことからこれは拒否される。最終的に \(2f\) のレプリカはあきらめて次のビューに移動する。そのとき、故障レプリカが \(l\) の提案に応答し、そして \(l\) は \({\it prepareQC}(v+1, b'')\) と一つのレプリカ、例えばそれに投票しロックされている \(r_{v+1}\) とをまとめる。

Complexity. HotStuff の各フェーズではリーダーのみがすべてのレプリカにブロードキャストし、レプリカは投票を認証するために部分署名で送信者に 1 回だけ応答する。リーダーのメッセージでは QC は以前に収集された \((n-f)\) 票の認証で構成され、これは単一のしきい値署名によってエンコードすることができる。レプリカの応答では、そのレプリカからの部分署名が唯一の認証子となる。従って、各フェーズでは合計で \(O(n)\) 個の認証子が受信される。フェーズの数は一定であるため、ビューごとの全体的な複雑性は \(O(n)\) である。

5 Chained HotStuff

Basic HotStuff のリーダーが提案を行うには 3 つのフェーズを必要とする。これらのフェーズはレプリカから投票を収集する以外に「役に立つ」作業を行わないが、それらはとても類似している。Chained HotStuff では、Basic HotStuff プロトコル機能を改善すると同時に大幅に単純化している。各 PREPARE フェーズでビューを変更するアイディアであるため、各提案には独自のビューが存在している。これにより、メッセージタイプの数が減り、決定のパイプライン化が可能となる。メッセージタイプ削減の類似アプローチは Casper[1] で提案された。

より具体的には、Chained HotStuff では PREPARE フェーズでの投票はビューでリーダーによって収集され \({\it genericQC}\) に入れられる。そして \({\it genericQC}\) は次のビューのリーダーに中継され、基本的に PRE-COMMIT となるはずだった次のフェーズの責任を次のリーダーに委任する。ただし、次のリーダーは実際には PRE-COMMIT フェーズを実施せず、代わりに新しい PREPARE フェーズを開始し独自の提案を追加する。このビュー \(v+1\) の PREPARE フェーズは、同時にビュー \(v\) の PRE-COMMIT フェーズとしても機能する。ビュー \(v+2\) の PREPARE フェーズはビュー \(v+1\) の PRE-COMMIT フェーズと、ビュー \(v\) の COMMIT フェーズとして同時に機能する。これは、すべてのフェーズの構造が同一であるためである。

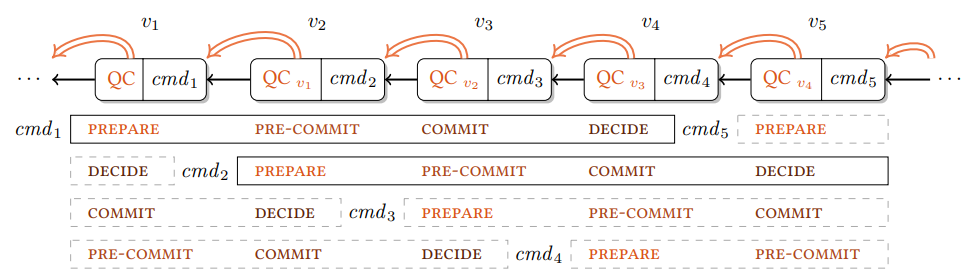
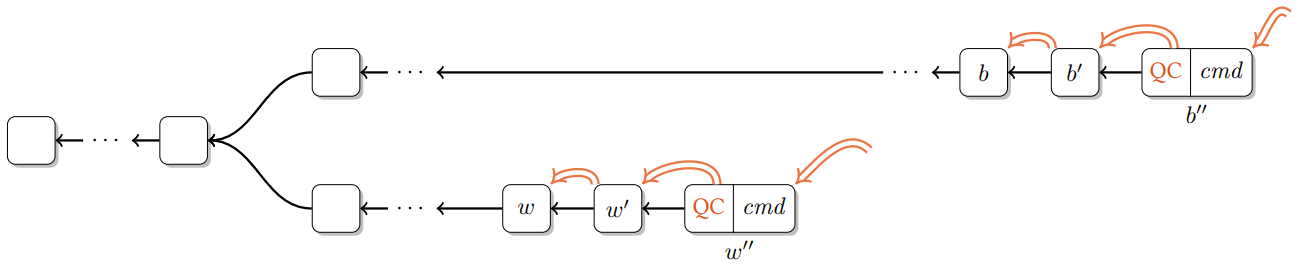
Figure 1: Chained HotStuff は QC が異なるフェーズで同時に実行できるパイプライン化された Basic HotStuff である。

Chained HotStuff 提案のチェーンに組み込まれた Basic HotStuff プロトコルフェーズのパイプラインを Figure 1 に示す。Chained HotStuff のビュー \(v_1\), \(v_2\), \(v_3\) は、\(v_1\) で提案された cmd1 の PREPARE, PRE-COMMIT および COMMIT の Basic Stuff フェーズとして機能する。このコマンドは \(v_4\) の終わりまでにコミットされる。ビュー \(v_2\), \(v_3\), \(v_4\) は \(v_2\) で提案された cmd2 の 3 つの Basic HotStuff フェーズとして機能し、\(v_5\) の終わりまでにコミットされる。これらのフェーズで生成された追加の提案は同様にパイプラインを続行し、破線のボックスで示されている。Figure 1 での単一の矢印はノード \(b\) に対する \(b.{\it parent}\) フィールドを示し、二重矢印は \(b.{\it justify}.{\it node}\) を示している。

従って、Chained HotStuff には NEW-VIEW と generic-phase の GENERIC メッセージの 2 タイプのメッセージのみが存在する。generic QC はすべての論理的なパイプライン化されたフェーズで機能する。次に、Basic HotStuff の COMMIT と DECIDE フェーズでのみ発生する、ロックとコミットを処理するパイプラインのメカニズムについて説明する。

Figure 2: ビュー \(v_4\), \(v_5\), \(v_6\) のノードは Three-Chain を形成する。ビュー \(v_8\) のノードは Chained HotStuff で有効な One-Chain を作成しない (ただしセクション 6 のアルゴリズムで緩和した後は有効な One-Chain である)。

Dummy nodes. 一部のビュー \({\it viewNumber}\) でリーダーが使用する \({\it genericQC}\) は直前のビュー \({\it viewNumber}-1\) の提案を直接参照しない場合がある。この理由は、競合する提案や両性のクラッシュによって前のビューのリーダーが QC を取得できないからである。ツリー構造を簡素化するために、\({\rm createLeaf}\) は提案するビューの高さ (ノードの枝上の親リンクの数) まで \({\it genericQC}.{\it node}\) を空白ノードで拡張するため、ビュー番号はノードの高さと同等になる。その結果、ノード \(b\) に埋め込まれた QC はその親を参照しない場合がある; すなはち \(b.{\it justify}.{\it node}\) は \(b.{\it parent}\) と等しくない可能性がある (Figure 2 の最後のノード)。

One-Chain, Two-Chain, and Three-Chain. ノード \(b^*\) が直接の親、つまり \(b^*.{\it justify}.{\it node} = b^*.{\it parent}\) を参照する QC を持っている場合それは One-Chain を形成していると言う。\(b''=b^*.{\it justify}.{\it node}\) と表記する。ノード \(b^*\) が One-Chain を形成しているのに加えて \(b''.{\it justify}.{\it node} = b''.{\it parent}\) である場合に Two-Chain を形成する。\(b''\) が Two-Chain を形成する場合、Three-Chain を形成する。

チェーン \(b=b_0.{\it justify}.{\it node}\), \(b_0=b''.{\it justify}.{\it node}\), \(b''=b^*.{\it justify}.{\it node}\) を見ると、いずれかのノードで先祖ギャップが発生する可能性がある。これらの状況は Basic HotStuff においてリーダーが 3 つのフェーズのいずれかを完了できず \({\rm nextView}\) によって次のビューに割り込まれるのと似ている。

\(b^*\) が One-Chain を形成しているのであれば \(b''\) の PREPARE フェーズは成功している。従ってレプリカが \(b^*\) に投票するとき \({\it genericQC} \leftarrow b^*.{\it justify}\) を記憶しておく必要がある。我々は One-Chain が直接ではない場合でも、現在の \({\it genericQC}\) より高い限り \({\it genericQC}\) を更新しても安全であることを述べた。セクション 6 で説明した実装コードでは、この場合に実際に \({\it genericQC}\) を更新する。

\(b^*\) が Two-Chain を形成する場合、\(b'\) の PRE-COMMIT フェーズは成功している。従ってレプリカは \({\it lockedQC} \leftarrow b''.{\it justify}\) を更新する必要がある。繰り返しになるが、Two-Chain が直接でなくともロックを更新できることに注意 -- 安全性は損なわれない -- 実際、これはセクション 6 の実装コードで示される。

最後に、\(b^*\) が Three-Chain を形成する場合、\(b\) の COMMIT フェーズは成功し、\(b\) はコミットされた決定となる。

Algorithm 3 は Chained HotStuff の疑似コードを示している。Appendix A の定理 5 によって与えられた safety の証明は Basic HotStuff のものと類似している。有効なノードの QC はその祖先を参照する必要がある。簡潔にするため、この制約が常に保持されると仮定しコードの検証は省略する。

Algorithm 3 Chained HotStuf protocol.

6 Implementation

HotStuff は効率的な SMR システムを構築するための実用的なプロトコルである。そのシンプルさにより、我々は Algorithm 3 をプロトタイプ実装のコードスケルトンのようなイベント駆動型の仕様に簡単に変えることができる。

Algorithm 4 に示されているように、本体から Pacemaker という名前のモジュールに liveness メカニズムを抽出することによりコードはされに単純化および一般化される。次のリーダーは GENERIC フェーズの終わりに常に \({\it genericQC}\) 待ってから統治を開始する代わりに、そのロジックを Pacemaker に委譲する。安定したリーダーはこのステップを省略して複数の height に渡る提案を合理化することができる。さらに我々は、有効なノードの QC が常にその祖先を参照しているという要件を維持している間、最も高い \({\it genericQC}\) と \({\rm lockedQC}\) を維持するための直接の親の制約を緩和する。正しさの証明は Chained HotStuff と似ており、我々は [50] の付録に従う。

Algorithm 4 Event-driven HotStuff (for replica \(u\)).

Data structures. 各レプリカ \(u\) は以下の主要な状態変数を追跡する:

\(V[\cdot]\) あるノードからその票へのマッピング。
\({\it vheight}\) 最後に投票されたノードの高さ。
\(b_{lock}\) ロックされているノード (\(lockedQC\) 相当)。
\(b_{exec}\) 最後に実行されたノード。
\(qc_{height}\) Pacemaker が保持する最も高い既知の QC (\(genericQC\) 相当)。
\(b_{leaf}\) Pacemaker が保持する葉ノード。

また全ての正しいレプリカで認識されている同じジェネシスノードである定数 \(b_0\) も保持している。ブートストラップを行うために \(b_0\) はハードコードされた自分自身の QC を含んでおり、\(b_{block}\), \(b_{exec}\), \(b_{leaf}\) は全て \(b_0\) に初期化されており、\(qc_{height}\) は \(b_0\) に対する QC を含んでいる。

Pacemaker. Pacemaker は GST 後に進行していることを保証するメカニズムである。これは 2 つの要素によって達成される。

1 つ目は "同期" (synchronization) であり、全ての正しいレプリカと一意のリーダーを十分な期間に渡って共通の高さにする。文献 [25, 20, 15] の一般的な同期メカニズムは、レプリカがより大きな高さで費やした \(\Delta\) の数を進行が得られるまで増加させるものである。リーダーを決定論的に選出する一般的な方法は、全ての正しいレプリカが事前定義されたリーダースケジュールを保持し、リーダーが降格されると次のものに切り替わるローテーションリーダースキームを使用することである。

2 つ目は、Pacemaker は正しいレプリカに支持されるであろう提案を選択する方法をリーダーに提供する必要がある。Algorithm 5 で示すように、ビューの変更後の \({\rm onReceiveNewView}\) で新しいリーダーが \({\rm onNextSyncView}\) を介してレプリカが送信した NEW-VIEW メッセージを収集し、liveness に対する \({\rm onReceiveProposal}\) 条件 (Algorithm 4 の 18 行目) の 2 番目を満たす最も高い QC を発見する。ただし、現職のリーダーは、同じビューの中で、自身が提案した最後の葉に新しいノードを連結する。ここで NEW-VIEW メッセージは必要ない。いくつかのアプリケーション固有のヒューリスティックに基づいて (例えば以前に提案されたノードが QC を取得するまで待つ間待機するため)、現在のリーダーは \({\rm onBeat}\) を呼び出し、実行するコマンドを持つ新しいノードを提案する。

不良 Pacemaker が任意に \({\rm onPropose}\) を呼び出したり、親と QC を気まぐれに選択したり、またどのようなスケジュール遅延に対しても、safety は常に保証される。従って Algorithm 4 のみによって保証される safety は、Algorithm 5 の潜在的なインスタンス化によって liveness から切り離される。

Algorithm 5 Code skeleton for a Pacemaker (for replica \(u\)).

Two-phase HotStuff variant. HotStuff フレームワークの柔軟さをさらに実証するために Algorithm 6 では HotStuff の 2-phase 変種を示す。UPDATE 手続きのみが影響を受け、コミット決定に達するには Two-Chain が必要であり、One-Chain がロックを決定する。前述 (セクション 4.4) で説明したとおり、この 2-phase 変種は楽観的応答性を失っており、Tendermint/Casper と同様である。利点はフェーズ数が少ないことだが、ネットワーク遅延の最大値に基づいた待機時間を Pacemaker に組み込むことによって liveness には対処できる。詳細についてはセクション 7.3 を参照。

Algorithm 6 \({\rm \small UPDATE}\) replacement for two-phase HotStuff.

7 One-Chain and Two-Chain BFT Protocols

このセクションではビザンチン障害耐性における 40 年に及ぶ研究の 4 つの BFT レプリケーションプロトコルを調査し、それらを Chained HotStuff に似たチェーンフレームワークにキャストする。

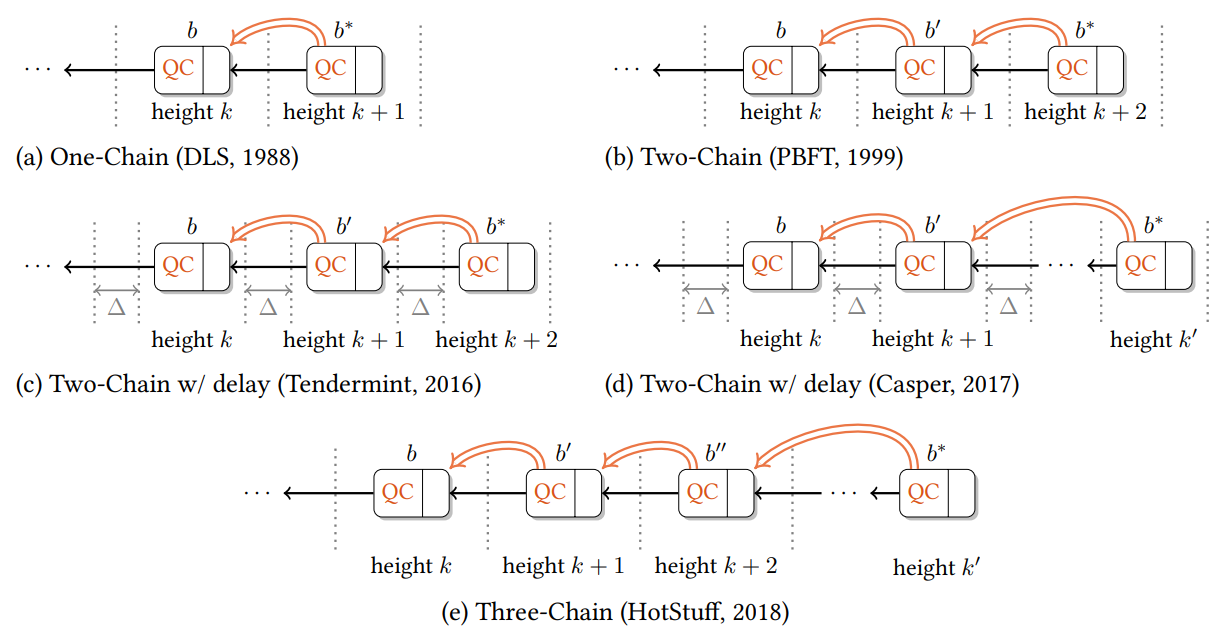
Figure 3 は HotStuff を含む 5 つのプロトコルのコミットルールの鳥瞰図を示している。

Figure 3: 様々な BFT プロトコルのコミットルール

簡単に言えば、DLS[25] のコミットルールは One-Chain であり、ノードはそれ自体のリーダーによってのみコミットされる。PBFT[20], Tendermint[15, 16], Casper[17] のコミットルールはほとんど同じで Two-Chain で構成される。liveness のために導入したメカニズムと区別するため、PBFT は 2 次サイズの "Proof" を持ち (線形性 (linearity) なし)、Tendermint と Casper は各リーダー提案の前に必須の \(\Delta\) 遅延を導入する (楽観的応答性 (optimistic responsiveness) なし)。HotStuff は Three-Chain ルールを使用し、遅延のない線形リーダープロトコルを備えている。

7.1 DLS

最も単純なコミットルールは One-Chain である。このルールは最初の既知の非同期ビザンチン合意ソリューションである Dwork, Lynch, Stockmeyer (DLS) をモデルとしていて Figure 3 (a) に示されている。レプリカは投票した最上位ノードの DLS でロックされる。

残念ながら、このルールはある高さでリーダーが曖昧になり、2 つの正しいレプリカがその高さで対立する提案にロックされた場合に容易にデッドロックを引き起こす。ロックされた値に投票しなかったことを示す \(2f+1\) が存在しない限り、いずれかのロックを放棄することは安全ではない。

実際、DLS では、各高さのリーダーのみが One-Chain コミットルールによるコミット決定に到達することができる。従ってもしそれが曖昧となった場合、リーダー自身だけが被害を受けることになる。レプリカは \(2f+1\) レプリカが投票しなかった場合、または競合する (リーダーによって署名された) 提案がある場合にロックを放棄できる。DLS の各高さの終了時点で発生するロック解除のプロトコルはかなり複雑でコストが高いことが判明している。各高さのリーダーのみが決定を行えるという事実と併せて、ネットワークに障害が発生しておらずタイムリーである最良のシナリオでも、DLS は 1 回の決定ごとに \(n\) 回のリーダーローテーションと \(O(n^4)\) メッセージ送信を必要とする。DLS は安全な非同期プロトコルを実証するという新たな道を開いたが実用的なソリューションとしては設計されていなかった。

7.2 PBFT

PBFT をモデルとしている、より実用的なアプローチでは Two-Chain コミットルールを使用する (Figure 3 (b) 参照)。レプリカが One-Chain を形成するノードに投票すると、レプリカはそのノードにロックされる。同じ高さで競合している One-Chain は、それぞれに QC を持つため DLS のようなデッドロック状態は回避され、単純には不可能である。

しかし、あるレプリカが他のレプリカより高いロック保持している場合、リーダーは \(n-f\) レプリカから情報を収集してもそのことを知る事ができない可能性がある。これはリーダーが決定に到達することを無限に妨げる可能性があり、純粋にスケジューリングの問題である。この "スタック" を解消するために、PBFT は最も大きい One-Chain と \(2f+1\) レプリカから成る証明書を運ぶことにより、全てのレプリカのロックを解除する。以下に説明するようにこの証明は非常に複雑である。

オープンソース[20]化され、いくつかのフォローアップ研究[13, 34]で採用されたオリジナルの PBFT は、各メンバーが投票した最高の One-Chain を報告する \(n-f\) レプリカから集められたメッセージのセットを含むリーダー署名である。各 One-Chain には QC が含まれているため合計の通信コストは \(O(n^3)\) である。SBFT[30]は署名結合法[45, 18]を使用して各 QC を単一値に変えることによってこのコストを \(O(n^2)\) に軽減した。

[21] の PBFT 変種においては、リーダー署名はリーダーが定足数から一度だけ収集した最も大きい One-Chain を含んでいる。それはまた定足数の各メンバーから署名された値を一つ含み、より高い One-Chain に投票しなかったことを証明している。この証明をブロードキャストすると通信複雑度 \(O(n^2)\) が生じる。QC 上の署名は単一の値に結合されるかもしれないが、定足数の異なるメンバーからのメッセージは異なる値を持つかも知れないため、証明選対を一定のサイズに縮小できないことに注意されたい。

どちらのバリエーションでも、正しいレプリカはリーダーの署名より高い One-Chain を持っていたとしてもロックを解除する。従って、正しいリーダーは同期期間中にその提案を受け入れさせることがっでき liveness は保証される。コストはリーダーの交代ごとに 2 次式の通信である。

7.3 Tendermint and Casper

Tendermint は PBFT と同一の Two-Chain コミットルールがあり、Casper は葉が親と繋がるために QC を持つ必要がない Two-Chain ルールを持っている。つまり Casper では、Figure 3 (c, d) はそれぞれ Tendermint と Casper のコミットルールを示している。

どちらの方法でもリーダーは自分が分かっている最も大きい One-Chain を提案と共に送信するだけである。レプリカはリーダーからより高い One-Chain を受け取るとそのロックを解除する。

ただし、正しいレプリカはリーダーのノードに投票しない場合があるため、進行を保証するために新しいリーダーは最大ネットワーク遅延まで待機して最も大きい One-Chain を獲得しなければならない。そうでなければ、リーダーが新しい height を開始するために最初の \(n-1\) メッセージを待つだけでは進行は保証されない。リーダーの遅延は liveness を提供するために Tendermint と Casper の両方に固有のものである。

この単純なリーダープロトコルは HotStuff が借用しているリーダープロトコルの通信複雑性の線形増加を具体化している。前述のように、QC はしきい値署名を使用して単一の値で補足することができるため、リーダーは線形の通信複雑性を持つ最も大きい One-Chain を収集して配布することができる。ただし重要なことだが、HotStuff は追加の QC ステップによってリーダーが最大ネットワーク遅延を待機することを要求していない。

8 Evaluation

HotStuff を C++ コード約 4k 行のライブラリとして実装した。最も顕著なのは擬似コードで指定されたコアコンセンサスロジックが 200 行しか消費しなかったことだ。このセションでは、まず最先端のシステムである BFT-SMaRt[13]と比較してベースラインのスループットとレイテンシを調査する。次にビュー変更のメッセージコストに焦点を当てこのシナリオでの利点を確認する。

8.1 Setup

我々の実験は Amazon EC2 の c5.4xlarge インスタンスを使用して実施した。各インスタンスには Intel Xeon Platinum 8000 プロセッサのサポートする 16 個の vCPU が存在した。全てのコアは最大 3.4GHz の Turbo CPU クロック速度を維持した。各レプリカを単一の VM インスタンスで実行したため、元の評価[13]のようにスレッドを多用する BFT-SMaRt はレプリカ事に 16 コアを使用できた。iperf が計測した最大 TCP 帯域幅は約 1.2 ギガバイト/秒だった。我々は実行中に帯域幅調整を行わなかった。2 つのマシン間のネットワーク遅延は 1 ミリ秒未満だった。

我々の HotStuff プロトタイプ実装は投票および定足数証明書の両方すべての電子署名に secp256k1 を使用する。BMT-SMaRt では通常の操作中はメッセージの MAC (メッセージ認証コード) に hmac-sha1 を使用し、ビュー変更中は MAC に加えデジタル署名を使用する。

HotStuff の全ての結果はクライアントからの end-to-end の測定を反映している。BFT-SMaRt については BFT-SMaRt の Web サイト (https://github.com/bft-smart/library) のマイクロベンチマークプログラム ThroughputLatencyServer および ThroughputLatencyClient を使用した。クライアントプログラムは end-to-end のレイテンシを計測しスループットは計測しないが、サーバ側のプログラムはスループットとレイテンシの両方を計測する。サーバからのスループット結果とクライアントからの遅延の結果を使用した。

8.2 Base Performance

我々は最初に他の BFT レプリケーションシステムの評価でよく見られる構成でスループットとレイテンシを測定した。システムが飽和するまで操作要求レートを変えながら、単一の障害、つまり \(f=1\) を許容する構成で 4 つのレプリカを実行した。このベンチマークでは空の (サイズがゼロの) 操作要求を応答を使用し、ビューの変更をトリガーしなかった; 以下に他の設定を展開する。応答性 HotStuff は 3-phase だが、BFT-SMaRt ベースラインは 2-phase しかないため、追加のベースラインとして 2-phase 変種も実行している。

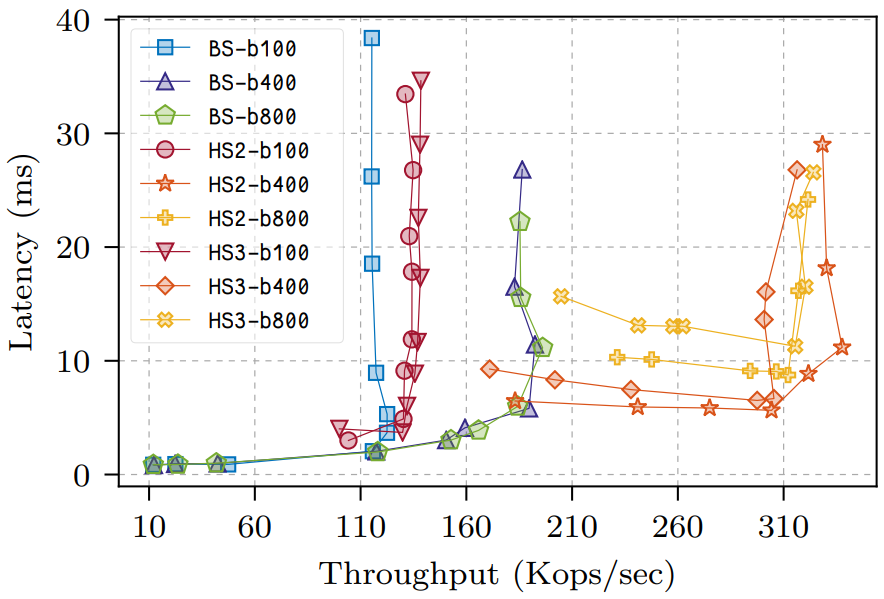
Figure 4: 異なるバッチサイズ, 4 レプリカ, 0/0 ペイロードのスループット vs レイテンシ

Figure 4 は両方のシステムでの 3 つのバッチサイズ、100, 400, 800 を示しているが、これらのシステムには異なるバッチスキームがあるため、これらの値はそれぞれのシステムでわずかに異なることを意味している。BFT-SMaRt は操作ごとに個別のコンセンサス決定を行い、複数のコンセンサスプロトコルからのメッセージをバッチ処理する。従って、典型的な L 字型のレイテンシ/スループットパフォーマンスとなる。HotStuff は各ノードで複数の操作をバッチ処理しているため決定ごとの電子署名コストを軽減している。ただし、バッチごとに 400 を超える操作を行うと、バッチ処理で発生するレイテンシは暗号のコストよりも高くなる。これらの違いにもかかわらず 3-phase ("HS3-") と 2-phase ("HS2-") の両方の HotStuff は 3 つのバッチサイズの全てで BFT-SMaRt ("BS-") と同等のレイテンシ性能を実現し、スループットは BFT-SMaRt を著しく上回った。

バッチサイズが 100 および 400 の場合、最低レイテンシの HotStuff ポイントは、最高のスループットで BFT-SMaRt によって同時に達成できるレイテンシとスループットよりも良好なレイテンシとスループットを提供するが、レイテンシはわずかに増加する。この増加は HotStuff で採用しているバッチ処理の戦略に一部起因する: バッチの決定に達するには 3 つの追加の完全バッチ (2-phase 変種では 2 つ) が必要となる。我々の実験では未処理のリクエスト数を多く維持したが、バッチサイズが大きくなるほど、バッチ処理パイプラインを満たすのに時間がかかる。実際の展開をさらに最適化して未処理の操作数にバッチサイズを適合することができる。

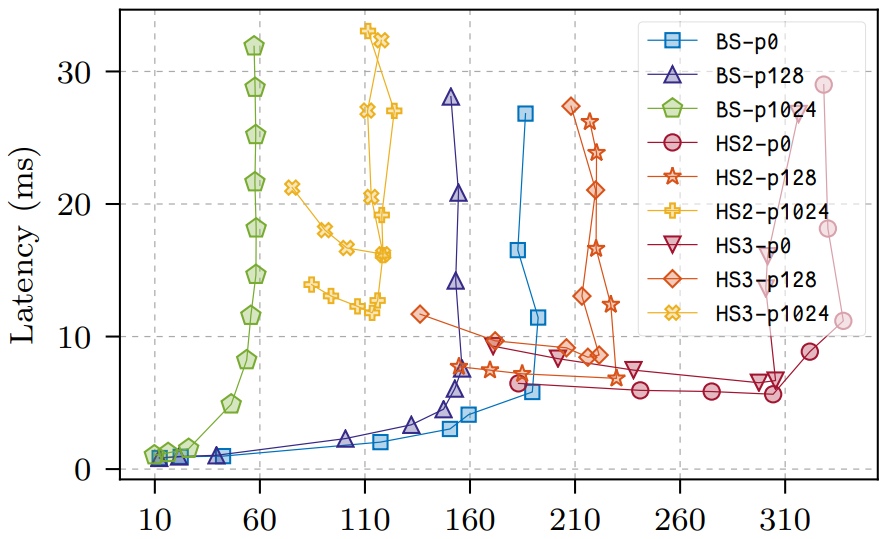
Figure 5: 異なるペイロードサイズ, 4 レプリカ, バッチサイズ 400 のスループット vs レイテンシ

Figure 5 でそれぞれ "p0", "p128", "p1024" の表示は 0/0, 128/128, 1024/1024 の 3 つのクライアント要求/応答ペイロードサイズ (バイト数) を示している。全てのペイロードサイズに対して、3-phase と 2-phase の両方で HotStuff のスループットが BFT-SMaRt を上回り、同等か同程度のレイテンシを実現した。

BFT-SMaRt は HotStuff が使用する電子署名の非対称暗号よりも桁違いに速い、対称鍵に基づく MAC を使用する。また 3-phase HotStuff は BFT-SMaRt が使用する 2-phase PBFT 変種と比較してより多くのラウンドトリップを行う。それでも HotStuff は同等のレイテンシと遙かに高いスループットを実現している。以下では HotStuff のパフォーマンス上の利点がより顕著になる、より困難な状況で両方のシステムを評価する。

8.3 Scalability

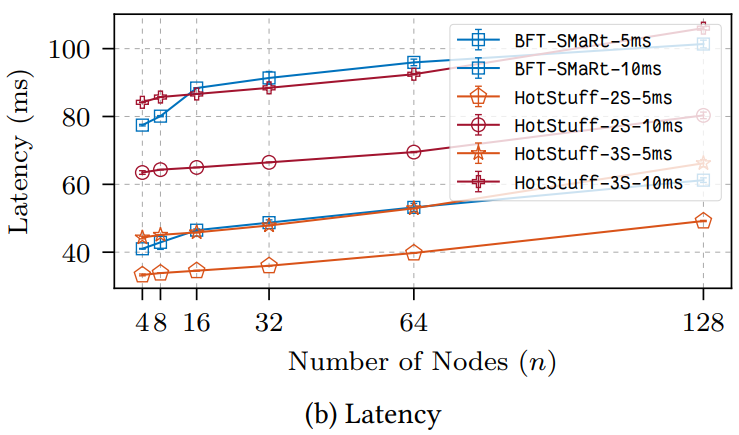
HotStuff のスケーラビリティを様々な次元で評価するために 3 の実験を行った。ベースラインではレプリカの数を変えながらサイズがゼロの要求/応答ペイロードを使用した。2 番目の評価では 128 バイトと 1024 バイトの要求/応答ペイロードを使用してベースライン実験を繰り返した。3 番目のテストでは NetEm (https://www.linux.org/docs/man8/tc-netem.html 参照) を使用して実装された 5ms ±0.5ms または 10ms ±1.0ms に均一に分散されたレプリカ間にネットワーク遅延を導入しながら (ペイロードが空の) ベースラインを繰り返した。各データポイントに対して、同じ設定で 5 回の実行を繰り返し、全ての実行の標準偏差を示すエラーバーを表示している。

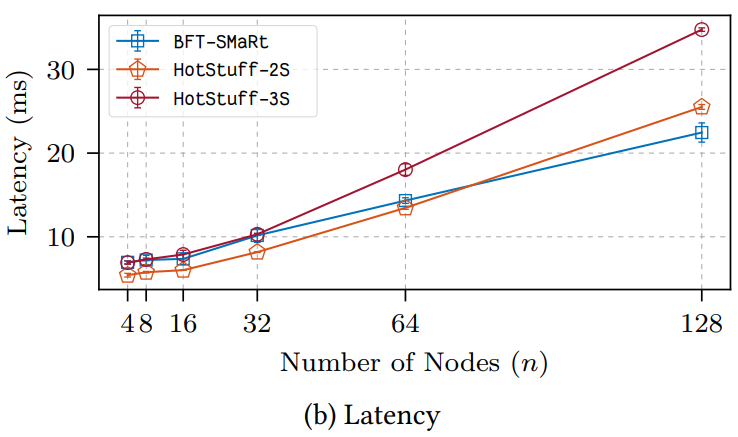
最初の設定は Figure 6a (スループット) と Figure 6b (レイテンシ) に示されている。3-phase および 2-phase のHotStuff は BFT-SMaRt よりも一貫して優れたスループットを示すが、それらのレイテンシは BFT-SMaRt と同等であり緩やかに劣化している。\(n\lt 32\) の場合、パフォーマンスは BFT-SMaRt より優れている。これは現在我々が QC に secp256k1 署名のリストを使用しているためである。将来的には高速しきい値署名方式を使用して HotStuff の暗号計算オーバーヘッドを削減する予定である。

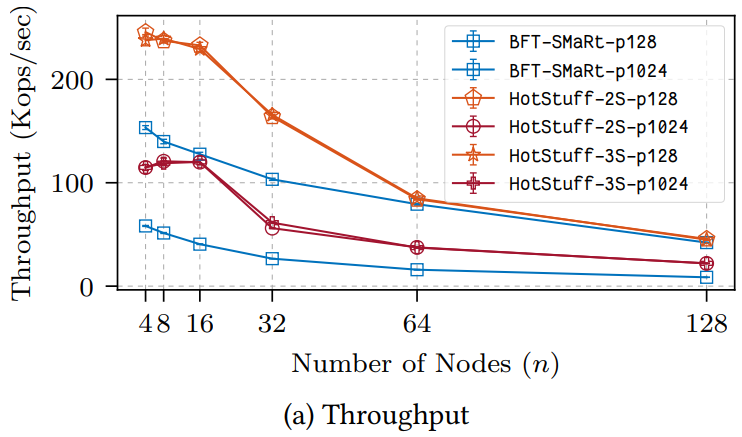
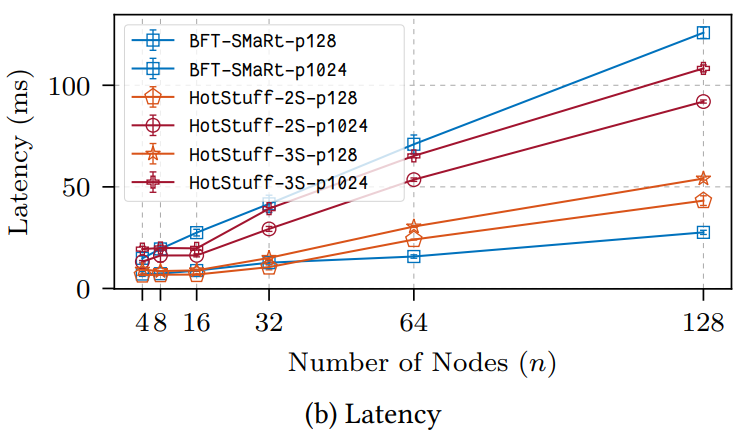
Figure 6: 0/0 ペイロード、バッチサイズ 400 のスケーラビリティ

ペイロードサイズが 128 または 1024 バイトとして 2 番目の設定は Figure 7a (スループット) および Figure 7b (レイテンシ) で "p128" または "p1024" で示されている。二次関数的な帯域幅コストのため BFT-SMaRt のスループットは適度なペイロードサイズ (1024バイト) で HotStuff よりも悪くなる。

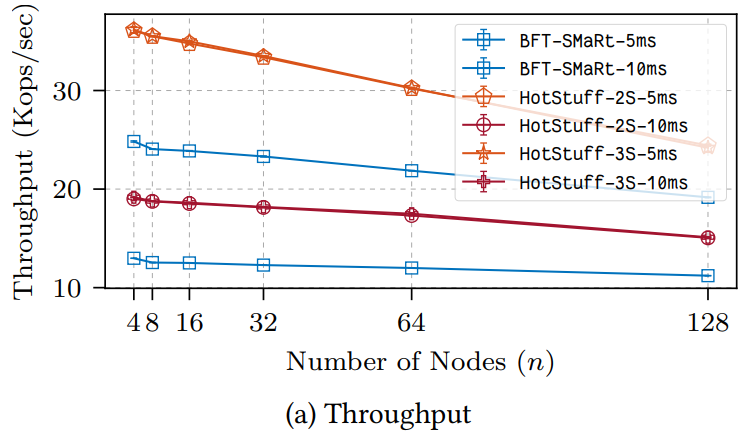
Figure 7: 128/128 または 1024/1024 ペイロード、バッチサイズ 400 のスケーラビリティ

3 番目の設定は Figure 8a (スループット) と Figure 8b (レイテンシ) に "5ms" と "10ms" として示している。繰り返すが、BFT-SMaRt での大きな帯域消費により HotStuff は両方のケースで一貫して BFT-SMaRt を上回った。

Figure 8: 0/0 ペイロード、バッチサイズ 400 でのレプリカ間レイテンシ 5ms ± 0.5ms と 10ms ± 1.0ms　のスケーラビリティ

8.4 View Change

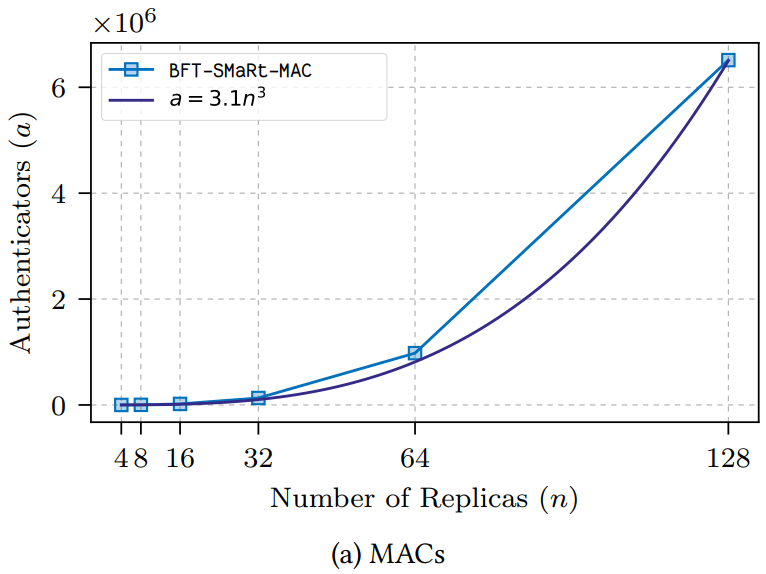
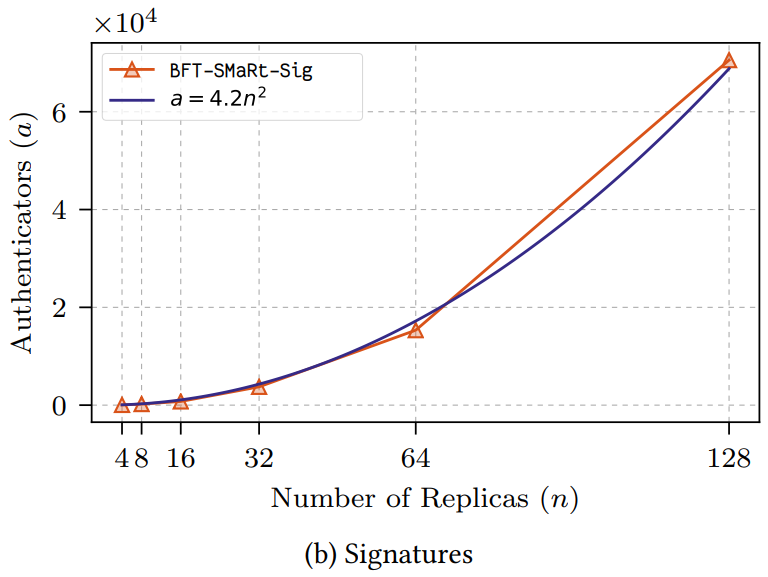
リーダー交代時の通信の複雑さを評価するために BFT-SMaRt のビュー変更プロトコルないで実行された MAC と署名の検証回数をカウントした。我々の評価戦略は以下の通り。我々は BFT-SMaRt の 1000 回の決定ごとにビュー変更を挿入した。ビュー変更プロトコル内でメッセージを受信したり処理する際に検証する回数をカウントするコードを BFT-SMaRt のソースに装備した。通信複雑性以上に、この測定はこれらの認証済み値の転送に関連する暗号計算負荷を協調している。

Figure 9a と Figure 9b (訳注:原文中に Figure 9a/b は存在せず 10a/b がこれに相当) はビューの変更ごとに処理される追加の認証子 (それぞれ MAC と署名) の数を示している。この定義では、リーダーが同じかどうかに関係なく認証子の数が同じままであるため、HotStuff に "余計な" 認証子は存在しないことに注意。2 つの図は BFT-SMaRt が 3 次数の MAC と 2 次数の署名を使用していることを表している。HotStuff はビュー変更に追加の認証子を必要としないためグラフからは省略されている。

リーダー交代の実時間パフォーマンスを評価することは難しい。第一に、頻繁なビュー変更をトリガーすると BFT-SMaRt はスタックした; 我々の認証子カウントプログラムはシステムがスタックする前に可能な限り多くの成功したビュー変更について平気な為る必要があり実験を何度も繰り返した。第二に、リーダー交代の実際の経過時間はタイムアウトパラメータとリーダー選挙メカニズムに大きく依存する。従って意味のある比較を提供することは不可能である。

Figure 10: Number of extra authenticators used for each BFT-SMaRt view change.

9 Conclusion

部分同期モデルにおける最初の実用的な BFT レプリケーションソリューションである PBFT の導入以来、2-phase コアパラダイムを中心に多数の BFT ソリューションが構築された。第一フェーズでは QC を通じた提案の一意性を保証し、第二フェーズでは QC を通じて新しいリーダーがレプリカを調整して安全な提案に投票できるようにしている。このためにリーダーは \((n-f)\) 個のレプリカからの情報を中継し、それぞれが最も大きい QC または投票を報告する必要があった。このように 2-phase 研究世代はリーダー交代に関する二次的な通信ボトルネックに悩まされている。

HotStuff は 3-phase コアを中心に展開しており、新しいリーダーは自分が知っている最も大きい QC を選択するだけでよい。これにより、上記の複雑さが緩和されると同時に、リーダー交代プロトコルが大幅に簡素化される。フェーズを (ほぼ) 正規化したため HotStuff のパイプライン化と頻度の高いリーダーローテーションが非常に容易となった。

Acknowledgements

We are thankful to Mathieu Baudet, Avery Ching, George Danezis, François Garillot, Zekun Li, Ben Maurer, Kartik Nayak, Dmitri Perelman, and Ling Ren, for many deep discussions of HotStuff, and to Mathieu Baudet for exposing a subtle error in a previous version posted to the ArXiv of this manuscript.

References

  1. Casper ffg with one message type, and simpler fork choice rule. https://ethresear.ch/t/casper-ffg-with-one-message-type-and-simpler-fork-choice-rule/103, 2017.
  2. Istanbul bft’s design cannot successfully tolerate fail-stop failures. https://github.com/jpmorganchase/quorum/issues/305, 2018.
  3. A livelock bug in the presence of byzantine validator. https://github.com/tendermint/tendermint/issues/1047, 2018.
  4. Ittai Abraham, Guy Gueta, Dahlia Malkhi, Lorenzo Alvisi, Ramakrishna Kotla, and Jean-Philippe Martin. Revisiting fast practical byzantine fault tolerance. CoRR, abs/1712.01367, 2017.
  5. Ittai Abraham, Guy Gueta, Dahlia Malkhi, and Jean-Philippe Martin. Revisiting fast practical Byzantine fault tolerance: Thelma, velma, and zelma. CoRR, abs/1801.10022, 2018.
  6. Ittai Abraham and Dahlia Malkhi. The blockchain consensus layer and BFT. Bulletin of the EATCS, 123, 2017.
  7. Ittai Abraham, Dahlia Malkhi, Kartik Nayak, Ling Ren, and Alexander Spiegelman. Solida: A blockchain protocol based on reconfigurable byzantine consensus. In 21st International Conference on Principles of Distributed Systems, OPODIS 2017, Lisbon, Portugal, December 18-20, 2017, pages 25:1–25:19, 2017.
  8. Ittai Abraham, Dahlia Malkhi, and Alexander Spiegelman. Validated asynchronous byzantine agreement with optimal resilience and asymptotically optimal time and word communication. In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, PODC 2019, Toronto, ON, Canada, July 29-August 2, 2019, 2019.
  9. Yair Amir, Brian A. Coan, Jonathan Kirsch, and John Lane. Prime: Byzantine replication under attack. IEEE Trans. Dependable Sec. Comput., 8(4):564–577, 2011.
  10. Hagit Attiya, Cynthia Dwork, Nancy A. Lynch, and Larry J. Stockmeyer. Bounds on the time to reach agreement in the presence of timing uncertainty. J. ACM, 41(1):122–152, 1994.
  11. Pierre-Louis Aublin, Rachid Guerraoui, Nikola Knezevic, Vivien Quéma, and Marko Vukolic. The next 700 BFT protocols. ACM Trans. Comput. Syst., 32(4):12:1–12:45, 2015.
  12. Michael Ben-Or. Another advantage of free choice: Completely asynchronous agreement protocols (extended abstract). In Proceedings of the Second Annual ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing, Montreal, Quebec, Canada, August 17-19, 1983, pages 27–30, 1983.
  13. Alysson Neves Bessani, João Sousa, and Eduardo Adílio Pelinson Alchieri. State machine replication for the masses with BFT-SMART. In 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, DSN 2014, Atlanta, GA, USA, June 23-26, 2014, pages 355–362, 2014.
  14. Dan Boneh, Ben Lynn, and Hovav Shacham. Short signatures from the weil pairing. J. Cryptology, 17(4):297–319, 2004.
  15. Ethan Buchman. Tendermint: Byzantine fault tolerance in the age of blockchains. PhD thesis, 2016.
  16. Ethan Buchman, Jae Kwon, and Zarko Milosevic. The latest gossip on BFT consensus. CoRR, abs/1807.04938, 2018.
  17. Vitalik Buterin and Virgil Grifith. Casper the friendly finality gadget. CoRR, abs/1710.09437, 2017.
  18. Christian Cachin, Klaus Kursawe, and Victor Shoup. Random oracles in constantinople: Practical asynchronous byzantine agreement using cryptography. J. Cryptology, 18(3):219–246, 2005.
  19. Christian Cachin and Marko Vukolic. Blockchain consensus protocols in the wild. CoRR, abs/1707.01873, 2017.
  20. Miguel Castro and Barbara Liskov. Practical byzantine fault tolerance. In Proceedings of the Third USENIX Symposium on Operating Systems Design and Implementation (OSDI), New Orleans, Louisiana, USA, February 22-25, 1999, pages 173–186, 1999.
  21. Miguel Castro and Barbara Liskov. Practical byzantine fault tolerance and proactive recovery. ACM Trans. Comput. Syst., 20(4):398–461, 2002.
  22. Allen Clement, Manos Kapritsos, Sangmin Lee, Yang Wang, Lorenzo Alvisi, Michael Dahlin, and Taylor Riche. Upright cluster services. In Proceedings of the 22nd ACM Symposium on Operating Systems Principles 2009, SOSP 2009, Big Sky, Montana, USA, October 11-14, 2009, pages 277–290, 2009.
  23. Danny Dolev and Rüdiger Reischuk. Bounds on information exchange for byzantine agreement. J. ACM, 32(1):191–204, 1985.
  24. Danny Dolev and H. Raymond Strong. Polynomial algorithms for multiple processor agreement. In Proceedings of the 14th Annual ACM Symposium on Theory of Computing, May 5-7, 1982, San Francisco, California, USA, pages 401–407, 1982.
  25. Cynthia Dwork, Nancy A. Lynch, and Larry J. Stockmeyer. Consensus in the presence of partial synchrony. J. ACM, 35(2):288–323, 1988.
  26. Ittay Eyal, Adem Efe Gencer, Emin Gün Sirer, and Robbert van Renesse. Bitcoin-ng: A scalable blockchain protocol. In 13th USENIX Symposium on Networked Systems Design and Implementation, NSDI 2016, Santa Clara, CA, USA, March 16-18, 2016, pages 45–59, 2016.
  27. Michael J. Fischer, Nancy A. Lynch, and Mike Paterson. Impossibility of distributed consensus with one faulty process. J. ACM, 32(2):374–382, 1985.
  28. Juan A. Garay, Aggelos Kiayias, and Nikos Leonardos. The bitcoin backbone protocol: Analysis and applications. In Advances in Cryptology - EUROCRYPT 2015 - 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, April 26-30, 2015, Proceedings, Part II, pages 281–310, 2015.
  29. Yossi Gilad, Rotem Hemo, Silvio Micali, Georgios Vlachos, and Nickolai Zeldovich. Algorand: Scaling byzantine agreements for cryptocurrencies. In Proceedings of the 26th Symposium on Operating Systems Principles, Shanghai, China, October 28-31, 2017, pages 51–68, 2017.
  30. Guy Golan-Gueta, Ittai Abraham, Shelly Grossman, Dahlia Malkhi, Benny Pinkas, Michael K. Reiter, DragosAdrian Seredinschi, Orr Tamir, and Alin Tomescu. SBFT: a scalable decentralized trust infrastructure for blockchains. CoRR, abs/1804.01626, 2018.
  31. Timo Hanke, Mahnush Movahedi, and Dominic Williams. DFINITY technology overview series, consensus system. CoRR, abs/1805.04548, 2018.
  32. Jonathan Katz and Chiu-Yuen Koo. On expected constant-round protocols for byzantine agreement. J. Comput. Syst. Sci., 75(2):91–112, 2009.
  33. Eleftherios Kokoris-Kogias, Philipp Jovanovic, Nicolas Gailly, Ismail Khoff, Linus Gasser, and Bryan Ford. Enhancing bitcoin security and performance with strong consistency via collective signing. CoRR, abs/1602.06997, 2016.
  34. Ramakrishna Kotla, Lorenzo Alvisi, Michael Dahlin, Allen Clement, and Edmund L. Wong. Zyzzyva: Speculative byzantine fault tolerance. ACM Trans. Comput. Syst., 27(4):7:1–7:39, 2009.
  35. Leslie Lamport. Time, clocks, and the ordering of events in a distributed system. Commun. ACM, 21(7):558–565, 1978.
  36. Leslie Lamport. The part-time parliament. ACM Trans. Comput. Syst., 16(2):133–169, 1998.
  37. Leslie Lamport, Robert E. Shostak, and Marshall C. Pease. The byzantine generals problem. ACM Trans. Program. Lang. Syst., 4(3):382–401, 1982.
  38. James Mickens. The saddest moment. ;login:, 39(3), 2014.
  39. Andrew Miller, Yu Xia, Kyle Croman, Elaine Shi, and Dawn Song. The honey badger of BFT protocols. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, October 24-28, 2016, pages 31–42, 2016.
  40. Satoshi Nakamoto. Bitcoin: A peer-to-peer electronic cash system. https://bitcoin.org/bitcoin.pdf, 2008.
  41. Rafael Pass, Lior Seeman, and Abhi Shelat. Analysis of the blockchain protocol in asynchronous networks. In Advances in Cryptology - EUROCRYPT 2017 - 36th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, April 30 - May 4, 2017, Proceedings, Part II, pages 643–673, 2017.
  42. Rafael Pass and Elaine Shi. Thunderella: Blockchains with optimistic instant confirmation. In Advances in Cryptology - EUROCRYPT 2018 - 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, April 29 - May 3, 2018 Proceedings, Part II, pages 3–33, 2018.
  43. Marshall C. Pease, Robert E. Shostak, and Leslie Lamport. Reaching agreement in the presence of faults. J. ACM, 27(2):228–234, 1980.
  44. HariGovind V. Ramasamy and Christian Cachin. Parsimonious asynchronous byzantine-fault-tolerant atomic broadcast. In Principles of Distributed Systems, 9th International Conference, OPODIS 2005, Pisa, Italy, December 12-14, 2005, Revised Selected Papers, pages 88–102, 2005.
  45. Michael K. Reiter. The rampart toolkit for building high-integrity services. In Theory and Practice in Distributed Systems, International Workshop, Dagstuhl Castle, Germany, September 5-9, 1994, Selected Papers, pages 99–110, 1994.
  46. Phillip Rogaway and Thomas Shrimpton. Cryptographic hash-function basics: Definitions, implications, and separations for preimage resistance, second-preimage resistance, and collision resistance. In Bimal K. Roy and Willi Meier, editors, Fast Software Encryption, 11th International Workshop, FSE 2004, Delhi, India, February 5-7, 2004, Revised Papers, volume 3017 of Lecture Notes in Computer Science, pages 371–388. Springer, 2004.
  47. Fred B. Schneider. Implementing fault-tolerant services using the state machine approach: A tutorial. ACM Comput. Surv., 22(4):299–319, 1990.
  48. Victor Shoup. Practical threshold signatures. In Advances in Cryptology - EUROCRYPT 2000, International Conference on the Theory and Application of Cryptographic Techniques, Bruges, Belgium, May 14-18, 2000, Proceeding, pages 207–220, 2000.
  49. Yee Jiun Song and Robbert van Renesse. Bosco: One-step byzantine asynchronous consensus. In Distributed Computing, 22nd International Symposium, DISC 2008, Arcachon, France, September 22-24, 2008. Proceedings, pages 438–450, 2008.
  50. Maofan Yin, Dahlia Malkhi, Michael K. Reiter, Guy Golan Gueta, and Ittai Abraham. Hotstuff: Bft consensus in the lens of blockchain. CoRR, abs/1803.05069, 2018.

A - Proof of Safety for Chained HotStuff

定理5. \(b\) と \(w\) を 2 つの競合したノードとする。この場合、それらは両方とも正直なレプリカにコミットされることはない。

Proof. 我々はこの定理を矛盾によって証明する。補題 1 と同類の論議により \(b\) と \(w\) は異なるビューでなければならない。実行中に \(b\) が QC Three-Chain \(b\), \(b'\), \(b''\) , \(b^*\) を介してある正しいレプリカでコミットされ、同様に、\(w\) が QC Three-Chain \(w\), \(w'\), \(w''\), \(w^*\) を介してある正しいレプリカでコミットされると仮定する。\(b\), \(b'\), \(b''\), \(w\), \(w'\), \(w''\) それぞれが QC を取得するため、一般性を失わず Figure 11 に示すように \(b\) が \(w''\) より高いビュー、つまり \(b'.{\it justify}.{\it viewNumber} \gt w^*.{\it justify}.{\it viewNumber}\) で作成されると仮定する。

Figure 11: \(w\) and \(b\) both getting committed (impossible). Nodes horizontally arranged by view numbers.

ここで \({\it qc}_s.{\it node}\) が \(w\) と競合するような \({\it qc}_s\) が存在する \(v_{w''} = w^*.{\it justify}.{\it viewNumber}\) よりも高いなかで最も小さいビューを \(v_s\) で示す。\(v_b = b'.{\it justify}.{\it viewNumber}\) とする。正式には任意の \({\it qc}\) に対して次の判定を定義する: \[ E({\it qc}) := (v_{w''} \lt {\it qc}.{\it viewNumber} \le v_b) \land ({\it qc}.{\it node} \ \mbox{conflicts with} \ w) \] ここで最初のスイッチングポイント \({\it qc}_s\) を設定することができる: \[ {\it qc}_s := \argmin_{\it qc} \left\{ {\it qc}.{\it viewNumber} \ | \ {\it qc} \ \mbox{is valid} \ \land E({\it qc}) \right\} \]

仮定によりそのような \({\it qc}_s\) が存在する。例えば \({\it qc}_s\) は \(b'.{\it justify}\) となる。\(r\) が \(w^*.{\it justify}\) と \({\it qc}_s\) の交点にある正しいレプリカを表すとする。\({\it qc}_s\) の最小性に関する仮定より、\(r\) が \(w\) 上に持つロックは \({\it qc}_s\) が形成される前に変更されることはない。ここで、競合しているノード \(m.{\it node} = {\it qc}_s.{\it node}\) を伝搬するメッセージ \(m\) を使用した、\(r\) によるビュー \(v_s\) での \({\rm safeNode}\) 呼び出しを考慮する。仮定より、ロック条件 (Algorithm 1 の 26 行目) は false である。一方でプロトコルでは \(t=m.{\it node}.{\it justify}.{\it node}\) が \({\lt qc}_s.{\it node}\) の先祖である必要がある。\({\it qc}.{\it node}\) が \(w\) と競合するため \(t\) は \(w\), \(w'\) または \(w''\) となることはできない。そして \(m.{\it node}.{\it justify}.{\it viewNumber} \lt w'.{\it justify}.{\it viewNumber}\) より孤立 (disjunct) の残り半分も false である。従って \(r\) は \({\it qc}_s.{\it node}\) に投票せず、\(r\) の仮定と矛盾する。

liveness 議論は Basic HotStuff とほぼ同じだが、決定を保証するため GST 後に 2 連続でリーダーが正しいことを仮定しなければならない点が異なっている。簡潔のため省略する。

B - Proof of Safety for Implementation Pseudocode

補題6. \(b\) と \(w\) を \(b.{\it height} = w.{\it height}\) となるような 2 つの競合したノードとしたとき、双方は有効な定足数証明書を持つことができない。

Proof. \(b\) と \(w\) の両方が \(2f+1\) 票を受け取り、少なくとも \(f+1\) の正しいレプリカがそれぞれのノードに投票することができたとした場合、両方に投票した正しいレプリカが存在しなければならず、\(b\) と \(w\) は同じ高さであることから不可能である。

Notation 1. 任意のノード \(b\) に対して、"\(\leftarrow\)" を親への関係、つまり \(b.{\it parent} \leftarrow b\) とする。"\(\xleftarrow{*}\)" は祖先、つまり親への関係の再帰的推移的閉包を示すものとする。ここで 2 つノード \(b\), \(w\) は \(b \ \mbox{not} \ \xleftarrow{*} w \land w \ \mbox{not} \ \xleftarrow{*} b\) の場合にのみ競合する。QC が参照するノードを "\(\Leftarrow\)"、つまり \(b.{\it justify}.{\it node} \Leftarrow b\) で表す。

補題7. \(b\) と \(w\) を 2 つの競合したノードとしたとき、正しいレプリカによってそれぞれ両方ともコミット状態になることはできない。

Proof. この重要な補題を矛盾によって証明する。\(b\) と \(w\) を異なる高さで競合するノードとする。実行中に \(b\) が QC Three-Chain \(b(\Leftarrow \land \leftarrow)b'(\Leftarrow \land \leftarrow)b'' \Leftarrow b^*\) を介して正しいレプリカでコミットさると仮定する; 同様に \(w\) が QC Three-Chain \(w(\Leftarrow \land \leftarrow)w'(\Leftarrow \land \leftarrow)w''\) を介して正しいレプリカでコミットされる。補題1より、各ノード \(b\), \(b'\), \(b''\), \(w\), \(w'\), \(w''\) に QC があるため、一般性を失うことなく Figure 11 に示すように \(b.{\it height} \gt w''.{\it height}\) と仮定する。

ここで \(w''.{\it height}\) よりも大きい中で最小の高さを持ち、\(w\) と競合しているノードの QC を \({\it qc}_s\) で示す。正確には、任意の \({\it qc}\) に次の判定を定義する: \[ E(qc) := (w''.{\it height} \lt {\it qc}.{\it node}.{\it height} \le b.{\it height}) \land ({\it qc}.{\it node} \ \mbox{conflicts with} \ w) \]

仮定により、例えば \({\it qc}_s\) が \(b'.{\it justify}\) となる事ができるような \({\it qc}_s\) が存在する。\(r\) を \(w^*.{\it justify}\) と \({\it qc}_s\) の交点に存在する正しいレプリカを示すものとする。\({\it qc}_s\) の最小性の仮定により、\(r\) が \(w\) 上に持つロックは \(qc_s\) が形成される前に変更されることはない。ここで \(b_{new} = qc_s.node\) のように競合したノード \(b_{new}\) を伝搬するメッセージを使った \({\rm onReceiveProposal}\) の呼び出しについて考える。仮定により、ロックの条件 (Algorithm 4 の 17 行目) は false である。一方、プロトコルは \(t=b_{new}.justify.node\) が \(b_{new}\) の祖先である必要がある。\(qc_s\) の最小性により、\(t.height \le w''.height\) である。\(qc_s.node\) が \(w\) と競合しているため、\(t\) は \(w\), \(w'\), \(w''\) とはならない。そして \(t.height \lt w.height\) であるため、孤立の残り半分も false である。従って \(r\) は \(b_{new}\) には投票せず \(r\) の仮定と矛盾する。

定理 8. \(cmd_1\) と \(cmd_2\) を任意の 2 つのコマンドとし、\(cmd_1\) が \(cmd_2\) より前にある正しいレプリカによって実行される場合、\(cmd_2\) を実行する正しいレプリカは \(cmd_2\) の前に \(cmd_1\) を実行しなければならない。

Proof. \(cmd_1\) を伝播するノードを \(w\)、\(cmd_2\) を伝播するノードを \(b\) と表す。補題 6 からコミットされたノードが個別の高さであることは明かである。一般性を失うことなく \(w.height \lt b.height\) と仮定する。\(w\) のコミットは、UPDATE で \(b\) がある \({\rm onCommit}(w')\) と \({\rm onCimmit}(b')\) によってトリガーされるものである。ここで \(w \xleftarrow{*} w'\), \(b \xleftarrow{*} b'\) である。補題 7 によると \(w'\) は \(b'\) と競合してはならず、そのため \(w\) は \(b\) と競合していない。そして \(w \xleftarrow{*} b\) で任意の正しいノードが \(b\) を実行するとき、\({\rm onCommit}\) の再帰ロジックにより先に \(w\) ｗ実行しなければならない。

B.1 Remarks

HotStuff 設計で得られるトレードオフについての洞察を得るために我々は safety に対して特定の制約が必要な理由を説明する。

Why monotonic vheight? (なぜ単調な高さなのか?) 各高さに対して複数回投票しない限り、レプリカが単調に投票する必要がないように投票ルールを変更すると、この弱められた制約は safety を破壊するだろう。例えばレプリカは最初に \(b\) に投票し次に \(w\) に投票できる。\(b'\), \(b''\) について認識する前に、\(w\) 上にロックがあると仮定してまず \(w'\), \(w''\) に配信し \(w''\) に投票する。最終的に \(b''\) を配信すると、ロックに的確でアリ \(b\) が \(w\) より高いことから \(b\) を先頭に持つ枝にフリップする。最後にレプリカも \(b''\) に投票するため \(w\) と \(b\) の両方がコミットされる。

Why direct parent? (なぜ直接の親か?) 直接の親を持つ制約は、補題 6 に補強されるように、証明で使用される関係式 \(b.height \gt w''.height\) を満たすために使用される。我々はコミットのルールを強制しないため、コミット制約は \(w \leftarrow w' \leftarrow w''\) の代わりに \(w \xleftarrow{*} w' \xleftarrow{*} w''\) に弱められる (\(b\) も同様)。\(w'.height \lt b.height \lt b'.height \lt w''.height \lt b''.height\) のケースについて考慮する。レプリカは最初に \(w''\) に投票することができ、次に \(b''\) を発見して \(b\) によって枝をスイッチすることができるが、\(w\) がコミットされている可能性があるため遅すぎる。

翻訳抄

State Machine Replication を行うための BFT 合意アルゴリズム HotStuff に関する 2019 年の論文。ブロックチェーンのような頻繁なリーダー変更を行う環境向けに、通信コストが \(O(n^2)\) から \(O(n)\) となっている。

  1. Maofan Yin, Dahlia Malkhi, Michael K. Reiter, Guy Golan Gueta, Ittai Abraham (2019) HotStuff: BFT Consensus in the Lens of Blockchain
  2. BFT in Lens of Blockchain