論文翻訳: The Part-Time Parliament
Digital Equipment Corporation
 序文
序文
近年の Paxos 島での考古学的発見により、兼業の議員 (part-time legislators) が放浪していたにもかかわらず議会 (parliament) が機能していたことが明らかとなっている。議員たちが頻繁に議会を離れたり、また伝令者 (messengers) が伝令を忘れていたとしても、彼らは議会記録の一貫したコピーを維持していた。Paxos 議会のプロトコルは分散システムの設計においてステートマシンのアプローチを実装する新しい方法を提供している。
カテゴリと主題記述: C.2.4 [Computer-Communication Networks]: Distributed Systems - network operating systems; D.4.5 [Operating System]: Reliability - fault-tolerance; J.1 [Computer Applications]: Administrative Data Processing - government
一般用語: Design, Reliability
その他のキーワードとフレーズ: State machines, three-phase commit, voting
Table of Contents
- 序文
- 1. 問題
- 2. 単一法令の教会会議
- 3. 複数法令の議会
- 4. コンピュータ科学との関連性
- APPENDIX - 教会会議プロトコルの一貫性の証明
- ACKNOWLEDGEMENTS
- REFERENCES
- 翻訳抄
この論文で言及している Paxos 島やその議会はすべて Paxos のアルゴリズムを説明するための Lamport によるフィクションです。
 1. 問題
1. 問題
 1.1 Paxos 島
1.1 Paxos 島
この千年紀の初頭、エーゲ海に浮かぶ Paxos 島は商取引の中心地として繁栄していた1。豊かさは政治的な洗練をもたらし、Paxon 人は古代の神権政治から議会政治へと移行していった。しかし市民の義務よりも貿易が優先され Paxos では議会に人生を捧げるような人はいなかった。Paxon 議会は議員が絶えず出入りしても機能する必要があった。
この問題は今日のフォールトトレラント (障害耐性) 分散システムが直面している問題と見事に一致している。つまり、議員はプロセスに相当し、議会を去ることは故障に相当する。したがって Paxon 人の解決策はコンピュータ科学者にとっても興味深いものであろう。ここでは Paxos 議会のプロトコルの歴史を簡単に紹介し、続いてその分散システムとの関連性についてさらに簡単に説明する。

この投稿は、最近 TOCS 編集部のファイルキャビネットから発見された。古いものだが編集長は掲載する価値があると考えた。著者は現在、ギリシャの島々でフィールドワークをしていて連絡が取れないため、私に掲載の準備を依頼してきた。
著者は考古学者でコンピュータ科学にはほとんど興味がないようだ。彼が記述している名もなき古代 Paxon 文明は、残念なことにほとんどのコンピュータ科学者にとっては興味のないものだが、その立法システムは非同期環境における分散型コンピュータシステムの実装方法の優れたモデルとなっている。実際、Paxon 人がプロトコルに加えた改良点のいくつかはシステム文献では知られていないものもあった。
著者はセクション 4 で Paxon 議会と分散コンピューティングとの関連性を簡単に述べている。コンピュータ科学者はまずこのセクションを読むと良いだろう。その前に Lampson [1996] によるコンピュータ科学者向けのアルゴリズムの説明を読みたいと思うかも知れない。このアルゴリズムは De Prisco ら [1997] によって公式に記述されている。セクション 4 の最後に、古代のプロトコルと最近の研究との関連性についてより詳細なコメントを加えた。
Keith Marzullo
カリフォルニア大学サンディエゴ校
Paxon 文明が外敵の侵入により滅亡し、考古学者がその歴史を発掘し始めたのはごく最近のことである。そのため Paxon 議会に関する我々の知識は断片的なものである。基本的なプロトコルについては知られているが多くの詳細については知られていない。そこで興味のある部分については勝手に Paxon 人の行動を推測してみたいと考えている。
 1.2 要件
1.2 要件
議会の主な仕事は国の法律を決めることであり、それは議会が通過させる一連の法令によって定義される。現在の議会ではその行動を記録するために秘書を雇うが、Paxos では会期中ずっと議場に残って秘書の役割を果たすものはいなかった。その代わりに Paxon の各議員は、可決された法令の順番を番号で記録する台帳 (ledger) を管理していた。例えば \(\Lynch\) 議員の台帳は、議会で可決された 155 番目の法令がオリーブ税を 1 トンあたり 3 ドラクマに設定したと確信した場合、
155: オリーブ税は 1 トンあたり 3 ドラクマ
という項目を持っていた。台帳は消えることのないインクで書かれており、その記入内容を変更することはできなかった。
議会規約の第一の要件は台帳の整合性 (consistency of ledgers) で、2 つの台帳に矛盾した情報があってはならないというものである。\(\Fischer\) 議員が彼の台帳に
132: ランプにはオリーブオイルのみを使用すること
と記載されているなら、他の議員の台帳での法令 132 号が異なることはない。しかし、他の議員がこの法令が可決されたことをまだ知らなかった場合、自分の台帳に法令 132 号の記載がないかもしれない。
すべての台帳を空白にしておけば自明のこととして満たされるため、これだけでは台帳の一貫性は十分ではない。法令が最終的に可決され、台帳に記録されることを保証するためには何らかの要件が必要であった。現代の議会では議員の間で意見の相違があると法令の通過が妨げられる。しかし Paxos ではそのようなことはなく相互に信頼し合う雰囲気があった。Paxon の議員たちは提案された法令を喜んで可決した。しかし彼らの放浪癖が問題となった。一つの議員グループが法令
37: 寺院の壁に絵を書くことを禁止する
を通過させ、その後に別の議員グループが議場に入り、何も知らずに矛盾する法令
37: 芸術表現の自由を保証する
を可決してしまった場合、整合性が失われてしまう。
十分な数の議員が十分に長い時間議場にいなければ進行を保証することはできない。Paxon の議員は外での活動を抑えようとしないため、どんな法令も確実に通過させることはできなかった。しかし、Paxon の議員たちが議場にいる間は、議員とその側近が議会に関する全ての事項を迅速に処理することを保証していた。このような保証があったからこそ Paxon 人は次のような進行条件 (progress condition) を満たす議会プロトコルを考案することができたのである。
議員の過半数2が会議場におり、十分に長い期間、誰も会議場に出入りしなければ、会議場にいる議員が提案した法令はすべて可決され、可決されたすべての法令は会議場にいるすべての議員の台帳に記載されることになる。
 1.3 前提
1.3 前提
議会規則の要件は議員に必要なリソースを提供することによってのみ達成することができた。各議員には法令を記録するための頑丈な台帳、ペン、消せないインクが与えられた。議員は議場を離れると何をしていたか忘れてしまうため3、台帳の裏にメモを書いて議会の重要な仕事を思い出せるようにしていた。法令の一覧の記入内容は変更できないが、メモは消すことができる。進行条件を達成するためは議員が時間の経過を測定できる必要があり、そのために彼らには簡単な砂時計が与えられた。
議員たちは常に台帳を持ち歩き、常に法令の一覧や消していないメモを読むことができた。台帳は最高級の羊皮紙で作られており、最も重要な記録帳としてのみ使われた。議員は他のメモを紙片に書いておき、議場を出たときにそれをなくす (なくさない) かもしれない。
議場の音響は悪く演説は不可能であった。議員たちは伝令者を使ってしかコミュニケーションを取ることができず、必要なだけの伝令者を雇うための資金が与えられていた。伝令者は言葉を濁さないことを期待されていたが、すでに伝えたことを忘れて再度伝えてしまうこともあった。伝令者は自分が仕える議員と同じように、時間の一部だけを議会の仕事にあてていた。伝令者はメッセージを伝える前に議場を離れ用事を済ませることもあり、半年間の航海に出ることもあった。その場合、メッセージは決して届けられることはない。
議員や伝令者は議場にいつでも出入りできるが、議場にいる間は議会の仕事に専念していた。議場にいる間、伝令者は適時メッセージを届け、議員は受け取ったメッセージに迅速に対応した。
Paxos の公式記録では、議員や伝令者は正直者で議会の手順を厳守していたとされている。しかし、これは Paxos が東欧諸国に比べて道徳的に優れていたというプロパガンダであると多くの学者は考えている。まれにではあるが、不誠実な行為があったことは確かである。しかしそれは公文書に記載されることがなかったため、議会が不誠実な議員や伝令者にどのように対処したかについてはほとんど知られていない。これまでに明らかになっている証拠についてはセクション 3.3.5 で説明する。
- 1Ionian 諸島の Paxoi 島と混同しないように。Paxoi 島の名前は Paxos と誤表示されることがある。
- 2進行条件を訳すにあたり Paxon 語の \(\majority\) を議員の過半数 (majority of the legislators) とした。この単語の別の翻訳が提案されており、セクション 2.2 で述べている。
- 3議員の \(\Toyer\) は議場のすぐ外で落ちてきた彫像に頭を打ち不可逆的な記憶喪失となるという悲劇的な事件もあった。
 2. 単一法令の教会会議
2. 単一法令の教会会議
Paxon 議会はただ一つの象徴的な法令を選ぶために 19 年ごとに開催されていた司祭たちの初期の教会会議 (Synod) 儀式から発展したものである。何世紀にも渡ってこの教会会議はすべての司祭が出席しなければならない慣例的な手順で法令を決定していた。しかし商業が盛んになるにつれ、教会会議開催中に司祭が議場を出入りするようになった。ついには従来の手順が破綻し、法令が決まらないまま教会会議が終了してしまっていた。このような神学上の惨事を繰り返さないために、Paxon の宗教家たちは数学者に教会会議の法令を選ぶためのプロトコルの策定を依頼した。このプロトコルの要件と前提条件は、のちの議会のものと基本的には同じであったが、台帳には一連の法令の代わりに多くても 1 つの法令が記載されることになっていた。結果として得られた教会会議のプロトコルをここで説明し、議会のプロトコルはセクション 3 で説明する。
数学者たちは教会会議のプロトコルを一連のステップで導き出した。まず、ある制約を満たすプロトコルであれば一貫性を保証し進行が可能であるという結果が証明された。次に、これらの制約から直接予備プロトコル (preliminary protocol) を導き出した。この予備プロトコルを制限して、一貫性を保証するが進行はできない基本プロトコル (basic protocol) を提供した。一貫性と進行を満たす完全な教会会議プロトコルは基本プロトコルを宣言することで得られた4。
数学的な結果はセクション 2.1 で、プロトコルはセクション 2.2-2.4 で非公式に説明されている。基本プロトコルのより正式な説明と正しさの証明は付録に記載されている。
 2.1 数学的結果
2.1 数学的結果
教会会議の法令は、一連の番号付き票決 (ballots) を通して選ばれた。票決は単一の法令に対する一般投票 (referendum) だった。各票決では、司祭は法令に賛成するか投票しないかの選択肢しかなかった5。票決に関連付けられていたのはクォーラム (quorum) と呼ばれる司祭の集合だった。投票が成功するのはクォーラムのすべての司祭が法令に投票した場合に限られる。形式的には、票決 \(B\) は以下の 4 つの要素で構成されている (特に断りのない限り、集合とは有限集合を意味するものとする6)。
- \(B_{dec}\): 法令 (投票される対象)
- \(B_{qrm}\): 空ではない司祭の集合 (投票のクォーラム)
- \(B_{vot}\): 司祭の集合 (法令に票を投じた人)7
- \(B_{bal}\): 票決番号
票決 \(B\) は \(B_{qrm} \subseteq B_{vot}\) の場合にのみ成功した (successful) と呼ばれ、つまり成功した票決はクォーラムのメンバー全員が投票した (投票者である) ことを指している。
票決番号は無制限に並べられた番号の集合から選ばれた。\(B_{bal}' \gt B_{bal}\) であれば票決 \(B'\) は票決 \(B\) よりあと (later) と言われていた。ただしこれは票決が行われた順序を示すものではなく、あとの票決が実際には前の票決より先に行われることもある。
Paxon の数学者は票決の集合 \(\mathfrak{B}\) に 3 つの条件を定義し、その条件を満たす票決の集合があれば、一貫性が保証され、進行が可能であることを示した。最初の 2 つの条件は簡単で、非形式的に次のように述べることができる。
- \(B1(\mathfrak{B})\): \(\mathfrak{B}\) の各票決には一意な票決番号が付けられている。
- \(B2(\mathfrak{B})\): \(\mathfrak{B}\) の任意の 2 つの票決のクォーラムは、少なくとも 1 人の司祭が共通している。
3 つめの条件はより複雑である。Paxon の記録には、それについて次のようなかなり混乱した記述があった。
- \(B3(\mathfrak{B})\): \(\mathfrak{B}\) のすべての票決 \(B\) に対して、\(B\) のクォーラムに含まれる司祭が \(\mathfrak{B}\) の以前の票決で投票している場合、\(B\) の法令はそのような以前の票決のうち最も新しい法令と等しい。
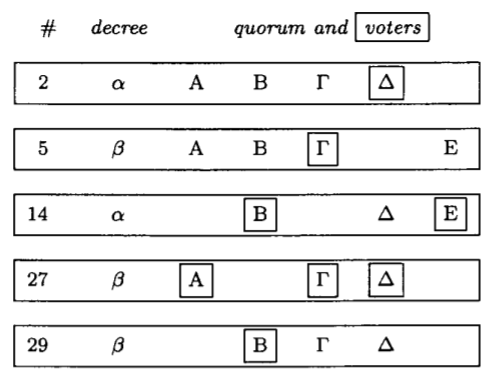
この暗号文の解読には Fig 1 の記録が役に立った。この記録は 5 人の司祭 \(A\), \(B\), \(\Gamma\), \(\Delta\), \(E\) で構成される教会会議の 5 つの票決の集合 \(\mathfrak{B}\) を使用して条件 \(B3(\mathfrak{B})\) を示している。この集合 \(\mathfrak{B}\) には 5 つの票決が含まれており、各票決の投票者の集合は四角形で囲まれた名前を持つクォーラムの司祭の部分集合である。例えば、票決番号 14 は法令 \(\alpha\)、3 人の司祭を持つクォーラム、2 人の投票者集合を持っている。条件 \(B3(\mathfrak{B})\) は "\(\mathfrak{B}\) 内のすべての \(B\) に対して: ..." の形式であり、ここで "..." は票決 \(B\) の条件である。Fig 1 の 5 つの票決 \(B\) の条件は次の通り:
- 2: 票決番号 2 は一番最初の票決なので、その票決の条件は明らかに成り立つ (trivially true)。
- 5: 票決 5 の 4 人のクォーラムメンバーのうち、以前の票決で投票した人はいないので、票決 5 の条件も明らかに成り立つ。
- 14: 票決 14 のクォーラムの中で、先の票決で投票しているメンバーは、投票番号 2 で投票した \(\Delta\) だけであるため、条件として、票決 14 の法令が票決 2 の法令と等しくなければならない。
- 27: (これは成功した票決である) 票決 27 のクォーラムのメンバーは \(A\), \(\Gamma\), \(\Delta\) である。司祭 \(A\) は以前の票決で投票しておらず、\(\Gamma\) が以前に投票したのは票決 5、\(\Delta\) が以前に投票したのは票決 2 だけである。この、以前に投票されている 2 つのうち最も遅い票決は 5 であるから、条件として、票決 27 の法令は票決 5 の法令と等しくなければならない。
- 29: 投票番号 29 のクォーラムのメンバーは \(B\), \(\Gamma\), \(\Delta\) である。\(B\) が以前に投票したのは票決 14、司祭 \(\Gamma\) は票決 5 と 27 で投票し、\(\Delta\) は票決 2 と 27 で投票した。これら、以前に投票されている 4 つのうち最も遅い票決は 27 であるため、条件として、票決 29 の法令は票決 27 の法令と等しくなければならない。
\(B1(\mathfrak{B})\)〜\(B3(\mathfrak{B})\) を形式的に述べるにはもう少し記述が必要である。票 (votes) \(v\) は、司祭 \(v_{pst}\)、票決番号 \(v_{bal}\)、法令 \(v_{dec}\) の 3 つの要素からなる量と定義された。これは司祭 \(v_{pst}\) が票決番号 \(v_{bal}\) で法令 \(v_{dec}\) に投じた票を表している。Paxon 人は無効票 (null votes) を \(v_{bal} = - \infty\) かつ \(v_{dec} = {\rm BLANK}\) として定義していた。ここで任意の票決番号 \(b\) に対して \(-\infty \lt b \lt \infty\) であり、\({\rm BLANK}\) は有効な法令ではない。また彼らは任意の司祭 \(p\) に対して \(v_{pst}=p\) を持つ唯一の無効票 \(v\) を \({\it null}_p\) と定義した。
Paxon の数学者はすべての票の集合に全順序を定義したが、その定義を記した記録の一部は失われてしまった。残された断片は、任意の票 \(v\) と \(v'\) について、\(v_{bal} \lt v'_{bal}\) であれば \(v \lt v'\) であることを示している。
票決の任意の集合 \(\mathfrak{B}\) に対して、\(\mathfrak{B}\) 内の票の集合 \({\it Votes}(\mathfrak{B})\) は、ある \(B \in \mathfrak{B}\) に対して \(v_{pst} \in B_{vot}\), \(v_{bal} = B_{bal}\), \(v_{dec} = B_{dec}\) となるすべての票 \(v\) で構成されると定義されていた。\(p\) を司祭とし、\(b\) を票決番号または \(\pm \infty\) とすると、\({\it MaxVote}(b,p,\mathfrak{B})\) は集合 \[ \{v \in {\it Votes}(\mathfrak{B}) : (v_{pst} = p) \land (v_{bal} \lt b) \} \cup \{{\it null}_p\} \] である。任意の殻でない司祭の集合 \(Q\) に対して、\({\it MaxVote}(b,Q,\mathfrak{B})\) は、\(Q\) の中に \(p\) を持つすべての票の最大値 \({\it MaxVote}(b, p, \mathfrak{B})\) に等しいと定義されている。
条件 \(B1(\mathfrak{B})\)〜\(B3(\mathfrak{B})\) は形式的に次のように記述される8: \[ \begin{eqnarray*} B1(\mathfrak{B}) & \triangleq & \forall B,B' \in \mathfrak{B}\,:\, (b \ne B') \Rightarrow (b_{bal} \ne B'_{bal}) \\ B2(\mathfrak{B}) & \triangleq & \forall B,B' \in \mathfrak{B}\,:\, B_{qrm} \cap B'_{qrm} \ne \emptyset \\ B3(\mathfrak{B}) & \triangleq & \forall B \in \mathfrak{B} \, : \, ({\it MaxVote}(B_{bal}, B_{qrm}, \mathfrak{B})_{bal} \ne - \infty) \\ & & \Rightarrow (B_{dec} = {\it MaxVote}(B_{bal}, B_{qrm}, \mathfrak{B})_{dec} ) \end{eqnarray*} \] \({\it MaxVote}\) の定義は票の順序に依存するが、\(B1(\mathfrak{B})\) は \({\it MaxVote}(b,Q,\mathfrak{B})_{dec}\) が票決番号の等しい票の順序に依存しないことを意味する。
これらの条件が一貫性を意味することを示すために、Paxon 人はまず \(B1(\mathfrak{B})\)〜\(B3(\mathfrak{B})\) が、\(\mathfrak{B}\) での票決 \(B\) が成功した場合、\(\mathfrak{B}\) 内でそれより後の票決は \(B\) と同じ法令に対するものであることを意味することを示した。
補題. \(B1(\mathfrak{B})\)、\(B2(\mathfrak{B})\) および \(B3(\mathfrak{B})\) が成り立つならば、\(\mathfrak{B}\) の任意の \(B\), \(B'\) に対して \[ \left( (B_{qrm} \subseteq B_{vot}) \land (B'_{bal} \gt B_{bal}) \right) \Rightarrow (B'_{dec} = B_{dec}) \]
補題の証明. \(\mathfrak{B}\) の任意の票決 \(B\) に対して、\(\Psi(B,\mathfrak{B})\) を \(B\) よりも後で \(B\) とは異なる法令を出した \(\mathfrak{B}\) 内の票決の集合とする: \[ \Psi(B, \mathfrak{B}) \triangleq \{ B' \in \mathfrak{B} : (B'_{bal} \gt B_{bal}) \land (B'_{dec} \ne B_{dec}) \} \] 補題を証明するには \(B_{qrm} \subseteq B_{vot}\) ならば \(\Psi(B,\mathfrak{B})\) が空であることを示せば良い。Paxon 人は矛盾による証明を行った。彼らは \(B_{qrm} \subseteq B_{vot}\) となる \(B\) と、\(\Psi(B, \mathfrak{B}) \ne \emptyset\) が存在すると仮定し、以下のように矛盾を得た9。
- \(C_{bal} = \min\{B'_{bal} : B' \in \Psi(B,\mathfrak{B})\}\) となるような \(C \in \Psi(B,\mathfrak{B})\) を選ぶ。
証明: \(\Psi(B, \mathfrak{B})\) は空でなく有限であるため \(C\) は存在する。 - \(C_{bal} \gt B_{bal}\)
証明: 1. と \(\Psi(B,\mathfrak{B})\) の定義により。 - \(B_{vot} \cap C_{qrm} \ne \emptyset\)
証明: \(B2(\mathfrak{B})\) と、仮説 \(B_{qrm} \subseteq B_{vot}\) により。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})_{bal} \ge B_{bal}\)
証明: 2., 3. と \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})\) の定義により。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B}) \in {\it Votes}(\mathfrak{B})\)
証明: 4. (\({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})\) が無効票でないことを意味している) と \({\it MaxVote}(C_{bal},C_{qrm},\mathfrak{B})\) の定義により。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})_{dec} = C_{dec}\)
証明: 5. と \(B3(\mathfrak{B})\) により。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})_{dec} \ne B_{dec}\)
証明: 6.、1. と \(\Psi(B,\mathfrak{B})\) の定義により。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})_{bal} \gt B_{bal}\)
証明: 4. により、7. と \(B1(\mathfrak{B})\) が \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})_{bal} \ne B_{bal}\) を意味するため。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B}) \in {\it Votes}(\Psi(B,\mathfrak{B}))\)
証明: 7.、8. と \(\Psi(B,\mathfrak{B})\) の定義により。 - \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B}) \lt C_{bal}\)
証明: \({\it MaxVote}(C_{bal}, C_{qrm}, \mathfrak{B})\) の定義により。 - 矛盾
証明: 9.、10.、および 1. により。∎
この補題により、\(B1\)〜\(B3\) が成り立つなら、成功した 2 つの票決は同じ法令に対するものであることを容易に示すことができる。
定理 1. \(B1(\mathfrak{B})\)、\(B2(\mathfrak{B})\) および \(B3(\mathfrak{B})\) が成り立つならば、\(\mathfrak{B}\) の任意の \(B\), \(B'\) に対して \[ \left( (B_{qrm} \subseteq B_{vot}) \land (B'_{qrm} \subseteq B'_{vot}) \right) \Rightarrow (B'_{dec} = B_{dec}) \]
定理の証明. \(B'_{bal} = B_{bal}\) ならば \(B1(\mathfrak{B})\) は \(B' = B\) を意味している。\(B'_{bal} \ne B_{bal}\) ならば定理は補題から直ちに導かれる。∎
そして Paxon 人は、議場に十分な数の司祭がいれば \(B1\)〜\(B3\) を維持したまま票決を成功させることが可能であると主張する定理を証明した。これは進行を保証するものではないが、少なくとも \(B1\)〜\(B3\) に基づいた票決プロトコルがデットロックしないことを示している。
定理 2. \(b\) を票決番号、\(Q\) を各 \(B \in \mathfrak{B}\) に対して \(b \gt B_{bal}\) かつ \(Q \cap B_{qrm} \ne \emptyset\) となるような司祭の集合とする。\(B1(\mathfrak{B})\)、\(B2(\mathfrak{B})\) および \(B3(\mathfrak{B})\) が成り立つならば、\(B1(\mathfrak{B} \cup \{B'\})\), \(B2(\mathfrak{B} \cup \{B'\})\), \(B3(\mathfrak{B} \cup \{B'\})\) が成り立つような \(B'_{bal} = b\) かつ \(B'_{qrm} = B'_{vot} = Q\) の票決 \(B'\) が存在する。
定理の証明. 条件 \(B1(\mathfrak{B} \cup \{B'\})\) は、\(B1(\mathfrak{B})\)、\(B'_{bal}\) の選択、および \(b\) に関する仮定から従う。条件 \(B2(\mathfrak{B} \cup \{B'\})\) は \(B2(\mathfrak{B})\)、\(B'_{qrm}\) の選択、および \(Q\) に関する仮定から従う。もし \({\it MaxVote}(b,Q,B)_{bal} = - \infty\) であれば、\(B'_{dec}\) を任意の法令とし、それ以外では \({\it MaxVote}(b,Q,B)_{dec}\) とすると、条件 \(B3(\mathfrak{B} \cup \{B'\})\) は \(B3(\mathfrak{B})\) から従う。∎
 2.2 予備プロトコル
2.2 予備プロトコル
Paxon 人は条件 \(B1(\mathfrak{B})\)〜\(B3(\mathfrak{B})\) が真であるという要件から予備プロトコルを導き出した。ここで \(\mathfrak{B}\) は、これまでに実施された、または実施中のすべての票決の集合である。プロトコルの定義は集合 \(\mathfrak{B}\) がどのように変化するかが規定されていたが、その集合が明示的に算出されてはいなかった。Paxon では \(\mathfrak{B}\) は神々のみが観察する量であり、人間は決して知ることができないかもしれないと考えていた。
各票決は一人の司祭から開始し、司祭はその番号、法令、クォーラムを選択した。その後、クォーラムの各司祭はその票決に投票するかどうかを決定した。開始者が票決の番号、法令、クォーラムをどのように選ぶか、また司祭が投票するかどうかをどのように決めるかを決定する規則は、\(B1(\mathfrak{B})\) 〜\(B3(\mathfrak{B})\) を維持する必要性から直接導き出されたものである。
\(B1\) を維持するために、それぞれの票決には固有の番号を付ける必要があった。司祭は自分が以前にどのような投票を行ったかを台帳に書き留めておくことで、同じ番号の 2 つの異なる票決の開始を容易に回避することができた。別の司祭が同じ番号の票決を開始しないようにするために、可能な票決番号の集合を司祭の間で分割していた。これがどのように行われたかは不明だが、明らかな方法として、票決番号を整数と司祭からなるペアとし、辞書順を用いて \[ (13, \Gray) \lt (13, \Lindsay) \lt (15, \Gray) \] Paxon アルファベットでは \(\Gamma\) は \(\Lambda\) より前に来る。いずれにしても、すべての司祭は自分が使用するために確保された無制限の投票番号の集合を持っていたことが分かっている。
\(B2\) を維持するためには、票決のクォーラムは \(\majority\) の司祭を含むように選ばれていた。当初 \(\majority\) は単純に過半数を意味していたが、その後、太った司祭は痩せた司祭に比べて移動が少なく、議場での滞在時間が長いことが判明したため、\(\majority\) は司祭の単純な過半数ではなく、体重の合計が全司祭の体重の半分以上になる司祭の集合を意味するようになった。痩せた司祭のグループがこれでは不公平だと訴えたため、実際の重さではなく、司祭の出席記録に基づく抽象的な重さに変更された。\(\majority\) の主な条件は、司祭の \(\majority\) を含む任意の 2 つの集合が少なくとも 1 人の共通の司祭を持つことであった。\(B2\) を維持するために、票決 \(B\) を開始する司祭は \(B_{qrm}\) を過半数の集合になるように選択した。
条件 \(B3\) は、\({\it MaxVote}(b,Q,\mathfrak{B})_{dec}\) が \({\rm BLANK}\) と等しくなければ、票決番号 \(b\) とクォーラム \(Q\) は法令 \({\it MaxVote}(b,Q,\mathfrak{B})_{dec}\) を持たなければならない。もし \({\it MaxVote}(b,Q,\mathfrak{B})\) が \({\rm BLANK}\) に等しければ、その票決は任意の法令を持つことができる。\(B3(\mathfrak{B})\) を維持するために、票決番号 \(b\) とクォーラム \(Q\) の新しい票決を開始する前に、司祭 \(p\) は \({\it MaxVote}(b,Q,\mathfrak{B})_{dec}\) を見つけなければならない。これを行うため \(p\) は \(Q\) のそれぞれの司祭 \(q\) に対して \({\it MaxVote}(b,Q,\mathfrak{B})\) を見つける必要があった。
前述の通り、\({\it MaxVote}(b,Q,\mathfrak{B})_{dec}\) は、\(q\) が投票したすべての票のうち \(b\) より小さい最大の票決番号を持つ票であり、\(q\) が \(b\) より小さい票決番号のいずれでも投票しなかったのであれば \({\it null}_q\) となる。司祭 \(p\) はメッセージの交換によって \(q\) から \({\it MaxVote}(b,q,\mathfrak{B})\) を得る。したがって、\(p\) が開始した一つの票決を行うためのプロトコルの最初の 2 つのステップは次のようになる10:
- 司祭 \(p\) は新しい票決番号 \(b\) を選び、ある司祭集合に \({\it NextBallot}(b)\) メッセージを送る。
- 司祭 \(q\) は \({\it NextBallot}(B)\) メッセージの受け取りに対して、\(p\) に \({\it LastVote}(b,v)\) メッセージを送ることで応答する。ここで \(v\) は \(b\) より小さく \(q\) が投じたなかで最も大きい票決番号の票、または、\(q\) が \(b\) より小さい番号の票決に投票していなかった場合は彼の無効票 \({\it null}_q\) である。
司祭 \(q\) は過去にどのような票を投じたかを台帳の裏のメモで憶えておかなければならない。
\(q\) が \({\it LastVote}(b,v)\) メッセージを送ると、\(v\) は \({\it MaxVote}(b,q,\mathfrak{B})\) と等しくなる。しかし、新しい票決が始まり票が投じられると、票決の集合 \(\mathfrak{B}\) は変化する。司祭 \(p\) が法令を選択するときに \(v\) を \({\it MaxVote}(b,q,\mathfrak{B})\) の値として使うことになるので、\(B3(\mathfrak{B})\) を真に保つためには、\(q\) が \({\it LastVote}(b,v)\) メッセージを送ったあとで \({\it MaxVote}(b,q,\mathfrak{B})\) が変わらない必要がある。\({\it MaxVote}(b,q,\mathfrak{B})\) を変えないために、\(q\) は \(v_{bal}\) から \(b\) の間の票決番号に新しい票を投じてはならない。\({\it LastVote}(b,v)\) メッセージを送ることで \(q\) はそのような票を投じないことを約束している (この約束を守るために \(q\) は自分の台帳に必要な情報を記録しなければならない)。
票決プロトコルの次の 2 つのステップ (司祭 \(p\) がステップ 1 で始めたもの) は]
- ある多数派の集合 \(Q\) のすべての司祭から \({\it LastVote}(b,v)\) メッセージを受け取った後、司祭 \(p\) は番号 \(b\)、クォーラム \(Q\)、法令 \(d\) で新しい票決を開始する。ここで \(d\) は \(B3\) を満たすように選択される。そして、その票決を自分の台帳の裏に記録し、\(Q\) のすべての司祭に \({\it BeginBallot}(b,d)\) メッセージを送る。
- \({\it BeginBallot}(b,d)\) メッセージを受け取った司祭 \(q\) は票決番号 \(b\) に自分の票を投じるかどうかを決定する (投票することで、彼が別の票決に送った \({\it LastVote}(b',v')\) メッセージの意味する約束に反する場合には、票を投じないこともある)。\(q\) が票決番号 \(b\) に投票すると決めた場合、\(q\) は \(p\) に \({\it Voted}(b,q)\) メッセージを送り、その票を自分の台帳の裏に記録する。
ステップ 3 の実行は、\(B_{bal}=b\), \(B_{qrm} = Q\), \(B_{vot} = \emptyset\) (まだ誰もこの票決に投票していない), そして \(B_{dec} = d\) となるような票決 \(B\) を \(\mathfrak{B}\) に追加することと考えられる。ステップ 4 では、司祭 \(q\) が票決に投票すると決めたのなら、そのステップを実行することは票決 \(B \in \mathfrak{B}\) で票を投じた人の集合 \(B_{vot}\) に \(q\) を加えることで、票決の集合 \(\mathfrak{B}\) を変更することと考えられる。
司祭は、投票が過去の約束に違反しない場合であっても、ステップ 4 で投票しないという選択肢がある。実際、このプロトコルのすべてのステップはオプションである。例えば、司祭 \(q\) はステップ 2 を実行する代わりに \({\it NextBallot}(b)\) メッセージを無視することができる。アクションを実行しないことで進行が妨げられる可能性があるが、\(B1(\mathfrak{B})\)~\(B3(\mathfrak{B})\) を偽とすることはできないため、不整合を引き起こすことはできない。メッセージを受け取らないことで得られる唯一の効果はアクションを起こせないことであるため、メッセージの損失も不整合の原因とはならない。したがって、このプロトコルは司祭が退室したりメッセージを紛失しても一貫性を保証する。
複数のコピーを受け取るとアクションが繰り返される。ステップ 3 を除いて、アクションを 2 回実行しても効果はない。例えば、ステップ 4 で複数の \({\it Voted}(b,q)\) メッセージを送っても、1 つだけ送るのと効果は同じである。ステップ 3 が実行されたときに、台帳の裏に記載された項目を使うことでステップ 3 の繰り返しを防ぐことができる。このように、伝令者が同じメッセージを何度届けても一貫性の条件は保たれる。
ステップ 1~4 は票決を開始してそこに投票するための完全なプロトコルである。あとは票決の結果を判断して、法令が選ばれたときに発表するだけである。前述の通りクォーラムのすべての司祭が投票した場合に限り票決は成功する。成功した票決の法令は教会会議で選ばれたものである。プロトコルの残りの部分は:
- \(p\) は \(Q\) のすべての司祭 \(q\) (票決番号 \(b\) のクォーラムとする) から \({\it Voted}(b,q)\) メッセージを受け取ったなら、自分の台帳に \(d\) (票決の法令) を書き込み、すべての司祭に \({\it Success}(d)\) を送る。
- \({\it Success}(d)\) メッセージを受け取ると、司祭は自分の台帳に法令 \(d\) を記入する。
ステップ 1~6 は個別の票決がどのように行われるかを説明している。予備プロトコルではどの司祭でもいつでも票決を開始することができる。各ステップは \(B1(\mathfrak{B})\)~\(B3(\mathfrak{B})\) を維持しているため、プロトコル全体もこれらの条件を維持している。司祭は票決が成功した場合にのみ自分の台帳に法令を記入するため、定理 1 はすべての司祭の台帳が一貫していることを意味している。このプロトコルでは進行の問題には触れない。
ステップ 3 において、条件 \(B3\) により法令 \(d\) が決定された場合、この法令がすでにどこかの司祭の台帳に書き込まれている可能性がある。その司祭はクォーラム \(Q\) に含まれている必要はなく、議場を離れてしまっていても構わない。したがって、ステップ 3 で \(d\) を選択する際の自由度を高くしてしまうと一貫性が保証されない。
 2.3 基本プロトコル
2.3 基本プロトコル
予備プロトコルでは、司祭は (1) 自分が開始した各票決の番号、(2) 自分が投じた各票、(3) 自分が送った \({\it LastVote}\) メッセージ、を記録しなければならない。このような情報をすべて記録することは、多忙な仔細にとっては難しいことだった。そこで Paxon 人は予備プロトコルを制限し、各司祭 \(p\) が台帳の裏に以下の情報だけを保持するという、より実用的な基本プロトコル (basic protocol) を得た:
- \({\it lastTied}[p]\): \(p\) が開始を試みた最後の票決の番号、またはそのようなことがなければ \(- \infty\)。
- \({\it prevVote}[p]\): \(p\) が投票した中で、最も高い番号の票決の票、または投票してなければ \(- \infty\)。
- \({\it nextBal}[p]\): \(p\) が \({\it LastVote}(b,v)\) を送ったことのある \(b\) の最大値、またはそのようなメッセージを送ったことがなければ \(- \infty\)。
予備プロトコルのステップ 1~6 では、開始者である司祭 \(p\) が 1 つの票決をどのように実施するかを説明している。予備プロトコルでは \(p\) は任意の番号の票決を同時に行うことができるが、基本プロトコルでは一度に一つの票決 - 票決番号 \({\it lastTried}[p]\) しか行うことができない。\(p\) がこの票決を開始したあと、過去に開始している他の票決に関連しているメッセージを無視する。司祭 \(p\) は票決番号 \({\it lastTried}[p]\) の進行状況に関する全ての情報を紙切れに書いて保存している。もしその紙切れを紛失した場合はその票決の実施を中止する。
予備プロトコルでは、司祭 \(q\) が送る各 \({\it lastVote}(b,v)\) メッセージは \(v_{bal}\) と \(b\) の間の番号に投票しないという約束を表していたが、基本プロトコルでは \(b\) 以下の票決番号には新しい票を投じないというより強い約束を表している。この強い約束により、\(q\) は基本プロトコルのステップ 4 で、予備プロトコルでは許されていた投票を行うことができなくなるかもしれない。しかし、予備プロトコルでは \(q\) は投票しないという選択肢が常に与えられているため、基本プロトコルは予備プロトコルで認められていないことを \(q\) に要求しているのではない。
予備プロトコルのステップ 1~6 は、基本プロトコルでは票決を行うための以下の 6 つのステップとなる (\(p\) が票決を行うために使用する、\({\it lastTried}[p]\), \({\it prevVote}[p]\), \({\it nextBal}[p]\) 以外の情報はすべて紙切れに記録しておく)。
- 司祭 \(p\) は \({\it lastTried}[p]\) より大きい新しい票決番号 \(b\) を選び \({\it lastTried}[p]\) を \(b\) に設定する。そして司祭のある集合に \({\it NextBallet}(b)\) メッセージを送る。
- \(b \gt {\it nextBal}[q]\) となるような \({\it NextBallet}(b)\) メッセージを \(p\) から受け取ると、司祭 \(q\) は \({\it nextBal}[q]\) を \(b\) に設定し \(p\) に \({\it LastVote}(b,v)\) メッセージを送る。ここで \(v\) は \({\it prevVote}[q]\) と等しい (\(b \le {\it nextBal}[q]\) であれば \({\it NextBallet}(b)\) メッセージは無視される)。
- ある多数の集合 \(Q\) のすべての司祭から、\(b = {\it lastTried}[p]\) となるような \({\it LastVote}(b,v)\) を受け取ったあと、司祭 \(p\) は番号 \(b\)、クォーラム \(Q\)、法令 \(d\) で票決を開始する。ここで \(d\) は \(B3\) を満たすように選択される。そして \(Q\) のすべての司祭に \({\it BeginBallot}(b,d)\) メッセージを送信する。
- \(b = {\it nextBal}[q]\) となるような \({\it BeginBallot}(b,d)\) メッセージを受け取ると、司祭 \(q\) は票決番号 \(b\) に自身の票を投じ、\({\it prevVote}[q]\) にこの票を設定し、\(p\) に \({\it Voted}(b,q)\) を送信する (\(b \ne {\it nextBal}[q]\) であれば \({\it BeginBallot}(b,d)\) メッセージは無視される)。
- \(p\) が \(Q\) (票決番号 \(b\) のクォーラム) のすべての司祭 \(q\) から \({\it Voted}(b,q)\) メッセージを受け取った場合、\(p\) は自身の台帳に \(d\) (この票決での法令) を書き込み、すべての司祭に \({\it Success}(d)\) メッセージを送る。
- \({\it Success}(d)\) メッセージを受け取った司祭は、自身の台帳に法令 \(d\) を記入する。
基本プロトコルは予備プロトコルの制約版で、基本プロトコルで許可される動作は予備プロトコルでも許可されていることを意味する。予備プロトコルは一貫性の条件を満たしているため基本プロトコルもその条件を満たしている。予備プロトコルと同様に、基本プロトコルもアクションを実行する必要がないため進行の問題には対応していない。
\(B1\)~\(B3\) から基本プロトコルを導き出すと、一貫性の条件が満たされることが明らかになった。しかし、同様に "明白な" (obvious) 古代の知恵の中には誤りがあることが判明したため、懐疑的な市民はより厳密な証拠を要求した。プロトコルが一貫性条件を満たすことを示す Paxon の数学者の証明は付録として再現している。
 2.4 完全教会会議プロトコル
2.4 完全教会会議プロトコル
基本プロトコルは一貫性を保っているが、司祭ができることを述べているだけで司祭に何かを要求しているわけではなく、進行を保証することはできない。完全プロトコルは基本プロトコルと同じ 6 つの票決実施手順で構成されている。進行を達成するために、司祭がプロトコルの 2~6 の手順をできるだけ早く実施するという明白な追加条件が含まれている。しかし、進行条件を満たすには票決を開始するステップ 1 を実行する司祭が必要である。このプロトコルを完成させる鍵は司祭がいつ票決を開始するかにあった。
投票を一度も開始しないことをは確かに進行を妨げるが、しかしあまりにも多くの票決を開始することも進行を妨げることになる。もし \(b\) が他のどの票決番号よりも大きければ、ステップ 2 で司祭 \(q\) が \({\it NextBallot}(b)\) メッセージを受け取ると、ステップ 4 で過去に開始されたどの票決に対しても投票しない約束を引き出すことができる。したがって新しい票決の開始は過去に開始された票決が成功することを防ぐことができる。もし、過去の票決が成功する前に新しい票決が連続して開始され、票決番号が増え続けてゆくなら、進行は達成できないかもしれない。
進行条件を満たすためには成功するまで新しい票決を行う必要があるが、あまり頻繁に行わないようにする必要がある。プロトコルを完成させる前に、Paxon 人はまず伝令者がメッセージを届けるのにかかる時間と、司祭が応答するのにかかる時間を知る必要があった。議場を出ない伝令者は常に 4 分以内にメッセージを届け、議場に残った司祭は起因するイベントから 7 分以内に行動を起こすと判断した11。このように、\(p\) と \(q\) が議場にいて、あるイベントで \(p\) が \(q\) にメッセージを送り、\(q\) が \(p\) に返信した場合、どちらの伝令者も議場を離れることがなければ、\(p\) は 22 分以内にその返事を受け取ることになる (司祭 \(q\) はイベントから 7 分以内にメッセージを送り、\(q\) はさらに 4 分以内にメッセージを受け取り、\(q\) は 7 分以内に返信し、その返信はさらに 4 分以内に \(p\) に届くことになる)。
ただ一人の司祭 \(p\) が票決を開始し、プロトコルのステップ 1 ですべての司祭にメッセージを送って票決を行ったとする。多数の司祭が議場にいるときに \(p\) が票決を開始した場合、\(p\) は票決を開始してから 22 分以内にステップ 3 を実行し、さらに 22 分以内にステップ 5 を実行することが期待できる。その時間までにステップを実行できなかった場合、\(p\) が票決を開始したあとに、司祭や伝令者の誰かが議場から退出したか、(\(p\) が票決を開始した唯一の司祭となる前に) 他の司祭がより大きな数字の票決を開始していたかのいずれかである。後者の可能性に対応するために、\(p\) は他の司祭が使用した \({\it lastTried}[p]\) よりも大きい番号の票決を知る必要がある。これはプロトコルを拡張して、司祭 \(q\) が \(p\) から \(b \lt {\it nextBal}[q]\) となる \({\it NextBallet}(b)\) または \({\it BeginBallet}(b,d)\) メッセージを受け取った場合、\(p\) に \({\it nextBal}[q]\) を含むメッセージを送ることを要求することで実現できる。その後、司祭 \(p\) はより大きな票決番号で新しい票決を開始する。
\(p\) が唯一の投票を開始した司祭と仮定して、(1) 直前の 22 分以内にステップ 3 またはステップ 5 を実行しなかったり、(2) 他の司祭がより高い番号の票決を開始したことを知った場合には、新しく票決を開始する必要があるとする。\(p\) と多数の司祭がいる状態で議場のドアをロックした場合、99 分以内に法令が可決され、議場にいるすべての司祭の台帳に記録される (\(p\) が次の票決を開始するのに 22 分、他の司祭がより大きい番号の票決を開始したことを知るのにさらに 22 分、そして票決を成功させるためにステップ 1~6 を完了するのに 55 分かかる可能性がある)。したがって議場を出ない 1 人の司祭だけが投票を開始すると進行条件は満たされることになる。
そのため、完全プロトコルには票決を開始するときに議長 (president) と呼ばれる一人の司祭を選ぶ手続きが含まれていた。ほとんどの政府形態では大統領を選ぶのは難しい問題である。しかし、それはほとんどの政府で大統領はどんな時でも正確に一人であると定められているためである。例えばアメリカの 1988 年の選挙後、ブッシュが大統領に選ばれたと考える人と、デュカキスが大統領に選ばれたと考える人がいた場合に混乱が生じる。しかし Paxon 教会会議では、複数の議長が存在することは進行を妨げるだけで矛盾を引き起こすことはない。完全プロトコルは進行条件を満たすためには議長を選ぶ方法が以下の議長選択要件 (presidential selection requirement) を満たすだけでよい:
議場に誰も入室したり退出しなければ、\(T\) 分後に議場にいる正確に 1 人の司祭が自分を議長とみなす。
もし議長選択要件が満たされているなら、司祭の過半数集合が議場におり、\(T+99\) 分間、議場に誰も出入りしなければ、完全プロトコルはその期間の終わりにすべての司祭の台帳に法令が記入されるという特性を持つことになる。
Paxon 人は議場にいるすべての司祭の名前をアルファベット順に並べて最後になった名前の司祭を議長に選んだが、これがどのように行われたかは正確には分からない。議長選択要件は、議場内の司祭が少なくとも \(T+11\) 分に 1 回、自分の名前を含むメッセージを他のすべての司祭に送っていれば満たされ、司祭は \(T\) 分間 "上位の名前" を持つ司祭からのメッセージを受け取らなければ自分が議長であると考えた。
完全教会会議プロトコルは、基本プロトコルから司祭に 2~6 の手順を速やかに行うことを要求し、票決を開始する議長を選ぶ方法を追加し、議長に適切な期間に票決を開始することを要求して得られたものである。このプロトコルの詳細は不明な点が多い。私は、議長を選ぶ簡単な方法と、議長がいつ新しい票決を開始すべきかを決定するための方法を説明したが、それらは間違いなく Paxos で使用されているものではない。私が提示した規則では法令が決議されたあとも議長は票決を開始し続けなければならず、それによって議場に入ったばかりの司祭が決議された法令について知ることができるようになっている。法令が決議された後に司祭がその法令を知るようにするにはもっと良い方法があったはずである。また、議長を選ぶ過程で、各司祭は自分の \({\it lastTried}[p]\) 値を他の司祭に送り、議長が最初の試行で十分に大きな票決番号を選択できるようにしていただろう。
Paxon 人は進行条件を達成するためのプロトコルには時間の経過を観測するものが必要だと考えた12。先述の議長選出や票決開始のプロトコルは、タイマーを設定し、タイムアウトが発生したときにアクションを実行する正確なアルゴリズムとして簡単に定式化できる (完全に正確なタイマーを仮定する)。さらに詳しく分析すると、このようなプロトコルはタイマーの精度に既知の制限がある場合にも機能することがわかる。Paxos の熟練した吹きガラス職人はそれに適した砂時計を作るのに苦労しなかった。
Paxon の数学者が洗練されていたことを考えると、彼らは議長選択要件を満たす最適なアルゴリズムを発見していたに違いないと広く信じられている。今後の Paxos 発掘調査でそのアルゴリズムが発見されることを期待するしかない。
- 4教会会議プロトコルが発見された経緯については完全には分かっていない。Paxon の数学者は現代のコンピュータ科学者のようにエレガントで論理的な導出を説明していたが、実際にアルゴリズムがどのように導出されたかとは似ても似つかないものだった。しかし数学的な成果 (セクション 2.1 の定理 1 および 2) が実際にプロトコルに先行していたことがわかっている。この数学的成果はプロトコルの要請を受けた数学者が満足の行くプロトコルが不可能であることを証明しようとしたときに発見された。
- 5いくつかの近代国家と同様に、Paxos はアテナイの民主主義の本質を完全に理解していなかった。
- 6Paxon の数学者は当時としては非常に進んでいたが、明らかに集合論の知識は持っていなかった。私は Paxon 人の原始的な表記法を現代の集合論の言葉に翻訳することにした。
- 7実際に投票するのはクォーラム内の司祭だけだったが、Paxon の数学者は証明の際に、どの司祭もどの投票用紙でも投票できるようにしておけば、プロトコルが正しいことを人々に納得させることが簡単であると考えた。
- 8定義上等しい (equals by definition) を意味する Paxon の数学記号 \(\triangleq\) を使用する。
- 9Paxon の数学者は、重要な定理の証明を常に注意深く構造的に行っていた。しかし現代の数学者のように細部を省略して段落形式の証明を書いても間違いがないほど洗練されていたわけではない。
- 10司祭 \(p\) と \(q\) は同じかもしれない。単純化のために、この場合は \(p\) が自分自身にメッセージを送ることでプロトコルを説明する。実際には、司祭は伝令者を使わずに自分自身に話しかけることができる。
- 11Paxon 人の時間単位である \(\dzifi\) 値を 30 秒と想定している。この値は、砂時計の破片の研究から得られた範囲内である。司祭の反応時間は、多数のメッセージが同時に到着しても 7 分 (\(14\,\dzifi\)) 以内にすべてのメッセージに応答しなければならなかったため非常に長かった。
- 12しかし、この結果の厳密な証明 [Fischer et al. 1985] が成されるまでには何世紀もの時間がかかった。
 3. 複数法令の議会
3. 複数法令の議会
議会が設立されたとき、その一貫性と進行の要件を満たすプロトコルが教会会議のプロトコルから派生した。オリジナルの議会プロトコルの派生と特性についてはセクション 3.1 と 3.2 で説明する。セクション 3.3 ではプロトコルのさらなる進化について説明する。
 3.1 プロトコル
3.1 プロトコル
Paxon 議会は 1 つの法令を可決するのではなく、番号の付けられた一連の法令を通過させなければならなかった。教会会議プロトコルと同様に議長が選出される。法令を通過させたい人は議長に報告し、議長はその法令に番号をつけて通過させようとする。論理的には、議会プロトコルでは法令の番号ごとに完全教会会議プロトコル使用された。しかし、これらすべてのインスタンスには 1 人の大統領が選ばれ、プロトコルの最初の 2 つのステップを 1 回だけ実行した。
議会プロトコルを導出する鍵は、教会会議プロトコルでは議長はステップ 3 まで法令やクォーラムを選択しないという観察にある。新たに選出された議長 \(p\) は、ある議員集合に教会会議プロトコルのすべてのインスタンスの \({\it NextBallet}(b)\) メッセージとして機能する単一のメッセージを送ることができる (インスタンスの数は無限で、法令番号ごとに 1 つである)。議員 \(q\) は教会会議プロトコルのすべてのインスタンスのステップ 2 の \({\it LastVote}\) メッセージとして機能する単一のメッセージを返信することができる。\(q\) は有限個のインスタンスでしか投票できないため、このメッセージには有限この情報しか含まれていない。
新しい議長が過半数集合のすべてのメンバーから返信を受け取ったとき、新議長は教会会議プロトコルのすべてのインスタンスに対してステップ 3 を実行する準備ができている。ある有限数のインスタンス (法令番号) について、ステップ 3 での法令の選択は \(B3\) によって決定される。議長は直ちにそのそれらのインスタンスごとにステップ 3 を実行して超えらの法令の通過を試みる。そして、議長は法令を通過させる要求を受け取るたびに、まだ自由に選択できる最も低い番号の法令を選択し、この法令番号 (教会会議プロトコルのインスタンス) に対してステップ 3 を実行して、その法令を通過させようとする。
このシンプルなプロトコルに次のような修正を加えることで実際の Paxon 議会のプロトコルとなる。
- 結果がすでに分かっている法令番号に対して教会会議プロトコルを使用する理由はない。したがって、新しく選出された議長 \(p\) が \(n\) 以下の番号を持つすべての法令を台帳に書き込んでいる場合、教会会議プロトコルにおいて \(n\) より大きい法令番号に対するすべてのインスタンスでの \({\it NextBallet}(b)\) メッセージと同じように機能する \({\it NextBallet}(b,n)\) メッセージを送信する。このメッセージに対する応答の中で、議員 \(q\) は自身の台帳にすでに記載されている \(n\) より大きい番号を持つ法令を \(p\) に通知し (自身の台帳にない法令については通常の \({\it LastVote}\) 情報を送信することに加えて)、自身の台帳にない法令番号 \(n\) 以下の法令を送るように \(p\) に依頼する。
金曜日の午後遅くに法令 125 と 126 が導入され、法令 126 は可決されて 1 つまたは 2 つの台帳に書き込まれたが、何も起きないうちに議員たちは全員週末のために帰宅したとする。また、次の月曜日に \(\Dwork\) が新しい議長に選出され、法令 126 について知ったが、前の議長とそれに賛同した議員全員がまだ議場にいないため、彼女は法令 125 について知らないとする。彼女は法令 126 を可決する決を行うので台帳に空白ができてしまう。新しい法令に 125 を割り当てると、前の週に可決された法令 126 より早く台帳に載ることになる。このように順序を変えて法令と可決すると、たとえば新しい法案を提案した市民が法令 126 がすでに可決されていることを知っていた場合に混乱を招く可能性がある。代わりに \(\Dwork\) は Paxos の誰にとっても全く意味のない伝統的な法令
125: 2月8日は国際オリーブの日である
を可決しようとする。一般的に、新しい議長は "オリーブの日" 法令を通過させることで自身の台帳の空白を埋めることになる。
議会プロトコルの一貫性と進行の特性は、それが派生した教会会議プロトコルの対応する特性からすぐに導かれる。我々が知る限り、議会プロトコルが教会会議プロトコルから非常に簡単に導き出せたため、Paxon 人は議会プロトコルの正確な説明をわざわざ書くことはなかった。
 3.2 プロトコルの特性
3.2 プロトコルの特性
 3.2.1 法令の順序
3.2.1 法令の順序
票決は、さまざまな議員によって開始された多くの異なる法令番号に対して同時に行われることができる ─ それぞれが、票決を開始したときには自分が議長だと考えていた。どのような順序で法令が可決されているのか、特に議長をどのように選ばれるのかを知らない限り正確なことは言えない。しかし法令の順番については推論できる一つの重要な性質がある。
法令は教会会議プロトコルの対応するインスタンスのステップ 3 で議長によって選択された時に提案された (proposed) とされる。法令は、それが最初に台帳に書き込まれたときに可決された (passed) とされる。議長が新しい法案を提案する前に、過半数集合のすべてのメンバーから彼らが投票した法令を知らなければならない。すでに可決されている法令は過半数集合の議員のうち少なくとも 1 人が投票していなければならない。したがって、議長は新しい法令を開始する前に、以前に可決しているすべての法令について知っていなければならない。議長は重要な法令、つまり "オリーブの日" 以外の法令で台帳の空白を埋めることはない。また、議長は順序どおりではない法令を提案しない。そのため、このプロトコルは次のような法令順序特性 (decree-ordering property) を満たしている。
法令 \(A\) と \(B\) が重要であり、法令 \(A\) は法令 \(B\) より前に提案されているなら、\(A\) は \(B\) より低い法令番号を持つ。
 3.2.2 閉ざされたドアの向こう
3.2.2 閉ざされたドアの向こう
新しい議長の選出に関する詳細は分からないが、議長が決まって議場に誰も出入りしなかったときに議会がどのように機能したかは正確に分かっている。議長は、市民から直接、あるいは他の議員から法令の可決要請を受けると、法令に番号を割り当て次のようなメッセージ交換で可決していた (番号は教会会議プロトコルの対応するステップを示している)。
- 議長はクォーラム内のそれぞれの議員に \({\it BeginBallet}\) メッセージを送る。
- クォーラムのそれぞれの議員は議長に \({\it Voted}\) メッセージを送る。
- 議長はすべての議員に \({\it Success}\) メッセージを送る。
全 \(N\) 人の議員と約 \(N/2\) のクォーラムを持つ議会を想定した場合、これは合計 3 つのメッセージの遅延と約 \(3N\) 個のメッセージを意味する。さらに、議会が忙しい場合には議長はある法令の \({\it BeginBallot}\) メッセージと前の法令の \({\it Success}\) メッセージを組み合わせて、一つの法令に付き合計 \(2N\) 個のメッセージしか送らない。
 3.3 今後の展開
3.3 今後の展開
島の統治は Paxon 人が実際に考えていた以上に複雑なものであった。いくつかの問題が発生し、その解決のためにもプロトコルの変更が必要となった。その中でも特に重要なものを以下にに紹介する。
 3.3.1 議長選び
3.3.1 議長選び
議会の議長は、もともと教会会議で行われていたアルファベット順に名前を並べる方法で選ばれていた。そのため、半年間の休暇を終えて戻った \(\Oki\) 議員は何が起きているかわからないのにすぐに議長に任命されてしまった。遅筆の \(\Oki\) が半年分の法令を台帳に複写している間、議会活動は停止していた。
この事件をきっかけに議長の選び方についての論議が始まった。Paxon 人の中には、一度議長になった議員は議場を去るまで議長でいるべきだと主張するものもいた。ある有力な市民グループは議会で最も裕福な議員が議長になることを望んでいた。なぜならその議員は議長の任務を手伝う書紀やその他の使用人をより多く雇う余裕があるからである。しかし、裕福層とは関係なく、最も立派な市民が議長になるべきだと主張するものもいた。立派であるということは、不正をする可能性が低いということだろうが、公的な不正行為の可能性を公に認める Paxon 人はいない。残念ながらこの議論の結論は不明で、最終的にどのような議長選考方法がされたのかは記録に残っていない。
 3.3.2 長い台帳
3.3.2 長い台帳
年月が経ち、議会がより多くの法令を可決するようになると、Paxon 人は現在のオリーブ税や、どのような色のヤギを売ることができるのかを調べるために、ますます長い法令のリストを熟読しなければならなかった。長期間の公開を終えて議場に戻ってきた議員は、自分の台帳を最新状態にするあtめにかなりの量を複写しなければならなかった。最終的に議員たちの台帳は、法令のリストから、現在の法令の状態とその状態に反映された最後の法令の番号だけが記載された法律書に変えざるを得なかった。
現在のオリーブ税を知るためには、法令集の "税法" の項目を見て、どのような色のヤギを売ることができるかを知るためには "商取引法" の項目を見ていた。議員の台帳に法令 1298 までの法令が記載されていて、法令 1299 でオリーブ税が 1 トン当たり 6 ドラクマになったと知ったとき、オリーブ税の法律の項目を変更し、台帳は法令 1299 までで完結すると記載するだけであった。その後、法令 1302 を知るとそれを台帳の後ろに書き留め、法令 1302 を法令集に組み込むのは法令 1300 と 1301 を知った後とした。
短期間不在だった議員が法令集のすべてを複写しなくても追いつけるように、議員は先週の法令のリストを本の後ろに置いていた。この一覧表は紙片に書いておくこともできたが、議員にとっては判決が出るたびに台帳の後ろに書き込んで、週に 2,3 回だけ法令集を更新するのが便利だったのである。
 3.3.3 官僚制度
3.3.3 官僚制度
Paxos が繁栄すると議員たちは非常に忙しくなった。議会では、政府のすべての詳細を扱うことができなくなったため官僚制度 (bureaucracy) が設立された。議会は、チーズの各ロットが販売に適しているかどうかを宣言する代わりに、その判断を行うチーズ検査官を任命する法令を通過させた。
官僚選びがそれほど簡単ではないことはすぐに分かった。議員は \(\Dijkstra\) を最初のチーズ検査官とする法令を可決した。数カ月後、商人たちは \(\Dijkstra\) が厳しすぎて完全に良質なチーズを拒否していると訴えた。そこで議会は \(\Dijkstra\) に変わって次のような法令を可決した。
1375: \(\Gwysa\) を新しいチーズ検査官とする
しかし \(\Dijkstra\) は議会の動きを注視していなかったため、この法令をすぐに知ることができなかった。\(\Dijkstra\) と \(\Gwysa\) の両者がチーズを検査し、相反する判断を下したことで、チーズ市場は混乱した時期が合った。
このような混乱を避けるために Paxon 人は、一つの役職に就くことができるのは常に一人の官僚に限られていることを保証しなければならなかった。そのために、議長は各法令の一部としてその法令が提案された日時を記載した。\(\Gwysa\) をチーズ検査官にする法令は次のようになる。
2716: 8:30 15 Jan 72 - \(\Dijkstra\) を 3 ヶ月のチーズ検査官とする
これにより彼の任期は、1 月 15 日の 8:30 か、前任の検査官の任期終了時のいずれか遅い方から始まると宣言される。彼の任期は、彼が議長に次のような法令の制定を求めて明確に辞任しない限り、3 月 15 日の 8:30 に終了する。
2834: 9:15 3 Mar 72 - \(\Dijkstra\) はチーズ検査官を辞任
官僚の任期は短く、島を離れるなどですぐに交代できるようになっていた。官僚が満足の行く仕事をしていれば議会はその完了の人気を延長する法令を制定するだろう。
官僚が現在ポストに付いているかを判断するには時間を知る必要があった。Paxos 島には機械式時計はありませんでしたが、Paxon 人は太陽や星の位置で 15 分以内の正確な時間を知ることができた13。\(\Dijkstra\) の任期が 8:30 からだとしたら、天球観測で 8:45 になるまでチーズ検査を始めないだろう。
法令の番号が大きいほど提案の日時が遅くなるのであれば、この官僚登用方法を機能させるのは簡単である。しかし、もし、どちらも議長だと思っている別々の議員が 9:30 から 9:35 の間に次の法令を可決してしまうとどうなるだろうか?
2854: 9:45 9 Apr 78 - \(\Fransez\) は 2 ヶ月のワインテスターを務める
2855: 9:20 9 Apr 78 - \(\Pnueli\) は 1 ヶ月のワインテスターを務める
このような提案時間のズレは、議会プロトコルが以下の特性を満たしているため簡単に防ぐことができる。
2 つの法令が異なる議長によって可決された場合、どちらかの議長がもう一方の法令が提案されたことを知った後に自分の法令を提案したことになる。
この特性が満たされていることを確認するために、票決番号 \(b\) が法令 \(D\) に対して成功し、\(b \lt b'\) となる票決番号 \(b'\) が法令 \(D'\) に対して成功したと仮定する。\(q\) を両方の票決に投票した議員とする。\(D'\) の票決は \({\it NextBallet}(b',n)\) メッセージで開始した。もしこのメッセージの送信者が \(D\) についてまだ知らなかったとすれば、\(n\) は \(D\) の法令番号より小さく、\(q\) の \({\it NextBallot}\) メッセージに対する返信は \(D\) に投票したことが書かれていなければならない。
 3.3.4 法律を知る
3.3.4 法律を知る
一般市民は法令の制定を求めるだけではなく、現在の国の法律を調べる必要があった。Paxon 人は当初、市民が議員の台帳を調べれば良いと考えていたが、次のような出来事があったためより高度のアプローチが必要であることが分かった。何世紀にも渡って白ヤギだけは売ることが許されていた。\(\Dolev\) という農夫が議会で次のような法令を可決し
77: 黒ヤギの販売を許可する
\(\Dolev\) はヤギ飼いに黒山羊を \(\Skeen\) という商人に売るよう指示した。法律を遵守する市民として \(\Skeen\) は議員の \(\Stockmeyer\) にそのような販売が合法化を尋ねた。しかし \(\Stockmeyer\) は議会を離れていたため、法令 76 を過ぎても彼の台帳には記載はなかった。彼は \(\Skeen\) に、現行法ではこの販売は違法であると忠告し \(\Skeen\) はヤギの購入を拒否した。
この事件をきっかけに法律に関する問い合わせについて次のような単調性条件 (monotonicity condition) が設定された。
第 1 の問い合わせが第 2 の問い合わせに先行する場合、第 2 の問い合わせは第 1 の問い合わせより早い法令の状態を明らかにすることはできない。
ある市民が特定の法令が可決されたことを知った場合、その知識を得るプロセスは、この条件が適用される暗黙との問い合わせであるとみなされる。後述するように、単調性条件の解釈は年々変化していった。
当初、単調性条件は問い合わせごとに法令を通すことで実現していた。\(\Schneider\) がオリーブに対する現在の税金を知りたければ、議会に次のような法令を可決させる。
87: 市民 \(\Schneider\) は法律を読んでいる
そして、少なくとも法令 86 までの台帳を読み、その法令の時点でオリーブ税を知ることになる。別の市民 \(\Greez\) がオリーブ税について問い合わせたとき、その問い合わせ法令が法令 87 が可決された後に提案されたものであれば、法令順序特性 (セクション 3.2.1) により 87 よりも大きい法令番号を割り当てられたことになる。そのため、\(\Greez\) は \(\Schneider\) より早くオリーブ税の値を得ることができなかった。このような法律の読み方では先行 (precedes) が単調性条件を満たすと解釈され、問い合わせ \(A\) が問い合わせ \(B\) に先行するのは、\(A\) が \(B\) の開始よりも早い時間に終了した場合に限られるとされていた。
問い合わせのたびに法令を可決していたのではとても間に合わないことから、Paxon 人は単調性条件を緩和して先行の解釈を変えればもっと簡単な方法にできると考えた。ある事象が他の事象に先行するためには、最初の事象がより早い時間に起きるだけではなく、2 番目の事象に因果関係を与えることができなければならないと考えた。この弱い単調性条件により、農夫 \(\Dolev\) による暗黙の問い合わせの終了と商人 \(\Skeen\) による問い合わせの開始には因果のある出来事の連鎖があることから、農夫の \(\Dolev\) と商人の \(\Skeen\) が最初に遭遇した問題は回避された。
弱い単調性の条件は、すべての商取引や問い合わせに法令番号を使うことで満たされた。例えば、白以外のヤギを多く飼っていた農夫 \(\Dolev\) は議会で次のような法令を可決させた。
277: 茶色いヤギの販売は許可されている
茶色いヤギを \(\Skeen\) に売るとき、彼は商人に法令 277 の時点で販売が合法であることを伝えた。\(\Skeen\) は次に議員 \(\Stockmeyer\) に少なくとも法令 277 までは販売が合法であるかを尋ねた。もし \(\Stockmeyer\) の台帳が法令 277 まで揃っていなければ、揃うまで待つか、他の人に尋ねるように \(\Skeen\) に伝える。\(\Stockmeyer\) の台帳が法令 298 まであった場合は、法令 298 の時点で販売が合法であることを \(\Skeen\) に伝える。商人 \(\Skeen\) は次の商取引や法令に関する問い合わせの際に使用するために 298 を憶えておく。
Paxon 人は単調性条件を満たしていたが、一般市民は法令番号を憶えておくことを嫌った。繰り返すが、Paxon 人は単調性条件を再解釈することで問題を解決した ─ 今度は法律の状態 (state of low) の意味を変更した。法律を分野別に分け、それぞれの分野の専門家として議員を選んだ。そして、その専門家の台帳によって、各分野の法律の現状を把握することにした。例えば法令 1517 で関税法が変わり、法令 1518 で税法が変わったとする。税法の専門家が関税法の専門家よりも先に両方の法令を知った場合、税法が先に変更されることになり、法令を番号順に制定した状態とは異なる法律の状態をもたらすことになる。
現在の状態の定義に矛盾が生じないように、Paxon 人はどの分野にも最大 1 人の専門家がいる必要があった。この要件は官僚を選ぶときと同じ方法で専門家を選ぶことで満たされた (セクション 3.3.3 参照)。それぞれの問い合わせが法律の 1 つの分野にしか関係していない場合は、その分野の専門家に問い合わせをして、その専門家が自分の台帳から回答することで単調性を実現した。ある法律が可決されたことを知ることは暗黙のうちに行われる問い合わせの結果であるため、Paxon 人は法令の変更が最大 1 つの法律分野であり、法令の可決の通知はその領域の専門家からのみ行うことができることを要求した。
複数の分野に跨がる問い合わせでも対応は難しくなかった。商人 \(\Liskov\) が輸入した金羊毛 (golden fleece) の関税は、現地で購入した金羊毛の消費税より高いのかと質問したとき、税法と関税法の専門家が協力して答えを出す必要があった。例えば税法の専門家は、まず関税の専門家に金羊毛の関税を聞いてから \(\Liskov\) に答えることができ、返事をもらうまでに台帳を変更しなければ良い。
この方法は一度にいくつかの分野の法律を大幅に変更する必要が生じるまで満足のゆくものだった。そして Paxon 人は、単調性を保つために必要な条件は、ある法令が単一の分野にのみ影響を与えることではなく、その法令が影響を与えるすべての分野に同じ専門家がいることであると考えた。議会はまず、一人の議員をすべての分野の専門家として任命することで、一回の法令で複数の分野の法律を変更することができる。さらに、同じ分野に複数の専門家がいても、その分野の法律を変えてはいけないということになっていた。所得税の納税期限が近づくと、議会では数人の税法専門家が任命され、季節的に殺到する税法に関する問い合わせに対応することになる。
 3.3.5 不誠実な議員と正直者の間違い
3.3.5 不誠実な議員と正直者の間違い
公式には間違いと言われているが、Paxos の歴史上には不誠実な議員が何人かいたはずである。逮捕された者はおそらく追放された。悪意のある議員は、矛盾したメッセージを送ることで別の議員の台帳に矛盾を生じさせることができる。矛盾は、正直な議員の伝令者の記憶の欠落によっても起こりうる。
矛盾が認知されれば法令を通過させることで容易に修正することができた。例えば、現在のオリーブ税についての意見の相違は、オリーブ税に一定の価値があることを宣言する新たな法令を可決することで解消できる。難しいのは、誰も気づいてなくても矛盾している台帳を修正することである。
議員の不正やミスの存在は、議会成立から数年後に台帳に現れ始めた冗長な法令からも推測できる。例えば法令
2605: オリーブ税は 1 トンあたり 9 ドラクマ
は、法令 2155 でオリーブ税がすでに 1 トン当たり 9 ドラクマに設定されており、その後の法令では変更されていなかったにも関わらず可決された。議会は 6 ヶ月ごとに法律を巡回していたため、議員の台帳が最初は矛盾していても、6 ヶ月以内にはすべての議員が現行の法律に同意するようになっていた。これらの冗長な法令を用いることで、Paxon 人は議会を自己安定化させていたと考えられている (自己安定化 (self-stabilizing) は Dijkstra [1974] による現代用語である)。
議員が自由に出入りする議会において、自己安定化が何を意味するのかは正確にはわからない。一貫性を保証するためにすべての議員が一度に議場にいなければならないという定義では Paxon 人は満足しなかっただろう。しかし一貫性を実現するには、ある議員が台帳に特定の法令番号を記入していて、別の議員が記入していない場合、2 番目の議員が最終的にその番号を記入する必要があった。
残念ながら Paxon 議会がどのような自己安定可読性を持っていたのか、そしてそれがどのようにして実現されていたのかは正確には分かっていない。Paxon の数学者がこの問題に取り組んだのは間違いないが、その研究はまだ見つかっていない。今後の Paxos の考古学調査で自己安定化に関する古文書の探索が優先されることを願っている。
 3.3.6 新しい議員の選択
3.3.6 新しい議員の選択
当初、議会の議員は親から子への世襲制であった。長老の \(\Parnaz\) 議員が引退すると台帳を息子に渡し、息子はそれを引き継いだ。他の議員にとってどの \(\Parnaz\) と連絡をとっているかは重要ではなかった。
旧来の家族が転出し、新しい家族が転入してくるようになると、このシステムは変更せざるを得なかった。Paxon 人は議会のメンバーを法令で追加・削除することにした。議会のメンバーはどの法令を可決させるかによって決まるが、法令を通過させるには何をもって多数派とするかを知らなければならず、それには誰が議会のメンバーであるかが重要になる、という循環性 (circularity) の問題を提起した。この循環性は、法令 \(n-3\) の時点で法令 \(n\) を可決する議員メンバーを指定することで解消された。議長は、法令 3252 までのすべての法令を知るまでは、法令 3255 を通そうとすることはできなかった。実際には法令
3252: \(\Strong\) は新しい議員である
を可決した後、議長は直ちに "オリーブの日" 法令を 3253 と 3254 として可決する。
議会の構成をこのように変えることは危険であり、慎重に行わなければならなかった。一貫性と進行の条件は常に維持される。しかし、進行条件は議会に過半数集合がある場合にのみ進行を保証するものであり、過半数集合があることを保証するものではなかった。実際、この議員選出の仕組みが Paxos の議会制度を崩壊させるきっかけとなった。筆記者のミスにより、難破船で溺死した船員を称えるはずの法令は、その船員たちを議会の議員とすると宣言した。この法令が可決されたことで、ミスを修正する法令も含めて、新たな法令を可決できなくなってしまった。Paxos の政治は停止した。混乱に乗じてクーデターを起こした \(\Lampson\) という将軍は軍事独裁政権を樹立し、何世紀にも渡る進歩的な政治を終わらせた。腐敗した独裁者の下で弱体化した Paxos は東からの侵略を退けることができず、その文明は破壊されてしまった。
- 13Paxos の温暖な気候では曇りの日はほとんどなかった。
 4. コンピュータ科学との関連性
4. コンピュータ科学との関連性
 4.1 ステートマシンアプローチ
4.1 ステートマシンアプローチ
Paxos 議会は何世紀も前に破壊されたがそのプロトコルは現代でも有用である。例えば、ネームサーバとして使用される可能性のある簡単な分散型データベースシステムを考えてみよう。データベースの状態は、名前に対する値の割当で構成されている。データベースのコピーは複数のサーバで管理されている。クライントプログラムはどのサーバに対しても、名前に割り当てられた値の読み取りや変更を要求することができる。読み取り要求には 2 種類あり、現在名前に割り当てられている値を返す低速読み取り (slow read) と、高速ではあるがデータベースに最近行われた変更が反映されていない可能性がある高速読み取り (fast read) がある。
| 議会 | 分散データベース |
|---|---|
| 議員 | サーバ |
| 市民 | クライアントプログラム |
| 現在の法律 | データベース状態 |
Table 1 はこのデータベースシステムと Paxon 議会との明らかな対応関係を示している。値を変更するクライアントの要求は、法令を可決することによって実行される。低速読み取りはセクション 3.3.4 で説明されているように法令を可決することで行われる。高速読み取りはサーバの現在のバージョンのデータベースを読み取ることによって実行される。Paxon 議会プロトコルはデータベースシステムの分散型フォールトトレラント実装を提供する。
この分散型データベースの実装方法は Lamport [1978] によって最初に提案されたステートマシンアプローチの一例である。このアプローチではまずステートマシンを定義する。ステートマシンは、状態の集合、コマンドの集合、応答の集合、および、コマンド/状態のそれぞれのペアに応答/状態ペア (応答と状態からなるペア) を割り当てる関数で構成されている。直感的に、ステートマシンは応答を生成して状態を変更することでコマンドを実行し、コマンドとマシンの現在の状態が応答と新しい状態を決定する。分散型データベースでは、ステートマシンの状態は単なるデータベースの状態である。ステートマシンのコマンドと、応答と新しい状態を指定する関数を Fig 2 に示す。
| コマンド | read(name, client) | update(name, val, client) |
| 応答 | (client, value of name) | (client, "ok") |
| 新しい状態 | 現在の状態と同じ | name の値が val である以外は現在の状態と同じ |
ステートマシンのアプローチでは、システムはサーバプロセスのネットワークで実装される。サーバは、クライアントの要求をステートマシンのコマンドに変換し、コマンドを実行し、ステートマシンの応答をクライアントへの応答に変換する。一般的なアルゴリズムでは、すべてのサーバが同じコマンドシーケンスを取得し、それによってすべてのサーバが同じシーケンスのレスポンスと状態を生成することが保証される。データベースの例では、クライアントが低速読み取りや値の変更を要求すると、ステートマシンは read または udpate コマンドに変換される。このコマンド時が実行されると、ステートマシンの応答がクライアントへの返信に変換され、要求を受け取ったサーバからクライアントに送信される。すべてのサーバが同じシーケンスのステートマシンコマンドを実行するため、すべてのサーバがデータベースの一貫したバージョンを維持する。ただし、あるステートマシンコマンドがすべてのサーバで同時に実行される必要はないため、サーバによっては他のサーバより古いバージョンの場合がある。サーバはステートマシンコマンドを実行することなく、現在のバージョンの状態を使用して高速読み取り要求に応答する。
システムの機能は、コマンド/状態のペアから応答/状態のペアとなる単なる関数であるステートマシンによって表現される。同期やフォールトトレランスの問題は、サーバがコマンドのシーケンスを取得するための一般的なアルゴリズムによって処理される。新しいシステムを設計するときはステートマシンだけが新しくなる。サーバは、すでに正しいことが証明されている標準的な分散アルゴリズムによってステートマシンコマンドを取得する。関数は分散アルゴリズムよりも設計が容易であり、また正しい結果を得ることも容易である。
任意のステートマシンを実装する最初のアルゴリズムは Lamport [1978] によるものである。その後、Lamport [1984] で任意の固定数 \(f\) までの任意障害 (arbitrary failures) を許容するアルゴリズムが考案された。こののアルゴリズムは \(f\) 以下のプロセスが故障しても一定時間内にステートマシンのコマンドが実行されることが保証されている。このアルゴリズムはリアルタイムな応答を必要とするアプリケーションに適している14。しかし \(f\) 個以上の故障が発生した場合、別々のサーバがステートマシンの矛盾したコピーを持つ可能性がある。さらに、2 つのサーバが互いに通信できない状況は、一方のサーバが故障したことと同じである。システムが一貫性を失う可能性を低くするためには \(f\) の値が大きいアルゴリズムを使用する必要がある。これは、冗長ハードウェア、通信帯域幅、および応答時間における大きなコストを意味する。
Paxon 議会プロトコルは任意のステートマシンを実装する別の方法を提供している。議員の法律書がマシンの状態に対応し、法令を可決することがステートマシンのコマンドを実行することに対応する。その結果、以前のアルゴリズムと比べて堅牢性やコストが低くなっている。恣意的で悪意のある故障を許容するものではなく、有限時間の応答を保証するものでもない。しかし、任意の数のプロセスや通信経路が (良性の) 故障をしても一貫性は維持される。Paxon アルゴリズムは適度な信頼性を必要とするシステムに適しているが、極端なフォールトトレラントなリアルタイム実装のコストを正当化するものではない。
有限時間での応答を保証するアルゴリズムを用いてステートマシンを実行できれば、時間を状態の一部とすることができ、時間の経過によってマシンのアクションを引き起こすことができる。例えばリソースの所有権を付与するシステムについて考える。状態には、クライアントがリソースを付与された時間を含めることができ、ステートマシンはクライアントがリソースを長く保持していた場合に所有権を取り消すコマンドを自動的に実行することができる。
Paxon アルゴリズムでは、このような自然な形で時間を状態の一部とすることはできない。障害が発生すると、コマンドの実行 (法令の可決) に任意の時間がかかったり、あるコマンドが先に発行された別のコマンドよりも先に実行される (つまり法令の順序で先に現れる) 可能性がある。ただしステートマシンは Paxon 議会と同じように実時間を使うことができる。例えばセクション 3.3.3 で説明したような、現在のチーズ検査官が誰なのかを決定する方法はリソースの所有権を決定するのにも使用できる。
この記事が書かれて以来、この分野では多くの研究が行われてきた。ステートマシンアプローチは Schneider [1990] で調査されている。Keidar and Dolev [1996] のリカバリープロトコルと Fekete et al. [1996] の全順序ブロードキャストアルゴリズムはここで説明した Paxon プロトコルに非常によく似ている。また著者は Oki and Liskov [1988] の View Management プロトコルが Paxon プロトコルと同等であるように思われることに気づいていなかったようである。
この投稿で提示された改良お店の多くは、現代またはその後の記事にも登場している。セクション 3.3.3 で説明されている委任の方法は Gray and Cheriton [1989] のリースメカニズムと非常によく似ている。Paxon 人が法令番号を使用して単調性条件を満たす手法は Ladin et al. [1992] によって説明されている。セクション 3.3.6 の新しい議員を追加する手法は Schneider [1990] でも提供されている。
 4.2 コミットプロトコル
4.2 コミットプロトコル
Paxon 教会会議プロトコルは標準的な 3-フェーズコミットプロトコル [Bernstein 1087; Skeen 1982] と類似している。Paxon の票決と 3-フェーズコミットプロトコルはどちらもコーディネーター (議長) と他のクォーラムメンバー (議員) の間で 5 つのメッセージを交換する。コミットプロトコルは commit か abort の 2 値のうち 1 つを選択し、教会会議プロトコルは任意の法令を選択する。コミットプロトコルを教会会議プロところに変換するには、メッセージの最初のラウンドで法令を送信する。commit の決定はこの法令が可決したことを意味し、abort の決定は "オリーブの日" 法令が可決されたことを意味する。
教会会議プロトコルは第 2 フェーズまで法令が送信されない点で、変換されたコミットプロトコルとは異なる。これにより、対応する議会プロトコルでは、すべての法令に対して第 1 フェーズを 1 回だけ実行することができるため、個々の法令を通過させるために必要なメッセージのやり取りは 3 回だけとなる。
教会会議プロトコルの基礎となる定理は Dwork, Lynch, and Stockmeyer [Dwork et al. 1988] によって得られた結果と類似している。ただし、それらのアルゴリズムは票決を別のラウンドで順次実行するものであり、教会会議プロトコルとは無関係のようである。
- 14これらのアルゴリズムは地中海に面した別の国の軍事プロトコルを参考にしている (ビザンチン将軍問題のこと)。
 APPENDIX - 教会会議プロトコルの一貫性の証明
APPENDIX - 教会会議プロトコルの一貫性の証明
 A.1 基本プロトコル
A.1 基本プロトコル
教会会議の基本的なプロトコルはセクション 2.3 で非形式的に説明されているが、ここでは現代的なアルゴリズム表記を使用して説明する。まず司祭 \(p\) が保持しなければならない変数から始める。最初に、司祭の台帳に記載されている情報を表す変数がある (便宜上、セクション 2.3 で使用されている票 \({\it prevVote}[p]\) はその構成要素である \({\it prevBal}[p]\) と \({\it prevDec}[p]\) に置き換えられている)。
| \({\it outcome}[p]\) | \(p\) の台帳に書かれて法令、またはまだ何も書かれていなければ \({\rm BLANK}\)。 |
| \({\it lastTried}[p]\) | \(p\) が最後に開始しようとした票決の番号、またはなければ \(-\infty\)。 |
| \({\it prevBal}[p]\) | \(p\) が最後に投票した投票用紙の番号、または一度も投票していない場合は \(- \infty\)。 |
| \({\it prevDec}[p]\) | \(p\) が最後に投票した法令、または一度も投票していなければ \({\rm BLANK}\)。 |
| \({\it nextBal}[p]\) | \(p\) が票決に参加することに同意した最後の票決の番号、または一度も票決に参加することに同意していなければ \(-\infty\)。 |
次は司祭 \(p\) が紙片に書いておく情報を表す変数である。
| \({\it status}[p]\) | 次のいずれかの値:
|
||||||
| \({\it prevVotes}[p]\) | 現在の票決 (票決番号 \({\it lastTried}[p]\) のそれ) に対して \({\it LastVote}\) メッセージで受け取った票の集合。 | ||||||
| \({\it quorum}[p]\) | \({\it status}[p] = {\it polling}\) ならば、現在の票決のクォーラムを形成している司祭の集合、そうでなければ意味はない。 | ||||||
| \({\it voters}[p]\) | \({\it status}[p] = {\it polling}\) ならば、\(p\) が現在の票決で \({\it Voted}\) メッセージを受信したクォーラムメンバーの集合、そうでなければ意味はない。 | ||||||
| \({\it decree}[p]\) | \({\it status}[p] = {\it polling}\) ならば、現在の票決の法令、そうでなければ意味はない。 |
また履歴変数 \(\mathfrak{B}\) もあり、これは開始された票決の集合とその進行、つまりどの司祭が票を投じたかを表している (履歴変数はアルゴリズムの開発や証明に使われるが、実際には実装されていない)。
次に司祭 \(p\) が受け取るだろうアクションがある。これらのアクションはアトミックであると想定されている。つまり一度アクションを開始したら司祭 \(p\) が他のアクションを開始する前に完了しなければならない。アクションは有効化条件 (enabling condition) と効果のリスト (list of effects) で記述されている。有効化条件はアクションがいつ実行できるかを示す。メッセージを受信するアクションは、伝令者が適切なメッセージとともに到着するたびに有効化される。効果のリストには、アクションがアルゴリズムの変数をどのように変更するかと、送信するメッセージ (存在するなら) が記載されている (個々のアクションごとに最大で 1 つのメッセージが送信される)。
前述のように票決番号は司祭の間で分割されている。Paxon 人は任意の投票番号 \(b\) に対して、その投票番号を使うことを許された司祭を \({\it owner}(b)\) と定義した。
基本プロトコルのアクションは許可に対するアクションであり、司祭が何かを行うことを要求していない。効率化の試みはされていない。アクションは、\(p\) がすでに \({\it LastVote}\) メッセージを受け取っている司祭に別の \({\it BeginBallot}\) メッセージを送るような馬鹿げたことを可能にしている。
- 新しい票決を試行
常に有効化されている。- \({\it lastTried}[p]\) を、\({\it owner}(b)=p\) であるような以前の値より大きい任意の票決番号 \(b\) に設定する
- \({\it status}[p]\) を \({\it trying}\) に設定する。
- \({\it prevVotes}[p]\) を \(\emptyset\) に設定する。
- \({\it NextBallet}\) メッセージの送信
\({\it status}[p] = {\it trying}\) であればいつでも有効化されている。- 任意の司祭に \({\it NextBallot}({\it lastTried}[p])\) メッセージを送信する。
- \({\it NextBallot}(b)\) メッセージの受信
もし \(b \ge {\it nextBal}[p]\) なら- \({\it nextBal}[p]\) を \(b\) に設定する。
- \({\it LastVote}\) メッセージの送信
\({\it nextBal}[p] \gt {\it prevBal}[p]\) であればいつでも有効化されている。- 司祭 \({\it owner}({\it nextBal}[p])\) に \({\it LastVote}({\it nextBal}[p])\) メッセージを送信する。ここで \(v_{pst}=p\), \(v_{bal}={\it prevBal}[p]\), \(v_{dec}={\it prevDec}[p]\) である。
- \({\it LastVote}(b,v)\) メッセージの受信
もし \(b = {\it lastTried}[p]\) かつ \({\it status}[p] = {\it trying}\) であれば、- \({\it prevVote}[p]\) をその元の値と \(\{v\}\) の和集合に設定する。
- 過半数集合 \(Q\) のポーリングを開始
\(Q\) を過半数集合とし、\({\it status}[p] = {\it trying}\) かつ \(Q \subseteq \{v_{pst}: v \in {\it prevVotes}[p]\}\) のとき有効化されている。- \({\it status}[p]\) を \({\it polling}\) に設定する。
- \({\it quorum}[p]\) を \(Q\) に設定する。
- \({\it voters}[p]\) を \(\emptyset\) に設定する。
- \({\it decree}[p]\) を次のような法令 \(d\) に設定する: \(v\) を \({\it prevVotes}[p]\) の最大の要素とする。もし \(v_{bal} \ne -\infty\) であれば \(d = v\)、そうでなければ \(d\) は任意の票決。
- \(\mathfrak{B}\) を元の値と \(\{B\}\) の和集合に設定する。ここで \(B_{dec}=d\), \(B_{qrm}=Q\), \(B_{vot}=\emptyset\), \(B_{bal}={\it lastTried}[p]\) である。
- \({\it BeginBallot}\) メッセージの送信
\({\it status}[p] = {\it polling}\) であれば有効化されている。- \({\it BeginBallog}({\it lastTried}[p],{\it decree}[p])\) メッセージを \({\it quorum}[p]\) 内の任意の司祭に送信する。
- \({\it BeginBallot}(b,d)\) メッセージの受信
もし \(b = {\it nextBal}[p] \gt {\it prevBal}[p]\) であれば- \({\it prevBal}[p]\) を \(b\) に設定する。
- \({\it prevDec}[p]\) を \(d\) に設定する。
- \(\mathfrak{B}\) 内に \(B_{bal}=b\) となるような票決 \(B\) が存在する (存在しそう) ならば、そのような任意の \(B\) を選び (一つしか無いだろう)、\(B_{vot}\) をその旧値と \(\{p\}\) の和集合に設定することで、\(\mathfrak{B}\) の新しい値をその旧値から得るようにする。
- \({\it Voted}\) メッセージを送信
\({\it prevBal}[p] \ne -\infty\) であればいつでも有効化されている。- \({\it owner}({\it prevBal}[p]\) に \({\it Voted}({\it prevBal}[p])\) メッセージを送信する。
- \({\it Voted}(b,q)\) メッセージを受信
もし \(b = {\it lastTried}[p]\) かつ \({\it status}[p] = {\it polling}\) であれば- \({\it voters}[p]\) を旧値と \(\{q\}\) の和集合に設定する。
- 後を継ぐ
\({\it status}[p] = {\it polling}\), \({\it quorum}[p] \subseteq {\it voters}[p]\), \({\it outcome}[p] = {\rm BLANK}\) であればいつでも有効化されている。- \({\it outcome}[p]\) を \({\it decree}[p]\) に設定する。
- \({\it Success}\) メッセージの送信
\({\it outcome}[p] \ne {\it BLANK}\) であればいつでも有効化されている。- 任意の司祭に \({\it Success}({\it outcome}[p])\) を送信する。
- \({\it Success}(d)\) メッセージの受信 \({\it outcome}[p] = {\rm BLANK}\) であれば
- \({\it outcome}[p]\) を \(d\) に設定。
このアルゴリズムは Paxon の司祭が実際に行っているプロトコルを抽象化したものである。このアルゴリズムの動作は実際の司祭のアクションを正確にモデル化しているだろうか? 司祭が "原子的に" 実行できるアクションは、メッセージの受信、メモや台帳への書き込み、メッセージの送信の 3 種類だった。これらはそれぞれアルゴリズムの単一のアクションで表現されているが、受信アクションはメッセージの受信と変数の設定の両方を行う。メッセージの受信は、司祭がそのメッセージに基づいてアクションしたときに発生したと見なすことができる。もし司祭がメッセージを受信する前に議場を去った場合、そのメッセージは受信されなかったと見なすことができる。この見なしは一貫性の条件には影響しないため、アルゴリズムの一貫性から基本的な教会会議プロトコルの一貫性を推測することができる。
 A.2 一貫性の証明
A.2 一貫性の証明
一貫性の条件を証明するためには、\({\it outcome}[p]\) と \({\it outcome}[q]\) の両方が \({\rm BLANK}\) と異なる場合、それらが等しいことを示す必要がある。厳密な正しさの証明にはアルゴリズムの完全な記述が必要である。上記の記述はほぼ完全だが、送信中のすべてのメッセージの多重集合の値である \(\mathcal{M}\) 変数が不足している15。各 Send アクションは多重集合にメッセージを追加し、各 Receive アクションはメッセージを削除する。またメッセージの紛失や重複を表すアクションや、司祭が紙片をなくすことを表す Forget アクションも必要である。
これらを追加することで取りうる振る舞いの集合を定義するアルゴリズムが得られ、各状態の変化は取りうるアクションの一つに対応する。Paxon 人は次のような述語 (predicate) \(I\) を見つけることで正しさを証明した。
- 初期状態で \(I\) は真。
- \(I\) は望ましい正しい条件を意味する。
- 取りうるアクションはそれぞれ \(I\) を真にする。
述語 \(I\) は論理積 \(I1 \land \ldots \land I7\) として記述された。ここで \(I1\)~\(I5\) はすべての司祭 \(p\) に対しての述語 \(I1(p)\)~\(I5(p)\) の論理積である。ほとんどの変数はいくつかの論理積 (conjunct) で言及されているが、\({\it status}[p]\) を除く各変数は当然 1 つの論理積に関連しており、各論理積はその関連する変数に対する制約と考えることができる。\(I\) の個々の論理積の定義は Fig 3 に示されており、\(\land\) 記号で示された項目のリストはそれらの論理積を示している。論理積に関する変数は角括弧付きのコメントに記載している。
Paxon 人は \(I\) が上記の 3 つの条件を満たすことを証明しなければならなかった。最初の条件、すはなち \(I\) が初期状態で成立するという条件は、すべての変数の初期値に対して各論理積が真であることを確認する必要がある。この初期値は明示されていないものの、変数の記述から推測できるため 1 つ目の条件を確認することは簡単である。\(I\) が一貫性を意味する、という 2 つ目の条件は、\(I1\)、\(I6\) の最初の論理積、そして定理 1 から導かれる。難しいのは 3 つ目の条件である \(I\) の不変性の証明で、これは \(I\) がすべてのアクションに対して真となることを証明することを意味する。この条件は、\(I\) の各論理積について、\(I\) が真のときに何らかのアクションを実行すると、その論理積が真のままであることを示すことで証明される。その証明を以下に示す。
Proof Sketch for \(I1(p)\). \(\mathfrak{B}\) は、ある \(B \in \mathfrak{B}\) に対して新しい票決を追加するか、\(B_{vot}\) に新しい司祭を追加することによってのみ変化するが、どちらも \(I1(p)\) を偽ることはできない。\({\it outcome}[p]\) の値は Succeed と Receive Success Message アクションによってのみ変化する。有効化条件と \(I5(p)\) は \(I1(p)\) が Succeed アクションによって真のままであることを意味している。有効化条件、\(I1(p)\)、\(I7\) の最後の論理積は、Receive Success Message アクションによって \(I1(p)\) が真のままであることを意味する。∎
Proof Sketch for \(I2(p)\). この論理積は \({\it lastTried}[p]\), \({\it status}[p]\), および \(\mathfrak{B}\) にのみ依存する。\({\it lastTried}[p]\) を変更するのは Try New Ballot アクションのみであり、このアクションのみが \({\it status}[p]\) を \({\it trying}\) にすることができる。このアクションは \({\it lastTried}[p]\) を \({\it owner}(b) = p\) となるような値 \(b\) に増加させるため \(I2(p)\) は真のままである。全く新しい要素が \(\mathfrak{B}\) に追加されるのは Start Polling アクションによるものだけである。\(I2(p)\) の最初の論理積とアクションの仕様は、この新しい要素を追加しても \(I2(p)\) の 2 つ目の論理積が偽とならないことを意味する。\(\mathfrak{B}\) が変更される唯一の方法は、ある \(B \in \mathfrak{B}\) に対して \(B_{vot}\) に新しい司祭を追加することであり、これは \(I2(p)\) に影響を与えない。∎
Proof Sketch for \(I3(p)\). \(\mathfrak{B}\) から票が削除されることはないため、\({\it MaxVote}(\infty,p,\mathfrak{B})\) を変更することができる唯一のアクションは、\(p\) の投じた票を \(\mathfrak{B}\) に追加するアクションである。Receive BeginBallot Message のみがそれを行うことができ、そのアクションだけが \({\it prevBal}[p]\) と \({\it prevDec}[p]\) を変更することができる。\(I7\) の BeginBallot 論理積は、このアクションが実際に \(\mathfrak{B}\) に票を追加することを意味し、\(B1(\mathfrak{B}\) (\(I6\) の最初の論理積) は表を追加できる票決が一つだけであることを意味する。有効化条件、アクションを実行する前に \(I3(p)\) が成立しているという仮定、\({\it MaxVote}\) の定義から、アクションは \(I3(p)\) の最初の 2 つの論理積を真のままにするということになる。\({\it prevBal}[p]\) は \({\it nextBal}[p]\) に設定することでのみ変更され、\({\it nextBal}[p]\) が減少することはないため、3 つ目の論理積は真のままとなる。∎
Proof Sketch for \(I4(p)\). この論理積は \({\it status}[p]\)、\({\it prevVotes}[p]\)、\({\it lastTried}[p]\)、何名かの司祭 \(q\) に対する \({\it nextBal}[q]\)、\(\mathfrak{B}\) に値にのみ依存する。\({\it status}[p]\) は Try New Ballot アクションによってのみ \({\it idle}\) から非 \({\it idle}\) に変更され、これは \({\it prevVotes}[p]\) を \(\emptyset\) に設定し、\(I4(p)\) は空虚に真 (vacuously true)となる。\({\it prevVotes}[p]\) を変更する他のアクションは、\({\it status}[p]\) を \({\it idle}\) に設定するため \(I4(p)\) を真のままにする Forget アクションと、Receive LastVote Message アクションだけである。有効化条件と \(I7\) の \({\it LastVote}\) 論理積から Receive LastVote Message アクションが \(I4(p)\) を保持することがわかる。\({\it lastTried}[p]\) の値は Try New Ballot アクションによってのみ変更され、\({\it status}[p]\) を \({\it trying}\) に設定するため \(I4(p)\) は真のままである。\({\it nextBal}[q]\) の値は増加するだけなので \(I4(p)\) を偽にすることはできない。最後に \({\it MaxVote}({\it lastTried}[p], v_{pst}, \mathfrak{B})\) は、\(B_{bal} \lt {\it lastTried}[p]\) を持つある \(B \in \mathfrak{B}\) に対して、\(B_{vot}\) に \(v_{pst}\) が追加された場合にのみ変更できる。しかし (Receive BeginBallot Message によって) \(v_{pst}\) が \(B_{vot}\) に追加されるのは \({\it nextBal}[v_{pst}] = B_{bal}\) の場合のみであり、この場合 \(I4(p)\) は \(B_{bal} \ge {\it lastTried}[p]\) を意味している。∎
Proof Sketch for \(I5(p)\). \({\it status}[p]\) は Start Polling アクションによってのみ \({\it polling}\) に設定される。このアクションの有効化条件は、最初の論理積が真になることを保証し、2 つ目の論理積を真にする票決を \(\mathfrak{B}\) に追加する。他のアクションでは \({\it status}[p]\) を \({\it polling}\) と等しいままで \({\it quorum}[p]\)、\({\it decree}[p]\)、\({\it lastTried}[p]\) を変更することはできない。\({\it prevVote}[p]\) の値は \({\it status}[p]={\it polling}\) の間は変更できず、\(\mathfrak{B}\) は新しい要素を追加するか、\(B_{vot}\) に新しい司祭を追加することによってのみ変更される。\(I5(p)\) を偽にする唯一残された可能性は、Receive Voted Message アクションによって \({\it voters}[p]\) に新しい要素が追加されることである。\(I7\) の \({\it Voted}\) 論理積、\(B1(\mathfrak{B})\) (\(I6\) の最初の論理積)、およびアクションの有効化条件は、\({\it voters}[p]\) に追加された要素が \(B_{vot}\) であることを意味し、\(B\) は \(I5(p)\) で存在が主張されている票決である。∎
Proof Sketch for \(I6\). \(B_{bal}\) と \(B_{qrm}\) はどの \(B \in \mathfrak{B}\) に対しても変更されることはないので、\(B1(\mathfrak{B})\)、\(B2(\mathfrak{B})\)、そして \(I6\) の 2 つ目の論理積が偽となる唯一の方法は、\(\mathfrak{B}\) に新しい票決を追加することであり、それは \({\it status}[p]\) が \({\it trying}\) と等しいときに Start Polling Majority Set \(Q\) アクションによってのみ行われる。\(I2(p)\) の 2 つ目の論理積から、このアクションは \(B1(\mathfrak{B})\) を真のままにしておくことができる。また有効化条件で \(Q\) が過半数集合であると主張していることから、このアクションは \(B2(\mathfrak{B})\) と \(I6\) の 2 つ目の論理積を真のままにしておくことができる。\(B3(\mathfrak{B})\) を偽とするには、\(\mathfrak{B}\) に新しい票を追加して \({\it MaxVote}(B_{bal},B_{qrm},\mathfrak{B})\) を変更する方法と、\(\mathfrak{B}\) に新しい票決を追加する方法の 2 つが考えられる。新しい票は Receive BeginBallot Message アクションによってのみ追加されるが、\(I3(p)\) はアクションが \(\mathfrak{B}\) で \(p\) が投じた他の票よりも後に票を追加することを暗示しているため、\(\mathfrak{B}\) の任意の \(B\) に対して \({\it MaxVote}(B_{bal},B_{qrm},\mathfrak{B})\) を変更することはできない。論理積 \(I4(p)\) は Start Polling アクションによって追加された新しい票決が \(B3(\mathfrak{B})\) を偽としないことを意味している。∎
Proof Sketch for \(I7\). \(I7\) は、\(\mathcal{M}\) に新しいメッセージを追加するか、\(I7\) が依存している他の変数の値を変更することで偽にすることができる。\({\it lastTried}[p]\) と \({\it nextBal}[p]\) が減少することはないため、これらを変更しても \(I7\) を偽にすることはできない。\({\it outcome}[p]\) は、その値が \({\rm BLANK}\) でなければ変化することはないため、これを変化させて \(I7\) を偽にすることはできない。\(\mathfrak{B}\) は票決の追加と票の追加によってのみ変更されるため、\(I7\) を偽にできる唯一の変更は \(v_{pst}\) による票の追加で、\({\it MaxVote}(b,v_{pst},\mathfrak{B})\) を変更して \({\it LastVote}(b,v)\) の論理積を偽にすることである。これは \(v_{pst}\) が \(B_{bal} \lt b\) であるような票決 \(B\) に投票するときのみ起きる。しかし、\(v_{pst}\) は票決番号 \({\it nextBal}[v_{pst}]\) にしか投票することができず、この論理積が最初に成立するという仮定は \({\it nextBal}[v_{pst}] \ge b\) を意味している。したがって、送信されるすべてのメッセージが \(I7\) の適切な論理積の条件を満たすことだけを確認すればよい。
- NextBallot: Send NextBallot Message アクションの定義と \(I2(p)\) の最初の論理積から導かれる。
- LastVote: Send LastVote Message アクションの優子か条件と \(I3(p)\) は \({\it MaxVote}({\it nextBal}[p], p, \mathfrak{B}) = {\it MaxVote}(\infty, p, \mathfrak{B})\) であることを意味している。このことから、アクションが送信する LastVote メッセージは \(I7\) の条件を満たしていることがわかる。
- BeginBallot: \(I5(p)\) と Send BeginBallot Message アクションの定義に従う。
- Voted: \(I3(p)\)、\({\it MaxVote}\) の定義、Send Voted Message アクションの定義に従う。
- Success: Send Success Message の定義に従う。∎
- 15多重集合は同じ要素の複数のコピーを含む可能性のある集合。
 ACKNOWLEDGEMENTS
ACKNOWLEDGEMENTS
Daniel Duchamp pointed out to me the need for a new state machine implementation. Discussions with Martín Abadi, Andy Hisgen, Tim Mann, and Garret Swart led me to Paxos. \(\Lambda\epsilon\omega\nu\acute{\iota}\delta\alpha\varsigma\) \(\Gamma\kappa\acute{\iota}\mu\pi\alpha\varsigma\) provided invaluable assistance with the Paxon dialect.
 REFERENCES
REFERENCES
- BERNSTEIN, P. A., HADZILACOS, V., AND GOODMAN, N. 1987. Concurrency Control and Recovery in Database Systems. Addison-Wesley Longman Publ. Co., Inc., Reading, MA.
- DE PRISCO, R., LAMPSON, B., AND LYNCH, N. 1997. Revisiting the Paxos algorithm. In Proceedings of the 11th International Workshop on Distributed Algorithms, M. Mavronicolas and P. Tsigas, Eds., Lecture Notes in Computer Science, vol. 1320. Springer-Verlag, Berlin, Germany, 111–125.
- DIJKSTRA, E. W. 1974. Self-stabilizing systems in spite of distributed control. Commun. ACM 17, 11, 643–644.
- DWORK, C., LYNCH, N., AND STOCKMEYER, L. 1988. Consensus in the presence of partial synchrony. J. ACM 35, 2 (Apr.), 288–323.
- FEKETE, A., LYNCH, N., AND SHVARTSMAN, A. 1997. Specifying and using a partitionable group communication service. In Proceedings of the 16th Annual ACM Symposium on Principles of Distributed Computing. ACM Press, New York, NY, 53–62.
- FISCHER, M. J., LYNCH, N. A., AND PATERSON, M. S. 1985. Impossibility of distributed consensus with one faulty process. J. ACM 32, 1 (Jan.), 374–382.
- GRAY, C. AND CHERITON, D. 1989. Leases: An efficient fault-tolerant mechanism for distributed file cache consistency. SIGOPS Oper. Syst. Rev. 23, 5 (Dec. 3–6), 202–210.
- KEIDAR, I. AND DOLEV, D. 1996. Efficient message ordering in dynamic networks. In Proceedings of the 15th Annual ACM Symposium on Principles of Distributed Computing. ACM Press, New York, NY.
- LADIN, R., LISKOV, B., SHRIRA, L., AND GHEMAWAT, S. 1992. Providing high availability using lazy replication. ACM Trans. Comput. Syst. 10, 4 (Nov.), 360–391.
- LAMPORT, L. 1978. Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21, 7, 558–565.
- LAMPORT, L. 1984. Using time instead of timeout for fault-tolerant distributed systems. ACM Trans. Program. Lang. Syst. 6, 2 (Apr.), 254–280.
- LAMPSON, B. W. 1996. How to build a highly available system using consensus. In Distributed Algorithms, O. Babaoglu and K. Marzullo, Eds. Springer Lecture Notes in Computer Science, vol. 1151. Springer-Verlag, Berlin, Germany, 1–17.
- OKI, B. M. AND LISKOV, B. H. 1988. Viewstamped replication: A general primary copy. In Proceedings of the 7th Annual ACM Symposium on Principles of Distributed Computing (Toronto, Ontario, August 15-17, 1988). ACM Press, New York, NY, 8–17.
- SCHNEIDER, F. B. 1990. Implementing fault-tolerant services using the state machine approach: A tutorial. ACM Comput. Surv. 22, 4 (Dec.), 299–319.
- SKEEN, M. D. 1982. Crash recovery in a distributed database system. Ph.D. thesis. University of California at Berkeley, Berkeley, CA.
翻訳抄
Paxos に関する 1998 年の論文。戯曲めいた説明がしばしば理解を阻害すると言われるので Paxos Made Simple (2001) をあわせて読むと良い。Paxos 島やその議会は Lamport によるフィクションで実在しない。文中のギリシャ文字で表記されている登場人物は実在する計算機科学者のオマージュのようである。以下に推測で該当者を示す。
| ギリシャ文字表記 | アルファベット対応 | 人名/意味 | 配役 |
|---|---|---|---|
| \(\majority\) | madzthōritiōet | majority | 過半数 (定足数) |
| \(\Dijkstra\) | Dikōtra | Edsger W. Dijkstra [3] | 厳しすぎるチーズ検査官 |
| \(\Dolev\) | Dōlef | Danny Dolev [8] | 白以外のヤギを多く飼う農夫 |
| \(\Dwork\) | Dphōrk | Cynthia Dwork [4] | 月曜に "125:オリーブの日" を可決 |
| \(\Fischer\) | Fisther | Michael J. Fischer [6] | "132:ランプはオリーブオイルのみ" を可決 |
| \(\Lampson\) | Lampsōn | Butler Lampson [2] [12] | クーデターを起こす |
| \(\Liskov\) | Liskōf | Barbara Liskov [9] [13] | 金羊毛の関税で質問 |
| \(\Lynch\) | Linchth | Nancy Lynch [2] [4] [5] [6] | "155:オリーブ税は1トンあたり3ドラクマ" を台帳に記入 |
| \(\Oki\) | Ōki | Brian Oki [13] | 半年の休暇直後に議長に任命 |
| \(\Schneider\) | Sthnider | Fred B. Schneider [14] | オリーブ税額問い合わせを提案 |
| \(\Skeen\) | Skeen | Dale Skeen [15] | Dolev から茶色いヤギを飼う商人 |
| \(\Stockmeyer\) | Stōkmeir | Larry Stockmeyer [4] | Skeen から問い合わせを受けた議員 |
| \(\dzifi\) | dzthiphi | jiffy (ちょっとの間) | Paxon時間単位 |
| \(\Parnaz\) | Parnas | David Parnas | 世襲議員の息子 |
| \(\Toyer\) | Tōueg | Sam Toueg | 落下物で記憶喪失 |
| \(\Gray\) | Grai | Cary Gray [7] または Jim Gray | 票決を辞書順にする例 |
| \(\Lindsay\) | Linsei | おそらく Bruce G. Lindsay | 票決を辞書順にする例 |
| \(\Gwysa\) | Gōuda | M. Gopal Gouda | Dijkstra に代わるチーズ検査官 |
| \(\Fransez\) | Fransez | Nissim Francez | ワインテスター |
| \(\Pnueli\) | Pnueli | Amir Pnueli | ワインテスター |
| \(\Greez\) | Grees | David Gries | オリーブ税で問い合わせ |
| \(\Strong\) | Strōng | H. Raymond Strong | 新しく参加する議員 |
| \(\Lambda\epsilon\omega\nu\acute{\iota}\delta\alpha\varsigma\) \(\Gamma\kappa\acute{\iota}\mu\pi\alpha\varsigma\) | Leonidas Gkimpas | Leonidas J. Guibas | 謝辞 |
- L. Lamport. The Part-Time Parliament, In ACM Transactions on Computer Systems 16, 2 (May 1998), 133-169. Minor corrections were made on 29 August 2000.

