論文翻訳: Practical Byzantine Fault Tolerance

Abstract

この論文では Byzantine 障害に堪えることのできる新しい複製アルゴリズムについて説明する。悪意のある攻撃やソフトウェアエラーがますます一般的になり故障ノードに任意の動作をさせる可能性があるため Byzantine 障害耐性アルゴリズムは今後ますます重要になると考えられる。これまでのアルゴリズムは同期システムを想定したか、実際に使用するには遅すぎたのに対して、この論文で説明するアルゴリズムは実用的である: インターネットのような非同期環境で動作し、過去のアルゴリズムの応答速度を 1 桁以上に改善するいくつかの重要な最適化を組み込んでいる。我々はこのアルゴリズムを使って Byzantine-fault-tolerant NFS サービスを実装しその性能を測定した。その結果、我々のサービスは標準の複製されていない NFS よりわずか 3% 遅いことが分かった。

Table of Contents

1. Abstract
2. Introduction
3. 2 System Model
4. 3 Service Properties
5. 4 The Algorithm
   1. 4.1 The Client
   2. 4.2 Normal-Case Operation
   3. 4.3 Garbage Collection
   4. 4.4 View Changes
   5. 4.5 Correctness
      1. 4.5.1 Safety
      2. 4.5.2 Liveness
   6. 4.6 Non-Determinism
6. 5 Optimizations
   1. 5.1 Reducing Communication
   2. 5.2 Cryptography
7. 6 Implementation
   1. 6.1 The Replication Library
   2. 6.2 BFS: A Byzantine-Fault-tolerant File System
   3. 6.3 Maintaining Checkpoints
   4. 6.4 Computing Checkpoint Digests
8. 7 Performance Evaluation
   1. 7.1 Experimental Setup
   2. 7.2 Micro-Benchmark
   3. 7.3 Andrew Benchmark
9. 8 Related Work
10. 9 Conclusions
11. Acknowledgements
12. References
13. 翻訳抄

Introduction

悪意のある攻撃やソフトウェアエラーはますます一般的になっている。産業や政府によるオンライン情報サービスへの依存度の高まりにより、悪意のある攻撃はより魅力的になり、攻撃が成功した場合の影響はさらに深刻となっている。さらに、ソフトウェアエラーの数はソフトウェアのサイズの増大と複雑さのために増加している。悪意のある攻撃やソフトウェアエラーは故障したノードに Byzantine (すなはち任意障害) の振る舞いを見せることがあることから Byzantine 耐性アルゴリズムはますます重要となっている。

この論文では Byzantine 障害を許容するステートマシンレプリケーション [17, 34] の新しい実用的アルゴリズムを紹介する。このアルゴリズムは合計 \(n\) 個のレプリカのうち最大で \(\lfloor \frac{n-1}{3} \rfloor\) 個が同時に故障している場合でも Liveness と Safety の両方を提供する。つまり、クライアントは最終的に自分の要求に対する応答を受け取り、それらの応答は線形化可能性 (linearizability) [14, 4] に従って正しいということである。このアルゴリズムはインターネットのような非同期システムで機能し、効率的に実行するための重要な最適化を組み込んでいる。

Byzantine 障害を許容する合意と複製の技術に関する研究はとても多く存在する ([19 から始まる)。最も初期の研究は (例えば [3, 24, 10]) どれも実際に使用するにはあまりにも非効率的であったり、同期、つまりメッセージ遅延やプロセス速度の限界に関して既知であると仮定しており、理論の実現可能性を実証するように設計された技術に関するものであった。我々のシステムに最も近い Rampart [30] や SecureRing [16] は実用的に設計されているが correctness に対して同期性を仮定することに頼っており、悪意のある攻撃が存在する場合に危険である。攻撃者は故障とタグ付けされレプリカグループから除外されるまでの間、非故障ノードやノード間の通信を遅らせることによってサービスの Safety を危うくすることができる。通常、このような DoS 攻撃は非故障ノードの制御を試みるよりも簡単である。

我々のアルゴリズムは Safety に対して同期性に頼っていないためこのタイプの攻撃に対して脆弱ではない。さらにセクション 7 で説明するようにRampart と SecureRing のパフォーマンスを一桁以上向上させる。read-only 操作の実行には 1 回、read-write 操作には 2 回のメッセージラウンドトリップのみを使用する。また、通常操作としてメッセージ認証コードに基づく効率的な任所方法を使用する; Rampart の主な遅延 [29] とスループット [22] ボトルネックとして挙げられていた公開鍵暗号は障害があった場合にのみ使用される。

我々のアプローチを評価するために、我々はレプリケーションライブラリを作成し実際のサービス: NFS プロトコルをサポートする Byzantine-fault-tolerant 分散ファイルシステムを実装するために使用した。我々はシステムの性能を評価するために Andrew ベンチマーク [15] を使用した。その結果、通常の操作では Digital Unix カーネルの標準 NFS デーモンよりわずか 3% 遅いことが示された。

従ってこの論文では次のような寄稿を行う:

• 非同期ネットワークで Byzantine 障害を正しく解決した最初のステートマシンレプリケーションプロトコルについて説明する。
• 実際のシステムで使用できるように、アルゴリズムがうまく機能できるための重要な最適化について説明する。
• Byzantine-fault-tolerant 分散ファイルシステムの実装について説明する。
• レプリケーション技術のコストを定量化する実験結果を提供する。

本稿の残りの分は次のように構成されている。我々は障害の仮定を含むシステムモデルを説明することから始める。セクション 3 ではアルゴリズムによって解決される問題を説明し correctness 条件を述べる。アルゴリズムについてはセクション 4 で説明しいくつかの重要な最適化についてはセクション 5 で説明する。セクション 6 では、我々のレプリケーションライブラリと、それを使って Byzantine-fault-tolerant NFS を実装する方法について説明する。セクション 7 で我々の実験結果を示す。セクション 8 では関連作業について論議し、最後に我々が達成したことのまとめと今後の研究の方向性について論議する。

2 System Model

ノードがネットワークによって接続されている非同期分散システムを想定する。ネットワークはメッセージの配信に失敗したり、遅延したり、重複させたり、あるいは順序を入れ違えて配信する可能性がある。

我々は Byzantine 障害モデルを使用する。つまり、故障したノードは以下に言及する制約のみに従う任意の振る舞いを行うことができる。我々は独立したノード障害を仮定する。悪意のある攻撃が存在する場合にこの仮定が当てはまるにはいくつかのステップが必要となる。例えば各ノードはサービスコードとオペレーティングシステムの異なる実装で実行し、異なる root パスワードと異なる管理者を持つべきである。同じコードベース[28]から異なる実装を取得することが可能であるし、複製の度合いが低い場合は異なるベンダーからオペレーティングシステムを購入することができる。\(N\)-バージョンプログラミング、すなはち異なるプログラマチームが異なる実装を提供することはいくつかのサービスにとって別のオプションである。

我々はなりすましやリプレイ攻撃を防ぎメッセージの破損を検出するために暗号化技術を使用している。我々のメッセージは公開鍵署名[33]、メッセージ認証コード[36]、そして衝突耐性ハッシュ関数[32]によって生成されたメッセージダイジェストを含んでいる。ノード \(i\) によって署名されたメッセージ \(m\) を \(\langle m \rangle_{\sigma_i}\)、メッセージ \(m\) のダイジェストを \(D(m)\) と表す。メッセージ全体に署名するのではなく、メッセージのダイジェストに署名し、それをメッセージの平文に追加するという一般的な慣習に従う (\(\langle m \rangle_{\sigma_i}\) はそのように解釈する必要がある)。全てのレプリカは署名を検証するために他の公開鍵を知っている。

我々は、レプリケーションサービスに最大の損害を与えるために欠陥のあるノードを調整し通信を遅らせる、あるいは正しいノードを遅らせることのできる非常に強力な敵対者を許容する。我々は敵対者が正しいノードを無制限に遅らせることができないと仮定する。また、敵対者 (およびそれが支配する障害ノード) は (非常に高い確率で) 上記の暗号技術を突破することができないような計算上の上限があると仮定する。例えば、攻撃者は非故障ノードの有効な署名を生成したり、ダイジェスト値からダイジェストで要約された情報を算出したり、同じダイジェスト値となる 2 つのメッセージを見つけることはできない。我々が使用する暗号化技術はこれらの特性を持っていると考えられている[33, 36, 32]。

3 Service Properties

我々のアルゴリズムは状態といくつかの操作に基づいて決定論的なレプリケーションサービスを実装するために使うことができる。操作はサービス状態の一部の単純な読み書きには制限されていない; それらは状態と操作の引数を使用して任意の決定論的演算を実行できる。クライアントはレプリケーションサービスの操作を呼び出すためにリクエストを発効し、応答を待つあいだブロックする。レプリケーションサービスは \(n\) 個のレプリカによって実装される。クライアントとレプリカがセクション 4 のアルゴリズムに従い、攻撃者がそれらの署名を偽造できなければ、それらは非故障である。

このアルゴリズムは \(\lfloor \frac{n-1}{3} \rfloor\) 以下のレプリカが故障していると仮定し Safety と Liveness を提供する。Safety とはレプリケーションサービスが (Byzantine 障害クライアント[4]を考慮して修正された) 線形可能性[14] (linearizability) を満たすことを意味する: これは、一度に 1 つずつの操作をアトミックに実行する集中型の実装のように動作する。故障したレプリカは任意に振る舞う可能性がある。例えば、その状態を破壊する可能性があるため、Safety は故障したレプリカの数の制限を必要とする。

どれだけの障害クライアントがサービスを利用しても Safety は確保される (たとえそれらが故障したレプリカと共謀したとしても): 障害のあるクライアントによって実行されるすべての操作は、障害のないクライアントによって一貫した方法で監視される。特に、サービス操作がサービス状態に関するいくつかの不変性を保持するように設計されている場合、障害のあるクライアントはそれらの不変性を破ることができない。

Safety は障害クライアントに対して防護するには不十分であり、例えばファイルシステムにおいて障害クライアントが何らかの共有ファイルにごみデータを書き込むことができる。しかし、我々はアクセス制御を提供することで障害クライアントのもたらす事のできる損害の量を制限する: リクエストを発行したクライアントに操作を呼び出す権限がない場合、我々はクライアントを認証してアクセスを拒否する。また、サービスはクライアントに対するアクセス許可を変更するための操作を提供することができる。個のアルゴリズムはアクセス取り消し捜査の影響がすべてのクライアントによって一貫して観測されることを保証するため、これは欠陥のあるクライアントによる攻撃から回復するための強力なメカニズムを提供する。

アルゴリズムは safety を提供するために同期性には依存しない。従って、liveness を提供するために同期生に頼らなければならない; さもなくば非同期システムでコンセンサスを実装するために使用することができ、これは不可能である[9]。我々は、最大で \(\lfloor \frac{n-1}{3} \rfloor\) 個のレプリカ故障を許容し、遅延が \(t\) より無制限に速く成長しないという条件で、我々は liveness、つまりクライアントがそのリクエストに対して最終的に応答を受け取ることを保証する。ここで \({\rm delay}(t)\) は (送信者がメッセージの受信が行われるまで再送信し続けると仮定して) メッセージが最初に送信される瞬間 \(t\) とそれが送信先で受信されるまでの間の時間を示す。(より正確な定義は[4]で見つけることができる。) ネットワーク障害が最終的に修理されるのであれば、どんな現実のシステムでも真であると感じられるかなり弱い同期性だが、それは我々が不可能な結果を回避することを可能にする[9]。

我々のアルゴリズムの resiliency は最適である: \(3f+1\) は \(f\) 個までのレプリカが故障しているとき非同期システムが safety と liveness を提供することのできる最小数のレプリカである (証明は[2])。\(f\) 個のレプリカが故障し応答しない可能性があるとき、\(n-f\) 個のレプリカと通信した後で処理を進めることができなければならないためこのような多くのレプリカが必要となる。しかし、応答しなかった \(f\) 個のレプリカが故障ではなく、従って応答した \(f\) 個の方が故障である可能性がある。そうであっても故障のないレプリカからのものが故障したレプリカからのものより多い、すなはち \(n-2f \gt f\) の十分な応答が存在しなければならない。従って \(n \gt 3f\) である。

このアルゴリズムはフォールトトレラントなプライバシー問題に対処しない: 故障レプリカは攻撃者に情報を漏らす可能性がある。サービス操作はそれらの引数とサービス状態を使用して任意の計算を実行することができるため、一般的なケースではフォールトトレラントなプライバシーを提供することは実現不可能である; レプリカはこのような操作を効率的に実行するために明確に必要とする。秘密共有方式[35]を使用することで、サービス操作に対して不透明な状態の引数と部分に対する悪意のある複製の閾値[13]が存在する場合でもプライバシーを得ることができる。将来的にこれらの手法を調査することを計画している。

4 The Algorithm

我々のアルゴリズムはステートマシンレプリケーション[17, 34]の方式である: サービスは分散システムの異なるノードにまたがってレプリケーションされるステートマシンとしてモデル化される。各ステートマシンレプリカはサービス状態を保持しサービス操作を実装する。レプリカの集合を \(\mathcal{R}\) とし、\(\{1,\ldots,|\mathcal{R}|-1\}\) の整数を使って各レプリカを識別する。単純化のために我々は \(|\mathcal{R}|=3f+1\) と仮定する。ここで \(f\) は故障しても良いレプリカの最大数である; \(3f+1\) を超えるレプリカが存在することもできるが、追加のレプリカは resiliency を改善することなくパフォーマンスを劣化させる (より多く大きいメッセージが交換されるため)。

レプリカはビューと呼ばれる一連の構成を移動する。1つのビューの中では一つのレプリカがプライマリでそのほかはバックアップである。ビューには連続した番号が付けられる。ビューのプライマリは \(p=v \mod |\mathcal{R}|\) となるレプリカ \(p\) である。ここで \(v\) はビューの番号である。プライマリがフェイルしたと思われるときにビュー変更が発生する。Viewstamped Replication [26] と Paxos [18] は良性の障害を許容するために同様のアプローチを使用している (セクション 8 で説明する)。

アルゴリズムはおおよそ以下のように機能する:

1. クライアントはサービス操作を呼び出す要求をプライマリに送信する。
2. プライマリは要求をバックアップにマルチキャストする。
3. レプリカは要求を実行してクライアントに応答を送信する。
4. クライアントは同じ結果を持つ異なる \(f+1\) 個のレプリカからの応答を

すべてのステートマシンレプリケーション手法[34]と同様に我々はレプリカに 2 つの要件を課している: それらは決定論的ではならず (つまり与えられた状態において与えられた引数の集合での操作の実行が常に同じ結果をもたらさなければならない)、そしてそれらは同一の状態から始まらなければならない。これらの 2 つの要件が与えられると、アルゴリズムはすべての非故障レプリカが失敗にもかかわらず要求の実行に対して全順序で合意することを保証することによって Safety を保証する。

このセクションの残りの部分ではアルゴリズムの簡素化されたバージョンを説明する。ノードがスペース不足の障害から回復する方法についての説明は省略する。さらに、メッセージ認証はメッセージ認証コードに基づくより効率的な方法ではなくデジタル署名を使用して達成されると想定してる; セクション 5 でこの問題についてさらに説明する。I/O オートマトンモデル [21] を使ったアルゴリズムの詳細な定式化は [4] に示されている。

4.1 The Client

クライアント \(c\) は \(\langle {\rm REQUEST},o,t,c \rangle_{\sigma_c}\) メッセージをプライマリに送信することによってステートマシン操作 \(o\) の実行を要求する。タイムスタンプ \(t\) はクライアントリクエストの実行に対して exactly-once セマンティクスを保証するために使用される。\(c\) のリクエストに対するタイムスタンプは、遅いリクエストが早いリクエストより高いタイムスタンプを持つように完全に順位付けられている; 例えばタイムスタンプはリクエストが発行されたときのクライアントのローカルクロック値でよい。

レプリカによってクライアントに送信されるそれぞれのメッセージは現在のビュー番号を含んでおり、クライアントがビューつまり現在のプライマリを追跡できるようにする。クライアントは point-to-point メッセージを使用して現在のプライマリと判断したものに対して要求を送信する。プライマリは自動的に、次のセクションで詳述するプロトコルを使用してすべてのバックアップにリクエストをマルチキャストする。

レプリカはリクエスト対して応答を直接クライアントに送信する。応答の形式は \(\langle {\rm REPLY},v,t,c,i,r \rangle_{\sigma_i}\) であり \(v\) は現在のビュー番号、\(t\) は対応するリクエストのタイムスタンプ、\(i\) はレプリカ番号、\(r\) はリクエストされた操作の実行結果である。

クライアントは \(r\) を受け入れる前に、異なるレプリカから有効な署名と同一の \(t\) および \(r\) を持つ \(f+1\) 応答を待機する。これは多くても \(f\) 個のレプリカが故障できるため結果が有効であることを保証する。

クライアントが十分に早く応答を受け取らなかった場合、すべてのレプリカにリクエストをブロードキャストする。もしリクエストが既に処理されているのであれば、レプリカは応答を単純に再送信する; レプリカは応答した最後のメッセージをクライアントごとに覚えている。そうでなく、もしレプリカがプライマリではなければプライマリにリクエストを中継する。もしプライマリがグループにリクエストをマルチキャストしなければ、ビュー変更を引き起こすのに十分なレプリカによって最終的にそれが故障していると想定される。

この論文では、我々はあるリクエストが完了するまで次のリクエストの送信を待機するクライアントを想定する。しかし、クライアントが非同期リクエストを行えるようにしながら、そのリクエストに対する順序の制約を保持することができる。

4.2 Normal-Case Operation

各レプリカの状態には、サービスの状態とレプリカが受け取っているメッセージを含んでいるメッセージログ、レプリカの現在のビューを示す整数が含まれている。セクション 4.3 でログを切り捨てる方法について記述する。

プライマリ \(p\) がクライアントリクエスト \(m\) を受信すると、自動的にレプリカにそのリクエストをマルチキャストすることで 3-フェーズプロトコルを開始する。プライマリはプロトコル処理中のメッセージ数が既定の最大数を超えない限り直ちにプロトコルを開始する。このとき、リクエストをバッファリングする。バッファリングされたリクエストは、高負荷下でのメッセージトラフィックと CPU オーバーヘッドを削減するために後でグループとしてマルチキャストされる; この最適化はトランザクションシステム [11] におけるグループコミットと類似している。簡略化のため以下ではこの最適化については省略する。

3つのフェーズは pre-prepare, prepare, commit である。pre-prepare および prepare は、リクエストの順序付けを提案しているプライマリが故障したときでも、同一のビューで送信されたリクエストを完全に順序付けるために使用される。prepare と commit フェーズはコミットされたリクエストがビュー間で完全に順序付けられていることを確認するために使用される。

pre-prepare フェーズにおいて、プライマリはリクエストにシーケンス番号 \(n\) を割り当て、\(m\) を乗せた pre-prepare メッセージをすべてのバックアップにマルチキャストし、そのログにメッセージを追加する。このメッセージは \(\langle\langle {\rm PRE-PREPARE},v,n,d\rangle_{\sigma_p},m\rangle\) の形式をもつ。ここで \(v\) はメッセージが送信されたビューを示し、\(m\) はクライアントのメッセージ、\(d\) は \(m\) のダイジェストである。

メッセージを小さくするために pre-prepare メッセージにはリクエストは含まれていない。これはビュー変更においてビュー \(v\) のリクエストにシーケンス番号 \(n\) が割り当てられたことを証明するために、pre-prepare メッセージが使用されるため重要である。さらに、これはリクエストをレプリカに転送するプロトコルと、リクエストを完全に順序付けるプロトコルとを分離する; プロトコルメッセージには小さなメッセージに最適化されたトランスポート層を使用し、大きなリクエストには大きなメッセージに最適化されたトランスポート層を使用することができる。

バックアップは以下に提供される pre-prepare メッセージを受け入れる:

• リクエストと pre-prepare メッセージの署名が正しく \(d\) が \(m\) に対するダイジェストである。
• 現在、ビュー \(v\) である。
• 同一のビュー \(v\) とシーケンス番号 \(n\) を持ち異なるダイジェスト値を含む pre-prepare メッセージを受付済みではない。
• pre-prepare メッセージのシーケンス番号が最低水準 \(h\) と最高水準 \(H\) の間にある。

最後の条件は、故障したプライマリが非常に大きなシーケンス番号を選択することによってシーケンス番号の空間を使い果たすことを防止する。我々は \(H\) と \(h\) がどのように進展するかについてセクション 4.3 で論議する。

バックアップ \(i\) が \(\langle\langle {\rm PRE-PREPARE},v,n,d\rangle_{\sigma_p},m\rangle\) メッセージを受け入れると他のすべてのレプリカに \(\langle{\rm PREPARE},v,n,d,i\rangle_{\sigma_i}\) メッセージをマルチキャストすることで prepare フェーズに入り、両方のメッセージをログに追加する。そうでなければ何もしない。

(プライマリを含む) レプリカは prepare メッセージを受け入れ、署名が正しく、ビュー番号がそのレプリカの現在のビュー番号と一致し、シーケンス番号が \(h\) と \(H\) の間であればそれらをログに追加する。

レプリカ \(i\) がログに挿入している場合に限り true となる判定式 \({\it prepared}(m,v,n,i)\) を定義する: リクエスト \(m\)、ビュー \(v\) のシーケンス番号 \(n\) を持つ \(m\) に対する pre-prepare、そして pre-prepare と一致する、異なるバックアップからの \(2f\) 個の prepare を。レプリカは、prepare が pre-prepare が同じビュー、シーケンス番号、ダイジェストを持つことをチェックすることで一致するかを検証する。

アルゴリズムの pre-prepare と prepare フェーズはビュー内で非故障レプリカがリクエストに対する完全な順序で合意することを保証する。より正確にはそれらは以下の不変条件を保証する: もし \({\it prepared}(m,v,n,i)\) が true ならば、任意の非故障レプリカ \(j\) (\(i=j\) を含む) かつ \(D(m') \neq D(m)\) である任意の \(m'\)に対して \({\it prepared}(m',v,n,j)\) は false である。これは \({\it prepared}(m,v,n,i)\) と \(|\mathcal{R}|=3f+1\) は少なくとも \(f+1\) の非故障レプリカがビュー \(v\) 内でシーケンス番号 \(n\) の \(m\) に対する pre-prepare または prepare を送信したことを示しているため真である。従って \({\it prepared}(m',v,n,j)\) が true であるためにはそれらのレプリカの少なくとも一つが 2 つの矛盾した prepare (または \(v\) のプライマリの場合は pre-prepare)、つまり同じビューとシーケンス番号と異なるダイジェストを持つ 2 つの prepare を送信する必要がある。しかしレプリカが故障していないためこれは不可能である。最後に、メッセージダイジェストの強度に関する我々の仮定は \(m \ne m'\) において \(D(m)=D(m')\) である確率が無視できることを保証している。

\({\it prepared}(m,v,n,i)\) が true となるとレプリカ \(i\) は \(\langle{\rm COMMIT},v,n,D(m),i\rangle_{\sigma_i}\) をほかのレプリカにマルチキャストする。これは commit フェーズを開始する。レプリカは適切に署名され、メッセージ内のビュー番号がレプリカの現在のビューと一致し、シーケンス番号が \(h\) から \(H\) の間であれば commit メッセージを受け入れてログに挿入する。

我々は判定式 \({\it committed}\) と \({\it committed\_local}\) を次のように定義する: ある \(f+1\) 個の非故障レプリカ集合でのすべての \(i\) に対して \({\it prepared}(m,v,n,i)\) が true であれば \({\it committed}(m,v,n)\) は true である; \({\it prepared}(m,v,n,i)\) が true であり、\(m\) に対する pre-prepared と一致する異なるレプリカからの \(2f+1\) 個の commit (おそらく自身を含む) を受け入れているならば \({\it committed\_local}(m,v,n,i)\) は true である; 同一のビュー、シーケンス番号、ダイジェストを持つとき commit は pre-prepare と一致する。

commit フェーズでは次のような不変条件が保証される: もしある非故障 \(i\) に対して \({\it committed\_local}(m,v,n,i)\) が true ならば \({\it committed}(m,v,n)\) は true である。この不変条件とセクション 4.4 で説明するビュー変更プロトコルにより、非故障レプリカは、レプリカごとに異なるビューでコミットされる場合でも、ローカルでコミットされるリクエストのシーケンス番号で合意することを保証する。さらに、非故障レプリカのローカルにコミットされるどのようなリクエストも最終的に \(f+1\) 以上の非故障レプリカでコミットされることを保証する。

各レプリカ \(i\) は \({\it committed\_local}(m,v,n,i)\) が true となった後に \(m\) によって要求された操作を実行し、\(i\) の状態はより小さいシーケンス番号のすべてのリクエストの順次実行結果を反映する。これは、すべての非故障レプリカが safety 特性を提供するのために必要であるように、同一順序でリクエストを実行することを保証する。要求された操作を実行した後、レプリカはクライアントに応答を送信する。レプリカは exactly-once セマンティクスを保証するために、クライアントに送信した最後の応答におけるタイムスタンプより小さいタイムスタンプを持つ要求を破棄する。

我々は順序付けられたメッセージ配信に依存しておらず、従ってレプリカは順序通りにリクエストをコミットできない可能性がある。これは、対応するリクエストが実行できるようになるまで pre-prepare, prepare, commit メッセージがログに保持されるため問題とはならない。

Figure 1 はプライマリが故障していない通常ケースでのアルゴリズム操作を表している。レプリカ 0 がプライマリでレプリカ 3 が故障している。そして \({\it C}\) がクライアントである。

4.3 Garbage Collection

このセクションではログからメッセージを破棄するために使われるメカニズムについて説明する。Safety 条件を満たすために、関係するリクエストが少なくとも \(f+1\) 個の非故障レプリカによって実行され、ビュー変更によって他に証明できるようになるまで、メッセージをレプリカのログに保存する必要がある。さらに、すべての非故障レプリカによって破棄されたメッセージを一部のレプリカが紛失した場合は、サービス状態のすべてまたは一部を転送して最新の状態にする必要がある。そのためにはレプリカは状態が正しいことを証明する必要もある。

すべての操作を実行した後にこれらの証明を生成することは高コストだろう。代わりに、ある定数 (例えば 100) で割り切れるシーケンス番号を持つリクエストが実行されるとき周期的に生成される。我々はこれらのリクエストの実行によって生成された状態をチェックポイントと呼び、証明付きのチェックポイントを安定チェックポイント (stable checkpoint) と呼ぶ。

レプリカはサービス状態 ─ 最後の安定チェックポイント、安定ではない 0 個以上のチェックポイント、および現在の状態 ─ のいくつかの論理コピーを保持する。セクション 6.3 で説明するように、状態の余計なコピーを保存するスペースのオーバーヘッドを削減するために copy-on-write 手法を使うことができる。

チェックポイントに対する正しさの証明は以下のように生成される。レプリカ \(i\) がチェックポイントを作成するとき、レプリカはメッセージ \(\langle {\rm CHECKPOINT},n,d,i\rangle_{\sigma_i}\) を他のレプリカにマルチキャストする。ここで \(n\) は実行が状態に反映されている最後のリクエストのシーケンス番号、\(d\) は状態のダイジェストである。各レプリカは、異なるレプリカによって署名された同じダイジェスト \(d\) を持つシーケンス番号 \(n\) に対して、\(2f+1\) 個のチェックポイントメッセージ (多分、自分自身のメッセージを含む) をログに収集する。これらの \(2f+1\) メッセージはチェックポイントに対する正しさの証明である。

証明付きのチェックポイントは安定 (stable) となり、レプリカはそのログから \(n\) 以下のシーケンス番号を持つすべての pre-prepare, prepare, commit メッセージを破棄する; また過去のチェックポイントとチェックポイントメッセージをすべて破棄する。

セクション 6.3 で議論するように、ダイジェストは増分暗号 (incremental cryptography) [1] を使用して算出することができるため証明の算出は効率的であり、証明が生成されるのはまれである。

チェックポイントプロトコルは (メッセージを受け入れるかを制限する) 最低水準点と最高水準点を進めるために使用される。最低水準点 \(h\) は最後の安定チェックポイントのシーケンス番号と等しい。最高水準点は \(H=h+k\) であり、\(k\) はチェックポイントが安定となるのを待つためにレプリカが停止しない十分に大きい値である。例えばチェックポイントが 100 リクエストごとにとられるのであれば \(k\) は 200 が可能だろう。

4.4 View Changes

ビュー変更プロトコルはプライマリで障害が起きたときにもシステムが処理を進めることを可能にすることで liveness を提供する。ビュー変更は、バックアップがリクエストの実行を無期限に待機しないためのタイムアウトによって引き起こされる。バックアップは、有効なリクエストを受信して実行していない場合、リクエストを待機している。バックアップはリクエストを受信したときタイマーがまだ実行されていなければタイマーを開始する。リクエストの実行を待機していない場合はタイマーを停止するが、その時点で別のリクエストの実行を待機している場合は再起動する。

バックアップ \(i\) のタイマーがビュー \(v\) で期限切れになると、バックアップはシステムをビュー \(v+1\) に移行するためにビュー変更を開始する。バックアップは (checkpoint, view-change, new-view メッセージ以外の) メッセージの受付を停止し、すべてのレプリカに対して \(\langle{\rm VIEW\_CHANGE},v+1,n,\mathcal{C},\mathcal{P},i\rangle_{\sigma_i}\) メッセージをマルチキャストする。ここで \(n\) は \(i\) が分かっている最後の安定チェックポイント \(s\) のシーケンス番号であり、\(\mathcal{C}\) は \(s\) の正しさを証明する \(2f+1\) 個の有効なチェックポイントメッセージの集合、\(\mathcal{P}\) は、\(i\) で prepare されており \(n\) よりも大きいシーケンス番号をっているすべてのリクエスト \(m\) に対する集合 \(\mathcal{P}_m\) を含んでいる集合である。各集合 \(\mathcal{P}_m\) は、(対応するクライアントメッセージを除く) 有効な pre-prepare メッセージと、異なるバックアップによって署名された同一のビュー、シーケンス番号、そして \(m\) のダイジェストをもつ \(2f\) 個と一致する有効な prepare メッセージを含んでいる。

ビュー \(v+1\) のプライマリ \(p\) がほかのレプリカからビュー \(v+1\) に対する有効な view-change メッセージを \(2f\) 個受信したとき、\(p\) はほかのすべてのレプリカに対して \(\langle{\rm NEW\_VIEW},v+1,\mathcal{V},\mathcal{O}\rangle_{\sigma_p}\) メッセージをマルチキャストする。ここで \(\mathcal{V}\) はプライマリが受信した有効な view-change メッセージに加えてプライマリが送信した (または既に送信されている) \(v+1\) に対する view-change メッセージを含む集合、\(\mathcal{O}\) は (リクエストが乗せられていない) pre-prepare メッセージの集合である。\(\mathcal{O}\) は以下のように算出される:

1. プライマリは \(\mathcal{V}\) における最新の安定チェックポイントのシーケンス番号 \({\it min\_s}\) と \(\mathcal{V}\) における prepare メッセージの最大シーケンス番号 \({\it max\_s}\) を決定する。
2. プライマリは \({\it min\_s}\) から \({\it max\_s}\) までの各シーケンス番号 \(n\) に対するビュー \(v+1\) に対する新しい pre-prepare メッセージを作成する。ここで 2 のケースがある: (1) シーケンス番号 \(n\) を持つ \(\mathcal{V}\) 内のある view-change メッセージの \(\mathcal{P}\) 成分に少なくとも 1 つの集合がある、または (2) そのような集合がない。前者の場合、プライマリは新しいメッセージ \(\langle{\rm PRE\_PREPARE},v+1,n,d\rangle_{\sigma_p}\) を生成する。ここで \(d\) は \(\mathcal{V}\) における最大ビュー番号を持つシーケンス番号 \(n\) に対する pre-prepare メッセージのリクエストダイジェストである。後者のケースでは、新しい pre-prepare メッセージ \({\rm PRE\_PREPARE},v+1,n,d^{\it null}\rangle_{\sigma_p}\) を生成する。ここで \(d^{\it null}\) は特別な null リクエストのダイジェストである; null リクエストは他のリクエストと同様にプロトコルを通過するが、その実行は何も行わない。(Paxos [18] も同様の方法を使ってギャップを埋めている。)

次に、プライマリは \(\mathcal{O}\) のメッセージをログに追加する。\({\it min\_s}\) が最新の安定チェックポイントのシーケンス番号より大きい場合、プライマリは安定チェックポイントの証明をシーケンス番号 \({\it min\_s}\) でログに追加し、セクション 4.3 で論議したようにログから情報を廃棄する。次にビュー \(v+1\) に入る: この時点でビュー \(v+1\) に対するメッセージを受け付けることができる。

バックアップは、ビュー \(v+1\) に対する new-view メッセージが適切に署名されており、それが含む new-change メッセージがビュー \(v+1\) に対して有効であり、集合 \(\mathcal{O}\) が正しい場合、new-view メッセージを受け入れる; バックアップはプライマリが \(\mathcal{O}\) を作成するために使用したものと同様の計算を実行することで \(\mathcal{O}\) の正しさを検証する。それから、バックアップはプライマリに対して詳述されるようにログに新しい情報を追加し、ほかのすべてのレプリカに \(\mathcal{O}\) のそれぞれのメッセージに対する prepare をマルチキャストし、それらの prepare をログに追加し、ビュー \(v+1\) に入る。

その後、プロトコルはセクション 4.2 で説明されているように進行する。レプリカは \({\it min\_s}\) から \({\it max\_s}\) までのメッセージに対するプロトコルをやり直すが、(各クライアントに送信された最新の応答に関すして保存されている情報を使うことで) クライアントリクエストの再実行は回避する。

レプリカはあるリクエストメッセージ \(m\) または安定チェックポイントを欠落しているかもしれない (これらは new-view メッセージでは送信されない)。欠落した情報は他のレプリカから得ることができる。例えばレプリカ \(i\) は、欠落したチェックポイント状態 \(s\) を checkpoint メッセージでその正当性を証明されているレプリカの一つから得ることができる。これらのレプリカの \(f+1\) は正しいため、レプリカ \(i\) は常に \(s\) またはそれ以降の安定チェックポイントを得ることができる。我々は、状態を分割しそれを変更した最後のリクエストのシーケンス番号でそれぞれのパーティションをスタンプすることでチェックポイント全体を送信することを避けることができる。レプリカを最新にするためには、チェックポイントの全体ではなく、古くなったパーティションのみを送信する必要がある。

4.5 Correctness

このセクションでは Safety と Liveness を提供するアルゴリズムの証明をスケッチする; 詳細は [4] で見つけることができる。

4.5.1 Safety

前述のように、このアルゴリズムはすべての非故障レプリカがローカルで commit するリクエストのシーケンス番号に合意する場合に Safety を提供する。

セクション 4.2 で我々はもし \({\it prepared}(m,v,n,i)\) が true であれば \({\it prepared}(m',v,n,j)\) はすべての非故障レプリカ \(j\) (\(i=j\) を含む) と \(D(m') \neq D(m)\) となる \(m'\) に対して false であることを示した。これは 2 つのレプリカが同じビューでローカルに commit するリクエストのシーケンス番号について 2 つの非故障レプリカが合意することを意味する。

ビュー変更プロトコルは異なるレプリカの異なるビューでローカルに commit するリクエストのシーケンス番号についても合意することが保証される。リクエスト \(m\) は \({\it committed}(m,v,n)\) が true となる場合のみビュー \(v\) のシーケンス番号 \(n\) を持つ非故障レプリカのローカルにコミットされる。これは、集合内のすべてのレプリカ \(i\) に対して \({\it prepared}(m,v,n,i)\) が true となる、少なくとも \(f+1\) 個の非故障レプリカを含んでいる集合 \(R_1\) が存在することを意味している。

非故障レプリカは、(new-view メッセージを受信した時点でそのビューに入るため) ビュー \(v'\) に対する new-view メッセージを受信していないのであればビュー \(v' \gt v\) に対する pre-prepare を受け付けないだろう。しかし、ビュー \(v' \gt v\) に対する正しい new-view メッセージは、\(2f+1\) レプリカのセット \(R_2\) のすべてのレプリカ \(i\) からの正しい view-change メッセージを含んでいる。\(3f+1\) レプリカが存在するため、\(R_1\) と \(R_2\) は少なくとも一つの非故障レプリカ \(k\) において交差しなければならない。\(k\) の view-change メッセージは、new-view メッセージが \(n\) より大きなシーケンス番号を持つ安定チェックポイントの view-change メッセージを含まない限り、\(m\) が直前のビューで prepare されるという事実が後続のビューに伝播されることを保証するだろう。最初のケースでは、アルゴリズムは同じシーケンス番号 \(n\) と新しいビュー番号を持つ \(m\) に対してアトミックマルチキャストプロトコルの 3 フェーズをやり直す。これは、直前のビューでシーケンス番号 \(n\) が割り当てられた異なるリクエストが commit されないようにするために重要である。第二のケースでは、新しいビューのどのレプリカも \(n\) より小さいシーケンス番号のメッセージを受け入れないだろう。どちらの場合でも、レプリカはシーケンス番号 \(n\) でローカルにコミットされるリクエストに合意するだろう。

4.5.2 Liveness

Liveness を提供するため、レプリカはリクエストを事項できなければ新しいビューに移行しなければならない。しかし、少なくとも \(2f+1\) 個の非故障レプリカが同じビューに存在するときに期間を最大化し、あるリクエストされた操作が実行されるまでこの期間を指数関数的に増加させることを保証することは重要である。我々は 3 つの方法でこれらの目標を達成する。

第1に、ビュー変更の早すぎる開始を回避するため、ビュー \(v+1\) に対する view-change メッセージをマルチキャストするレプリカはビュー \(v+1\) に対する \(2f+1\) 個の view-change メッセージを待機し、その後、時間 \(T\) が経過すると期限切れとなるタイマーを開始する。もし \(v+1\) に対する有効な new-view メッセージを受信する前、もしくは新しいビューで過去に実行されたことのないリクエストを実行する前にタイマーが期限切れになると、ビュー \(v+2\) に対するビュー変更が開始するが、ビュー \(v+3\) に対するビュー変更を開始する前に待機する時間は \(2T\) である。

第2に、レプリカが、現在のビューより大きいビューに対して他のレプリカから \(f+1\) 個の有効な view-change メッセージを受信した場合、タイマーが期限切れになっていなくても集合のもっとも小さいビューに対する view-change メッセージを送信する; これにより次のビュー変更が遅くなりすぎることを防ぐことができる。

第3に、故障レプリカは頻繁なビュー変更を強制することによって進捗を妨げることができない。ビュー変更は少なくとも \(f+1\) 個のレプリカが view-change メッセージを送信したときのみ起きるため、故障レプリカが view-change メッセージを送信してビュー変更を引き起こすことはできない。ただし故障レプリカがプライマリの場合には (メッセージを送らなかったり破損したメッセージを送ることで) それを引き起こすことができる。しかしながら、ビュー \(v\) のプライマリが \(p=v \mod |\mathcal{R}|\) となるレプリカ \(p\) であるため、プライマリが \(f\) 回を超える連続したビューに対して障害を発生させることはできない。

これらの 3 つの手法は、タイムアウト期間よりもメッセージ遅延が実際のシステムではあり得ないほど無制限に早く成長しない限り Liveness を保証する。

4.6 Non-Determinism

ステートマシンレプリケーションは決定論的でなければならないが、多くのサービスは非決定論的な何らかの設計を抱えている。例えば、NFS での最終更新時刻はサーバのローカル時刻を読み取ることによって設定される; もしこれがそれぞれのレプリカで個別に行われた場合、非故障レプリカの状態は分岐するだろう。従って、全てのレプリカが同じ値を選択することを保証するための何らかのメカニズムが必要である。一般的に、クライアントは十分な情報がないため値を選択することができない; 例えば他のクライアントによる同時刻のリクエストと比較してリクエストを順序づけることはできないだろう。代わりに、プライマリの独自によるか、またはバックアップから提供される値に基づくかのどちらかで値を選択する必要がある。

プライマリが独自に非決定論的な値を選択する場合、非故障レプリカがリクエストに対するシーケンス番号とその値とで合意することを保証するため、その値を関連するリクエストと連結して 3 フェーズプロトコルを実行する。これは故障したプライマリが異なる値を異なるレプリカに送信することによってレプリカの状態に差異が出ることを防ぐ。ただし、故障したプライマリは全てのレプリカに同じだが不正な値を送信する可能性がある。従って、レプリカはサービス状態にのみ基づいてその値が正しいかどうか (そして正しくない場合はどうするか) を決定論的に判断できなければならない。

このプロトコルは (NFS を含む) ほとんどのサービスに適しているが、レプリカはサービスの仕様を満たすために値の選択に参加しなければいけないことがある。これはプロトコルに追加のフェーズを導入することで実現することができる: プライマリはバックアップによって提案された認証済みの値を取得し、\(2f+1\) 個のそれらを関連づけられたリクエストと連結し、連結したメッセージに対して 3 フェーズプロトコルを開始する。レプリカは \(2f+1\) 個の値とそれらの状態で決定論的な計算、例えば中央値を取るなどの処理によって値を選択する。追加のフェーズは一般的に最適化することができる。例えば、レプリカがローカル時刻の値に "十分に近い" 値を必要とする場合、レプリカの時刻があるデルタ内で同期されているのであれば追加のフェーズは回避することができる。

5 Optimizations

このセクションでは、通常の操作でアルゴリズムのパフォーマンスを向上させるいくつかの最適化について説明する。全ての最適化は Liveness と Safety 特性を維持する。

5.1 Reducing Communication

我々は通信コストを削減するために 3 つの最適化を使用する。1 つ目は大量の応答を送信しないようにすることである。クライアントリクエストは結果を送信するレプリカを指定する; それ以外の全てのレプリカは結果のダイジェストだけを含む応答を送信する。クライアントはこのダイジェストを使用して結果の正当性を確認しながら、大量の応答に対する深刻なネットワーク帯域の消費と CPU オーバーヘッドを削減することができる。クライアントが指定したレプリカから正しい結果を受け取らなかった場合、ウライアントは通常通りに要求を再送信し、全てのレプリカに完全な応答を送信するように要求する。

2 番目の最適化は操作呼び出しに対するメッセージ遅延の数を 5 から 4 に削減する。レプリカは prepare された評価式がリクエストを正しいとみなし、それらの状態がシーケンス番号の小さい全てのリクエストの実行結果を反映しており、それらのリクエストが全てコミット済みであることが分かっていると、速やかに仮置きでそのリクエストを実行する。リクエストを実行した後、レプリカはクライアントに暫定的な応答を送信する。クライアントは \(2f+1\) に一致する暫定応答を待機する。この数を受け取ったとき、リクエストは結果的にコミットされていることが保証される。そうでない場合クライアントはリクエストを再送信し \(f+1\) の非暫定応答を待機する。

暫定的に実行されたリクエストはビュー変更があり null リクエストによって置き換えられた場合に中止させられることがある。この場合、レプリカはその状態を new-view メッセージ内の最後の安定チェックポイント、またはそれが最後にチェックポイントとした状態 (どちらがより大きなシーケンス番号を持つかによる) に戻す。

3 番目の最適化は、サービス状態を変更しない read-only 操作のパフォーマンスを向上させる。クライアントは read-only リクエストを全てのレプリカにマルチキャストする。レプリカはリクエストが正しく認証されていること、鞍アントがアクセス権を持っていること、リクエストが実際に read-only であることを確認した後に、その暫定的な状態に対してすぐにリクエストを実行する。それらは暫定状態に反映された全てのリクエストがコミットされた後にのみ応答を送信する; これは、クライアントがコミットされていない状態を観測できないようにするために必要である。クライアントは異なるレプリカからの同一の応答が \(2f+1\) 個集まるまで待機する。結果に影響を与えるデータの書き込みがある場合、クライアントはそのような \(2f+1\) 個の応答を受信できない可能性がある; この場合、再送信タイマーが期限切れになった後に通常の read-write 操作としてリクエストを再送信する。

5.2 Cryptography

セクション 4 で我々は全てのメッセージを認証するための電子署名を使用するアルゴリズムを説明した。しかし、我々は実際には滅多に送信されない view-change と new-view メッセージのみに電子署名を使用し、それ以外の全てのメッセージをメッセージ認証コード (MAC) で認証する。これにより以前のシステム [29, 22] における主なパフォーマンスボトルネックが解消される。

しかし MAC は電子署名と比べて根本的な制限が存在する ─ つまり第三者に対してメッセージが本物であることを証明できない。ステートマリンレプリケーションのためのセクション 4 でのアルゴリズムと以前の Byzantine-fault-tolerant アルゴリズム [31,16] は電子署名の過剰な力に頼っている。我々はアルゴリズムを修正して特定の不変条件、例えば 2 つの非故障レプリカが同じビューおよび同じシーケンス番号を持った 2 つの異なるリクエストを prepare しないという不変条件を利用することにより問題を回避した。修正したアルゴリズムは [5] で説明している。ここで我々は MAC を使用することの主な意味をスケッチする。

MAC は電子署名と比較して 3 桁速く算出することができる。例えば我々の実装では 200MHz Pentium Pro では MD5 ダイジェストの 1024bit モジュラス RSA 署名を生成するのに 43ms、署名の検証に 0.6ms かかる [37] が、同一のハードウェア 64byte MAC メッセージの算出にはたった 10.3μs しかかからない。例えば楕円曲線公開鍵暗号システムのように、署名をより速く生成する他の公開鍵暗号システムも存在するが、しかし署名検証は遅く [37]、我々のアルゴリズムにおいて各所名は何度も検証される。

各ノード (アクティブなクライアントを含む) は各レプリカと 16byte のシークレットセッションキーを共有する。我々はメッセージにこの秘密鍵を連結し MD5 を適用することによってメッセージ認証コードを算出する。最終的な MD5 ダイジェストの 16 バイトを使用する代わりに最下位 10 バイトのみを使用する。この切り捨ては MAC サイズを削減するという明確な利点があり、特定の攻撃 [27] に対する resilience も改善する。これは secret suffix method [36] の変種だが、MD5 が衝突耐性であるかぎり安全である [27,8]。

応答メッセージの電子署名は単一の MAC に置き換えることができる。これらのメッセージは単一の明確な受信者を持つためそれで十分である。(クライアントリクエストを含むが view-change は除く) それ以外の全てのメッセージは、我々が認証子 (authenticators) と呼ぶ MAC のベクトルによって置き換えられる。認証子は送信者を除く全てのレプリカのエントリを持っている; それぞれのエントリはエントリに対応する送信者とレプリカによって共有された鍵から算出した MAC である。

認証子を検証する時間は一定だが、一つの認証子を生成するための時間はレプリカの数によって線形に増加する。我々はレプリカの数が大きくなることは想定しておらず、MAC と電子署名の算出には大きなパフォーマンスの格差があるため問題とはしていない。さらに我々は効率的に認証子を算出する; MD5 はメッセージに一度適用され、結果のコンテキストは対応するセッションキーに MD5 を適用することによって各ベクトルエントリを計算するために使用される。例えば 37 レプリカのシステム (すなはち 12 個の同時障害を許容できる) であっても、認証子は 1024bit モジュラス RSA 署名よりも 2 桁以上速く算出することができる。

認証子のサイズはレプリカの数によって線形増加するが、ただしそれはゆっくりである: これは \(30 \times \lfloor \frac{n-1}{3} \rfloor\) バイトに等しい。認証子は \(n \le 13\) (つまり最大 4 つの同時障害を許容することができるシステム) に対する 1024bit モジュラスの RSA 署名よりも小さい。これはほとんどの構成において当てはまると想定している。

6 Implementation

このセクションは我々の実装を説明する。最初に我々はどのようなレプリケーションサービスでも基盤として使用することのできるレプリケーションライブラリを論議する。セクション 6.2 ではレプリケーションライブラリの上にどのようにレプリケーション NFS を実装したかを説明する。次に我々はチェックポイントを維持してチェックポイントダイジェストを効率的に算出する方法について説明する。

6.1 The Replication Library

レプリケーションライブラリのクライアントインターフェースは、ステートマシン操作を起動するリクエストを含んでいる入力バッファを引数に取る単一のプロシジャ invoke からなる。invoke プロシジャはリクエストされた操作をレプリカ上で実行し、それぞれのレプリカの応答の中から正しい応答を選択するために、我々のプロトコルを使用する。これは捜査結果を含むバッファへのポインタを返す。

サーバサイドでは、アプリケーションが実装しなければならないサーバ部分のプロシジャがレプリケーションコードによって何度も呼び出される。リクエストを実行する (execute)、サービス状態のチェックポイントを維持する (make_checkpoint, delete_checkpoint)、特定のチェックポイントのダイジェストを得る (get_digest)、欠落した情報を得る (get_checkpoint, set_checkpoint) ためのプロシジャが存在する。execute プロシジャはリクエストされた操作を含んでいるバッファを入力として受け取り、その操作を実行し、出力バッファに結果を入れる。その他のプロシジャはセクション 6.3 および 6.4 で説明する。

ノード間の point-to-point 通信は UDP を、レプリカのグループへのマルチキャストは UDP over IP マルチキャスト [7] を使用して実装される。それぞれのサービスに対して単一の IP マルチキャストグループが存在する。これらの通信プロトコルは信頼性が低低く、メッセージの重複や紛失、順序の違う配信などを行う可能性がある。

アルゴリズムは順序外の配信を許容し重複を除外している。ビュー変更はメッセージ紛失から回復するために使用できるが、これはコストが高いため再送信を実行することが重要である。通常操作の間はメッセージ紛失からの回復は受信側によって行われる: バックアップは期限が切れたときにプライマリに拒否応答を送信し、プライマリは長いタイムアウトの後に pre-prepare メッセージを再送信する。拒否応答に対する応答は安定チェックポイントの一部と紛失メッセージの両方を含むだろう。ビューが変更されている間、レプリカは view-change と一致する new-view メッセージを受信するか、新しいビューに移行するまで view-change メッセージを再送信する。

このレプリケーションライブラリは今のところビュー変更と再送信を実装していない。これは (ビュー変更をトリガーするタイマー操作を含む) 残りのアルゴリズムが完全に実装されており、我々は完全なアルゴリズムを定式化して正しさの証明も行っているため [4]、セクション 7 で与えられる結果の正確さを損なうことはない。

6.2 BFS: A Byzantine-Fault-tolerant File System

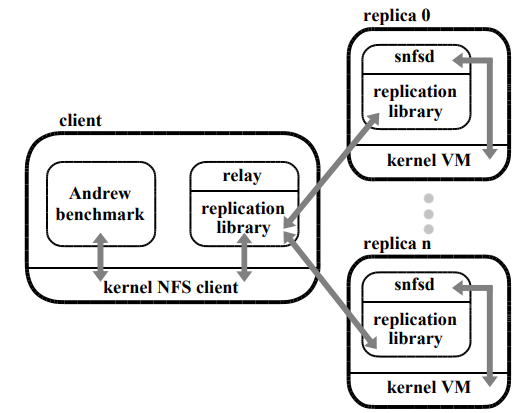
我々はレプリケーションライブラリを使用して BFS, ビザンチン障害耐性 NFS サービスを実装した。Figure 2 は BFS のアーキテクチャを表している。我々は Digital Unix カーネルのソースを持っていなかったため NFS　クライアントとサーバのカーネルは書き換えないことを選択した。

障害耐性 NFS サービスによってエクスポートされたファイルシステムは通常の NFS ファイルシステムと同様にクライアントマシンにマウントされる。アプリケーションプロセスは変更せずに実行し、カーネル内の NFS クライアントを介してマウントされたファイルシステムと対話する。標準の NFS クライアントとレプリカ間の通信を仲介するために、ユーザレベルリレープロセスに依存している。リレーは NFS プロトコルリクエストを受け取り、レプリケーションライブラリの invoke プロシジャを呼び出し、NFS クライアントに結果を送り返す。

各レプリカはレプリケーションライブラリと我々の NFS V2 デーモンを使用してユーザレベルプロセスを実行する。このデーモンを snfsd (simple nfsd) とする。レプリケーションライブラリはリレーからリクエストを受信し、upcall を行って snfsd と対話し、リレーに送信するレプリケーションプロトコル応答に NFS 応答をパッケージする。

我々は snfsd を固定サイズのメモリマップファイルを使用して実装した。全てのファイルシステムデータ構造、例えば inode やブロック、それらの空きリストは、マップファイル内に存在する。メモリマップファイルページのキャッシュの管理、更新ページのディスクへの非同期書き込みはオペレーティングシステムに頼っている。現在の実装は 8kB のブロックと NFS ステータス情報、プラス、ディレクトリエントリをディレクトリに格納するために使用され、ファイル内のブロックへのポインタ、およびシンボリックリンクのテキストを保存するための 256byte データを持つ inode を使用して実装している。ディレクトリとファイルは Unixo と同様に間接ブロックも使うことができる。

我々の実装はすべてのレプロかが同一の初期状態で開始し、それらが決定論的であることを保証する。これは、我々のプロトコルを使って実装されたサービスの正しさのために必要な条件である。プライマリは最終更新日時と最終アクセス日時に対する値を propose し、レプリカは propose された値のうち大きい方と、以前のリクエストで選択された全ての値の最大値より大きい方を選択する。BFS がレプリケーションによって更新されたデータとメタデータの安定性を達成するため [20]、我々は NFS V2 プロトコルセマンティクスを実装するための同期書き込みを必要としない。

6.3 Maintaining Checkpoints

このセクションでは snfsd がどのようにファイルシステム状態のチェックポイントを管理するかを説明する。各レプリカが現在の状態、まだ安定していないいくつかのチェックポイント、最後の安定チェックポイントといういくつかの状態の論理コピーを管理していることに注意。

snfsd は局所性を保つためにメモリマップファイル内で直接ファイルシステム操作を実行し、copy-on-write を使ってチェックポイントの維持に関連する空間と時間のオーバーヘッドを削減する。snfsd はメモリマップファイル内の 512byte ごとのブロックに copy-on-write ビットを保持する。レプリケーションコードが make_checkpoint を呼び出すと、snfsd は全ての copy-on-write ビットを設定し、呼び出しの引数として受信した現在のシーケンス番号とブロックのリストを含む (一時的な) チェックポイントレコードを作成する。このリストにはチェックポイントを取得したときから変更されたブロックのコピーが含まれている。したがって初期状態では空である。レコードは現在の状態のダイジェストも含んでいる; 我々はセクション 6.4 でどのようにダイジェストを算出するか説明する。

クライアントリクエストの実行中にメモリマップファイル内のブロックが書き換えられると、snfsd はブロックの copy-on-write ビットをチェックし、もし設定されていたら最後のチェックポイントに対するチェックポイントレコードにブロックの現在の内容とその識別子を保存する。そしてブロックを新しい値で上書きし copy-on-write ビットをリセットする。snfsd は delete_checkpoint 呼び出しを介してチェックポイントレコードを破棄するよう指示されるまでチェックポイントレコードを保持する。これは後のチェックポイントが安定となったときにレプリケーションコードによって行われる。

レプリケーションコードが別のレプリカに送信するためのチェックポイントが必要としている場合 get_checkpoint を呼び出す。ブロックに対する値を取得するために snfsd は最初に安定チェックポイント内のチェックポイントレコードに含まれるブロックを検索し、次にそれ以降のチェックポイントのチェックポイントレコードを検索する。ブロックがどのチェックポイントレコードにも含まれていない場合、現在の状態から値を返す。

copy-on-write 技法の使用と最大 2 つのチェックポイントを維持するという事実によって、状態のいくつかの論理コピーを維持する空間と時間のオーバーヘッドは確実に低くなる。例えば、セクション 7 で詳述する Andrew ベンチマーク実験では、チェックポイントレコードの平均サイズは 182 ブロック、最大 500 ブロックである。

6.4 Computing Checkpoint Digests

snfsd は make_checkpoint の一部としてチェックポイント状態のダイジェストを算出する。チェックポイントはまれにしか使用されないが、状態は大きくなる可能性があるため、状態のダイジェストは加算的に計算することが重要である。snfsd は AdHash [1] と呼ばれる加算的衝突耐性一方向ハッシュ関数を使用する。この関数は状態を固定サイズにブロックに分割し、それぞれのブロックに対してブロックインデックスとブロック値を連結することによって得られる列のダイジェストを計算するために別の何らかのハッシュ関数 (例えば MD5) を使用する。状態のダイジェストはブロックのダイジェストをある大きな整数で割った余りの合計である。現在の実装では copy-on-write 技法の 512byte ブロックを使用し MD5 を使用してそれらのダイジェストを算出している。

加算的に状態のダイジェストを算出するために、snfsd は各 512byte ブロックのハッシュ値を管理する。このハッシュ値は最後のチェックポイントの時点でのブロック値を連結したインデックスに MD5 を適用することによって得られる。make_checkpoint が呼ばれたとき、snfsd は前の (関連するチェックポイントレコードからの) チェックポイント状態に対するダイジェスト \(d\) を得る。現在のブロック値を連結したブロックインデックスに MD5 を適用することによって copy-on-write ビットがリセットされている各ブロックに新しいハッシュ値を算出する。続いて新しいハッシュ値を \(d\) に加算し、\(d\) から古いハッシュ値を減算し、新しいハッシュ値を含むようにテーブルを更新する。このプロセスは更新されるブロック数が少ない限り有効である; 前述のように Andrew ベンチマークのチェックポイントごとの平均 182 ブロックが更新される。

7 Performance Evaluation

このセクションではマイクロベンチマークと Andrew ベンチマーク [15] の 2 つのベンチマークを使用して我々のシステムのパフォーマンスを評価する。マイクロベンチマークはレプリケーションライブラリのパフォーマンスのサービスに依存しない評価を提供する; これは null 操作つまり何もしない命令を呼び出すレイテンシーを計測する。

Andrew ベンチマークは BFS を他の 2 つのファイルシステムと比較するために使用する: 1 つは Digital Unix での NFS V2 実装で、もう一つはレプリケーションを行わない点を除いて BFS と同じである。最初の比較では、多くのユーザによって毎日利用されている商用システムのレイテンシーと我々のシステムのレイテンシーが同程度であることを示すことによって、我々のシステムが実用的であることを実証する。第二の比較では、実サービスの実装内でアルゴリズムのオーバーヘッドを正確に評価できるようにする。

7.1 Experimental Setup

通常ケースの挙動がシステムのパフォーマンスを決定することからこの実験では通常ケースの挙動を計測する (つまりビュー変更はしない)。全ての実験は 2 つのリレープロセスを実行している 1 つのクライアントと 4 つのレプリカを実行している状態で実行した。4 つのレプリカは 1 つの Byzantine 障害を許容する; この信頼性レベルはほとんどのアプリケーションに十分であると我々は想定している。レプリカとクライアントは同一の DEC 3000/400 Alpha ワークステーションで実行した。これらのワークステーションは 133MHz Alpha 21064 プロセッサ、128MB メモリを搭載し Digital Unix version 4.0 を実行している。ファイルシステムは各レプリカの DEC RZ26 ディスク上に保存される。全てのワークステーションは 10Mbit/s switched Ethernet で接続され DEC LANCE Ethernet インターフェースを持っていた。このスイッチは DEC EtherWORKS 8T/TX であった。実験は独立したネットワーク上で実行された。

チェックポイント間の間隔は 128 リクエストとし、どの実験でもガーベッジコレクションが数回発生した。pre-prepare メッセージでレプリカが受け付ける最大シーケンス番号は 256 プラス最後の安定チェックポイントのシーケンス番号であった。

7.2 Micro-Benchmark

(原文参照)

7.3 Andrew Benchmark

(原文参照)

8 Related Work

レプリケーション技法に関する過去の研究のほとんどは Byzantine 障害を無視していたか同期システムモデルを仮定していた [17, 26, 18, 34, 6, 10]。Viewstamped Replication [26] と Paxos [18] は非同期システムにおける問題のない障害を許容するためにプライマリとバックアップをもつビューを使用する。Byzantine 障害を許容するには暗号技術を使用した遙かに複雑なプロトコル、追加の pre-prepare フェーズ、ビュー変更の起動とプライマリ選択を行う別の手法が必要である。さらに、我々のシステムは新しいプライマリを選択するためだけにビュー変更を使用するが、[26, 18] のように新しいビューを形成するために別のレプリカセットを選択することは決して行わない。

いくつかの合意およびコンセンサスアルゴリズムは非同期システムで Byzantine 障害に耐性を持つ (例えば [2, 3, 24])。しかし、それらはステートマシンレプリケーションに対して完全な解決策を提供しておらず、さらにそれらのほとんどは論理的な実現可能性を実証するように設計されていて、実際に使用するにはとても遅い。通常ケース操作内での我々のアルゴリズムは [2] での Byzantine 合意アルゴリズムと似ているが、そのアルゴリズムはプライマリ故障に耐えることができない。

我々の研究に最も密接に関連している 2 つのシステムは Rampart [29, 30, 31, 22] と SecureRing [16] である。これらはステートマリンレプリケーションを実装しているが我々のシステムより一桁以上遅く、最も重要なことに同期性の仮定に依存している。

Rampoart と SecureRing の両方とも、処理を進めるため (例えば故障プライマリを削除して新しいものを選択するため)、そしてガーベッジコレクションを実行するためにグループから故障レプリカを除外しなければならない。それらはどのレプリカが故障しているかを判断するために障害検出機能に依存している。しかしながら、障害検出は非同期システムにおいて正確に行うことはできない [21]。すなはちレプリカを故障していると誤分類するかもしれない。correctness は故障がグループメンバーの 1/3 未満であることを必要とするため、グループから非故障レプリカを削除することによって誤分類は correctness を脆弱にすることができる。これにより攻撃の道が開かれる: 攻撃者は単一のレプリカを制御することができるが、その動作を検出可能な方法で変更することはない; 次に、グループから十分な数のレプリカが除外されるまで、正しいレプリカまたはレプリカ間の通信を遅くする。

誤分類の可能性を減らすために、レプリカを障害と分類するのを送らせるように障害検知を調整することができる。しかし、確率が無視できるほどとなるには遅延を非常に大きくしなければならず、これは望ましくない。例えばプライマリが実際に故障したとき、グループは遅延が期限切れになるまでクライアントリクエストを処理することができないだろう。我々のアルゴリズムはグループからレプリカを除外する必要が無いため、この問題に対する脆弱性は存在しない。

Phalanx [23, 25] は非同期システムで Byzantine 障害耐性を達成するために定足数レプリケーション手法 [12] を適用する。この研究は一般的なステートマシンレプリケーションを提供しない代わりに、それぞれの変数の読み書きとロックを得るための操作を備えたデータリポジトリを提供する。それが読み書き操作のために提供するセマンティクスは我々のアルゴリズムによって提案されるものより弱い; 任意の数の変数にアクセスする任意の操作を実装できるが、Palanx ではそのような操作を実行するためにロックの獲得/解放を行う必要がある。Phalanx に公表されているパフォーマンス値はありませんが、クリティカルパスでのメッセージ遅延が少なく、公開鍵暗号の代わりに MAC を使用しているため我々のアルゴリズムより速いだろうと考えている。Phalanx のアプローチはスケーラビリティを向上させる可能性を提供している; 各操作はレプリカのサブセットでのみ実行される。しかし、このスケーラビリティへのアプローチは高コストである: \(f\) 個の障害を許容するには \(n \gt 4f+1\) が必要である; それぞれのレプリカは状態のコピーを必要とする; そして各レプリカの付加は \(n\) と共に (\(O(1/\sqrt{n})\) で) ゆっくり減少する。

9 Conclusions

この論文は Byzantine 障害を許容することができ、そして実際に使用することができる新しいステートマシンレプリケーションアルゴリズムに付いて述べた: 現在のところ Internet のような非同期システムで最初の研究であり以前のアルゴリズムから一桁以上パフォーマンスを改善している。

この論文ではまた BFS、NFS の Byzantine-fault-tolerant 実装も説明した。BFS は、我々のアルゴリズムが、複製されていないサービスと近いパフォーマンス ─ Digital Unix の標準 NFS 実装と比べて 3% だけ劣化したパフォーマンスで実際のサービスに利用することができることを示している。この優れたパフォーマンスは公開鍵署名をメッセージ認証コードのベクトルに置き換え、メッセージのサイズと数を削減し、加算的なチェックポイント管理手法を含むいくつかの重要な最適化によるものである。

将来的に Byzantine 障害耐性アルゴリズムが重要になると考えられる理由の一つは、ソフトウェアエラーが存在したときでもシステムが正しい動作を継続することを可能にするためである。あらゆるエラーが生き残り可能ではない; 我々のアプローチは全てのレプリカで発生するソフトウェアエラーを隠すことはできない。しかしながら、検出が最も困難なため最も難問で永続的なエラーである非決定的ソフトウェアエラーを含む、異なるレプリカで個別に発生するエラーを隠すことができる。事実、我々のシステムを実行している間にそのようなソフトウェアバグに遭遇したが、それにもかかわらず我々のアルゴリズムは正しく実行を継続することができた。

我々のシステムを改善するために行うべき研究はまだたくさん存在する。特に興味深い問題の一つはアルゴリズムを実装するために必要なリソース量の削減である。あるフルレプリカが故障したときのみプロトコルに関与する目撃者として \(f\) 個のレプリカを使用することでレプリカの数を減らすことができる。また我々は状態のコピー数を \(f+1\) 個のコピーに減らすことが可能だと考えているが、詳細は研究中である。

Acknowledgements

We would like to thank Atul Adya, Chandrasekhar Boyapati, Nancy Lynch, Sape Mullender, AndrewMyers, LiubaShrira, and the anonymous referees for their helpful comments on drafts of this paper.

References

1. M. Bellare and D. Micciancio. A New Paradigm for Collision-free Hashing: Incrementality at Reduced Cost. In Advances in Cryptology – Eurocrypt 97, 1997.
2. G. Bracha and S. Toueg. Asynchronous Consensus and Broadcast Protocols. Journal of the ACM, 32(4), 1995.
3. R. Canneti and T. Rabin. Optimal Asynchronous Byzantine Agreement. Technical Report #92-15, Computer Science Department, Hebrew University, 1992.
4. M. Castro and B. Liskov. A Correctness Proof for a Practical Byzantine-Fault-Tolerant Replication Algorithm. Technical Memo MIT/LCS/TM-590, MIT Laboratory for Computer Science, 1999.
5. M. Castro and B. Liskov. Authenticated Byzantine Fault Tolerance Without Public-Key Cryptography. Technical Memo MIT/LCS/TM-589, MIT Laboratory for Computer Science, 1999.
6. F. Cristian, H. Aghili, H. Strong, and D. Dolev. AtomicBroadcast: From Simple Message Diffusion to Byzantine Agreement. In International Conference on Fault Tolerant Computing, 1985.
7. S. Deering and D. Cheriton. Multicast Routing in Datagram Internetworks and Extended LANs. ACM Transactions on Computer Systems, 8(2), 1990.
8. H. Dobbertin. The Status of MD5 After a Recent Attack. RSA Laboratories’ CryptoBytes, 2(2), 1996.
9. M. Fischer, N. Lynch, and M. Paterson. Impossibility of Distributed Consensus With One Faulty Process. Journal of the ACM, 32(2), 1985.
10. J. Garay and Y. Moses. Fully Polynomial Byzantine Agreement for n 3t Processors in t+1 Rounds. SIAM Journal of Computing, 27(1), 1998.
11. D. Gawlick and D. Kinkade. Varieties of Concurrency Control in IMS/VS Fast Path. Database Engineering, 8(2), 1985.
12. D. Gifford. Weighted Voting for Replicated Data. In Symposium on Operating Systems Principles, 1979.
13. M. Herlihy and J. Tygar. How to make replicated data secure. Advances in Cryptology (LNCS 293), 1988.
14. M. Herlihy and J. Wing. Axiomsfor Concurrent Objects. In ACM Symposium on Principles of Programming Languages, 1987.
15. J. Howard et al. Scale and performance in a distributed file system. ACM Transactions on Computer Systems, 6(1), 1988.
16. K. Kihlstrom, L. Moser, and P. Melliar-Smith. The SecureRing Protocols for Securing Group Communication. In Hawaii International Conference on System Sciences, 1998.
17. L. Lamport. Time, Clocks, and the Ordering of Events in a Distributed System. Commun. ACM, 21(7), 1978.
18. L. Lamport. The Part-Time Parliament. Technical Report 49, DEC Systems Research Center, 1989.
19. L. Lamport, R. Shostak, and M. Pease. The Byzantine Generals Problem. ACM Transactions on Programming Languages and Systems, 4(3), 1982.
20. B. Liskov et al. Replication in the Harp File System. In ACM Symposium on Operating System Principles, 1991.
21. N. Lynch. Distributed Algorithms. Morgan Kaufmann Publishers, 1996.
22. D. Malkhi and M. Reiter. A High-Throughput Secure Reliable Multicast Protocol. In Computer Security Foundations Workshop, 1996.
23. D. Malkhi and M. Reiter. Byzantine Quorum Systems. In ACM Symposium on Theory of Computing, 1997.
24. D. Malkhi and M. Reiter. Unreliable Intrusion Detection in Distributed Computations. In Computer Security Foundations Workshop, 1997.
25. D. Malkhi and M. Reiter. Secure and Scalable Replication in Phalanx. In IEEE Symposium on Reliable Distributed Systems, 1998.
26. B. Oki and B. Liskov. Viewstamped Replication: A New Primary Copy Method to Support Highly-Available Distributed Systems. In ACM Symposium on Principles of Distributed Computing, 1988.
27. B. Preneel and P. Oorschot. MDx-MAC and Building Fast MACs from Hash Functions. In Crypto 95, 1995.
28. C. Pu, A. Black, C. Cowan, and J. Walpole. A Specialization Toolkit to Increase the Diversity of Operating Systems. In ICMAS Workshop on Immunity-Based Systems, 1996.
29. M. Reiter. Secure Agreement Protocols. In ACM Conference on Computer and Communication Security, 1994.
30. M. Reiter. The Rampart Toolkit for Building High-Integrity Services. Theory and Practice in Distributed Systems (LNCS 938), 1995.
31. M. Reiter. A Secure Group Membership Protocol. IEEE Transactions on Software Engineering, 22(1), 1996.
32. R. Rivest. The MD5 Message-Digest Algorithm. Internet RFC1321, 1992.
33. R. Rivest, A. Shamir, and L. Adleman. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Communications of the ACM, 21(2), 1978.
34. F. Schneider. Implementing Fault-Tolerant Services Using The State Machine Approach: A Tutorial. ACM Computing Surveys, 22(4), 1990.
35. A. Shamir. How to share a secret. Communications of the ACM, 22(11), 1979.
36. G. Tsudik. Message Authentication with One-Way Hash Functions. ACM Computer Communications Review, 22(5), 1992.
37. M. Wiener. Performance Comparison of Public-Key Cryptosystems. RSA Laboratories’ CryptoBytes, 4(1), 1998.

翻訳抄

Byzantine Fault Tolerance 合意アルゴリズムを実装面で補強した 1999 年の論文。

1. Miguel Castro, Barbara Liskov (1999) Practical Byzantine Fault Tolerance
2. Leslie Lamport, Robert Shostak, Marshall Pease (1982) The Byzantine Generals Problem