分散アルゴリズム

論文翻訳: Algorand: Scaling Byzantine Agreements for Cryptocurrencies

Takami Torao 2017年の論文 #Algorand
  • このエントリーをはてなブックマークに追加
Yossi Gilad, Rotem Hemo, Silvio Micali, Georgios Vlachos, Nickolai Zeldovich
MIT CSAIL

概要

Algorand は 1 分程度のレイテンシでトランザクションを確定する新しい暗号通貨である。Algorand は、一部のユーザが悪意を持っておりネットワークが一時的に分断されている場合でも、ユーザが確定したトランザクションについて異なる見え方ができないことを保証する。対照的に、既存の暗号通貨では一時的な分岐が可能であるために高い信頼性でトランザクションを確定するには 1 時間程度の長い時間が必要である。

Algorand は新しいビザンチン合意 (BA ; Byzantine Agreement) プロトコルを使用して次のトランザクションのセットでユーザ間のコンセンサスに到達する。多くのユーザにコンセンサスをスケールするために、Algorand は Verifiable Random Function に基づく新しいメカニズムを使用している。これにより、ユーザは BA に参加して次の一連のトランザクションに合意するために選択されているかをプライベートで確認し、それらのネットワークメッセージにその選択の証明を含むことができる。Algorand の BA プロトコルでは、ユーザは自身の秘密鍵以外の秘密状態を保持しない。これにより Algorand はメッセージを送信した直後に参加者を置き換えることができる。これは特定の参加者の身元が明らかになった後、選択された参加者に対する標的型攻撃を軽減することができる。

Algorand を実装し 1,000 の EC2 仮想マシンでパフォーマンスを評価し、最大 500,000 人のユーザをシミュレートする。実験結果は Algorand が 1 分未満でトランザクションを確定し、125 × Bitcoin のスループットを達成し、より多くのユーザにスケールしてもほとんどペナルティがないことを示している。

Table of Contents

  1. 概要
  2. 1 導入
  3. 2 RELATED WORK [under construction]
  4. 3 GOALS AND ASSUMPTIONS
  5. 4 オーバービュー
  6. 5 暗号抽選
    1. 5.1 選択手続き
    2. 5.2 シードの選択
    3. 5.3 シードに先行した \(sk_u\) の選択
  7. 6 ブロック提案
  8. 7 \(BA\star\)
    1. 7.1 \(BA\star\) の主な手順
    2. 7.2 Voting
    3. 7.3 Reduction
    4. 7.4 Binary Agreement
    5. 7.5 Committee size
  9. 8 ALGORAND
    1. 8.1 Block format
    2. 8.2 Safety and liveness
    3. 8.3 Bootstrapping
    4. 8.4 Communication
  10. 9 IMPLEMENTATION
  11. 10 EVALUATION
    1. 10.1 Latency
    2. 10.2 Throughput
    3. 10.4 Misbehaving users
    4. 10.5 Timeout parameters
  12. 11 FUTURE WORK
  13. 12 CONCLUSION
  14. ACKNOWLEDGEMENTS
  15. REFERENCES
  16. 翻訳抄

1 導入

Bitcoin などの暗号通貨はスマートコントラクト[24, 50]や fair protocols [2] などの新しいアプリケーションを利用可能にし、通貨変換[12]を簡素化し、トランザクションを規制する信頼された中央当局の設置を回避することができた。しかし現在の提案はトランザクションのレイテンシとシラン性のトレードオフに苦しめられている。例えば Bitcon でトランザクションが確定されたという高い信頼を得るには約 1 時間の長い待ち時間が必要である[7]。一方、低レイテンシを必要とするアプリケーションは、トランザクションが確定されるかどうかを確実に確認することはできず、支払い者が二重支出 (double spending) を行わないことを信頼する必要がある[46]。

二重支出は暗号通貨が直面する革新的な問題であり、1 ドルしか保有していない敵対者が 2 人の異なるユーザに 1 ドルずつを提供するというものである。暗号通貨は、トランザクションの順序付きログ ("ブロックチェーン") でコンセンサスに達することにより二重支出を防いでいる。オープンな構成のため合意に至ることは難しい: 誰でも参加できるため、攻撃者は任意の数の偽名 ("Sybils") [21] を作成でき、正直なユーザの一部を必要とする伝統的な合意プロトコル[15]に依存することは不可能である。

Bitcon[42]やその他の暗号通貨[23, 54]は、ユーザがブロックチェーンを成長させるためにハッシュ計算を繰り返し行わなければならない Proof-of-Work (PoW) を使用してこの問題に対処しており、最も長いチェーンが信頼できるとみなされる。PoW は攻撃者が偽名を使うことで利益を得ないことを保証している。ただし、PoW は 2 つの異なるブロックチェーンが同じ長さを持ち、どちらのブロックチェーンも他方に取って代わることがないフォークの可能性を許容している。フォークを緩和するには 2 つの不幸な犠牲が必要である: チェーンを 1 つのブロックで成長させる時間をかなり長くする必要があり (例えば Bitcoin では 10 分)、アプリケーションは自分のトランザクションが信頼できるチェーンに取り込まれることを保証するためにいくつかのブロック (Bitcon では 6 ブロックが推奨されている[7]) を待機する必要がある。その結果、Bitcoin のトランザクションの確定には約1時間がかかる。

この論文では 1 分程度のオーダーでトランザクションを確定するように設計された新しい暗号通貨である Algorand を紹介する。Algorand のコアは \(BA\star\) と呼ばれるビザンチン合意プロトコルを使用している。これは多数のユーザにスケールし、Algorand が低レイテンシで分岐の可能性がない新しいブロックのコンセンサスに達することを可能にしている。\(BA\star\) を Algorand に適用する重要なテクニックは、プライベートで非インタラクティブな方法でユーザをランダムに選択する verifiable random functions (VRFs)[39] の使用である。\(BA\star\) は以前にハイレベルのワークショップ[38] で発表され、Chen と Micali [16] は Algorand の以前のバージョンについて説明している。

Algorand は 3 つの課題に直面している。第一に、Algorand は攻撃者がビザンチン合意プロトコルに影響を与えるために多数の偽名を作る Sybil 攻撃を回避する必要がある。第二に、\(BA\star\) は数百万のユーザに拡大しなければならない。これは最新のビザンチン合意プロトコルが機能する規模よりも遥かに大きいものである。最後に、Algorand は Denial of Service 攻撃に対して回復性を持ち、たとえ敵対者が一部のユーザ[30, 52]を切断しても運用し続けなければならない。

3 GOALS AND ASSUMPTIONS

4 オーバービュー

Algorand は各ユーザに公開鍵を要求する。Algorand はブロックチェーンと呼ばれるトランザクションのログを保持している。各トランザクションはあるユーザの公開鍵によって署名され、別のユーザの公開鍵に送金される支払いである。Algorand は Bitcoin に似た非同期ラウンドでブロックチェーンを成長させている。ラウンド事にトランザクションのセットと前方のブロックへのポインタを含む新しいブロックがブロックチェーンに追加される。この論文の残りの部分ではユーザのコンピュータ上で動作する Algorand ソフトウェアをそのユーザと呼ぶ。

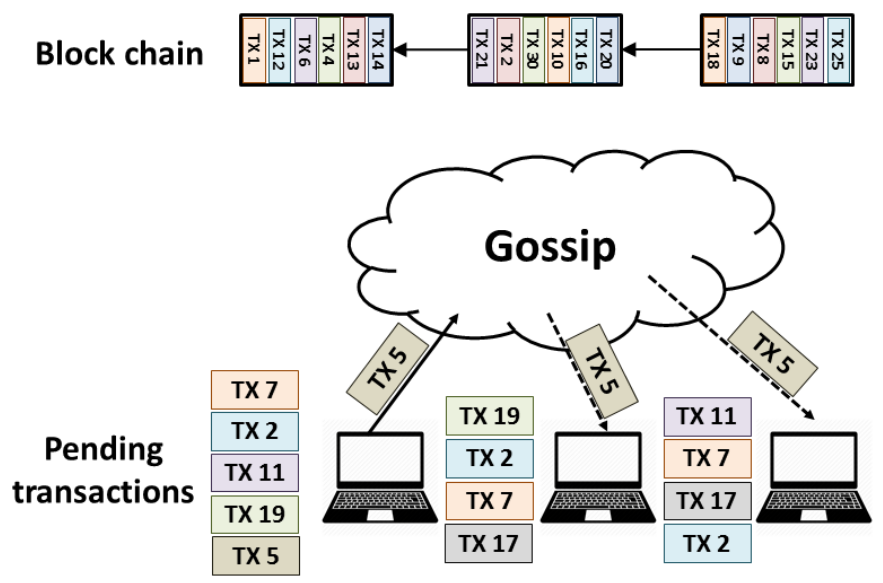
Algorand ユーザはゴシッププロトコルを介して通信する。ゴシッププロトコルは、ユーザが新しいトランザクションを送信するために使用される。各ユーザは Figure 1 に示すように、次のブロックを提案するために選択された場合に備えて、自分がリッスンした保留中のトランザクションのブロックを収集する。Algorand は \(BA\star\) を使用してこれらの保留中のブロックの 1 つについて合意に達する。

\(BA\star\) は段階的に実行され、同じようにゴシッププロトコルを介して通信し、新しい合意済みのブロックを生成する。\(BA\star\) は最終的なコンセンサスと暫定的なコンセンサスの 2 種類のコンセンサスを生成することができる。あるユーザが合意に達した場合、これは同じラウンドで最終合意または暫定合意に達した他の全てのユーザが同じブロック値に合意しなければならないことを意味する (強い同期の仮定が成り立つかどうかにかかわらず)。これにより、将来の全てのトランザクションがこの最終ブロック (および一時的のその前身) にチェーンされるため、Algorand の安全性が確保される。従って Algorand はトランザクションのブロック (または任意の後続ブロック) が最終合意に達したときにトランザクションを確定する。一方、仮合意は他のユーザが別のブロックで仮合意に達した可能性があることを意味する (ユーザが最終的な合意に達していない場合)。ユーザは後続ブロックが最終合意に達した場合にのみ仮ブロックからトランザクションを確定する。

\(BA\star\) は 2 つのケースで暫定的なコンセンサスをもたらす。一つ目は、ネットワークが強力に同期している場合、敵対者は小さな確率で \(BA\star\) をブロックに関する暫定的な合意に至らせることができる。この場合、\(BA\star\) は 2 つの異なるブロックでコンセンサスに達することはないが、ネットワークが強く同期されていることを確認することができない。Algorand は最終的には (数ラウンドで) 圧倒的な確率で後続ブロックに関する最終的な合意に達するため、このように以前のトランザクションを確定する。

もう一つのケースは、ネットワークの同期が弱い (つまり完全に敵対者に支配されており、敵対者が制御を維持できる期間の上限が設定されている) ことである。この場合 \(BA\star\) は 2 つの異なるブロックで暫定的な合意に達し、複数の分岐を形成することができる。その結果、ユーザは以前のブロックについて見解の相違がある異なるグループに分割されるため、\(BA\star\) が再び合意に達することを防ぐことができる。liveness を回復するために Algorand は定期的に \(BA\star\) を呼び出して今後殿分岐を使うべきかについて合意に達する。ネットワークが強力な同期を取り戻すと Algorand は分岐の一つを選択しその分岐の後続のブロックで最終的な合意に達することができる。

次に Algorand のコンポーネントがどのように適合するかを説明する。

Figure 1. Algorand でのトランザクションフローのオーバービュー
Figure 2. \(BA\star\) の 1 ステップの概要。図を簡略化するために各ユーザは 2 回表示されている。1 回は図の上部に、2回は下部に表示されている。各矢印の色は特定のユーザからのメッセージを示している。

ゴシッププロトコル. Algorand は (Bitcoin に類似した) ゴシップネットワークを実装し、各ユーザがゴシップメッセージの送信先となるピアの小さなランダムセットを選択する。メッセージが偽造されないように、全てのメッセージは下の送信者の秘密鍵で署名される。他のユーザは、中継する前に署名が有効であることを確認する。転送ループを回避するためにユーザは同じメッセージを 2 回中継してはいけない。Algorand は TCP を介してゴシップを実装し、所有する金額に基づいてピアの選択を比較検討し汚染攻撃 (pollution attack) を軽減する。

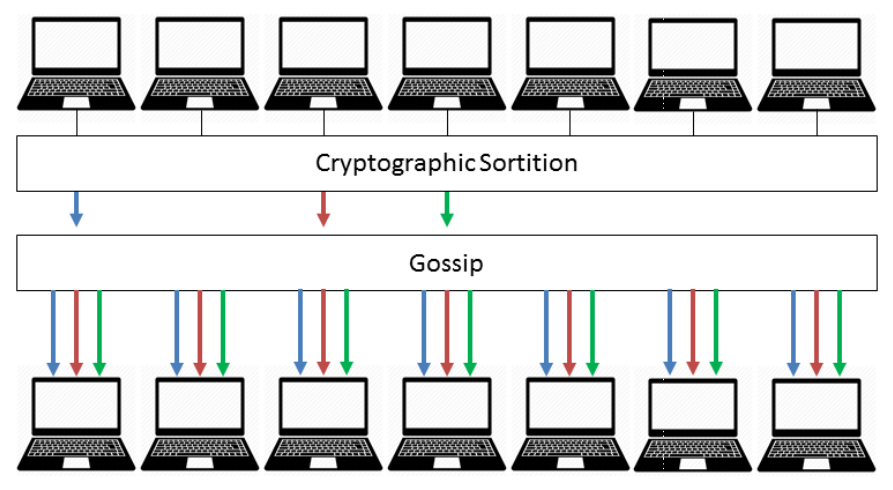
ブロック提案 (§6). 全ての Algorand ユーザは暗号抽選を実行して特定ラウンドでブロックを提案するために選択されているかを判定する。§5 で抽選について説明しているが、高レベルでは、抽選によって少数のユーザがランダムに選択され、そのアカウントの残高で重み付けされ、選択された各ユーザの間で比較可能な優先順位と、選択されたユーザの優先度の証明を各選択ユーザに提供する。確率はランダムであるため、ブロックを提案するために選択された複数のユーザが存在する可能性があり、優先度は、全てのユーザが採用すべきブロックを決定する。選ばれたユーザは、未処理のトランザクションのブロックを優先順位と証明と共にゴシッププロトコルを通じて配布する。ユーザが高い確率で 1 つのブロックに収束することを保証するために、ブロックの提案は提案ユーザの優先度に基づいて優先され、ユーザはブロックを受信するために一定時間待機する。

\(BA\star\) を使用した合意. ブロック提案は全てのユーザが同じブロックを受信したことを保証するものではなく、Algorand は安全のためにブロック提案プロトコルには依存しない。1 つのブロックでコンセンサスを得るために Algorand は \(BA\star\) を使用する。各ユーザは受信した最高優先度のブロックで \(BA\star\) を初期化する。\(BA\star\) は Figure 2 で示すように繰り返し実行される。各ステップは全てのユーザがそのステップで委員会に選ばれたかを確認するための (§5) で始まる。それらのステップは \(BA\star\) のあるステップで委員会の十分なユーザが合意に達するまで繰り返される。(ステップはユーザ間で同期されない; 各ユーザは前のステップが終了したことを確認するとすぐに選択をチェックする。) 前述のように \(BA\star\) の重要な特徴は、委員会メンバーが秘密鍵以外の秘密情報を保持しないため、標的型攻撃を軽減するために全てのステップの後で置き換えることができるという点である。

効率. ネットワークが強力に同期している場合、\(BA\star\) は全ての正直なユーザが同じ最初のブロックで開始する場合 (すなはち最高優先度のブロック提案者が正直であった場合)、\(BA\star\) はそのブロックに対する最終合意を確立し、ユーザ間の 4 つのインタラクティブなステップで正確に終了することを保証する。テクニカルレポート [27] の Appendix C で分析されているように、同じネットワーク条件下で、特に幸運な敵対者の最悪ケースでは、全ての正直なユーザは予想される 13 ステップ以内に次のブロックについて合意に達する。

5 暗号抽選

暗号抽選 (cryptographic sortition) はユーザごとの重みに応じてランダムなユーザサブセットを選択するアルゴリズムである; つまり、重みの集合 \(w_i\) とすべてのユーザの重み \(W=\sum_i w_i\) が与えられると、ユーザ \(i\) が選択される確率は \(w_i/W\) に比例する。抽選アルゴリズムのランダム性は公開されているランダムシードに由来する; 我々はこのシードをどうやって選択するかについて後述する。ユーザが、自分が選択されたことを証明できるように、抽選では各ユーザ \(i\) が公開鍵/秘密鍵ペア \((pk_i,sk_i)\) を持つ必要がある。

抽選は Verifiable Random Functions (VRFs) [39] を使用して実装されている。簡単に言うと任意の入力文字列 \(x\) に対して \(VRF_{sk}(x)\) はハッシュと証明の 2 つの値を返す。ハッシュは \(sk\) と \(x\) によって一意に決定する\(hashlen\)-bit 長の値だが、\(sk\) を知らない人には乱数と区別がつかない。証明 \(\pi\) によって、\(pk\) を知っていれば \(sk\) を知らなくても、そのハッシュが実際に \(x\) に対応しているかを検証することができる。セキュリティのため、攻撃者が \(pk\) と \(sk\) を選択したとしても VRF はこれらの特性を提供する必要がある。

5.1 選択手続き

Algorand は VRF を使用して Algorithm 1 に示すように暗号化抽選を実装する。抽選にはユーザが選択できる、様々なロールを区別するロールパラメータを必要とする; 例えば、ユーザはあるラウンドでブロックを提案するように選択されたり、\(BA\star\) の特定のステップで committee のメンバーとして選択されたりする。Algorand はそのロールに対して選択される予想ユーザ数を決定するしきい値 \(\tau\) を指定する。

抽選はユーザの重みに比例してユーザを選択することが重要である; さもなくば抽選は Sybil 攻撃を防衛できないだろう。一つの微妙な含みは (訳注: 同一のラウンド内の同一のロールに対して) ユーザが複数回選択される可能性があるということである (つまり重みが高いことによって)。抽選手続きはユーザが何回選択されたかを示すパラメータ \(j\) を返すことによってこれを示す。\(j\) 回選択されるということは、ユーザが \(j\) 人の異なる "サブユーザ" として参加することを意味している。

金額に比例して選択を行うために Algorand の通貨単位それぞれを異なる "サブユーザ" と考える。ユーザ \(i\) が Algorand の (統合) ユニット \(w_i\) を所有している場合、\(j \in \{1,\ldots,w_i\}\) を持つシミュレーションユーザ \((i,j)\) は \(i\) が所有している \(j^{th}\) 番目の通貨単位を表し、確率 \(p=\frac{\tau}{W}\) で選択される。ここで \(W\) は Algorand における通貨単位の総量である。

\( {\bf procedure} \ {\rm Sortation}(sk, seed, \tau, role, w, W):\)
\( \langle hash, \pi \rangle \leftarrow {\it VRF}_{sk}(seed \ || \ role) \)
\( p \leftarrow \frac{\tau}{W} \)
\( j \leftarrow 0 \)
\( {\bf while} \ \frac{hash}{2^{hashlen}} \notin \left[ \sum_{k=0}^j B(k; w,p), \ \sum_{k=0}^{j+1} B(k; w, p) \right) {\bf do} \)
\( \qquad j ++ \)
\( {\bf return} \ \langle hash, \pi, j \rangle \)
Algorithm 1 : 暗号化抽選アルゴリズム

Algorithm 1 に示すように、ユーザは \(\langle hash, \pi \rangle \leftarrow {\rm VRF}_{sk}(seed \ || \ role) \) を計算して抽選を実行する。ここで \(sk\) はユーザの秘密鍵である。擬似乱数のハッシュは次のようにしてサブユーザの数を決定する。\(w\) (ユーザの重み) のサブユーザから正確に \(k\) 個が選択される確率は二項分布 \(B(k;w,p) = \binom{w}{k} p^k (1-p)^{w-k}\) に従う。ここで \(\sum_{k=0}^w B(k;w,p) = 1\) である。ここで \(B(k_1;n_1,p)+B(k_2;n_2,p)=B(k_1+k_2;n_1+n_2,p)\) であるため、ユーザの重み (通貨) 量を Sybil に分割しても、彼/彼女の制御下にある選択されたサブユーザの数には影響しない。

ユーザの \(w\) 個のサブユーザのうち何人が選択されているかを判断するために、抽選アルゴリズムは区間 \([0, 1)\) を連続した区間 \(I^j = \left[ \sum_{k=0}^j B(k;w,p), \sum_{k=0}^{j+1} B(k;w,p) \right)\) に分割する。ここで \(j \in \{0,1,\ldots,w\}\) である。\(hash / 2^{hashlen}\) (\(hashlen\) はハッシュのビット長) が区間 \(I^j\) に入る場合、ユーザはまさに選択されたサブユーザ \(j\) を持っている。選択されたサブユーザの数は (VRF 出力からの) 証明 \(\pi\) を使用してパブリックに検証可能である。

抽選には２つの重要な特徴を提供する。１つ目は、VRF はランダムシードが与えられると擬似乱数ハッシュ値を出力する。これは本質的に \(0\) から \(2^{hashlen-1}\) の間で均一に分散されている。その結果、ユーザは重みに基づいてランダムに選択される。第二に、\(sk_i\) を知らない敵対者は、ユーザ \(i\) が何回選択されたか、あるいはそもそも \(i\) が選ばれたのかを推測することができない (より正確には、敵対者は重みに基づいて推測する以上の推測はできない)。

\( {\bf procedure} \ {\rm VerifySort}(pk, hash, \pi, seed, \tau, role, w, W):\)
\( {\bf if} \ \lnot VerifyVRF_{pk}(hash, \pi, seed \ || \ roke) \ {\bf then \ return} \ 0; \)
\( p \leftarrow \frac{\tau}{W} \)
\( j \leftarrow 0 \)
\( {\bf while} \ \frac{hash}{2^{hashlen}} \notin \left[ \sum_{k=0}^j B(k; w,p), \ \sum_{k=0}^{j+1} B(k; w, p) \right) {\bf do} \)
\( \qquad j ++ \)
\( {\bf return} \ j \)
Algorithm 2 : 公開鍵 \(pk\) を持つユーザの抽選を検証する擬似コード

Algorithm 2 に示されている抽選証明を検証するための擬似コードは、同じ構造に従ってそのユーザが選択されたかを検証する (ユーザの公開鍵に対する重みはその台帳から取得する)。この関数は選択されたサブユーザの数を返す (あるいはユーザが全く選択されなかった場合はゼロ)。

5.2 シードの選択

抽選には無作為に選ばれた公開シードが必要である。Algorand の場合、各ラウンドですべての人に公開されていて敵対者が制御することができないシードを必要とする; そうでなければ攻撃者は故障したユーザの選択を支持するシードを選択できる可能性がある。

Algorand の各ラウンドで新しいシードが公開される。Algorand のラウンド \(r\) で公開されるシードは前のラウンド \(r-1\) のシード値を用いて VRF によって決定される。具体的には、ラウンド \(r-1\) のブロック提案段階で、ブロック提案のために選択された各ユーザ \(u\) が \(\langle seed_r,\pi\rangle \leftarrow {\rm VRF}_{sk_u}(seed_{r-1} \ || \ r)\) としてラウンド \(r\) に対する提案シードを算出する。Algorand ではそのラウンドのシードが決定される前に \(u\) が \(sk_u\) を選択することを要求する (§5.3)。これにより \(u\) が悪意のある場合でも結果の \(seed_r\) は擬似乱数となることを保証する。

このシード (および対応する VRF 証明 \(\pi\)) は提案されたすべてのブロックに含まれているため、Algorand がラウンド \(r-1\) のブロックに対して合意に達すると、ラウンド \(r\) の開始時には全員が \(seed_r\) を認識する。もしブロックが有効なシードを含んでいない場合 (例えばブロックが悪意のあるユーザによって提案され、無効なトランザクションが含まれていた場合など)、ユーザは提案されたブロック全体を空のように扱い、暗号化ハッシュ関数 \(H\) (ランダムオラクルと想定) を使用してラウンドに関するシードを \(seed_r = H(seed_{r-1} \ || \ r)\) として計算する。シード選択をブートストラップする \(seed_0\) の値は分散乱数生成 [14] を使用して、最初の参加者 (公開鍵が宣言されたあと) によって Algorand の開始時にランダムに選択することができる。

敵対者による抽選操作、つまり別の committee に対するユーザの選択操作を制限するために、(Algorithm 1 と Algorithm 2 に渡される) 選択シードを \(R\) ラウンドごとに再生成する。つまりラウンド \(r\) において Algorand は \(seed_{r-1 - (r \mod R)}\) で Sortition 関数を呼び出す。

5.3 シードに先行した \(sk_u\) の選択

\(seed_r\) を計算するには、各ユーザの秘密鍵 \(sk_u\) が、そのラウンドで使用される選択シード、つまり \(seed_{r-1-(r \mod R)}\) に先立って選択されている必要がある。ネットワークが強力に同期していない場合、攻撃者はリンクを完全に制御できるため、ブロックの提案を破棄し、将来の選択シードを計算できるように空のブロックに対してユーザに同意させることができる。そのような攻撃を緩和するために Algorand は弱い同期の仮定に依存している (長さ \(b\) のすべての期間で、長さ \(s \lt b\) となる強く同期した周期がなければならない)。Algorand はラウンド \(r\) の暗号化抽選を実行するたびに、ラウンド \(r-1-(r \mod R)\) の合意済みブロックに含まれるタイムスタンプをチェックし、ブロック \(r-1-(r \mod R)\) の前の \(b\) 時点で作成された最後のブロックの鍵 (および関連する重み) を使用する。強い同期期間の長さ \(s\) の下限は、少なくとも 1 つのブロックが正しいことを圧倒的な確率で確実にするために、十分に多くのブロックが作成されることを可能にすべきである。これは、\(s\) が適切に大きい限り、鍵 \(sk_u\) を選択する敵対者 \(u\) はラウンド \(r\) のシードを予測できないことを保証する。

この look-back 期間 \(b\) には次のトレードオフが存在する: 大きな \(b\) は攻撃者が弱い同期性の仮定を破るリスクを軽減するが、ユーザが自分の通貨を他人に送金してしまい、システムのセキュリティが破られても失うものがない可能性が高くなる。これは俗に "nothing at stake" (危険なものはなにもない) 問題として知られている; このトレードオフを回避する 1 つの可能な方法は、Algorand では取り上げていないが、現在のユーザ残高と look-back ブロックからのユーザ残高の小さい方をユーザの重みとして取得することである。

テクニカルレポート [27] の Appendx A では、ネットワークが強く接続されている期間 \(s\) において Algorand が作成する必要のあるブロック数の数を正式に分析している。我々は、故障確率 \(F\) が小さいことを保証するために、ブロック数は \(\frac{1}{F}\) の対数であることを示した。これは、必要なブロック数が適度に少ない場合に高いセキュリティを得ることを可能にしている。

6 ブロック提案

各ラウンドであるブロックが提案されることを保証するために、Algorand はブロック提案役に 1 より大きい抽選しきい値 \(\tau_{rm PROPOSER}\) を設定する (ただし Algorando は提案されたこれらのブロックの多くとも 1 でコンセンサスに到達する)。テクニカルレポート [27] の Appendix B では \(\tau_{\rm PROPOSER}=26\) を選択すると妥当な数 (妥当な上限として、少なくとも一つ、多くても 70) の提案者が非常に高い確率 (\(1-10^{-11}\) など) で選択されることが証明されている。

不要なブロック転送の最小化. 複数の提案者を選ぶリスクの一つは、それぞれが自分の提案するブロックをゴシップすることである。ブロックが大きい場合 (例えば 1MB)、これはかなりの通信コストを生じうる。このコストを削減するために抽選ハッシュを使用してブロック提案に優先順位を付ける: ユーザ \(\) の選択されたサブユーザ \(1,\ldots,j\) それぞれに対して、ブロック提案の優先度はサブユーザのインデックスと連結した VRF の (verifiable random) ハッシュ出力をハッシュ化することによって得られる。ブロック提案者が選択した全てのサブユーザの中で最も高い優先順位はブロックの優先度である。

Algorand ユーザは、そのユーザが現在までに表示した最高の優先順位を持たないブロックに関するメッセージを破棄する。Algorand は 2 種類のメッセージをゴシップする: 一つは (抽選から) 選択されたブロック提案者の優先度と証明のみを含み、もう一つはブロック全体を含んでいる。これには提案者の抽選ハッシュと証明も含まれている。最初の種類のメッセージは小さく (約 200 バイト)、ゴシップネットワークを通じて迅速に伝播する。これらのメッセージにより、ほとんどのユーザは誰が最も優先度の高い提案者を知ることができるため、他に提案されたブロックをすぐに破棄できる。

ブロック提案の待機. 各ユーザはゴシッププロトコルを介してブロック提案を受け取るために一定の時間待たなければならない。この時間間隔を選択しても Algorand の安全性保証には影響しないがパフォーマンスにとっては重要である。待機時間を短くすると提案を受信できなくなる。ユーザがブロック提案を受け取れなければ、ユーザは \(BA\star\) を空のブロックで初期化し、もし多くのユーザがそのようにすれば Algorand は空のブロックで合意に達するだろう。一方、待機時間が長すぎると全てのブロック提案が受信されるが確認待ち時間が不必要に長くなる。

ブロック提案を待機する適切な時間を決定するために、我々はユーザが自分自身を見つける可能性のあるシナリオを考察した。ユーザがラウンド \(r\) のブロック提案の待機を開始するとき、彼らはラウンド \(r-1\) でコンセンサスに達した最初のユーザの 1 人である可能性がある。そのユーザはラウンド \(r-1\) を完了したため、十分な数のユーザがそのラウンドにおける \(BA\star\) の最初のステップのメッセージを送信したため、ネットワークの大部分はこのユーザより最大でも 1 ステップ遅れ居ている。従って、ユーザは他のユーザが \(r-1\) ラウンドから \(BA\star\) の最後のステップを完了するのをどうにかして待たなければならない。この時点で、たまたま最高優先順位を持っているラウンド \(r\) の提案者がその優先順位と証明メッセージをゴシップし、ユーザはそのメッセージを受け取るのを何とか待たなければならない。そしてユーザは最も優先度の高い証明に対応するブロックを受信するまで待つだけで良い (1 分程度のタイムアウト \(\lambda_{\rm BLOCK}\) を指定するとユーザは空のブロックに戻る)。

上記のシナリオの最初の 2 ステップでユーザが正確に正しい量を待つことは不可能である。従って Algorand はこれらの量 (異なるユーザが \(BA\star\) の最後のステップを完了するのにかかる時間の分散 \(\lambda_{\rm STEPVAR}\)、優先順位と証明メッセージをゴシップするのにかかる時間 \(\lambda_{\rm PRIORITY}\)) を推定し、\(\lambda_{\rm STEPVAR} + \lambda_{\rm PRIORITY}\) 時間帯記して最高の優先順位を特定する。§10 では、これらのパラメータがそれぞれ 5 秒であることが実験的に示されている。前述のようにこれらの推定値が不正確であっても Algorand は安全である。

悪意的な提案者. 一部のブロック提案者が悪意的だったとしても、最悪のシナリオは別の Algorand ユーザを騙して異なるブロックで \(BA\star\) を初期化することである。これにより Algorand は空のブロックでコンセンサスに達する可能性があり、そのために追加のステップを実行する可能性がある。しかし、このシナリオでさえ比較的起きそうにないことが判明している。特に、敵対者がラウンドにおいて最高優先順位の提案者でない場合、最高優先順位の提案者は全てのユーザに一貫したバージョンをゴシップするだろう。もし敵対者がラウンドで最高優先順位の提案者であるなら、彼らは空のブロックを提案することができ、従って実際のどのようなトランザクションも確定することが妨害される。ただしこれは加重ユーザの少なくとも \(h \gt 2/3\) が正直であるという Algorand の仮定により、多くても \(1-h\) の確率で起きる。

7 \(BA\star\)

\(BA\star\) の実行は 2 つのフェーズで構成されている。最初のフェーズでは \(BA\star\) は 2 のオプションのいずれかに合意するためにブロックに合意する問題を減らす。次のフェーズでは \(BA\star\) は提案されたブロックに合意するか、または空のブロックに合意するかのオプションに合意する。

各フェーズはいくつかのインタラクティブなステップで構成されている; 最初のフェーズは常に 2 ステップをとり、次のフェーズは最高優先順位のブロック提案者が正直 (全てのユーザに同じブロックを送信している) であったならば 2 ステップを取る。そして、我々の分析で示しているように、それぞれのステップで委員会参加者の大部分と共謀した悪意を持つ最高優先順位の提案者という最悪ケースの場合 11 ステップが予想される。

各ステップでは全ての委員会メンバーが何らかの値に対して投票を行い、全てのユーザがその投票をカウントする。ある値に対してしきい値を超える投票を受け取ったユーザは、次のステップで (委員会に選ばれた場合) その値に投票する。ユーザがどの値に対しても十分な票を得られない場合、タイムアウトし、次のステップに対する投票の選択はステップ番号によって決まる。

一般的なケースでは、ネットワークが強力に同期しており、最高優先順位のブロック提案者が正直だった場合 \(BA\star\) は最終ステップを使用して同じラウンド内に他の合意済みブロックが存在しないことを確認することで最終的な合意に達する。ただし、ネットワークの非同期の可能性のために他のブロックが存在しないことを確認できない場合、\(BA\star\) は仮合意を宣言するかも知れない。

\(BA\star\) のデザインの重要な特徴は、ユーザの秘密鍵を除いて秘密を保持しないことである。これによりメッセージを監視している全てのユーザがプロトコル内で "受動的に参加" することができる。つまり署名を確認し、票を数え、合意に達することができる。

7.1 \(BA\star\) の主な手順

Algorand によって呼び出される \(BA\star\) を実装する最上位レベルのプロシジャは Algorithm 3 に示されている。このプロシジャは最高優先順位のブロック生成者 (§6) から台帳の現在の状態、ラウンド番号、新しく提案されたブロックを取り込むコンテキスト ctx を取る。Algorand はブロックが有効であることを保証する (§8 に記述されているように、提案されたブロックの内容を検証しそれが無効である場合は空ブロックを使用することによって)。コンテキストは抽選のためのシード、ユーザの重み、最後に合意したブロックで構成される。

効率化のために \(BA\star\) はブロックの内容全体ではなくブロックハッシュに投票する。\(BA\star\) アルゴリズムの最後に \({\rm BlockOfHash}()\) 関数を使用して \(BA\star\) が合意したハッシュの事前イメージをまだ受信していない場合には他のユーザ (そしてブロックが合意されたので正直なユーザの多くはブロック提案の間にそれを受け取っているに違いない) からそのイメージを取得する必要があることを示す。

\(BA\star\) アルゴリズムは最終的なコンセンサスを確立したか、暫定的なコンセンサスを確立したかも判断する。このチェックについては Algorithm 8 で詳述する。

7.2 Voting

7.3 Reduction

7.4 Binary Agreement

7.5 Committee size

8 ALGORAND

8.1 Block format

8.2 Safety and liveness

8.3 Bootstrapping

8.4 Communication

9 IMPLEMENTATION

10 EVALUATION

10.1 Latency

10.2 Throughput

10.4 Misbehaving users

10.5 Timeout parameters

11 FUTURE WORK

12 CONCLUSION

ACKNOWLEDGEMENTS

REFERENCES

  1. M. Abd-El-Malek, G. R. Ganger, G. R. Goodson, M. K. Reiter, and J. J. Wylie. Fault-scalable Byzantine fault-tolerant services. In Proceedings of the 20th ACM Symposium on Operating Systems Principles (SOSP), pages 59–74, Brighton, UK, Oct. 2005.
  2. I. Bentov and R. Kumaresan. How to use Bitcoin to design fair protocols. In Proceedings of the 34th Annual International Cryptology Conference (CRYPTO), Santa Barbara, CA, Aug. 2014.
  3. I. Bentov, C. Lee, A. Mizrahi, and M. Rosenfeld. Proof of activity: Extending Bitcoin’s proof of work via proof of stake. In Proceedings of the 2014 Joint Workshop on Pricing and Incentives in Networks and Systems, Austin, TX, June 2014.
  4. I. Bentov, A. Gabizon, and A. Mizrahi. Cryptocurrencies without proof of work. In Proceedings of the 2016 Financial Cryptography and Data Security Conference, 2016.
  5. I. Bentov, P. Hubáček, T. Moran, and A. Nadler. Tortoise and hares consensus: the Meshcash framework for incentive-compatible, scalable cryptocurrencies. Cryptology ePrint Archive, Report 2017/300, Apr. 2017. http://eprint.iacr.org/.
  6. D. J. Bernstein. Curve25519: New Diffie-Hellman speed records. In Proceedings of the 9th International Conference on Theory and Practice in Public-Key Cryptography (PKC), pages 207–228, New York, NY, Apr. 2006.
  7. Bitcoin Wiki. Confirmation. https://en.bitcoin.it/wiki/Confirmation, 2017.
  8. BitcoinWiki. Mining hardware comparison, 2016. https://en.bitcoin.it/wiki/Mining_hardware_comparison.
  9. BitcoinWiki. Bitcoin scalability. https://en.bitcoin.it/wiki/Scalability, 2017.
  10. BitcoinWiki. Proof of stake. https://en.bitcoin.it/wiki/Proof_of_Stake, 2017.
  11. D. Boneh and M. K. Franklin. Identity-based encryption from the Weil pairing. In Proceedings of the 21st Annual International Cryptology Conference (CRYPTO), Santa Barbara, CA, Aug. 2001.
  12. G. Brockman. Stellar, July 2014. https://stripe.com/blog/stellar.
  13. V. Buterin. Minimal slashing conditions. https://medium.com/@VitalikButerin/minimalslashing-conditions-20f0b500fc6c, Mar. 2017.
  14. C. Cachin, K. Kursawe, F. Petzold, and V. Shoup. Secure and efficient asynchronous broadcast protocols. In Proceedings of the 21st Annual International Cryptology Conference (CRYPTO), pages 524–541, Santa Barbara, CA, Aug. 2001.
  15. M. Castro and B. Liskov. Practical Byzantine fault tolerance and proactive recovery. ACM Transactions on Computer Systems, 20(4), Nov. 2002.
  16. J. Chen and S. Micali. Algorand. Technical report, 2017. URL http://arxiv.org/abs/1607.01341.
  17. A. Clement, E. L. Wong, L. Alvisi, M. Dahlin, and M. Marchetti. Making Byzantine fault tolerant systems tolerate Byzantine faults. In Proceedings of the 6th Symposium on Networked Systems Design and Implementation (NSDI), pages 153–168, Boston, MA, Apr. 2009.
  18. C. Decker and R. Wattenhofer. Information propagation in the Bitcoin network. In Proceedings of the 13th IEEE International Conference on Peer-to-Peer Computing, Sept. 2013.
  19. R. Dingledine, N. Mathewson, and P. Syverson. Tor: The second-generation onion router. In Proceedings of the 13th Usenix Security Symposium, pages 303–320, San Diego, CA, Aug. 2004.
  20. N. Döttling and S. Garg. Identity-based encryption from the Diffie-Hellman assumption. In Proceedings of the 37th Annual International Cryptology Conference (CRYPTO), pages 537–569, Santa Barbara, CA, Aug. 2017.
  21. J. R. Douceur. The Sybil attack. In Proceedings of the 1st International Workshop on Peer-to-Peer Systems (IPTPS ’02), Cambridge, MA, Mar. 2002.
  22. P. Erdős and A. Rényi. On the evolution of random graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences, 5:17–61, 1960.
  23. Ethereum Foundation. Ethereum, 2016. https://www.ethereum.org/.
  24. Ethereum Foundation. Create a democracy contract in Ethereum, 2016. https://www.ethereum.org/dao.
  25. I. Eyal and E. G. Sirer. Majority is not enough: Bitcoin mining is vulnerable. In Proceedings of the 2013 Financial Cryptography and Data Security Conference, Mar. 2014.
  26. I. Eyal, A. E. Gencer, E. G. Sirer, and R. van Renesse. Bitcoin-NG: A scalable blockchain protocol. In Proceedings of the 13th Symposium on Networked Systems Design and Implementation (NSDI), pages 45–59, Santa Clara, CA, Mar. 2016.
  27. Y. Gilad, R. Hemo, S. Micali, G. Vlachos, and N. Zeldovich. Algorand: Scaling Byzantine agreements for cryptocurrencies. Cryptology ePrint Archive, Report 2017/454, Version 20170924:210956, Sept. 2017. http://eprint.iacr.org/.
  28. S. Goldberg, M. Naor, D. Papadopoulos, and L. Reyzin. NSEC5 from elliptic curves: Provably preventing DNSSEC zone enumeration with shorter responses. Cryptology ePrint Archive, Report 2016/083, Mar. 2016. http://eprint.iacr.org/.
  29. E. Heilman, A. Kendler, A. Zohar, and S. Goldberg. Eclipse attacks on Bitcoin’s peer-to-peer network. In Proceedings of the 24th Usenix Security Symposium, pages 129–144, Washington, DC, Aug. 2015.
  30. S. Higgins. Bitcoin mining pools targeted in wave of DDoS attacks. Mar. 2015. https://www.coindesk.com/bitcoin-mining-pools-ddos-attacks/.
  31. A. Kiayias, I. Konstantinou, A. Russell, B. David, and R. Oliynykov. Ouroboros: A provably secure proof-of-stake blockchain protocol. Cryptology ePrint Archive, Report 2016/889, 2016. http://eprint.iacr.org/.
  32. S. King and S. Nadal. PPCoin: Peer-to-peer cryptocurrency with proof-of-stake, Aug. 2012. https://peercoin.net/assets/paper/peercoinpaper.pdf.
  33. E. Kokoris-Kogias, P. Jovanovic, N. Gailly, I. Khoffi, L. Gasser, and B. Ford. Enhancing Bitcoin security and performance with strong consistency via collective signing. In Proceedings of the 25th Usenix Security Symposium, pages 279–296, Austin, TX, Aug. 2016.
  34. R. Kotla, L. Alvisi, M. Dahlin, A. Clement, and E. L. Wong. Zyzzyva: Speculative Byzantine fault tolerance. ACM Transactions on Computer Systems, 27(4):7:1–39, 2009.
  35. L. Lamport. The part-time parliament. ACM Transactions on Computer Systems, 16(2):133–169, 1998.
  36. J. Li and D. Mazières. Beyond one-third faulty replicas in Byzantine fault tolerant systems. In Proceedings of the 4th Symposium on Networked Systems Design and Implementation (NSDI), Cambridge, MA, Apr. 2007.
  37. D. Mazières. The Stellar consensus protocol: A federated model for internet-level consensus. https://www.stellar.org/papers/stellarconsensus-protocol.pdf, 2014.
  38. S. Micali. Fast and furious Byzantine agreement. In Proceedings of the Innovations in Theoretical Computer Science (ITCS) Conference, 2017.
  39. S. Micali, M. O. Rabin, and S. P. Vadhan. Verifiable random functions. In Proceedings of the 40th Annual IEEE Symposium on Foundations of Computer Science (FOCS), New York, NY, Oct. 1999.
  40. A. Miller, Y. Xia, K. Croman, E. Shi, and D. Song. The Honey Badger of BFT protocols. In Proceedings of the 23rd ACM Conference on Computer and Communications Security (CCS), pages 31–42, Vienna, Austria, Oct. 2016.
  41. A. Monaghan. US wealth inequality: top 0.1% worth as much as the bottom 90%, Nov. 2014. https://www.theguardian.com/business/2014/nov/13/us-wealth-inequality-top-01-worthas-much-as-the-bottom-90.
  42. S. Nakamoto. Bitcoin: A peer-to-peer electronic cash system. https://bitcoin.org/bitcoin.pdf, 2008.
  43. R. Pass and E. Shi. Hybrid consensus: Efficient consensus in the permissionless model. Cryptology ePrint Archive, Report 2016/917, 2016. http://eprint.iacr.org/.
  44. Peercointalk. Peercoin invalid checkpoint. https://www.peercointalk.org/t/invalidcheckpoint/3691, 2015.
  45. O. Riordan and N. Wormald. The diameter of sparse random graphs. Combinatorics, Probability and Computing, 19(5-6):835–926, Nov. 2010.
  46. P. Rizzo. BitGo launches “instant” Bitcoin transaction tool, Jan. 2016. http://www.coindesk.com/bitgoinstant-bitcoin-transaction-tool/.
  47. J. Rubin. The problem of ASICBOOST, Apr. 2017. http://www.mit.edu/~jlrubin/public/pdfs/Asicboost.pdf.
  48. Y. Sompolinsky and A. Zohar. Secure high-rate transaction processing in Bitcoin. In Proceedings of the 2015 Financial Cryptography and Data Security Conference, 2015.
  49. Y. Sompolinsky, Y. Lewenberg, and A. Zohar. SPECTRE: A fast and scalable cryptocurrency protocol. Cryptology ePrint Archive, Report 2016/1159, 2016. http://eprint.iacr.org/.
  50. N. Szabo. Smart contracts: Formalizing and securing relationships on public networks. First Monday, 2(9), Sept. 1997. http://firstmonday.org/ojs/index.php/fm/article/view/548/469.
  51. R. Turpin and B. A. Coan. Extending binary Byzantine agreement to multivalued Byzantine agreement. Information Processing Letters, 18(2):73–76, Feb. 1984.
  52. M. Vasek, M. Thornton, and T. Moore. Empirical analysis of denial-of-service attacks in the Bitcoin ecosystem. In Proceedings of the 18th International Financial Cryptography and Data Security Conference, Barbados, Mar. 2014.
  53. WonderNetwork. Global ping statistics: Ping times between WonderNetwork servers, Apr. 2017. https://wondernetwork.com/pings.
  54. Zerocoin Electric Coin Company. ZCash: All coins are created equal, 2017. https://z.cash.

翻訳抄

PoS に VRF (Verifiable Random Function) を組み合わせた選出を行う BFT 合意アルゴリズム Algorand に関する 2017 年の論文。

  1. Yossi Gilad, Rotem Hemo, Silvio Micali, Georgios Vlachos, Nickolai Zeldovich (2017) Algorand: Scaling Byzantine Agreements for Cryptocurrencies