CometBFT: コンセンサス
 概要
概要
分散システムにおけるコンセンサスとは、分散ネットワーク上のすべての正常なノード間で合意を形成して共通の状態を確立するためのメカニズムである。よりブロックチェーン向けの表現では、コンセンサスに参加しているノードが「提案されたブロックを受理 (または拒否)」という共通の結論に到達するためのメカニズムを意味する。コンセンサスで受理されたブロックは確定した (confirmed) みなされブロックチェーン上の 1 つの正当なブロックとなる。
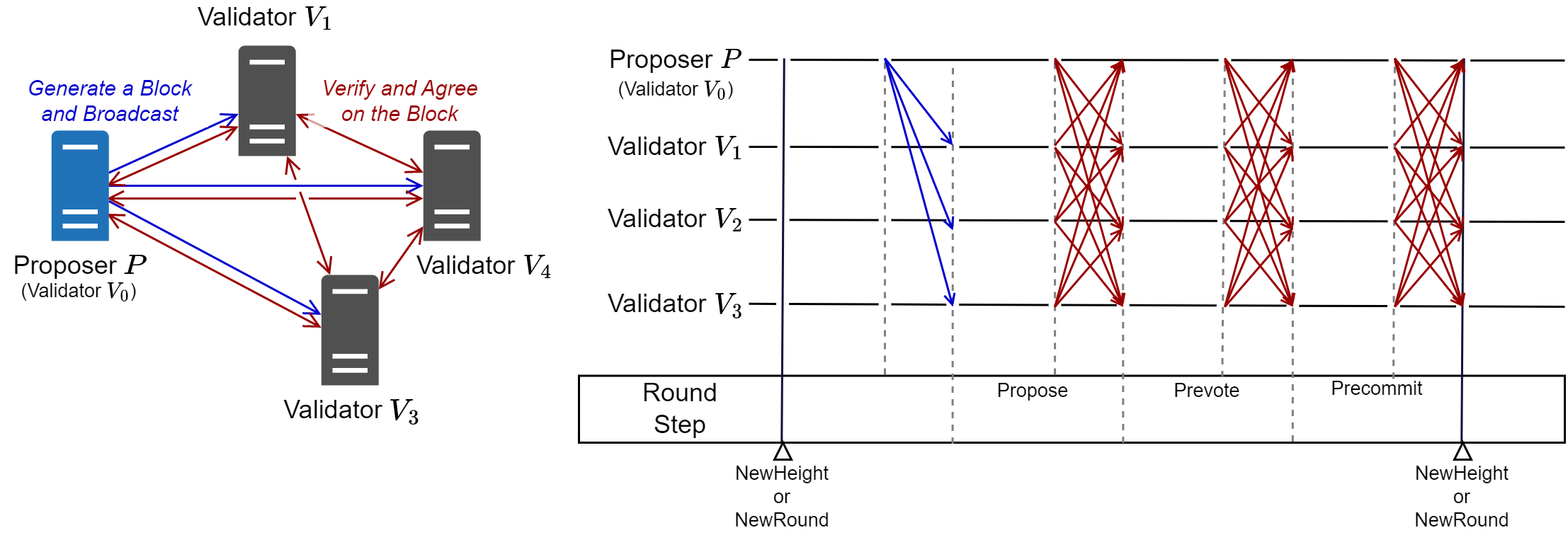
CometBFT のブロック生成プロセスは Fig 1 に示すような CometBFT (フレームワークと同じアルゴリズム名; 旧名 Tendermint-BFT) と呼ばれる pBFT 派生の分散合意アルゴリズムに基づいている。これはビザンチン障害耐性 (BFT; Byzantine fault tolerance) を持つ強い一貫性の分散合意アルゴリズムである。このプロセスによってすべての正常な Validator は不正なブロックの作成や改ざんを検出し、受理か拒否かで合意に到達し、受理されたブロックのみが正しいブロックとして CometBFT ネットワークで受け入れられる。
Table of Contents
 構成
構成
CometBFT のコンセンサスクラスタは、提案ブロック (proposal block) を作成する 1 つの Proposer ノードと、提案ブロックを検証し受理か拒否かを BFT プロトコルで合意して確定する 1 つ以上の Validator ノードの 2 種類で構成されている。Proposer は Validator の中から選ばれるため Validator の役割も併せて持つ。
CometBFT ではブロックチェーンに含まれるブロックの数をそのブロックチェーンの高さ (height) と呼ぶ。また特定のブロック \(B_h\) がブロックチェーン上に現われる位置をそのブロックの高さとも呼び 64-bit 値 \(h \in \{1,2,\ldots,2^{64}-1\}\) で表す。ブロックチェーンにおける最初のブロック \(B_1\) はジェネシスブロック (genesis block) であり、これは CLI ツールでブロックチェーンのインスタンスを構築したときに作成される genesis.json で定義されている。ブロックチェーンの高さはまた、物理クロックを使えない P2P ネットワーク環境において論理クロックとして使用されることも多い。
コンセンサスクラスタ \(\vector{V}_h\) は特定の高さのブロック \(B_h\) を生成し確定することを目的とした Validator の集合である。ブロック \(B_h\) を確定するまで \(\vector{V}_h\) を構成する Validator が変化することはない。Proposer は \(\vector{V}_h\) の中から選出される。Proposer ノードの故障などの理由でブロックの生成に失敗すると、同じ \(\vector{V}_h\) から別の Proposer が選出されてブロック生成を続行する。
ある Proposer が提案ブロックを生成し \(\vector{V}_h\) の Validator がそれを受理または拒否する 1 つのサイクルをラウンド (round) と呼び 31-bit 値 \(r \in \{0,1,\ldots,2^{31}-1\}\) で表す。\(\vector{V}_h\) は提案ブロック \(B'_{h,r}\) の合意に失敗すると、ラウンドを一つ進めて新しい Proposer ノード \(P_{h,r+1}\) を選出し、新しい提案ブロック \(B'_{h,r+1}\) に対しての合意を再実行する (ただしラウンドの進行状況よってはラウンド \(r\) の途中から再実行することもある)。
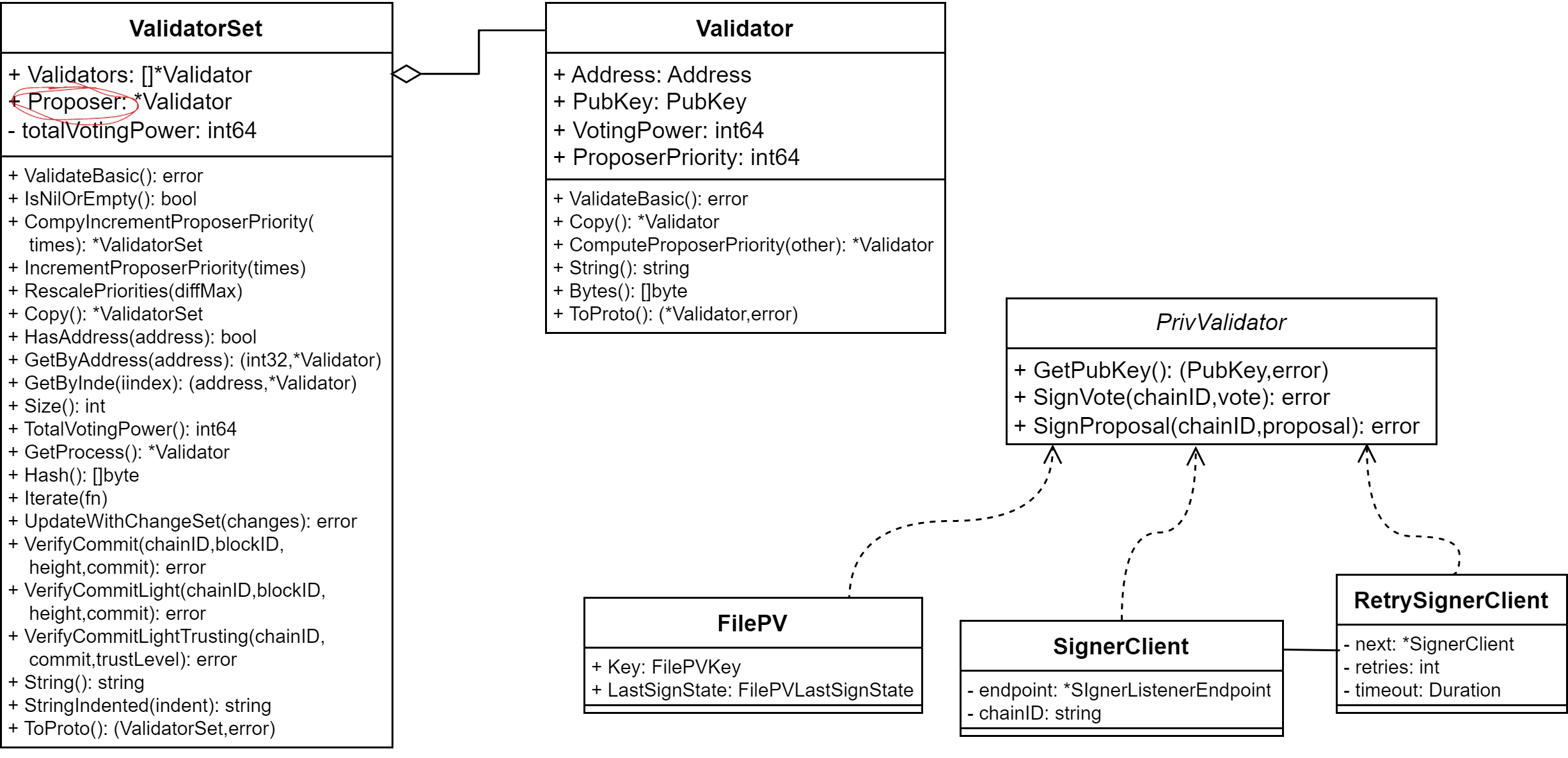
CometBFT では ValidatorSet クラスがコンセンサスクラスタを表している。提案ブロックを生成する Proposer ノードはブロック生成ラウンドごとに ValidatorSet の中から選出される。あるラウンドを担当する Proposer は新しい提案ブロックを作成してクラスタに提出する。ValidatorSet に含まれる各 Validator は提案ブロックを検証し、受理または拒否を判断して ValidatorSet 内の他の Validator と BFT で合意する。
ValidatorSet は ブロックを実行した後の EndBlock 応答ごとにアプリケーション実装で変更することができる。言い換えるとコンセンサスクラスタ \(\vector{V}_h\) の構成は高さ \(h\) に対して決定する。これは、例えばコンセンサスに参加する権利の NFT を流通しインセンティブを付与するといった "マイニング" に似たアプリケーション実装を意図した設計である (逆に言えばアプリケーション実装はコンセンサスクラスタのノードを変更する機能や責務を持つ必要がある)。なお、最初のジェネシスブロックを確定する ValidatorSet はジェネシスブロックを定義する genesis.json に定義されている。
ValidatorSet には Proposer フィールドがあり、ラウンドが進行するごとに Proposer フィールドのみが変化する。ValidatorSet が参照する Validator の各インスタンスは、アドレス、署名検証のための公開鍵、Proposer 選出のための属性といった情報を持っている単なるリモートノードのエイリアスである。
一方、実際の署名機能 (秘密鍵) を持つローカルノードに相当する Validator は PrivValidator インターフェースとして定義されている。これは秘密鍵を管理する方法によって実装を変更できるように設計されている。例えば FilePV 実装は秘密鍵を単純にローカルファイルに保存する PrivValidator であるし (これは扱いやすいがセキュリティは低い)、SignerClient 実装はファイアウォールの内側に配置された KMS を利用してよりセキュリティの高い Validator ノードを構築することができる。
Validator はブロックを検証するが、トランザクションの内容はアプリケーション実装によって定義されるため検証の対象ではなく、CometBFT のコンセンサス層ではトランザクションを単なるバイト配列のデータとみなすだけである。トランザクションの検証は、提案ブロックが作成されるより前の、mempool に保存される時点で CheckTx ABCI でアプリケーション実装によって行われる。
 状態遷移
状態遷移
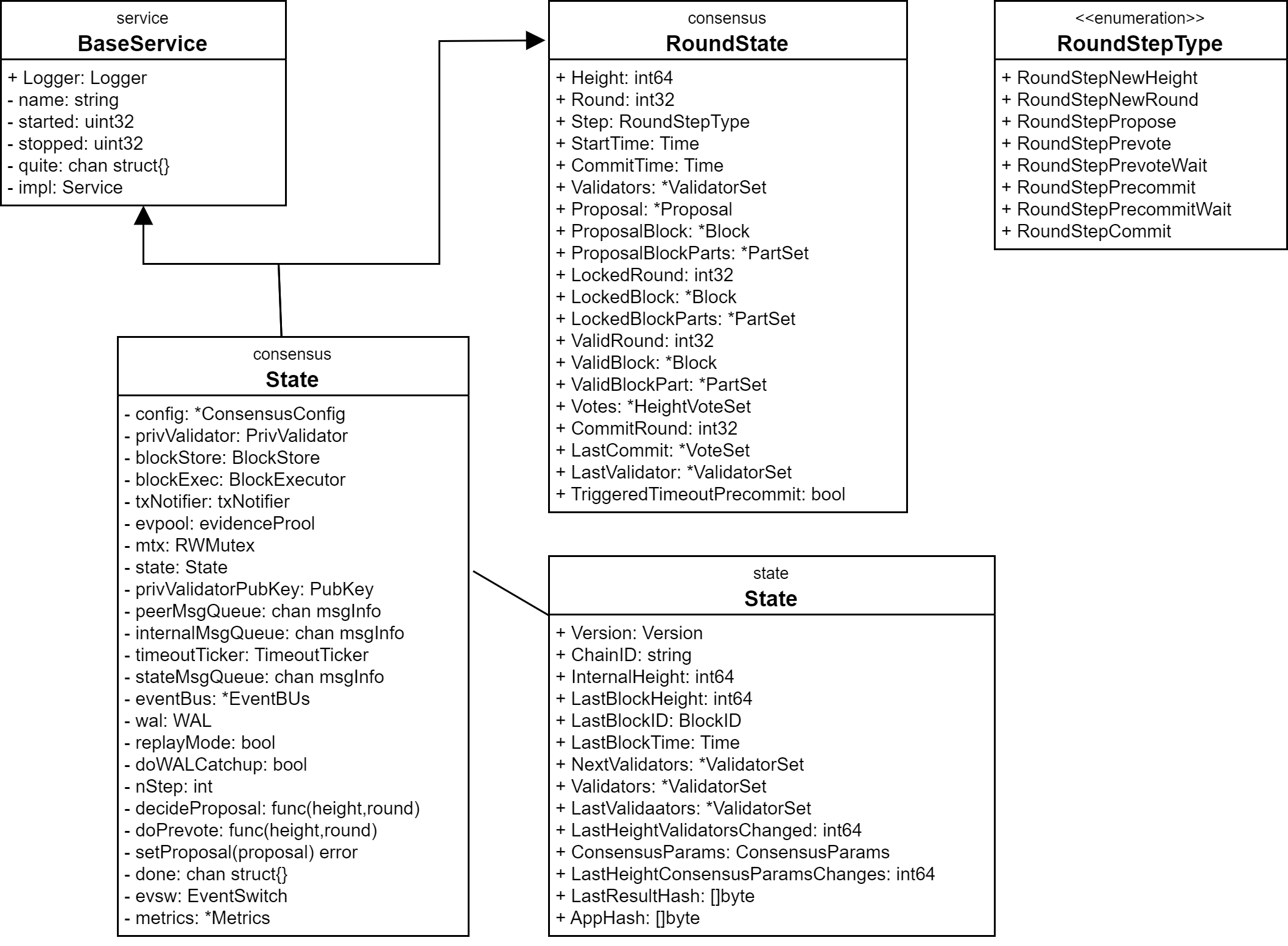
CometBFT のコンセンサスに関連する状態変数は多く、またその変更経路や関連する非同期イベントも多岐にわたるため非常に複雑である。CometBFT のコンセンサスの状態遷移を追跡しようとする人は consensus.State という巨大なクラスを読み解くことになる。
State という名のクラスが 2 つ登場することからして混乱の元凶だが、それぞれは次のような違いがある。
consensus.Stateは進行中のコンセンサスの状態であり、またコンセンサスの各フェーズを実行するメソッドを定義したステートマシンである。state.Stateはコミットされたブロックごとのメタ情報である。そのブロックを生成するために使用された Validator やコンセンサスパラメータなど、そのブロックを後で検証するために必要な情報をすべて保持している。
コンセンサスの状態遷移は consensus.State が行っているので以下はそちらに注目する。
 非同期処理
非同期処理
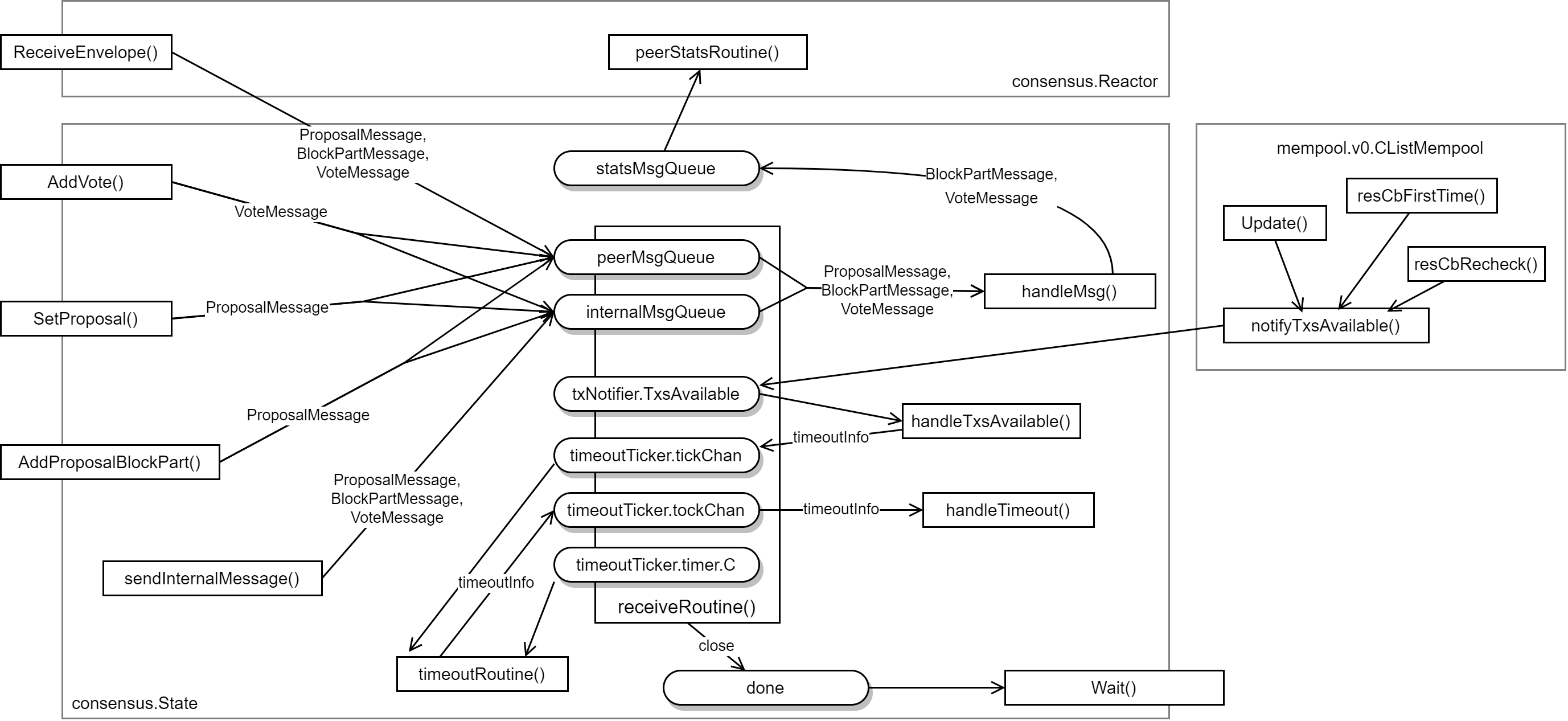
状態遷移のスレッド境界を知るためにキュー (Go で言うところの chan) によって分断されている非同期処理に注目する。consensus.State には peerMsgQueue, internalMsgQueue, statsMsgQueue, done の 4 つのキューが存在する。
Proposal, BlockPart, Vote メッセージは internalMsgQueue か peerMsgQueue を経由し、Proposal は State 内部で保持し BlockPart と Vote は consensus.Reactor に伝達される。internal プレフィクスは内部で発生したメッセージ、peer プレフィクスはピアから受信したメッセージを処理するが、どちらに投入されたメッセージも最終的に handleMsg() を経由して consensus.Reactor に伝達する。
timeoutTicker は
 Round Step の遷移
Round Step の遷移
ラウンドはステップ (フェーズ) に分かれている。ラウンド内のステップの切り替わりは RoundState.Step の遷移を追跡すれば良い。
 NewHeight ステップ
NewHeight ステップ
前のラウンドで提案ブロックが受理されるなどして新しいブロック生成フェーズが始まると、次のブロックを生成するためにコンセンサス状態が設定される。
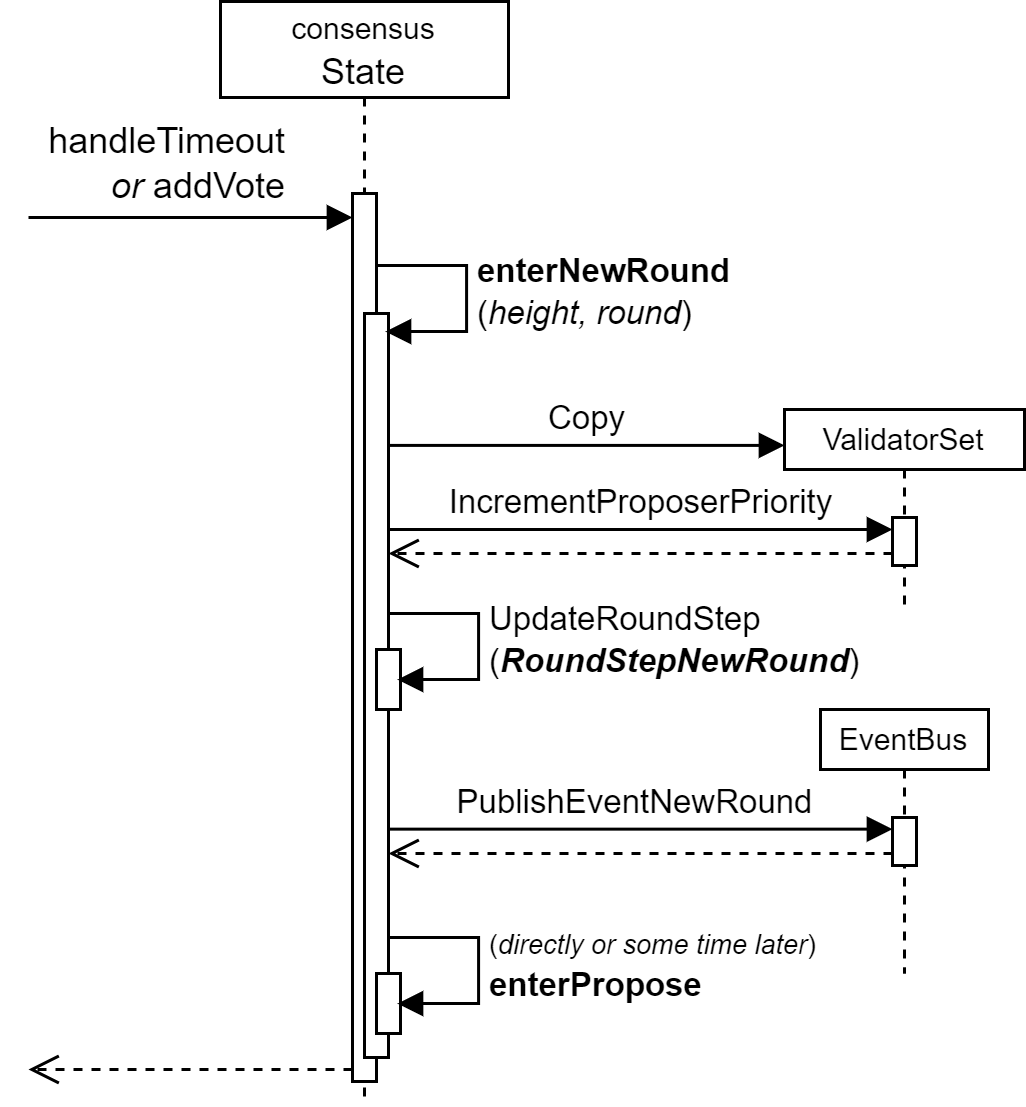
 NewRound ステップ
NewRound ステップ
- NewHeight から一定時間が経過するか、または
- NewHeight 状態で直前のラウンドの Precommit 票を受信しすべての票が揃った
ときに呼び出され、NewRound ステップへ移行したあとすぐに Propose ステップに移行する。
enterNewRound ではラウンドの進行で新しい Proposer を選出するために ValidatorSet の ProposerPriority が調整される。
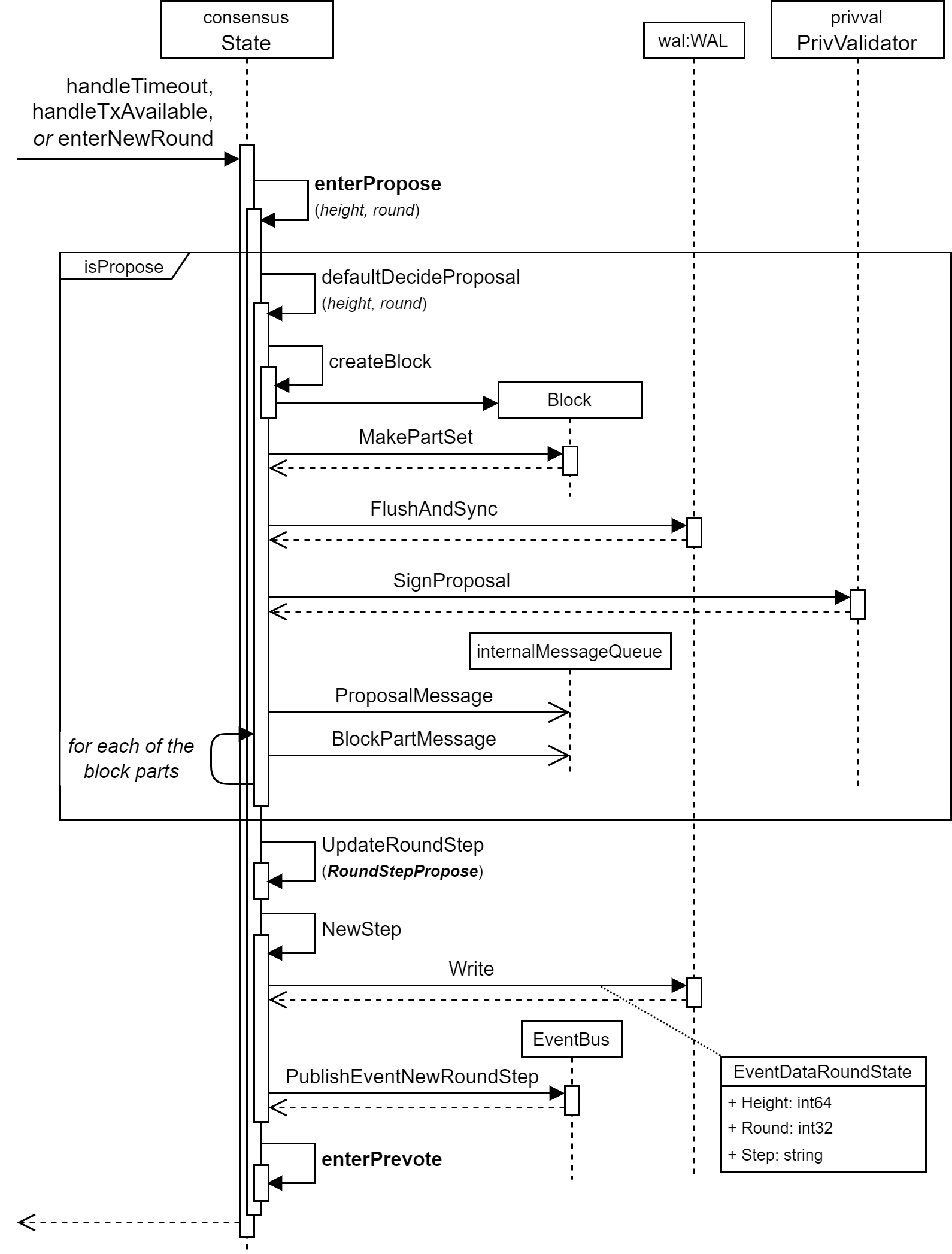
 Propose ステップ
Propose ステップ
- NewHeight から一定時間が経過するか、または
- NewHeight 状態で直前のラウンドの Precommit 票を受信しすべての票が揃った
ときに呼び出され、NewRound ステップへ移行したあとすぐに Propose ステップに移行する。
enterNewRound ではラウンドの進行で新しい Proposer を選出するために ValidatorSet の ProposerPriority が調整される。
 合意アルゴリズム
合意アルゴリズム
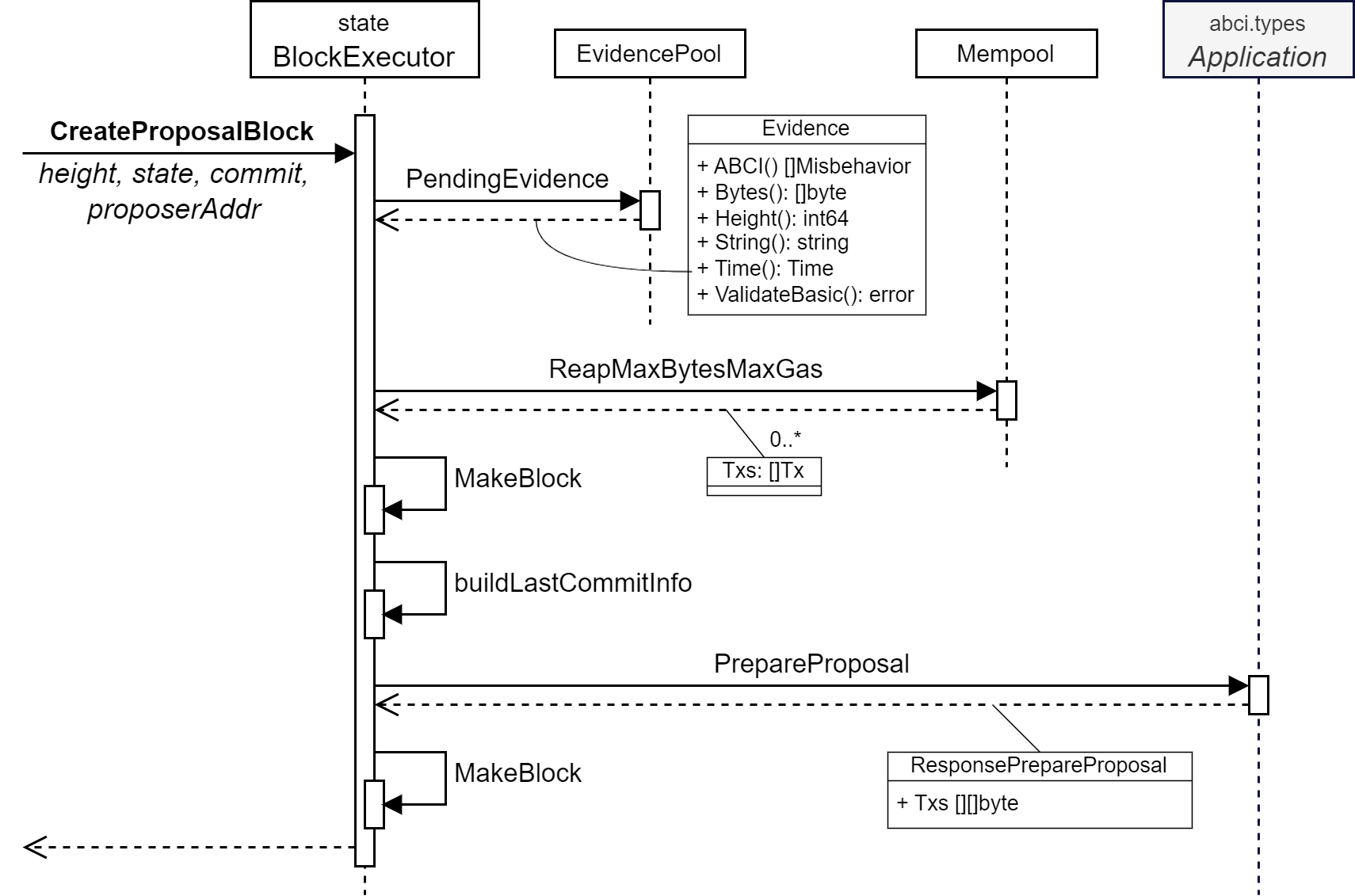
 提案ブロックの生成
提案ブロックの生成
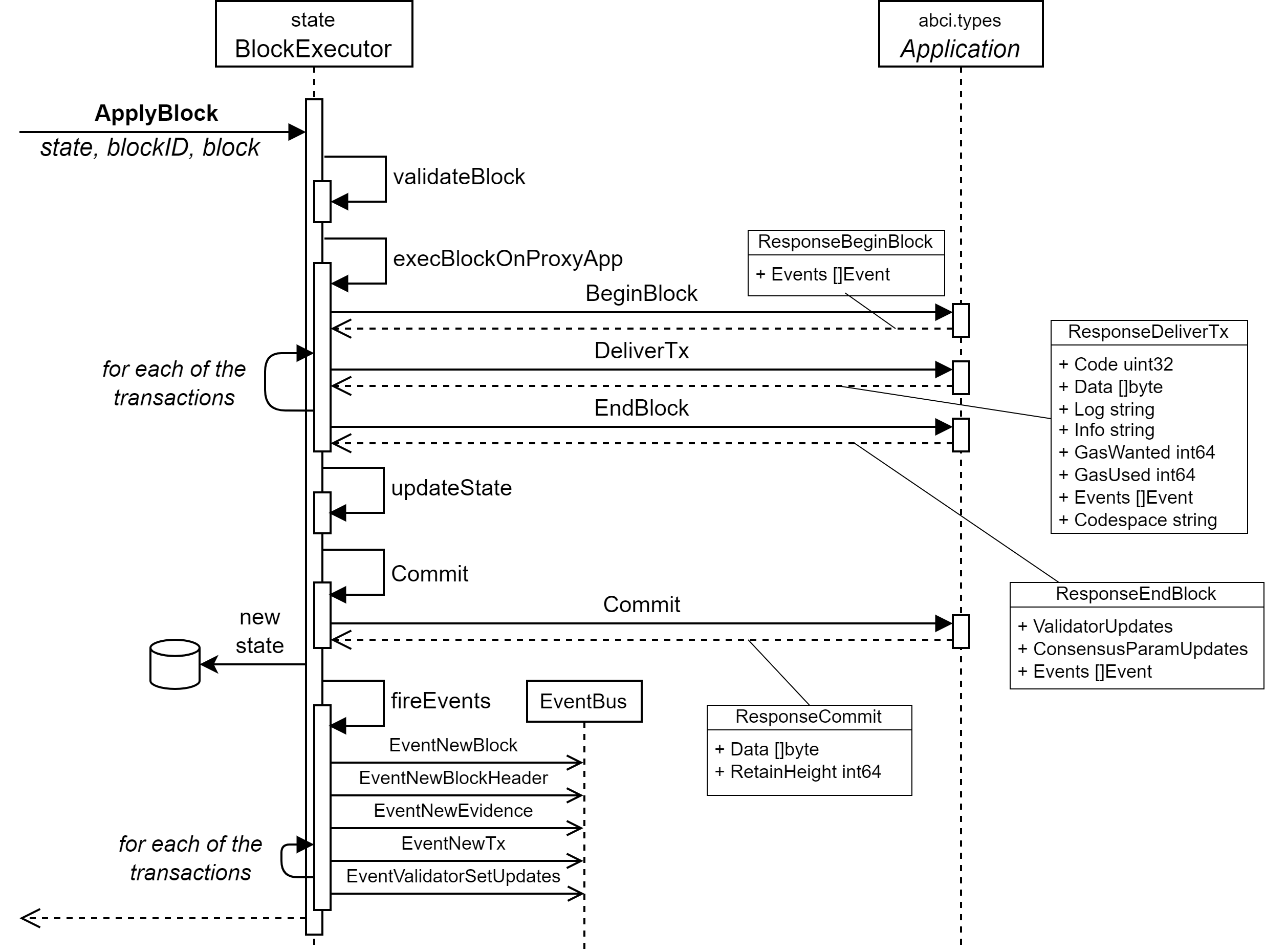
 ブロックの適用
ブロックの適用
Validator の合意によってブロックが確定すると BlockExecutor がブロックの適用を開始する。
- ブロックの検証。
- ブロックの実行。これはブロックに含まれるすべてのトランザクションをアプリケーション実装が実行し状態を更新する。
- コミット。
ブロックの適用が正常に終了すると現在の height に対するラウンドが終了し、次の height に対するラウンド用の State が生成される。
 ビュー変更
ビュー変更
アプリケーション実装は EndBlock のレスポンスで有効な ValidatorUpdates を返して次回以降のブロック生成を担当する ValidatorSet を指定することができる。これは一般的な分散システムでのビュー変更 (view change) あるいは構成変更と呼ばれるイベントをアプリケーション実装の主導で行うことができるという意味である。合意に参加する ValidatorSet をどのように選ぶかはアプリケーション実装が完全に制御できるため、アプリケーション定義の通貨保有量やトークン所有で合意に参加する ValidatorSet を選ぶことができる。
 選出アルゴリズム
選出アルゴリズム
CometBFT は Validator 集合からラウンドごとに Proposer を選択する。このアルゴリズムは、それぞの Validator が持つ票数 (voting power) で重み付けられた Round Robin アルゴリズムであり Proof of Stake の一種と言える。具体的な実装アルゴリズムは Priority Queue で要素を選択する方法と同じである。
\(t = S\) となる時にそれぞれの Validator の選出頻度が概ね Voting Power \(s_i\) と一致することが分かるだろう。
基本的な選出方針は、ラウンドごとに各 Validator の Proposer Priority に Stake を加算してゆき、最も大きい Priority を持つ Validator を次のラウンドの Proposer とする。Proposer に選出されると Priority は最下位程度まで減算される。ラウンドロビン設計だが、ラウンドごとに Stake を累積してゆくことで Stake 保有量が多く長期間保有している Validator が高い頻度で選出される構造になっている。また実際には加算によってオーバーフローしないように正規化 (再スケーリング) を行っている。
ある Validator 集合 \(\vector{V}\), \(|\vector{V}| = N\) に含まれる Validator \(V_i\) が持つ票数 (voting power \(\simeq\) Stake) を \(s_i\)、ラウンド \(t\) における \(V_i\) の Priority を \(p_{i,t}\) とすると Priority の初期状態は以下のように表される。\[ \begin{equation} p_{i,0} = - C S + s_i \label{initial_priority} \end{equation} \] ここで \(S\) は \(\vector{V}\) 全体の総評数 \(\sum_{i=i}^{N} s_i\)、\(C \simeq 1.125\) は定数である。式 (\(\ref{initial_priority}\)) より初回は Validator の持つ票数の多さで Proposer が選択されることが分かる。また途中から合意に参加する Validator もこの初期値から始まる。
ラウンド \(t\) の各 \(p_{i,t}\) は概ね 0 を中心に \(\pm S\) となるように正規化される。より正確には \(\max p - \min p = 2S\) となるように線形返還され、さらにそれぞれから平均値を減算する。正規化後、Validator ごとに \(q_{i,t+1} = p_{i,t} + s_i\) を求め、最も大きい \(q_{i,t+1}\) を持つ Validator が \(t+1\) ラウンドでの Proposer となる。\[ \begin{array}{rcl} r & = & \left\lceil \frac{\max p_t - \min p_t}{2S} \right\rceil \\ \bar{p}_t & = & \frac{r}{N} \sum_{i=1}^N p_{i,t} \\ q_{i,t+1} & = & (r \ p_{i,t} - \bar{p}) + s_i \\ P_{t+1} & = & \argmax_i q_{i,t+1} \end{array} \] Proposer に選出された Validator の \(q_{P_{t+1},t+1}\) からは \(S\) が減算されて次のラウンドの Proposer Priority となる。\[ p_{i,t+1} = \left\{ \begin{array}{ll} q_{i,t+1} - S \ \ & \mbox{if} \ \ i = P_{t+1} \\ q_{i,t+1} \ \ & \mbox{otherwise} \end{array} \right. \]
\(q_{i,t} = q_{j,t}\) となるような Validator \(i\), \(j\) が存在する場合、そのアドレスのバイナリ表現が小さい方が優先される。票を持たない \(s_i=0\) の Validator は初期状態で最下位であり累積も行われないため (\(S \ne 0\) ならば) Proposer として選出されることはない。