論文翻訳: The latest gossip on BFT consensus
Tendermint
 Abstract
Abstract
この論文は敵対的な条件下で分散ネットワーク内のイベントを順序付けるための新しいプロトコルである Tendermint を紹介する。この問題はビザンチンフォールトトレラント (BFT) コンセンサスやアトミックブロードキャストとしてよく知られているが、近年、ビットコインやイーサリアムなどのブロックチェーンベースのデジタル通貨が広く普及し、中央機関を介さずにパブリックな設定でこの問題を解決することに成功したことにより大きな注目を集めている。Tendermint はこの問題に関する古典的な学術研究を現代化し、ノード間のピアツーピアゴシッププロトコルに依存することにより BFT アルゴリズムの設計を簡素化している。
Table of Contents
- Abstract
- 1 導入
- 2 定義
- 3 Tendermint コンセンサスアルゴリズム
- 4 Tendermint コンセンサスアルゴリズムの証明
- 5 結論
- Acknowledgements
- References
- 翻訳抄
 1 導入
1 導入
コンセンサスは分散コンピューティングにおける最も基本的な問題の一つである。これは、決定論的ステートマシンとしてモデル化できるサービスを複製するための一般的なアプローチであるステートマシンレプリケーション (SMR) において重要な役割を果たしている [1], [2]。このアプローチの重要な考え方は、サービスレプリカが同じ状態で開始し、同じ順序でリクエスト (トランザクションとも呼ばれる) を実行することで、レプリカが互いに動悸していることを保証するということである。SMR アプローチにおけるコンセンサスの役割は、全てのレプリカが同じ順序でトランザクションを受信することを保証することである。従来 SMR ベースのシステムはデータセンター (ローカルエリアネットワーク) の構成で展開され、レプリカの数が少数 (3〜7) であり、一般的には単一の管理ドメインの一部である (例えば Chubby [3])。そのため、より一般的な障害 (特に悪意のある障害またはビザンチン障害) はごく僅かな確率でしか発生しないと想定しており、良性の障害 (クラッシュ) のみを扱っている。
近年の暗号通貨やブロックチェーンシステムの成功 (例: [4], [5] は SMT ベースのシステムの設計と展開に新たな課題を提起している: これは同じ管理ドメインに属していない多数の (数百または数千) ノード間で、広域ネットワーク上で合意に達すること、そして、ノードのサブセットが悪意 (ビザンチン障害) を持って行動する可能性があるということである。さらにノードが相互に完全に接続されている以前のデータセンター展開とは異なり、ブロックチェーンシステムでのノードは他のノードのサブセットにしか接続されていないため、通信はゴシップベースのピアツーピアプロトコルによって実現される。新しい要件は、主旨の焦点が異なる設定であったため、古典的なビザンチンフォールトトレラントコンセンサス (または SMR) システムに関する学術論文 (例えば [6], [7]) に必ずしも存在しない設計とアルゴリズムを要求する。
この論文では Tendermint1 と呼ばれる BFT SMR プラットフォームのコアである新しいビザンチン耐障害性コンセンサスアルゴリズムについて説明する。Tendermint のプラットフォームは Go で記述された高性能な BFT SMR 実装、コンセンサス以上の任意の決定論的アプリケーションを構築するための柔軟なインターフェースおよび展開と管理のためのツール群で構成されている。
Tendermint のコンセンサスアルゴリズムは PBFT SMR アルゴリズム [8] および認証された障害用の DLS アルゴリズム ([6] の Algorithm 2) に触発されている。DLS アルゴリズムと同様に Tendermint はラウンド2 で進行する。各ラウンドには専用の提案者 (コーディネーターやリーダーとも呼ばれる) が存在し、プロセスは通常の処理の一部として新しいラウンドに進む (PBFT のように提案者に問題があったり多くのプロセス欠陥が疑われる場合だけではない)。各ラウンドの通信パターンは PBFT の "normal" の場合と非常によく似ている。したがって、好ましい条件 (正常な提案者、プロセス間のタイムリーで信頼性の高い通信) の下では Tendermint は (PBFT と同じ) 3 つの通信ステップで決定する。
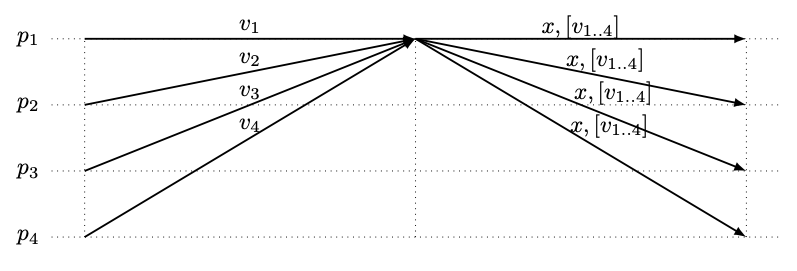
Tendermint コンセンサスアルゴリズムの主な新規性と貢献は新しい終了メカニズムである。[9], [10] で説明されているように、部分同期システムモデルに対する既存の BFT コンセンサス (および SMR) アルゴリズムは (例えば PBFT [8], [6, [11]) は、通常、Fig 1 に示すような通信パターンに依存して終了している。Fig 1 はプロセスが新しいラウンド3を開始する際の提案者の変更中に交換されるメッセージを示している。これは、最終的に (つまりグローバル安定時間 (GST) が経過した後に) 正しい提案車を持つラウンドが存在し、システムを一本化することを保証するものである。直感的には、提案された値が全ての正しいプロセスに受け入れられ、正しいプロセス間のコミュニケーションがタイムリーで信頼できるラウンドでは、全ての正しいプロセスが決定に到達する。
提案された値が全ての正しいプロセス4で受け入れられるように、提案者は 1) 他のプロセスからのメッセージを受信してグローバルな状態を構築し 2) 提案する安全な値を選択し 3) 選択された値を、最初のステップで受信した署名付きメッセージとともに、それを支持するために送信する。正しいプロセスが次の提案者に送る値 \(v_i\) は、通常、そのプロセスが決定のために許容できると考える値に対応する:
- PBFT [8] や DLS [6] では、値そのものではなく同じ値 ID を持つ \(2f+1\) 符号付きメッセージの集合である。
- 高速ビザンチン Paxos [11] では、値自身が送信されている。
どちらの場合でも、我々のシステムモデル (すなはちゴシップベースネットワークの多数のノード) でこのメカニズムを使用すると、プロセスの数とともに通信複雑性が高くなる: 最初のケースではプロセスの総数に応じたメッセージが送信され、2つ目のケースではそれぞれのプロセスによって値 (トランザクションのブロック) が送信される。最初のステップで受信したメッセージのセットは、通常、選択された値 \(x\) の選択を正当化するために提案メッセージ (Fig 1 で \([v_{1..4}]\) で示される) に便乗している。
我々は、我々が検討しているシステムモデルにより適した Tendermint の新しい終了メカニズムを設計した。これは追加の通信を必要とせず (新しいメッセージを送信したり、既存のメッセージに情報を便乗させたりする必要もない) PBFT [8] の normal の場合と非常によく似た通信パターンに基づいている。したがって Tendermint の実行モードは単一であり、他の PBFT ライクなプロトコル ([8], [12], [13] など) に見られるような normal モードとリカバリーモードの分離は存在しない。これにより Tendermint の理解と実装がよりシンプルとなり、正しく実装できるようになると考えている。
BFT コンセンサスアルゴリズムのスケーラビリティと分散化 (プロセス数) を向上させるためにメッセージの複雑性を減らすための直行的なアプローチは、例えば SBFT [15] で行われているような高度な暗号 (例えば Boneh-Lynn-Shacham (BLS) 署名 [14]) を使用することであることに注意。
論文の残りの部分は以下の通りである。セクション 2 ではシステムモデルを定義し問題を定義する。セクション 3 では Tendermint コンセンサスアルゴリズムを提示し、セクション 4 でその証明を提示する。最後にセクション 5 で結論を述べる。
- 1 Tendermint プラットフォームは https://github.com/tendermint/tendermint でオープンソースとして公開されている。
- 2 Tendermint は [6] の基本的なラウンドモデルには含まれていない。さらに [6] とは異なる用語としてラウンドを用いている。
- 3 分散コンピューティングの用語には論理単位 (logical unit) に対応する通信ステップのシーケンスの命名に関する一貫した用語は存在しない。ラウンド、フェーズ、ビューと呼ばれることもある。
- 4 BFT アルゴリズムにおいて、提案された値が正しいプロセスによって盲目的に受け入れられることはない。コンセンサスの安全性特性が侵害されないように、提案された値が安全に受け入れられるかどうかを正しいプロセスは常に検証する。
 2 定義
2 定義
 A. モデル
A. モデル
我々はメッセージを交換して通信するプロセスのシステムについて考える。プロセスには正常なものと故障したものがあり、故障プロセスは任意の動作をすることができる (つまりビザンチン故障を考慮する)。各プロセスはある量の投票権 (voting power) を持っていると仮定する (あるプロセスが投票権 0 でも構わない)。このモデルではプロセスは特定の管理ドメインに属していないため、すべてのプロセス間で直接的なネットワーク接続を強制することはできない。代わりに各プロセスはピアと呼ばれるプロセス部分集合に接続しており、すべての正常なプロセスの間には間接的な通信チャネルが存在すると仮定する。プロセス間の通信はゴシッププロトコル [16] を用いて確立される。
形式的には、部分同期システムモデル [6] の変種を使用してネットワーク通信をモデル化する。システムのすべての実行で、境界 \(\Delta\) と instant GST (Global Stabilization Time) が存在し、正しいプロセス間の GST 後のすべての通信は信頼性が高く、\(\Delta\) 時間的に安定している。つまり、例えば正常なプロセス \(p\) が時刻 \(t \ge {\it GST}\) にメッセージ \(m\) を正常なプロセス \(q\) 宛に送ったとすると、\(q\) は \(t + \Delta\) 以前に \(m\) を受信することになる5。標準的な部分同期システムモデル [6] に加えて、我々は通信のゴシップベースの性質を捉える補助的な特性を仮定している6:
- ゴシップ通信: 正常なプロセス \(p\) が時刻 \(t\) に何らかのメッセージ \(m\) を送信した場合、すべての正常なプロセスは \(\max \{ t, {\it GST} \} + \Delta\) 以前に \(m\) を受信する。さらに、正常なプロセス \(q\) が時刻 \(t\) に何らかのメッセージ \(m\) を受信すると、すべての正常なプロセスは \(\max \{t, {\it GST}\} + \Delta\) 以前に \(m\) を受信する。
境界時間 \(\Delta\) と \({\it GST}\) はこのアルゴリズムの安全性に関して知る必要のないシステムパラメータである。アルゴリズムの終了は \({\it GST}\) 以後の境界時間内に保証されている。実際には、システムが (十分な長さので) 良好期間と不良期間を相互に繰り返すという、やや弱い変則でもアルゴリズムは正しく動作するが、\({\it GST}\) モデルを考慮することで論議を単純化することができる。ここで良好時間はシステムが信頼でき、かつ \(\Delta\) 時間的に安定している \({\it GST}\) 後の期間に相当し、不良時間はシステムが非同期でありメッセージが喪失する可能性がある \({\it GST}\) 前の期間に相当する。
我々はプロセスのステップにかかる時間 (メッセージの送受信を含む) がゼロであると仮定する。プロセスには時計が搭載されており、ローカルなタイムアウトを計測することができる。公開鍵暗号方式を採用していることでなりすまし/偽装攻撃は常に不可能であると仮定している。つまり、すべてのプロトコルメッセージにはデジタル署名が含まれていると仮定している。したがって、正常なプロセス \(q\) がピアから署名付きメッセージ \(m\) を受信した場合、プロセス \(q\) はメッセージ \(m\) のオリジナルの送信者が誰であるか、メッセージの署名が有効かどうかを検証することができる。読みやすさを向上させるため、アルゴリズムの擬似コードでは署名検証のステップを明示していない。そのレベルでは有効な署名を持つメッセージのみが考慮されると仮定している (無効な署名を持つメッセージは削除される)。
- 5すべての正常なプロセス間で直接的な通信チャネルを想定しているわけではないため、メッセージ \(m\) が \(q\)に到達する前にゴシッププロトコルを用いてメッセージ \(m\) を \(q\) に転送する複数の正常なプロセスを通過する可能性があることに注意。
- 6Tendermint ゴシッププロトコルの詳細については別の技術文書で説明する。
 B. ステートマシンレプリケーション
B. ステートマシンレプリケーション
決定論的なステートマシンとしてモデル化されたステートマシンレプリケーション (SMR) はサービスを複製するための一般的なアプローチである [1], [2]。このアプローチの重要なアイディアは、すべてのレプリカが同じ状態で開始し、クライアントからの要求を同じ順序で適用することで、レプリカの状態が発散しないことを保証することである。Schneider [2] によれば (ビザンチン) 故障に体制のある複製ステートマシンを実装するには以下の点が重要であると指摘されている:
- レプリカの協調: すべての [故障していない] レプリカは同じ順序のリクエストを受け取り処理する。
さらに、Schneider も指摘しているように、この特性は「合意」と「順序」の 2 つに分解することができる。「合意」とはすべての (故障していない) レプリカがすべてのリクエストを受信することを必要とし、「順序」とは受信したリクエストの順序がすべてのレプリカで同じであることを必要とする。
ビザンチン耐性ステートマシンレプリケーションにはクライアントから提案されたリクエスト (Tendermint ではトランザクションと呼ばれる) のみが実行されるという追加の要件がある。Tendermint では、トランザクションの検証は複製されるサービスの責任である。クライアントからトランザクションを受け取ると、Tendermint プロセスはサービスにリクエストが有効であるかを尋ねて有効なリクエストのみが処理される。
 C. コンセンサス
C. コンセンサス
Tendermint は、複製サービスが実行するトランザクションの各ブロックに合意するために、コンセンサス実体を順次実行することでステートマシンレプリケーションを解決する。我々はブロックチェーンシステムに動機づけられた [17] Validity Predicate-based Byzantine Consensus と呼ばれるビザンチン合意問題の変種について考える。この問題は合意、終了及び有効性の特性によって定義される。
- 合意: 2 つの正常なプロセスが異なる値を決定しない。
- 終了: すべての正常なプロセスが最終的にある値を決定する。
- 有効性: 決定された値が有効であること、つまり \({\it valid}()\) と表記される定義済みの述語を満たすこと。
ビザンチン合意問題は値が有効であるかどうかを示すためにアプリケーション固有の \({\it valid}()\) 述語を持つ。例えばブロックチェーンシステムの文脈では、ブロックチェーンに追加された最後の値 (ブロック) は適切なハッシュが含まれていなければ有効な値ではない。
 3 Tendermint コンセンサスアルゴリズム
3 Tendermint コンセンサスアルゴリズム
このセクションでは Tendermint ビザンチン障害耐性コンセンサスアルゴリズムを紹介する。このアルゴリズムは Algorithm 1 に記載されている擬似コードで表現される。アルゴリズムはアトミックに実行される upon rule の集合として提示している7。プロセスはゴシッププロトコルを使用してプロトコルメッセージを交換し、受信メッセージと送信メッセージの両方がすべてのプロセスのローカルメッセージログに保存されると想定している。メッセージがメッセージログに含まれ、対応する条件が true と評価されると upon rule がトリガーされる。特定のタイプと内容の \(X\) 個のメッセージの受信を想定する条件は、少なくとも \(X\) に等しい総投票権を持つ送信者のメッセージの受信を意味する。例えば \(2f+1\) 個の \(\langle {\sf PRECOMMIT}, h_p, r, {\it id}(v) \rangle\) という条件は、高さ \(h_p\)、ラウンド \(r\)、\({\it id}(v)\) に等しい値の \({\sf PRECOMMIT}\) メッセージで、送信者が少なくとも \(2f+1\) に等しい総投票権を持っているものを受信したときに真と評価される。ルールの中には対応する条件が初めて true と評価されたときのみトリガーされることを示す "for the first time" 制約が付いているものもある。これは、該当するルールが常にアルゴリズムの状態変数を変更するわけではないため、この制約をつけることでアルゴリズムが永遠にこのルールを実行し続けることを防止するためである。添字の \(p\) はプロセスのローカル状態変数で、添字 \(p\) の付かない変数は値のプレースホルダーである。記号 \(*\) は任意の値を示す。
このアルゴリズムは \(n \gt 3f\)、すなはち故障したプロセスの総投票権が全体の投票権の 3 分の 1 より小さいことを前提としている。簡略化のために \(n=3f+1\) のケースのアルゴリズムを示す。
アルゴリズムはラウンドごとに進行し、各ラウンドには専用の提案者 (proposer) がいる。ラウンドと提案者のマッピングはすべてのプロセスが知っており、コンセンサス実体 \(h\) のラウンド \({\it round}\) の提案者を返す関数 \({\sf proposer}(h,{\it round})\) で得られる。この提案者選択巻数はプロセスの投票権に比例して交代する、重み付きラウンドロビンと仮定する8。プロトコルの内部状態の遷移はメッセージ受信とタイムアウトによってトリガーされる。Algorithm 1 には \({\it timeoutPropose}\), \({\it timeoutPrevote}\), \({\it timeoutPrecommit}\) の 3 つのタイムアウトが存在する。これらのタイムアウトはアルゴリズムがブロックしたままある条件の成立を永遠に待機することを防ぎ、プロセスがラウンド間で継続的に移行することを保証し、最終的に (\({\it GST}\) 後に) 正常なプロセス間の通信が時間的で信頼性があり、そして決定できることを保証する。最後の役割は新しいラウンド \(r\) ごとにタイムアウトを増加させることで、つまり \({\it timeoutX}(r) = {\it initTimeoutX} + r * {\it timeoutDelta}\) のように達成される。これらは新しい高さ (コンセンサス実体) のたびにリセットされる。
プロセスは Tendermint で PROPOSAL、PREVOTE、PRECOMMIT のメッセージを交換する。PROPOSAL メッセージは現在のラウンドの提案者が潜在的な決定値を提案するために使用され、PREVOTE と PRECOMMIT は提案された値に対する投票である。コンセンサスアルゴリズムの分類 [10] によると、Tendermint は PBFT [7] や DLS [6] と同様にクラス 3 に属することから、値を決定するために 2 回の投票ステップ (全体で 3 回の通信) を必要とする。Tendermint のコンセンサスアルゴリズムは決定値がトランザクションのブロックである (つまり多くのトランザクションで構成される非常に大きくなる可能性がある) ようなブロックチェーンの文脈のために設計されている。したがって Algorithm 1 ([7] と同様) では値 (トランザクションのブロック) と、小さな一定サイズの ID (一意の値の識別子、たとえば \({\it id}(v)={\it id}(v')\) であれば \(v=v'\)) の送信を明示している。PROPOSAL メッセージは値を運搬する唯一のもので、PREVOTE と PRECOMMIT メッセージは値の ID を運搬する。正常なプロセスは、あるラウンド \(r\) で \(v\) に対する PROPOSAL と \({\it id}(v)\) に対する \(2f+1\) 投票権に相当する PRECOMMIT メッセージ受信したときに Tendermint で値 \(v\) を決定する。正常なプロセスは、ラウンド \(r\) で \(v\) に対する PRECOMMIT メッセージを送信するために、そのラウンド \(r\) の PROPOSAL メッセージと \(2f+1\) に対応する PREVOTE メッセージを待機する。それ以外の場合は特別値 \({\it nil}\) を持つ PRECOMMIT メッセージを送信する。これにより正しいプロセスは一つのラウンドで単一の値 (または \({\it nil}\)) のみに PRECOMMIT できることが保証される。提案者は故障しているかもしれないため、正常なプロセスはその提案値を単なる案 (suggestion) として扱い (盲目的に受け入れられることはない)、正常なプロセスは値 \(v\) の PROPOSAL を受け入れたかどうかを \({\it id}(v)\) に対する PREVOTE メッセージを送信することで他のプロセスに伝える。そうでなければ特別値 \({\it nil}\) を含む PREVOTE メッセージを送信する。
1: Initialization:
2: h_p := 0 /* current height, or consensus instance we are currently executing */
3: round_p := 0 /* current round number */
4: step_p ∈ {propose, prevote, precommit}
5: decision_p[] := nil
6: lockedValue_p := nil
7: lockedRound_p := −1
8: validValue_p := nil
9: validRound_p := −1
10: upon start do StartRound(0)
11: Function StartRound(round):
12: round_p ← round
13: step_p ← propose
14: if proposer(h_p, round_p) = p then
15: if validValue_p ≠ nil then
16: proposal ← validValue_p
17: else
18: proposal ← getValue()
19: broadcast 〈PROPOSAL, h_p, round_p, proposal, validRound_p〉
20: else
21: schedule OnTimeoutPropose(h_p , round_p) to be executed after timeoutPropose(round_p)
22: upon 〈PROPOSAL, h_p, round_p, v, −1〉 from proposer(h_p, round_p) while step_p = propose do
23: if valid(v) ∧ (lockedRound_p = −1 ∨ lockedValue_p = v) then
24: broadcast 〈PREVOTE, h_p, round_p, id(v)〉
25: else
26: broadcast 〈PREVOTE, h_p, round_p, nil〉
27: step_p ← prevote
28: upon 〈PROPOSAL, h_p, round_p, v, vr〉 from proposer(h_p, round_p) AND 2f + 1 〈PREVOTE, h_p, vr, id(v)〉 while
step_p = propose ∧ (vr ≥ 0 ∧ vr < round_p) do
29: if valid(v) ∧ (lockedRound_p ≤ vr ∨ lockedValue_p = v) then
30: broadcast 〈PREVOTE, h_p, round_p, id(v)〉
31: else
32: broadcast 〈PREVOTE, h_p, round_p, nil〉
33: step_p ← prevote
34: upon 2f + 1 〈PREVOTE, h_p, round_p, ∗〉 while step_p = prevote for the first time do
35: schedule OnTimeoutPrevote(h_p , round_p) to be executed after timeoutPrevote(round_p)
36: upon 〈PROPOSAL, h_p, round_p, v, ∗〉 from proposer(h_p, round_p) AND 2f + 1 〈PREVOTE, h_p, round_p, id(v)〉 while
valid(v) ∧ step_p ≥ prevote for the first time do
37: if step_p = prevote then
38: lockedValuep ← v
39: lockedround_p ← round_p
40: broadcast 〈PRECOMMIT, h_p, round_p, id(v))〉
41: step_p ← precommit
42: validValuep ← v
43: validRound_p ← round_p
44: upon 2f + 1 〈PREVOTE, h_p, round_p, nil〉 while step_p = prevote do
45: broadcast 〈PRECOMMIT, h_p, round_p, nil〉
46: step_p ← precommit
47: upon 2f + 1 〈PRECOMMIT, h_p, round_p, ∗〉 for the first time do
48: schedule OnTimeoutPrecommit(h_p , round_p) to be executed after timeoutPrecommit(round_p)
49: upon 〈PROPOSAL, h_p, r, v, ∗〉 from proposer(h_p, r) AND 2f + 1 〈PRECOMMIT, h_p, r, id(v)〉 while decision_p[h_p] = nil do
50: if valid(v) then
51: decision_p[h_p] = v
52: h_p ← h_p + 1
53: reset lockedRound_p, lockedValue_p, validRound_p and validValue_p to initial values and empty message log
54: StartRound(0)
55: upon f + 1 〈∗, h_p, round, ∗, ∗〉 with round > round_p do
56: StartRound(round)
57: Function OnTimeoutPropose(height, round):
58: if height = h_p ∧ round = round_p ∧ step_p = propose then
59: broadcast 〈PREVOTE, h_p, round_p, nil〉
60: step_p ← prevote
61: Function OnTimeoutPrevote(height, round):
62: if height = h_p ∧ round = round_p ∧ step_p = prevote then
63: broadcast 〈PRECOMMIT, h_p, round_p, nil〉
64: step_p ← precommit
65: Function OnTimeoutPrecommit(height, round):
66: if height = h_p ∧ round = round_p then
67: StartRound(round_p + 1)すべてのプロセスは Algorithm 1 の step, lockedValue, lockedRound, validValue, validRound の変数を保持している。step は Tendermint 内部のステートマシンの現在の状態、つまり現在のラウンドでのアルゴリズムの実行段階を反映している。lockedValue は PRECOMMIT メッセージが送信された最新の値 (ラウンド数に関する値) が格納されている。lockedRound はこのプロセスが \({\it nil}\) ではない PRECOMMIT メッセージを最後に送信したラウンドである。これは、正常なプロセスが \({\it id}(v)\) に対する PRECOMMIT メッセージを送信する前に lockedValue = v および lockedRound = r と設定することで、ラウンド \(r\) の値 \(v\) をロックすると言うこともできる。正常なプロセスは \({\it id}(v)\) に対する \(2f+1\) 個の PRECOMMIT メッセージを受信した場合のみ値 \(v\) を決定できるため、決定可能な値は少なくとも \(f+1\) の投票権に相当する正常なプロセスによってロックされている値であることを意味する。したがって、あるラウンド \(r\) で PROPOSAL とそれに対応する \(2f+1\) の PREVOTE メッセージを受信すればどのような値 \(v\) も決定可能 (possible decision) な値となる。validValue 変数の役割は可能な限り最新の決定可能値を保持することであり、validRound は validValue が最後に更新されたラウンドである。これらの変数とは別に、プロセスは現在のコンセンサス本体 (\(h_p\), Tendermint では \({\it height}\) と呼ぶ) と現在のラウンド数 (\({\it round}_p\)) も保存し各メッセージにそれらを添付している。最後に、プロセスは \({\it decision}_p\) という決定の配列も保存している (Tendermint では高さごとに 1 つずつのコンセンサス本体の連続を想定している)。
すべてのラウンドは提案者が PROPOSAL メッセージで値を提案することから始まる (19行目参照)。各 height の初期ラウンドでは、提案者は提案する値を自由に選ぶことができる。Algorithm 1 では、正常なプロセスは提案値を返す外部関数 getValue() を用いて提案値を得ることができる。次のラウンドの正常な提案者は validValue = nil の場合のみ新しい値を提案し、そうでなければ validValue を提案する (15-18行目)。提案された値に加えて PROPOSAL メッセージには validRound も含まれているため、他のプロセスは提案者が validValue を決定可能値として観測した最後のラウンドについて知ることができる。正常な提案者 \(p\) が PROPOSAL に validRound を付加した validValue を送信したのであれば、プロセス \(p\) がラウンド validRound において validValue に対する PROPOSAL と \(2f+1\) の PREVOTE を受信したことを意味していることに注意。正常なプロセスが validValue (validRound > -1) を持つ PROPOSAL メッセージを \(t \gt {\it GST}\) に送信した場合、ゴシップ通信特性により対応する PROPOSAL と VREVOTE メッセージは時間 \(t+\Delta\) より前にすべての正常なプロセスが受信する。したがって、すべての正常なプロセスは PROPOSAL とそれに対応する \(2f+1\) 投票権相当の PREVOTE メッセージによって支持されている提案値の正しさを検証することができる。
正常なプロセスは外部関数 valid() が値 \(v\) に対して true を返し、\(p\) がどのような値のロックも持っていない (lockedRound = -1) か \(p\) が値 \(v\) のロックを持っている (lockedValue = v) ときに値 \(v\) に対する提案を受け入れる (そして \({\it id}(v)\) に対する PREVOTE を送信する); 23行目参照。提案されたペアが \((v,vr \gt 0)\) であり正常なプロセス \(p\) が何らかの値をロックしている場合、\(v\) がより最近の決定可能値9 \(vr \gt {\it lockedRound}_p\) か、\({\it lockedValue} = v\) であれば \(v\) を受け入れる (29行目参照)。そうでなければ正常なプロセスは \({\it nil}\) を持つ PREVOTE メッセージを送信して提案を拒否する。正常なプロセスは (正常なプロセスが新しいラウンドを開始するときにトリガーした) timeoutPropose() の期限が切れ、現在のラウンドの PREVOTE メッセージをまだ送信していない場合にも \({\it nil}\) を持つ PREVOTE メッセージを送信する (57行目)。
正常なプロセスがある値 \(v\) に対する PROPOSAL メッセージと \({\it id}(v)\) に対する 2f+1 PREVOTE メッセージを受信した場合、\({\it id}(v)\) をもつ PRECOMMIT メッセージを送信する。そうでなければ \({\it nil}\) の PRECOMMIT を送信する。正常なプロセスは (正常なプロセスが PREVOTE メッセージを送信し任意の \(2f+1\) PREVOTE を受信したときに開始される) timeoutPrevote() が期限切れし、まだ現在のラウンドで PRECOMMIT メッセージを送信していない場合も \({\it nil}\) 値の PRECOMMIT メッセージを送信する (65行目参照)。正常なプロセスは、あるラウンド \(r\) で \(v\) に対する PROPOSAL メッセージと \({\it id}(v)\) の \(2f+1\) PRECOMMIT メッセージを受信した場合にある値 \(v\) を決定する (51行目参照)。この条件が true となるまでアルゴリズムが永遠にブロックし待機することを防ぐために Algorithm 1 は timeoutPrecommit() を使用している。これはプロセスが現在のラウンドの \(2f+1\) となる PRECOMMIT メッセージの任意の集合を受信した後にトリガーされる。もし timeoutPrecommit() が期限切れしプロセスがまだ決定していなければプロセスは次のラウンドを開始する (65行目参照)。正常なプロセス \(p\) が決定したとき、プロセスは (次の height に対する) 次のコンセンサス実体を開始する。ゴシップ通信特性により \(p\) が決定するきっかけとなった PROPOSAL および \(2f+1\) PREVOTE メッセージは最終的にすべての正常なプロセスに受信されるため、それらのプロセスも決定することが保証される。
- 7複数のルールが同時にアクティブになっている場合、最初に実行されるルールはランダムに選択される。アルゴリズムの正しさはルールの実行順序に依存しない。
- 8投票権の高い検証者はその投票権に比例してより頻繁に選択される。より正確には、サイズ \(n\) のラウンドの連続において
- 9前述のとおり、あるラウンド \(r\) で決定可能な値は、そのラウンド \(r\) で PROPOSAL とそれに対応する \(2f+1\) PREVOTE メッセージを受信したものである。
 A. Termination メカニズム
A. Termination メカニズム
Tendermint はゴシップベースの通信特性を利用した新しいメカニズムで終了 (termination) を保証する (ゴシップ通信特性参照)。これには、上で説明したような提案ステップ中に提案者が使用する validValue と validRound の 2 つの追加の変数を管理する必要がある。validValue と validRound は、正常なプロセスがラウンド \(r\) と値 \(v\) に対する有効な PROPOSAL メッセージと対応する \({\it id}(v)\) に対する \(2f+1\) PREVOTE メッセージを受信したときに、正常なプロセスによってラウンド \(r\) で \(v\) と \(r\) に更新される (36行目のルールを参照)。
ここで validValue と validRound を管理し提案することがどのようにして終了を保証するかについて直観的に説明する。形式的な扱いはセクション IV に譲る。
最初に注意すべきことは、ゴシップ通信特性により、正常なプロセス \(p\) があるラウンド \(r\) で値 \(v\) をロックしたとすると、すべての正常なプロセスはラウンド \(r\) の終了前に validateValue を \(v\) へ、validRound を \(r\) へ更新する (これはセクション IV で形式的に証明する)。直観的には、\(p\) がラウンド \(r\) で値 \(v\) をロックするに至ったメッセージはラウンド \(r\) の終了前にすべての正常なプロセスにごシッピングされることによって validValue と validRound を更新することになる (36行目)。したがって、正常なプロセスが good 期間に何らかの値をロックした場合、すべての正常なプロセスによって validValue と validRound が更新され、次のラウンドで提案される値がすべての正常なプロセスに受け入れられるようになる。ただし good 期間に正常なプロセスが値をロックせず、あるラウンドで正常なプロセス \(q\) が validValue と validRound を更新することも起きうることに注意。この場合、正常なプロセスが値をロックしていないため、すべての正常なプロセス \(c\) に対して \({\it validRound}_q \gt {\it valieRound}_c\) となり、またゴシップ通信の特性により \(q\) が対応するラウンド validRound_q で受信する PREVOTE メッセージを \(\Delta\) 時間後にすべての正常なプロセスが受信するため validValue_q と validRound_q もすべての正常なプロセスに受け入れられることになる。
最後に、GST のあと、正常なプロセスが値をロックせず、validValue と validRound を更新しないラウンドが長く続く可能性がある。この場合、一連のラウンドの間に、正常なプロセスが提案した値がすべての正常なプロセスに受け入れられなかったことになる。ただしこの一連のラウンドは、すべてのラウンドの最初にすべての正常なプロセスによって validValue と validRound が受け入れられるような正常なプロセス \(c\) が少なくとも一つ存在するため常に有限である点に注意。これは、他のすべての正常なプロセス \(p\) に対して、\({\it validRound}_c \gt {\it validRound}_p\) または \({\it validValue}_c = {\it validValue}_q\) となるような正常なプロセス \(c\) が存在するためである。これは、すべての正常なプロセスの中で直近のラウンドで値をロックしたプロセスが \(c\) であるため (またはどの正常なプロセスも値をロックしていないため) 真である。したがって、最終的にはどこかのラウンドで \(c\) が適正となり提案された値がすべての正常なプロセスに受け入れられこの一連のラウンドが終了することとなる。
したがって、変数 \({\it validValue}\) と \({\it validRound}\) の更新およびゴシップ通信特性を併用することで、提案された値が最終的に good 期間中のどこかですべての正常なプロセスによって受け入れられる正常なプロセスのいるラウンドが存在し、そのラウンドですべての正常なプロセスが終了することとなる。Fig 1 に示した一般的な終了メカニズムとは対照的に、このメカニズムは "通常" と呼ばれるケースで既に送信されているメッセージに加えてさらに追加の情報を交換する必要はない。
 4 Tendermint コンセンサスアルゴリズムの証明
4 Tendermint コンセンサスアルゴリズムの証明
補題 1. すべての \(f \ge 0\) について、投票権が少なくとも \(2f+1\) に等しいプロセスの集合は、少なくとも一つの正常なプロセスを共有している。
証明: …
補題 2: もし \(f+1\) の正常なプロセスがラウンド \(r_0\) で値 \(v\) をロックしたならば (\({\it lockedValue}=v\) と \({\it lockedRound}=r_0\))、それらは \(r \gt r_0\) となるすべてのラウンドで \({\it id}(v)\) または \({\it nil}\) に対する PREVOTE を送信する。
証明: …
補題 3: Algorithm 1 は合意 (agreement) を満たす。
証明: …
補題 4: Algorithm 1 は有効性 (validity) を満たす。
証明: …
補題 5: 以下を仮定すると:
- 正常なプロセス \(p\) は時刻 \(t \gt {\it GST}\) にラウンド \(r \gt 0\) に入る最初の正常なプロセスである (すべての正常なプロセス \(c\) に対して時刻 \(t\) に \({\it round}_c \le r\) となる)
- ラウンド \(r\) の提案者は正常なプロセス \(q\) である
- すべての正常なプロセス \(c\) について、時刻 \(t\) で \({\it lockedRound}_c \le {\it validRound}_q\) である
- \({\it timeoutProposer}(r) \gt 2\Delta + {\it timeoutPrecommit}(r-1)\), \({\it timeoutPrevote}(r) \gt 2\Delta\), そして \({\it timeoutPrecommit}(r) \gt 2\Delta\)
すべての正常なプロセスは \(t + 4\Delta + {\it timeoutPrecommit}(r-1)\) より前のラウンド \(r\) で決定する。
証明: …
補題 6: 正常なプロセス \(p\) があるラウンド \(r\) で時刻 \(t_0 \gt {\it GST}\) に値 \(v\) をロックし (つまり \({\it lockedValue} = v\) かつ \({\it lockedRound} = r\))、かつ \({\it timeoutPrecommit(r) \gt 2\Delta\) ならば、すべての正常なプロセスはラウンド \(r+1\) が始まる前に \({\it validValue}\) を \(v\) に、\({\it validRound}\) を \(r\) に設定する。
証明: …
補題 7: Algorithm 1 は終了 (termination) を満たす。
証明: …
 5 結論
5 結論
我々は Tendermint BFT SMR プラットフォームの中核となる新しいビザンチン障害耐性を持つコンセンサスアルゴリズムを提案した。このアルゴリズムはゴシップベースの peer-to-peer ネットワークで通信する、相互に接続されていないノードが多数存在する広域ネットワーク向けに設計されている。このアルゴリズムは単一の実行モードしか持たず、通信パターンは最先端の PBFT アルゴリズムの "通常" ケースと非常によく似ている。このアルゴリズムはノード間のゴシップベース通信を使用した新しいメカニズムにより終了を保証している。提案されたアルゴリズムとその証明はシンプルかつエレガントであり、それは理解と正しい実装をより容易にすると考えている。
 Acknowledgements
Acknowledgements
We would like to thank Anton Kaliaev, Ismail Khoffi and Dahlia Malkhi for comments on an earlier version of the paper. We also want to thank Marko Vukolic, Ming Chuan Lin, Maria Potop-Butucaru, Sara Tucci, Antonella Del Pozzo and Yackolley Amoussou-Guenou for pointing out the liveness issues in the previous version of the algorithm. Finally, we want to thank the Tendermint team members and all project contributors for making Tendermint such a great platform.
 References
References
- L. Lamport, “Time, clocks, and the ordering of events in a distributed system,” Commun. ACM, 1978.
- F. B. Schneider, “Implementing fault-tolerant services using the state machine approach: a tutorial,” ACM Comput. Surv., vol. 22, no. 4, Dec. 1990.
- M. Burrows, “The chubby lock service for loosely-coupled distributed systems,” in OSDI, 2006, pp. 335–350.
- S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” 2009. [Online]. Available: http://www.bitcoin.org/bitcoin.pdf
- V. Buterin, “Ethereum: A next-generation smart contract and decentralized application platform,” https://github.com/ethereum/wiki/wiki/White-Paper, 2014, accessed: 2018-07-11. [Online]. Available: https://github.com/ethereum/wiki/wiki/White-Paper
- C. Dwork, N. Lynch, and L. Stockmeyer, “Consensus in the presence of partial synchrony,” JACM, 1988.
- M. Castro and B. Liskov, “Practical byzantine fault tolerance and proactive recovery,” ACMTCS, 2002.
- ——, “Practical byzantine fault tolerance and proactive recovery,” in Proceedings of the 3rd Symposium on Operating Systems Design and Implementation, Feb. 1999.
- Z. Milosevic, M. Hutle, and A. Schiper, “Unifying Byzantine consensus algorithms with Weak Interactive Consistency,” to appear in OPODIS 2009.
- O. R ütti, Z. Milosevic, and A. Schiper, “Generic construction of consensus algorithms for benign and byzantine faults,” in DSN, 2010, pp. 343–352.
- J.-P. Martin and L. Alvisi, “Fast Byzantine consensus,” TDSC, 2006.
- G. S. Veronese, M. Correia, A. N. Bessani, and L. C. Lung, “Spin one’s wheels? byzantine fault tolerance with a spinning primary,” in SRDS, 2009.
- A. Clement, E. Wong, L. Alvisi, M. Dahlin, and M. Marchetti, “Making byzantine fault tolerant systems tolerate byzantine faults,” in NSDI, 2009, pp. 153–168.
- D. Boneh, B. Lynn, and H. Shacham, “Short signatures from the weil pairing,” in Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security: Advances in Cryptology, ser. ASIACRYPT ’01. Berlin, Heidelberg: Springer-Verlag, 2001, pp. 514–532. [Online]. Available: http://dl.acm.org/citation.cfm?id=647097.717005
- G. Golan-Gueta, I. Abraham, S. Grossman, D. Malkhi, B. Pinkas, M. K. Reiter, D. Seredinschi, O. Tamir, and A. Tomescu, “SBFT: a scalable decentralized trust infrastructure for blockchains,” CoRR, vol. abs/1804.01626, 2018. [Online]. Available: http://arxiv.org/abs/1804.01626
- A. Demers, D. Greene, C. Hauser, W. Irish, J. Larson, S. Shenker, H. Sturgis, D. Swinehart, and D. Terry, “Epidemic algorithms for replicated database maintenance,” in Proceedings of the Sixth Annual ACM Symposium on Principles of Distributed Computing, ser. PODC ’87. New York, NY, USA: ACM, 1987, pp. 1–12. [Online]. Available: http://doi.acm.org/10.1145/41840.41841
- T. Crain, V. Gramoli, M. Larrea, and M. Raynal, “Leader/randomization/signature-free byzantine consensus for consortium blockchains,” CoRR, vol. abs/1702.03068, 2017. [Online]. Available: http://arxiv.org/abs/1702.03068
翻訳抄
Tendermint のコンセンサスに関する 2018 年の論文。
- Ethan Buchman, Jae Kwon and Zarko Milosevic (2018) The latest gossip on BFT consensus