S2 Geometry Library
 概要
概要
S2 Geometry Library は球面上の領域を扱うための空間インデクシング (spatial indexing) ライブラリ。主に地球を対象としており、地理データを分割統治や索引付けのためのセル (区画) に分割することを目的としている。また非常にコンパクトで 64bit 整数で地球表面上の 1cm 四方を表す解像度を持つ。
 変換方法
変換方法
S2 Geometry Library は以下の方法で球体状の領域を 64bit 整数の幅にパックする。
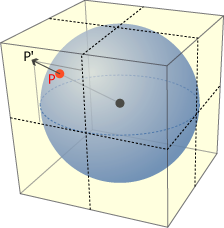
球面上の点 \(P\) を、球体に接する立方体に投影する。この投影により点 \(P\) は立方体の 6 面のうちのある面 \({\rm face}\) 上の点 \(P'\) として表すことができる。
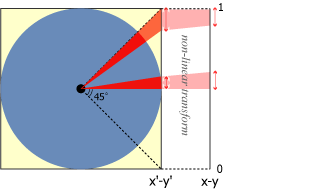
投影した状態では角度が小さい位置の領域は小さく、45°に近い位置の領域は大きくなり配置に偏りが生じるため、投影後に拡大率を調整し \((0, 1)\) の範囲となるように変換する。S2 では正確で速度の遅い \(\arctan\) を使った計算ではなく 2 次式を使用している。
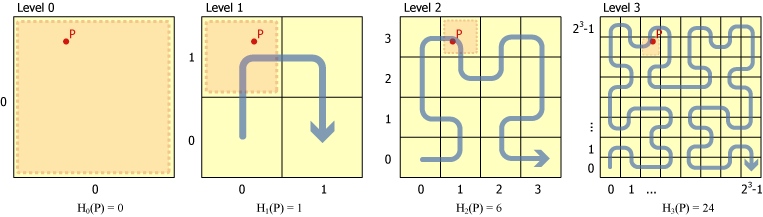
点 \(P'\) を含む立方体の面 (正方形) が適切な精度のセルとなるよう四分木に分割する。四分木の深さを表すレベルは 0 から 30 の範囲をとり、大きくなるほど精度が高く (セルが小さく) なる。分割された正方形から点 \(P\) を含むセルのヒルベルト曲線上の距離 (ステップ数) を求める。
立方体上の面 \(0 \leq {\rm face} \leq 5\)、四分木の深さレベル \(0 \leq {\rm level} \leq 30\)、ヒルベルト曲線上の位置 \(0 \leq p \leq 2^{2\times{\rm level}}-1\) を 64 ビット整数にパックした値をそのセルの ID とする。

 レベルの精度とセルの解像度
レベルの精度とセルの解像度
地球を半径 \(R\)=6,378km の球体と仮定した場合、その総面積 \(S = 4\pi R^2\) を立方体の 6 面で分割した \(S_0 = \frac{4\pi R^2}{6}\) がレベル 0 のセル相当の面積である。\(S_0\) をレベルごとのセル数 \(2^{2\times{\rm level}}\) で割った面積がそのレベルで表現できる大まかな精度 (解像度) と考えることができる。
| Level | Cell |
|---|---|
| 0 | 85,201,305km² |
| 1 | 21,300,326km² |
| 2 | 5,325,082km² |
| 3 | 1,331,270km² |
| 4 | 332,818km² |
| 5 | 83,204km² |
| 6 | 20,801km² |
| 7 | 5,200.3km² |
| 8 | 1,300.1km² |
| 9 | 325.0km² |
| Level | Cell |
|---|---|
| 10 | 81.25km² |
| 11 | 20.31km² |
| 12 | 5.08km² |
| 13 | 1.27km² |
| 14 | 317,400m² |
| 15 | 79,350m² |
| 16 | 19,837m² |
| 17 | 4,959.4m² |
| 18 | 1,239.8m² |
| 19 | 310.0m² |
| Level | Cell |
|---|---|
| 20 | 77.49m² |
| 21 | 19.37m² |
| 22 | 4.84m² |
| 23 | 1.21m² |
| 24 | 3027.0cm² |
| 25 | 756.7cm² |
| 26 | 189.2cm² |
| 27 | 47.30cm² |
| 28 | 11.82cm² |
| 29 | 2.96cm² |
| 30 | 0.74cm² |
レベル 30 では地球上の領域を 1cm×1cm より高い解像度で表すことができる。