オートマトン

2022年8月20日 #automaton

概要

オートマトン (automaton; ムーア型順序機械) は計算理論における数学的なモデルの総称。ある既定の手続きに従って行う自動計算の機構、つまりプログラミングやインタープリタ、文字列解析などを表すモデルとしてしばしば使われている。

歴史的に、ランダムアクセスが高速に可能なメモリというより、一次元の穿孔テープ (入力専用) や磁気記録テープ (読み書き可能) と少数の ON/OFF スイッチで構成される原初的な状態機械を組み合わせて可能な処理を強く意識したモデルである。

概要
有限オートマトン
1. 決定性有限オートマトン
2. 非決定性有限オートマトン
プッシュダウンオートマトン
線形拘束オートマトン
チューリングマシン
参考文献

有限オートマトン

オートマトンは状態を持ち、状態は入力によって変化し、出力は内部状態によって決まる。この動作はしばしばテープに記録された入力とそれを読み出して状態を更新しながら移動するヘッドに例えられる。Fig 1 は初期状態を $q_0$ とし、$n$ 個の記号の並び $a_1 a_2 \ldots a_n$ を入力として状態を更新する様子を表している ($\$$ は入力が終端に達したことを示すエンドマーカーである)。

Fig 1. テープに記録された入力記号と、それを読み出して内部状態を更新しながら移動するヘッド。

取り得る状態の集合 $Q$ が有限のオートマトンを有限オートマトン (finite automaton) または有限状態機械 (finite state machine) と呼ぶ。

オートマトンが取り得る内部状態の集合を $Q$ とする。オートマトンの入力は記号 (symbol) の並びとして表され、記号の集合を $\Sigma$ で表す。記号の並びは列 (string) であり、特に長さ 0 の列を空列 (empty string) として $\epsilon$ で表す。オートマトン $M$ によって受理されるすべての列の集合を言語 (language) $L(M)$ と呼ぶ。

1 個の記号が入力されたときにオートマトンがどの内部状態に遷移するかは現在の内部状態と入力された記号によって決まる。内部状態 $q$ のときに入力 $a$ があったことを $(q,a)$ とすると、すべての内部状態と入力記号の組み合わせを直積 $Q \times \Sigma$ と表すことができる。また入力 $a$ によってオートマトンの内部状態 $q$ が $r$ に変化することを写像 $\delta$ を用いて $\delta(q,a)=r$ のように表す。

$F \subseteq Q$ を受理状態の集合とすると、オートマトンが入力をすべて読みきったときの内部状態が $q_n \in F$ であればオートマトンは入力を受理している。$P(w)$ をオートマトン $M$ によって列 $w$ が受理されるかを判定する関数とすると、$\Sigma$ 上の言語は $\{w \in \Sigma^* \ | \ P(w)\}$ と表すことができる。

以上より、オートマトンの初期状態を $q_0$ とするとオートマトンは式 ($\ref{m}$) のタプルで表すことができる。\[ \begin{equation} M = \langle Q,\Sigma, \delta, q_0, F\rangle \label{m} \end{equation} \]

ある時点のオートマトン $M$ の様相 (configuration) は内部状態と未読込の入力列のタプル $(q_i, a_{i+1} a_{i+2} \ldots a_n)$ で表すことができる。つまりオートマトンの開始時の様相は $(q_0,a_1 a_2 \ldots a_n)$ である。また様相 $(q_i,a_{i+1}\ldots a_n)$ が次の入力 $a_{i+1}$ によって状態 $q_{i+1}$ に遷移するという動作を $(q_i,a_{i+1}\ldots a_n) \vdash_M (q_{i+1},a_{i+2}\ldots a_n)$ のように表す。したがって、入力の先頭から終端までの $n$ 個の読み込むという一連の動作は式 ($\ref{all_conf}$) のように表すことができる。\[ \begin{equation} (q_0, \ a_1 a_2 \ldots a_n) \vdash_M (q_1,\ a_2 a_3 \ldots a_n) \vdash_M \ldots \vdash_M (q_n,\ \epsilon) \label{all_conf} \end{equation} \]

$A$ と $B$ を $\Sigma$ 上の 2 つの言語とするとき、$A$ に属する列の後に $B$ に属する列が続く列 $\{w \ | \ w = uv, u \in A, v \in B\}$ を言語 $A$ と $B$ の連接 (concatenation) と呼び $AB$ で表す。

記号 $\Sigma$ 上のすべての列の集合を $\Sigma^*$ で表す。例えば $\{a,b\}^*$ $=$ $\{\epsilon$, $a$, $b$, $aa$, $ab$, $bb$, $aaa$, $\ldots\}$ である。$\Sigma^*$ もまた $\Sigma$ 上の言語の一つである。$\Sigma^*$ から空列を除いたものを $\Sigma^+=\Sigma^*-\{\epsilon\}$ と表す。

決定性有限オートマトン

すべての状態 $q \in Q$ においてすべての記号 $\Sigma$ に対する状態遷移が必ず 1 つ定まっている有限オートマトンを決定性有限オートマトン (deterministic finite automaton; dfa) と呼ぶ。言い換えると決定性有限オートマトンの写像は式 ($\ref{dfa_delta}$) のように表され $\delta(q,a) = q' \in Q$ となる。\[ \begin{equation} \delta: Q \times \Sigma \to Q \label{dfa_delta} \end{equation} \]

Fig 2 の状態遷移として表される決定性有限オートマトン $M_1$ は、内部状態 $Q=\{q_0,q_1\}$ を持ち、入力記号 $\Sigma=\{0,1\}$ を取り、初期状態 $q_0$ で開始し、入力終了時点で $q_1$ であれば入力された記号列はオートマトンによって受理され、$q_0$ であれば拒否されることを示している。

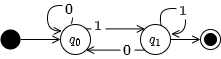
Fig 2. 記号 $\Sigma = \{0,1\}$ を入力とし、1 で終了する記号列を受理するオートマトン $M_1$ の例。

このオートマトン $M_1$ は 1 で終了するすべての入力を受理することが見て取れる。例えば 001 という入力は受理するが 10 という入力は拒否するだろう。同時にこのオートマトンは 1 で終了する列の集合によって構成される言語 $L(M_1)$ を定めていることにもなる。

オートマトン $M_1$ に対する各表記は以下のようになる。\[ \begin{eqnarray*} Q & = & \{q_0, q_1\} \\ \Sigma & = & \{0, 1\} \\ F & = & \{q_1\} \\ \Sigma^* & = & \{0, 1\}^* = \{\epsilon, 0, 1, 00, 01, 10, 11, 000, 001, \ldots\} \\ L(M) & = & \{1, 01, 11, 001, \ldots\} \\ Q \times \Sigma & = & \{(q_0, 0), (q_0, 1), (q_1, 0), (q_1, 1)\} \end{eqnarray*} \]

また決定性有限オートマトンでは内部状態と入力による状態遷移先が一意に決まっていることから $\delta$ は表で表すこともできる。

\[ \begin{eqnarray*} \delta(q_0, 0) & = & q_0 \\ \delta(q_0, 1) & = & q_1 \\ \delta(q_1, 0) & = & q_0 \\ \delta(q_1, 1) & = & q_1 \end{eqnarray*} \]

	0	1
$q_0$	$q_0$	$q_1$
$q_1$	$q_0$	$q_1$

非決定性有限オートマトン

ある内部状態 $q \in Q$ において、ある入力記号に対する状態遷移先が 1 つに定まっていない有限オートマトンを非決定性有限オートマトン (non-deterministic finite automaton; nfa) と呼ぶ。これは非決定性有限オートマトンの写像 $\delta(q,a)$ が状態 $Q$ の部分集合である。非決定性有限オートマトンの写像 $\delta$ はべき集合¹を使用して式 ($\ref{nfa_delta}$) のように表すことができる。\[ \begin{equation} \delta: Q \times \Sigma \to 2^Q \label{nfa_delta} \end{equation} \] 例えば $\delta(q,a)=\{s,t\}$ であれば状態 $q$ での入力 $a$ は $s$ または $t$ のどちらの状態に遷移しても良いということを意味する。また $\delta(q,a)=\emptyset$ であれば状態 $q$ で入力 $a$ は起きえないことを意味している。

空動作 ($\epsilon$-move) は空列 $\epsilon$ によって引き起こされる状態遷移である。非決定性有限オートマトンが空動作を許しているときの写像 $\delta$ は式 ($\ref{enfa_delta}$) のように表される。\[ \begin{equation} \delta: Q \times (\Sigma \cup \{\epsilon\}) \to 2^Q \label{enfa_delta} \end{equation} \] 式 ($\ref{e_move}$) はある状態 $q$ において空列 $\epsilon$ と記号 $a,b$ に対する状態遷移を定めている。このケースでは、状態 $q$ における入力 $a$ は、入力を消費せず $r$ に遷移するか、あるいは入力を消費して $s$ か $t$ に遷移することができる。しかし入力が $b$ だった場合は入力を消費せず $r$ に遷移するしかない。\[ \begin{equation} \left\{ \begin{array}{lcl} \delta(q, \epsilon) & = & \{r\} \\ \delta(q, a) & = & \{s, t\} \\ \delta(q, b) & = & \emptyset \end{array} \right. \label{e_move} \end{equation} \]

決定性有限オートマトンは非決定性有限オートマトンの特殊ケースであり、非決定性有限オートマトンは空動作のある非決定性オートマトンの特殊ケースであると言える。

決定性有限オートマトン ${\rm dfa}$、非決定性オートマトン ${\rm nfa}$、空動作のある非決定性オートマトン $\epsilon{\rm -nfa}$ それぞれに対する言語族を $\mathcal{L}$ とすると、\[ \mathcal{L}(\mathrm{dfa}) = \mathcal{L}(\mathrm{nfa}) = \mathcal{L}(\epsilon\mathrm{-nfa}) \] つまり、ある言語を受理する (空動作のある) 決定性有限オートマトンが存在するなら、同じ言語を受理する決定性有限オートマトンが存在する。

同じ言語を受理する決定性有限オートマトンは無限に存在するが、その中でも最も状態数の少ないものを最簡形 (reduced form) という。

¹$Q$ のべき集合 $2^Q$ とは $Q$ のすべての部分集合で構成される集合のこと。例えば $Q=\{0,1,2\}$ のとき $2^Q$ $=$ $\{\emptyset,$ $\{0\},$ $\{1\},$ $\{2\},$ $\{0,1\},$ $\{0,2\},$ $\{1,2\},$ $Q\}$ となる。

プッシュダウンオートマトン

プッシュダウンオートマトン (pushdown automaton) は有限オートマトンに無限の長さを持つスタック (pd-スタック) を追加した構造である。動作関数 $\delta$ は内部状態と入力記号に加えてスタックから pop した値を使用して次に遷移する状態を決定し、状態遷移時に pd-スタックへ $\Gamma$ 上の列を push する。この pd-スタックにより有限オートマトンに短期的な記憶を追加している。

pd-スタックの実体はプッシュダウン記号の有限集合 $\Gamma$ 上の列である。この列の先頭に $\Gamma$ 上の記号を push したり pop することでスタックとしての機能を持たせる。pd-スタックは初期状態で $z_0=\epsilon$ であり $z_i \in \Gamma^*$ の状態を取る。入力を最後まで読み切ったときに $q_n \in F$ かつ $z_n=\epsilon$ であればオートマトンは入力された列を受理したことを意味する。

例えば記号 $\Sigma = \{a,b\}$ を入力として $a^n b^n$, $n\in\mathbb{Z}$ の列を受理するオートマトンを考えるとき、長さ $n$ の $a$ 列を観測した後に $n$ 個の $b$ を確認しなければならない。つまり直前の $n$ を短期記憶として保持しなければならないが、$n$ を内部状態 $q$ として持つことは状態の数が整数 $\mathbb{Z}$ と同じ数だけ (つまり無限に) 存在することになり有限オートマトンではない。

プッシュダウンオートマトンは直前に記憶した繰り返し数と同じ回数の繰り返しを再現することができるため、動作関数 $\delta$ を以下のように定義することで $a^nb^n$ を受理するオートマトンを構築することができる。

\[ \begin{eqnarray*} Q & = & \{q_0, q_1, q_2\} \\ \Sigma & = & \{a,b\} \\ \Gamma & = & \{A\} \\ F & = & \{q_2\} \end{eqnarray*} \]

\[ \begin{array}{lcl} \delta(q_0, a, \epsilon) & = & (q_0, A) \\ \delta(q_0, a, A) & = & (q_0, AA) \\ \delta(q_0, b, A) & = & (q_1, \epsilon) \\ \delta(q_1,b,A) & = & (q_1, \epsilon) \\ \delta(q_1, \epsilon, \epsilon) & = & (q_2, \epsilon) \end{array} \]

\[ \begin{eqnarray*} (q_0, aaabbb, \epsilon) & \vdash_M & (q_0, aabbb, A) \\ & \vdash_M & (q_0, abbb, AA) \\ & \vdash_M & (q_0, bbb, AAA) \\ & \vdash_M & (q_1, bb, AA) \\ & \vdash_M & (q_1, b, A) \\ & \vdash_M & (q_1, \epsilon, \epsilon) \\ & \vdash_M & (q_2, \epsilon, \epsilon) \end{eqnarray*} \]

pd-スタックの導入により繰り返し回数を再現できるプッシュダウンオートマトンは有限オートマトンより言語識別能力や表現能力が高いと言える。ただし、例えば $a^nb^nc^n$, $n\in\mathbb{Z}$ に対しては $c$ の繰り返しを評価する時点で $n$ はすでにスタックから消費されてしまっていることからプッシュダウンオートマトンでも表現することはできない。

線形拘束オートマトン

線形拘束オートマトン (linear bounded automaton; lba) は非決定性チューリングマシンと同様に書き換え可能で読み込み位置を左右に移動できるが、入力記号の範囲からは出ることができない構造。

チューリングマシン

チューリングマシン (Turing machine) は有限オートマトンに左右に移動可能と書き換えが可能な 1 次元の作業領域を追加した機構。有限オートマトンやプッシュダウンオートマトンと同様に入力記号を一方向に読み出すが、読み込んだ記号を作業領域に記録することができることから、最初から作業領域上に入力記号列が存在する構造と同じと考えても良い。

チューリングマシンの初期状態は $q_0$ で、読み出し位置は作業領域内の入力記号列の先頭を指している。読み出した記号と現在の状態から内部状態を更新し、現在の読み出し位置の記号を書き換え、読み出し位置を左右のどちらかに 1 つ移動する。このとき、読み出した記号をそのまま書き込むのであれば、書き込まずに読み出し位置を移動することと同等である。

もし内部状態と入力記号に対する動作が定義されていなければチューリングマシンは停止する。このとき、内部状態が $q_m \in F$ であればチューリングマシンは入力列を受理したことを意味する。また無限ループのようにチューリング機械が停止しない状況は拒否とみなされる。

チューリングマシン $M$ は式 ($\ref{tm}$) のタプルで表される。\[ \begin{equation} M = \langle Q, \Gamma, \Sigma, \delta, q_0, B, F \rangle \label{tm} \end{equation} \] ここで $Q$ は状態の有限集合、$q_0 \in Q$ は初期状態、$\Gamma$ は作業領域の取り得る記号の有限集合、$\Sigma \subset \Gamma$ は入力記号の有限集合、$B \in \Gamma - \Sigma$ は空白を表す作業領域記号、$F \subseteq Q$ は受理状態である。動作関数 $\delta:$ $Q$ $\times$ $\Gamma$ $\to$ $Q$ $\times$ $\Gamma$ $\times$ $\{L,R\}$ は内部状態と入力から次の状態と出力、左右の移動方向を決定する。

参考文献

オートマトン・言語理論の基礎 (2003) 近代科学社

	0	1
\(q_0\)	\(q_0\)	\(q_1\)
\(q_1\)	\(q_0\)	\(q_1\)