論文翻訳: Incremental Packrat Parsing
Y Combinator Research, USA
pat.dubroy@ycr.org
Y Combinator Research, USA
alex.warth@ycr.org
 Abstract
Abstract
Packrat 構文解析 (Packrat parsing) は線形時間での動作を保証するトップダウン、無制限先読みパーサを実装するための一般的な技法である。この論文では標準的な Packrat パーサをメモ化ストラテジーによる簡単な修正でインクリメンタルパーサにする方法を説明する。"インクリメンタル" とは、入力に対する編集操作の後にパーサが入力全体を再パースすることなく構文解析を実行できることを意味する。これにより Packrat 構文解析はコードエディタや IDE での対話的な仕様に適しており、大きな入力であっても使用することができる。我々の実験によれば、この技術を用いた JavaScript のインクリメンタル Packrat パーサは、手作業で最適化された非インクリメンタルパーサよりも優れた性能を発揮することがわかっている。
Patrick Dubroy and Alessandro Warth. 2017. Incremental Packrat Parsing. In Proceedings of 2017 ACM SIGPLAN International Conference on Software Language Engineering (SLE’17) . ACM, New York, NY, USA, 12 pages. https://doi.org/10.1145/3136014.3136022
Table of Contents
- Abstract
- 1 導入
- 2 Packrat 構文解析の概要
- 3 インクリメンタル Packrat 構文解析
- 4 Evaluation
- 5 Related Work
- 6 Conclusion and Future Work
- Appendix: Source Code
- Acknowledgements
- References
- 翻訳抄
 1 導入
1 導入
Packrat パーサ [3, 4] はバックトラック型の再帰降下パーサで、線形解析時間を保証しながら無制限先読みをサポートする。これは "算出したすべての中間解析結果を保存してどの結果も 2 回以上評価されないようにする" [4] ことで実現されている。
この手法のよく知られた欠点はその大きなメモリフットプリントである。Packrat パーサは "入力テキストに対してそれまで算出したすべてを文字通りため込む" [4] ため、そのメモリ消費量も入力サイズに比例して大きくなる。これは通常、中程度の大きさの入力では問題にはならないが、研究者はより大きな入力に対して Packrat 構文解析を実用化するために構文解析のメモ表のサイズを小さくする技術を数多く導入している [1, 8, 11, 16]。
我々はこの論文で Packrat パーサのメモ表を問題としてではなく機会としてアプローチする。すなはち、我々は Packrat パーサが使用するメモ化機構に簡単な修正を加えてインクリメンタルパース [6, 7] のサポートが可能であることを提示する。これはコードエディタや統合開発環境 (IDE) のようなインタラクティブな環境において特に有用で、入力サイズに関係なく構文強調表示やタイプチェックなどの応答性の高いユーザ体験を提供するためにほぼ瞬時の解析時間が要求されている。
この論文の主なコントリビューションは:
- Packrat 構文解析のための対話的アルゴリズム。これは (我々の知る限り) 最初のアルゴリズムである。このアルゴリズムは文法を無変更で加算性をサポートする。
- Packrat 構文解析の中核データ構造であるメモ表への 2 つの修正により、我々のアルゴリズムが実世界の文法による大規模入力に効率的に機能できるようにする。
- 単純な Packrat パーサの JavaScript ソースコードと、我々のアルゴリズムに基づくインクリメンタルな Packrat パーサの JavaScript ソースコード。これらはともに標準的な Packrat パーサをインクリメンタルにするために必要な修正点を正確に示している。
対話的に実装した我々のプロトタイプでの実験 (セクション 4 参照) では、標準的な Packrat パーサと比較してわずかなメモリオーバーヘッド (約 12%) しか発生せずに大きな速度向上 (2 桁の速さ) が得られることが示された。対話的に使用した場合、我々のプロトタイプは best-of-breed の非インクリメンタル JavaScript パーサである Acorn [9] よりも高速であることも示されている。
この論文の構成は次の通り: セクション 2 では Packrat 構文解析の概要を説明する。セクション 3 ではメモ化機構に対する我々の修正と、アルゴリズムをより効率的にするための 2 つの最適化について説明する。セクション 4 ではバッチモードとインクリメンタルで使用した場合の解析時間に対する我々の方針の効果について議論し、我々のプロトタイプの性能を一般的な非インクリメンタル JavaScript パーサである Acorn と比較する。セクション 5 は関連する作業を論じ、セクション 6 は結論を述べる。付録として我々のアルゴリズムに基づくインクリメンタルパーサの完全な JavaScript ソースコードを示す。
 2 Packrat 構文解析の概要
2 Packrat 構文解析の概要
Packrat 構文解析の主旨は、すべての中間解析結果を算出時にメモ化することによってバックトラッキングや無制限の先読みがある場合でも線形解析時間を保証できるということである1。この仕組みを理解するために簡単な算術式の言語から次のような文法の断片2を考えてみよう:
expr = num "+" num
| num "-" num
num = digit+
digit = "0".."9"再帰降下パーサが上に示した expr 規則で入力 "869-7" をマッチングするとき、最初の選択肢である num "+" num から開始する。最初の項である num は 1 桁以上の数字列にマッチする。ここでは入力ストリームから最初の 3 文字 ("869") を消費して成功する。パーサは次に "+" 文字にマッチさせようとするが、入力ストリームの次の文字が "-" であるため失敗する。このためパーサは現在の選択肢を開始した位置 0 にバックトラックする。次にパーサは 2 番目の選択肢 num "-" num を試行する。
この時点で従来の再帰降下パーサは num 規則を再度適用し、最初の選択肢に対して行われた評価、つまり位置 0, 1, 2 の数値をマッチングして消費する評価を重複して行う。しかし Packrat パーサでは位置 0 に num を適用した結果は最初の試行でメモ (記録、キャッシュ) されるため、次の試行ではほとんど何もする必要がない。パーサは num が 3 文字を消費して位置 0 で成功したことをすでに知っているので、位置を 3 に更新し、パターンの次の部分 ("-") に一致させるだけでよく、これは成功する。パーサは最後に num を位置 4 で適用し、最後の文字 ("7") を消費して expr の解析全体が成功する。
- 1Packrat パーサは、バックトラッキングと従来の先読み (つまりトークンを調べるが消費しない) の間に実用的な違いがほとんどないことから "無制限の先読み" [4] をサポートすると言われている。
- 2具体的な構文は Packrat 構文解析と密接に関連する文法形式である構文解析式文法 (parsing expression grammars) [5] の変種をベースにしている。
 2.1 Packrat パーサのメモ化
2.1 Packrat パーサのメモ化
中間解析結果 (たとえば位置 0 の num とのマッチングの結果) がメモ化されると、その結果はパーサのメモ表 (memo table) に格納される。メモ表は \(m \times n\) 行列としてモデル化でき、入力の \(n\) 文字ごとに 1 列、文法内の各規則ごとに 1 行が存在する。行列の各要素をメモ表エントリ (memo table entry) と呼ぶことにする。
Figure 1 は前述のように expr をマッチン議した後のメモ表の内容 (疎行列表現を使用) である。各メモ表項目は 2 つのフィールドを持つ:
- \({\it nextPos}\): 入力文字列のオフセットで、残りの入力がどこから始まるかを示す。
- \({\it tree}\): アプリケーションが正解した場合は解析ツリー、または特別値 Fail。
規則 \(r\) が位置 \(p\) で適用されるたびに、パーサはその位置に \(r\) のメモ表エントリがあるかどうかを確認する。エントリが存在する場合、パーサの現在の位置は \({\it nextPos}\) に更新され \({\it tree}\) に格納されている値が返される。存在しない場合はパーサは \(r\) を評価し新しいメモ表エントリに結果を記録する。Packrat パーサはこのようにしてある位置で同じ規則が 2 回以上評価されないようにしている。
 3 インクリメンタル Packrat 構文解析
3 インクリメンタル Packrat 構文解析
インクリメンタル構文解析の目標は以前の結果をできる限り再利用し変更された入力文字列を効率的に解析することである。好都合なことに通常の (非インクリメンタルな) Packrat パーサはその中間結果をすべてのメモ表に記録する - が、そのメモ表は解析が完了すると破棄される。インクリメンタル Packrat 構文解析のアイディアは単純である: メモ表を保持 (あるいは可能な限り保持) し、構文解析の複数の起動にわたって中間解析結果を使用できるようにすることである。
標準的な Packrat パーサは関数: \[ \textsc{PARSE} : (G, s) \to T \] でモデル化される。ここで \(G\) は文法、\(s\) は入力文字列、\(T\) は構文木 (または特別値 \(T\)) である。同様にインクリメンタル Packrat パーサは: \[ \textsc{PARSE} : (G, S, M) \to (M', T) \] ここで \(M\) と \(M'\) は (理想的には) ある構造を共有する記憶可能なものである。\(G\), \(s\), \(M\) はパーサの状態または環境を構成し、明示的な環境パッシングスキームで転送される。
入力が変更された場合はその変更に対応するためにメモ表も更新する必要がある。このため我々は新しい関数: \[ \textsc{APPLY}\textsc{EDIT} : (s, M, e) \to (s', M') \] を導入する。ここで \(e\) は:
- 開始位置 \(p_s\)
- 終了位置 \(p_e\)
- 置換文字列 \(r\)
からなる編集操作 (edit operation) である。
一般に \(e\) を適用することは任意の長さの区間 \([p_s,p_e)\) の文字列を \(r\) の文字列で置き換えることを意味する。この定義では挿入 (\(p_s=p_e\) の場合) と削除 (\(r\) が空の場合) は置き換えの特殊なケースである。
\(s\) を修正して \(s'\) を生成した後、\(\textsc{APPLY}\textsc{EDIT}\) は \(M\) と可能な限り多くのエントリを共有する新しいメモ表 \(M'\) を生成する。この手順の詳細は以下に説明する我々のアルゴリズムの中核である。
このセクションの残りの部分では本論文の主要なコントリビューション、つまり以下の点について説明する:
- メモ表のどのエントリが編集の影響を受けるかを検出し、他のエントリを次のパースで再利用できるようにする戦略 (セクション 3.1)。
- メモ表の表現の修正 (セクション 3.2) により \(\textsc{APPLY}\textsc{EDIT}\) が効率的に \(M'\) を計算できるようにする。
- 実世界の文法で大きな入力に対してより効率的に動作することを可能にする我々のアルゴリズムの最適化 (セクション 3.4)。
 3.1 影響を受けたメモ表エントリの検出
3.1 影響を受けたメモ表エントリの検出
インクリメンタルパーサの基本的な正しさの基準は、ゼロから解析するのと同じ結果を生成することである。編集後に正しさを保つためにエントリを修正または削除しなければならない場合、メモ帳エントリは編集の影響を受ける (affected) という。
影響を受けるメモ表のエントリを検出するための戦略を説明する前に、まず利用可能な編集操作のサブセット、つまり入力の長さを変更しない置換操作について説明する。入力文字列に編集を加えた次のステップは、どのエントリが編集の影響を受けるか (もし受けるのであれば) を判断することである。
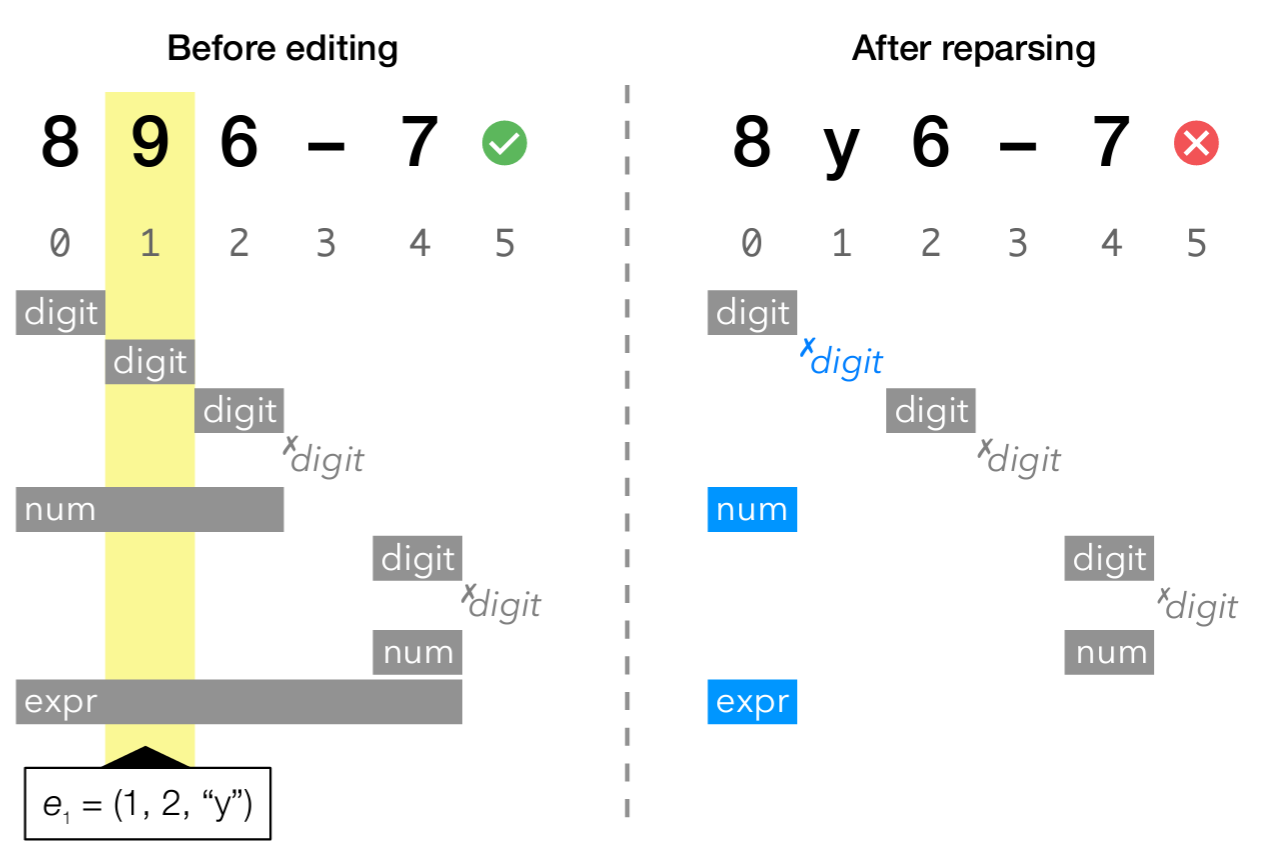
例えばセクション 1 で使用した入力 "896-7" と 9 を y に置き換える編集操作 \(e_1 = (1,2,"y")\) について考えると、この操作を適用したあとの新しい入力文字列は Figure 2 のように "8y6-7" である。
以前は digit 規則は位置 1 で成功していたが、今度は変更された入力のゼロからのパースで失敗する ("y" は数字ではないため)。正しさを維持するにはメモ表から位置 1 の digit エントリを削除して、パーサがその位置で digit を再度評価させる。
 3.1.1 "オーバーラップ規則" の基本
3.1.1 "オーバーラップ規則" の基本
一般に、あるメモ表エントリの範囲が編集操作 \(e\) と重なる場合、そのエントリは \(e\) の影響を受ける可能性があると観察できる。編集によって影響を受けない可能性もあるが (例えば置換テキストが元のテキストと同じ場合)、ここでは編集と重なるメモ表エントリを無効とみなしてメモ表から削除する保守的アプローチを採用した。
この "オーバーラップ規則" をメモ表全体に適用すると位置 0 にある expr と num のエントリも削除しなければならないことが分かる (Figure 2 の左)。再解析の結果 (Figure 2 の右)、位置 0 に 2 つの新しいエントリ (num と expr)、位置 1 に digit の新しいエントリが存在する。num は位置 0 でまだ成功しているが、今度は単一の文字 ("8") のみを消費する。expr も成功して "8" を消費するが、expr が入力全体を消費しなかったため全体の解析は失敗したことになる。
 3.1.2 問題: 基本的なオーバーラップでは不十分
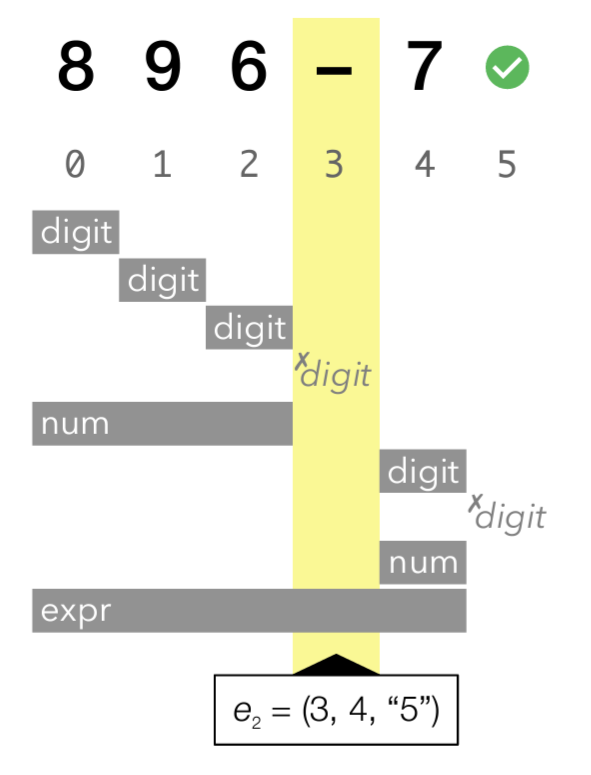
3.1.2 問題: 基本的なオーバーラップでは不十分
ここで Figure 3 に示す別の編集操作 \(e_2=(3,4,"5")\) について考える。これは "-" を "5" に置き換えるものである。前述の "オーバーラップ規則" を用いると 2 つの項目だけが無効になるが、しかしこれだけでは不十分である。位置 0 に num を適用すると入力全体が消費されるはずだが、メモ表のエントリは "896" しか消費していないため不正確なインクリメンタルパースになっている。
この例は基本的な "オーバーラップ規則" が無効なメモ帳エントリをすべて検出するには十分ではないことを示している。位置 0 での num 適用は位置 3 の文字 "6" を消費しなかったが、位置 3 の digit の貪欲な繰り返し式 digit+ を介してそれに依存している。このように、最終的に文字を消費しない場合でも num ルールは digit を介して次の文字を調べなければならない。
Packrat 構文解析の無制限の先読み機能によって規則が何文字消費するかに関わらず任意の数の文字を調べるられることに注意。例えば: \[ {\tt allOrNothing} = {\tt "abcdefg"} \ | \ {\tt ""} \] "abcdef!" とマッチしたとき、この規則は最初の選択肢のために入力全体を調べ、その後にバックトラックして 2 番目の選択肢で成功して何も消費しない。
 3.1.3 解決策: 最大検査位置
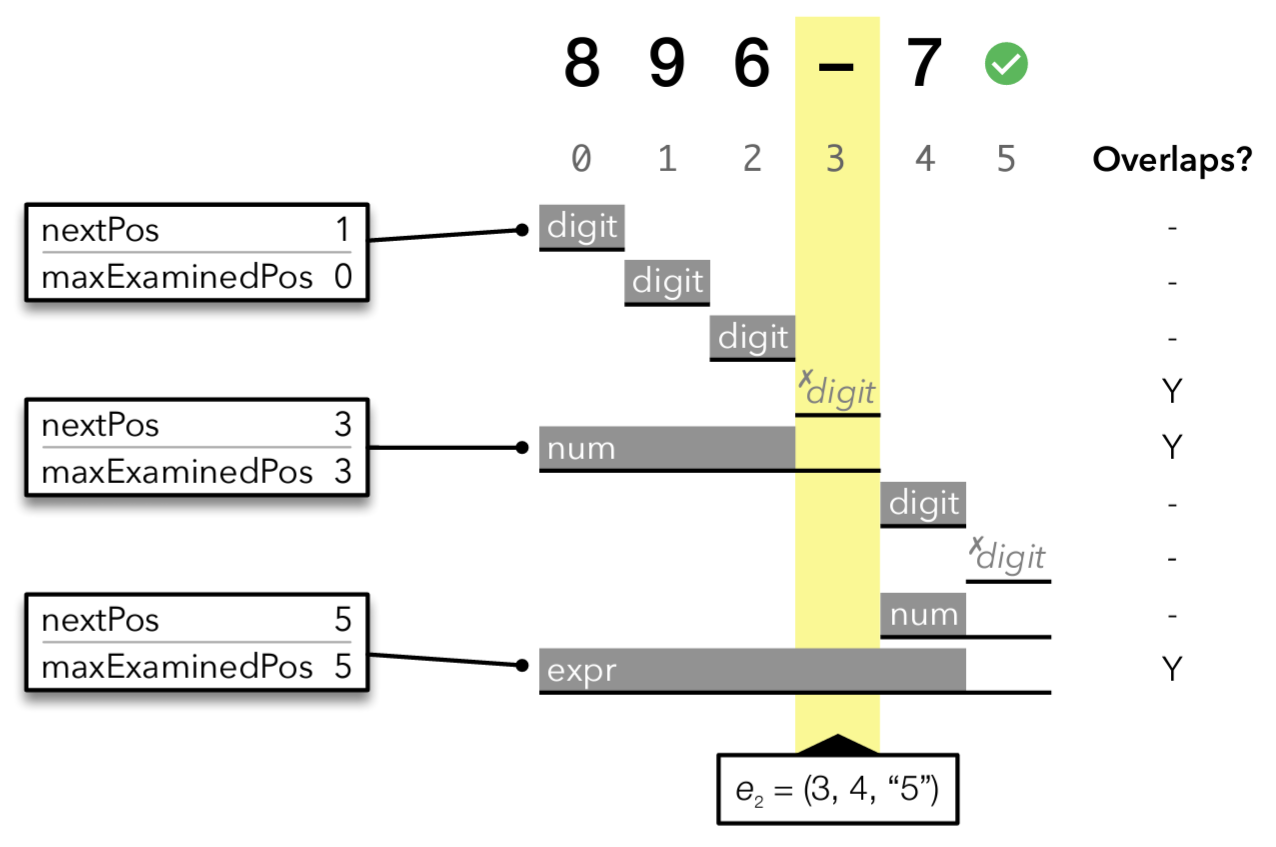
3.1.3 解決策: 最大検査位置
この問題に対処するため、メモ表のエントリに最大検査済み位置 (maximum examined position) または \({\it maxExaminedPos}\) という別のフィールドを導入した。これは規則を解析する全過程において入力ストリームで最も遠くにある位置を記録するものである。入力位置が検査 (examined) されるのは (a) その一の文字が消費されるか、(b) その文字の値が解析の判断に使用されるか、のいずれかである。
実用的には規則適用の検査済み区間 (examined interval) (閉区間 \([p,{\it maxExaminedPos}]\) として定義) には、その検査の解析結果に影響を与えた可能性のある文字が全て含まれている。定義によりある式の検査済み区間はそのすべての部分式の検査済み区間を含む。
Figure 4 はエントリが次の位置と最大検査済み位置の両方を記録するメモ表である。位置 0 にある num の検査済み区間は、実際には編集操作 \(e_2\) と重なっていることに注意。したがって、消費された間隔ではなく、検査された間隔に基づいてエントリを無効化することで正しさを保つことができる。
直感的にこれは理にかなっている。規則適用の検査済み区間は、その結果に影響を与える可能性のある入力の全領域を表している。編集操作が入力のその部分に影響を与える場合にのみ操作可能なエントリは無効となるはずである。
 3.2 メモ表エントリの再配置
3.2 メモ表エントリの再配置
入力の長さが変わらない限りは前述の無効化戦略でも十分である。重複するエントリを無効化した後、メモ表の残りは新しい入力を解析するために再利用することができる。しかし挿入や削除などによって入力の長さが変化した場合はメモ表の一部のエントリには追加の処理が必要になる。
例えば \(e_3=(1,2,"")\) という編集によって元の入力から "9" を削除して "86-7" とすることを考える。"9" を削除すると位置 1 以降の文字 ("6-7") が一つ左に移動する。入力の変更後にそれに合わせてメモ表も変更しなければならない。つまり Figure 5 に示すように、1 列目を削除して次の列を 1 ポジション左にシフトさせる。
以前は位置 2 にあった digit のエントリは今 1 の位置にある。しかし \({\it nextPos}\) の値は 3 であり、これは 2 文字消費することを示している (これは正しいとはいえない)。\({\it nextPos}\) と \({\it maxExaminedPos}\) は絶対位置であるため、メモ表の項目が再配置されるたびにそれらの値を修正する必要がある。
大きなファイルの先頭に文字を挿入するような現実的なシナリオでは、このような更新のコストによってインクリメンタル構文解析の利点はほとんどが失われてしまう。この問題に対する我々の解決策は、ここのメモ表エントリを位置非依存にし、余計なコストを掛けずに再配置できるようにすることである。これを実現するために、メモ表エントリの \({\it nextPos}\) プロパティを相対オフセットで置き換え、これを \({\it matchLength}\) と呼ぶことにする。同様に、あるエントリの検査済み間隔を \({\it examinedLength}\) として保存する。これはほとんどの Packrat 構文解析の実装において単純な変更であり、構文解析の漸近的な複雑さには影響しない。
 3.3 ApplyEdit のアルゴリズム
3.3 ApplyEdit のアルゴリズム
セクション 3.1 では編集操作によって無効化されたメモ表エントリを検出するために検査済み区間を使用する方法について説明した。セクション 3.2 では、メモ表エントリを効率的に再配置できるように、位置に依存しない方法で保存する手法について説明した。次に、\(\textsc{APPLY}\textsc{EDIT}\) 手続きを実装するためにこれら 2 つの手法をどのように一緒に使うことができるかを説明する。
\(\textsc{APPLY}\textsc{EDIT}\) の定義は本節の冒頭で紹介した。\[ \textsc{APPLY}\textsc{EDIT} : (s, M, e) \to (s', M') \]
\(\textsc{APPLY}\textsc{EDIT}\) は入力文字列 \(s\)、メモ表 \(M\)、編集操作 \(e\) を与えると修正された入力文字列 \(s'\) と、\(s'\) をインクリメンタルに解析するために使用できる新しいメモ表 \(M'\) を生成する。基本的な実装は以下のステップからなる:
- Step 1. \(s\) に編集操作を適用し \(s'\) を生成する。
- Step 2. メモ表を調整する。編集区間内の列から全てのエントリを削除し、必要に応じて列を追加または削除し、区間の右側に列を移動させる。
- Step 3. メモ表をスキャンして検査済み区間が編集区間と重なる残りのエントリを削除する。最後に \(s'\) と \(M'\) を返す。
Step 3 では編集区間の左側の部分のみをスキャンする必要があることに注意。編集区間の内側で始まる無効なエントリは Step 2 で削除され、右側のエントリ (再配置されたエントリ) は編集によって影響を受けることはない。しかしそれらのエントリは、例えば編集によってそれらの文字がコメントの一部になった場合など、現在の解析ではもはや使用されていない可能性がある。
これら 3 つのステップをあわせて \(\textsc{APPLY}\textsc{EDIT}\) の完全な実装とインクリメンタル Packrat 構文解析技術の中核を構成している。次のセクションではこれを最適化する一つの方法について説明する。
 3.4 解析と最適化
3.4 解析と最適化
上記の \(\textsc{APPLY}\textsc{EDIT}\) の実装は \(O(m \times n)\) の複雑性を持つ。ここで \(n\) は入力のサイズ、\(m\) は文法の規則の数である。文字列連結 (step 1) と配列連結 (step 2) がともに \(O(n)\) であると仮定すると実行時間は step 3 のメモ表無効化によって支配される。最悪ケースでは無効化でメモ表の \(O(n)\) 列を訪れ、各列で \(O(m)\) のメモ表エントリをスキャンして編集区間に重なるかをチェックする必要がある。これは Packrat 区分解析の漸近的な複雑さ (すでに \(O(m \times n)\)) には影響しないが、実際の仕様では性能低下を招く可能性がある。
 3.4.1 最大検査済み長
3.4.1 最大検査済み長
この無効化アルゴリズムのパフォーマンスを向上させるために、メモ表のレイアウトを変更して各行がそのすべてのエントリの最大検査済み間隔を追跡できるようにする。この値を \({\it maxExaminedLength}\) と呼ぶカラムごとのプロパティに格納する。これにより、\(\textsc{APPLY}\textsc{EDIT}\) の step 3 で列をスキャンするときに \({\it maxExaminedLength}\) でその列のエントリがどれも編集と重ならないことを示していれば、その列のすべてのエントリをスキャンしないようにすることができる。
解析中にメモ表エントリが削除されることはないため、解析中はカラムの \({\it maxExaminedLength}\) は単調増加する。これは、新しいメモ表エントリが列に追加されるたびに \({\it maxExaminedLength}\) を定数時間で更新できることを意味する。
個々のメモ表エントリは \(\textsc{APPLY}\textsc{EDIT}\) がすでに与えられた列のすべてのエントリをスキャンしている時にのみ削除することができる。したがって \({\it maxExaminedLength}\) の新しい値 (より小さい場合) も、一定の追加時間で算出することができる。したがって列ごとに最大珪砂済み長を維持することは検査アルゴリズムや Packrat 解析一般の漸近的な複雑性に影響を与えない。
 3.5 総括
3.5 総括
Figure 6 は最大検査済み長 (maximum examined length) 最適化を含む \(\textsc{APPLY}\textsc{EDIT}\) アルゴリズムの最終版を示している。入力文字列 \(s\)、メモ表 \(M\)、編集操作 \(e\) が与えられると、\(\textsc{APPLY}\textsc{EDIT}\) は修正された入力 \(s'\) と編集によって影響を受けないすべてのエントリを \(M\) と共有する新しいメモ表 \(M'\) を生成する。
▷ Step 1: 編集を \(s\) に適用
| 1. | \( s' = \textsc{CONCAT}(s[0..e.pos_s], e.r, s[e.pos_e..]) \) | |
| 1. | \( M' = \textsc{CONCAT}(M[0..e.pos_s], e.r.lenght \mbox{個の新しい列のリスト}, M[e.pos_e..]) \) | |
| 1. | \( {\bf for} \ i = 0 \ {\bf to} \ e.pos_s \) | |
| 2. | \( \hspace{12pt}col = M'[i] \) | |
| 3. | \( \hspace{12pt} \)// この列には \(e\) とオーバーラップしているものがあるか? | |
| 4. | \( \hspace{12pt}{\bf if} \ i+col.maxExaminedLength \le e.pos_s \) | |
| 5. | \( \hspace{24pt}{\bf continue} \ to \ next \ column \) | |
| 6. | \( \hspace{12pt}newMax = 0 \) | |
| 7. | \( \hspace{12pt}{\bf for} \ {\rm each} \ entry \ {\bf in} \ col \) | |
| 8. | \( \hspace{24pt}{\bf if} \ i + entry.examinedLength \gt e.pos_s \) | |
| 9. | \( \hspace{36pt}{\rm Delete} \ entry \ {\rm from} \ M' \) | |
| 10. | \( \hspace{24pt}{\bf elseif} \ entry.examinedLength \gt newMax \) | |
| 11. | \( \hspace{36pt}newMax = entry.examinedLength \) | |
| 12. | \( \hspace{12pt}col.maxExaminedLength = newMax \) | |
| 13. | \( {\bf return} \ s', M' \) | |
インクリメンタルな解析を行うために \(\textsc{APPLY}\textsc{EDIT}\) の結果は \(\textsc{PARSE}\) に渡され、より多くのエントリを持つ新しいメモ表を返す。\(\textsc{PARSE}\) は事前に満たされた (pre-filled) メモ表エントリを利用する。コードエディタや IDE では、編集を適用するたびに入力を再解析するのが一般的な使い方だろう:
| 1. | \( M = \mbox{新しいメモ表} \) | |
| 2. | \( s = \mbox{空の文字列} \) | |
| 3. | \( {\bf for} \ {\rm each} \ {\rm edit} \ {\rm operator} \ e \) | |
| 4. | \( \hspace{12pt}s, M = \textsc{APPLY}\textsc{EDIT}(s,M,e) \) | |
| 5. | \( \hspace{12pt}M = \textsc{PARSE}(G,s,M) \) | |
また \(\textsc{PARSE}\) に結果を渡す前に \(\textsc{APPLY}\textsc{EDIT}\) を複数回呼び出すことで、編集スキャンを一括して行うことも可能である。
\(\textsc{PARSE}\) の実装は以下の例外を除いて標準的な Packrat パーサとほぼ同じである:
- メモ表エントリの \({\it examinedLength}\) プロパティとメモ表列の \({\it maxExaminedPos}\) プロパティを保持する。
- 解析の終了時にそのメモ表を返す。
詳細は実装に依存するため、ここでは (1) のアルゴリズムは示さない (ただし単純である)。例として本論文付録の IncrementalMatcher と IncRuleApplication のマッチメソッドを参照されたい。
 4 Evaluation
4 Evaluation
 4.1 Parsing Performance
4.1 Parsing Performance
 4.1.1 Improving Initial Parse Time
4.1.1 Improving Initial Parse Time
 4.2 Space Efficiency
4.2 Space Efficiency
 4.3 Discussion
4.3 Discussion
 5 Related Work
5 Related Work
 5.1 Incremental Parsing
5.1 Incremental Parsing
 5.2 Optimization of Packrat Parsers
5.2 Optimization of Packrat Parsers
 6 Conclusion and Future Work
6 Conclusion and Future Work
 Appendix: Source Code
Appendix: Source Code
 Acknowledgements
Acknowledgements
T heauthors would like to thank Jonathan Edwards, Marijn Haverbeke, Marko R¨oder, Nada Amin, Saketh Kasibatla, Sean McDirmid, Yoshiki Ohshima, and the anonymous reviewers for feedback on this work and earlier drafts of the paper.
 References
References
- Ralph Becket and Zoltan Somogyi. 2008. DCGs + Memoing = Packrat Parsing but Is It Worth It?. In Proc. of Practical Aspects of Declarative Languages: 10th International Symposium (PADL 2008). Springer, 182–196. https://doi.org/10.1007/978-3-540-77442-6
- Stuart K. Card, Thomas P. Moran, and Allen Newell. 1980. The Keystroke-Level Model for User Performance Time with Interactive Systems. Commun. ACM 23, 7 (1980), 396–410. https://doi.org/10.1145/358886.358895
- Bryan Ford. 2002. Packrat Parsing: A Practical Linear-Time Algorithm with Backtracking. Master’s thesis. Massachusetts Institute of Technology.
- Bryan Ford. 2002. Packrat Parsing: Simple, Powerful, Lazy, Linear Time. In Proc. of the Seventh ACM SIGPLAN International Conference on Functional Programming (ICFP ’02), Vol. 37. ACM, 36–47. https://doi.org/10.1145/581478.581483
- Bryan Ford. 2004. Parsing Expression Grammars: A Recognition-Based Syntactic Foundation. In Proc. of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL ’04). ACM, 111–122. https://doi.org/10.1145/964001.964011
- Carlo Ghezzi and Dino Mandrioli. 1979. Incremental Parsing. ACM Transactions on Programming Languages and Systems (TOPLAS) 1, 1 (Jan. 1979), 58–70. https://doi.org/10.1145/357062.357066
- Carlo Ghezzi and Dino Mandrioli. 1980. Augmenting Parsers to Support Incrementality. J. ACM 27, 3 (July 1980), 564–579. https://doi.org/10.1145/322203.322215
- Robert Grimm. 2006. Better Extensibility Through Modular Syntax. In Proc. of the 27th ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI ’06). ACM, 38–51. https://doi.org/10.1145/1133981.1133987
- Marijn Haverbeke. 2017. Acorn webpage. (2017). https://github.com/ternjs/acorn
- Israel Herraiz, Daniel M. German, and Ahmed E. Hassan. 2011. On the Distribution of Source Code File Sizes.. In ICSOFT (2). 5–14.
- Kimio Kuramitsu. 2015. Packrat Parsing with Elastic Sliding Window. Journal of Information Processing 23, 4 (7 2015), 505–512. https://doi.org/10.2197/ipsjjip.23.505
- Ilya Lakhin. 2013. Incremental Parser Based on Invariant Syntax Fragments (LtU post). (2013). http://lambda-the-ultimate.org/node/4840
- Ilya Lakhin. 2013. Papa Carlo webpage. (2013). http://lakhin.com/projects/papa-carlo/
- J.-M. Larchevˆeque. 1995. Optimal Incremental Parsing. ACM Transactions on Programming Languages and Systems (TOPLAS) 17, 1 (Jan. 1995), 1–15. https://doi.org/10.1145/200994.200996
- Robert B. Miller. 1968. Response Time in Man-Computer Conversational Transactions. In Proc. of the December 9–11, 1968, Fall Joint Computer Conference, Part I. ACM, 267–277. https://doi.org/10.1145/1476589.1476628
- Kota Mizushima et al. 2010. Packrat Parsers Can Handle Practical Grammars in Mostly Constant Space. In Proc. of PASTE ’10. ACM, 29–36. https://doi.org/10.1145/1806672.1806679
- Arvind M. Murching, Y.V. Prasad, and Y.N. Srikant. 1990. Incremental Recursive Descent Parsing. Computer Languages 15, 4 (1990), 193–204. https://doi.org/10.1016/0096-0551(90)90020-P
- John J. Shilling. 1993. Incremental LL (1) Parsing in Language-Based Editors. IEEE Transactions on Software Engineering 19, 9 (1993), 935–940. https://doi.org/10.1109/32.241775
- Tim A. Wagner and Susan L. Graham. 1998. Efficient and Flexible Incremental Parsing. ACM Transactions on Programming Languages and Systems (TOPLAS) 20, 5 (Sept. 1998), 980–1013. https://doi.org/10.1145/293677.293678
- Alessandro Warth, Patrick Dubroy, et al. 2016. Ohm webpage. (2016). https://ohmlang.github.io/
- Alessandro Warth, Patrick Dubroy, and Tony Garnock-Jones. 2016. Modular Semantic Actions. In Proc. of the 12th Symposium on Dynamic Languages (DLS 2016). ACM, 108–119. https://doi.org/10.1145/2989225.2989231
翻訳抄
Packrat 構文解析のメモ表を利用して、構文解析済みの入力テキストが変更されたときに (全体の再パースなしに) テキスト変更分をインクリメンタルに構文解析結果に反映する Packrat 構文解析の改良に関する 2017 年の論文。
- Patrick Dubroy and Alessandro Warth. 2017. Incremental Packrat Parsing. In Proceedings of 2017 ACM SIGPLAN International Conference on Software Language Engineering (SLE’17). ACM, New York, NY, USA, 12 pages. https://doi.org/10.1145/3136014.3136022