構文解析

概要

一般に構文解析 (syntactic analysis) とは文章を解析してその構文構造を導き出すという意味を持つ。

Table of Contents

1. 概要
2. 導入
   1. トップダウンとボトムアップ
      1. ボトムアップ構文解析
   2. 最左導出と最右導出
3. 正規言語
4. 文脈自由文法
5. LL 構文
6. 構文解析器の実装
   1. 入力方法
   2. 出力方法
7. 参考文献

導入

自由文脈文法 (context-free grammar) の生成規則は \((A, w)\) で表される。この LHS (左要素) の \(A\in N\) は単一の非終端文字 (つまりコンテキストを含まない) であり、RHS (右要素) の \(w \in V^*\) は任意の終端記号/非終端記号の混合列である。

トップダウンとボトムアップ

トップダウン解析 (top-down parsing) は文法の開始記号を起点に様々な生成規則を適用し、最終的に文から構文木を構築する。ボトムアップ解析 (bottom-up parsing) は与えられた文の処理から初めて、最終的に 1 つの構文木にマージされる逆生成を適用して森を木にする。自動生成されるほとんどの構文解析器は後述する SR や LALR 構文解析器はボトムアップ解析である。

例1. 次のように表される文法を仮定する。ここで \((A,B)\) は変換規則 \(p:A \to B\) である。 \[ \begin{equation} \begin{split} G & = & \langle (S,L,D), (a,b,\ldots,z,0,1,\ldots,9), P, S \rangle \\ P & = & \{(S,L), (S,SL), (S,SD), \\ && (L,a), (L,b), \ldots, (L,z), \\ && (D,0), (D,1), \ldots, (D,9)\} \end{split} \label{ex1} \end{equation} \] 式 (\(\ref{ex1}\)) の文法 \(G\) に \(s3\) という記号列を適用したとき、トップダウンは次のように構文木を構築する。\[ S \Rightarrow SD \Rightarrow LD \Rightarrow s D \Rightarrow s 3 \] 最初のステップでは \(L\), \(SL\), \(SD\) の 3 つの選択肢があるが、その中で \(s3\) に適合可能な生成規則を暗に選択している点に注意。一方、ボトムアップは次のように行われる。\[ s3 \Rightarrow L3 \Rightarrow S3 \Rightarrow SD \Rightarrow S \]

ボトムアップ構文解析

ボトムアップ構文解析は入力記号列に対してボトムアップで構文木を構築する。構文木は末端の葉 (下) から根 (上) へ向かって構築される。

最左導出と最右導出

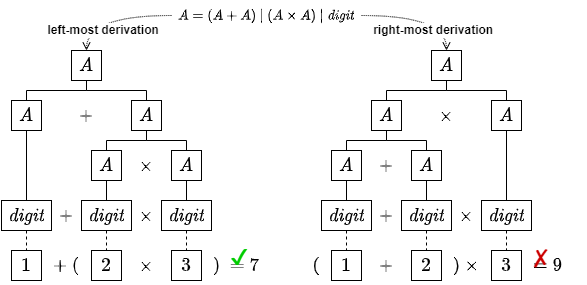
最も左から導出する方法を最左導出 (left-most derivation)、最も右から導出する方法を最右導出 (right-most derivation) という。例えば式 (\(\ref{md_smpl}\)) のような構文定義があった場合、最左導出は式 (\(\ref{lmd}\)) の順序で導出し、最右導出は式 (\(\ref{rmd}\)) の順序で導出する。\[ \begin{equation} A = (A + A) \ | \ (A \times A) \ | \ {\it digit} \label{md_smpl} \end{equation} \]

これらは最終的に同じ導出結果をもたらす。一般に、最右導出はより強力で多くの言語に適用され、最左導出はより簡単で再帰下降パーサの実装演習に用いられる。最右導出、最左導出はそれぞれ後述する LR パーサ、LL パーサの方針に対応する。

ただし、最左導出と最右導出から生成される抽象構文木は Fig 1 のように異なることから、異なる評価順序の演算子が混在するケースでは間違ったセマンティクスを生成する。

また同一の演算子であっても左結合 (left-associative) と右結合 (right-associative) とで異なる結果をもたらす。例えば数学の減算記号は左結合であるため Fig 2 のように右結合の評価順序では間違った結果をもたらす。

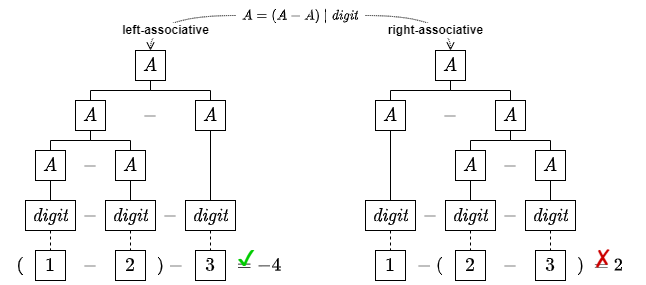
構文定義はこのような形式文法の表現はあいまいさを解決するために優先順位と結合規則を正しく設計する必要がある。例えば Fig 1 は \(A\) \(=\) \((A + B)\) \(|\) \(B;\) \(B\) \(=\) \((B \times {\it digit})\) \(|\) \({\it digit}\) のように定義することで乗算演算子 \(\times\) を加算演算子 \(+\) より優先することができる。同様に Fig 2 では左結合性の文脈を左再帰によって帰納するように結合性を正し、\(A = (A - {\it digit}) \ | \ {\it digit}\) のように定義すれば LL パーサでも LR パーサでも左結合を強制することができる。

中でも LALR(1) は、記号列を再帰することなく左から右へ一度だけ走査する現実的なパーサである。fast stable driven parser

正規言語

正規文法は有限オートマトンで受理される文法、正規言語は正規文法によって生成される言語である。

正規言語 \(L\) 上の長さ \(n\) 以上のすべての記号列 \(z\) は \(z = u v w\), \(0 \lt |v| \lt n\) となるように分解できる。この性質は繰り返し定理 (iteration theorem) またはポンピング定理 (pumping theorem) と呼ばれ式 (\(\ref{iter}\)) のように表される。\[ \begin{equation} \forall i \ge 0, \ u\,v^i\,w \in L \label{iter} \end{equation} \] この定数 \(n\) は \(L\) を受理する有限オートマトンの状態数である。

文脈自由文法

LL 構文

LL 構文 (LL parser) 再帰下降パーサー (recursive-decent parser) 列の前方の \(k\) 個の記号を読み込んで

構文解析器の実装

入力方法

パーサが対象とする初期記号列の入力は:

1. 解析対象の入力記号列全体をパーサに指定する方法。
   1. 任意の位置から入力記号を読み出すことのできる (つまり低コストでシーク可能な) メモリ領域やブロックデバイス。
   2. 入力記号列の前方から逐次読み出しが可能だが読み出し位置を戻すことのできない抽象化されたストリーム。
2. 断片化された入力記号を繰り返し指定する方法。

下になるほどパーサの実装は困難になるが、アプリケーションやデータサイズの制約は少なく、下の形態のパーサが存在するのであれば上のパーサを代替することが可能である。

出力方法

push パーサ (push parser) はパーサが自主的に入力記号列を読み進めて構文解析を進行し、その解析結果をアプリケーションに "push する" という利用方法を表している (一般にアプリケーションの用意した関数に解析結果をコールバックする方法で行われる)。一方で pull パーサ (pull parser) はアプリケーションから get 要求があった時に入力記号列を読み進めて次の解析結果を返す利用方法を表している。

これらの言葉は Java での SAX (simple API for XML) パーサに対する StAX (streaming API for XML) パーサの利用形態を表現するために使われ始めた。どちらもパーサ構築時に初期入力記号列を意味する入力ストリームを指定するが、その解析結果をアプリケーションの用意したハンドラに ”push" するか、アプリケーションが "pull" したときに解析結果を返すかの違いを表している。現在でも Java XML API 以外文脈でパーサの利用形態を表現するためにしばしば使用されている。

参考文献

1. オートマトン・言語理論の基礎 (2003) 近代科学社