論文翻訳: Packrat Parsing: Simple, Powerful, Lazy, Linear Time

Abstract

Packrat 構文解析は遅延評価を持つプログラミング言語でパーサを実装するための新しい技法である。Packrat パーサはバックトラックと無制限の先読みを備えたトップダウン構文解析のパワーと柔軟性を備え、なおかつ線形構文解析時間を保証している。Packrat パーサは、\(LL(k)\) あるいは \(LR(k)\) 文法によって定義されるあらゆる言語に加えて、従来の線形時間アルゴリズムではサポートできない多くの言語を認識することができる。この付加能力により、広く普及しているが厄介な最長一致規則のような一般的な構文イディオムの扱いを簡略化でき、構文述語や意味述語のような高度な曖昧性解消戦略が使えるようになり、より良い構文構成特性が得られ、また字句解析が構文解析にシームレスに統合される。しかしその強力さにも関わらず Packrat 構文解析は再帰降下構文解析と同じ単純さと優雅さを共有している。実際、バックトラック型再帰降下構文解析器を線形時間 Packrat 構文解析器に変換するには、しばしばかなり単純な構造変更のみで十分である。この論文では、実用的なアプリケーションでの使用に重点を置いて、Packrat 構文解析について非公式に説明し、より伝統的な代替手段に対する利点と欠点を探る。

Table of Contents

1. Abstract
2. 1 導入
3. 2 パーサの構築
   1. 2.1 再帰降下構文解析
   2. 2.2 バックトラック型と予測型の比較
   3. 2.3 表形式トップダウン構文解析
   4. 2.4 Packrat 構文解析
4. 3 アルゴリズムの拡張
   1. 3.1 左再帰
   2. 3.2 統合字句解析
   3. 3.3 モナド的 Packrat 構文解析
5. 4 LL と LR 構文解析の比較
   1. 4.1 先読み
   2. 4.2 文法構成
   3. 4.3 認識の限界
6. 5 実用上の問題点と限界
   1. 5.1 決定論的構文解析
   2. 5.2 ステートレス構文解析
   3. 5.3 空間消費
7. 6 パフォーマンス結果
   1. 6.1 空間効率
   2. 6.2 解析性能
8. 7 関連研究
9. 8 今後の課題
10. 9 考察
11. Acknowledgements
12. References
13. 翻訳抄

1 導入

関数型言語でパーサを実装する方法は数多くある。最も単純で直接的な方法はトップダウン (top-down) または再帰降下構文解析 (recursive descent parsing) である。この方法では多かれ少なかれ言語文法の構成要素が再帰関数の集合に直接変換される。トップダウンパーサは 2 つのカテゴリに分けられる。予測パーサ (predictive parsers) は入力ストリーム中の限られた個数のシンボルを "先読み" (looking ahead) することにより、ある時点で予測される言語構成要素の種類を予測しようとする。一方でバックトラッキングパーサ (backtracking parsers) は異なる選択肢を連続して試すことで推測的に判断する。これは、ある選択肢が一致しない場合、パーサはもとの入力位置に "バックトラック" して別の選択肢を試す。予測パーサは高速で線形時間の解析が保証されていているが、バックトラックパーサ概念的に単純とはいえ指数関数的な実行時間を示すことがある。

この論文では予測型とバックトラック型の選択を回避するトップダウン構文解析戦略を紹介する。Packrat 構文解析 (packrat parsing) はバックトラックモデルの単純さ、優雅さ、一般性を提供するが、すべての構文解析の計算時に中間結果を保存し、どの結果も 2 回以上評価されないことを保証することによって解析時間が超線形となるリスクを排除している。個のアルゴリズムの理論的基礎は 1970 年代に研究されたが [3, 4]、当時のコンピュータのメモリサイズが限られていたため、線形時間バージョンは実用化されなかったようである。しかし現代のマシンでは個のアルゴリズムのストレージコストは多くのアプリケーションにおいて妥当である。さらにこの特殊な記憶法は現代の遅延関数型プログラミング言語で非常にエレガントかつ効率的に実装することができ、ハッシュテーブルや他の明示的なルックアップ構造を必要としない。このように、古典的ではあるが無視されてきた線形時間構文解析アルゴリズムと最新の関数型プログラミングの融合が本論文の主要な技術的貢献である。

Packrat 構文解析は線形時間を保証しているにも関わらず非常に強力である。Packrat パーサは \(LL(k)\) または \(LR(k)\) 文法で記述できるあらゆる言語、また無限の先読みを必要とする \(LR\) でない多くの言語に対して容易に構築できる。この柔軟性により YACC 系のパーサジェネレータが課す厄介な制限の多くを排除できる。また Packrat 構文解析はボトムアップ LR パーサよりもはるかにシンプルに構成されており、手作業で構築することも現実的である。本論文では手作業による構築のアプローチを探るが、Packrat パーサの自動構築は将来の有望な方向性である。

Packrat パーサは文脈自由文法では曖昧さなく表現することが難しく、従来の線形時間では実装が困難な longest-match (最長一致), followed-by, not-followed-by といった一般的な曖昧性解消規則 (disambiguation rule) を直接的かつ効率的に実装できる。例えば、字句解析における識別子や数字の認識、C-like 言語における if-then-else 文の解析、Haskell に於ける do, let や lambda 式の処理などは本質的に最長一致の曖昧性解消を含んでいる。また Packrat パーサは LR パーサよりも簡単かつ自然に構成可能であり、動的構文や拡張可能な構文に適した基盤となっている [1]。最後に、字句解析と改装解析は統一された単一の Packrat パーサにシームレスに統合することができ、字句解析と階層的言語機能は、例えば式を埋め込んだ文字列リテラルや構造化文書マークアップを含むリテラルコメントを扱うように一緒に混ぜることさえも可能である。

Packrat 構文解析の主な欠点はその空間消費である。その漸近的な最悪ケース (asymptotic worst-case) の境界は従来のアルゴリズムと同じで入力に対して線形だが、その空間利用は最大再帰深ではなく、入力の大きさに直接比例し、それらは一桁違うかもしれない。しかし最新の最適化コンパイラのような多くのアプリケーションでは Packrat パーサの記憶コストは皇族の処理ステージのコストより大きくないと考えられる。したがってこのコストは無制限の先読みを持つ線形時間解析の能力と柔軟性のための合理的なトレードオフである可能性がある。

この論文では Packrat 構文解析をどのように実装し、どのような場合に有用であるかの実用的な間隔を提供することを目的として Packrat 構文解析について検討する。文脈自由文法とトップダウン構文解析の基本的な知識は持っているものとする。完結でわかり易い表現にするために、本文中ではコードの例だけを少し抜粋している。しかしこの論文で説明しているすべての例は、完全に動作する Haskell コードとして以下で利用可能である:
http://pdos.lcs.mit.edu/˜baford/packrat/icfp02

この論文は次のように構成されている。セクション 2 では Packrat 構文解析を紹介し、従来の再帰降下構文解析を出発点としてその動作について説明する。セクション 3 では左再帰、字句解析、モナド解析のサポートなど基本的なアルゴリズムの有用な拡張を紹介する。セクション 4 では従来の線形時間パーサと比較した場合の Packrat パーサの認識能力をより詳細に検討する。セクション 5 では Packrat 構文解析の 3 つの主要な実用上の制限、すなはち決定性、ステートレス性、および空間消費について論じる。セクション 6 では実際の言語に対する Packrat 構文解析の実用性を実証するためにいくつかの実験結果を示す。セクション 7 は関連する研究について、セクション 8 は今後の研究の方向性を指摘し、セクション 9 か結論を述べている。

2 パーサの構築

Packrat 構文解析は本質的にトップダウン構文解析戦略であり、そのため Packrat 構文解析は再帰降下構文解析と密接に関係している。このため、まずありふれた言語の再帰降下パーサを構築し、それを Packrat パーサに変換する。

2.1 再帰降下構文解析

Figure 1 に示したありふれた算術式言語のような文法に再帰降下パーサを構築する標準的なアプローチを考えてみよう。規則の左辺の非終端記号 (nonterminals) のそれぞれについて 4 つの関数を定義する。各関数は解析対象の文字列を受け取り、入力文字列のいくつかの接頭辞を対応する非終端記号の派生として認識しようと試み、"成功" または "失敗" のどちらかの結果を返す。成功した場合、関数は認識した部分の直後にある残りの入力文字列と、認識した部分から算出した何らかの意味的な値を返す。各関数は対応する文法規則の右辺に現れる非終端記号を認識するために自分自身や他の関数を再帰的に呼び出すことができる。

このパーサを Haskell で実装するにはまず解析関数の結果を記述する方が必要である:

data Result v = Parsed v String
              | NoParse

異なる種類の意味値を生成する異なる解析関数に対して汎用的にするために、この Result 型は関連付けられた意味値の型を表す型パラメータ \(v\) をとる。成功した結果は Parsed コンストラクタで構築され (型 \(v\) の) 意味値と (String 型の) 残りの入力テキストを含んでいる。失敗した結果は単純な値 NoParse で表される。このパーサでは 4 つの解析関数がそれぞれ String 型を受け取り Int 型の意味値を持つ Result を生成する。

pAdditive  :: String -> Result Int
pMultitive :: String -> Result Int
pPrimary   :: String -> Result Int
pDecimal   :: String -> Result Int

これらの関数の定義は Figure 1 の文法で表現される相互再帰性をそのまま反映した次のような一般的な構造を持っている:

pAdditive  s = ... (calls itself and pMultitive) ...
pMultitive s = ... (calls itself and pPrimary) ...
pPrimary   s = ... (calls pAdditive and pDecimal) ...
pDeciaml   s = ...

例えば pAdditive 関数は Haskell の原始的なパターンマッチング構文だけを用いて次のようにコード化することができる:

-- Parse an additive-precedence expression
pAdditive :: String -> Result Int
pAdditive s = alt1 where

    -- Additive <- Multitive ’+’ Additive
    alt1 = case pMultitive s of
             Parsed vleft s’ ->
               case s’ of
                 (’+’:s’’) ->
                   case pAdditive s’’ of
                     Parsed vright s’’’ ->
                       Parsed (vleft + vright) s’’’
                     _ -> alt2
                 _ -> alt2
             _ -> alt2

    -- Additive <'- Multitive
    alt2 = case pMultitive s of
             Parsed v s’ -> Parsed v s’
             NoParse -> NoParse

まず pAdditive の結果を計算するためにこの文法規則の選択肢を表す alt1 の値を計算する。次にこの選択肢は pMultitive を呼び出して乗法的優先順位の式を認識させる。pMultitive が成功した場合、その式の意味値 vleft と、認識された入力の部分に続く残りの入力 s' が返される。次に s' の位置に '+' 演算子があるかをチェックし、成功すれば '+' 演算子のあとに残った入力を返す文字列 s'' が生成される。最後の pAdditive 自身を再帰的に呼び出して位置 s'' にある別の加法的優先順位の式を認識する。これが成功すると右辺の結果 vright と最後に余った文字列 s''' が生成される。これらの 3 つすべてのマッチがすべて成功した場合に pAdditive の最初の呼び出しの結果として加算の意味値である vleft + vright と、最終的なあまりの文字列 s''' が返される。これは単に元の入力位置 s にある単一の情報的優先順位の式を認識しようとするもので、成功であれ失敗であれその結果をそのまま返す。

同様に他の 3 つの解析関数も文法に直接対応するように作られている。もちろんヘルパー関数やコンビネータの適切なライブラリを使ってこれらの解析関数をより簡単かつ簡潔に記述する方法もある。これらの手法についてはセクション 3.3 で後述するが、わかりやすさのために今は単純なパターンマッチにこだわることにする。

2.2 バックトラック型と予測型の比較

上記で開発したパーサはバックトラック型パーサである。例えばもし pAdditive 関数で alt1 が失敗するとパーサは元の入力位置まで事実上 "バックトラック" し、1 つ目の選択肢の最初か二番目か三番目かどのステージでマッチしなかったかにかかわらず、2 つ目の選択肢 alt2 を元の入力文字列 s で再実行する。入力 s が単一の乗算式からなる場合、pMultitive 関数は同じ文字列に対して 2 回呼び出されることに注意。1 回目は最初の選択肢で存在しない '+' 演算子にマッチしようとして失敗し、2 回目は 2 つ目の選択肢で適用に成功しながらも失敗する。このようなバックトラックと解析関数の冗長な評価により解析時間は入力の大きさに応じて指数関数的に増加する。これが上記のような "ナイーブな" バックトラック戦略が現実的なパーサで大きなサイズの入力に対して使用されない主な理由である。

トップダウンパーサを実用化するための標準的な戦略は、実際に再帰的な呼び出しを行う前にいくつかの選択肢の規則の中から適用すべき規則を "予想" できるように設計することである。この方法により、解析関数が冗長に呼び出されることがなくなり、どのような入力でも線形時間で解析できることが保証される。例えば Figure 1 の文法は予測型パーサには直接適さないが、Additive と Multitive 非終端記号を次のように "左因子化" (left-factoring) することで 1 つの先読みトークンを持つような予想に適した LL(1) 文法に変換することができる: \[ \begin{eqnarray*} {\rm Additive} & \leftarrow & {\rm Multitive} \ \ {\rm AdditiveSuffix} \\ {\rm AdditiveSuffix} & \leftarrow & {\tt "+"} \ \ {\rm Additive} \ \ | \ \ \epsilon \\ {\rm Multitive} & \leftarrow & {\rm Primary} \ \ {\rm MultitiveSuffix} \\ {\rm MultitiveSuffix} & \leftarrow & {\tt "*"} \ \ {\rm Multitive} \ \ | \ \ \epsilon \end{eqnarray*} \] これで AdditiveSuffix の 2 つの選択肢の決定は、再帰呼び出しを行う前に次の入力文字が "+" であるかどうかをチェックするだけで行うことができるようになる。しかし予測メカニズムは "生の" (raw) 入力トークン (この場合は文字) しか扱えず、それ自体は一定時間で動作しなければならないため、予測的に解析可能な文法のクラスは非常に限定的である。また予測メカニズムが文法と矛盾しないように注意する必要があるが、これは手作業では難しく、言語の大域的な性質に大きく影響される。例えばより優先順位の高い指数演算子 '**' が言語に追加された場合 MultitiveSuffix の予測メカニズムは長征されなければならない。そうでないと指数演算子は乗算式の予測を誤って起動し、有効な入力に対してパーサが失敗する原因となる。

トップダウンパーサの中にはほとんどの判断で予測を使用し、より柔軟性が必要な場合に完全なバックトラックにフォールバックするものも存在する。この戦略は柔軟性と性能の良い組み合わせを実現することが多い一方で、予測という複雑な要素が加わるため、パーサの設計者は予測を使用できる場所とバックトラックが必要な場所を密接に意識する必要がある。

2.3 表形式トップダウン構文解析

Birman と Ullman [4] が指摘するように、セクション 2.1 で紹介した種類のバックトラック型パーサは予測による複雑さや成約を追加することなく線形時間で動作させることが可能である。バックトラッキング型パーサが超線形時間を要する根本の理由は、同じ部分入力文字列に対して同じ解析関数を冗長に呼び出すためであり、これらの冗長な呼び出しはメモ化によって排除することができる。

例の各解析関数は単一のパラメータである入力文字列にのみ依存している。解析関数が自分自身や他の解析関数を再帰的に呼び出すときは常に、与えられた文字列ものと同じ入力文字列か (例えば pAdditive から pMultitive への呼び出し)、元の入力文字列の先頭部分 (たとえば "+" 演算子にマッチした後の pAdditive から自分自身への再帰呼び出し) が提供される。もし入力文字列の長さが \(n\) ならこれらの再帰呼び出しで使用される可能性のある後方部分は、元の入力文字列自身と空文字列を含めて \(n+1\) 種類だけである。解析関数は 4 種類しかないため解析処理に必要な中間結果は最大でも \(4 (n+1)\) 個しかない。

これらの中間結果を表に格納することでそれらを何度も計算することを避けることができる。表には 4 つの解析関数ごとに 1 行、入力文字列の異なる位置ごとに 1 列がある。入力文字列の右側から左に向かって 1 列ずつ、各入力位置に対する各解析関数の結果を表に格納する。各列の中では一番下のセルから始めて上に向かって処理する。あるセルの結果を計算するまでに、対応する解析関数のすべての再帰呼び出しの結果は算出されて別の場所に記録されている。

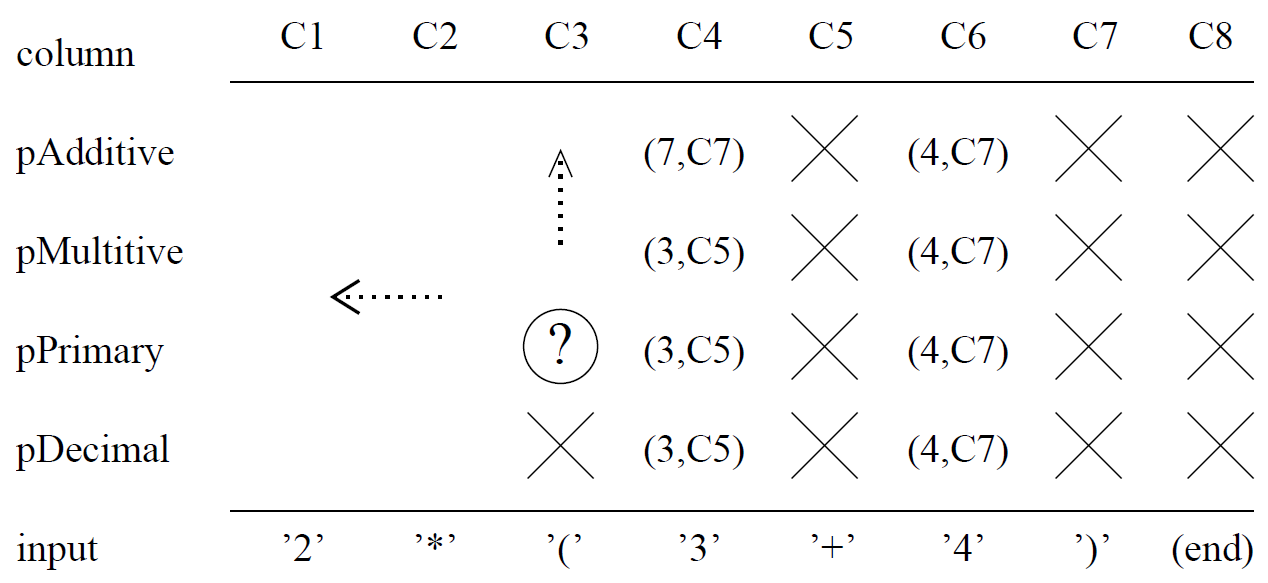
Figure 2 は入力文字列 "2*(3+4)" に対する部分的に完成された結果の表である。簡潔さのために Parse の結果は \(v,c)\) のように表記していて、\(v\) は意味値、\(c\) は関連する余りの後方部分が始まる列番号である。整数の意味値との混乱を避けるために、列は C1, C2, とラベル付けしている。NoParse 結果はセルに X と表示している。次に埋めるべきセルは C3 列の pPrimary セルであり、丸で囲んだクエスチョンマークで示されている。

Primary 式の規則には括弧付きの Additive 式と Decimal 数字の 2 つの選択肢がある。もし文法で示されている順序で選択肢を試すとすると pPrimary はまず括弧化された Addtive 式のチェックを行う。そのために pPrimary は C3 列の開き括弧 '(' とのマッチを試み、これが成功すると C4 列から始まる残りの後方文字列、つまり '3+4)' が得られる。単純な再帰降下パーサでは pPrimary はこの余った文字列に対して再帰的に pAdditive を呼び出すことになる。しかし我々は表を持っているので、表の C4 列で pAdditive の結果を簡単に調べることができ、これは (7,C7) である。このエントリは加算式 '3+4' の結果である 7 の意味値と、C7 列から始まる残りの後方文字列 ')' を示している。このマッチングは成功するため、pPrimary は最終的に位置 C7 の閉じ括弧とのマッチを試み、成功して進行し、残りの空文字列 C8 が得られる。従って C3 列で pPrimary に入力された結果は (7,C8) である。

長い入力文字列と複雑な文法ではこの結果の表は大きくなるかもしれないが、文法の非終端記号の数が一定であれば入力の大きさに比例して大きくなるに過ぎない。さらに Backus-Naur Form [2] を使用する限り、新しい結果を計算するために行列内に以前に記録された一定数のセルにアクセスする必要があるだけである。従って表の検索が一定時間で行われると仮定すると、構文解析プロセス全体は線形時間で終了する。

結果の表に埋め込まれた "forward pointers" により、ある結果の計算では行列の中で大きく離れたセルを調べることがある。例えば上記の C3 での pPrimary の計算では C3, C4, C7 列の結果が使用されている。このように、解析の決定時に任意の距離をスキップできることがこのアルゴリズムの無制限の先読み能力の源であり、この能力によりアルゴリズムは線形時間予測パーサや LR パーサよりも強力なものとなっている。

2.4 Packrat 構文解析

前述の表形式 right-to-left 解析アルゴリズムにおける実用上の明白な問題は、必ずしも必要とされない多くの結果を算出することである。さらに pAdditive や pMultitive のように、同じ列のほかの結果に依存する解析関数が正しく動作するように、特定の列の結果が計算される順序を慎重に決定しなければならないという不便もある。

Packrat 構文解析 (packrat parsing) はこれらの問題を解決するための表形式アルゴリズムの遅延バージョンである。Packrat 解析は必要な時に必要な分だけ、本来の再帰降下パーサと同じ順序で結果を計算する。ただし、最初に一度算出された結果はその後の呼び出しで再利用できるように保存される。

Haskell のような非厳格関数型プログラミング言語は Packrat パーサの理想的な実装プラットフォームを提供している。実際、Haskell での Packrat 構文解析は、配列や、言語の通常の代数的データ型以外の明示的なルックアップ構造を必要としないため特に効率的である。

まず我々は解析結果の行列で単一の列を表す新しい型を導入する必要がある。これを Derives ("derivations") と呼ぶことにする。この型は文法中の各非終端記号ごとに 1 つの要素を持つ単なるタプルである。各要素の方は対応する解析関数の結果型である。Derivs 型には dvChar という追加の要素が 1 つあり、入力文字列の "生の" 文字を、それ自体が何らかの解析関数の結果であるかのように表現する。この例のパーサでの Derivs 型は Haskell では次のように簡単に宣言することができる:

data Derivs = Derivs {
                dvAdditive  :: Result Int,
                dvMultitive :: Result Int,
                dvPrimary   :: Result Int,
                dvDecimal   :: Result Int,
                dvChar      :: Result Char}

この Haskell 構文では Derivs 型に指定されている 5 つの型に対応する要素を持つ Derivs という名前の 1 つのコンストラクタを宣言している。また dvAdditive が Derivs → Result Int 型の関数として使用でき、Derivs タプルの第一要素を抽出するように、各要素に対して関連するデータアクセス関数も自動的に生成する。

次に我々は Result 型を変更し、成功結果の "remainder" 要素が単なる String 型ではなく Derivs のインスタンスとなるようにする:

data Result v = Parsed v Derivs
              | NoParse

Derivs と Result 型は相互に再帰が可能である。ある Derivs インスタンスでの成功結果は他の Derivs インスタンスへのリンクとして機能する。これらの結果値は、実際には解析結果の行列の異なる列の間に必要な唯一のリンクとなる。

ここで元の再帰降下構文解析関数を修正し、それぞれがパラメータとして文字列の代わりに Derivs を受け取るようにする:

pAdditive  :: Derivs -> Result Int
pMultitive :: Derivs -> Result Int
pMprimary  :: Derivs -> Result Int
pDecimal   :: Derivs -> Result Int

元の解析関数が入力文字を直接調べるとき、新しい解析関数は代わりに Derivs オブジェクトの dvChar 要素を参照する。元の関数が文法中の非終端文字にマッチさせるために自分自身や他の解析関数を再帰的に呼び出していた場合、新しい解析関数は代わりにその非終端記号に対応する　Derivs アクセス関数を使用する。終端記号と非終端記号のシーケンスは複数の Derivs インスタンスを経由して成功結果の連鎖をたどることでマッチングされる。例えば新しい pAdditive 関数では次のように dvMultitive, dvChar および dvAdditive アクセス関数を使用し、直接的な再帰呼び出しは行わない。

-- Parse an additive-precedence expression
pAdditive :: Derivs -> Result Int
pAdditive d = alt1 where

      -- Additive <- Multitive ’+’ Additive
      alt1 = case dvMultitive d of
               Parsed vleft d’ ->
                 case dvChar d’ of
                   Parsed ’+’ d’’ ->
                     case dvAdditive d’’ of
                       Parsed vright d’’’ ->
                         Parsed (vleft + vright) d’’’
                       _ -> alt2
                     _ -> alt2
                   _ -> alt2

      -- Additive <- Multitive
      alt2 = dvMultitive d

最後に、特別な "トップレベル" 関数である parse を作成し、Derivs 型のインスタンスを生成して個々の解析関数感の再帰を "束ねる" ようにする:

-- Create a result matrix for an input string
parse :: String -> Derivs
parse s = d where
    d = Derivs add mult prim dec chr
    add = pAdditive d
    mult = pMultitive d
    prim = pPrimary d
    dec = pDecimal d
    chr = case s of
            (c:s’) -> ParseParsed c (parse s’)
            [] -> NoParse

Packrat パーサの "魔法" はこの二重再帰関数にある。第一レベルの再帰は case 文の中でパース関数自身を参照することによって行われる。この比較的一般的な再帰の形式は入力文字列を位置文字ずつ繰り返し処理し、入力位置ごとに 1 つの Derivs インスタンスを生成するために使用される。空文字を表す最後の Derivs インスタンスには NoParse の dvChar 結果が割り当てられ、結果の行列の列のリストが実質的に終了する。

第二レベルの再帰は記号 d を経由して行われる。この識別子はパース関数が構築して返す Derivs インスタンスの名前であると同時に個々のパース関数のパラメータでもある。これらの解析関数は順番に、まさにこの Derivs オブジェクトを形成する残りの要素を生成する。

もちろんこの形式のデータ再帰性 (data recursion) は同じオブジェクトの他の部分が利用可能になる前にオブジェクトのいくつかの要素にアクセスすることができる非厳格な言語でのみ機能する。例えば上記のいくつかの関数で作成された Derivs インスタンスはタプル内の他の要素が利用可能になる前に dvChar 要素にアクセスすることができる。このタプルの dvDecimal 要素にアクセスしようとすると pDecimal が呼び出され dvChar 要素を使用するが、他の "上位レベル" 要素は必要ない。同様に dvPrimary にアクセスすると pPrimary が呼び出され dvChar と dvAdditive にアクセスすることができる。後者では pPrimary は "上位レベル" 要素にアクセスしていることになるが、この場合 dvAdditive は呼び出された要素とは異なる Derivs オブジェクト、つまり冒頭の括弧に続く位置のオブジェクト上で呼び出されているだけなので、循環的な依存関係は発生しない。parse によって生成されるすべての Derivs オブジェクトの各要素はこの方法で遅延評価することができる。

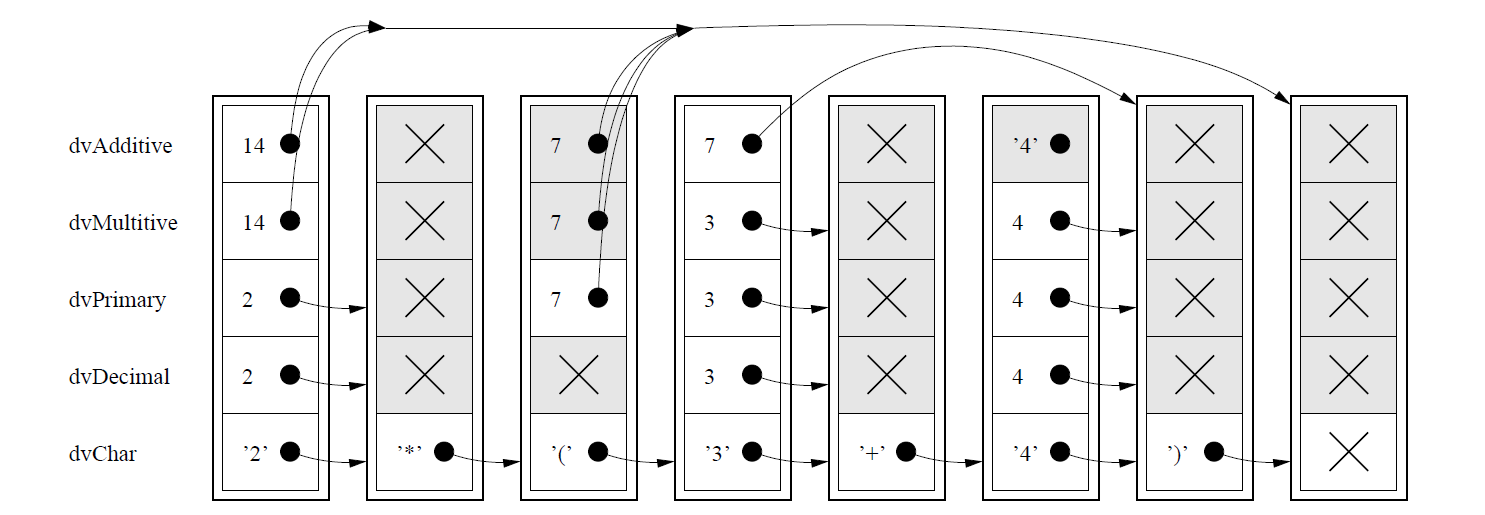
Figure 3 は入力テキストの例 '2*(3+4)' に対してパーサが生成したデータ構造で、最新の関数型評価器 (a modern functional evaluator) ですべてのセルを完全に縮小した後のメモリを示している。各縦列は 5 つの結果要素を持つ Derivs インスタンスを表している。'Parsed \(v\) \(d\)' 形式の結果では意味値 \(v\) が適切なセルに表示され、行列内の別の Derivs インスタンスにつながる "余り" (remainder) ポインタを示す矢印も表示される。評価時に共有関係を適切に保持する最新の遅延評価言語実装では、図中の矢印は文字通りヒープ内のポインタに対応し、構造体内の任意のセルが 2 回評価されることはない。網掛けは、左端の列の dvAdditive の結果がアプリケーションで最終的に必要とされている唯一の値である可能性が高い場合に、全く評価されないセルを表している。

この図は、このアルゴリズムが長さ \(n\) の入力文字列に対して遅延評価器の下で \(O(n)\) 時間で実行できる理由を明らかにするものである。最上位の解析関数は Derivs 型のインスタンスを生成する唯一の関数であり、常に正確に \(n+1\) 個のインスタンスを生成する。解析関数は互いに呼び出し合うのではなく、この構造体のエントリにのみアクセスし、各関数は与えられた結果を計算する間に他のセルを西田でも固定数だけ調べる。各セルが最大 1 回評価されることを遅延評価機が保証するため、これらの結果が評価される順序が先に示した表形式、right-to-left、bottom-to-top アルゴリズムとは全く異なる可能性があるにも関わらず、重要なメモ化特性が提供されて線形解析時間が保証される。

3 アルゴリズムの拡張

前セクションでは Packrat パーサを構築するために必要な基本原理とツールを提供した。しかし実際のアプリケーションのためにパーサを作成するためには追加的な詳細を必要とし、そのうちのいくつかは Packrat 構文解析パラダイムに影響される。このセクションでは、前述で開発した Packrat パサーの例を徐々に構築しながら、より重要で実用的ないくつかの問題を探る。まず、左再帰という厄介だが簡単な問題を検討する。次に軸解析の問題を取り上げ、このタスクを Packrat パーサにシームレスに統合する。最後に、モナドコンビネータを使用してより簡潔に Packrat パーサを表現することを検討する。

3.1 左再帰

Packrat 構文解析がほかのトップダウン方式と共有している制限の一つは左再帰 (left recursion) を直接サポートしない点である。例えば上の例に減算演算子を追加して、加算と減算が適切に左結合 (left-associative) となるようにしたいとする。自然なアプローチは加算式の文法規則を次のように変更し、それに応じてパーサを変更することである。\[ \begin{eqnarray*} {\rm Additive} & \leftarrow & {\rm Additive} \ {\tt '+'} \ {\rm Multitive} \\ & | & {\rm Additive} \ {\tt '-'} \ {\rm Multitive} \\ & | & {\rm Multitive} \end{eqnarray*} \] この文法に対する佐伯港かパーサでは pAdditive 関数は与えられたものと同じ入力で再帰的に自分自身を呼び出すだろう。従って無限の再帰サイクルに入ることになる。この文法に対する Packrat パーサでは pAdditive は自分自身の Derivs タプルの dvAdditive 要素 (算出するはずの要素と同じもの) にアクセスしようとするため循環データ依存関係が発生する。どちらの場合でもパーサは失敗する。最新の遅延評価器はしばしば実行時に循環データ依存性を検出するが、無限再帰を検出できないため Packrat パーサの失敗モードは少し "友好的" (friendlier) であるように見えるかもしれない。

幸いなことに、左再帰文法は常に同等の右再帰文法に書き換えることができ [2]、目的の左結合の意味動作はパーサの中間結果として工事関数を使って簡単に再構築できる。例えば例のパーサで Additive と AddtiveSuffix という 2 つの非終端記号に分割すればよい。pAdditive 関数は AddtiveSuffix が続く 1 つの Multitive 式を認識する。

pAdditive :: Derivs -> Result Int
pAdditive d = case dvMultitive d of
                Parsed vl d’ ->
                  case dvAdditiveSuffix d’ of
                    Parsed suf d’’ ->
                      Parsed (suf vl) d’’
                    _ -> NoParse
                  _ -> NoParse

pAddtiveSuffix 関数は中置演算子 (infix operator) と右辺オペランドを集約し、左辺オペランドを受け取って結果を生成する 'Int → Int' 型の意味値を構築する:

pAdditiveSuffix :: Derivs -> Result (Int -> Int)
pAdditiveSuffix d = alt1 where

  -- AdditiveSuffix <- ’+’ Multitive AdditiveSuffix
  alt1 = case dvChar d of
           Parsed ’+’ d’ ->
             case dvMultitive d’ of
               Parsed vr d’’ ->
                 case dvAdditiveSuffix d’’ of
                   Parsed suf d’’’ ->
                     Parsed (\vl -> suf (vl + vr))
                            d’’’
                     _ -> alt2
                   _ -> alt2
                 _ -> alt2

  -- AdditiveSuffix <- <empty>
  alt3 = Parsed (\v -> v) d

3.2 統合字句解析

従来の構文解析アルゴリズムは "生の" 入力テキストがすでに別の字句解析器 (lexical analyzer) によって部分的に消費されトークンのストリームになっていることを前提としている。そしてパーサは、それぞれが複数の連続した入力文字を表していたとしても、それらのトークンを原子単位として扱う。従来の線形時間パーサは先読みの判断に原始的な終端記号しか使用できず、上位の非終端記号を参照できないため、通常この分離が必要である。この制限はセクション 2.2 で予測型トップダウンパーサについて説明したが、ボトムアップ LR パーサでも同じ問題を共有する同様のトークンベースの先読みメカニズムに依存する。もしパーサが先読みの判断にアトミックなトークンのみを使用できるなら、そのトークンが生の文字列ではなくキーワード、識別子、リテラルの全体を表すのであれば、解析がはるかに容易になる。

Packrat パーサは真のバックトラックモデルを反映しているため、ある解析関数における選択肢間の決定は、ほかの解析関数によって生成された完全な結果に依存することができる。このため字句解析は特別な処理をすることなく Packrat パーサにシームレスに統合することができる。

Packrat パーサの例を "本当の" 字句解析器で拡張するために、いくつかの新しい非終端記号を Derivs 型に追加する:

data Derivs = Derivs {
                -- Expressions
                dvAdditive :: Result Int,
                ...

                -- Lexical tokens
                dvDigits :: Result (Int, Int),
                dvDigit :: Result Int,
                dvSymbol :: Result Char,
                dvWhitespace :: Result (),

                -- Raw input
                dvChar :: Result Char}

pWhitespace 解析関数は字句トークンを区切る空白をすべて消費する:

pWhitespace :: Derivs -> Result ()
pWhitespace d = case dvChar d of
                  Parsed c d’ ->
                    if isSpace c
                    then pWhitespace d’
                    else Parsed () d
                  _ -> Parsed () d

より完全な言語では、この関数はコメントも消費するというタスクも持っているかもしれない。字句解析のために Packrat 構文解析の全能力が利用できるため、コメントはそれ自身の複雑な階層構造、例えばリテラルプログラミングのためのネストやマークアップを持つことができる。構文認識は一方向のパイプラインに分割されないため、字句構造より上位の構文要素を "上方から" (upwards) 参照することさえ可能である。例えばある言語の構文ではコメント内に埋め込まれた識別子やコード断片をマークしてパーサが実際の士気や分として見つけて分析できるようにすることができ、知的ソフトウェア工学ツールをより効率的に使用できるようになる。同様に、文字列リテラル内のエスケープシーケンスには静的または動的な置換を表す一般的な式を含めることができる。

pWhitespace の例は、純粋な文脈自由文法では表現することが難しい、ありふれた最長一致 (longest-match) 曖昧性解消規則がいかに簡単に Packrat パーサに実装できるかを示している。実際に入力テキストを消費することなく構文先読み情報に基づいて構文解析の決定に影響を与える一般構文述語 (general syntactic predicates) [14] を含む、より洗練された決定及び曖昧性解消戦略もまた簡単に実装することができる。例えば便利な followed-by と notfollowd-by 規則は、解析している選択肢がその選択肢にマッチするテキストに続く (または続かない) 場合にのみ使用されることを可能にするものである。この種の構文述語は一般に無制限の先読みを必要とするため、他のほとんどの線形時間構文解析アルゴリズムの能力の範囲外である。

字句解析の例を続けると、関数 pSymbol は演算子文字と任意の空白からなる "演算子トークン" を識別する:

-- Parse an operator followed by optional whitespace
pSymbol :: Derivs -> Result Char
pSymbol d = case dvChar d of
              Parsed c d’ ->
                if c ‘elem‘ "+-*/%()"
                then case dvWhitespace d’ of
                       Parsed _ d’’ -> Parsed c d’’
                       _ -> NoParse
                else NoParse
              _ -> NoParse

ここで、演算子や括弧のスキャンの dvChar の代わりに dvSymbol を使うように式の上位の解析関数を変更する。例えば pPrimary は次のように実装することができる:

-- Parse a primary expression
pPrimary :: Derivs -> Result Int
pPrimary d = alt1 where

    -- Primary <- ’(’ Additive ’)’
    alt1 = case dvSymbol d of
             Parsed ’(’ d’ ->
               case dvAdditive d’ of
                 Parsed v d’’ ->
                   case dvSymbol d’’ of
                     Parsed ’)’ d’’’ -> Parsed v d’’’
                   _ -> alt2
                 _ -> alt2
               _ -> alt2

    -- Primary <- Decimal
    alt2 = dvDecimal d

この関数は、構文解析の決定が Symbol などの非終端記号の任意の位置での一致の有無だけではなくその非終端記号に関連する意味値にも依存しうることを示すものである。この場合、すべての記号トークンがまとめて解析され、pSymbol によって一様に扱われるとしても、pPrimary などの他のルールによって特定のシンボルを区別することができる。複数文字の演算子、識別し、予約後を持つより高度な言語では、トークンパーサによって生成される意味値は Char ではなく String 型になるかもしれないが、これらの値は同じ方法でマッチさせることができる。このような意味値に対する構文の依存性は意味述語 (semantic predicates) [14] として知られ、実際には非常に強力で有用な能力を提供する。構文述語と同様に意味述語は一般に無限の先読みを必要とし、従来の構文解析アルゴリズムでは線形時間保証を諦めなければ実装することができない。

3.3 モナド的 Packrat 構文解析

Haskell のような関数型言語でパーサを構築する一般的な方法はモナドコンビネータ [11, 13] を使用することである。しかし残念なことに、通常モナド的なアプローチは性能上のペナルティを伴う。これまでに説明したように Packrat パーサの実装は非終端記号のセットとそれに対応する結果型が静的に分かっていて、それらが単一の固定タプルで結合され Derivs 型を形成できることを前提としている。コンビネータを介して他の Packrat パーサから動的に全体の Packrat パーサを構築するには Derivs を動的なルックアップ構造に変更し、対応する結果と非終端記号の可変セットを関連付けることが必要となる。この方法は遙かに遅く空間効率も悪くなる。

コンビネータの利便性の多くをあまり影響のない性能ペナルティで提供するためのより実用的な戦略は、Packrat パーサを構成する個々の解析関数を Derivs 型と "トップレベル" 再帰を前述のように静的に実装したままでモナドで定義することである。、

必要な解析関数を直接構築するためには、単純な方エイリアスでコンビネータを動作させるのが明らかな方法であろう:

type Parser v = Derivs -> Result v

残念ながら Haskell の便利な do 構文を利用するためにコンビネータは特殊なクラス Monad 型を使用しなければならず、単純なエイリアスには型クラスが割り当てられない。その代わりに解析関数を "本当の" ユーザ定義型でラップしなければならない:

newtype Parser v = Parser (Derivs -> Result v)

これで Haskell の標準的なシーケンス (>>=)、結果生成 (return)、エラー生成の各コンビネータを実装することができる:

instance Monad Parser where

        (Parser p1) >>= f2 = Parser pre
                where pre d = post (p1 d)
                      post (Parsed v d’) = p2 d’
                        where Parser p2 = f2 v
                      post (NoParse) = NoParse
        return x = Parser (\d -> Parsed x d)

        fail msg = Parser (\d -> NoParse)

最後に、構文解析のために alternation コンビネータが必要である:

(<|>) :: Parser v -> Parser v -> Parser v
(Parser p1) <|> (Parser p2) = Parser pre
                 where pre d = post d (p1 d)
                       post d NoParse = p2 d
                       post d r = r

特定の文字を認識するための些細な組み合わせに加えて、これらの組み合わせで元の Packrat パーサの例の pAdditive 関数は次のように書くことができる。

Parser pAdditive =
            (do vleft <- Parser dvMultitive
                char ’+’
                vright <- Parser dvAdditive
                return (vleft + vright))
        <|> (do Parser dvMultitive)

繰り返しや中置式など、より高度なイディオムのために追加のコンビネータを構築することは魅力的である。しかし Packrat 構文解析において反復型コンビネータを使用することは、結果行列のセルはそれに依存するほかのセルの結果が利用可能になった時点で一定時間内に算出できるという仮定に違反することになる。反復的コンビネータは中間結果が結果行列にメモされない "隠れた" 再帰を効果的に作り出してパーサを超線形時間で実行させる可能性がある。セクション 6 の結果が示すようにこの問題は実際には必ずしも深刻ではないが反復的コンビネータを使用する際には考慮する必要がある。

本論文のオンラインサンプルには大規模な Packrat パーサを構築するために使用できるフル機能のモナド型コンビネータライブラリも含まれている。このライブラリは実質的に Parsec [13] に触発されているが、字句解析を別のフェーズとして実装したり、従来のトップダウンパーサで使われていたワントークン先読み予想機構 (one-token-lookahead prediction mechanism) を実装する必要がないため、Packrat 構文解析コンビネータはずっと単純なものとなっている。完全なコンビネータライブラリは様々な "安全な" 定数時間コンビネータを提供し、またいくつかの "危険な" 反復型コンビネータも提供する。これらは便利ではあるがパーサを構築するために必須というわけではない。コンビネータライブラリは Derivs 型が異なる複数のパーサで同時に使用することができ、使いやすいエラー検出とレポート機能をサポートしている。

4 LL と LR 構文解析の比較

これまでのセクションは Packrat パーサをどのように構築するかのチュートリアルを提供したが、残りのセクションでは Packrat 構文解析が実際にいつ有用なのかという問題に目を向ける。このセクションでは Packrat 構文解析の言語認識能力をより深く掘り下げ LL(\(k\)) や LR(\(k\)) のような従来の線形時間アルゴリズムとの関係を明らかにすることを非公式に行う。

LR 構文解析は一般に限定先読みトップダウン構文や LL 構文よりも "より強力" であると考えられているが、これらの構文解析が認識できる言語のクラスは同じである [3]。Pepper が指摘 [17] するように、LR 解析は単純に左再帰を排除しすべての重要な解析決定をできるだけ遅らせるように文法を書き換えた LL 解析と見なすことができる。その結果、LR は文法の表現方法の柔軟性を高めるが実際の認識能力の向上はない。このため、ここでは LL パーサと LR パーサは本質的に等価であるとして扱う。

4.1 先読み

Packrat 構文解析と LL/LR 構文解析の実用上の最も重要な違いは先読みメカニズムである。Packrat パーサの決定は、どの時点でも入力文字列の最後までのすべてのテキストに基づくことができる。解析行列の個々の結果の算出では、一定数の "基本操作" しか実行できないが、これらの基本操作には解析行列の前方ポインタをたどることも含まれ、それぞれが一度に大量のテキストを読み飛ばすことができる。したがって LL および LR パーサが入力の一定数の終端記号しか先読みできないのに対して Packrat パーサは終端記号と非終端記号を任意の組み合わせで一定数先読みすることが可能である。このように任意の非終端記号を考慮して構文解析を決定できることが Packrat 構文解析に無制限の先読み機能を与えている。

言語認識力の違いを示すと、次の文法はどのような \(k\) に対しても LR(\(k\)) とはならないが、Packrat パーサにとっては問題のない文法である: \[ \begin{eqnarray*} S & \leftarrow & A \ | \ B \\ A & \leftarrow & x \ A \ y \ | \ x \ z \ y \\ B & \leftarrow & x \ B \ y \ y | x \ z \ y \ y \end{eqnarray*} \]

LR パーサは上記の言語の文字列で 'z' とそれに続く最初の 'y' に遭遇すると、非終端記号 \(A\) または \(B\) のどちらを介して推論を開始するか直ちに決定しなければならないが、左側にある 'x' と同数の 'y' が遭遇するまでこの決定を行う方法がない。一方、Packrat パーサは基本的に投機的に動作し、入力をスキャンしながら並行して非終端記号 \(A\) と \(B\) に対する導出を生成する。\(A\) と \(B\) の最終的な判断は事実上入力文字列全体が解析されるまで遅延する。上記の文法を左から右にミラーリングしても状況は変わらない。この違いは、LR が入力を右から左にスキャンするのに対して、Packrat 構文解析は逆に動作するという事実上の副作用に過ぎないことが明らかである。

4.2 文法構成

実用的な言語のパーサを設計する際に、固定先読みによる LR 文法解析の限界を感じることが多いが、その多くは LL 文法と LR 文法がきれいに合成できないことに起因している。例えば次の文法は式と代入を持つ単純な言語を表しており、代入の左辺には単純な識別子しか許さない: \[ \begin{eqnarray*} {\rm S} & \leftarrow & {\rm R \ | \ ID \ '=' \ R} \\ {\rm R} & \leftarrow & {\rm A \ | \ A \ EQ \ A \ | A \ NE \ A} \\ {\rm A} & \leftarrow & {\rm P \ | \ P \ '+' \ P \ | \ P \ '-' \ P} \\ {\rm P} & \leftarrow & {\rm ID \ | \ '(' \ R \ ')'} \end{eqnarray*} \] ID, EQ, NE が終端記号、つまり別の字句解析フェーズで生成されたアトミックトークンであれば LR(1) パーサはこの文法を問題なく扱える。しかし、トークンかを以下のような簡単なルールでパーサ自体に組み込もうとすると、この文法はもはや LR(1) ではなくなってしまう: \[ \begin{eqnarray*} {\rm ID} & \leftarrow & {\rm 'a' \ | \ 'a' \ ID} \\ {\rm EQ} & \leftarrow & {\rm '=' \ '='} \\ {\rm NE} & \leftarrow & {\rm '!' \ '='} \end{eqnarray*} \]

問題は、LR パーサは識別子をスキャンした後にそのあとのトークンだけに基づいてそれが一次式であるか代入の左辺であるかを直ちに決定しなければならないことである。しかしトークンが '=' の場合、パーサはそれが代入演算子なのか、それとも '==' の前半部分なのかを知るすべがない。この場合、文法は LR(2) パーサによって解析できるだろう。実際には LR(\(k\)) パーサや LALR(\(k\)) パーサでさえも \(k\gt1\) は一般的ではない。近年開発された left-to-right 構文解析アルゴリズムの拡張 [18, 16, 15] により状況はいくらか改善はしたものの、線形時間の保証を維持しながら無限の先読み機能を提供することはまだできない。

字句解析と構文解析を分離したとしても、LR パーサの限界は他の現実的な状況でしばしば表面化し、進化する文法に対する一見無害な変更の結果として表れることがある。たとえば上記の言語に簡単な配列インデックスを追加し、配列インデックス演算子を代入の左辺または右辺に表示できるようにしたいとする。一つの方法として、左辺または "lvalue" 式を表す新しい非終端記号 L を追加し、以下のように両方の方の式に配列インデックス演算子を組み込むことができる: \[ \begin{eqnarray*} {\rm S} & \leftarrow & {\rm R \ | \ L \ '=' \ R} \\ {\rm P} & \leftarrow & {\rm A \ | \ A \ EQ \ A \ | \ A \ NE \ A} \\ {\rm A} & \leftarrow & {\rm P \ | \ P \ '+' \ P \ | \ P \ '-' \ P} \\ {\rm P} & \leftarrow & {\rm ID \ | \ '(' \ R \ ')' \ | \ P \ '[' \ A \ ']'} \\ {\rm L} & \leftarrow & {\rm ID \ | \ '(' \ L \ ')' \ | \ L \ '[' \ A \ ']'} \end{eqnarray*} \] ID, EQ, NE 記号が再び終端として扱われるとしても、この文法はどのような \(k\) に対しても LR(\(k\)) ではない。パーサは識別子を確認した後にそれが P または L 式の一部であるかを直ちに決定しなければならないが、皇族の配列インデックス演算子が完全に解析されるまでそれを知るすべがないためである。繰り返しになるが、Packrat パーサではこの文法は何の問題もない。なぜなら P と L の選択肢を "並行して" 効率的に評価し、重要な判断を下すまでに完全な導出 (または導出がないという知見) を得ることができるためである。

Packrat パーサは選択肢の間で決定を下すために使う先読みは、最初の例では EQ、二番目は P と L のような任意の非終端記号を考慮に入れられることから、一般に Packrat パーサの文法は合成可能である。Packrat パーサは LL や LR パーサのように "原始的な" (primitive) 構文構造 (終端記号) に特別な意味を与えないため、文法中に現れる終端記号や終端記号の固定シーケンスはパーサを "壊す" ことなく非終端記号に置き換えることができる。この置換機能により Packrat 構文解析はより柔軟な構文解析が可能となる。

4.3 認識の限界

Packrat パーサは LL(\(k\)) や LR(\(k\)) アルゴリズムのよりも広い範囲の言語を線形時間で認識できるとすると、どのような文法が認識できないだろうか? このアルゴリズムの正確な理論的能力はまだ十分に明らかになっていないが、以下の些細であいまいさのない文脈自由文法は LL や LR パーサと同様に Packrat パーサにとっても厄介な例である: \[ {\rm S} \leftarrow {\rm x \ S \ x \ | \ x} \] この文法がどちらの種類のパーサにとっても問題なのは、'x' の文字をスキャンするときに、LR の場合は左から右に、Packrat の場合は右から左に、アルゴリズムが文字列の真ん中がどこにあるかをあらかじめ "知って" いて、その位置で第 2　の選択肢を適用し、それから入力ストリームに第 1 の選択肢を使って "外側に構築" (build outwords) しなければならない点である。しかしストリームは完全に均質であるため、入力全体が解析されるまでパーサは中間を見つける方法がない。従ってこの文法は、不自然ではあるが、より一般的な非線形時間 CFG 構文解析アルゴリズムを必要とする例を提供する。

5 実用上の問題点と限界

Packrat 構文解析は多くのアプリケーションにとって十分に強力で効率的なものであるが、いくつかの状況でそれを不適切にする 3 つの主要な問題がある。第 1 に、Packrat 構文解析は決定論的なパーサ、つまり最大でも 1 つの結果を生成できるパーサを構築することにのみ有効である。第 2 に、Packrat パーサはその効率性のためにほとんど、あるいは完全にステートレスであることに依存している。最後に、Packrat 構文解析はメモ化に依存しているため本質的に空間集約的 (space intensive) である。このセクションではこれらの 3 つの問題を議論する。

5.1 決定論的構文解析

これまでの重要な仮定は Packrat パーサを構築する相互に再帰的な解析関数のそれぞれが決定論的に少なくとも一つの結果を返すということであった。パーサを構築する文法にあいまいさがある場合、構文解析関数はそれを局所的に解決できなければならない。この論文で開発したパーサの例では、複数の選択肢をテストする順番によって常に暗黙のうちにあいまいさを解消している。この動作は実装が簡単で、最長一致やそのほかの明示的な局所曖昧性解消の実行に便利である。解析関数は可能な限りの選択肢を試し、複数の候補がマッチした場合は失敗という結果を返すこともできる。Packrat パーサの解析関数ができないことは、複数の結果を返して並列に使用したり、後で何らかの大域的な戦略によって曖昧さを解消して利することである。

機械による利用を想定した言語では、そもそも曖昧性は通常望ましいことではないし、局所的な曖昧性解消規則は人間が理解しやすいことから大域的なものよりも好まれるため、複数のマッチング候補で局所的にあいまいさを解消するという要件は実際にはそれほど問題にはならない。しかし自然言語やそのほかの文法で大局的な曖昧さが想定される場合は Packrat 構文解析はあまり役に立たない。解析関数が結果のリストを返す古典的な非決定論的トップダウンパーサ [23, 8] も同様にメモ化できるが、得られるパーサは線形時間ではなく、曖昧文脈自由文法 (ambiguous context-free grammars) [3, 20] の既存の表形式アルゴリズムと同等になる可能性が高いと思われる。非決定論的構文解析は計算量においてブーリアン行列の乗算 [12] と同等であるため、このより一般的な問題に対する線形時間解は見つかりそうにない。

5.2 ステートレス構文解析

Packrat 構文解析の第2の制限は、基本的にステートレス解析に向いているということである。Packrat 解析のメモ化システムは、各終端記号の解析関数が入力文字列のみに依存し、解析処理中に蓄積された他の情報には依存しないことを想定している。

純粋な文脈自由文法は定義上ステートレスだが、多くの実用的な言語は構文解析中に状態の概念を必要とするため、本当の意味での文脈自由ではない。例えば C や C++ では型が宣言されるとパーサが型名のテーブルを段階的に構築する必要がある。これは、パーサが型名を他の識別子と区別して、後続のテキストを正しく解析できるようにする必要があるためである。

従来のトップダウン (LL) およびボトムアップ (LR) パーサは解析中に状態を維持することにほとんど問題がない。これらのパーサは入力を左から右へ 1 回だけスキャンし、1 つ以上のトークン、またはせいぜい数個のトークンを先に見ることはないため、状態の変更が発生しても何も "失われ" ない。これに対して Packrat パーサは無制限の先読み機能を効率化するためにステートレスに依存している。ステートフルな Packrat パーサを構築することはできるが、パーサの状態が変わるたびに新しい結果行列を構築し始めなければならない。このためステートフル Packrat 構文解析は状態変化が頻繁に起こる場合は実用的ではないかもしれない。状態を伴う Packrat 構文解析の詳細については私の修士論文 [9] を参照。

5.3 空間消費

Packrat パーサの最も顕著な特徴は、入力テキストを含め、入力テキストについて今まで算出したすべてのものをも文字通りため込んでしまうという事実である。このため Packrat 解析は常に入力サイズの実質的な定数倍に相当する記憶容量を必要とする。これに対して LL(\(k\)), LR(\(k\)) および単純なバックトラックパーサは、入力に現れる構文構造の最大ネスト深によってのみ容量が増大するように設計することができ、実際にはテキストの合計サイズよりも数桁小さくなることがよくある。あらゆる非正規言語の LL(\(k\)) および LR(\(k\)) パーサは最悪ケースで線形空間要件となるが、この "平均ケース" での違いが実際には重要であるかもしれない。

導出構造、特に非終端記号が多い文法のパーサで必要な空間を減らす方法の一つは Derivs 型を福栖のレベルに分割することである。例えば、ある言語の非終端記号が軸トークン、式、分、宣言など、いくつかの大きなカテゴリに分類されるとする。この場合、Derivs タプル自体には dvChar の他にこれらの非終端記号のカテゴリごとに 1 つずつ、合計 4 つの要素しかないかもしれない。これらのコンポーネントはそれぞれ、そのカテゴリのすべての非終端記号の結果を含むタプルとなる。"トークン間" の文字位置を表す大部分の Derivs インスタンスでは、非終端記号のカテゴリを表す構成要素はどれも評価されないため、小さなトップレベルオプジェクトとその構成要素の未評価クロージャだけが空間を占めることになる。トークンの先頭に対する Derivs インスタンスであっても、その位置にどのような言語構成要素があるかによって、1 つか 2 つのカテゴリから結果だけが必要になることがよくある。

このような最適化を行っても Packrat パーサは元の入力テキストの何倍もの作業用ストレージを消費することがある。このような理由から Packrat パーサがおそらく最良の選択ではないアプリケーション領域がある。例えば XML ストリームを解析する場合、それはかなり単純な構造だが、しばしば比較的フラットではない機械的に生成されたデータを大量にエンコードしている。

一方、言語のパワーと表現力が最優先される複雑な現代のプログラミング言語で人間が通常書くようなソースコードを解析する場合、Packrat 解析の空間コストはおそらく妥当なものになるだろう。標準的なプログラミング手法では大規模なプログラムを独立してコンパイルできるサイズのモジュールに分割する。また、最近のマシンのメインメモリのサイズでは、典型的な 10～100kB のソースファイルの解析を拡張するために少なくとも 3 桁の "ヘッドルーム" が確保されている。より大きなソースファイルを解析する場合でも、現実的な言語の強力な構造的局所性により作業セットは比較的小さくなる可能性がある。最後に、解析が完了した後に導出構造全体を捨てることができるため、Packrat パーサが使用したのと同程度のスペースを必要とするような、大域的オプティマイザといった他の複雑な計算に解析結果が投入された場合、パーサの空間消費は無関係になる可能性が高い。セクション 6 ではこの空間消費量が実際には妥当であるという証拠を提示する。

6 パフォーマンス結果

(省略)

6.1 空間効率

(省略)

6.2 解析性能

(省略)

7 関連研究

このセクションでは Packrat 構文解析と関連する先行研究について簡単に説明する。他のアルゴリズムと比較した Packrat 構文解析のより詳細な分析については私の修士論文 [9] を参照。

Barman と Ullman [4] はバックトラックを用いた決定論的構文解析アルゴリズムの形式的特性を初めて開発した。この研究は Aho と Ullman [3] によって改良され "トップダウン限定バックトラック構文解析" (top-down limited backtrack parsing) と分類された。これは、それぞれの構文解析関数が最大 1 つの結果を生成でき、したがってバックトラックは局所的であるという制限に言及している。彼らはこの種のパーサ、正式には Generalized Top-Down Parsing Language (GTDPL) として知られるパーサが非常に強力であることを示した。GTDPL パーサは任意のプッシュダウンオートマトンをシミュレートできるため、任意の LL または LR 言語を認識でき、文脈自由でない言語も認識可能である。それにもかかわらず、左再帰によって引き起こされるようなすべての "失敗" は GTDPL 文法から検出して除去することができアルゴリズムが良好に動作することが保証される。Barman と Ullman は結果の集計を通じて線形時間 GTDPL パーサを構築する可能性も指摘したがこの線形時間アルゴリズムは実用化されなかったようだ。当時はメインメモリがはるかに限られており、コンパイラはほぼ一定の空間で実行できるストリーミング ”フィルタ" として動作しなければならなかったためであることは間違いないだろう。

Adams [1] は最近 LR アルゴリズムと比較して GTDPL 構文解析が優れた複合性を持つことを認識し、モジュール式言語プロトタイピングのフレームワークのコンポーネントとして復活させた。さらにポピュラーな ANTLR [15] や Haskell の PARSEC コンビネータライブラリ [13] など多くの実用的なトップダウン構文解析ライブラリやツールキットも、予測構文解析の制限を克服するためにパーサ設計者が選択的に呼び出せるような同様の制限付きバックトラック機能を提供している。しかしこれらのパーサはすべてメモ化を行わずに従来の再帰降下方式でバックトラックを実装しているため、解析時間は最悪ケースで指数関数的に増加する危険がある。このためバックトラックを予測の代わりとして使用したり字句解析と構文解析を統合することは非現実的になっている。

統合字句解析、つまり "スキャンレス構文解析" を効果的にサポートする唯一の既知の線形時間構文解析アルゴリズムは、Tai [19] が最初に作成し Salomon と Cormack [18] がこの目的のために実用化した NSLR(1) アルゴリズムである。このアルゴリズムは非終端記号に基づく先読みの決定に対する限定的なサポートを追加することで、従来の LR クラスのアルゴリズムを拡張している。NSLR(1) に対する Packrat 構文解析の相対的な力は不明である。Packrat 構文解析は右方向の先読みをあまり制限しないが、NSLR(1) は左後方の文脈を考慮することも可能である。実際には NSLR(1) はおそらく空間効率に優れているが Packrat はよりシンプルでクリーンである。他の最新のスキャナレスパーサ [22, 21] は線形時間決定論的アルゴリズムを放棄し、曖昧さを許容しより一般的だが遅い CFG 構文解析を採用している。

8 今後の課題

ここで紹介した結果は Packrat 構文解析の力と実用性を示しているが、より多様な言語での柔軟性、パフォーマンス、空間消費を評価するためにさらなる実験を必要としている。例えば C や C++ のようにパーサの状態に大きく依存する言語や、ML や Haskell のようにレイアウトに敏感な言語は Packrat パーサが効率的に処理することがより困難であることが分かる。

一方、実用的な言語の構文は一般的に特定の構文解析技術を念頭に置いて設計されている。このため Packrat 構文解析の "自由な" 無制限先読みと無制限の文法構成能力によってどのような新しい構文設計の可能性が生まれるかということも、同様に説得力のある質問である。セクション 3.2 では、統合された字句解析に依存するいくつかの簡単な拡張を提案したが、文法構成の柔軟性が重要な拡張可能な構文 [7] を持つ言語では、Packrat 構文はさらに有用であると思われる。

Packrat 構文解析は遅延関数型言語では手作業で実装できるほど簡単だが、C 言語の世界では YACC、Haskell の世界では Happy [10] と Mímico [6] のような文法コンパイラが実用的な利益をもたらすと思われる。構文解析関数そのものに加えて、文法コンパイラは静的な "導出” タプル型と最上位の再帰的 "連結" 関数を自動的に生成し、セクション 3.3 で論議したモナド表現の問題を解決することができるだろう。またコンパイラは、よく使われる '+' や '*' といった反復演算子を、千傾向分解析時間の保証を維持したまま、原始的な定数時間演算のみを使用する低レベル文法に落とし込むことができる。最後に、コンパイラは左再帰規則を書き換えて文法中の左結合構文をより簡単に表現できるようにすることができる。

Packrat 構文解析の適用が難しくさらなる研究が必要な分野の一つは対話型ストリームの構文解析である。例えば言語インタープリタの "read-eval-print" ループはしばしばパーサが各行の終わりで次の文を終了するためにさらなる入力が必要かどうかを検出する必要がある。この要求は入力ストリームが前もって利用可能であるという Packrat アルゴリズムの前提に違反する。同様の未解決問題はどのような条件下で Packrat 構文解析が無限ストリームの構文解析に適するかということである。

9 考察

Packrat 解析は非厳格な関数型言語で実装されたバックトラック型再帰降下パーサを、無制限の先読み能力を放棄することなく線形時間パーサに変換するシンプルでエレガントな方法である。このアルゴリズムは複雑な依存関係を持つ再帰的データ構造を直接表現する非厳格な関数型言語の能力にその単純さを依存し、その実用的な効率は遅延評価に依存している。Packrat パーサは従来の決定論的線形時間アルゴリズムが認識できる言語はもちろん、認識できない多くの言語を認識することができ、より優れた構成特性を提供し、字句解析を構文解析に統合することができる。このアルゴリズムの主な制約は、決定論的構文解析しかサポートしないことと、(漸近的に線形ではあるが) かなりのストレージを必要とすることである。

Acknowledgements

I wish to thank my advisor Frans Kaashoek, my colleagues Chuck Blake and Russ Cox, and the anonymous reviewers for many helpful comments and suggestions.

References

1. Stephen Robert Adams. Modular Grammars for Programming Language Prototyping. PhD thesis, University of Southampton, 1991.
2. Alfred V. Aho, Ravi Sethi, and Jeffrey D. Ullman. Compilers: Principles, Techniques, and Tools. Addison-Wesley, 1986.
3. Alfred V. Aho and Jeffrey D. Ullman. The Theory of Parsing, Translation and Compiling - Vol. I: Parsing. Prentice Hall, Englewood Cliffs, N.J., 1972.
4. Alexander Birman and Jeffrey D. Ullman. Parsing algorithms with backtrack. Information and Control, 23(1):1–34, Aug 1973.
5. Dmitri Bronnikov. Free Yacc-able Java(tm) grammar, 1998. http://home.inreach.com/bronikov/grammars/java.html.
6. Carlos Camarão and Lucília Figueiredo. A monadic combinator compiler compiler. In 5th Brazilian Symposium on Programming Languages, Curitiba – PR – Brazil, May 2001. Universidade Federal do Paraná.
7. Luca Cardelli, Florian Matthes, and Mart´ın Abadi. Extensible syntax with lexical scoping. Technical Report 121, Digital Systems Research Center, 1994.
8. Jeroen Fokker. Functional parsers. In Advanced Functional Programming, pages 1–23, 1995.
9. Bryan Ford. Packrat parsing: a practical linear-time algorithm with backtracking. Master’s thesis, Massachusetts Institute of Technology, Sep 2002.
10. Andy Gill and Simon Marlow. Happy: The parser generator for Haskell. http://www.haskell.org/happy.
11. Graham Hutton and Erik Meijer. Monadic parsing in Haskell. Journal of Functional Programming, 8(4):437–444, Jul 1998.
12. Lillian Lee. Fast context-free grammar parsing requires fast boolean matrix multiplication. Journal of the ACM, 2002. To appear.
13. Daan Leijen. Parsec, a fast combinator parser. http://www.cs.uu.nl/˜daan.
14. Terence J. Parr and Russell W. Quong. Adding semantic and syntactic predicates to LL(k): pred-LL(k). In Computational Complexity, pages 263–277, 1994.
15. Terence J. Parr and RussellW. Quong. ANTLR: A predicated-\(LL(k)\) parser generator. Software Practice and Experience, 25(7):789–810, 1995.
16. Terence John Parr. Obtaining practical variants of \(LL(k)\) and \(LR(k)\) for \(k > 1\) by splitting the atomic \(k\)-tuple. PhD thesis, Purdue University, Apr 1993.
17. Peter Pepper. LR parsing = grammar transformation + LL parsing: Making LR parsing more understandable and more efficient. Technical Report 99-5, TU Berlin, Apr 1999.
18. Daniel J. Salomon and Gordon V. Cormack. Scannerless NSLR(1) parsing of programming languages. In Proceedings of the ACM SIGPLAN’89 Conference on Programming Language Design and Implementation (PLDI), pages 170–178, Jul 1989.
19. Kuo-Chung Tai. Noncanonical SLR(1) grammars. ACM Transactions on Programming Languages and Systems, 1(2):295–320, Oct 1979.
20. Masaru Tomita. Efficient parsing for natural language. Kluwer Academic Publishers, 1985.
21. M.G.J. van den Brand, J. Scheerder, J.J. Vinju, and E. Visser. Disambiguation filters for scannerless generalized LR parsers. In Compiler Construction, 2002.
22. Eelco Visser. Scannerless generalized-LR parsing. Technical Report P9707, Programming Research Group, University of Amsterdam, 1997.
23. Philip Wadler. How to replace failure by a list of successes: A method for exception handling, backtracking, and pattern matching in lazy functional languages. In Functional Programming Languages and Computer Architecture, pages 113–128, 1985.

翻訳抄

複数の選択肢をもつ構文解析時に、解析済みのパターンの結果を記録しておき別の選択肢を評価するときに使用する Packrat 構文解析に関する 2002 年の論文。

1. Patrick Dubroy and Alessandro Warth. 2017. Incremental Packrat Parsing. In Proceedings of 2017 ACM SIGPLAN International Conference on Software Language Engineering (SLE’17). ACM, New York, NY, USA, 12 pages. https://doi.org/10.1145/3136014.3136022