Julia: 目的別機能
以下、例示に使用するサンプルデータは主に RDatasets の Iris を使用する。
julia> using RDatasets
julia> iris = dataset("datasets", "iris")
150×5 DataFrames.DataFrame
│ Row │ SepalLength │ SepalWidth │ PetalLength │ PetalWidth │ Species │
├─────┼─────────────┼────────────┼─────────────┼────────────┼───────────┤
│ 1 │ 5.1 │ 3.5 │ 1.4 │ 0.2 │ setosa │
│ 2 │ 4.9 │ 3.0 │ 1.4 │ 0.2 │ setosa │
│ 3 │ 4.7 │ 3.2 │ 1.3 │ 0.2 │ setosa │
⋮
│ 150 │ 5.9 │ 3.0 │ 5.1 │ 1.8 │ virginica │
データ変換
DataFrame を 2 次元行列に変換する
CSV ファイルや RDatasets から取得したデータはカラム名と行番号付きの DataFrame 構造を持っている。Iris データセットから 1-2 列を取り出し 2 次元行列に変換するには該当範囲を Matrix() に渡せば良い。
julia> Matrix(iris[:, 1:2])
150×2 Array{Float64,2}:
5.1 3.5
4.9 3.0
4.7 3.2
⋮
5.9 3.0
ただし、CSV から読み込んだデータなどは数値を正しく認識できず Missing 型を含む Union 型になっていることがある。この場合は convert() を使用して Array{Float64,2} に変換する。
julia> using CSV
julia> iris = CSV.read("iris.csv")
# 一部が Missings.Missing と認識されている
julia> Matrix(iris[:, 1:2])
150×2 Array{Union{Float64, Missings.Missing},2}:
5.1 3.5
4.9 3.0
4.7 3.2
⋮
5.9 3.0
# すべての要素を Float64 に変換した 2 次元行列を作成
julia> convert(Array{Float64}, iris[:, 1:2])
150×2 Array{Float64,2}:
5.1 3.5
4.9 3.0
4.7 3.2
⋮
5.9 3.0k-means によるクラスタリング
Iris データセットの Sepal, Petal を 4 次元ベクトル空間上の点として \(k=3\) のクラスタリングを行う。データが DataFrame の場合は 2 次元行列に変換して転置する必要がある。
julia> using Clustering
julia> r = kmeans(Matrix(iris[:, 1:4])', 3; maxiter=200, display=:iter)
julia> assignments(r)
150-element Array{Int64,1}:
1
1
1
...PCA による次元削減
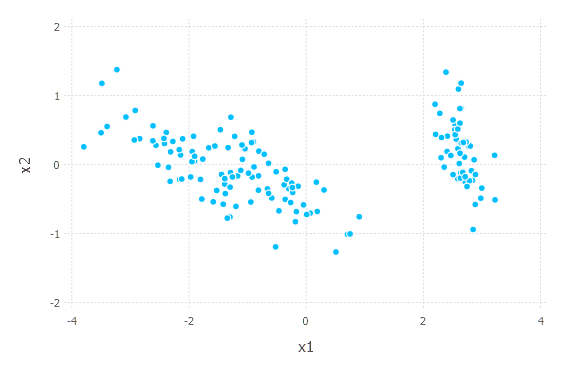
Iris データセットの Sepal, Petal を 4 次元ベクトル空間上の点として PCA を使用いて 2 次元に削減する。
julia> using MultivariateStats
julia> pca = fit(PCA, Matrix(iris[:,1:4])'; maxoutdim=2)
julia> xy = transform(pca, Matrix(iris[:,1:4])')
2×150 Array{Float64,2}:
2.68413 2.71414 2.88899 2.74534 2.72872 … -1.94411 -1.52717 -1.76435 -1.90094 -1.39019
0.319397 -0.177001 -0.144949 -0.318299 0.326755 0.187532 -0.375317 0.0788589 0.116628 -0.282661
julia> p = plot(convert(DataFrame, xy'), x = :x1, y = :x2, Geom.point)
julia> img = PNG("iris_pca.png", 15cm, 10cm)
julia> draw(img, p)
