Rust: nom によるパーサー実装
 概要
概要
nom は Rust で実装された字句解析ライブラリ (Lexer, Lexical Analyzer, Tokenizer) およびパーサコンビネーターです。プログラムのソースコードや DSL (domain specific language) のようなテキストデータの字句解析を実装できるのに加えて、バイナリデータの解析も前提に設計されています (実際、nom の作者は nom を使って GIF 画像ファイルのデコーダーを実装しています)。この記事は nom 5 に基づいてテキストデータを解析するチュートリアルを目的としています。
Table of Contents
過去の nom は Rust のマクロを使用してパーサーコンビネーターを実装する思想でしたが、nom 5 からは関数合成に基づく使い方のみでパーサーを実装できる設計に変更されています。この記事でもマクロを使った実装方法は省略します。対象とする nom バージョンは以下の通り。
nom = "^5.1.0" パーサーフレームワーク
パーサーフレームワーク
字句解析におけるパーサーとは文字列やバイト列のような入力データをトークンに分割する処理を意味します。nom ではパーサー自身が定義するパターンと前方一致する部分とそれ以降の部分に分割し、場合によっては一致した文字列を別の型に変換する関数を指しています。例えば 1 つ以上の連続した数字を抽出し整数として認識するパーサーは、入力 "0123ABC" を次のように分割します。\[ f_{\rm digit}({\tt "0123ABC"}) = (123, {\tt "ABC"}) \] \(123\) は文字列ではなく整数化されていることに注意。また、1 つ以上のアルファベットを認識する別のパーサーを定義します。\[ f_{\rm alpha}({\tt "ABC"}) = ({\tt "ABC"}, {\tt ""}) \] これらを合成したパーサー \(F = f_{\rm digit} \circ f_{\rm alpha}\) は 1 つ以上の数字に続く 1 つ以上のアルファベットを認識するパーサーとなります。\[ F({\tt "0123ABC"}) = f_{\rm alpha}(f_{\rm digit}({\tt "0123ABC"})) = (123, ({\tt "ABC"}, {\tt ""})) \] パーサーコンビネーターとは、このようにして基本的なパーサーを合成して構文定義全体を解析できるパーサーを組み立てるフレームワークです。
もう少し具体的に見てみましょう。nom では引数にデータ列を取り IResult を返す関数をパーサーとして合成することができます。データ列とは一般に文字列やバイト列を指します。
fn my_parser(in:I) -> IResult<I, O, E>ここで、例えば文字列を解析して浮動小数点として返すパーサーを実装するのであれば、型 I は &str;、O は f64 となるでしょう。IResult の実体は Result<(I, O), Err<E>> であるため、関数は Ok((残りのデータ, 結果)) か Err((残りのデータ, ErrorKind)) を返せば良いことになります。
type IResult<I, O, E=(I, ErrorKind)> = Result<(I, O), Err<E>>nom における解析エラーの報告手段は少々貧弱で、位置情報や詳細な情報などの付加的な情報を付けることができません。また ErrorKind は nom で用意しているパーサーに対応したエラーしか準備されていないという難点があります。
 モジュール概要
モジュール概要
関数末尾の 0 と 1 はそれぞれ「0 個以上の繰り返し」「1 個以上の繰り返し」を意味しています。complete と streaming の違いは、complete はメモリ上に存在する (既に読み込まれている) データを解析する用途、streaming はストリームとして読み込みながら解析する用途とされています (ただし構成はあまり変わらない)。
 パターン認識
パターン認識
| Module | Function | 説明と例 |
|---|---|---|
| nom:: character:: complete |
alpha0, alpha1 | アルファベットの連続: [a-zA-Z]*, [a-zA-Z]+ |
| digit0, digit1 | 数字の連続: [0-9]*, [0-9]+ | |
| hex_digit0, hex_digit1 | 16進数字の連続: [0-9a-fA-F]*, [0-9a-fA-F]+ | |
| oct_digit0, oct_digit1 | 8進数字の連続: [0-7]*, [0-7]+ | |
| alphanumeric0, alphanumeric1 | アルファベットと数字の連続: [a-zA-Z0-9]*, [a-zA-Z0-9]+ | |
| space0, space1 | 空白やタブの連続: [ \t]*, [ \t]+ | |
| multispace0, multispace1 | 空白、タブ、復帰改行の連続: [ \t\r\f]*, [ \t\r\f]+ | |
| tab, newline, crlf, line_ending, not_line_ending | 各種制御文字: \t, \n, \r\n, \n|\r\n, [^\r\n] | |
| anychar | 任意の一文字: . | |
| char | 指定した一文字: $1 | |
| one_of | いずれかの一文字: [$1$2$3...] | |
| none_of | いずれにも一致しない一文字: [^$1$2$3...] | |
| nom:: bytes:: complete |
tag, tag_no_case | 指定したバイト列: $1, (?i)$1 |
| is_a | いずれかの文字の連続: [$1]+ | |
| is_not | いずれにも一致しない文字の連続: [^$1]+ | |
| take | 固定長の任意の文字列: .{$1} | |
| take_till, take_till1, | 条件に一致する文字までまたは終端までの連続 | |
| take_until | 指定した文字列または終端までの連続 | |
| take_while, take_while1, take_while_m_n, | 条件に一致する文字の連続 | |
| nom:: number:: complete |
(be | le)_(i | u)(8 | 16 | 24 | 32 | 64 | 128), (be | le)_f(32 | 64) | 固定長バイナリ整数または浮動小数点 (Big Endian, Little Endian) |
| hex_u32 | 1 文字以上の16進数文字: [0-9a-fA-F]{1,8} → u32 | |
| recognize_float, float, double | 浮動小数点表記またはその変換 |
 パーサーの条件分岐や繰り返し
パーサーの条件分岐や繰り返し
| Module | Function | 説明と例 |
|---|---|---|
| nom:: branch |
alt | いずれかのパーサーが成功した結果: $1 | $2 | ... |
| permutation | パーサーの逐次実行: $1$2$3... | |
| nom:: combinator |
not | サブパーサが成功したときに Err を返す |
| opt | サブパーサーが失敗した時に None を返す | |
| cond | 条件が true ならサブパーサーを実行 | |
| all_consuming | サブパーサーがすべてのデータを解析できたら成功 (それ以上データがないことを保証) | |
| iterator | パターンに一致する限り繰り返す列挙子を作成 | |
| map, map_opt, map_res | パターンの一致結果を別の型に変換 | |
| map_parser | パターンの一致結果を別のパーサーに適用する | |
| rest | 残りの部分全てと一致 | |
| rest_len | 残りの部分の文字数 (データは消費しない) | |
| value | サブパーサーが一致したときに固定値を返す (map) | |
| verify | サブパーサーの一致したパターンを検証 (map_res) | |
| nom:: multi |
count | 固定回数のパターンの繰り返し |
| many0, many1, | 任意回数のパターンの繰り返し | |
| many_m_n | 指定回数のパターンの繰り返し | |
| many_till | 終端パターンが検出されるまで任意回数のパターンの繰り返し | |
| many0_count, many1_count, | パターンの繰り返し回数 | |
| fold_many0, fold_many1, | 任意回数のパターンの繰り返しと結果の集約 | |
| fold_many_m_n | 指定回数のパターンの繰り返しと結果の集約 | |
| length_data | サブパーサーが抽出した個数のバイト値を抽出 | |
| length_value | サブパーサーが抽出した個数のバイト値を抽出し第二のサブパーサーを適用 | |
| separated_list, separated_nonempty_list | 区切り文字で区切られたパターンの繰り返し |
 括弧の中の数字を抽出する
括弧の中の数字を抽出する
まず最初に簡単な例として (123) のように括弧に囲まれた数字を取り出す字句解析を実装します。目的は以下のパターンを解析して DIGIT+ に相当する部分を取得することです。

"(" SP* DIGIT+ SP* ")" 手続き型スタイルで解析する
手続き型スタイルで解析する
nom の基本的なデザインでは、パーサーは与えられたデータを前方から解析し、パーサーが解釈可能なトークンと残りの部分を分割して返す処理を実装します。もしパーサーの解釈できないパターンであれば構文エラーを返します。
括弧で囲まれた数字の抽出を手続型のスタイルで記述すると以下のような実装となります。
extern crate nom;
use nom::{Err, IResult};
use nom::character::complete::{char, digit1, multispace0};
use nom::error::ErrorKind;
fn numeric_in_parentheses(s: &str) -> IResult<&str, &str> {
let (s, _) = char('(')(s)?;
let (s, _) = multispace0(s)?;
let (s, num) = digit1(s)?;
let (s, _) = multispace0(s)?;
let (s, _) = char(')')(s)?;
Ok((s, num))
}
fn main() {
assert_eq!(numeric_in_parentheses("(0)"), Ok(("", "0")));
assert_eq!(numeric_in_parentheses("( 123 )"), Ok(("", "123")));
assert_eq!(numeric_in_parentheses("(123)456"), Ok(("456", "123")));
assert_eq!(numeric_in_parentheses("1234"), Err(Err::Error(("1234", ErrorKind::Char))));
assert_eq!(numeric_in_parentheses("()"), Err(Err::Error((")", ErrorKind::Digit))));
}関数 char は単一の文字、ここでは括弧の文字と一致します。また multispace0 は 0 個以上の空白文字 (タブや改行を含む) と一致し、digit1 は 1 個以上の数字と一致します。nom::character::complete にはこのような文字パターン解析のためのシンプルな関数が用意されています。
パーサーコンビネーターは (その名が示すように) サブパーサーを組み合わせて新しいパーサーを定義することが多く、実際その方がコードが簡潔となり記述性も高くなります。しかし関数合成は必須ではなく、デバッグの目的でログを挿入したりステップ実行するためにこのような手続き型スタイルで記述することも可能です。

delimited: 括弧に囲まれた部分を取得する
さて、ここで対象とするパターンの定義を再考すると "(" と ")" で囲まれた中に、さらに SP* で囲まれた DIGIT+ という構造を持っていると考えることができます。

nom には特定のパターンで囲まれた部分を取り出すための便利な関数 delimited が用意されています。ここで delimited を使用してパーサーを合成してみましょう。
fn numeric_in_parentheses(s: &str) -> IResult<&str, &str> {
delimited(
char('('),
delimited(multispace0, digit1, multispace0),
char(')'),
)(s)
}上記は「"(" と ")" に囲まれた、0 個以上の空白に囲まれた数字列」というネストされた意味を持っています。delimited により 3 つのサブパーサーが 1 つのパーサーに合成され、最終的に合成された 1 つの関数のみが呼び出されていることが分分かるでしょうか? nom にはこのようなパーサーを合成するための関数も豊富に含まれています。

alt: 対応する括弧の種類を増やす
ここでパターンを拡張して対応する括弧の種類を増やしてみましょう。ただし開き括弧と閉じ括弧は同じ種類で対応しなければならないものとします。
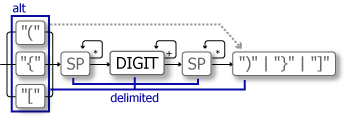
"(" | "{" | "[") SP* DIGIT+ SP* (")" | "}" | "]")以下では関数 alt を使用して対応する開き括弧のいずれか一つに一致するパーサを作成し、開き括弧に対応した閉じ括弧を明示的に選択しています。
extern crate nom;
use nom::{Err, IResult};
use nom::branch::alt;
use nom::character::complete::{char, digit1, multispace0};
use nom::error::ErrorKind;
use nom::sequence::delimited;
fn numeric_in_parentheses(s: &str) -> IResult<&str, &str> {
let (s, open) = alt((
char('('), char('{'), char('['),
))(s)?;
let close = match open {
'(' => ')', '{' => '}', '[' => ']', _ => panic!(),
};
let (s, num) = delimited(multispace0, digit1, multispace0)(s)?;
let (s, _) = char(close)(s)?;
Ok((s, num))
}
fn main() {
assert_eq!(numeric_in_parentheses("( 123 )"), Ok(("", "123")));
assert_eq!(numeric_in_parentheses("{ 456 }"), Ok(("", "456")));
assert_eq!(numeric_in_parentheses("[ 789 ]"), Ok(("", "789")));
assert_eq!(numeric_in_parentheses("<999>"), Err(Err::Error(("<999>", ErrorKind::Char))));
assert_eq!(numeric_in_parentheses("(123}"), Err(Err::Error(("}", ErrorKind::Char))));
}今回のような単一の文字から選ぶのであれば関数 one_of を使用しても良いでしょう。
let (s, open) = nom::character::complete::one_of("({[")(s)?; 数値リテラルを解析する
数値リテラルを解析する
次の例として小数点付きの数値を解析するパーサーを実装してみましょう。ポイントとしては正負の符号は省略可能とし、省略時には + が指定されたものとみなします。

"+" | "-")? DIGIT+ "." DIGIT+
opt: 符号を省略可能にする
opt は省略可能なパターンを定義するときに使用することができます。この関数はサブパーサーが解析に失敗したときに None を返します。以下のコードでは opt を使用して「+ か -、または符号が省略されている」結果を返すパーサを合成し即時実行しています。
extern crate nom;
use nom::{Err, IResult};
use nom::character::complete::{char, digit1, one_of};
use nom::combinator::opt;
use nom::error::ErrorKind;
fn decimal(s: &str) -> IResult<&str, f64> {
let (s, sign) = opt(one_of("+-"))(s)?;
let (s, int) = digit1(s)?;
let (s, _) = char('.')(s)?;
let (s, frac) = digit1(s)?;
let sign: f64 = if sign.unwrap_or('+') == '+' { 1.0 } else { -1.0 };
let integer: f64 = int.parse::<f64>().unwrap();
let fraction: f64 = frac.parse::<f64>().unwrap() / 10f64.powf(frac.len() as f64);
Ok((s, (integer + fraction).copysign(sign)))
}
fn main() {
assert_eq!(decimal("3.14"), Ok(("", 3.14)));
assert_eq!(decimal("+3.14"), Ok(("", 3.14)));
assert_eq!(decimal("-3.14"), Ok(("", -3.14)));
assert_eq!(decimal("+3"), Err(Err::Error(("", ErrorKind::Char))));
assert_eq!(decimal(".14"), Err(Err::Error((".14", ErrorKind::Digit))));
}
permutation: パーサの並びを合成する
上記のように直列に配置することができるパーサは permutation を使ってタプルでまとめて結果を得る関数に合成することができます。delimited の一般形とも言えますが、delimited が囲みパターンを無視して内部だけを抽出するのに対して permutation は配置されたすべてのパターンの一致結果をタプルで返します。
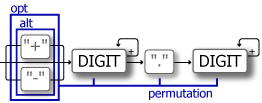
let (s, (sign, int, _, frac)) = nom::branch::permutation((
opt(one_of("+-")), digit1, char('.'), digit1
))(s)?; 
map_res: 結果を変換する
permutation によって解析処理を合成することができましたが、文字列を f64 に変換する部分が残ったままです。パーサーは入力のシーケンスから一致部分を抽出するだけではなく、適切な適切な型への変換も同時に行います。ここで map_res を使用して結果を適切な型に変関する処理も合成することができます。
extern crate nom;
use nom::{Err, IResult};
use nom::branch::permutation;
use nom::character::complete::{char, digit1, one_of};
use nom::combinator::{map_res, opt};
use nom::error::ErrorKind;
use std::num::ParseFloatError;
fn floating_point(s: &str) -> IResult<&str, f64> {
map_res(
permutation((opt(one_of("+-")), digit1, char('.'), digit1)),
|(sign, int, _, frac): (Option<char>, &str, char, &str)| -> Result<f64, ParseFloatError> {
let sign: f64 = if sign.unwrap_or('+') == '+' { 1.0 } else { -1.0 };
let integer: f64 = int.parse::<f64>()?;
let fraction: f64 = frac.parse::<f64>()? / 10f64.powf(frac.len() as f64);
Ok((integer + fraction).copysign(sign))
},
)(s)
}
fn main() {
assert_eq!(floating_point("3.14"), Ok(("", 3.14)));
assert_eq!(floating_point("+3.14"), Ok(("", 3.14)));
assert_eq!(floating_point("-3.14"), Ok(("", -3.14)));
assert_eq!(floating_point("+3"), Err(Err::Error(("", ErrorKind::Permutation))));
assert_eq!(floating_point(".14"), Err(Err::Error(("", ErrorKind::Permutation))));
}変換処理は、直前の解析処理の結果を受け取り Result<T,Err> を返す関数です。もし変換処理に失敗する可能性がないなら map を使用することができます。

recognize_float: 浮動小数点を解析する
浮動小数点表記 0.0e+0 への拡張ははこれまでに挙げたパーサの組み合わせでも可能ですが、nom に用意されている double![]() はまさに浮動小数点のパーサーです。
はまさに浮動小数点のパーサーです。
extern crate nom;
use nom::{Err, IResult};
use nom::error::ErrorKind;
use nom::number::complete::double;
fn floating_point(s: &str) -> IResult<&str, f64> {
double(s)
}
fn main() {
assert_eq!(floating_point("1.234e-8+0.24"), Ok(("+0.24", 1.234e-8)));
assert_eq!(floating_point("1.234"), Ok(("", 1.234)));
assert_eq!(floating_point("1234"), Ok(("", 1234f64)));
assert_eq!(floating_point(".234"), Ok(("", 0.234)));
assert_eq!(floating_point("EFG"), Ok(("FG", 0.0))); // !
assert_eq!(floating_point("ABC"), Err(Err::Error(("ABC", ErrorKind::Float))));
}ただしこの double 関数は単独の "e" に対しても正しい浮動小数点表記と認識して 0.0 を返すことから、recognize_float と parse::<f64>() を組み合わせた方が良いかも知れません。
fn floating_point(s: &str) -> IResult<&str, f64> {
let (s, value) = nom::number::complete::recognize_float(s)?;
Ok((s, value.parse::<f64>().unwrap()))
} 文字列リテラルを解析する
文字列リテラルを解析する
一般的なプログラミング言語における文字列リテラルのエスケープシーケンスや XML の文字参照のように、コンテキストに特殊な文字を埋め込むための書式が存在することがあります。これは人が認識しやすいように構文というより埋め込みの書式として定義されています。

escaped_transform: エスケープ文字を含む文字列を解析する
関数 escaped_transform は特定のパターンに一致する埋め込みのシーケンスを抽出し、エスケープ表記と一致する部分を別の値で置き換えます。
ESCAPED_CHAR := "\" ("\" | '"' | "'" | "r" | "n" | "t" | ("u" HEXDIGIT{4}))UNESCAPED := ^('"' | "\")STRING_LITERAL := '"' (ESCAPED_CHAR | UNESCAPED)* '"'extern crate nom;
use nom::{Err, IResult};
use nom::branch::{alt, permutation};
use nom::bytes::complete::{escaped_transform, take_while_m_n};
use nom::character::complete::{char, none_of};
use nom::combinator::{map, value};
use nom::error::ErrorKind;
use nom::sequence::delimited;
use std::char::{decode_utf16, REPLACEMENT_CHARACTER};
use std::u16;
fn string_literal(s: &str) -> IResult<&str, String> {
delimited(
char('\"'),
escaped_transform(none_of("\"\\"), '\\', alt((
value('\\', char('\\')),
value('\"', char('\"')),
value('\'', char('\'')),
value('\r', char('r')),
value('\n', char('n')),
value('\t', char('t')),
map(
permutation((char('u'), take_while_m_n(4, 4, |c: char| c.is_ascii_hexdigit()))),
|(_, code): (char, &str)| -> char {
decode_utf16(vec![u16::from_str_radix(code, 16).unwrap()])
.nth(0).unwrap().unwrap_or(REPLACEMENT_CHARACTER)
},
)
))),
char('\"'),
)(s)
}
fn main() {
assert_eq!(string_literal("\"a\\\"b\\\'c\""), Ok(("", String::from("a\"b\'c"))));
assert_eq!(string_literal("\" \\r\\n\\t \\u2615 \\uDD1E\""), Ok(("", String::from(" \r\n\t ☕ �"))));
assert_eq!(string_literal("\"abc"), Err(Err::Error(("", ErrorKind::Char))));
assert_eq!(string_literal("\"ab\\zc\""), Err(Err::Error(("zc\"", ErrorKind::Permutation))));
}この例では C/C++/Java のように \ に続く文字によって所定の文字に置き換えています。最後の分岐は少し複雑ですが \uXXXX 形式の 16 進数 4 文字を UTF-16 の文字コードと認識して Unicode 文字を作成しています。
escaped_transform の第三引数はトレイト ExtendInto を実装している型、つまり [u8], &[u8], str, &str, char のいずれかを成功結果型とする関数を指定することができます。
 繰り返し構造を解析する
繰り返し構造を解析する

count: RGB 表記を解析する
固定個数の繰り返しパターンを解析する例として CSS で使用されている RGB 表記を u32 に変換するパーサーを考えてみます。全体のパターンは以下のように # に続く 16 進数 2 文字 × 3 個で構成されているものとします。

"#" HEX{2} HEX{2} HEX{2}extern crate nom;
use nom::bytes::complete::take_while_m_n;
use nom::character::complete::char;
use nom::character::is_hex_digit;
use nom::combinator::{map, map_res};
use nom::{IResult,Err};
use nom::multi::count;
use nom::sequence::preceded;
use nom::error::ErrorKind;
fn hex_to_u8(s: &str) -> IResult<&str, u8> {
map_res(
take_while_m_n(2, 2, |ch| is_hex_digit(ch as u8)),
|x| u8::from_str_radix(x, 16),
)(s)
}
fn rbg(s: &str) -> IResult<&str, u32> {
preceded(
char('#'),
map(
count(hex_to_u8, 3),
|hex| (hex[0] as u32) << 16 | (hex[1] as u32) << 8 | hex[2] as u32,
),
)(s)
}
fn main() {
assert_eq!(rbg("#000000"), Ok(("", 0)));
assert_eq!(rbg("#FFFFFF"), Ok(("", 0xFFFFFF)));
assert_eq!(rbg("#7F0000"), Ok(("", 0x7F0000)));
assert_eq!(rbg("#007F00"), Ok(("", 0x007F00)));
assert_eq!(rbg("#00007F"), Ok(("", 0x00007F)));
assert_eq!(rbg("$FFFFFF"), Err(Err::Error(("$FFFFFF", ErrorKind::Char))));
assert_eq!(rbg("#FFFGHI"), Err(Err::Error(("FGHI", ErrorKind::TakeWhileMN))));
assert_eq!(rbg("#FF"), Err(Err::Error(("", ErrorKind::TakeWhileMN))));
}この例では固定個数の繰り返しパターンに 2 つの方法を使っています。最初の take_while_m_n は条件に一致する長さ \(n \le \ell \le m\) のバイト値を取得するためのパーサーです。条件関数は u8 を取るため char へキャストしています。もう一つの count は 3 つの u8 値を読み込んで u32 に変換しています。
map_res と map はそれぞれサブパーサーの解析結果を別の値にマップしています。上記では &str → u8 と Vec<u8>[3] → u32 の変換を行っています。この 2 つのマップ関数の違いは変換関数が Err となる可能性があるかです。
preceded![]() はこの例のように識別子から始まる構造に適した機能といえます。最初のパーサに一致した値を破棄し、二番目のパーサに一致した値を返します。
はこの例のように識別子から始まる構造に適した機能といえます。最初のパーサに一致した値を破棄し、二番目のパーサに一致した値を返します。

many0: 数値の並びを解析する
count![]() が固定数の繰り返しだったのに対して
が固定数の繰り返しだったのに対して many0![]() はパターンに一致する任意数の並びを解析することができます。これを使って空白で区切られた数値の並びを解析してみましょう。
はパターンに一致する任意数の並びを解析することができます。これを使って空白で区切られた数値の並びを解析してみましょう。
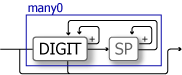
NUM := DIGIT+NUMS := (NUMS SP+ NUM) | NUMnom に用意されている関数 many0 は特定のパターンの繰り返しが出現する限り解析を続けます。
extern crate nom;
use nom::IResult;
use nom::character::complete::{digit1, multispace0};
use nom::combinator::map_res;
use nom::multi::many0;
use nom::sequence::delimited;
fn number_list(s: &str) -> IResult<&str, Vec<u32>> {
many0(
map_res(
delimited(multispace0, digit1, multispace0),
|x: &str| x.parse::<u32>(),
)
)(s)
}
fn main() {
assert_eq!(number_list("1 2 3 4"), Ok(("", vec![1, 2, 3, 4])));
}many0 は 0 個を許容しますが many1 は少なくとも 1 つの要素が必要であることを意味しています。many0_count は要素ではなく出現数のみを返します。many_m_n は出現数の上限と下限を指定できます。many_till は終了パターンが出現するまで特定のパターンの繰り返しを抽出します。

separated_list: リスト表記を解析する
JavaScript やいくつかのプログラミング言語でリストとして解釈されるような [AB, C, DEF] の表記のリストを解析します。リストの要素は 0 個以上の任意個数とします。
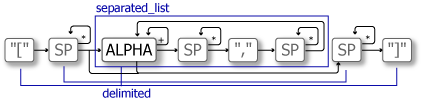
ELEM := ALPHA+ELEMS := ELEM | (ELEMS SP* "," SP* ELEM)LIST := "[" SP* (ELEMS | \(\emptyset\)) SP* "]"separated_list はコンマ区切りのようなセパレータによって分けられた書式を解析します。今回の例では SP* "," SP* のシーケンスをセパレータと見なすことができるため以下のように記述できます。
extern crate nom;
use nom::{Err, IResult};
use nom::branch::permutation;
use nom::character::complete::{alpha1, char, multispace0};
use nom::error::ErrorKind;
use nom::multi::separated_list;
use nom::sequence::delimited;
fn list(s: &str) -> IResult<&str, Vec<&str>> {
delimited(
char('['),
delimited(
multispace0,
separated_list(permutation((multispace0, char(','), multispace0)), alpha1),
multispace0,
),
char(']'),
)(s)
}
fn main() {
assert_eq!(list("[]"), Ok(("", vec!())));
assert_eq!(list("[AB, C, DEF]"), Ok(("", vec!("AB", "C", "DEF"))));
assert_eq!(list("AB,C,DEF"), Err(Err::Error(("AB,C,DEF", ErrorKind::Char))));
assert_eq!(list("[A,]"), Err(Err::Error((",]", ErrorKind::Char))));
assert_eq!(list("[A,,BC]"), Err(Err::Error((",,BC]", ErrorKind::Char))));
assert_eq!(list("[AB, 2, DEF]"), Err(Err::Error((", 2, DEF]", ErrorKind::Char))));
assert_eq!(list("[AB, C; DEF]"), Err(Err::Error(("; DEF]", ErrorKind::Char))));
assert_eq!(list("[AB, C, DEF)"), Err(Err::Error((")", ErrorKind::Char))));
}リストが 1 個以上の要素となる場合 (つまり空集合とならない場合) は separated_nonempty_list を使用することができます。

