\( \def\ldef{≜} \) \( \def\globally{□} \) \( \def\eventually{◇} \) \( \def\openleftarrowplus{\overset{+}{⇾}} \) \( \def\equalv{⫤} \)
翻訳: Summary of TLA+
Table of Contents
- モジュールレベルの構成
- ┌──── MODULE \(M\) ────┐
- EXTENDS \(M_1, \ldots, M_n\)
- CONSTANTS \(C_1,\ldots,C_n\)(1)
- VARIABLES \(\ x_1,\ldots,x_n\)(1)
- ASSUME \(P\)
- \(F(x_1,\ldots,x_n) \ldef {\it exp}\)
- \(f[x \in S] \ldef {\it exp}\)(2)
- INSTANCE \(M\) WITH \(p_1 \leftarrow e_1,\ldots,p_m \leftarrow e_m\)
- \(N(x_1,\ldots,x_n) \ldef\) INSTANCE \(M\) WITH \(p_1 \leftarrow e_1,\ldots,p_m \leftarrow e_m\)
- THEOREM \(\ P\)
- LOCAL \({\it def}\)
- └───────────────┘
- 定数演算子
- 論理
- 集合
- 関数
- レコード
- タプル
- その他の構成
- アクション演算子
- 時相演算子
- ユーザ定義可能な演算子記号
- 中置演算子
- 接尾辞演算子(12)
- 演算子の優先順位範囲
- 接頭演算子
- 中置演算子
- 接尾演算子
- 標準モジュールで定義されている演算子
- Naturals, Integers, Reals モジュール
- Sequences モジュール
- FiniteSets モジュール
- Bags モジュール
- RealTime モジュール
- TLC モジュール
- タイプセット記号の ASCII 表現
- 参照
 モジュールレベルの構成
モジュールレベルの構成
 ┌──── MODULE \(M\) ────┐
┌──── MODULE \(M\) ────┐
\(M\) という名前のモジュールまたはサブモジュールを開始する。
 EXTENDS \(M_1, \ldots, M_n\)
EXTENDS \(M_1, \ldots, M_n\)
\(M_1,\ldots,M_n\) という名前のモジュールから宣言、定義、仮定、および定理を現在のモジュールに組み込む。
 CONSTANTS \(C_1,\ldots,C_n\)(1)
CONSTANTS \(C_1,\ldots,C_n\)(1)
\(C_j\) を定数パラメータ (リジッド変数; rigid variable) として宣言する。各 \(C_j\) は識別子か、\(C(\_,\ldots,\_)\) 形式をとる。後者の形式は \(C\) が指定された数の引数を持つ演算子であることを示す。
 VARIABLES \(\ x_1,\ldots,x_n\)(1)
VARIABLES \(\ x_1,\ldots,x_n\)(1)
\(x_j\) を変数 (フレキシブル変数であるパラメータ) として宣言する。
 ASSUME \(P\)
ASSUME \(P\)
\(P\) を仮定としてアサートする。
 \(F(x_1,\ldots,x_n) \ldef {\it exp}\)
\(F(x_1,\ldots,x_n) \ldef {\it exp}\)
各識別子 \(x_k\) を \(e_k\) に置き換えた \(F(e_1,\ldots,e_n)\) が \({\it exp}\) に等しいような演算子として \(F\) を定義する (\(n=0\) の場合、\(F \ldef {\it exp}\) と記述する)。
\(f[x \in S] \ldef {\it exp}\)(2)
\(S\) 内の全ての \(x\) に対して \(f[x] = {\it exp}\) であるような定義域 \(S\) の関数として \(f\) を定義する (記号 \(f\) は \({\it exp}\) で出現でき再帰的定義が許可)。
INSTANCE \(M\) WITH \(p_1 \leftarrow e_1,\ldots,p_m \leftarrow e_m\)
モジュール \(M\) の定義済み演算子 \(F\) それぞれに対して、演算子として \(F\) を定義する。この定義は \(M\) の各宣言済み定数または変数 \(p_j\) を \(e_j\) に置き換えることによって、\(M\) の \(F\) の定義から得られる (\(m=0\) であれば WITH は省略される)。
\(N(x_1,\ldots,x_n) \ldef\) INSTANCE \(M\) WITH \(p_1 \leftarrow e_1,\ldots,p_m \leftarrow e_m\)
モジュール \(M\) の定義済み演算子 \(F\) それぞれに対して、演算子として \(N(d_1,\ldots,d_n) ! F\) を定義する。この定義は \(M\) の各宣言済み定数または変数 \(p_j\) を \(e_j\) に置き換え、各識別子 \(x_k\) を \(d_k\) に置き換えることによって、\(M\) の \(F\) の定義から得られる (\(m=0\) であれば WITH は省略される)。
THEOREM \(\ P\)
\(P\) が現在のモジュールの定義や仮定から証明できることをアサートする。
LOCAL \({\it def}\)
(定義またはインスタンス宣言かもしれない) \({\it def}\) の定義を現在のモジュールに対してローカルにする。これにより、モジュールを拡張したりインスタンス化する時に取得されない。
└───────────────┘
現在のモジュールまたはサブモジュールを終了する。
 定数演算子
定数演算子
 論理
論理
| \(\land\) \(\lor\) \(\lnot\) \(\Rightarrow\) \(\equiv\) |
| TRUE FALSE BOOLEAN [TRUE とFALSE の集合] |
| \(\forall x \in S: p\)(3) |
|
| \(\exists x \in S: p\)(3) |
|
| CHOOSE \(x \in S: p\) |
[\(S\) に属する\(x\) は \(p\) を満たす] |
 集合
集合
| \(=\) \(\neq\) \(\in\) \(\not\in\) \(\cup\) \(\cap\) \(\subseteq\) \(\backslash\) [差集合] |
| \(\{e_1,\ldots,e_n\}\) |
[要素 \(e_i\) で構成される集合] |
| \(\{x \in S: p\}\)(4) |
[\(S\) に属し \(p\) を満たす要素 \(x\) の集合] |
| \(\{e: x \in S\}\)(3) |
[\(S\) に属する \(x\) のような要素 \(e\) の集合] |
| SUBSET \(S\) |
[\(S\) の部分集合の集合] |
| UNION \(S\) |
[\(S\) のすべての要素の和集合] |
 関数
関数
| \(f[e]\) |
[関数適用] |
| DOMAIN \(f\) |
[関数 \(f\) の定義域] |
| \([x \in S \mapsto e]\)(3) |
[\(x \in S\) に対して \(f[x]=e\) となるような関数 \(f\)] |
| \([S \to T]\) |
[\(x \in S\) に対して \(f[x] \in T\) となる関数 \(f\) の集合] |
| \([f\) EXPECT \(![e_1] = e_2]\)(5) |
[\(\hat{f}[e_1]=e_2\) を除く \(f\) と等しい関数 \(\hat{f}\)] |
 レコード
レコード
| \(e.h\) |
[レコード \(e\) の \(h\)-フィールド] |
| \([h_1 \mapsto e_1,\ldots,h_n \mapsto e_n]\) |
[\(h_i\) フィールドが \(e_i\) であるようなレコード] |
| \([h_1: S_1,\ldots,h_n:S_n]\) |
[\(S_i\) であるような \(h_i\) フィールドを持つすべてのレコードの集合] |
| \([r\) EXPECT \(!.h = e]\)(5) |
[\(\hat{r}.h=e\) を除く、\(r\) と等しいレコード \(\hat{r}\)] |
 タプル
タプル
| \(e[i]\) |
[タプル \(e\) の \(i\) 番目の要素] |
| \(\langle e_1,\ldots,e_n\rangle\) |
[\(i\) 番目の要素が \(e_i\) であるような \(n\)-タプル] |
| \(S_1\times\ldots\times S_n\) |
[\(S\) の \(i\) 番目の要素を持つ全ての \(n\)-タプルの集合] |
 その他の構成
その他の構成
| IF \(p\) THEN \(e_1\) ELSE \(e_2\) |
[\(p\) が true であれば \(e_1\)、そうでなければ \(e_2\)] |
| CASE \(p_1 \to e_1 □ \ldots □ p_n \to e_n\) |
[\(p_i\) が true となるある \(e_i\)] |
| CASE \(p_1 \to e_1 □ \ldots □ p_n \to e_n □\) OTHER \(\to e\) |
[\(p_i\) が true となるある \(e_i\), または全ての \(p_i\) が false なら \(e\)] |
| LET \(d_1 \ldef e_1 \ \ldots \ d_n \ldef e_n\) IN \(e\) |
[定義の文脈での \(e\)] |
\(\land p_1\)
\(\vdots\)
\(\land p_n\) |
[論理積 \(p_1 \land \ldots \land p_n\)] |
\(\lor p_1\)
\(\vdots\)
\(\lor p_n\) |
[論理和 \(p_1 \lor \ldots \lor p_n\)] |
 アクション演算子
アクション演算子
| \(e'\) |
[あるステップの最終状態における \(e\) の値] |
| \([A]_e\) |
[\(A \lor (e' = e)\)] |
| \(\langle A \rangle_e\) |
[\(A \land (e' \neq e)\)] |
| ENABLED \(A\) |
[ある \(A\) ステップが可能] |
| UNCHANGED \(e\) |
[e' = e] |
| \(A \cdot B\) |
[アクションの結合] |
 時相演算子
時相演算子
| \(\globally F\) |
[\(F\) は常に true] |
| \(\eventually F\) |
[\(F\) は結果的に true] |
| \(WF_e(A)\) |
[アクション \(A\) に対する弱い公平性] |
| \(SF_e(A)\) |
[アクション \(A\) に対する強い公平性] |
| \(F \rightsquigarrow G\) |
[\(F\) は \(G\) を導く] |
 ユーザ定義可能な演算子記号
ユーザ定義可能な演算子記号
 中置演算子
中置演算子
| \(+\)(6) |
\(-\)(6) |
\(*\)(6) |
\(/\)(7) |
\(\circ\)(8) |
\(++\) |
| \(\div\)(6) |
\(\%\)(6) |
\(\hat{}\)(6)(9) |
\(..\) |
\(\ldots\) |
\(--\) |
| \(\oplus\)(10) |
\(\ominus\)(10) |
\(\otimes\) |
\(\oslash\) |
\(\odot\) |
\(**\) |
| \(\lt\)(6) |
\(\gt\)(6) |
\(\le\)(6) |
\(\ge\)(6) |
\(⊓\) |
\(//\) |
| \(\prec\) |
\(\succ\) |
\(\preceq\) |
\(\succeq\) |
\(⊔\) |
\(\hat{}\hat{}\) |
| \(\ll\) |
\(\gg\) |
\(\lt:\) |
\(:\gt\)(11) |
\(\&\) |
\(\&\&\) |
| \(\sqsubset\) |
\(\sqsupset\) |
\(\sqsubseteq\)(10) |
\(\sqsupseteq\) |
\(|\) |
\(\%\%\) |
| \(\subset\) |
\(\supset\) |
\(\subseteq\) |
\(\supseteq\) |
\(\star\) |
\(@@\)(11) |
| \(\vdash\) |
\(\dashv\) |
\(\models\) |
\(\equalv\) |
\(\bullet\) |
\(\#\#\) |
| \(\sim\) |
\(\simeq\) |
\(\approx\) |
\(\cong\) |
\(\$\) |
\(\$\$\) |
| \(\bigcirc\) |
\(::=\) |
\(\asymp\) |
\(\doteq\) |
\(??\) |
\(!!\) |
| \(\propto\) |
\(\wr\) |
\(\asymp\) |
\(⊎\) |
|
|
| \(\hat{}+\) |
\(\hat{}*\) |
\(\hat{}\#\) |
 演算子の優先順位範囲
演算子の優先順位範囲
2 つの演算子の範囲が重複する場合、それらの相対的な優先順位は指定しない。左結合演算子は (a) で示している。
 接頭演算子
接頭演算子
| \(\lnot\) |
4-4 |
\(\globally\) |
4-15 |
UNION |
8-8 |
| ENABLED |
4-15 |
\(\eventually\) |
4-15 |
DOMAIN |
9-9 |
| UNCHANGED |
4-15 |
SUBSET |
8-8 |
\(-\) |
12-12 |
 中置演算子
中置演算子
| \(\Rightarrow\) |
1-1 |
\(\le\) |
5-5 |
\(\lt:\) |
7-7 |
\(\ominus\) |
11-11(a) |
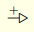 |
2-2 |
\(\ll\) |
5-5 |
\(\backslash\) |
8-8 |
\(-\) |
11-11(a) |
| \(\equiv\) |
2-2 |
\(\prec\) |
5-5 |
\(\cap\) |
8-8(a) |
\(--\) |
11-11(a) |
| \(\rightsquigarrow\) |
2-2 |
\(\preceq\) |
5-5 |
\(\cup\) |
8-8(a) |
\(\&\) |
13-13(a) |
| \(\land\) |
3-3(a) |
\(\propto\) |
5-5 |
\(..\) |
9-9 |
\(\&\&\) |
13-13(a) |
| \(\lor\) |
3-3(a) |
\(\sim\) |
5-5 |
\(\ldots\) |
9-9 |
\(\odot\) |
13-13(a) |
| \(\neq\) |
5-5 |
\(\simeq\) |
5-5 |
\(!!\) |
9-13 |
\(\oslash\) |
13-13 |
| \(\dashv\) |
5-5 |
\(\sqsubset\) |
5-5 |
\(\#\#\) |
9-13(a) |
\(\otimes\) |
13-13(a) |
| \(::=\) |
5-5 |
\(\sqsubseteq\) |
5-5 |
\($\) |
9-13(a) |
\(*\) |
13-13(a) |
| \(:=\) |
5-5 |
\(\sqsupset\) |
5-5 |
\(\$\$\) |
9-13(a) |
\(**\) |
13-13(a) |
| \(\lt\) |
5-5 |
\(\sqsupseteq\) |
5-5 |
\(??\) |
9-13(a) |
\(/\) |
13-13 |
| \(=\) |
5-5 |
\(\subset\) |
5-5 |
\(\sqcap\) |
9-13(a) |
\(//\) |
13-13 |
| \(\equalv\) |
5-5 |
\(\subseteq\) |
5-5 |
\(\sqcup\) |
9-13(a) |
\(\bigcirc\) |
13-13(a) |
| \(\gt\) |
5-5 |
\(\succ\) |
5-5 |
\(\uplus\) |
9-13(a) |
\(\bullet\) |
13-13(a) |
| \(\approx\) |
5-5 |
\(\succeq\) |
5-5 |
\(\wr\) |
9-14 |
\(\div\) |
13-13 |
| \(\asymp\) |
5-5 |
\(\supset\) |
5-5 |
\(\oplus\) |
10-10(a) |
\(\circ\) |
13-13(a) |
| \(\cong\) |
5-5 |
\(\supseteq\) |
5-5 |
\(+\) |
10-10(a) |
\(\star\) |
13-13(a) |
| \(\doteq\) |
5-5 |
\(\vdash\) |
5-5 |
\(++\) |
10-10(a) |
\(\hat{}\) |
14-14(a) |
| \(\ge\) |
5-5 |
\(\models\) |
5-5 |
\(\%\) |
10-11(a) |
\(\hat{}\hat{}\) |
14-14 |
| \(\gg\) |
5-5 |
\(\cdot\)(13) |
5-14(a) |
\(\%\%\) |
10-11(a) |
\(.\)(14) |
17-17(a) |
| \(\in\) |
5-5 |
\(@@\) |
6-6(a) |
\(|\) |
10-11(a) |
|
|
| \(\not\in\) |
5-5 |
\(:\gt\) |
7-7 |
\(||\) |
10-11(a) |
|
|
 接尾演算子
接尾演算子
| ^+ |
15-15 |
^* |
15-15 |
^# |
15-15 |
' |
15-15 |
 標準モジュールで定義されている演算子
標準モジュールで定義されている演算子
 Naturals, Integers, Reals モジュール
Naturals, Integers, Reals モジュール
| \(+\) |
\(-\)(15) |
\(*\) |
\(/\)(16) |
\(\hat{}\)(17) |
\(..\) |
Nat |
Real(16) |
| \(\div\) |
\(\%\) |
\(\le\) |
\(\ge\) |
\(\lt\) |
\(\gt\) |
Int(18) |
Infinity(16) |
 Sequences モジュール
Sequences モジュール
| \(\circ\) |
Head |
SelectSeq |
SubSeq |
| Append |
Len |
Seq |
Tail |
 FiniteSets モジュール
FiniteSets モジュール
 Bags モジュール
Bags モジュール
| \(\oplus\) |
BagIn |
CopiesIn |
SubBag |
| \(\ominus\) |
BagOfAll |
EmptyBag |
|
| \(\sqsubseteq\) |
BagToSet |
IsABag |
|
| BagCardinality |
BagUnion |
SetToBag |
|
RealTime モジュール
| RTBound |
RTnow |
now (変数として宣言) |
 TLC モジュール
TLC モジュール
| \(:\lt\) |
\(@@\) |
Print |
Assert |
JavaTime |
Permutations |
| SortSeq |
|
|
|
|
|
 タイプセット記号の ASCII 表現
タイプセット記号の ASCII 表現
| \(\land\) |
/\ または \land |
\(\lor\) |
\/ または \lor |
\(\Rightarrow\) |
=> |
| \(\lnot\) |
~ または \lnot または \neg |
\(\equiv\) |
<=> または \equiv |
\(\ldef\) |
== |
| \(\in\) |
/in |
\(\not\in\) |
\notin |
\(\neq\) |
# または /= |
| \(\langle\) |
<< |
\(\rangle\) |
>> |
\(\globally\) |
[] |
| \(\lt\) |
< |
\(\gt\) |
> |
\(\eventually\) |
<> |
| \(\le\) |
\leq または =< または <= |
\(\ge\) |
\geq または >= |
\(\rightsquigarrow\) |
~> |
| \(\ll\) |
\ll |
\(\gg\) |
\gg |
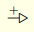 |
-+-> |
| \(\prec\) |
\prec |
\(\succ\) |
\succ |
\(\mapsto\) |
|-> |
| \(\preceq\) |
\preceq |
\(\succeq\) |
\succeq |
\(\div\) |
\div |
| \(\subseteq\) |
\subseteq |
\(\supseteq\) |
\supseteq |
\(\cdot\) |
\cdot |
| \(\subset\) |
\subset |
\(\supset\) |
\supset |
\(\circ\) |
\o または \circ |
| \(\sqsubset\) |
\sqsubset |
\(\sqsupset\) |
\sqsupset |
\(\bullet\) |
\bullet |
| \(\sqsubseteq\) |
\sqsubseteq |
\(\sqsupseteq\) |
\sqsupseteq |
\(\star\) |
\star |
| \(\vdash\) |
|- |
\(\dashv\) |
-| |
\(\bigcirc\) |
\bigcirc |
| \(\models\) |
|= |
\(\equalv\) |
=| |
\(\sim\) |
\sim |
| \(\to\) |
-> |
\(\rightarrow\) |
<- |
\(\simeq\) |
\simeq |
| \(\cap\) |
\cap または intersect |
\(\cup\) |
\cup または union |
\(\asymp\) |
\asymp |
| \(\sqcap\) |
\sqcap |
\(\sqcup\) |
\sqcup |
\(\approx\) |
\approx |
| \(\oplus\) |
(+) または \oplus |
\(\uplus\) |
\uplus |
\(\cong\) |
\cong |
| \(\ominus\) |
(-) または \ominus |
\(\times\) |
\X または \times |
\(\doteq\) |
\doteq |
| \(\odot\) |
(.) または \odot |
\(\wr\) |
\wr |
\(x^y\) |
x^y(20) |
| \(\otimes\) |
(\X) または \otimes |
\(\propto\) |
\propto |
\(x^+\) |
x^+(20) |
| \(\oslash\) |
(/) または \oslash |
“\(s\)” |
"s"(19) |
\(x^*\) |
x^*(20) |
| \(\exists\) |
\E |
\(\forall\) |
\A |
\(x^\#\) |
x^#(20) |
| \({\bf \exists}\) |
\EE |
\({\bf \forall}\) |
\AA |
\('\) |
' |
| \(]_v\) |
]_v |
\(\rangle_v\) |
>>_v |
|
|
| \({\rm WF}_v\) |
WF_v |
\({\rm SF}_v\) |
SF_v |
|
|
| ┌─── |
------(21) |
───┐ |
------(21) |
|
|
| ├───┤ |
------(21) |
└───┘ |
======(21) |
|
|
 参照
参照
- Leslie Lamport (2020), Summary of TLA+.
 モジュールレベルの構成
モジュールレベルの構成 CONSTANTS \(C_1,\ldots,C_n\)(1)
CONSTANTS \(C_1,\ldots,C_n\)(1) VARIABLES \(\ x_1,\ldots,x_n\)(1)
VARIABLES \(\ x_1,\ldots,x_n\)(1) \(F(x_1,\ldots,x_n) \ldef {\it exp}\)
\(F(x_1,\ldots,x_n) \ldef {\it exp}\) 定数演算子
定数演算子 論理
論理 集合
集合 関数
関数 レコード
レコード その他の構成
その他の構成 アクション演算子
アクション演算子 時相演算子
時相演算子 ユーザ定義可能な演算子記号
ユーザ定義可能な演算子記号 中置演算子
中置演算子 接尾辞演算子(12)
接尾辞演算子(12) 演算子の優先順位範囲
演算子の優先順位範囲 接頭演算子
接頭演算子 中置演算子
中置演算子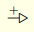
 接尾演算子
接尾演算子 標準モジュールで定義されている演算子
標準モジュールで定義されている演算子 Naturals, Integers, Reals モジュール
Naturals, Integers, Reals モジュール Bags モジュール
Bags モジュール タイプセット記号の ASCII 表現
タイプセット記号の ASCII 表現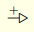
 参照
参照